将军饮马问题

将军饮马问题的11个模型及例题将军饮马问题是一个经典的逻辑问题，涉及到将军如何用有限数量的马和酒到达目的地。

本文将介绍将军饮马问题的11个模型及相应的例题。

1. 直线模型将军与目的地之间没有障碍物，可以直线前进。

此时，将军只需将马拉到目的地即可。

例题1：将军与目的地之间距离为10公里，马的速度为每小时5公里，将军能否在2小时内到达目的地？2. 单个障碍物模型在将军与目的地之间存在一个障碍物，将军可以绕过该障碍物。

例题2：将军与目的地之间距离为15公里，马的速度为每小时4公里，障碍物位于距离将军起点5公里处，将军能否在3小时内到达目的地？3. 多个障碍物模型在将军与目的地之间存在多个障碍物，将军需要逐一绕过这些障碍物。

例题3：将军与目的地之间距离为20公里，马的速度为每小时6公里，障碍物位于距离将军起点分别为5公里、10公里和15公里的位置，将军能否在4小时内到达目的地？4. 跳跃模型将军可以让马跳过障碍物，从而直接到达目的地。

例题4：将军与目的地之间距离为12公里，马的速度为每小时8公里，将军在距离起点6公里处设置一个障碍物，将军能否在2小时内到达目的地？5. 限时模型将军需要在规定的时间内到达目的地。

例题5：将军与目的地之间距离为30公里，马的速度为每小时10公里，将军需要在3小时内到达目的地，是否可能？6. 守备模型目标地点有守备军，将军需要巧妙规避守备军。

例题6：将军与目的地之间距离为25公里，马的速度为每小时7公里，目的地有一支守备军位于距离目标地点10公里处，将军能否在4小时内到达目的地？7. 短平快模型将军不借助马匹，直接徒步走到目的地。

例题7：将军与目的地之间距离为8公里，将军的步行速度为每小时2公里，将军能否在4小时内到达目的地？8. 时间窗模型将军只能在规定时间范围内到达目的地。

例题8：将军与目的地之间距离为18公里，马的速度为每小时6公里，将军需要在3小时到4小时之间到达目的地，是否可能？9. 兵变模型将军需要利用敌军马匹达到目的地。

“将军饮马”常见模型及18道典型习题何为将军饮马？2000多年以前。

古希腊的亚历山大城里住着一位睿智的数学家海伦。

一天，城里来了一位将军，听闻海伦盛名，特来向他请教一个问题。

将军说，每天早上，他都骑着马儿从营帐出发，到河边让马儿饮水，然后，再去河岸同一侧的一块草地上带着马儿去吃草，问题时，在河岸的哪个具体位置喝水，行程最短？海伦略做沉思，给出了将军最佳方案。

此之谓“将军饮马”。

最佳方案为何？且阅下文：一、将军饮马常见的5种模型：1、一动两定（和最小）：如图，点A是将军和马居住的营帐，点B是一块指定的草地，一条小河L潺潺流过，P是将军带着马儿喝水的地方，P点在何处时，将军和马儿走过的路PA+PB的值最小？解析：做A点关于L的对称点A’，连接A’B，与L的交点即为P点。

为什么这时PA+PB最小？假设L上有一点M（与P点不重合）。

∵A点与A’关于L对称∴AP=A’P；AM=A’M；∴AP + BP =A’P +BP =A’B而AM + BM = A’M +MB在△A’MB中，两边之和大于第三边∴A’B < A’M +MB；而M为L上任一点（与P点不重合）。

∴动点P在A’B与L交点处时AP+BP最小。

2、一定两动：如图，点A是将军和马居住的营帐，小河L1依然像上题中一样潺潺流过，P是将军带着马儿喝水的地方，不同的是，这次吃草的地方不在是一个指定的点，而是L2所代表的一片草地，Q则是将军骑马吃草的地方，水足草饱以后，将军和马儿会再回到营帐。

那么，P点、Q点在何处时，将军走过的路AP+PQ+QA的值最小？解析：做A点关于L1的对称点A’；做A点关于L2的对称点A‘’；连接A’A‘’，与L1和L2的交点即为P、Q。

为什么此时，AP+PQ+AQ的和最小？假设L1上有点M（不与P重合）、L2上有点N（不与Q重合）。

∵A点与A’关于L1对称；A点与A‘’关于L2对称。

∴AP=A’P；AQ=A”Q；AM=A’M；AN=A”N；∴AP+PQ+AQ = A’P+PQ+A”Q =A’A”；AM+MN+AN = A’M+MN+A”N在四边形A’MNA”中：A’M+MN+A”N >A’A”∴P、Q位于A’A”与L1和L2的交点处时，AP+PQ+AQ的和最小。

将军饮马问题例题
例题：一个将军饮马，有三个酒坛，其中一个酒坛里装着毒酒，另外两个酒坛里装着普通的酒。

这三个酒坛外观相同，将军无法通过外观来判断哪个酒坛是有毒的。

在喝下一杯毒酒后，将军将会立即死亡。

现在将军有一匹马，这匹马可以闻出毒酒，如果马喝下一杯毒酒，它将会在30分钟后死亡。

将军只有30
分钟的时间来确定哪个酒坛里装着毒酒，并且不允许酒坛之间进行任何类型的测量。

解法：将军可以按照以下步骤确定毒酒所在的酒坛：
1. 为了节省时间，将将军的马分成三组，每组10匹马。

标记
这三组马为A、B、C。

2. 让A组的马尝试第一个酒坛，让B组尝试第二个酒坛，C
组尝试第三个酒坛。

3. 让所有的马者都喝下一杯酒。

4. 等待15分钟。

5. 如果A组的马中有马死亡，那么第一个酒坛是有毒的；如
果B组的马中有马死亡，那么第二个酒坛是有毒的；如果C
组的马中有马死亡，那么第三个酒坛是有毒的。

6. 如果在15分钟内没有任何马死亡，那么第一个酒坛是安全的，因此第二个酒坛是有毒的；如果A和B组的马都没有死
亡，那么第三个酒坛是有毒的。

这样，将军可以在30分钟内确定哪个酒坛里装着毒酒。

将军饮马问题起源:古希腊亚里山大里亚城有一位久负盛名的学者，名叫海伦。

有一天，有位将军不远千里专程前来向海伦求教一个百思不得其解的问题：将军从A地出发到河边饮马，然后再到B地军营视察，显然有许多走法。

问走什么样的路线最短呢？精通数理的海伦稍加思索，便作了完善的回答。

这个问题后来被人们称作“将军饮马”问题。

让我们来看看数学家是怎样解决的。

海伦发现这是一个求折线和最短的数学问题。

根据公理1连接两点的所有线中，直线段最短。

只知道两点间直线段最短，那么显然要把折线变成直线再解。

如果直接连AB，与I不会相交，怎么办呢？当A、B位于I的异侧时，就有交点了。

于是我们就希望在I的另一侧找一点A '，使得连A ' B与I相交于P点后（这时A ' P+ PB最短）线段A ' P与AP 一样长.由对称的知识可知道，A关于I的对称点就有资格扮演A '的角色。

解：如图1先作A关于I的对称点A '，连接A ' B与I相交于P点，则AP + PB就最小.那么这样作出的AP + PB是否真的最小呢？要证明它只需要在I 上任取一点P',证明AP'+P‘ A >AP + PB就行了。

这点好证明：事实上因为A '、A关于I对称，有AP =A ' P、AP ' = A ' P'，又由公理2:三角形的两边之和大于第三边.AP'+ P‘ B=A ' P'+ P‘ B>A ' B = A ' P+ PB= AP+ PB.原来海伦解决本问题时，是利用作对称点把折线问题转化成直线问题求解的。

后来这一方法已形成了思想，它在解决许多问题中都在起作用。

现在人们把凡是用对称点来实现解题的思想方法叫对称原理。

例题分析：1、已知A，B两点在MN同侧，如图所示，在MN上求一点P,使:I PA- PB| 最大连接BA并延长交MN于P | PA-PB| =|AB|在MN上再任意取一点P'三角形P'AB中 | P'A-P'B | <AB=| PA —PB| 2、两点在直线的异侧如何做直线上一点是其到两点之差最短作线段AB 的中垂线，交直线I于点P，点P即为所求。

将军饮马做题顺序
“将军饮马”问题的做题顺序可以遵循以下步骤：
1.确定动点和定点：在题目中，将军的行走路径是动态的，而马的位置和军营是固定的。

因此，首先需要确定这些动点和定点。

2.转化动点为定点：根据“两点之间线段最短”的原则，可以通过找对称点的方法，将动点（将军的位置）转化为定点。

具体来说，就是找到将军关于河岸的对称点，这个点就是将军饮马的位置。

3.连接定点：连接军营（起点）、饮马点（转化后的定点）和B地（终点），形成一条线段。

这条线段就是将军行走的最短路径。

4.计算最短路径的长度：利用勾股定理或其他方法，计算出这条最短路径的长度。

以上就是“将军饮马”问题的做题顺序。

需要注意的是，在实际做题过程中，还需要根据题目的具体情况进行灵活处理。

将军饮马问题的原理
将军饮马问题是一个经典的数学问题，它的原理是利用线性方程组来解决实际问题。

这个问题的背景是：有一位将军要带兵过河，他手下有若干个骑兵和步兵，每个骑兵需要2匹马来驮运，每个步兵需要1匹马来驮运。

现在将军手中有一定数量的马，问能否满足所有人的渡河需求？
为了解决这个问题，我们可以设骑兵的数量为x，步兵的数量为y，马的数量为z。

根据题意，我们可以得到以下两个方程：2x + y = z （每匹马可以驮运一个骑兵或两个步兵）
x + y = z/2 （将军手中的马只能驮运部分人）
将第二个方程式变形得到 x = z/2 - y，将其代入第一个方程式中，消去x，得到：
2(z/2 - y) + y = z
化简后得到：
3y = z
因此，无论将军手中的马有多少只，只要骑兵和步兵的数量之比为2:1，就可以满足所有人的渡河需求。

这就是将军饮马问题的原理。

通过建立线性方程组并求解，我们可以找到问题的最优解。

将军饮马18道典型习题将军饮马"是一个古希腊数学问题，源于2000多年前。

当时，一位将军向城里的著名数学家海伦请教：他每天早上都要骑马到河边让马喝水，然后到河岸同一侧的一块草地上让马吃草。

将军想知道，在河岸的哪个具体位置让马喝水，可以让他和马儿走的路程最短。

经过思考，海伦给出了答案，这就是"将军饮马"问题。

以下是"将军饮马"问题的五种常见模型：1.一动两定（和最小）模型：假设点A是将军和马儿居住的营帐，点B是指定的草地，小河L在两点之间流过。

问题是，将军和马儿在哪个具体位置喝水，可以让他们走的路程最短？解决方法是，做A点关于L的对称点A'，连接A'B，与L的交点即为P点。

这时，PA+PB最小。

为什么呢？因为在L 上任意取一点M（不与P重合），根据几何原理，PA+PB=A'P+PB=A'B，AM+MB>A'B，所以动点P在A'B与L 交点处时，PA+PB最小。

2.一定两动模型：假设点A和小河L1与第一种模型一样，但是这次，草地不是指定的点，而是由L2代表的一片草地。

问题是，在哪个具体位置喝水和吃草，可以让将军和马儿走的路程最短？解决方法是，做A点关于L1的对称点A'，做A点关于L2的对称点A''，连接A'A''，与L1和L2的交点即为P、Q。

这时，AP+PQ+QA的和最小。

为什么呢？因为在L1上取点M（不与P重合），在L2上取点N（不与Q重合），根据几何原理，AP+PQ+AQ=A'P+PQ+A''Q=A'A''，AM+MN+AN>A'A''，所以动点P和Q在A'A''与L1、L2的交点处时，AP+PQ+QA的和最小。

3.两动一定模型：假设点A和小河L1与第一种模型一样，但是这次，将军要骑马到L2代表的一片草地吃草，然后再回到营帐。

关于将军饮马难题的练习10题
1. 将军饮马难题是著名的逻辑难题之一，以下是10个练题帮助理解和解决这个难题。

2. 题目一：题目一：
- 将军饮马难题描述了将军通过一条连续的河流骑马前行的情景。

- 请阐述将军饮马难题的具体要求和条件。

3. 题目二：题目二：
- 给定一个车辆的行驶速度、将军饮马的速度以及将军饮马的间隔时间，请计算将军饮马时车辆与将军的距离。

4. 题目三：题目三：
- 假设将军饮马的路径有所改变，如何调整速度和时间间隔，才能保持将军和车辆的固定距离？
5. 题目四：题目四：
- 假设将军饮马时遇到突发情况，需要停下来处理，重新上路后可以追上车辆吗？
6. 题目五：题目五：
- 若车辆的速度变化，将军饮马的速度还能保持不变吗？请解释为什么？
7. 题目六：题目六：
- 假设将军饮马的速度变化，车辆的速度保持不变，将军和车辆之间的相对距离如何变化？
8. 题目七：题目七：
- 将军饮马难题中是否有其他影响将军和车辆距离的因素？请列举并解释。

9. 题目八：题目八：
- 假设将军饮马的速度快于车辆的速度，将军和车辆之间的相对距离会怎样变化？
10. 题目九：题目九：
- 将军饮马难题中的数学模型是什么？使用该模型可以解决哪些相关问题？
11. 题目十：题目十：
- 将军饮马难题中是否存在法律或道德层面的问题？请阐述你的观点和理由。

以上是关于将军饮马难题的练习10题，希望能帮助你更好地理解和解决这个难题。

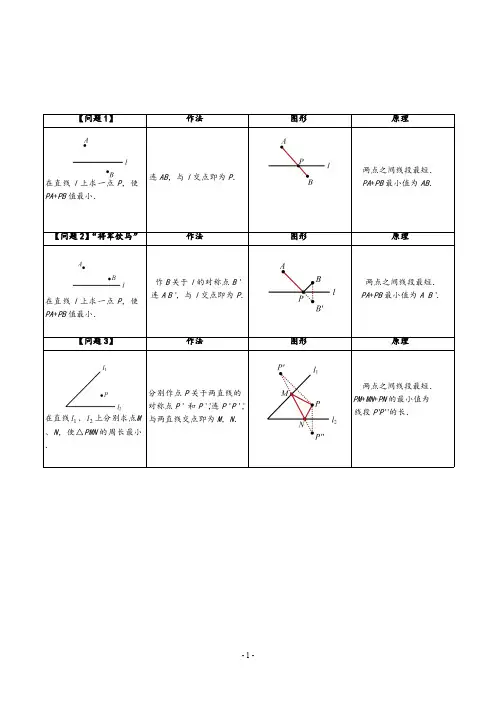
最短路径——“将军饮马”问题基本类型总结【问题1】作法图形原理在直线l 上求一点P ，使PA +PB 值最小．连AB ，与l 交点即为P ．两点之间线段最短．PA +PB 最小值为AB ．【问题2】“将军饮马”作法图形原理在直线l 上求一点P ，使PA +PB 值最小．作B 关于l 的对称点B ＇连A B ＇，与l 交点即为P ．两点之间线段最短．PA +PB 最小值为A B ＇．【问题3】作法图形原理在直线l 1、l 2上分别求点M 、N ，使△PMN 的周长最小．分别作点P 关于两直线的对称点P ＇和P ＇＇，连P ＇P ＇＇，与两直线交点即为M ，N ．两点之间线段最短．PM +MN +PN 的最小值为线段P ＇P ＇＇的长．在直线1l 、2l 上分别求点N ，使四边形PQMN 的周长最小．【问题5】“造桥选址”图形直线m ∥n ，在m 、上分别求点M 、N ，使m ，且AM +MN +BN 的值最小．【问题6】图形在直线l 上求两点M 、在左），使a MN ，并使MN +NB 的值最小．【问题7】图形1上求点A ，在2l ，使PA +AB 值最小．m n BA【问题8】作法图形原理A 为1l 上一定点，B 为2l 上一定点，在2l 上求点M ，在1l 上求点N ，使AM +MN +NB 的值最小．作点A 关于2l 的对称点A ＇，作点B 关于1l 的对称点B ＇，连A ＇B ＇交2l 于M ，交1l 于N ．两点之间线段最短．AM +MN +NB 的最小值为线段A ＇B ＇的长．【问题9】作法图形原理在直线l 上求一点P ，使PB PA -的值最小．连AB ，作AB 的中垂线与直线l 的交点即为P ．垂直平分上的点到线段两端点的距离相等．PB PA -＝0．【问题10】作法图形原理在直线l上求一点P，使PB PA -的值最大．作直线AB ，与直线l 的交点即为P ．三角形任意两边之差小于第三边．PB PA -≤AB ．PB PA -的最大值＝AB ．【问题11】作法图形原理在直线l 上求一点P ，使PB PA -的值最大．作B 关于l 的对称点B ＇作直线A B ＇，与l 交点即为P ．三角形任意两边之差小于第三边．PB PA -≤AB ＇．PB PA -最大值＝AB ＇．【问题12】“费马点”作法图形原理△ABC 中每一内角都小于120°，在△ABC 内求一点P ，使PA +PB +PC 值最小．所求点为“费马点”，即满足∠APB ＝∠BPC ＝∠APC ＝120°．以AB 、AC 为边向外作等边△ABD 、△ACE ，连CD 、BE 相交于P ，点P即为所求．两点之间线段最短．PA +PB +PC 最小值＝CD ．。

将军饮马问题模型的概述：唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B 点宿营。

问如何行走才能使总的路程最短。

模型一(两点在河的异侧)：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B 点宿营，将在何处渡河使行走距离最短并求最短距离。

方法：如右图，连接AB，与线段L交于点M,在M处渡河距离最短，最短距离为线段AB的长。

模型二(两点在河的同侧)：将军在观望烽火之后从山脚下的A点出发，需先走到河边让战马饮水后再到B点宿营，将在何处渡河使行走距离最短并求最短距离。

方法：如右图，作点B关于直线L的对称点B'，连接AB',与直线L的交点即为所求的渡河点，最短距离为线段AB'的长。

模型三：如图，将军同部队行驶至P处，准备在此驻扎，但有哨兵发现前方为两河AB、BC的交汇处，为防止敌军在对岸埋伏需派侦察兵到河边观察，再返回P处向将军汇报情况，问侦察兵在AB、BC何处侦查才能最快完成任务并求最短距离。

数学描述：如图在直线AB、BC上分别找点M、N，使得∆PMN周长最小。

方法：如右图，分别作点P关于直线AB、BC的对称点P'、P''，连接P'P''，与两直线的交点即为所求点M、N，最短距离为线段P'P''的长。

模型四如图，深夜为防止敌军在对岸埋伏，将军又派一队侦察兵到河边观察，并叮嘱观察之后先去存粮位置点Q处查看再返回P处向将军汇报情况，问侦察在AB、BC何处侦查才能最快完成任务并求最短距离。

数学描述：如图在直线AB、BC上分别找点M、N，使得四边形PQNM周长最小。

方法：如右图，分别作点P、点Q关于直线AB、BC的对称点P'、Q'，连接P'Q'，与两直线的交点即为所求点M、N，最短距离为线段(PQ+P'Q')的长。

将军饮马问题例题【原创版】目录1.将军饮马问题的背景和基本概念2.将军饮马问题的数学模型3.将军饮马问题的解决方法4.将军饮马问题的实际应用正文一、将军饮马问题的背景和基本概念将军饮马问题是一个古老的数学问题，最早出现在中国古代数学家刘徽的《九章算术》中。

问题的大致情景是这样的：一位将军要率领他的军队去一个水源地饮水，但水源地距离军队有一定距离，且水源地有两个方向可以到达。

为了保证军队能够尽快饮水，将军需要选择一条最短的路径。

这就是将军饮马问题的基本概念。

二、将军饮马问题的数学模型为了解决将军饮马问题，我们可以将其建立为一个数学模型。

假设将军所在的位置为 A，水源地为 B，两个方向分别由点 C 和 D 连接。

那么，将军可以通过 AC 和 AD 两条路径到达水源地。

为了使路径最短，我们需要求出 AC 和 AD 两条路径的长度，并选择较短的那一条。

三、将军饮马问题的解决方法解决将军饮马问题的方法主要有两种：一种是使用几何法，另一种是使用代数法。

这里我们主要介绍使用代数法的解决方法。

首先，我们可以设点 A 的坐标为 (a, b)，点 C 的坐标为 (c, 0)，点 D 的坐标为 (0, d)。

那么，路径 AC 的长度可以表示为√((a-c)+b)，路径 AD 的长度可以表示为√(a+d)。

为了求出最短路径，我们需要比较这两条路径的长度，并选择较短的那一条。

通过比较，我们可以得到一个不等式：(a-c)+b ≤ a+d。

将不等式进行化简，可以得到一个关于 a、b、c、d 的代数方程。

通过求解这个代数方程，我们就可以找到使路径最短的将军饮马问题的解。

四、将军饮马问题的实际应用将军饮马问题在实际生活中有很多应用，比如最短路径问题、物流配送问题、通信网络设计等。

这些问题都可以通过将军饮马问题的数学模型来解决，从而为实际问题提供有效的解决方案。

总之，将军饮马问题是一个古老而富有挑战性的数学问题，它的解决方法可以帮助我们在实际生活中解决许多实际问题。

将军饮马问题16大模型将军饮马问题源于中国古代的一个寓言故事，讲述的是三位将军跟随他们的军队来到一座河边准备渡河，但只有一条小船，这条小船一次只能搭载两人。

如果将军A和将军B在船上，将军C在岸边，将军C将会受到辱骂，如果将军A和将军C在船上，将军B在岸边，将军B也会受到辱骂，问题是如何让这三位将军都安全地渡河而不受辱骂。

这个问题启发了许多数学家和逻辑学家，有各种不同的解法。

下面将介绍将军饮马问题的16种不同模型。

模型1：最直接的解法最直接的解法是将将军A和将军B一同乘坐小船去对岸，然后将将军A带船返回，将将军C载到对岸。

模型2：穷举法穷举法是一种比较笨拙但可以解决问题的方法，即穷尽所有可能的情况。

这种方法虽然有效，但耗时较长。

模型3：递归法递归法是将问题分解成较小规模的子问题，并逐步解决。

这种方法可以节省时间和精力，但需要较高的逻辑思维能力。

模型4：数学推导法通过数学推导，可以将将军饮马问题转化为数学模型，从而得出解答。

这种方法需要较强的数学功底。

模型5：逻辑推理法逻辑推理法是通过逻辑推理和思维分析，得出解决将军饮马问题的方法。

这种方法强调思维的逻辑性和推理能力。

模型6：图论模型图论是数学的一个分支，可以用来描述将军饮马问题中的交叉关系和路径规划。

通过构建相应的图模型，可以更清晰地解决问题。

模型7：概率模型概率模型是通过概率计算和推测，找出解决将军饮马问题的可能性和概率分布。

这种方法适用于对问题进行全面分析和评估。

模型8：动态规划法动态规划法是针对多阶段决策问题的一种解决方法，可以在问题空间中寻找最优解。

这种方法适用于将军饮马问题的场景。

模型9：模拟法模拟法是通过模拟将军饮马问题的场景，以实验测算的方式找出最佳解决方案。

这种方法可以直观地展示问题的复杂性和解决路径。

模型10：启发式算法启发式算法是通过启发性的思考和优化方法，寻找将军饮马问题的最佳解决方案。

这种方法可以在复杂问题中找到较好的解决途径。

(完整版)将军饮马问题(总5页)
将军饮马问题是一个考查组合数学的有趣问题，它的背景故事是这样的：有一位准将，他有30匹马，要出发征战了，但是他想要对这30匹马进行饮马仪式，即把30匹马从一个桶里拿出三匹，立即喂食，然后又把它们放回去，以此重复30次，问最少要多少桶，才能保证每匹马都受到饮马仪式的次数？
将军饮马问题是一道传统的组合数学问题。

本题由英国数学家J. S. Wright 于1880 年发表在《数学月刊》上。

本问题是关于组合数学中的非可逆组合问题，也可以理解为组合排列问题。

将军饮马问题有两种解法，一种是使用概率论的方法，一种是使用组合数学的方法。

如果使用概率论的方法，根据鸽巢原理，可以得出答案是3桶。

如果使用组合数学的方法，问题可以表述为:从30个马中取出3个，相当于从30个空位中取出3个，一共有C30 3 = 27720 种可能，每一种可能就表示一次饮马仪式，所以需要27720 个桶，即28 桶。

将军饮马问题的另一个解法是使用组合数学的方法。

从题意中可以得出，饮马仪式的目的就是要把30 匹马分成。

将军饮马问题唐朝诗人李欣的诗《古从军行》开头两句说：“白日登山望峰火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题--将军饮马问题：如图1所示，诗中将军在观望烽火之后从山脚下的A点出发，走到河旁边的P 点饮马后再到B点宿营．请问怎样走才能使总的路程最短？作法如下：如（1）图，从B出发向河岸引垂线，垂足为D，在AD的延长线上，取B关于河岸的对称点B′，连接AB′，与河岸线相交于P，则P点就是饮马的地方，将军只要从A出发，沿直线走到P，饮马之后，再由P沿直线走到B，所走的路程就是最短的．（1）观察发现再如（2）图，在等腰梯形ABCD中，AB=CD=AD=2，∠D=120°，点E、F是底边AD与BC的中点，连接EF，在线段EF上找一点P，使BP+AP最短．作点B关于EF的对称点，恰好与点C重合，连接AC交EF于一点，则这点就是所求的点P，故BP+AP的最小值为2．（2）实践运用如（3）图，已知⊙O的直径MN=1，点A在圆上，且∠AMN的度数为30°，点B是弧AN的中点，点P在直径MN上运动，求BP+AP的最小值．（3）拓展迁移如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．①求这条抛物线所对应的函数关系式；②在抛物线的对称轴直线x=1上找到一点M，使△ACM周长最小，请求出此时点M的坐标与△ACM周长最小值．（结果保留根号）考点：二次函数综合题；垂径定理；圆周角定理；轴对称-最短路线问题．分析：（1）根据轴对称中最短路线问题，可以得出AC的长即为BP+AP的最小值，利用三角函数关系求出即可；（2）根据轴对称中最短路线问题，得出BP′+AP′=BP′+A′P′=A′B，即A′B是BP+AP 的最小值，求出即可；（3）运用待定系数法求二次函数解析式，再求出直线与坐标轴的交点坐标，当AM+CM取最小值时，△ACM周长最小值，求出AM+CM最小值，即可得出．解答：解：（1）∵在等腰梯形ABCD中，AB=CD=AD=2，∠D=120°，点E、F是底边AD与BC的中点，∴∠DAC=∠DCA=30°，∴∠ACB=30°，∴∠BAC=90°，∴tan∠ACB=ABAC，∴AC=23，故答案为：23；（2）如图，作点A关于MN的对称点A′，则A′在⊙O上，连接BA′交MN于P′点，此时BP′+AP′最小．由对称性可知AP′=A′P′，∴BP′+AP′=BP′+A′P′=A′B，连接OA、OB、OA′，可知弧AN=弧A′N，则∠NOA′=∠NOA=2∠M=60°，而点B为弧AN中点，∴∠BON=30°∴∠BOA′=90°而MN=1，∴在Rt△OA′B中，A′B=22即BP+AP的最小值22．（3）①∵抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，分别代入二次函数解析式得：∴-b2a=1a-b+c=0c=-3，解得：a=1，b=-2，c=-3，∴二次函数解析式为：y=x2-2x-3，②得到直线BC：y=x-3，∴M（1，-2），AC的长为：10，∴△ACM周长最小值即是：AM+CM最小时的值，∵AM+CM=BC=32，∴△ACM周长最小值为：．点评：此题主要考查了轴对称中最短路线问题以及圆周角定理和二次函数解析式的求法等知识，题目综合性较强，利用轴对称求最小值问题，是近几年中考中热点问题，应该引起同学们的注意．。