一 年 级 上 册 数 学 综 合 练 习 题

一年级上册数学奥数题附练习题与答案数学奥数的学习，是最大程度提高孩子思维能力的学习，所以很多人觉得这个知识要从小学的一年级抓起，小编整理了一年级上册数奥数题相关内容，希望能帮助到您。

一年级奥数经典试题1.楼层小宏与爸爸一起上楼，小宏走得慢，爸爸走得快，小宏上了1层时，爸爸已上了2层，问小宏上到3楼时，爸爸上到几楼?2.分水果一个小组有10个人，7个人爱吃香蕉，5个人爱吃苹果，问既爱吃香蕉又爱吃苹果的有几个人?3.小鸭子说稀奇，道稀奇，鸭子队里有只鸡，正着数，它第6，倒着数，它第7，小鸭一共有几只?4. 找规律填数：① 5、7、9、11、13、( )②0、1、1、2、3、5、8、( )5. 按要求填数：36、12、45、7、35、23、60、55 ( )>( )>( )>( )>( )>( )>( )>( )13、24、15、7、61、25、14、8 ( )<( )<( )<( )<( )<( )<( )<( )6、有一个两位数，个为是9十位是4，这个两位数是( )7、有14小朋友排成一队，从左往右数红红排在第4位，从右向左数明明也是排在第4位，那么红红和明明两人之间有多少人?8、最小三位数的是( )最大的三位数是( )。

9、用5、7、4三个数可以排成( )个不相同的三位数。

分别写出来。

10、要把一根木棒锯成5段需要4分钟，要是想锯成7段需要多少分钟?11、计算：3+5+7+9+11+13+15+17+19+21=5+10+15+20+25+30=12、有14个小朋友在玩捉迷藏的游戏，有6个小朋友被捉住了，还有多少个小朋友没被捉住啊?13、、有一个个位数，在它的右边加上一个零，构成一个两位数，这个两位比原来的数要大36，则原来的各位数是( )。

14、按要求填补算式完整：9+( )=21 21—( )=19 21—( )=18 24+( )=4315、老师让小朋友们植树，先植了10棵桃树，然后老师让同学们在每两棵桃树间植一棵梨树，那么一共还可以植多少棵梨树?16.分糖块三个小朋友分5块糖。

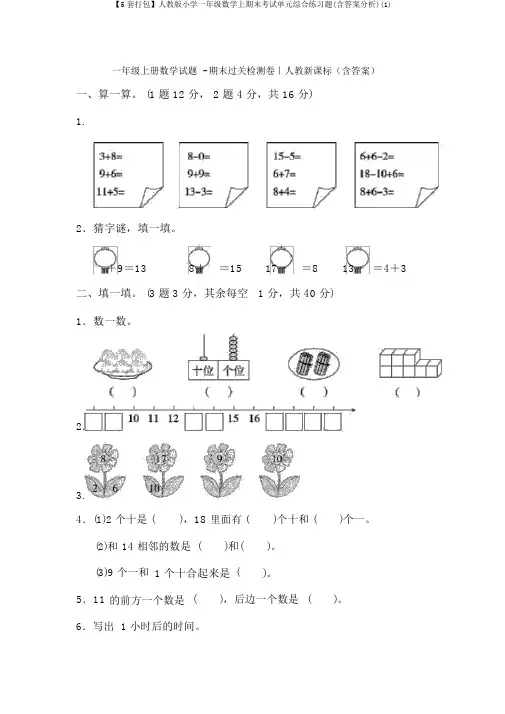
一年级上册数学试题 - 期末过关检测卷｜人教新课标（含答案）一、算一算。

(1 题 12 分， 2 题 4 分，共 16 分)1.2．猜字谜，填一填。

＋9＝13 8＋＝1517－＝813－＝4＋3二、填一填。

(3 题 3 分，其余每空 1 分，共 40 分)1．数一数。

2.3.4．(1)2 个十是 ()，18里面有 ()个十和 ()个一。

(2)和14 相邻的数是()和()。

(3)9 个一和1 个十合起来是()。

5．11的前方一个数是()，后边一个数是()。

6．写出 1 小时后的时间。

7．在里填上“＞”“＜”或“＝”。

105＋619－8 113＋66＋39＋86＋88．(1)右图中一共有 ()种物件。

(2)的()面是，的()面是。

(3)的()边是，()边是。

9.里最大能填几？8＋＜1519－＞912＋＜18－2＜17 10．要拼成一个大正方体，下面的图形起码还需要()个。

三、选一选。

(每题 2 分，共 10 分)1．13 和 15 之间的数是 ()。

① 12② 14③ 16④ 172.爸爸睡觉的时间是 ()。

①8时②9时③10时④11时3．从 8 数到 15，一共数了 ()个数。

①6②7③8④94．原定礼拜一开运动会，现推延 2 天开，开运动会是礼拜 ()。

①六②日③二④三5．起码用 ()个相同的小正方体能够拼成一个较大的正方体。

①4②6③8④9四、看图列式计算。

(每题 3 分，共 12 分)1. 2.＝(本)＝(颗)3. 4.＝(只) .＝(只)五、解决问题。

(1，2，3 题每题 4 分， 4 题 10 分，共 22 分)1.本来有多少个松果？＝(个) 2．今日来了 18 个同学，每个同学一个，还差多少个？＝(个)3.她可能买了多少支笔？＝(支)4.(1)一共有几个小鸡？方法一：＝(只)方法二：＝(只)(2)请你再提出一个数学识题，并解答。

答案一、 1.11 15 168 18 1010 13 1210 14112.4796二、 1.9162082.891314171819203.75491(后四空答案不独一 )4.(1)2018(2)1315(3)195.10126.2：00 11：00 12：007.＜＝＝＞8.(1)9 (2)下上(3)左右9.6 9 51810.3三、 1.② 2.③ 3.③ 4.④ 5.③四、 1.13－3＝10(本)2.9＋6＝15(颗)3.3＋3＋2＝8(只)4.6－3＋4＝7(只)五、 1.6＋8＝14(个)2.18－8＝10(个)3.5＋9＝14(支)(答案不独一 )4.(1)方法一： 5＋2＝7(只)方法二：3＋4＝7(只)(2)略一年级上册试题 - 期末模拟卷 - 人教新课标（含答案） (6)一.选择题(共 5题，共 10分)1. “4 4=0”，在里应填的运算符号是（）A.＋B.－C.×D.÷2. 看图，一人一块糖，应当准备（）A.7 块B.8 块C.9 块D.10 块3.12－8－4＝（）A.8B.18C.0D.44. 某班共有11 人，人人参加比赛，参加数学比赛的有 4 人，参加作文比赛的有9 人，那么有（）A. 1 人既参加数学比赛又参加作文比赛．B. 2 人既参加数学比赛又参加作文比赛.C. 3 人既参加数学比赛又参加作文比赛．D. 4 人既参加数学比赛又参加作文比赛．5. 看图列式计算 , 正确的选项是（）A. 15－ 10=5(个)B.15－5=10( 个)C. 15＋5=20( 个) D. 10－5=5(个)二.判断题(共 4题，共 8分)1.下面的题计算得对吗？对的画“√”，错的画“×”，并在横线上写出正确的得数 .13－5－4＝5（）_______________2.7＋6－8＝5 ()3.7+6-7+6=0（）4.7+6＞7-6 。

小学一年级上册数学综合练习题小学一年级上册数学综合练习题导语：小学数学是一门很有趣的课程，不仅开发了小朋友的动脑能力，还让小朋友们更加喜欢学习了，今天店铺收集了一些数学题，有需要的小朋友们可以看看一、算一算5+6-8=16-0-16=8-8+3=7+1+4=17-10-7=16-9=20+0-9=10+6-10=12-8=11+0-7=20-1=9+9-0=13-5+7=17-8-8=15+1-9=11+0-0=14+6-8=15-8-7=18+1+1=7+9-8=二、填空1、一个两位数，左边的数是( )位，右边的数是( )位。

2、1个一是( )3、6个一和1个十组成( )，它的`前面一个数是( )，比它大比20小的数有()、()、()。

4、现在是9时了，再过2个小时是( )时。

1时的前2个小时是( )时。

(24小时计时法)5、钟面上的时针指向11，分针指向12，现在是( )时。

6、17是( )个一。

它比10大( )。

7、最小的一位数是( )，最小的两位数是( )，他们和是( )8、11是( )位数，个位上是( )，十位上是( )9、比11小11的数是( )，比10大10的数是( )10、16-7=( )，在这个算式中，减数是( )，被减数是( )三、我会填1、上面一共有( )只昆虫?2、从左边起，青蛙是第( )个，排在第3个的是( )3、蜜蜂的右边有( )只昆虫，它的左边有( )只昆虫。

4、把左边起第4个昆虫圈起来，把右边3个昆虫圈起来。

5、七星瓢虫排在从右边起的第( )个。

四、我会找1、有( )个，有( )个，有( )个，有( )个。

2、有( )个有( )个，有( )个，有( )个。

五、再过三个小时是几时?( )时( )时( )时( )时六、在( )填上“+”或“-”7( +- )6=13 2( +- )8=10 9+9=17( +- )1 8( +- )2=16( +- )10 7( +-)9=20( +-)4 19( +- )1=20( +- )0 10( +- )3=13 19( +- )1=9( +- )9 10( +- )10=0( +- )0 4( +- )5=5( +- )4 12( +- )8=8( +- )4 7( +- )9( +- )9=7七、以下是张艺馨一年级上学期作业情况1、张艺馨小朋友的作业情况中，得( )的最多，得( )最少，继续加油哦。

一年级数学下册应用题综合练习题1、鱼缸里有13条热带鱼，爸爸送给他的同事4条，鱼缸里还有多少条热带鱼。

2、水果店有12筐苹果，卖了3筐后，店里还剩几筐苹果？3、妈妈买了12个水果中，其中7个是香蕉，剩下的是梨，梨有几个？4、幼儿园大班分到14个梨，小朋友们拿走了7个，还剩下多少个？5、啄木鸟妈妈捉了11条虫子，喂孩子们8条，给自己留下几条？6、妈妈买了15个苹果，我们吃了6个，还剩下多少个？7、小明有17支铅笔，用了8支后，现在有几支铅笔？8、停车场有20辆汽车，开走了8辆，又开来3辆，现在停车场有几辆汽车？9、家里还有2个苹果，妈妈下班后又买回9个，现在家里共有多少个苹果？10、草地上有15只羊，跑了6只，又来了5只，现在草地上有几只羊？11、河里有12只小鸭子，游走了3只，还有几只？12、图书馆上午借出14本连环画，下午借出的比上午少5本，下午借出多少本？13、花园里有13只蝴蝶，飞走了4只，又飞来5只，花园里现在有蝴蝶多少只？14、小丽家有红气球和花气球共15个，其中花气球有6个，红气球有几个？15、小玲和小娜共做了14朵花，小玲做了8朵，小娜做了几朵？16、教室里有13名同学在做作业，有4名同学写完后回家了，教室里现在还有几名同学？17、小丽有12本故事书，拿走《童话故事》书的一半后，还有9本，小丽有几本《童话故事》书？18、湖边有16只天鹅，飞走9只，还剩几只？19、学业校买来红、绿彩纸共13张，绿纸有8张，红纸有几张？20、小亮要练习写15个大字，已经写了7个，还要写几个大字？21、妈妈买来12个苹果，吃了6个，还剩几个？22、小玲和小英共做了12朵工艺花，小玲做了7朵，小英做了几朵？23、奶奶家养了11只兔子，送人4只，家里还剩几只？24、湖边有15只船，同学们划走了6只，还剩几只小船？25、把一根木头锯成3段，如果每锯一次用3分钟，同共要锯多少分钟？26、树上有12只小鸟，第一次飞走了3只，第二次飞走了2只，一共飞走了几只？27、弟弟今年4岁，哥哥今年12岁，10年后，哥哥比弟弟大几岁？28、小亮昨天做了6道题，今天做了同样多的题，小明两天做了8道题，小亮两天做了题比小明多几道？29、咪咪家有14个香蕉，吃了6个，还剩几个？30、河边有16只鸭子，游走了几只后，还剩下7只，游走了几只？31、停车场有15辆汽车，开走了7辆，还剩几辆？32、体操队有16个同学，其中女同学有8个，男同学有几个？33、一个小队17人排成一排，一、二报数，报二的人向后退两步，留在原地的还有多少人？34、小丽家有20条红金鱼，还有8条地图鱼，小丽家共有多少条鱼？35、饲养场有40匹白马和9匹花马，饲养场共有多少匹马？36、我们饲养场有40只小兔和20只大兔，共有多少只兔子？37、商店第一天卖出50件衣服，第二天上午卖出40件，下午卖出50件，第二天共卖出多少件？38、一根绳子，剪去40米，还剩30米，这根绳子有多长？39、学校买来20盒彩色粉笔，80盒白粉笔，学校共买来粉笔多少盒？40、一根绳子长100米，剪去50米，还剩多少米？41、体育室有20个篮球，15个足球，8个排球，借走了6个足球后，还剩几个足球？42、一个玩具狗要30元，我给了营业员50元，应找回多少钱？43、青蛙捉了16只虫子，吃了8只，还剩几只？44、班里的图书角原有图书40本，借出15本，还剩多少本？45、小明买一件上衣用30元，买一条裤子用35元，这套衣服共花多少元？46、小玲看一本连环画，已经看了20页，还有45页没看，这本连环画共有多少页？47、赵丽两天看了30页书，第一天看了9页，第二天看了多少页？48、大树上有12只小鸟，飞走了4只，还有几只？49、妈妈买回一些草莓，李英吃了一半后，还剩下30个，妈妈买回多少个草莓？50、学校原有20棵柳树，又种了35棵杨树，现在共有多少棵树？51、草地上有9头大牛，18头小牛，大牛比小牛少多少头？52、饲养组养了40只乌鸡，25只花鸡，卖掉20只后，还剩多少只？53、二年一班有男生26人，女生20人，男生比女生多多少人？54、二年一班有男生26人，女生20人，男、女生共有多少人？55、小华有一本95页的故事书，已经看了40页，还有多少页没看？56、修一条公路，工人叔叔第一天修50米，第二天修40米，两天一共修多少米？57、篮子里有35个鸡蛋，吃了一些后，还剩10个，吃了多少个鸡蛋？58、水果超市有30箱苹果，20箱水晶梨，水果超市共有水果多少箱？59、李丽看一本童话书，上午看了25页，下午比上午多年看了10页，下午看了多少页？60、动物园里有25只大猴子，10只小猴子，大猴子比小猴子多多少只？61、李奶奶家养了46只鸡，其中6只是公鸡，其余是母鸡，母鸡有多少只？62、校图书室有故事书100本，科技书80本，故事书比科技书多多少本？63、体育组有22个排球，有33个足球，体育组共有多少个球？64、二年级女生人数比男生少9人，男生有29人，女生有多少人？65、动物园的猴山上有大猴12只，小猴比大猴少3只，小猴有多少只？66、湖里有天鹅65只，野鸭比天鹅少20只，野鸭有多少只？67、菜店里有12筐黄瓜，黄瓜比西红柿少10筐，西红柿有多少筐？68、服装超市上午卖出25套西装，下午比上午多卖出20套，下午卖出多少套？69、学校原来有9台闭路电视，又买来8台，现在共有闭路电视多少台？70、丽丽和妈妈共包了20个饺子，其中丽丽包了5个，妈妈包了多少个？71、幼儿园有35个皮球，分给大班20个，其余的给中班，中班分到多少个皮球？72、广场上原有30只鸽子，又飞来25只，现在广场上共有多少只鸽子？73、步步家养了12只鸡，卖掉一些后，还剩下4只，卖了多少只？74、生态保护区内原有10只东北虎，后又运来15只华南虎，现在保护区内共有老虎多少只？75、学校开联欢会，准备安装45串彩灯，已经安装了30串，还有多少串没安装好？76、小芳上午写了9个生字，下午写了6个，今天小芳共写了多少生字？77、图收馆上午借出15本书，下午借出的比上午少5本，下午借出多少本书？78、草地上有8只羊，又跑来了4只，现在草地上有多少羊？79、草地上有8只羊，跑来了5只鸭和6头牛，现在草地上共有羊鸭、牛多少？80、河里有14只鸭子，游走了3只，还有几只？81、草地上有17只羊，跑了6只，又来了5只，现在草地上有几只羊？82、小明有17支铅笔，用了7支，又买来5支，现在小明有几支铅笔？83、停车场有20辆汽车，开走了8辆，又开来了3辆，现在停车场有几辆汽车？84、停车场上有13辆汽车，开走几辆后，还剩8辆，开走几辆？85、学校有白粉笔50盒，彩色粉笔20盒，白粉笔比彩色粉笔多多少盒？86、小华有8块奶糖，12块水果糖，小华一共有多少块糖？87、体育组有15个跳球，8个篮球，篮球比足球少多少个？88、妈妈买回一些巧克力，小明吃了3块，还剩9块，妈妈共买回多少块巧克力？89、农场的果园种梨树54棵，桃树比梨树多20棵，桃树有多少棵？90、车站有公交车18辆，长途汽车比公交车多10辆，长途汽车有多少辆？91、学校春季种树比秋季多种15棵，秋季种树50棵，春季种多少棵？92、少年宫的舞蹈组有24人，航模组比舞蹈组多10人，航模组有多少人？93、三年一班男生有28人，女生有25人，女生比男生少多少人？94、水果店运来一批苹果，卖出3筐，还剩9筐，水果店远来多少筐苹果？95、机场停了12架飞机，飞走了5架，还剩几架？96、学校原来有30棵树，又种了20棵，又种的树比原来的少多少棵？97、妈妈拿来4个梨和12个苹果，梨的个数比苹果少多少个？98、赵明今年8岁，他姐姐15岁，姐弟两人相差几岁？99、车站有货车15辆，客车比货车少6辆，客车有多少辆？100、书架上有些书，芳芳拿走了6本，剩下的比拿走的多6本，书架上原有书多少本？101、树上原来12只小鸟，飞走4只，又飞来6只，树上现在有多少只小鸟？102、树上有8只小鸟，飞来5只，又飞走6只，现在树上有几只小鸟？103、校园里有12盆月季花，牡丹花比月季花少4盆，牡丹花有几盆？104、爸爸买来15个香蕉，全家人吃了7个，还剩几个？剩下的比吃了的多几个？105、李丽走进教室，看见教室里只有10名同学，那么现在教室里有几名同学？106、小青蛙捉了11只虫子，吃了4只后，又捉了20只，现在共捉多少只虫子？107、奶奶家有20只鸡，其中公鸡有4只，剩下的是母鸡，母鸡比公鸡多多少只？108、学校体育组有篮球20个，足球比篮球多15个，足球有多少个？两种球共有多少个？109、班里有各种彩色气球20个，其中8个是花气球，剩下的是红气球，红气球有多少个？110、小红买了一本故事书，她第一天看了20页，第二天看了30页，第二天比第一天多看多少页？111、百货店购进20箱毛巾，卖出9箱，还剩几箱？剩下的比卖出的多几箱？112、湖边有16只天鹅，飞走8只后，又飞来9只，现在湖边共有多少只天鹅？113、娜娜买一本练习本5角，买一块橡皮5角，一共花了多少钱？114、妈妈买香蕉用去6元钱，钱包里还有14元，妈妈钱包里共有多少钱？115、弟弟花1元钱买了一个小皮球，哥哥花6元钱买了一个铅笔盒，哥哥比弟弟多花了多少钱？116、奶奶买肉用去9元，又买了10元的苹果，付给售货员20元钱，应找回多少钱？117、妈妈买了一个暖水瓶，她付给售货员20元钱，找回4元，这个暖水瓶多少钱？118、爸爸给小明花65元买了一个足球，他付给收银员100元，应找回多少元？119、商店有25个足球，又进来40个，今天卖出5个，现在还剩下多少个？120、钢厂计划投资20万元建厂房，因节约的原因，实际只用了17万元，为厂里节省多少万元？121、妈妈买苹果用去8元钱，给我买一个书包用去50元，妈妈应付给营业员多少钱？122、小英买了4个练习本用去1元2角，还剩8角钱，小英原来有多少钱？123、图书借出30本书后，还剩25本，图书角原来有多少本？124、停车场有小汽车9辆，大汽车16辆，大汽车比小汽车多几辆？125、停车场有大小汽车18辆，开走9辆后，又有3辆开来，停车场现有汽车多少辆？126、小刚体重38千克，比小华重10千克，小强比小华重5千克，小强有多重？127、赵明家有两种热带钱共15条，其中地图鱼有7条，另一种鱼有几条？128、公园里有柏树40棵，柳树60棵。

乡镇（街道）学校 班级 姓名 学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…上海教育版小学一年级数学上学期综合练习试题 含答案题号 一 二 三 四 五 六 七 八 九 十 总分 得分考试须知：1、考试时间：45分钟，满分为100分（含卷面分3分），附加题单独20分。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

3、不要在试卷上乱写乱画，卷面不整洁扣3分。

一、我会填（本题共10分，每题2分）1、19比（ ）少1，比（ ）多1。

2、找规律，填一填，画一画。

3、换人民币。

1、1张1元可以换成（ ）张5角。

2、1张10元可以换成（ ）张2元。

3、1张50元可以换成（ ）张10元。

4、1张10元可以换成（ ）张5元和（ ）张1元。

4、按要求填空。

17、1、6、19、4、13、20、71、上面一共有（ ）个数。

从右边数，第3个数是（ ）。

2、在这些数中，最小的一个数是（ ），最大的一个数是（ ）。

5、在( )里填上米或厘米。

①课本宽17( ) ②大树高大约10( )。

二、我会算（本题共20分，每题5分）1、看图列式。

2、看图写算式。

3、算一算，并给得数是3的格子用铅笔涂上颜色。

4、一根绳子对折后长7米，这根绳子原来长多少米？这根绳子用掉6米后，还剩几米？答：绳子原来长（）米，还剩（）米。

三、我会比（本题共10分，每题5分）1、哪把斧子最长？按从短到长的顺序排列.2、在○里填上＞、＜或＝。

9○10 1○0 6○7 5○57○6 3○4 8○6 6○10四、选一选（本题共10分，每题5分）1、哪些是蔬菜，是的画“√”。

哪些是水果，是的画“×”。

（）（）（）（）（）（）2、小动物要到小兔家玩，小朋友想想谁走的路最短，五、对与错（本题共5分，每题2.5分）1、正确的在（）里画√，错误的在（）里画×。

整理和复习▶教学内容教科书P85~87“整理和复习”、“练一练”以及“数学游戏。

▶教学目标1.梳理本单元知识内容，让学生熟练掌握20以内的数的顺序、序数含义、组成等知识，加深对加、减法含义的理解，提高计算能力。

2.通过整理和复习，让学生对11~20各数有一个全面的认识，培养学生有条理、多角度地思考问题。

3.通过多种形式的练习，加深学生对知识间的联系的认识，从而培养数感。

▶教学重点熟练掌握11~20以内数的认识，加深学生对加、减法含义的理解，提高计算能力。

▶教学难点自主建构知识间的联系，整体把握20以内数的特征。

▶教学准备课件。

一、知识回顾1.单元知识梳理。

师：同学们，这一单元我们学习了哪些知识？【学情预设】引导学生梳理本单元知识，学生可能会说：我知道了10根小棒捆成一捆，10个一就是1个十；我认识了11~20各数，会读写各数，知道了它们的组成；我会给数按从小到大的顺序排排队；我会比较数的大小；我会计算十加几、十几加几、十几减几、十几减十……师：你们说得非常好，学习这么多的知识。

下面，我们就一起来梳理一下本单元的知识结构。

【设计意图】通过简单的知识回顾，让学生建立初步的知识体系，为后面系统复习打下坚实的基础。

2.动手制作“知识图”。

师：（课件出示××整理的“知识图”）同学们请看，这是××同学制作的“知识图”。

我们来看看这张知识图上有哪些知识，××是怎样将它们排列起来的？【学情预设】预设1：我从××整理的“知识图”中看到了我们学习过的十加几，十几减几以及十几减十的计算。

预设2：我还发现整理了数位表，十位上的数是1，个位上的数是3，表示13这个数是由1个十和3个一组成的。

预设3：我也有发现，在××的“知识图”中，有我们学习过的用画图法解决问题的过程。

求12和16之间有几个数，通过图示我知道了这两个数之间有3个数。

人教版一上数学答案同步练习册人教版一年级上册数学同步练习册答案
一、认识数字
1. 填空题
- 1到10中，最大的数字是（10）。

- 比5大的最小整数是（6）。

2. 选择题
- 下列数字中，最大的是（C）。

A. 3
B. 7
C. 9
D. 5
3. 判断题
- 10比1大。

（正确）
- 2比4小。

（正确）
二、比较大小
1. 填空题
- 5和8相比，（8）更大。

2. 选择题
- 下列哪两个数字相加等于10？
A. 1和9
B. 2和8
C. 3和7
D. 4和6
- 正确答案：D
3. 判断题
- 如果一个数比另一个数大，那么这个数一定比10大。

（错误）
三、10以内的加减法
1. 计算题
- 3 + 2 = 5
- 7 - 4 = 3
2. 应用题
- 如果我有5个苹果，你再给我2个，我一共有多少个苹果？
答：一共有7个苹果。

四、认识图形
1. 选择题
- 下列哪个是圆形？
A. 正方形
B. 圆形
C. 三角形
- 正确答案：B
2. 判断题
- 所有的圆形都有相同的形状。

（正确）
五、综合应用题
1. 应用题
- 一个班级有20个学生，如果每个学生分到2个苹果，一共需要多少个苹果？
答：一共需要40个苹果。

结束语：
通过本练习册的练习，同学们应该已经对一年级上册数学的基础知识有了更深入的理解和掌握。

希望同学们能够继续努力，不断进步，在数学的海洋中遨游，享受学习的乐趣。

2017年小学一年级上册数学测试题+综合练习题D23456小学数学第一册第二单元测试题（2）姓名得分一、比长短(10分)1．长□√，短□○。

2．最长□√，最短□○。

二、比高矮(15分)1．最高□√，最矮□○。

2.重的画“□√”轻的画“□○”。

三、比远近(10分)1．小蚂蚁回家，走哪条路最近，在□里画“√”。

782．在最长的后面的“□”里画“√”。

四、实践能力题 (7分)把同样多的方糖放进下面的杯中，哪一杯水最甜，在( )里打√。

( )( ) ( )五、多□√,少□○ (6分)六、1. 比一比，厚的画□√,薄的画□○ 2．比一比，大□√,小□○□ □ □ 七、比一比（12分）□ □ □□9 1．最轻的画√，最重的画△。

2. 最快的画√，最慢的画△。

① ② ③ ④□ □ □ □ 八、 和 哪个重？重□√,轻□○(8分)。

十、两个杯里的水一样多，放进大小不同的石块后，哪个杯子里的水会变得更高？在更高□√。

(6分)（杯子一样大）①②③④ □ □①□②□十一、比一比，哪一种水果最重？在最重□√。

(10分)十二、益智题(10分,不计入总分)请同学们想一想,在一天中,大树是早晨的影子长,还是中午的影子长?早晨( ) 中午( )小学数学第一册第三单元测试题（3）姓名得分一、把同类的物体圈出来(8分)二、请把一类的东西用不同形状圈出来(8分)三、把应放在书包里的东西圈出来(8分)10四、圈出一个不同类的东西(12分)(1)(2)(3)五、看图说一说，图1和图2怎样分的(8分) 1． 2.六、把□涂上红色, 涂绿色,△涂黄色 (8分)七、想一想，可以怎样分(10分)八、把下面物品的序号填在下面相应的圈里(10分)文具玩具服装鞋帽2．怎样放合适呢？（用线连一连 8分）九、数一数、分一分，你能想出几种分类方法(10分)(7)十、下面这些动物你认识吗？它们各有几只脚？会游泳的是哪几个号？请把动物编号写在相应的圈内。

(10分)十一、拓展题(接着画，10分，不计入总分)△●△●●△●●●○○○□□□□小学数学第一册第四单元测试题（4）姓名得分一、说一说，的上面、下面、左面、右面是什么(8分)在的面，在的面；在的面，在的面；在的面，在的面；三、看一看，说一说。

人教版一年级上册同步练习数学题大全及答案目录1.1数一数 (1)1.2比多少 (2)2位置 (3)3.1 1~5 的认识 (4)3.2比大小 (5)3.3第几 (6)3.4分与合 (7)3.5加法 (8)3.6减法 (9)3.7 0 的认识和0 的加减法 (10)4立体图形的认识 (11)5.1 6 和 7 的认识 (12)5.2 6 和 7 的加减法 (13)5.4 8 和 9 的加减法 (15)5.5 10 的认识 (16)5.6 10 的加减法 (16)5.7连加连减 (18)5.8加减混合 (19)6.1 11~20 各数的认识 (20)6.2十加几、十几加几（不进位）和相应的减法 (20)7认识钟表 (21)8.1 9 加几 (22)8.2 8、 7、 6 加几 (23)8.3 5、 4、 3、 2 加几 (24)8.4解决问题 (25)1.1数一数1.看数涂上颜色。

2.连一连。

3. 看数画。

396 24.看数圈一圈。

2318 55.照样子画○。

答案：1—4. 答案不唯一，合理即可。

5.提示：分别 2 个○、 7 个○、 10 个○。

1.2比多少1.在多的后面画“√” 。

2.在多的后面画“√”。

3.在少的后面画“√” 。

4.填一填。

5.5 个人吃饭，椅子够坐吗？答案：1.在骨头后面画√。

2.在绿球后面话√。

3.在鸡后面画√。

4.多5.够2位置1. 苹果的下面是（），西瓜的上面是（），香蕉的左边是（），桃子的右边是（）。

2. 在○的上面画△，下面画□，左面画? ，右面画☆。

3.填一填。

4.（1）（）排在最前面，（）排在最后面。

（2）刺猬的前面是（），后面是（）。

5.按要求做题。

答案：1.桃子香蕉桃子香蕉2.略3.上下下上4.（1）小狗恐龙（2）猴子猫5.5涂色略3.1 1~5 的认识1.看图写数。

2.看数涂色。

3.连一连。

4.圈一圈。

5.把右边前 3 只小鸟圈起来，黄鸟的左边有（）只，右边有（）只。

一年级数学下册应用题综合练习题1、鱼缸里有13 条热带鱼. 爸爸送给他的同事 4 条. 鱼缸里还有多少条热带鱼。

2、水果店有12筐苹果.卖了3筐后.店里还剩几筐苹果？3、妈妈买了12 个水果中. 其中7 个是香蕉. 剩下的是梨. 梨有几个？4、幼儿园大班分到14 个梨. 小朋友们拿走了7 个. 还剩下多少个？5、啄木鸟妈妈捉了11 条虫子.喂孩子们8 条.给自己留下几条？6、妈妈买了15个苹果.我们吃了6个.还剩下多少个？7、小明有17支铅笔.用了8支后.现在有几支铅笔？8、停车场有20辆汽车.开走了8辆.又开来3辆.现在停车场有几辆汽车？9、家里还有 2 个苹果. 妈妈下班后又买回9 个. 现在家里共有多少个苹果？10、草地上有15只羊. 跑了6只.又来了5只.现在草地上有几只羊？11、河里有12 只小鸭子. 游走了 3 只. 还有几只？12、图书馆上午借出14 本连环画. 下午借出的比上午少 5 本. 下午借出多少本？13、花园里有13 只蝴蝶. 飞走了 4 只.又飞来 5 只.花园里现在有蝴蝶多少只？14、小丽家有红气球和花气球共15个. 其中花气球有6个. 红气球有几个？15、小玲和小娜共做了14 朵花.小玲做了8 朵.小娜做了几朵？16、教室里有13名同学在做作业. 有4名同学写完后回家了. 教室里现在还有几名同学？17、小丽有12 本故事书. 拿走《童话故事》书的一半后. 还有9 本. 小丽有几本《童话故事》书？18、湖边有16 只天鹅. 飞走9 只. 还剩几只？19、学业校买来红、绿彩纸共13张. 绿纸有8张.红纸有几张？20、小亮要练习写15个大字.已经写了7个.还要写几个大字？21、妈妈买来12 个苹果. 吃了6个. 还剩几个？22、小玲和小英共做了12 朵工艺花. 小玲做了7朵. 小英做了几朵？奶奶家养了 11只兔子 .送人 4 只.家里还剩几只？湖边有 15 只船.同学们划走了 6 只.还剩几只小船？把一根木头锯成 3 段. 如果每锯一次用 3分钟. 同共要锯多少分钟？树上有 12 只小鸟 . 第一次飞走了 3 只. 第二次飞走了 2只. 一共飞走了几只？弟弟今年 4岁.哥哥今年 12 岁.10 年后.哥哥比弟弟大几岁？小亮昨天做了 6道题. 今天做了同样多的题 .小明两天做了 8道题.小亮两天做了题比小明多几道？ 咪咪家有 14 个香蕉 . 吃了 6个. 还剩几个？河边有 16 只鸭子 . 游走了几只后 .还剩下 7 只.游走了几只？停车场有 15 辆汽车 . 开走了 7 辆. 还剩几辆？ 体操队有 16个同学 .其中女同学有 8个.男同学有几个？ 一个小队 17 人排成一排 . 一、二报数 . 报二的人向后退两步 . 留在原地的还有多少人？ 小丽家有 20 条红金鱼 . 还有 8 条地图鱼 . 小丽家共有多少条鱼？ 饲养场有 40 匹白马和 9 匹花马 . 饲养场共有多少匹马？ 我们饲养场有 40只小兔和 20 只大兔.共有多少只兔子？ 商店第一天卖出 50件衣服 .第二天上午卖出 40件. 下午卖出 50件. 第二天共卖出多少件？ 一根绳子 . 剪去 40 米. 还剩 30 米. 这根绳子有多长？ 学校买来 20 盒彩色粉笔 .80 盒白粉笔 . 学校共买来粉笔多少盒？ 一根绳子长 100米.剪去 50 米.还剩多少米？ 体育室有 20 个篮球 .15 个足球 .8 个排球 .借走了 6 个足球后 .还剩几个足球？ 一个玩具狗要 30元. 我给了营业员 50元.应找回多少钱？ 青蛙捉了 16 只虫子 . 吃了 8只. 还剩几只？ 班里的图书角原有图书 40 本. 借出 15 本. 还剩多少本？23、24、25、26、27、28、29、30、31、32、33、34、35、36、37、38、39、40、41、42、43、44、45、小明买一件上衣用30 元.买一条裤子用35元. 这套衣服共花多少元？46、小玲看一本连环画. 已经看了20 页. 还有45 页没看.这本连环画共有多少页？47、赵丽两天看了30页书.第一天看了9页.第二天看了多少页？48、大树上有12 只小鸟. 飞走了 4 只. 还有几只？49、妈妈买回一些草莓.李英吃了一半后. 还剩下30个. 妈妈买回多少个草莓？50、学校原有20 棵柳树. 又种了35 棵杨树. 现在共有多少棵树？51、草地上有9 头大牛.18 头小牛. 大牛比小牛少多少头？52、饲养组养了40只乌鸡.25 只花鸡.卖掉20 只后.还剩多少只？53、二年一班有男生26人.女生20人. 男生比女生多多少人？54、二年一班有男生26人.女生20人. 男、女生共有多少人？55、小华有一本95页的故事书.已经看了40 页.还有多少页没看？56、修一条公路. 工人叔叔第一天修50 米. 第二天修40 米. 两天一共修多少米？57、篮子里有35 个鸡蛋. 吃了一些后.还剩10 个.吃了多少个鸡蛋？58、水果超市有30箱苹果.20 箱水晶梨. 水果超市共有水果多少箱？59、李丽看一本童话书.上午看了25 页.下午比上午多年看了10页.下午看了多少页？60、动物园里有25只大猴子.10 只小猴子. 大猴子比小猴子多多少只？61、李奶奶家养了46只鸡.其中6只是公鸡.其余是母鸡.母鸡有多少只？62、校图书室有故事书100 本. 科技书80 本. 故事书比科技书多多少本？63、体育组有22 个排球. 有33 个足球. 体育组共有多少个球？64、二年级女生人数比男生少9人.男生有29 人.女生有多少人？65、动物园的猴山上有大猴12只. 小猴比大猴少3只.小猴有多少只？66、湖里有天鹅65只. 野鸭比天鹅少20只.野鸭有多少只？67、菜店里有12 筐黄瓜. 黄瓜比西红柿少10 筐. 西红柿有多少筐？68、服装超市上午卖出25 套西装. 下午比上午多卖出20套. 下午卖出多少套？69、学校原来有9 台闭路电视. 又买来8台. 现在共有闭路电视多少台？70、丽丽和妈妈共包了20 个饺子. 其中丽丽包了 5 个. 妈妈包了多少个？71、幼儿园有35 个皮球. 分给大班20 个. 其余的给中班. 中班分到多少个皮球？72、广场上原有30只鸽子.又飞来25只. 现在广场上共有多少只鸽子？73、步步家养了12只鸡. 卖掉一些后.还剩下4只.卖了多少只？74、生态保护区内原有10 只东北虎. 后又运来15只华南虎. 现在保护区内共有老虎多少只？75、学校开联欢会.准备安装45串彩灯.已经安装了30串.还有多少串没安装好？76、小芳上午写了9个生字.下午写了6个.今天小芳共写了多少生字？77、图收馆上午借出15 本书. 下午借出的比上午少 5 本. 下午借出多少本书？78、草地上有8只羊.又跑来了4只. 现在草地上有多少羊？79、草地上有8只羊.跑来了5只鸭和6头牛.现在草地上共有羊鸭、牛多少？80、河里有14 只鸭子. 游走了3只. 还有几只？81、草地上有17只羊. 跑了6只.又来了5只.现在草地上有几只羊？82、小明有17 支铅笔. 用了7 支. 又买来 5 支. 现在小明有几支铅笔？83、停车场有20辆汽车. 开走了8 辆.又开来了3辆. 现在停车场有几辆汽车？84、停车场上有13辆汽车.开走几辆后.还剩8辆. 开走几辆？85、学校有白粉笔50盒. 彩色粉笔20盒.白粉笔比彩色粉笔多多少盒？86、小华有8 块奶糖.12 块水果糖. 小华一共有多少块糖？87、体育组有15 个跳球.8 个篮球. 篮球比足球少多少个？88、妈妈买回一些巧克力. 小明吃了3块. 还剩9块.妈妈共买回多少块巧克力？89、农场的果园种梨树54 棵. 桃树比梨树多20 棵. 桃树有多少棵？90、车站有公交车18辆. 长途汽车比公交车多10辆. 长途汽车有多少辆？91、学校春季种树比秋季多种15棵. 秋季种树50棵. 春季种多少棵？92、少年宫的舞蹈组有24 人. 航模组比舞蹈组多10 人. 航模组有多少人？93、三年一班男生有28人.女生有25人. 女生比男生少多少人？94、水果店运来一批苹果. 卖出3筐. 还剩9 筐.水果店远来多少筐苹果？95、机场停了12 架飞机. 飞走了 5 架. 还剩几架？96、学校原来有30 棵树. 又种了20 棵. 又种的树比原来的少多少棵？97、妈妈拿来 4 个梨和12 个苹果. 梨的个数比苹果少多少个？98、赵明今年8岁.他姐姐15岁. 姐弟两人相差几岁？99、车站有货车15辆. 客车比货车少6辆. 客车有多少辆？100、书架上有些书. 芳芳拿走了 6 本. 剩下的比拿走的多6本. 书架上原有书多少本？101、树上原来12 只小鸟. 飞走 4 只. 又飞来 6 只. 树上现在有多少只小鸟？102、树上有8 只小鸟. 飞来 5 只. 又飞走 6 只. 现在树上有几只小鸟？103、校园里有12 盆月季花. 牡丹花比月季花少4盆. 牡丹花有几盆？104、爸爸买来15 个香蕉. 全家人吃了7 个. 还剩几个？剩下的比吃了的多几个？105、李丽走进教室. 看见教室里只有10名同学. 那么现在教室里有几名同学？106、小青蛙捉了11只虫子. 吃了4只后.又捉了20只. 现在共捉多少只虫子？107、奶奶家有20 只鸡.其中公鸡有4只. 剩下的是母鸡.母鸡比公鸡多多少只？108、学校体育组有篮球20 个. 足球比篮球多15个. 足球有多少个？两种球共有多少个？109、班里有各种彩色气球20个. 其中8个是花气球. 剩下的是红气球.红气球有多少个？110、小红买了一本故事书.她第一天看了20 页.第二天看了30 页.第二天比第一天多看多少页？111、百货店购进20箱毛巾.卖出9箱.还剩几箱？剩下的比卖出的多几箱？112、湖边有16只天鹅.飞走8只后.又飞来9只.现在湖边共有多少只天鹅？113、娜娜买一本练习本 5 角.买一块橡皮 5 角.一共花了多少钱？114、妈妈买香蕉用去6元钱.钱包里还有14 元.妈妈钱包里共有多少钱？115、弟弟花 1 元钱买了一个小皮球. 哥哥花 6 元钱买了一个铅笔盒. 哥哥比弟弟多花了多少钱？116、奶奶买肉用去9元. 又买了10元的苹果.付给售货员20元钱. 应找回多少钱？117、妈妈买了一个暖水瓶.她付给售货员20元钱.找回4元.这个暖水瓶多少钱？118、爸爸给小明花65 元买了一个足球.他付给收银员100 元. 应找回多少元？119、商店有25个足球.又进来40 个.今天卖出5个.现在还剩下多少个？120、钢厂计划投资20 万元建厂房.因节约的原因.实际只用了17万元. 为厂里节省多少万元？121、妈妈买苹果用去8元钱.给我买一个书包用去50元. 妈妈应付给营业员多少钱？122、小英买了 4 个练习本用去 1 元 2 角. 还剩8角钱. 小英原来有多少钱？123、图书借出30 本书后. 还剩25 本. 图书角原来有多少本？124、停车场有小汽车9辆.大汽车16辆. 大汽车比小汽车多几辆？125、停车场有大小汽车18 辆. 开走9 辆后. 又有 3 辆开来. 停车场现有汽车多少辆？126、小刚体重38千克.比小华重10 千克.小强比小华重5千克.小强有多重？127、赵明家有两种热带钱共15条.其中地图鱼有7 条. 另一种鱼有几条？128、公园里有柏树40 棵. 柳树60 棵。

1.2 等差数列（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．在等差数列{}n a 中，若25=a ，43=a ，则6=aA. －1B. 0C. 1D. 6 【答案】C【解析】（解法一）因为25a =，43=a ，有2642+=a a a ，得6a =1，故选C ．（解法二）因为25a =，43=a ，所以2224-=-=a a d ，6421a a d ∴=+=，故选C ． 2．在等差数列{}n a 中，若34830a a a ++=，则19a a +=A ．15B ．20C ．25D ．30 【答案】B【解析】由34830a a a ++=，得5330a =，则195220a a a +==，故选B ． 3．等差数列{}n a 的前m 项和为30，前m 2项和为100，则它的前m 3项和为A ．130B ．170C ．210D ．260 【答案】C【解析】（解法一）m m m m m S S S S S 232--，， ，即10070 303-m S ，，成等差，1101003=-∴m S ，2103=∴m S ．故选C ．（解法二）特值法：取1=m 则100,3021211=+===a a S a S ，702=∴a ，1103=∴a ， 2103213=++=∴a a a S ．故选C ．4．设{}n a 是等差数列，则下列结论中正确的是A ．若021>+a a ，则032>+a aB ．若031<+a a ，则021<+a aC ．若210a a <<，则312a a a >D ．若01<a ，则0))((3212>--a a a a 【答案】C【解析】反例 A ： 2，-1，-4 B ：2，-1，-4 D:-3，-2，-1 或 02>-d 不成立．C ：210a a << ，3210a a a <<<∴，313122a a a a a >+=∴．故选C ．5．在等差数列{}n a 中，135105a a a ++=，24699a a a ++=，以n S 表示{}n a 的前n 项和， 则使n S 达到最大值的n 是A ．21B ．20C ．19D ．18 【答案】B【解析】（解法一） 135105a a a ++=，24699a a a ++=，∴335a =,433a =， ∴432d a a =-=-， ∴139a =，∴2240(20)400n S n n n =-+=--+， ∴当20n =时n S 取最大值20．故选B ．（解法二） 135105a a a ++=，24699a a a ++=，两式相减得：63=-d ，2-=∴d ． 又13533105a a a a ++==，335a ∴=，3(3)241n a a n d n ∴=+-=-+． 令0n a >,得412n <,∴当20n =时n S 取最大值20．故选B ． 6．数列{}n a 的首项为3，{}n b 为等差数列且n n n a a b -=+1．若23-=b ，1210=b ，则=8a A ．0 B ．3 C ．8 D ．11 【答案】B【解析】d b b 7310=- 且23-=b ，1210=b ,2=∴d,82622)3(3-=-+-=-+=∴n n d n b b n ,821-=-∴+n a a n n ,)()(.....)()(7867231218a a a a a a a a a a -+-++-+-+=∴36420)2()4()6(3=++++-+-+-+=．故选B ．二、填空题7．记n S 为等差数列{}n a 的前n 项和，10a ≠，213a a =，则105S S =___________． 【答案】4【解析】因为213a a =，所以113a d a +=，即12a d =，所以105S S =11111091010024542552a d a a a d⨯+==⨯+．8．已知n S 是等差数列{}n a 的前n 项和，且27S S =,6k S S =（6k ≠），则k = ．【答案】3【解析】（解法一）由27S S =,得1176272a d a d ⨯+=+, 所以14a d =-． 因为6k S S =，所以()11165622k k a d ka d -⨯+=+，所以()1241542k k d d kd d --+=-+，整理得，29180k k -+=，解得3k =，或6k =（舍去）． （解法二）因为()2111)222n n n d dS na d n a n -=+=--(， 所以对应的函数()21()22d df x x a x =--的图象是一条抛物线，因为27S S =， 所以()fx 的图象关于27922x +==对称． 又因为6k S S =，所以6922k +=，解得3k =． 9．已知}{n a 为等差数列，n S 表示}{n a 的前n 项和，}{n a 满足4560a a a ++>，100S <， 则n S 取得最大值时n 的取值为：___________． 【答案】5【解析】因为0)(510110<+=a a S ，所以065101<+=+a a a a ，又456530a a a a ++=>， 即05>a ， 所以06<a ，所以当5=n 时，n S 取得最大值．10．已知数列{}n a 的首项为1，其余各项为1或2，且在第k 个1和第1+k 个1之间有12-k 个2，即数列{}n a 为：1，2，1，2，2，2，1，2，2，2，2，2，1，…，记数列{}n a 的 前n 项和为n S ，则2019S =__________．（用数字作答） 【答案】3993【解析】（解法一）第1k +个1为数列{}n a 的第21(13521)1k k k k ++++++-=++项当44k =时211981k k ++=；当45k =时212071k k ++=； 所以前2019项有45个1和244(20191981)+-个2，所以22019452[44(20191981)]3993S =+⨯+-=．（解法二）把该数列排成如下格式 1，2 1，2，2，2 1，2，2，2，2，2 1，2，2，2，2，2，2，2 …设其前m 行共有m T 项，则)1(2642+=+⋯⋯+++=m m m T m , 令2019)1(≤+m m 则44≤m 又1980454444=⨯=T , 即前44行共有1980项，其中有44个1，1936441980=-个2,所以第2019项为第45行第3919802019=-项（其中有1个1，38个2）, 即前2019项共有45144=+个1，1974381936=+个2, 所以2019451197423993S =⨯+⨯=．三、解答题：解答应写出文字说明，证明过程或演算步骤．11．记n S 为数列{}n a 的前n 项和，已知0n a >，213a a =，且数列是等差数列，证明：{}n a 是等差数列．【解析】因为数列是等差数列，设公差为d ===(n -=，()n *∈N ，所以12n S a n =，()n *∈N所以当2n ≥时，()221111112n n n a S S a n a n a n a -=-=--=-， 当1n =时，11121=a a a ⨯-，满足112n a a n a =-，所以{}n a 的通项公式为112n a a n a =-，()n *∈N所以()()111111221=2n n a a a n a a n a a --=----⎡⎤⎣⎦，所以{}n a 是等差数列． 12．已知数列{}n a 的前n 项和为n S ，11=a ，0≠n a ，11-λ=+n n n S a a ，其中为常数，（I ）证明：λ=-+n n a a 2；（II ）是否存在λ，使得{}n a 为等差数列？并说明理由．【解析】（I ）11-λ=+n n n S a a ， 1121-λ=∴+++n n n S a a ，1121++++λ=-∴n n n n n a a a a a ， 又01≠+n a ， λ=-∴+n n a a 2．（II ）由（I ）可知：{}n a 的奇数项和偶数项均为等差数列． 若{}n a 为等差数列，则122++=+n n n a a a ，又λ=-+n n a a 2，λ+=∴++1222n n a a ，即212λ=-++n n a a ． 由11=a ，11-λ=+n n n S a a ，可得:12-λ=a ,13+λ=a ．3122a a a += ，即11)1(2+λ+=-λ，解得4=λ，212=-∴a a ，又2212=λ=-++n n a a ， ∴当4=λ时，{}n a 是以2为公差的等差数列．1．3 等比数列（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．等比数列t ，33+t ，66+t ，…的第四项等于A ．24-B ．0C ．12D ．24 【答案】A【解析】（解法一）23366=++=t t q ， t t 233=+∴，3-=∴t ， ∴第四项为：24233-=⨯-．故选A ．（解法二）依题意：)66()33(2+=+t t t ，091232=++∴t t ，即0)1)(3(32=++t t ，3-=∴t 或1-=t （舍去），所以该等比数列各项依次为：3-，6-，12-，24-． 即第四项为：24233-=⨯-．故选A ．2．我国古代数学著作（算法统宗》中有这样一个问题（意为）：“有一个人要走378里路， 第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了6天后到达目 的地．”那么，此人第4天和第5天共走路程是A ． 24里B ． 36里C ． 48里D ． 60里 【答案】B【解析】记每天走的路程里数为{}n a ，可知{}n a 是公比12q =的等比数列． 由6378S =，得16611)2378112(a S -==-，解得：1192a =，344511192()192()24123622a a ∴+=⨯+⨯=+=，所以此人第4天和第5天共走了241236+=里．故选B ． 3．已知正项等比数列{}n a 的前n 项和为n S ，已知374S =，6634S =，则=8a A ．8 B ．16 C ．32 D ． 64 【答案】C【解析】设等比数列{}n a 的公比为q )0(>q ，显然1≠q ，则有：⎪⎪⎩⎪⎪⎨⎧=--==--=4631)1(471)1(616313q q a S q q a S ，两式相除可得：91136=--q q ，即911)1)(1(3333=+=-+-q q q q ，2=∴q ，411=∴a ，3224178=⨯=∴a ．故选C ． 4．已知等比数列{}n a 中，各项都是正数，且1a ，312a ，22a 成等差数列，则91078a a a a +=+A．3+ B．1 C．1+ D．3- 【答案】A【解析】 1321,,22a a a 成等差数列，3122a a a ∴=+，∴2210q q --=，解得1q =± 又0>n a ，0>∴q，1q ∴=+∴2910783a a q a a +==++A ． 5．已知正项等比数列{}n a 的前n 项和为n S ，11=a ，且3a -，2a ，4a 成等差数列，则2021S与2021a 的关系是A. 2021202141S a =+ B ．2021202143S a =- C ．2021202121S a =- D ．2021202121S a =+ 【答案】C【解析】设等比数列的公比为)0(>q q ，由423,,a a a -成等差数列，得4322a a a +-=，又11=a ， 322q q q +-=∴， 即022=--q q ，0)1)(2(=+-∴q q ．又0>q ，2=∴q ，202020212=∴a ，122121202120212021-=--=S ，2021202121S a ∴=-．故选C ． 6．正项等比数列{}n a 中，463718+=a a a a ，则31323339log log log log ++++a a a a =A ．4B ．5C ．8D ．9 【答案】D【解析】因为246375218+==a a a a a 且{}n a 各项均为正数， ∴53=a ．所以()3132333931289log log log log log a a a a a a a a ++++=()()()()()423192837465355log log a a a a a a a a a a a ⎡⎤=⋅⋅⋅⋅=⋅⎡⎤⎣⎦⎢⎥⎣⎦99353log log 39a ===． 故选D ． 二、填空题7．等比数列{}n a 的前n 项和22nn S a a =⋅+-，则=a ________．【答案】1【解析】因为11()2211n n n a aS q a a q q=+-=⋅+---，所以20a a +-=，解得1a =． 8．记n S 为等比数列{}n a 的前n 项和．若24S =，46S =，则6S = ． 【答案】7【解析】因为n S 为等比数列{}n a 的前n 项和，所以2S ，42S S -，64S S -成等比数列， 所以24S =，42642S S -=-=，所以641S S -=，所以641167S S =+=+=． 9．已知{}n a 为等比数列，且334,12a S ==，则=q ． 【答案】1=q 或21-=q 【解析】（解法一）当1=q 时，31333a a S ==，显然1=q 符合题意；当1≠q 时，4213==q a a 214qa =∴．又12)1(1)1(21313=++=--=q q a q q a S ， 解得 21-=q ．∴综上可得：1=q 或21-=q ． （解法二）4213==q a a ，214q a =∴．又123113=++=a q a a S ， 可得：84422=+q q q ，即0122=--q q ，0)1)(12(=-+∴q q ，21-=∴q 或1=q ． 10．设等比数列{}n a 满足13+=10a a ，24+=5a a ，则123n a a a a ⋅⋅⋅⋅⋅的最大值为_________． 【答案】64【解析】设等比数列的公比为q ，由1324105a a a a +=+=⎧⎨⎩得，2121(1)10(1)5a q a q q +=+=⎧⎨⎩，解得1812a q =⎧⎪⎨=⎪⎩． 所以2(1)1712(1)22212118()22n n n n n n nn a a a a q--++++-==⨯=， 于是当3n =或4时，12n a a a 取得最大值6264=．三、解答题：解答应写出文字说明，证明过程或演算步骤． 11．设等比数列{}n a 满足124a a +=，318a a -=．（1）求{}n a 的通项公式；（2）记n S 为数列{}3log n a 的前n 项和．若13m m m S S S +++=，求m ． 【答案】（1）13n n a -=；（2）6m =．【解析】（1）设等比数列{}n a 的公比为q ，则1121148a a q a q a +=⎧⎨-=⎩，解得113a q =⎧⎨=⎩，所以13n n a -=． （2）令313log log 31n n n b a n -===-，所以(01)(1)22n n n n n S +--==，根据13m m m S S S +++=，可得(1)(1)(2)(3)222m m m m m m -++++=， 整理得2560m m --=，因为0m >，所以6m =． 12．已知为数列{}n a 的前项和，11=a ，241+=+n n a S ．（1）设数列{}n b 中，n n n a a b 21-=+，求证：{}n b 是等比数列； （2）求数列{}n a 的通项公式及前n 项和．【答案】（1）证明详见解析；（2）22)43(1+-=-n n n S ．【解析】（1）（解法一）241+=+n n a S ， 2,241≥+=∴-n a S n n 两式相减可得：1144-+-=n n n a a a ，)2(2211-+-=-∴n n n n a a a a ，即2,21≥=-n b b n n ， ∴{}n b 是以2为公比的等比数列．（解法二）241+=+n n a S ，2,241≥+=∴-n a S n n 两式相减可得：1144-+-=n n n a a a ，22422244221111111=--=---=--=∴-----+-n n n n n n n n n n n n n n n a a a a a a a a a a a a a b b ，2≥n ， ∴{}n b 是以2为公比的等比数列．（2）241212+=+=a a a S 且11=a ，52=∴a ，32121=-=∴a a b ，11232-+⨯=-=∴n n n n a a b ，432211=-∴++n n n n a a ， ⎭⎬⎫⎩⎨⎧∴n n a 2是以2121=a 为首项，以43为公差的等差数列， )13(41)1(43212-=-+=∴n n a n n ，22)13(--=∴n n n a ． 当2≥n 时，312)43(---=n n n a ，∴241+=-n n a S 22)43(1+-=-n n ，又111==a S 符合上式，∴数列{}n a 的通项公式及前n 项和22)43(1+-=-n n n S ．n2.1 直线的斜率（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．下列命题中正确的是A ．若两直线的倾斜角相等，则它们的斜率也一定相等B ．若两直线的斜率相等，则它们的倾斜角也一定相等C ．若两直线的倾斜角不相等，则它们中倾斜角越大的，斜率也越大D ．若两直线的斜率不相等，则它们中斜率越大的，倾斜角也越大 【答案】B【解析】当倾斜角都为2π时，斜率都不存在，所以A 项不正确； 钝角的正切是负值，锐角的正切是正值，不是角越大斜率越大，所以C 、D 都不正确； 因为直线的斜率确定，则倾斜角就确定了，直线的斜率相等，倾斜角一定相等，故选B ． 2．若图中的直线123l l l ，，的斜率分别为123k k k ，，，则A ．123k k k <<B ．312k k k <<C ．321k k k <<D ．132k k k << 【答案】D【解析】直线1l 的倾斜角α是钝角，故10k <．直线2l 与3l 的倾斜角β与γ均为锐角，且<γβ，所以320k k <<，因此132k k k <<．故选D ．3．已知直线过)4 2(，A ，)1(mB ，两点，且倾斜角为 45，则=m A ．0 B ．2C ．3D ．5 【答案】C【解析】因为直线过)4 2(，A ，)1(m B ，两点，所以直线的斜率为m m -=--4214， 又直线的倾斜角为 45，所以直线的斜率为145tan =，即14=-m ，所以3=m ．故选C ．4．已知三点)1 2(-，A ，)3 4(，B ，) 5(kC ，在同一条直线上，则k 的值为 A ．4 B ．5 C ．6D ．7 【答案】B【解析】因为)1 2(-，A ，)3 4(，B ，) 5(k C ，三点共线，所以BC AB k k =，即45324)1(3--=---k ， 解得5=k ．故选B ．5．直线02sin =++⋅y x α的倾斜角的范围是A ．)0[π，B ．]40[π，C ．)43[]40[πππ，， D ．)2[]4 0[πππ，， 【答案】C【解析】因为02sin =++⋅y x α，可化为2sin -⋅-=x y α，所以直线的斜率为αsin -． 设直线的倾斜角为θ，则有]1 1[sin tan ，-∈-=αθ， 又)0[πθ，∈，所以)43[]40[πππθ，， ∈．故选C ． 6．直线l 过点)0,1(P ，且与以)1,2(-A ，)3,0(B 为端点的线段有公共点，则直线l 斜率 的取值范围是A ．]31,3[--B ．]3,31[ C ．),31[]3,(+∞---∞ D ．),3[]31,(+∞-∞ 【答案】A【解析】如图，311201-=---=AP k ，31003-=--=BP k所以]31,3[--∈k ．故选A ． 二、填空题7．直线2-=x y 的倾斜角的大小为_______． 【答案】4π 【解析】由一次函数的图像及直线的斜率公式可知，直线2-=x y 的斜率为1， 设倾斜角为θ，则)0[πθ，∈，由1 tan =θ可得4πθ=．8． 直线l 经过点)1,3(A ，),2(2m B -，R m ∈两点，则直线l 的倾斜角α的取值范围是______． 【答案】)2,4[ππ【解析】直线l 的斜率1123122≥+=-+=m m k ，即1tan ≥α，又),0[πα∈，所以)2,4[ππα∈． 9．直线l 过点)0,1(P ，且与以)1,2(A ，)3,0(B 为端点的线段有公共点，则直线l 斜率的取值范围为________． 【答案】),1[]3,(+∞--∞ 【解析】如图，11201=--=AP k ，31003-=--=BP k ， 所以),1[]3,(+∞--∞∈ k ．10．已知0>ab ，且)0 (，a A ，) 0(b B ，，)2 2(--，C 三点共线，则ab 的最小值为________． 【答案】16【解析】因为)0 (，a A ，) 0(b B ，，)2 2(--，C 三点共线，所以BC AC k k =， 所以)2(0)2()2()2(0----=----b a ，即2222+=+b a ，所以)(2b a ab +-=． 又因为0>ab ，故0<a ，0<b ，所以ab b a b a ab 4)]()[(2)(2≥-+-=+-=． 从而0≤ab (舍去)或4≥ab ，故16≥ab ，当且仅当4-==b a 时取等号， 即ab 的最小值为16．三、解答题：解答应写出文字说明，证明过程或演算步骤．11．a 为何值时，过点(2,3)A a ，(2,1)B -的直线的倾斜角是锐角？是钝角？是直角？ 【答案】当1a >时，直线的倾斜角为锐角；当1a <时，直线的倾斜角为钝角；当1a =时，直线的倾斜角为直角.．【解析】当22a =，即1a =时，直线AB 的斜率不存在，直线的倾斜角为直角． 当1a ≠时，132221AB k a a --==--，若直线的倾斜角α是锐角，则2tan 01AB k a α==>-，即10a ->，得1a >； 若直线的倾斜角α是钝角，则2tan 01AB k a α==<-，即10a -<，得1a <． 综上，当1a >时，直线的倾斜角为锐角；当1a <时，直线的倾斜角为钝角； 当1a =时，直线的倾斜角为直角．12．在平面直角坐标系内，)32 1(，A ，)3 4(，B ． （1）求直线AB 的倾斜角θ的值；（2）若一束光线通过点A ，经x 轴反射，反射光线通过点B ，求入射光线与x 轴的交点P 的坐标．【答案】（1）65πθ=； （2） )0 3(，【解析】（1）因为)32 1(，A ，)3 4(，B ，所以直线AB 的斜率为3314323-=--=AB k ．又)0[πθ，∈，所以65πθ=． （2）依题意，有BPx APO ∠=∠，即直线AP 与直线BP 的倾斜角互补，所以BP AP k k -=． 设)0 (，a P ，则4301320---=--a a ，解得3=a ，即点P 的坐标为)0 3(，．13．如图，在矩形ABCD 中，2BC AB =，直线AC 的斜率为1，求直线BC 的斜率．【答案】3【解析】由题意，在Rt ABC ∆中，2ABC π∠=，2BC AB =，所以1tan 2AB ACB BC ∠==． 设直线AC 的倾斜角为θ，则tan 1θ=， 且直线BC 的倾斜角为ACB θ+∠， 所以tan()BC k ACB θ=+∠11tan tan 2311tan tan 112ACB ACB θθ++∠===-∠-⨯．2.2 直线的方程（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知直线022:=--y x l 的方向向量可以是A ．)2 1(-，B ．)2 1(，C ．)1 2(，-D ．)1 2(， 【答案】D【解析】（解法一）因为022=--y x ，可化为121-=x y ，所以直线l 的斜率为21， 所以直线l 所有的方向向量为)211(，λ，其中λ是不为零的任意实数， 又)1 2(，)21 1(2，=，所以)1 2(，是直线l 的一个方向向量．故选D ． （解法二）由0=++C By Ax 的一个方向向量为) (A B -，， 可知直线022=--y x 的一个方向向量为)1 2(--，， 又)1 2(，)1 2(---=，，所以)1 2(，是直线l 的一个方向向量．故选D ． 2．已知直线0=++c by ax 经过第一、第二、第四象限，则a ，b ，c 应满足A ．0>ab ，0<bcB ．0>ab ，0>bcC ．0<ab ，0>bcD ．0<ab ，0<bc 【答案】A【解析】由于直线0=++c by ax 经过第一、二、四象限， 所以直线存在斜率，将方程变形为bc x b a y --=， 如图，易知0<-b a 且0>-bc，故0>ab ，0<bc ．故选A ． 3．已知直线l 的一个法向量为)2 1(-，，且经过点)4 1(，，则直线l 的方程为 A ．092=-+y x B ．012=++y x C ．072=+-y x D ．012=--y x 【答案】C【解析】因为直线l 的法向量为)2 1(-，，可设直线的方程为02=+-C y x ． 又直线l 经过点)4 1(，，所以081=+-C ，即7=C ， 所以直线l 的方程为072=+-y x ．故选C ．4．如图，直线0:1=+-n y mx l 和0:2=+-m y nx l 在同一坐标系中正确的图形可能为A B C D 【答案】B【解析】0:1=+-n y mx l 和0:2=+-m y nx l 可分别化为n mx y +=和m nx y +=． 当00>>n m ，时，直线1l 和2l 的斜率都大于零，纵截距也都大于零，四个选项均不满足； 当0<mn 时，直线1l 和2l ，有一条直线的斜率大于零，纵截距小于零，而另一条直线的斜率小于零，纵截距大于零，选项B 满足；当00<<n m ，时，直线1l 和2l 的斜率都小于零，纵截距也都小于零，四个选项均不满足； 当0=mn 时，直线1l 和2l 至少一条经过原点，四个选项均不满足．故选B ． 5．直线l 经过点)4,3(，且与两坐标轴围成一个等腰直角三角形，则直线l 的方程为 A ．07=-+y x B ．01=--y xC ．07=-+y x 或01=+-y xD ．07=-+y x 或01=--y x 【答案】C【解析】设直线l 的方程为:1=+b y a x ，因为直线l 过点)4,3(，所以有143=+ba ． 因为直线l 与两坐标轴围成一个等腰直角三角形，所以b a =，即b a ±=． 当b a =时，有143=+aa ，故7==b a ； 当b a -=时，有143=-aa ，故1,1=-=b a ． 所以直线l 的方程为:177=+yx 或1=+-y x ，即07=-+y x 或01=+-y x ．故选C ． 6．已知直线1l ：422-=-a y ax ，2l ：42222+=+a y a x ，若20<<a 时，直线1l ，2l 与两坐标轴围成一个四边形，当四边形的面积最小时，实数=a A ．1- B ．21C ．1D ．2 【答案】B【解析】直线1l 可写成)2(22-=-x a y ，直线2l 可写成)2(222--=-x ay ，所以直线1l ，2l 恒过定点)2 2(，P ，直线1l 的纵截距为a -2，直线2l 的横截距为22+a ，又20<<a ，所以四边形的面积222111152(2)2(2)4()2224S a a a a a =⨯⨯-+⨯⨯+=-+=-+， 故当21=a 时，四边形的面积最小．故选B ． 二、填空题7．若直线过点)1 3(，和点)4 32(，，则该直线的方程为 ． 【答案】023=--y x【解析】（解法一）因为直线过点)1 3(，和点)4 32(，，所以直线的方程为0)1)(332()3)(14(=-----y x ，整理得；023=--y x ．（解法二）因为直线过)1 3(，和点)4 32(，，所以直线的斜率为333214=--=k ，所以直线的方程为)3(31-=-x y ，整理得023=--y x ．8．已知直线0322=-+-m my x ，当m 变化时，直线都通过定点 ．【答案】)3 1(--， 【解析】（解法一）当0≠m 时，0322=-+-m my x ，可化为)1(23+=+x my ， 即))1((2)3(--=--x my ，所以直线过定点)3 1(--，． 又当0=m 时，0322=-+-m my x ，可化为1-=x ，也过点)3 1(--，． 综上所述，当m 变化时，直线0322=-+-m my x 都通过定点)3 1(--，． （解法二）0322=-+-m my x 可化为)1(2)3(+=+x y m ,令03=+y ，得13-=-=x y ，，所以直线过定点)3 1(--，．9．已知直线l 经过点)3,1(--A ，且倾斜角等于直线x y 3=的倾斜角的2倍，则直线l 的方 程为 ． 【答案】01543=++y x【解析】设直线l 倾斜角为α，直线x y 3=的倾斜角为θ，则θα2=． 又因为直线x y 3=的斜率为3，即3tan =θ，所以直线l 的斜率为43tan 1tan 22tan tan 2-=-===θθθαk ． 又直线l 过点)3,1(--A ，所以其方程为：)1(433+-=+x y ，即01543=++y x ． 10．已知过点)2 2(，-P 的直线l 在第二象限与两坐标轴围成一个三角形，当该三角形的面积最小时直线l 的方程为 ． 【答案】04 =+-y x【解析】显然，直线l 的斜率存在且大于零，设直线l 的方程为)2 (2+=-x k y ，0>k ， 令0=x 得，22+=k y ；令0=y 得，)22(+-=kx ； 所以三角形的面积为8224)22)(22(21)22(2221≥++=++=+-+=k kk k k k S ， 当且仅当k k22=，即1=k 时取等．故三角形的面积的最小值为8． 此时直线l 的方程为2 2+=-x y ，即04 =+-y x ． 三、解答题：解答应写出文字说明，证明过程或演算步骤． 11．已知直线l 过点)2 3(，P ．（1）若直线l 在两坐标轴上的截距互为相反数，求直线l 的方程；（2）若直线l 分别交x 轴的正半轴和y 轴的正半轴于A 、B 两点，当OAB ∆的面积为12时求直线l 的方程．【答案】（1）032=-y x 或01=--y x ；（2）01232=-+y x ．【解析】（1）设若直线l 在x 轴和y 轴上的截距分别为a ，b 当0=-=b a 时，直线l 过原点，斜率为320302=--， 所以直线l 的方程为x y 32=，即032=-y x ； 当0≠-=b a 时，直线l 的方程为1=+b y a x ．又直线l 过点)2 3(，P ，所以123=+ba ． 因为b a -=，所以123=-aa ，故1=a ，1-=b ． 所以直线l 的方程为1=-y x ，即01=--y x ； 综上，直线l 的方程为032=-y x 或01=--y x ． （2）设直线l 的方程为)3(2-=-x k y ，0<k ， 令0=x 得，k y 32-=；令0=y 得，kx 23-=；因为直线l 与x 轴和y 轴交于正半轴，所以032>-k ，023>-k， 所以OAB ∆的面积12)23)(32(21=--=k k S ，解得32-=k ． 所以直线l 的方程为)3(322--=-x y ，即01232=-+y x ． 12．过点)1 2(，P 作直线l 分别交x 轴的正半轴和y 轴的正半轴于A 、B 两点． （1）求的最小值及此时直线l 的方程； （2）求最小值及此时直线l 的方程． 【解析】（1）根据题意可设直线l 的方程为，则， 直线l 过点，， 又(当且仅当，即时取等号)， ，即， 的最小值为8，此时直线l 的方程为；（2）由（1）可知，，则，(当且仅当，即时取等号)． 的最小值为4，此时直线l 的方程为．||||OA OB ⋅||||PA PB ⋅1(0,0)x ya b a b+=>>(,0),(0,)A a Bb (2,1)P 211(0,0)a b a b∴+=>>21a b +≥21a b =4,2a b ==1∴≤8ab ≥||||=OA OB ab ∴⋅240x y +-=211a b +=02ab a ∴=>-2a>||||PA PB ∴⋅4≥=221(2)=(2)a a --3a =||||PA PB ∴⋅30x y +-=2.3 两条直线的位置关系（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．若直线()120x m y ++-=和直线240mx y ++=平行，则m 的值为 A ．1 B ．2- C ．1或2- D ．23- 【答案】A【解析】直线()120x m y ++-=和240mx y ++=平行，可得11224m m +-=≠， 得1m =．故选A ．2．已知0b >，直线2(1)20b x ay +++=与直线210x b y --=垂直，则ab 的最小值为 A ．1 B ．2 C ．22 D ．23 【答案】B【解析】由已知两直线垂直，得22(1)0b ab +-=，即221ab b =+，又0b >，所以12ab b b=+≥，当且仅当1b =时等号成立，所以ab 的最小值为2．故选B ． 3．若直线:3l y kx =-与直线30x y +-=的交点在第一象限，则直线l 的倾斜角α的取 值范围为A ．(0 )30，B ．(30 )90，C ．(90 )135，D ．(135 )180， 【答案】B【解析】（解法一）已知直线:3l y kx =-过定点(03) P -，， 直线30x y +-=与x 轴，y 轴分别交于(30) A ，，(03) B ，，如图． 又33PA k =，通过数形结合可得， 33k >，即3tan 3α>，故3090α<< ，选B ．（解法二）由330y kx x y ⎧=-⎪⎨+-=⎪⎩得交点坐标为3333,)1+1+k k k +-（，又交点在第一象限， 所以3301+3301+kk k⎧+>⎪⎪⎨-⎪>⎪⎩，解得33k > ，即3tan 3α>，故3090α<< ，选B ．4．已知0a >，若y a x =与y x a =+的图象有两个交点，则a 的取范围为A ．0a >B ．01a <<C ．1a >D ．1a ≥ 【答案】C【解析】y a x =表示关于y 轴对称的两条射线，y x a =+表示斜率为1，在y 轴上的截距为a 的直线，根据题意，画出大致图形，如下图，若y a x =与y x a =+的图象有两个交点，且0a >，则根据图形可知1a >．故选C ．5．若(2 3)P ，既是11()A a b ，，22()B a b ，的中点，又是直线111:130l a x b y +-=与直线 222:130l a x b y +-=的交点，则线段AB 的垂直平分线的方程是A ．23130x y +-=B ．32120x y +-=C ．2350x y -+=D ．320x y -= 【答案】D【解析】将P 点坐标代入12,l l 的方程得1123130a b +-=，2223130a b +-=，所以,A B 两点在直线23130x y +-=上，故23AB k =-，所以线段AB 的垂直平分线的斜率为32，又AB中点为(2 3)P ，，所以线段AB 的垂直平分线的方程是()3322y x -=-，即320x y -=． 故选D ．6．已知直线1:310l x y --=，2:250l x y +-=，3:30l x ay --=不能围成三角形，则 实数a 的取值不可能为 A ．1 B ．13C ．1-D ．2- 【答案】A【解析】因为直线1l 的斜率为3，直线2l 的斜率为12-，所以直线1l ，2l 一定相交， 由3125x y x y -=⎧⎨+=⎩解得交点坐标为：(1,2)．当0a =时，3l 与横轴垂直，方程为：3x =不经过点(1,2)，所以三条直线能构成三角形；当0a ≠时，3l 的斜率为：1a． 当1l 与3l 的斜率相等即13a =，时，13a =，此时这两直线平行，这三条直线不能三角形； 当2l 与3l 的斜率相等即112a =-时，2a =-，此时这两直线平行，这三条直线不能三角形； 当3l 过12,l l 交点(1,2)即1230a --=时，1a =-，此时三条直线不能构成三角形；故选A ． 二、填空题7．过点()4,2P －与直线370l x y --=：平行的直线方程为： ． 【答案】3140x y -+=【解析】设所求直线的方程是()307x y m m -+=≠-， 因为点()4,2P －在直线上， 所以()3420m ⨯-+－＝，解得14m =，即所求直线方程是3140x y -+=． 8．已知ABC ∆三条边所在的直线方程分别为02:=+-y x l AB ，022:=++y x l AC ，1:=x l BC ，则AC 边上的高所在直线方程为： ．【答案】012=+-y x 【解析】由201x y x -+=⎧⎨=⎩，解得点B 坐标为(1 3)，． 因为直线AC 的斜率为12-，所以AC 边上的高所在直线的斜率为2， 所以AC 边上的高所在直线的方程为)1(23-=-x y ，即012=+-y x ．9．直线:(21)(31)730l x y λλλ+++--=恒过定点，则该定点的坐标为： ． 【答案】(2 1)，【解析】（解法一）将(21)(31)730x y λλλ+++--=化成(237)(3)0x y x y λ+-++-=，要使直线恒过定点，必须237030x y x y +-=⎧⎨+-=⎩，解得21x y =⎧⎨=⎩，即直线l 恒过定点(2 1)，．（解法二）将(21)(31)730x y λλλ+++--=化成21733131y x λλλλ++=-+++，即212(21)13131y x λλλλ++=-++++，即211(2)31y x λλ+-=--+，所以直线l 恒过定点(2 1)，． 10．已知m R ∈，动直线110l x my +-=：过定点A ，动直线2:230l mx y m --+=过定点B ，若1l 与2l 交于点P （异于A ，B 两点），则PA PB +的最大值为： ．【答案】【解析】由题意可得()()1,0,2,3A B ，因为1(1)0m m ⨯+⨯-=， 所以直线10x my +-=和直线230mx y m --+=垂直， 则()2222102PA PB PA PB AB++==≥，当且仅当PA PB ==时取等号，所以PA PB +≤PA PB +的最大值为 三、解答题：解答应写出文字说明，证明过程或演算步骤．11．在ABC ∆中，已知角C 的角平分线所在的直线方程为2y x =，顶点A ，B 的坐标分别是(4 2)-，，(3 1)，，求顶点C 的坐标． 【答案】(2 4)，．【解析】设(4 2)A -，关于直线2y x =的对称点为00( )A x y '，， 则0024AA y k x '-=+，AA '的中点坐标为0042( )22x y -+，，所以0000221424222y x y x -⎧⨯=-⎪+⎪⎨+-⎪=⨯⎪⎩， 解得0042x y =⎧⎨=-⎩，所以(4 2)A '-，，因为点A '在直线BC 上，且(3 1)B ，，所以BC 所在的直线方程为211(3)43y x ---=--，即3100x y +-=． 因为C 为直线BC 与直线2y x =的交点， 所以由31002x y y x +-=⎧⎨=⎩，31003100x y x y +-=⎧⎨-+=⎩，即(2 4)C ，．12．已知ABC ∆的顶点(5 1)A ，，AB 边上的中线CM 所在直线方程为250x y --=，AC 边上的高BH 所在直线方程为250x y --=． （1）求顶点C 的坐标； （2）求直线BC 的方程． 【答案】（1）(4 3)C ，； （2）6590x y --=．【解析】（1）由AC 边上的高BH 所在直线方程为250x y --=，得21=BH k ， 所以2-=AC k ，又(5 1)A ，，所以AC 边所在直线方程为2110x y +-=， 联立直线AC 与直线CM 方程得2110250x y x y +-=⎧⎨--=⎩，解得43x y =⎧⎨=⎩，即顶点C 的坐标为(4 3)，．（2）设00( )B x y ，，则AB 的中点M 为0051( )22x y ++，，由M 在直线250x y --=上，得005125022x y ++⨯--=，即00210x y --=， 由点B 在直线250x y --=上，得00250x y --=， 联立0000210250x y x y --=⎧⎨--=⎩，解得0013x y =-⎧⎨=-⎩，所以顶点B 的坐标为(1 3)--，．又(4 3)C ，，所以直线BC 的方程为333(1)14y x --+=+--，即6590x y --=．2.4 点到直线的距离（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．点 0)F0=的距离为 ABC ．3D ．m 3 【答案】A【解析】点F0=的距离d ==．故选A ．2．直线1:330l x y +-=与直线2:610l x my ++=平行，则1l 与2l 之间的距离为 A ．4 BCD【答案】D【解析】直线1:330l x y +-=可化为6260x y +-=，因为1l 与直线2:610l x my ++=平行，所以2=m ，即2:6210l x y ++=， 所以1l 与2l之间的距离为d ==故选D ． 3．已知12=+y x ，则22y x +的最小值为 A ．1 B ．14 C ．15 D ．110【答案】C【解析】22y x +表示)0,0(到12=+y x 上点的距离的平方， 所以22y x +的最小值是（0，0）到012=-+y x 的距离d 的平方，据点到直线的距离公式得d ==22y x +的最小值为15．故选C ． 4．直线1:320l x y --=和直线2:3100l x y +-=的夹角平分线的方程为 A ．240x y +-= B ．260x y --=C ．240x y +-=或260x y --=D ．240x y +-=或260x y --= 【答案】D【解析】设(,)P x y 为角平分线上的任意一点，由该点到两直线的距离相等，即可得：=32310x y x y --=+-，整理得240x y +-=或260x y --=．故选D ．5．知两点()1,2A ，()3,6B ，动点M 在直线y x =上运动，则MA MB +的最小值为 A ．25 B ．26 C ．4 D ．5 【答案】B【解析】根据题意画出图形，如图所示： 设点A 关于直线y x =的对称点()2,1A '， 连接A B '，则A B '即为MA MB +的最小值， 且()()22=32+61=26A B '--． 故选B ．6．已知点P 为直线013:=--y x l 上的动点，当点P 到(4 1)A ，和(0 4)B ，的距离之差最 大时，点P 坐标为A ．(1 2，）B ．4( 33，） C ．(2 5，）D ．(3 8，） 【答案】C【解析】如图，作点B 关于l 的对称点为B '，AB '的延长线交l 于0P ，在l 上任取一点P ，则00PA PB PA PB AB P A P B '''-=-≤=-，则点0P 即为所求．设(0 4)B ，关于直线l 的对称点为00( )B x y '，， 则004BB y k x '-=，BB '的中点坐标为004( )22x y +，， 所以0000431431022y x x y -⎧⨯=-⎪⎪⎨+⎪⨯--=⎪⎩，解得0033x y =⎧⎨=⎩，所以(3 3)B '，．所以直线AB '的方程为092=-+y x ．由290310x y x y +-=⎧⎨--=⎩，可得0P (2 5，）．故选D ．二、填空题7．若点Q P ，分别为直线01243=-+y x 与0343=++y x 上的动点，则PQ 的最小值 为： ． 【答案】3【解析】依题意知，两直线平行．所以PQ 的最小值为这两条平行直线间的距离， 即=min PQ 22|123|334--=+．8．若两条平行直线()1:200l x y m m -+=>与2:260l x ny +-=之间的距离是25m n += ．【答案】3【解析】由题意直线()1:200l x y m m -+=>与2:260l x ny +-=平行，则1226m n -=≠-， 即4n =-且3m ≠，所以2:2460l x y --=，化为2:230l x y --=，所以1l 与2l 之间的的距离为22(3)251(2)m --=+-，又0m >，所以7m =，所以3m n +=．9．已知点(1 2)A -，，(3 4)B ，．点P 在x 轴上，且PA PB =，则PAB ∆的面积为________． 【答案】152【解析】设AB 的中点坐标为M ，则(13)M ，， 因为241132AB k -==--，所以AB 的中垂线方程为)1(23--=-x y ，即052=-+y x ． 令=0y ，则52x =，即P 点的坐标为5( 0)2，，所以22(13)(24)25AB =--+-=， 点P 到AB 的距离为22535(1)(30)2PM =-+-= 所以113515252222PAB S AB PM ==⨯=△． 10．函数2291041y x x x =+-+_________． 74 【解析】()22222291041354y x x x x x =+-+=+-+设()0,3A ，()5,4B ，(),0C x ，则()2222354y x x AC BC =+-+=+，即x 轴上的一动点(),0C x 到()0,3A ，()5,4B 的距离之和．作()0,3A 点关于x 轴的对称点()10,3A -， 连接1BA ，则1BA 即为距离和的最小值， ()22153474BA =+--=min 74y ．三、解答题：解答应写出文字说明，证明过程或演算步骤．11．已知直线l 经过直线052=-+y x 与02=-y x 的交点．（1）若点)0 5(，A 到l 的距离为3，求l 的方程；（2）若直线l '经过原点O ，且与直线l 平行，求l '与l 的距离最大值时直线l '的方程．【答案】（1）2=x 或0534=--y x ；（2）02=+y x ．【解析】（1）（解法一）设经过两已知直线交点的直线方程为0)2(52=-+-+y x y x λ， 即05)21()2(=--++y x λλ3=．即02522=+-λλ，所以0)2)(12(=--λλ，解得21=λ或2-=λ．故l 的方程为2=x 或0534=--y x ． （解法二）由25020x y x y +-=-=⎧⎨⎩，解得交点)1 2(，P ． 当直线l 斜率不存在时，方程为：2=x ，此时点)0 5(，A 到l 的距离为3，故2=x 符合题意； 当直线l 斜率存在时，设其方程为：)2(1-=-x k y ，即021=-+-k y kx ，所以点)0 5(，A 到l 的距离为：31132=++k k ，解得34=k ， 所以直线l 的方程为：)2(341-=-x y ，即0534=--y x ． 综上，直线l 的方程为2=x 或0534=--y x ．（2）当两条平行直线l '，l 与P ，O 两点连线垂直时，两条平行直线间的距离最大． 又101202OP k -==-，所以两条平行直线的斜率为2-， 所以直线l '的方程是x y 2-=，即02=+y x ．12．已知直线方程为()()221340m x m y m -++++=．（1）证明：直线恒过定点；（2）当m 为何值时，点()3,4Q 到直线的距离最大，最大值为多少？（3）若直线分别与x 轴，y 轴的负半轴交于,A B 两点，求AOB ∆面积的最小值及此时直线的方程．【答案】（1）详见解析；（2）47m =； （3）AOB ∆面积的最小值为4，此时直线的方程240x y ++=．【解析】（1）证明：直线方程为()()221340m x m y m -++++=，可化为()()24230x y m x y +++-++=，对任意m 都成立，所以230240x y x y -++=⎧⎨++=⎩，解得12x y =-⎧⎨=-⎩，所以直线恒过定点()1,2--；（2）点()3,4Q 到直线的距离最大，可知点Q 与定点()1,2P --的连线的距离就是所求最=． 又 423312PQ k +==+， 且()()221340m x m y m -++++=的斜率为23-，故22321m m --=-+，解得47=m ． （3）由（1）可知，直线过定点，且分别与x 轴，y 轴的负半轴交于,A B 两点， 设直线方程为()21y k x +=+，0<k ，分别令=0x ，=0y ，可得2(1,0)A k -，()0,2B k -，则1212212(1)(2)2()24222AOB k S k k k k k -=--=--=++≥+=-△， 当且仅当2k =-时取等号，面积的最小值为4． 此时直线的方程240x y ++=．2.5 圆的方程（练习）一．单项选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．在平面内，,A B 是两个定点，C 是动点．若1AC BC ⋅=，则点C 的轨迹为A ．圆B ．椭圆C ．抛物线D ．直线【答案】A【解析】设()20AB a a =>，以AB 中点为坐标原点建立平面直角坐标系，则：( 0)( 0)A a B a -，，，，设(),C x y ，则()(),,,AC x a y BC x a y →→=+=-，所以()()21AC BC x a x a y →→⋅=+-+=，整理可得：22210x y a +=+>，即点C 的轨迹是以AB 为半径的圆．故选A ．2．已知点(1,1)a a +-在圆22240x y ay +--=的外部（不含边界），则实数a 的取值范围为A ．1a <B ．01a <<C ．15a >D ．1a > 【答案】D【解析】因为圆22240x y ay +--=，可化为()2224x y a a +-=+， 所以圆心()0,a ，半径24ra ． 因为点(1,1)a a +-在圆22240x y ay +--=的外部，所以点(1,1)a a +-到圆心()0,a 的距离大于半径，>1a >．故选D ． 3．若过点(2 1)，的圆与两坐标轴都相切，则圆心到直线032=--y x 的距离为 A ．55 B ．552 C ．553 D ．554 【答案】B【解析】由于圆上的点(2 1)，在第一象限，所以圆心必在第一象限， 因为圆与两坐标轴都相切，所以设圆的半径为a ，则圆心的坐标为()a a ，，故圆的标准方程为222()()x a y a a -+-=．由题意可得()()22221a a a -+-=，可得2650a a -+=，解得1a =或5a =，所以圆心的坐标为(11)，或(5 5)，，圆心到直线230x y --=的距离均为d ==，所以圆心到直线230x y --=．故选B ． 4．若方程22220x y kx y k ++++=所表示的圆取得最大面积，则直线(1)2y k x =-+的 倾斜角α等于A ．45B ．60C ．120D ．135【答案】D【解析】方程22220x y kx y k ++++=的标准方程为2223()(1)124k k x y +++=-， 则22314k r =-，当所表示的圆取得最大面积时，0k =，此时1r =， 则直线()12y k x =-+为2y x =-+，所以tan 1α=-，因为[0 180)α∈，，所以135α=︒．故选D ． 5．已知圆1C ：22(1)(1)1x y ++-=，圆1C 与圆2C 关于直线10x y --=对称，则圆2C 的 方程为A ．22(2)(2)1x y ++-=B ．22(2)(2)1x y +++=C ．22(2)(2)1x y -++=D ．22(2)(2)1x y -+-=【答案】C【解析】圆1C 的圆心为(11)-，，半径长为1，设圆2C 的圆心为( )a b ，， 由题意得111022a b -+--=且1=1+1b a --，解得22a b ==-，，即圆2C 的圆心为(2 2)-，， 又圆2C 的半径长为1，故圆2C 的方程为22(2)(2)1x y -++=．故选C ．6．设m R ∈，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于 点P ，则||||PA PB +（异于A ，B 两点）的取值范围是A ．B ．C ．D ．【答案】B【解析】由题意可得(0,0)A ，(1,3)B ，因为1(1)0m m ⨯+⨯-=，所以直线0x my +=和直线230mx y m --+=垂直，故点P 在以AB 为直径的圆上运动，故||||||cos ||sin PA PB AB PAB AB PAB +=∠+∠)4PAB π=∠+，因为(0 )2PAB π∠∈，，所以3( )444PAB πππ∠+∈，，所以2sin()(1]42PAB π∠+∈， 所以||||PA PB +(10,25]∈．故选B ．二、填空题7．已知圆C 经过(5 1)A ，，(1 3)B ，两点，圆心在x 轴上，则C 的方程为 ．【答案】22(2)10x y -+=【解析】依题意设圆C 的方程为222()x a y r -+=，把所给的两点坐标代入方程得2222(5)1(1)9a r a r⎧-+=⎨-+=⎩，解得2210a r =⎧⎨=⎩，所以圆C 的方程为：22(2)10x y -+=． 8．若方程222(2)4850a x a y x y a +++++=表示圆，则圆心坐标是_____，半径长为____．【答案】(2,4)--； 5．【解析】由题意22a a =+，即1a =-或2a =．当1a =-时，方程为224850x y x y +++-=，即22(2)(4)25x y +++=，圆心为(2,4)--，半径为5，当2a =时，方程为224448100x y x y ++++=，2215()(1)24x y +++=-不表示圆． 9．由曲线2222x y x y +=+围成的图形面积为 ．【答案】84π+【解析】由题意，作出如图的图形，由曲线关于原点对称，当0x ，0y 时，解析式为22(1)(1)2x y -+-=，故可得此曲线所围的力图形由一个边长为22的正方形与四个半径为2的半圆组成， 所围成的面积是2122224(2)842ππ⨯+⨯⨯⨯=+． 10．已知点(, )P x y 是圆22:4230C x y x y ++-+=上的动点，则22(1)(2)-++x y 的取值范围为 ．【答案】[8 32]，【解析】圆22:4230C x y x y ++-+=可化为22(2)(1)2x y ++-=，则圆心(2,1)C -，半径2r =， 故22(1)(2)-++x y 表示圆上的点(,)P x y 到点(1,2)Q -的距离的平方，因为22(21)(12)32QC =--++=，所以22QC PQ QC -≤≤+，即2242PQ ≤≤，所以2832PQ ≤≤，所以22(1)(2)-++x y 的取值范围为[8 32]，． 三、解答题：解答应写出文字说明，证明过程或演算步骤．11．直角三角形ABC 的顶点坐标(2,0)A -，直角顶点(0,22)B -，顶点C 在x 轴上．（1）求BC 边所在直线的方程；（2）圆M 是三角形ABC 的外接圆，求圆M 的方程．【答案】（1）240x y --=；（2）22(1)9x y -+=．【解析】（1）直线AB 的斜率为022220AB k +==---， 由题意可知AB BC ⊥，则直线BC 的斜率为122BC AB k k =-=． 因此，BC 边所在直线的方程为2222y x +=，即240x y --=； （2）直线BC 的方程为240x y --=，由于点C 在x 轴上，令0y =得，点()4,0C ． 由于ABC ∆是以ABC ∠为直角的直角三角形，则该三角形的外接圆圆心M 为线段AC 的中点()1,0M ，半径长为132AC ．因此，圆M 的标准方程为22(1)9x y -+=． 12．在平面几何中，通常将完全覆盖某平面图形且直径最小的圆，称为该平面图形的最小覆盖圆．最小覆盖圆满足以下性质：①线段AB 的最小覆盖圆就是以AB 为直径的圆；①锐角△ABC 的最小覆盖圆就是其外接圆．已知曲线W ：2416x y +=，(0,)A t ，(4,0)B ， (0,2)C ，(4,0)D -为曲线W 上不同的四点．（1）求实数t 的值及△ABC 的最小覆盖圆的方程；（2）求四边形ABCD 的最小覆盖圆的方程；（3）求曲线W 的最小覆盖圆的方程．【答案】（1）2t =-，22340x y x +--=；（2）2216x y +=；（3）22654x y +=． 【解析】（1）因为(0,)A t 在曲线W ：2416x y +=上，所以令0x =得，2t =-． 由于△ABC 为锐角三角形，外接圆就是△ABC 的最小覆盖圆．设△ABC 外接圆方程为220x y Dx Ey F ++++=， 则4201640420E F D F E F -+=⎧⎪++=⎨⎪++=⎩， 解得304D E F =-⎧⎪=⎨⎪=-⎩．。

人教版小学四年级上册数学综合练习题及答案(共八套)综合能力训练(一)一、直接写出下面各题得数：1.8×(125-25) = 80048+52÷4 = 60总和为：8602.160+40÷4(19-11)×125 = 160+40÷4×8×125160+800081603.(12+42÷7)×5×26×8÷26×8 = (12+6)×5×8×81920二、把下面运算中不正确的地方改过来：1.(841-41)÷25×42 ÷ 600×(1200-200÷25) 800÷25×42 ÷ 600×(1000÷25)32×42 ÷ 2401344 ÷ 2405.6三、把下面各组式子列成综合算式：1.3280÷16=20523×16=368205×10=2050625-368=2576000-2050=39501028÷257=4四、计算下面各题：1.280+840÷24×5 = 5002.85×(95-1440÷24) = 85×35 = 29753.÷(105+20×2) = 4904.-(4300+870÷15) =五、装订车间每人每小时装订课本640册，照这样计算，12人8小时装订课本多少册？答：640×12×8=册六、汽车队开展节约用油活动，12辆车一年共节约汽油7200千克，平均每辆车每个月节约汽油多少千克？答：7200÷12÷12=50千克七、一部电话机售价320元，一台“彩电”的售价是电话机售价的8倍，一台电脑的售价比“彩电”售价的3倍还多1000元，一台电脑多少元？答：320×8×3+1000=8680元八、两个车间生产零件，5天后甲车间生产1520个零件，乙车间生产1280个零件，若每天工作8小时，乙车间比甲车间每小时少生产多少个零件？答：(1520-1280)÷(8×5)=6个/小时综合能力训练(二)一、填空：1.学校有足球24个，是篮球的3倍，学校有足球，篮球共(24+72)=96个。

一、选择题1．在直尺上，与2相邻的两个数分别是（）。

A. 1，3B. 0，1C. 3，4 2．看图，数一数，圈一圈，两个圈在一起能圈出（）圈。

A. 3B. 4C. 5 3．选择题（1）下面多得是（）。

A.B.（2）下面少得是（）。

A.B.4．同样多的一组是（）。

A.B.5．数一数，填一填．（1）哪种水果最多？( )A.B.C.（2）最少的比最多的少( )A.1个B.2个C.3个6．下面3个盒子里原来有几个果子不知道，如果往盒里各放1个、2个、3个果子，3个盒里的果子数就一样多了。

原来第( )个盒里的果子最少A. B. C.7．与其他三行不同的那一行是（）A. 1 2 3B. 2 3 4C. 3 4 5D. 4 3 28．4＞，可以填写的正确答案是（）。

A. 1 、2 、3B. 2、 3、 4C. 3、4、5D. 0、1、2、3 9． 3003003的最高位是（）位A. 万B. 十万C. 百万10．一万一万地数，数十次是（）A. 十万B. 一百万C. 一千万11．下图中，（）多？A. 草莓B. 香蕉12．哪说的对？（）A. 我排第一我最多B. 我排第二我最多C. 我排第三我最多13．＋＝（）A. 1440B. 1800C. 540014．356再加3个十是（）A. 359B. 386C. 65615．1629后面第三个数是（）A. 1631B. 1632C. 1633二、填空题16．填一填：________________________________17．在横线上填“＞”、“＜”或“＝”。

6________4 7________7 0________1 3＋2________47________5 0________0 6________5 2＋3________6 18．5比4多________，3比5少________。

19．左边有________只小鸡，右边有________只小鸡。

一共有几只小鸡?□○□=□（只）________20．从小到大排列：3、1、0、4、5、2________<________＜________＜________＜________＜________ 21．看图列式计算① ________；② ________；③ ________；④ ________.22．填一填。

部编版一年级语文上全册课文课后习题参考答案部编一年级语文上册第1~3单元同步习题及答案一年级上册第一单元同步练习一、数一数，连一连。

（6分）二、选一选，填一填。

（填序号）（4分）三、看一看，写一写。

（8分）四、先写出汉字的笔顺，再按要求填空。

（18分）五、按笔顺规则写字。

（6分）六、选一选，填一填。

（填序号）（16分）七、背一背，写一写。

（18分）1. 对雨，雪对。

2. 四五，金木土。

天地分下，月照今古。

3.鹅，鹅，鹅，曲项向歌。

浮绿，红掌拨清波。

八、口语交际。

（9分）看下列图片，把图片中的动作和指令连一连。

九、读一读，做一做。

（15分）齐步走叽叽叽，叽叽叽，一二三四五六七。

七只小鸡齐步走，七六五四三二一。

1.写出对应的阿拉伯数字。

（10分）二三五七2.儿歌中齐步走的是（5分）（）A B C参考答案一、二、③ ④ ① ②三、手目虫火日云口田四、笔顺略 6 |五、三、二十、禾六、1.③ ① ④ ② 2.② ① ③ ④七、1.云风 2.一二三水火上日 3.天白毛水八、九、1.2 3 5 72.B一年级上册第二单元同步习题一、声母连连看。

（按声母表的顺序连一连）（5分）二、写出下面音节所对应的整体认读音节。

（8分）三、比一比，填一填。

（6分）四、拼一拼，写一写。

（7分）五、看图写音节。

（16分）六、读一读，把汉字和对应的韵母连线。

（20分）七、把下列不是同类的事物涂上颜色。

（9分）八、读一读，连成一句话。

（15分）1.cā gē ge bō li2.hé huā huà qí qi3.yì qǐ bà bɑ hé qí chē zi mā mɑ九、读一读，做一做。

（14分）1.用“○”圈出翘舌音的字。

（8分）2.用“——”在儿歌中画出动物的名字。

（6分）参考答案一、二、yu wu ri zi shi ci zhi yi三、d p t四、mǎ sh u x ǖ u á五、jú huā shī zi qì chē xī guā xià qí wū yā sǎo dì jī mù六、七、涂色：kè zhuō 2.chá yè 3.luó bo八、1.gē ge cā bō li.2.qí qi huà hé huā.3.bà bɑ hé mā mɑ yì qǐ qí chē zi.九、圈出：池抓只着2.小白鸭小虾一年级上册第三单元同步习题一、按要求给拼音分类。

小学一年级数学下册综合练习题篇一：2021新版小学一年级下册数学练习题全套小学一年级数学下册作业设计第1节：复习加减混合〔1〕一、算一算。

3+2= 2+7= 10+9= 6+3=7-4= 8-4= 6+4= 10-7=6+3= 6+5= 1+8= 8+2=9-4= 7+3= 9-8= 5-5=二、算一算。

4+3-2= 4-2+3= 2+3+4= 9-6+3= 8-2-2= 9+1-5= 4+5-7= 3+7-2= 1+4+5= 10-4-4=2+7+0= 7-6+5= 8-1-3= 2+6-7= 3+3+3= 7+2-5= 10-6+5=9-2-2= 9-8+5= 10-4+5=三、在□填数。

6+□=10 □+7=9 9+□=108+□=10 5+□=7 10+□=10□+5=9 □+7=10 □+3=82+□= □+3=75+□=10四、填空后写出四个算式。

6□○□=□ □○□=□ □○□=□□○□=□复习加减混合〔2〕一、算一算。

9-4=7-7= 10-5= 6+3= 8+2=10+0= 10-0= 0+9= 5+5= 10-6=9-9= 0+0= 0-0= 9+1= 10-1=二、算一算。

3+7-5=8-6+2=10-7+0= 9-6+5=10-6+0= 8-7+1=3+2+4=10-3-7=10-6+2= 8-8+8=10-9+7= 9+3-8=8+2-7=4+5+1=7-7+6=2+3-5=三、在括号里填上适当的数。

3+〔〕=10〔〕+2=8 〔〕+〔〕=109+〔〕=10 8+〔〕=9 4+〔〕=9〔〕+6=8 〔〕+2=7 〔〕+7=84+〔〕=10认识图形〔1〕一、填空。

〔1〕长方形有〔〕条边，正方形有〔〕条边，三角形有〔〕条边。

〔2〕用〔〕根小棒可以摆一个长方形。

〔3〕用〔〕根小棒可以摆一个正方形。

〔4〕用〔〕根小棒可以摆一个三角形。

〔5〕硬币是〔〕的。

二、有〔〕有〔〕三、给涂上颜色。

一年级数学上下册练习题汇总
一年级数学上下册练习题小学数学一年级上册5以内加减法口算题小学数学一年级上册期末常考题型小学一年级数学上册期末综合考试卷
小学一年级上册数学：比一比练习题人教版小学一年级上册数学：数一数练习题小学数学一年级上册数学提高测试题一年数学上册七单元《认识钟表》试卷小学数学一年级上册《数一数、比一比》练习题小学数学一年级上册综合练习题小学数学一年级下册“找规律”练习题小学数学一年级下册综合练习题总结：以上就是一年级数学上下册练习题，小朋友们会做哪些题呢？一年级数学上下册练习题并不复杂，请家长朋友帮助孩子一起把上学期学过的知识回忆起来吧！
浏览本文的孩子还看了：
小学数学一年级下册“找规律”练习题
小学数学一年级下册综合练习题
更多精彩内容尽在：一年级数学同步练习。