热力学第一定律在状态变化过程中的应用

物理化学论文论热力学第一定律学院：化学与化工学院专业：矿物加工工程班级：1301姓名：***学号：**********热力学第一定律的内容及应用【摘要】:热力学第一定律即能量守恒及转换定律,广泛地应用于学科的各个领域,和热力学第二定律一起构成了热力学的基础,因此,深刻地理解和掌握该定律显得尤为重要,本文阐述了其产生的历史背景,具体内容及其应用【关键字】:热力学第一定律；内能定理；焦耳定律；热机；热机效率;应用；影响【引言】在19世纪早期，不少人沉迷于一种神秘机械——第一类永动机的制造，因为这种设想中的机械只需要一个初始的力量就可使其运转起来，之后不再需要任何动力和燃料，却能自动不断地做功。

在热力学第一定律提出之前，人们一直围绕着制造永动机的可能性问题展开激烈的讨论。

直至热力学第一定律发现后，第一类永动机的神话才不攻自破。

本文就这一伟大的应用于生产生活多方面的定律的建立过程、具体表述、及生活中的应用——热机，进行简单展开。

1．热力学第一定律的产生1.1历史渊源与科学背景人类使用热能为自己服务有着悠久的历史,火的发明和利用是人类支配自然力的伟大开端,是人类文明进步的里程碑。

中国古代就对火热的本性进行了探讨,殷商时期形成的“五行说”——金、木、水、火、土,就把火热看成是构成宇宙万物的五种元素之一，古希腊米利都学派的那拉克西曼德（Anaximander,约公元前611—547) 把火看成是与土、水、气并列的一种原素,它们都是由某种原始物质形成的世界四大主要元素。

恩培多克勒（Empedocles,约公元前500—430）更明确提出四元素学说,认为万物都是水、火、土、气四元素在不同数量上不同比例的配合,与我国的五行说十分相似。

但是人类对热的本质的认识却是很晚的事情。

18世纪中期,苏格兰科学家布莱克等人提出了热质说。

这种理论认为,热是由一种特殊的没有重量的流体物质,即热质（热素）所组成,并用以较圆满地解释了诸如由热传导从而导致热平衡、相变潜热和量热学等热现象,因而这种学说为当时一些著名科学家所接受,成为十八世纪热力学占统治地位的理论。

热力学第一定律的表述方式及应用热力学第一定律是热力学中的基本定律之一，也被称为能量守恒定律。

它指出，在任何一个热力学系统中，系统的内能变化等于系统所吸收的热量与对外做的功的代数和。

这一定律为我们理解和描述热力学系统的行为提供了重要的理论依据。

一、热力学第一定律的表述方式热力学第一定律可以用以下三种方式进行表述：1. 微分形式在微分形式下，热力学第一定律可以表示为：[ = Q - W ]其中，( U ) 表示系统的内能，( Q ) 表示系统吸收的热量，( W ) 表示系统对外做的功。

2. 积分形式在积分形式下，热力学第一定律可以表示为：[ U = Q - W ]其中，( U ) 表示系统内能的变化量，( Q ) 表示系统吸收的热量，( W ) 表示系统对外做的功。

3. 宏观形式在宏观形式下，热力学第一定律可以表示为：[ _{i=1}^{n} i = {j=1}^{m} _j ]其中，( _i ) 表示系统从第 ( i ) 个热源吸收的热量，( _j ) 表示系统对外做第 ( j )项功。

二、热力学第一定律的应用热力学第一定律在工程、物理等领域有着广泛的应用，下面列举几个常见的应用实例：1. 热机效率的计算热机效率是指热机所做的功与吸收的热量之比。

根据热力学第一定律，热机所做的功等于吸收的热量减去内能的变化量。

因此，热机效率可以表示为：[ = ]2. 制冷机的性能分析制冷机的工作原理是利用工作物质在循环过程中吸收热量，从而实现低温环境的创造。

根据热力学第一定律，制冷机吸收的热量等于制冷量与制冷机压缩机所做的功之和。

因此，可以通过热力学第一定律来分析制冷机的性能。

3. 太阳能热水器的设计太阳能热水器利用太阳能将光能转化为热能，为用户提供热水。

根据热力学第一定律，太阳能热水器吸收的热量等于水温升高所吸收的热量与热水器损失的热量之和。

因此，在设计太阳能热水器时，需要考虑热量的损失，以提高热水器的效率。

4. 热传导过程的分析热传导是热量在物体内部由高温区向低温区传递的过程。

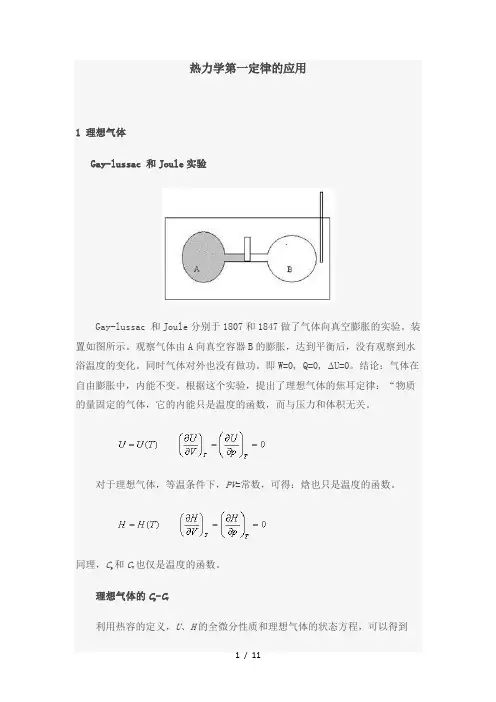
热力学第一定律的应用1 理想气体Gay-lussac 和Joule实验Gay-lussac 和Joule分别于1807和1847做了气体向真空膨胀的实验。

装置如图所示。

观察气体由A向真空容器B的膨胀，达到平衡后，没有观察到水浴温度的变化。

同时气体对外也没有做功。

即W=0, Q=0, U=0。

结论：气体在自由膨胀中，内能不变。

根据这个实验，提出了理想气体的焦耳定律：“物质的量固定的气体，它的内能只是温度的函数，而与压力和体积无关。

对于理想气体，等温条件下，PV=常数，可得：焓也只是温度的函数。

同理，C p和C V也仅是温度的函数。

理想气体的C p-C V利用热容的定义，U、H的全微分性质和理想气体的状态方程，可以得到证明：理想气体C p-C v= nR2 可逆过程体积功指体系反抗外力作用膨胀而与环境的功交换。

功是一个过程量。

考虑体系从状态(P1,V1)变化到(P2,V2)经4个不同的体积膨胀过程，所做功分别为：自由膨胀(真空膨胀)：外压为0，功We1=0。

体系膨胀但没有功。

抗恒外压膨胀：外压P e=P2不变，体积变化为V2-V1，W e2= -P2 (V2-V1)。

膨胀过程，V2>V1，W为负值，表示体系对环境做功。

抗二次恒外压：抗外压Pe1，体积变化V’-V1，再抗恒外压P e=P2，体积变化V 2-V’。

做功We3= -Pe1(V’-V1)-P2(V2-V’)。

准静态膨胀：环境压强比体系低一个微小的压差，P e = P-dP，体系发生一个微小的体积膨胀dV。

当这样的微小的外压降低连续发生，直至外压P e=P2，相应体积从V1变到V2时，过程所做功为其中忽略了2阶微小变化dPdV。

若气体近似按理想气体处理，可得：过程不同，体系所做功也不同。

比较四个功的绝对值，可以看到：|We4|>|We3|>|We2|>|We1|。

即准静态过程体系对外做功最大。

功的几何意义是P-V曲线所围面积。

小结：理想气体在各种过程中Q, W, ΔU, ΔH 的计算
（前提：封闭系统，W ′=0，无化学变化） 定温过程 WV=－psuΔV WV=－∫pdV
Q=W QV=ΔU Qp=ΔH Q=0
ΔU=0
ΔH=0
定容过程 定压过程 绝热过程
可逆相变化
End
WV=0 WV=－psuΔV WV=ΔU WV=－psuΔV
Hale Waihona Puke ①定压升温101.3 kPa, 25℃
H2O(g)
③定压降温
2mol H2O(l) ΔH1 =
101.3 kPa, 100℃
②可逆相变
H2O(g)
则 Qp=ΔH =ΔH1＋ΔH2＋ΔH3
∫
T2 T1
nC
p ,m
( l ) d T = nC
p ,m
(l ) Δ T
ΔH2 = n ·ΔvapHm ΔH3 = ∫ T nC
升华焓: ΔsubHm, 晶型转变焓: ΔtrsHm(α→β)
纯物质 B(α)
2、相变化过程的体积功和ΔU
定温、定压 WV =－p(Vβ－Vα)
B(β) Qp＝ΔαβH
由热一律, W′＝0 时 ΔU＝Qp＋WV 或 ΔU＝ΔH －p(Vβ－Vα) 1)对熔化和晶型转变 ΔV≈0，WV≈0， ΔU≈ΔH （s→l ， s1→s2） 2)若β为气相，α为凝聚相 (蒸发和升华) WV =－pVβ Vβ >>Vα，所以 ΔU =ΔH －pVβ 若气相视为理想气体 WV =－pVβ=－nRT 则 ΔU ＝ ΔH－nRT
（1-53）
典型例题
水的正常沸点
例1：2mol 水在101.3 kPa，100℃时蒸发，变成同温 同压下的水蒸气（设水蒸气为理想气体），求此过程 的Q、W、ΔU和ΔH。已知水在100℃及标准压力下的摩尔

第二章 热力学第一定律主要公式及使用条件1. 1. 热力学第一定律的数学表示式W Q U +=Δ或'amb δδδd δdU Q W Q p V W =+=−+规定系统吸热为正，放热为负。

系统得功为正，对环境作功为负。

式中 p amb 为环境的压力，W ’为非体积功。

上式适用于封闭体系的一切过程。

2. 2. 焓的定义式pVU H +=3. 3. 焓变（1） )(pV U H Δ+Δ=Δ式中为乘积的增量，只有在恒压下)(pV ΔpV )()(12V V p pV −=Δ在数值上等于体积功。

（2） 2,m 1d p H nC Δ=∫T 此式适用于理想气体单纯pVT 变化的一切过程，或真实气体的恒压变温过程，或纯的液体、固体物质压力变化不大的变温过程。

4. 4. 热力学能(又称内能)变此式适用于理想气体单纯pVT 变化的一切过程。

2,m 1d V U nC Δ=∫T5. 5. 恒容热和恒压热(d V Q U =Δ0,'0)V W ==p Q H =Δ(d 0,'0)p W ==6. 6. 热容的定义式（1）定压热容和定容热容δ/d (/)p p C Q T H T p ==∂∂δ/d (/)V V C Q T U T ==∂∂V p V R 3（2）摩尔定压热容和摩尔定容热容,m m /(/)p p C C n H T ==∂∂,m m /(/)V V C C n U T ==∂∂上式分别适用于无相变变化、无化学变化、非体积功为零的恒压和恒容过程。

（3）质量定压热容（比定压热容）,m //p p p c C m C M==式中m 和M 分别为物质的质量和摩尔质量。

（4）,m ,m p V C C −=此式只适用于理想气体。

（5）摩尔定压热容与温度的关系2,m p C a bT cT dT =+++式中a , b , c 及d 对指定气体皆为常数。

（6）平均摩尔定压热容21,m ,m 21d /()T p p T C T T T C =−∫7. 7. 摩尔蒸发焓与温度的关系21v ap m 2vap m 1v ap ,m ()()d T p T H T H T C T Δ=Δ+Δ∫或 vap m vap ,m (/)p p H T ∂Δ∂=ΔC d amb ∑−=−−=−−=式中 = C (g) —C (l)，上式适用于恒压蒸发过程。

热力学第一定律，又称热力学第一定律原理或热力学第一定律定理，是热力学的基本定理之一。

它指出：在任意一个过程中，物质的总热力量Q和总功率W之和是定值，即Q+W=定值。

热力学第一定律的实际运用广泛，可以用来解决各种热力学问题。

下面给出几个具体的例子。

制冷机的工作原理：制冷机是利用制冷剂的汽化-冷凝-膨胀过程来进行冷却的。

制冷剂从低压汽化到高压气体的过程中，汽化所吸收的热量就是制冷机所发出的冷量。

这个过程可以看作是制冷机消耗的功率W，对应的热力学第一定律式为Q+W=定值。

热水器的工作原理：热水器是利用电能将水加热的。

电能转化成热能的过程可以看作是热水器消耗的功率W，加热水所吸收的热量就是热水器发出的热量Q。

这个过程可以用热力学第一定律来表示，即Q+W=定值。

汽车发动机的工作原理：汽车发动机是利用燃料的燃烧来产生动力的。

燃料的燃烧过程中，消耗的燃料质量就是汽车发动机的功率W，燃烧所释放的热量就是汽车发动机发出的热量Q。

这个过程可以用热力学第一定律来表示，即Q+W=定值。

光伏发电的工作原理：光伏发电是利用光能转化成电能的过程。

光能转化成电能的过程可以看作是光伏发电的功率W，光伏发电所产生的电能就是光伏发电发出的热量Q。

这个过程可以用热力学第一定律来表示，即Q+W=定值。

以上就是热力学第一定律的几个具体运用例子。

可以看出，热力学第一定律是一个非常重要的定理，在各种热力学过程中都有着广泛的应用。

等容 dV 0
P C T
QV E E CV ,mT
等压 dP 0
V C T
QP E PV
E CV ,mT
等温 dT 0 PV C QT A
0
绝热
dQ 0
PV C1 V 1T C2 P 1T C3
Aa E
E CV ,mT
15
过程 等容
功A 0
热量Q
CV ,mT
热力学第一定律
微小过程：dQ dE dA 符号 d 表示
因为Q、A不是状态函数，不能写成“微元明确几点：
Q E A
①.注意内能增量、功、热量的正负规定。
②.热力学第一定律实际上是能量守恒定律在热力学中 的体现。热力学第一定律是从实验中总结出来的。
A V2 RT dV RT V2 dV
V1
V
V V1
V1
等温过程的功 A RT ln V2 （1）
V1
T
2 V2 V
8
由过程方程 P1V1 P2V2
则等温过程的功 6.热量
A RT ln V2
V1
RT ln P1
P2
（2）
无法使用 QT CT (T2 T1) 计算等温过程的热量。
原因：对于等温过程温度不变，Q=A，而功是过程量， 与过程有关，因而CT也与过程有关，没有意义。
第一类永动机：即不从外界吸收能量，而不断对外作 功的机械。
第一类永动机违反能量守恒定律。
热力学第一定律对准静态过程和非准静态过程均适 用。但为便于实际计算，要求初终态为平衡态。
3
二、热力学第一定律在等值过程中的应用
1.等容过程
等容过程也称等体过程。
V
1.过程特点 系统的体积不变 dV 0

又 dW = − dE
∴ dW = PdV = − 而 PdV + VdP =
dE =
M
M
µ
CV dT
(1) ( 2)
µ µ
CV dT RdT
M
由 （ 2） 得
dT = ( PdV + VdP )
µ
M R
代入(1)得 代入(
M µ PdV =－ CV ( PdV + VdP ) MR µ
PRdV =－CV ( PdV + VdP )
W = − ∫ dE = − ( E2 − E1 )
E1
E2
上式表明， 上式表明，在 绝热过程中， 绝热过程中，系统 对外做功完全依靠 自身热力学能的减 少.
p p1 p2 0
V1
绝热线
Ι
ΙΙ
V2
等温线
V
∵ E 2 − E1 =
∴ W =− M
M
µ
CV (T2 − T1 )
µ
CV (T2 − T1 )
3. 等温过程 温度保持不变的过程叫做等温过程 等温过程. 温度保持不变的过程叫做等温过程
∵ dT = 0 ∴ dE = 0
（热力学能只取决 于温度） 于温度）
p p1 p p2 0
Ι
∴ dQT = PdV M 1 又P＝ RT µ V
ΙΙ
V1 dV V2 V
dV RT ∴ W = ∫ PdV = ∫ V1 V1 µ V M V2 V2 RT ln = P1V1 ln = µ V1 V1
e a
d
V
沿曲线bea返回到状态 （2）当系统从状态 沿曲线 返回到状态 ）当系统从状态b沿曲线 返回到状态a 外界对系统做功84J ，问系统是吸热还是放 时，外界对系统做功 热？传递了多少热量？ 传递了多少热量？

热力学第一定律的实际运用热力学第一定律是物理学中的重要定律，它表明系统的热力学属性的变化与体系中所耗能量的大小是对应的。

热力学第一定律是热力学原理的基础，在许多科学和工程领域中有着重要的应用。

本文主要介绍热力学第一定律在实际应用中的一些典型案例。

首先，热力学第一定律可以用来解释不同体系中物质的状态变化，如温度、压强和密度等。

例如，当某种物质从固态变成液态时，根据热力学第一定律，所消耗的能量是定值的。

这使得我们可以通过计算它的温度及压强变化，从而确定物质在那个温度把固态变成液态的反应热。

另外，热力学第一定律也用于描述一定大小的系统中的能量变化。

一个典型的例子是发动机，它从燃料和空气中获得能量，将其转化为运动能量。

根据热力学第一定律，发动机的转速和所消耗的能量是相关的，即发动机的转速越高，所消耗能量就越多。

热力学第一定律还可以应用于热量转移。

例如，当物质从一个温度较高的区域传递到一个温度较低的区域时，根据热力学第一定律，可以确定传热量的大小。

因此，我们可以根据热力学第一定律来设计各种冷却系统，以达到将高温物体降温的目的。

此外，热力学第一定律还可以应用于量子力学中。

例如，根据热力学第一定律，系统发生变化时，系统的平均能量和平均熵也会发生变化。

这就是热力学定理的量子机械理论的基础。

综上所述，热力学第一定律是实际应用中的一个重要定律，应用范围很广，涉及到从物态变化、发动机运行到量子力学中的多个领域。

它的机理清晰，可以用来计算各种体系中物质的状态变化，设计各种冷却系统或者计算量子力学中的能量变化等。

由此可见，热力学第一定律在实际应用中发挥着重要的作用。

热力学第一定律在各种物理过程中的应用热力学是研究热、能量、功的关系的一门科学，其核心之一就是热力学第一定律。

热力学第一定律是热力学基本定律之一，指出能量不会消失，也不会从虚无中产生，只能从一种形式转换成另一种形式。

本文将探讨热力学第一定律在各种物理过程中的应用。

1、热力学第一定律的表述热力学第一定律有两种表述：一是能量守恒定律，也叫能量平衡定律；二是热与功的等价定律。

能量守恒定律是热力学第一定律的基本表述，其含义是在任何物理过程中，能量的总量都是不变的，即能量既不会凭空消失，也不会凭空出现。

在一个系统内，各部分之间的任何能量交换，必须遵守能量守恒定律。

热与功的等价定律是热力学第一定律的另一种表述。

它指出，在任何物理过程中，热与功的总量是等价的，即单位功所相当的热，叫做能量等价。

也就是说，热与功既可以相互转化，也可以相互作用。

这个定律能够正确地描述非平衡态下热力学过程的本质。

2、热力学第一定律在热机中的应用热机是一种将热能转换成机械能的装置，如蒸汽机、内燃机等。

在热机的工作过程中，热力学第一定律被广泛应用。

根据热力学第一定律，热机的过程中，输入的热量等于输出的机械功和散失的热量之和。

以汽车内燃机为例，其工作原理是使用气缸内燃机的方式，将汽油、氧气混合气体点燃，使爆炸产生的高温高压气体推动发动机活塞，从而让汽车启动。

在这一过程中，汽车内燃机通过将热量转化为机械能来推动汽车，同时也会散失一部分热量，如排气管的热气等等。

3、热力学第一定律在热传递中的应用热传递是将热量从高温对象传递到低温对象的过程，可以通过传导、对流、辐射等方式进行。

无论采用何种方式，热传递都遵循热力学第一定律。

例如，当我们在吃烧烤的时候，烤肉的过程也涉及到了热传递。

具体过程是，炭火不断地向烤肉传递热量，而烤肉也不断散发出热量，当烤肉的温度达到接近炭火的温度时，烤肉开始变得吸收不了炭火的热量，于是烤肉的内部变得越来越熟，烤出来的食物就变得更加美味了。

思考题、讨论题、作业
习题6,7
教学后记
本节课是本章的重难点.学生通过本节课的学习,基本上掌握了等容,等压,等温和绝热过程的特点,能运用这些特点解决一些相关问题,达到了预期效果.
绝热过程的特中，如果系统对外界做正功，就必须以消耗系统的内能为代价，即系统的内能减少；反之，如果系统对外界做负功（也叫做外界对系统做正功），则系统的内能就增加。按照内能增量的计算公式，我们有：
最后一步用到了 ，式中 是比热容比。绝热过程没有热量交换，摩尔热容为零。
3、绝热方程
由上面的式子可以看出，在等压过程中气体的吸热一部分用于增加内能，一部分用于对外做功。对于无限小的等压过程有
按摩尔热容的定义式，等压摩尔热容为：
其中
称为迈耶公式，表示等压摩尔热容和等体摩尔热容的关系。CP比CV,大一个R是因为系统在等压过程中，要多吸收一部分热量用来对外做功。这个关系也可以用比热容比 表示，比热容比 定义为等压摩尔热容和等容摩尔热容之比
绝热过程不是等值过程，系统的状态参量P、V、T在过程中均为变量，它和其它过程一样会有一个描写过程曲线的方程，这个方程叫做绝热方程。绝热过程的曲线叫做绝热线。下面推导理想气体的绝热过程方程。对于理想气体，将物态方程 全微分，有
对于平衡态绝热过程，由dA=－dE和dA=PdV以及 ，可得
将上面两式相除消去dT，得到
或
γ为比热容比。把上式分离变量为：
两端积分
得到
或
最后得到绝热方程
＝常量
上式称为绝热过程的泊松方程。再使用物态方程 ，上式可以替换成：
＝常量
＝常量
上面三个式子统称为绝热方程。
4、绝热过程讨论
下图是P－V图上的绝热过程曲线（1），以及它和等温过程曲线（2）的比较。从图中可以看出，一定量的理想气体从同一状态A出发，绝热线要比等温线变化陡一些，亦即发生相同的体积变化 时，绝热过程的压强变化绝对值 要比等温过程大一些。

3 2 V1(
pa
pc )
450R
300
c
b
循环过程中系统吸热
O
1
2 V（10-3m3）
Q1 Qab Qca 600R ln 2 450R 866R
循环过程中系统放热
此循环效率
Q2 Qbc 750R
1
Q2 Q1
1
750R 866R
13.4 00
29
例 逆向斯特林致冷循环的热力学循环原理如图所示
当高温热源的温度T1一定时，理想气体卡诺循环的致 冷系数只取决于T2 。 T2 越低，则致冷系数越小。
26
三、 卡诺定理
1. 在温度分别为T1 与T2 的两个给定热源之间工作的一切可 逆热机，其效率 相同，都等于理想气体可逆卡诺热机的
效率，即
1 Q2 1 T2
Q1
T1
2. 在相同的高、低温热源之间工作的一切不可逆热机，其
曲线起始于同一点. n可取任意值，不同n对应不同的过程曲线。
16
3种多方过程方程：
理想气体多方过程的定义 ：
pV n C
再根据理想气体的状态方程：
PV RT
以T、V或T、p为独立变量，还可有如下多方过程方程 ：
TV n1 C
p n1 Tn
C
17
二、多方过程摩尔热容
设多方过程的摩尔热容为Cn.m ，则：
dQ Cn,mdT
根据理想气体的热一律，可得：
Cn,m dT CV ,m dT pdV
在两边分别除以 dT
Cn,m
CV ,m
p( dVm dT
)n
CV ,m
p( Vm T
)n
式中的下标n 表示是沿多方指数为n 的路径变化。

第二章 热力学第一定律及其应用教学目的：使学生初步了解热力学的方法、建立内能和焓是状态函数的概念，并了解状态函数的性质、理解热力学第一定律，掌握理想气体在各种过程中、∆Η、Q 与W 的计算。

U ∆教学要求：1. 掌握热力学的一些基本概念2. 明确热、功与热力学能三者的区别与联系3. 明确准静态过程与可逆过程的意义4. 充分理解状态函数的意义及其数学性质5. 明确焓的定义，它和热力学能一样都是状态函数6. 熟练掌握气体在等温、等容、等压与绝热过程中△Ｕ、△Ｈ、Ｑ与Ｗ 的计算7. 掌握计算热效应的方法，熟悉掌握盖斯定律和基尔戈夫定律教学重点和难点: 热力学的一些基本概念，各种过程△Ｕ、△Ｈ、Ｑ与Ｗ 的计算，绝热过程、可逆过程与最大功是本章的重点和难点。

§2.1 热力学概论一、 热力学的研究对象1. 热力学：热力学是研究能量相互转换过程中所应遵循的规律的科学。

研究在一定条件下变化的方向和限度。

主要内容是热力学第一定律和第二定律。

这两个定律都是上一世纪建立起来的，是人类经验的总结，有着牢固的实验基础。

本世纪初又建立了热力学第三定律。

2. 化学热力学：用热力学原理来研究化学过程及与化学有关的物理过程就形成了化学热力学。

化学热力学的主要内容：（1）热力学第一定律-----解决化学变化的热效应问题。

（2）热力学第二定律----解决化学及物理变化的方向和限度问题。

^_^---（3）热力学第三定律-----利用热力学的数据解决有关化学平衡的计算问题。

二、热力学的方法及局限性1. 特点（1） 适用于大量质点构成的宏观体系，不适用于分子的个别行为。

（2）不考虑物质的微观结构和反应机理，只知道始终态即可。

2. 局限性：(1)只考虑平衡问题，只计算变化前后总账，无需知道物质微观结构的知识。

即只能对现象之间联系作宏观了解，不能作微观说明。

结果导致知其然而不知其所以然。

(2)只能告诉我们在某种条件下，变化能否发生，进行的程度如何，而不能说明所需的时间、经过的历程、变化发生的根本原因。

热力学第一定律及其应用§ 2. 1 热力学概论热力学的基本内容热力学是研究热功转换过程所遵循的规律的科学。

它包含系统变化所引起的物理量的变化或当物理量变化时系统的变化。

热力学研究问题的基础是四个经验定律（热力学第一定律，第二定律和第三定律，还有热力学第零定律），其中热力学第三定律是实验事实的推论。

这些定律是人们经过大量的实验归纳和总结出来的，具有不可争辩的事实根据，在一定程度上是绝对可靠的。

热力学的研究在解决化学研究中所遇到的实际问题时是非常重要的，在生产和科研中发挥着重要的作用。

如一个系统的变化的方向和变化所能达的限度等。

热力学研究方法和局限性研究方法：热力学的研究方法是一种演绎推理的方法，它通过对研究的系统（所研究的对象）在转化过程中热和功的关系的分析，用热力学定律来判断该转变是否进行以及进行的程度。

特点：首先，热力学研究的结论是绝对可靠的，它所进行推理的依据是实验总结的热力学定律，没有任何假想的成分。

另外，热力学在研究问题的时，只是从系统变化过程的热功关系入手，以热力学定律作为标准，从而对系统变化过程的方向和限度做出判断。

不考虑系统在转化过程中，物质微粒是什么和到底发生了什么变化。

局限性：不能回答系统的转化和物质微粒的特性之间的关系，即不能对系统变化的具体过程和细节做出判断。

只能预示过程进行的可能性，但不能解决过程的现实性，即不能预言过程的时间性问题。

§2. 2 热平衡和热力学第零定律－温度的概念为了给热力学所研究的对象－系统的热冷程度确定一个严格概念，需要定义温度。

温度概念的建立以及温度的测定都是以热平衡现象为基础。

一个不受外界影响的系统，最终会达到热平衡，宏观上不再变化，可以用一个状态参量来描述它。

当把两个系统已达平衡的系统接触，并使它们用可以导热的壁接触，则这两个系统之间在达到热平衡时，两个系统的这一状态参量也应该相等。

这个状态参量就称为温度。

那么如何确定一个系统的温度呢？热力学第零定律指出：如果两个系统分别和处于平衡的第三个系统达成热平衡，则这两个系统也彼此也处于热平衡。

第二章热力学第一定律及应用2.1 人们是怎样认识热的本质的?【答】“热是能量的一种形式。

”这就是热的本质。

回顾过去，人们为了认识热的本质曾走过了一段很长的弯路。

这里，我们不想过多地叙述物理学史中诸如“热质说”等人们认识热的本质时所走过的歧路。

但人们是怎样抛弃了热是物质的假说而承认热是能量的一种形式呢?我们认为这与当时著名的物理学家焦耳的辛勤工作分不开，重温这一历程对于我们认识热的本质也是很有益处的。

焦耳做过的最有名的实验如今已收集在教科书中，他把一个金属奖状搅拌器装到一个盛水的大铁罐中，当搅拌器被一个向下运动的重物驱动时，它就搅拌大铁罐中的水而产生热，产生热量的多少可以根据测量温度上升的多少及大铁罐中水的质量而计算出来。

而消耗的机械能量可以从重物下落的距离和重物的重量计算出来。

这个实验看起来很简单，但是，为了防止热量从实验装置上损失是很不容易的，焦耳采取了许多巧妙的措施才比较好地解决了这一问题。

为了使实验更令人信服，焦耳还曾把大铁罐中的水，换成水银、油等重做这个实验，其结果与水完全一样。

焦耳通过上述实验发现，一定数量的机械能总是产生柑同数量的热量。

也就是说，机械能和热量之间的转换率是一定的。

：焦耳根据自己的实验正确地指出’，热是机械能的另一 种形式，从而道出了热的本质。

实际上，在焦耳之前，有一些物理学家，象牛顿和玻意耳等人就已经认识到热与动能有关，并且推测到热可能是运动的一种形式。

现在人们认为热是分子的无规则运动，换句话说，热是物体分子运动的动能。

例如，当物体的机械能转变成热能时，用分子运动论的观点，我们可以用下述的物理图象来理解。

假定一个下落的物体，当它与地面碰撞时不反弹起来。

在物体下落的过程中，它损失了势能获得了动能。

这时物体中所有的分子都具有向下的运动，平均说来，它们是向一个方向运动，也就是说，运动是定向有规则的。

当物体到达地面而停止运动时，分子的定向有规则运动变成了杂乱的无规则的运动。

即分子的无规则热运动代替了有规则的定向运动。

c a b
d
V1 2V1
V
Ta Td
又根据物态方程
p1V1 Td Ta R
M pV RT M mol
p pcVc 4 p1V1 Tc 4Ta R R 2p1 1 1 再根据绝热方程 TcVc TdVd
Tc Vd ( ) Vc 4 .2V1 16V1 Td （2）先求各分过程的功
dQ 0
pdV M
pV
M RT

CV dT
M pdV Vdp RdT
联立消去dT
dp dV 0 p V
( CV R ) pdV CVVdp
pV 恒量
pV 恒量
M pV RT

V 1T 恒量 p 1T 恒量
绝热线与等温线比较
等温
p
pA
PS
PT
pV C
A
等温线
pdV Vdp 0 p dp V dV T
绝热
pV C
1
o
V
绝 热线
pV
V dp 0

p dp V dV S
dp dV S
P
例、一定质量的理想气体从 P-V 图中的初态 A 经历如图所示的（1）或（2）过程到达末态 B，
TA ，则这两个过程中气体吸收的热量 TB Q1 Q2 Q1 和 Q2的关系是_______________
已知
p
A
( 2)
(1)
B
O
V
例、如图所示， AB 、 DC 为绝热线， COA 为等
M i QP W E ( R R)T 2 QP i i2 CP RR R CV R M / T 2 2 M QP CP (T2 T1 )

热力学第一定律的应用1 理想气体Gay-lussac 和Joule实验Gay-lussac 和Joule分别于1807和1847做了气体向真空膨胀的实验。

装置如图所示。

观察气体由A向真空容器B的膨胀，达到平衡后，没有观察到水浴温度的变化。

同时气体对外也没有做功。

即W=0, Q=0, U=0。

结论：气体在自由膨胀中，内能不变。

根据这个实验，提出了理想气体的焦耳定律：“物质的量固定的气体，它的内能只是温度的函数，而与压力和体积无关。

对于理想气体，等温条件下，PV=常数，可得：焓也只是温度的函数。

同理，C p和C V也仅是温度的函数。

理想气体的C p-C V利用热容的定义，U、H的全微分性质和理想气体的状态方程，可以得到证明：理想气体C p-C v= nR2 可逆过程体积功指体系反抗外力作用膨胀而与环境的功交换。

功是一个过程量。

考虑体系从状态(P1,V1)变化到(P2,V2)经4个不同的体积膨胀过程，所做功分别为：自由膨胀(真空膨胀)：外压为0，功We1=0。

体系膨胀但没有功。

抗恒外压膨胀：外压P e=P2不变，体积变化为V2-V1，W e2= -P2 (V2-V1)。

膨胀过程，V2>V1，W为负值，表示体系对环境做功。

抗二次恒外压：抗外压Pe1，体积变化V’-V1，再抗恒外压P e=P2，体积变化V 2-V’。

做功We3= -Pe1(V’-V1)-P2(V2-V’)。

准静态膨胀：环境压强比体系低一个微小的压差，P e= P-dP，体系发生一个微小的体积膨胀dV。

当这样的微小的外压降低连续发生，直至外压P e=P2，相应体积从V1变到V2时，过程所做功为其中忽略了2阶微小变化dPdV。

若气体近似按理想气体处理，可得：过程不同，体系所做功也不同。

比较四个功的绝对值，可以看到：|We4|>|We3|>|We2|>|We1|。

即准静态过程体系对外做功最大。

功的几何意义是P-V曲线所围面积。