下载文档原格式
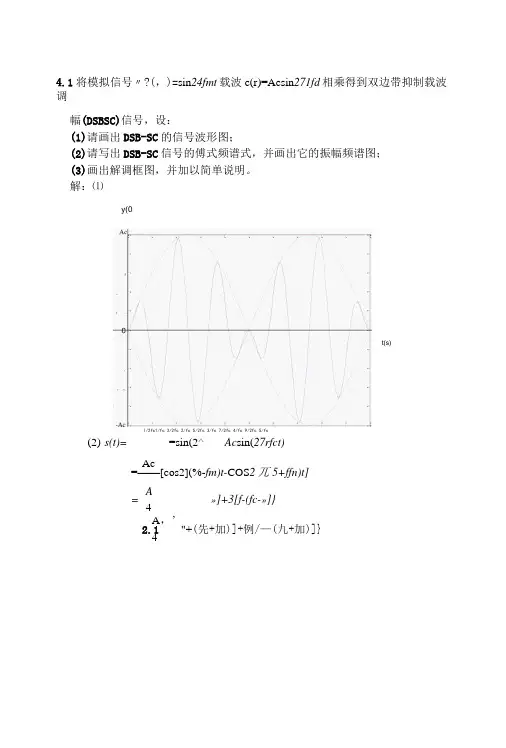
4.1将模拟信号〃?(，)=sin 24fmt 载波c(r)=Acsin 271fd 相乘得到双边带抑制载波调幅(DSBSC)信号，设：(1)请画出DSB-SC 的信号波形图；(2)请写出DSB-SC 信号的傅式频谱式，并画出它的振幅频谱图； (3)画出解调框图，并加以简单说明。
解：⑴(2) s(t)= =sin(2^ Ac sin(27rfct)Ac=——[cos2](%-fm)t-COS 2兀5+ffn)t] A = »]+3[f-(fc-»]} 4A ，’ 2.1 "+(先+加)]+例/—(九+加)]} 4y(0l/2fc1/fc 3/2fc 2/fc 5/2fc 3/fc 7/2fc 4/fc 9/2fc 5/fct(s)S ⑴八3Ac/4- Ac/2.Ac/4(3)相干解调Cos(Wct)与发端相干偏调相干解调：将接收信号与载波信号sin(2乙加)相乘，得至U A cr(t)sin(2^fct)=Acm(t)sin(2^fct)sin(2^fit)=--cos(44fct)]通过低通滤波器抑制载频的二倍频分量，得到解调信号为刈⑺=与机⑺ 2.2 已知某调幅波的展开式为：s(t)=cos(2/rxl()4r)+4COS (2TT xl.lxl040+cos(2万xl.2xl04r) (1)求调幅系数和调制信号频率；(2)写出该信号的傅式频谱式，画出它的振幅频谱图； (3)画出该信号的解调框图。
解：⑴sQ)=cos(24xl04r)+4cos(2乃xl.lxl04r)+cos(2万xl.2xl04r)=4cos(2%xl.lxl04r)[l+0.5cos(2万x0.1xl04r)] 调制系数是a=0.5;信号频率是f=1000Hz(2)S(/)=；U(/+104)+演f —i04)]+2[Mf+l.lxl()4)+5(/—1.1X104)]+-W+1.2X 104)+^(/-1.2X 104)]-fm-fc ・fc -fc+fm。
通信原理知到章节测试答案智慧树2023年最新青海民族大学第一章测试1.某独立发送的二进制信源，1符号出现概率为1/4，该信源的平均信息量为1.98 比特/符号。
（）参考答案:错2.设一数字传输系统传送二进制码元的速率为1200Baud，该系统的信息速率为1200比特/秒。
（）参考答案:错3.消息中所含的信息量是该消息出现的概率的函数。
（）参考答案:对4.概率越小，信息量越小。
（）参考答案:错5.设一个二进制离散信源，以相等的概率发送0和1，则信源每个输出的信息量为1比特。
（）参考答案:对第二章测试1.确定信号的的能量是（）。
参考答案:2.信号的平均功率是（）。
参考答案:13.信号的傅氏变换是（）。
参考答案:4.信号的傅氏变换是（）。
参考答案:5.若实信号的傅氏变换是，则的傅氏变换是（）。
参考答案:6.能量信号的自相关函数的性质有（）。
参考答案:自相关函数和能量谱密度是一对傅里叶变换;自相关函数是偶函数;自相关函数在零点的取值等于信号能量7.信号是非周期信号、且是能量信号。
（）参考答案:对8.信号是周期信号、且是功率信号。
（）参考答案:对9.信号是周期信号、且是功率信号。
（）参考答案:错10.互相关函数和两个信号相乘的前后次序无关。
（）参考答案:错第三章测试1.对随机过程作观测时，可以把随机过程看做是( )的集合，当对随机过程进行理论分析时，可以把随机过程看做是( )的集合。
参考答案:样本函数随机变量2.随机过程数字特征之间的关系是( ).参考答案:方差等于均方值和均值平方之差;在同一个时刻，自相关函数的值就是均方值;在同一个时刻，自协方差函数的值就是方差3.平稳随机过程自相关函数的主要性质是( )。
参考答案:偶函数;在时间差等于0时具有极大值4.随机过程经过线性系统的主要性质有( ).参考答案:如果输入是宽遍历的，则输出也是宽遍历的;如果输入是严平稳的，则输出也是严平稳的;如果输入是宽平稳的，则输出也是宽平稳的5.高斯过程经过线性变换后生成的过程还是高斯过程。
第四章 模拟调制系统已知调制信号 m(t)=cos(2000πt)+cos(4000πt)，载波为cos104πt ，进行单边带调制，试确定该单边带信号的表达试，并画出频谱图。
解：方法一：若要确定单边带信号，须先求得m(t)的希尔伯特变换 m ’（t ）=cos （2000πt-π/2）+cos （4000πt-π/2） =sin （2000πt ）+sin （4000πt ） 故上边带信号为S USB (t)=1/2m(t) cos w c t -1/2m ’(t)sin w c t =1/2cos(12000πt )+1/2cos(14000πt ) 下边带信号为S LSB (t)=1/2m(t) cos w c t +1/2m ’(t) sin w c t =1/2cos(8000πt )+1/2cos(6000πt ) 其频谱如图所示。
方法二：先产生DSB 信号：s m (t)=m(t)cos w c t =···，然后经过边带滤波器，产生SSB 信号。
1. 将调幅波通过残留边带滤波器产生残留边带信号。
若次信号的传输函数H(w )如图所示。
当调制信号为m(t)=A[sin100πt+sin6000πt]时，试确定所得残留边带信号的表达式。
解：设调幅波sm(t)=[m0+m(t)]coswct，m0≥|m(t)|max，且s m(t)<=>S m(w)根据残留边带滤波器在f c处具有互补对称特性，从H(w)图上可知载频f c=10kHz，因此得载波cos20000πt。
故有sm(t)=[m0+m(t)]cos20000πt=m0cos20000πt+A[sin100πt+sin6000πt]cos20000πt=m0cos20000πt+A/2[sin(20100πt)-sin(19900πt)+sin(26000πt)-sin(14000πt)Sm(w)=πm0[σ(w+20000π)+σ(W-20000π)]+jπA/2[σ(w+20100π)-σ(w+19900π)+σ(w-19900π)+σ(w+26000π)-σ(w-26000π)-σ(w+14000π)+σ(w-14000π)残留边带信号为F(t)，且f(t)<=>F(w)，则F(w)=Sm(w)H(w)故有：F(w)=π/2m0[σ(w+20000π)+σ(w-20000π)]+jπA/2[σ(w+20100π)σ(w-20100π)σ(w+19900π)+ σ(w-19900π)+σ(w+26000π)-σ(w-26000π)f(t)=1/2m0cos20000πt+A/2[ππt+sin26000πt]2.设某信道具有均匀的双边噪声功率谱密度Pn(f)=*10-3W/Hz，在该信道中传输抑制载波的双边带信号，并设调制信号m(t)的频带限制在5kHz，而载波为100kHz，已调信号的功率为10kW.若接收机的输入信号在加至解调器之前，先经过一理想带通滤波器滤波，试问：1.）该理想带通滤波器应具有怎样的传输特性H(w)2.）解调器输入端的信噪功率比为多少3.）解调器输出端的信噪功率比为多少4.）求出解调器输出端的噪声功率谱密度，并用图型表示出来。
第四章4-1设一条无线链路采用视距传播方式通信，其收发天线的架设高度都等于40m，若不考虑大气折射的影响，试求其最远通信距离。
解：D = J&R 花45km4-2设一条天波无线电信道，用高度等于400km的F2层反射电磁波，地球的等效半径等于（6370 x4/3）km，收发天线均架设在地面，试求其通信距离大约能达到多少千米?设地球的等效半径为r, F2层的高度为h，最大通信距离（直线距离）的一半为 d : 解: （图略）。
4-3米。
4-4dJ(r +h - J r2 -d2)2+d24式中，h = 400km，r =6374 x-km，3J r2 -d22d即为所求。
设有一平流台距离地面29km，试按上题给定的条件计算其覆盖地面的半径等于多少千解：将上式中的h=400km改为h=29km即可。
设一个接收机输入电路的等效电阻等于600 O，输入电路的带宽等于6MHz，环境温度为27 C，试求该电路产生的热噪声电压有效值。
解：V = j4kTRB = 丁4勺.38咒10"^3心00咒600咒6咒106 = 7.72AV4-5某个信息源有 A 、B 、C 和D 等四个符号组成。
设每个符号独立出现，其出现的概率分 别为1/4、1/4、3/16、5/16，经过信道传输后，每个符号正确接受的概率为1021/1024， 错为其他符号的条件概率 P(x /y j )均为1/1024，画出此信道的模型，并求出该信道的容量 C 等于多少b/符号。
解：此信源的平均信息量(熵)为33 5 5 H(x)弋 P( x i )log 2 P( X i ) -2 导瞄胡。
临胡og 2 花=1.977(b/符号)P®/" =1021/1024 (i =1,2,3,4)P(y i /X j )=1/1024 (iHj)P(X 1/V 1)「P(X 1)P SxJ2 P(X k )P(V 1/x k )kd ： (14)x(1021/1024)(1/4)x(1021/1024) +(1/4)咒(11024) +(3/16)x(1/1024) + ⑸ 16)"们024) 1021 1024=P 化仏)P(x / V )=2 X (14)天(1/1024)+ (3/16) X (1021/1024) + ⑸ 16)咒(1/1024) 30633076"x"%) "2x(1/4)x(们024) +(3/16)x(1/1024)+(5/16)x(1021/1024) 5105 5116(3/16)x(1021 1024)(5/16)咒(10211024)4 4H(x/y)=—2；P(y j)2；[P(^/y j)log2 P(X i/y j)]1 4 1 4 ---Z [P(x/y1)log2P(X i/y1)]-；送[P(X i/y2)log2 P^/y?)]4i 43 4 5 4--Z [P(X i/y3)log2 P(为/y3)] --2 [P化/y4)log2 P(^/y。
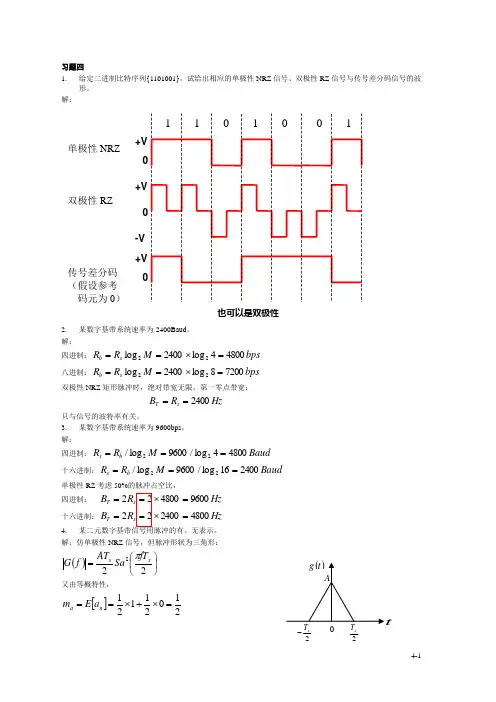
习题四 1. 给定二进制比特序列{1101001}，试给出相应的单极性NRZ 信号、双极性RZ 信号与传号差分码信号的波形。
解：2. 某数字基带系统速率为2400Baud 。
解：四进制：bps M R R s b 48004log2400log 22=⨯==八进制：bps M R R s b 72008log 2400log22=⨯==双极性NRZ 矩形脉冲时，绝对带宽无限，第一零点带宽： Hz R B s T 2400== 只与信号的波特率有关。
3. 某数字基带系统速率为9600bps 。
解：四进制：Baud M R R b s 48004log/9600log/22===十六进制：Baud M R R b s 240016log /9600log /22===单极性RZ 考虑50%的脉冲占空比，四进制： Hz R B s T 9600480022=⨯== 十六进制：Hz R B s T 4800240022=⨯== 4.某二元数字基带信号用脉冲的有、无表示。
解：仿单极性NRZ 信号，但脉冲形状为三角形：()⎪⎭⎫ ⎝⎛=222s sfT Sa AT f G π 又由等概特性，[]21021121=⨯+⨯==n a a E m单极性NRZ双极性RZ传号差分码 （假设参考 码元为0）也可以是双极性+V +V-V +V[][]4121021121222222=⎪⎭⎫⎝⎛-⨯+⨯=-=n na a E aE σ由教材P134公式（4.2.2），该数字基带信号的功率谱为：()()()∑∑∑∑∞±±±=∞-∞=∞-∞=∞-∞=⎪⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫⎝⎛⨯⨯=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+=.......5,3,144224242424222422222221621621621624412441k s s s k s s s k s s sss sss k s T sa T s as T k f k Af AfT Sa T A T k f k Sa A fT Sa T A T k f fT Sa T A T fT Sa T A T T k f T k G T m f G T f P δπδπδππδππδσ5.1和0概率为p 和1-p ，用()t g 和()t g -表示。
第四章模拟调制4.1学习指导4.1.1要点模拟调制的要点主要包括幅度调制、频率调制和相位调制的工作原理。
1.幅度调制幅度调制是用调制信号去控制载波信号的幅度，使之随调制信号作线性变化的过程。
在时域上，已调信号的振幅随基带信号的规律成正比变化；在频谱结构上，它的频谱是基带信号频谱在频域内的简单平移。
由于这种平移是线性的，因此，振幅调制通常又被称为线性调制。
但是，这里的“线性”并不是已调信号与调制信号之间符合线性变换关系。
事实上，任何调制过程都是一种非线性的变换过程。
幅度调制包括标准调幅（简称调幅）、双边带调幅、单边带调幅和残留边带调幅。
如果调制信号m(t)的直流分量为0，则将其与一个直流量A0相叠加后，再与载波信号相乘，就得到了调幅信号，其时域表达式为stAmttAtmttAM()0()cosc0cosc()cosc(4-1)如果调制信号m(t)的频谱为M(ω)，则调幅信号的频谱为1S()πA()()M()M()(4-2)AM0cccc2调幅信号的频谱包括载波份量和上下两个边带。
上边带的频谱结构与原调制信号的频谱结构相同，下边带是上边带的镜像。
由波形可以看出，当满足条件|m(t)|A0(4-3)时，其包络与调制信号波形相同，因此可以用包络检波法很容易恢复出原始调制信号。
否则，出现“过调幅”现象。
这时用包络检波将发生失真，可以采用其他的解调方法，如同步检波。
调幅信号的一个重要参数是调幅度m，其定义为m A m(t)Am(t)0max0minAm(t)Am(t)0max0min(4-4)AM信号带宽B AM是基带信号最高频率分量f H的两倍。
AM信号可以采用相干解调方法实现解调。
当调幅度不大于1时，也可以采用非相干解调方法，即包络检波，实现解调。
双边带信号的时域表达式为stmttDSB()()cosc(4-5)其中，调制信号m(t)中没有直流分量。
如果调制信号m(t)的频谱为M(ω)，双边带信号的频谱为1S()M()M()(4-6)DSBcc2与AM信号相比，双边带信号中不含载波分量，全部功率都用于传输用用信号，调制效率达到100%。
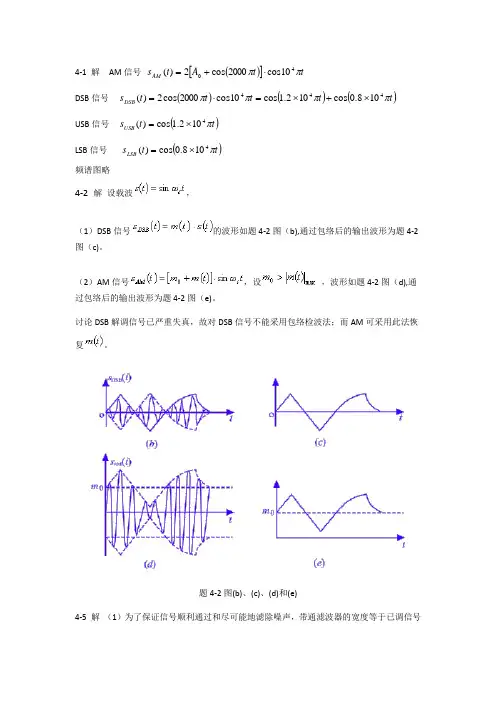
4-1 解 AM 信号 ()[]t t A t s AM ππ4010cos 2000cos 2)(⋅+=DSB 信号 ()()()t t t t t s DSB ππππ444108.0cos 102.1cos 10cos 2000cos 2)(⨯+⨯=⋅= USB 信号 ()t t s USB π4102.1cos )(⨯=LSB 信号 ()t t s LSB π4108.0cos )(⨯=频谱图略4-2 解 设载波，（1）DSB 信号的波形如题4-2图（b),通过包络后的输出波形为题4-2图（c)。
（2）AM 信号，设 ，波形如题4-2图（d),通过包络后的输出波形为题4-2图（e)。
讨论DSB 解调信号已严重失真，故对DSB 信号不能采用包络检波法；而AM 可采用此法恢复。
题4-2图(b)、(c)、(d)和(e)4-5 解 （1）为了保证信号顺利通过和尽可能地滤除噪声，带通滤波器的宽度等于已调信号带宽，即kHz f B m 8422=⨯==，其中心频率为100kHz ，故有为常数，其中其他，，K kHzf kHz K H ⎩⎨⎧≤≤=010496)(ω。
（2）已知解调器的输入信号功率W mW S i 31022-⨯==，输入噪声功率为)(1032101021082)(26633W f P B N n i ---⨯=⨯⨯⨯⨯⨯=⋅=故输入信噪比5.62=iiN S （3）因为DSB 调制制度增益2=DSB G ，故解调器的输出信噪比 1252==ii o o N SN S （4）根据相干解调器的输出噪声与输入噪声功率关系)(108416W N N i o -⨯==又因解调器中低通滤波器的截止频率为kHz f m 4=，故输出噪声的功率谱密度kHz f Hz W f N f P m o N o 4)/(1011081082)(336≤⨯=⨯⨯==--， μ 或者，根据相干解调器的输出噪声与输入噪声功率关系)(21)(t n t n c o =，其中)(t n c 是解调器输入端高斯窄带噪声的同相分量，其功率谱密度kHz f Hz W f P f P n nc 4)/(104)(2)(3≤⨯==-， μ因此输出噪声)(t n o 的功率谱密度kHz f Hz W f P f P nc no 4)/(101)(41)(3≤⨯==-， μ 功率谱图略4-6 解 方法如上题 （1）为常数，其中其他，，K kHzf kHz K H ⎩⎨⎧≤≤=010096)(ω（2）125=i i N S （3）125=oo N S4-7 解练习题4-7图 接收机模型（1）设双边带信号，则输入信号功率（2）双边带信号采用相干解调的输出为，故输出信号功率（3）因，则故输出信噪比或由，得4-8 解设发射机输出功率为，损耗，已知，（1）DSB/SC方式：因，则又因，则所以（2）SSB/SC 方式：因，则又因，则所以讨论 若要获得相同的输出信噪比，采用DSB 传输是所需的小于SSB 的。
通信原理课后习题答案思考题1-1 什么是通信？常见的通信⽅式有哪些？1-2 通信系统是如何分类的？1-3 何谓数字通信？数字通信的优缺点是什么？1-4 试画出模拟通信系统的模型，并简要说明各部分的作⽤。
1-5 试画出数字通信系统的⼀般模型，并简要说明各部分的作⽤。
1-6 衡量通信系统的主要性能指标是什么？对于数字通信具体⽤什么来表述？1-7 何谓码元速率?何谓信息速率?它们之间的关系如何?习题1-1 设英⽂字母E出现的概率=0.105，X出现的概率为＝0.002，试求E和X的信息量各为多少？1-2 某信源的符号集由A、B、C、D、E、F组成，设每个符号独⽴出现，其概率分别为1/4、1/4、1/16、1/8、1/16、1/4，试求该信息源输出符号的平均信息量。
1-3 设⼀数字传输系统传送⼆进制信号，码元速率RB2=2400B，试求该系统的信息速率Rb2=？若该系统改为传送16进制信号，码元速率不变，则此时的系统信息速率为多少？1-4 已知某数字传输系统传送⼋进制信号，信息速率为3600b/s，试问码元速率应为多少？1-5 已知⼆进制信号的传输速率为4800b/s，试问变换成四进制和⼋进制数字信号时的传输速率各为多少（码元速率不变）？1-6 已知某系统的码元速率为3600kB，接收端在l⼩时内共收到1296个错误码元，试求系统的误码率=？1-7 已知某四进制数字信号传输系统的信息速率为2400b/s，接收端在0.5⼩时内共收到216个错误码元，试计算该系统=？l-8 在强⼲扰环境下，某电台在5分钟内共接收到正确信息量为355Mb，假定系统信息速率为1200kb/s。
（l）试问系统误信率=？（2）若具体指出系统所传数字信号为四进制信号，值是否改变？为什么？（3）若假定信号为四进制信号，系统传输速率为1200kB，则＝？习题答案第⼀章习题答案1-1 解：1-2 解：1-3 解：1-4 解：1-5 解：1-6 解：1-7 解：1-8 解：思考题2-1 什么是狭义信道？什么是⼴义信道？（答案）2-2 在⼴义信道中，什么是调制信道？什么是编码信道？2-3 试画出调制信道模型和⼆进制⽆记忆编码信道模型。
第一章习题习题1.1 在英文字母中E 出现的概率最大，等于0.105，试求其信息量。
解：E 的信息量：()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题1.2 某信息源由A ，B ，C ，D 四个符号组成，设每个符号独立出现，其出现的概率分别为1/4，1/4，3/16，5/16。
试求该信息源中每个符号的信息量。
解：b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-=b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题1.3 某信息源由A ，B ，C ，D 四个符号组成，这些符号分别用二进制码组00，01，10，11表示。
若每个二进制码元用宽度为5ms 的脉冲传输，试分别求出在下列条件下的平均信息速率。
（1） 这四个符号等概率出现； （2）这四个符号出现概率如习题1.2所示。
解：（1）一个字母对应两个二进制脉冲，属于四进制符号，故一个字母的持续时间为2×5ms 。
传送字母的符号速率为Bd 100105213B =⨯⨯=-R等概时的平均信息速率为s b 2004log log 2B 2B b ===R M R R（2）平均信息量为比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 b 7.197977.1100B b =⨯==H R R习题1.4 试问上题中的码元速率是多少？解：311200 Bd 5*10B B R T -===习题1.5 设一个信息源由64个不同的符号组成，其中16个符号的出现概率均为1/32，其余48个符号出现的概率为1/96，若此信息源每秒发出1000个独立的符号，试求该信息源的平均信息速率。
解：该信息源的熵为96log 961*4832log 321*16)(log )()(log )()(22264121+=-=-=∑∑==i i i i Mi i x P x P x P x P X H=5.79比特/符号因此，该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
第四章模拟调制系统已知调制信号m(t)=cos(2000πt)+cos(4000πt)，载波为cos104πt，进行单边带调制，试确定该单边带信号的表达试，并画出频谱图。
解：方法一：若要确定单边带信号，须先求得m(t)的希尔伯特变换m’（t）=cos（2000πt-π/2）+cos（4000πt-π/2）=sin（2000πt）+sin（4000πt）故上边带信号为S USB(t)=1/2m(t) cos w c t-1/2m’(t)sin w c t=1/2cos(12000πt)+1/2cos(14000πt)下边带信号为S LSB(t)=1/2m(t) cos w c t+1/2m’(t) sin w c t=1/2cos(8000πt)+1/2cos(6000πt)其频谱如图所示。
方法二：先产生DSB信号：s m(t)=m(t)cos w c t=···，然后经过边带滤波器，产生SSB信号。
1.将调幅波通过残留边带滤波器产生残留边带信号。
若次信号的传输函数H(w)如图所示。
当调制信号为m(t)=A[sin100πt +sin6000πt]时，试确定所得残留边带信号的表达式。
解：设调幅波sm(t)=[m0+m(t)]coswct，m0≥|m(t)|max，且s m(t)<=>S m(w)根据残留边带滤波器在f c处具有互补对称特性，从H(w)图上可知载频f c=10kHz，因此得载波cos20000πt。
故有sm(t)=[m0+m(t)]cos20000πt=m0cos20000πt+A[sin100πt+sin6000πt]cos20000πt=m0cos20000πt+A/2[sin(20100πt)-sin(19900πt)+sin(26000πt)-sin(14000πt)Sm(w)=πm0[σ(w+20000π)+σ(W-20000π)]+jπA/2[σ(w+20100π)-σ(w+19900π)+σ(w-19900π)+σ(w+26000π)-σ(w-26000π)-σ(w+14000π)+σ(w-14000π)残留边带信号为F(t)，且f(t)<=>F(w)，则F(w)=Sm(w)H(w)故有：F(w)=π/2m0[σ(w+20000π)+σ(w-20000π)]+jπA/2[0.55σ(w+20100π)-0.55σ(w-20100π)-0.45σ(w+19900π)+ 0.45σ(w-19900π)+σ(w+26000π)-σ(w-26000π)f(t)=1/2m0cos20000πt+A/2[0.55sin20100πt-0.45sin19900πt+sin26000πt]-3W/Hz，在该信道中传输抑制载2.设某信道具有均匀的双边噪声功率谱密度Pn(f)=0.5*10波的双边带信号，并设调制信号m(t)的频带限制在5kHz，而载波为100kHz，已调信号的功率为10kW.若接收机的输入信号在加至解调器之前，先经过一理想带通滤波器滤波，试问：1.）该理想带通滤波器应具有怎样的传输特性H(w)?2.）解调器输入端的信噪功率比为多少?3.）解调器输出端的信噪功率比为多少?4.）求出解调器输出端的噪声功率谱密度，并用图型表示出来。
解：1.）为了保证信号顺利通过和尽可能的滤除噪声，带通滤波器的宽度等于已调信号带宽，即B=2fm=2*5=10kHz，其中中心频率为100kHz。
所以H(w)=K ，95kHz≤∣f∣≤105kHz0，其他2.）Si=10kWNi=2B* Pn(f)=2*10*103*0.5*10-3=10W故输入信噪比Si/Ni=10003.）因有GDSB=2故输出信噪比S0/N0=20004.）据双边带解调器的输出嘈声与输出嘈声功率关系，有：N0=1/4 Ni =2.5W故 Pn 双(f)= N0/2fm=0.25*10-3W/Hz =1/2 Pn(f) ∣f ∣≤5kHz4 若对某一信号用DSB 进行传输，设加至接收机的调制信号m(t)的功率谱密度为 Pm(f)= nm/2*│f │/fm ， │f │≤fm│f │≥fm试求：1） 接受机的输入信号功率 2） 接收机的输出信号功率3） 若叠加于DSB 信号的白噪声具有双边功率谱密度为n0/2，设解调器的输出端接有截止频率为fm 的理想低通滤波器，那么输出信噪功率比为多少?解：1）.设双边带信号sm(t)=m(t)coswct ，则输入信号功率 Si=s 2m (t)=1/2 m 2(t)=1/4 fm*nm2）双边带信号采用相干解调的输出为m0(t)=1/2m(t)，故输出信号功率 S0=m 20(t)=1/4 m 2(t)=1/8 fm*nm3）因Ni=n0B ，B=2fm ，则N0=1/4Ni=1/4·n0B=1/2·n0fm 故输出信噪比S0/N0=1/4·nm/n05 设某信道具有均匀的双边噪声功率谱密度Pn （f ）=5*10-3W/Hz ，在该信道中传输抑制载波的单边带信号，并设调制信号m （t ）的频带限制在5kHz 。
而载频是100kHz ，已调信号功率是10kW 。
若接收机的输入信号在加至解调器之前，先经过一理想带通滤波器，试问：1） 该理想带通滤波器应具有怎样的传输特性。
2） 解调器输入端信噪比为多少? 3） 解调器输出端信噪比为多少?解：1）H(f)= k ，100kHz ≤∣f ∣≤105kHz = 0 ， 其他2）Ni=Pn(f)·2fm=0.5*10-3*2*5*103=5W故Si/Ni=10*103/5=20003）因有G SSB=1，S0/N0= S i/N i =2000-9W，由发射机输出端到调制6某线性调制系统的输出信噪比为20dB，输出噪声功率为10器输入端之间总的传输耗损为100dB，试求：1）DSB/SC时的发射机输出功率。
2）SSB/SC时的发射机输出功率。
解：设发射机输出功率为ST，损耗K=ST/Si=1010(100dB)，已知S0/N0=100·（20dB），N0=10-9W1）DSB/SC方式：因为G=2，Si/Ni=1/2·S0/N0=50又因为Ni=4N0Si=50Ni=200N0=2*10-7WST=K·Si=2*103W2）SSB/SC方式：因为G=1，Si/Ni= S0/N0=100又因为Ni=4N0Si=100Ni=400N0=4*10-7WST=K·Si=4*103W7试证明：当AM信号采用同步检测法进行解调时，其制度增益G与公式(4-37)的结果相同。
证明：设AM信号为sm(t)=[A+m(t)]coswct式中，A≥∣m(t)∣max输入噪声为ni(t)=nc(t)coswct-ns(t)sinwct则解调器输入的信号功率Si和噪声功率Ni分别为Si=A2/2+m2(t)/2，Ni=n2i(t)=n0B设同步检测(相干解调)中，相干载波为coswct，则[sm(t)+ni(t)]coswct LPF A/2+m(t)/2+nc(t)故输出有用信号和输出噪声分别为m0(t)=m(t)/2，n0(t)=nc(t)/2所以S0=m2(t)/4，N0=n2c(t)/4=n0B/4故：G=2m2(t)/[A2+m2(t)]-3W/Hz，在该信道中传输振幅调8设某信道具有均匀的双边噪声功率谱密度Pn(f)=0.5*10制信号，并设调制信号m(t)的频带限制在5kHz，而且载频是100kHz，边带功率为10kW，载波功率为40kW。
若接收机的输入信号先经过一个合适的理想带通滤波器，然后再加至包络检波器进行调制。
试求：1）解调器输入端的信噪功率比2）解调器输出端的信噪功率比3）制度增益G解：1）.设sAM(t)=[A+m(t)]coswct，且m(t)=0，则Si=1/2A2+1/2m2(t)=Pc+Ps=50kW式中，Pc为载波功率，Ps为边带功率又Ni=Pn(f)·2B= Pn(f)·4fm=10W故S i/N i=5000（37dB）2）假定[A+m（t）]>>ni(t)，则理想包络检波输出为E(t)≈A+m(t)+nc(t) 则：S0=m2 (t)=2Ps=2*10=20kW；N0=n2c(t)=Ni=10kW故S0/N0=2000(33dB)3）G=2000/5000=2/56+104cos2π*103tHz，试求：9已知某单频调频波的振幅是10V，瞬时频率为f(t)=101）此调频波的表达式2）此调频波的频率偏移，调频指数和频带宽度3Hz，则调频波的频偏，调制指数和频带宽度如何变化?3）调制信号频率提高到2*10解：1）该调制博得瞬时角频率为w(t)=2πf(t)=2π*106+2π*104cos2π*103t rad/s此时，该调频波的总相位θ(t)=∫w(τ)dτ=2π*106t+10sin2π*103t因此，调频波的时域表达式sFM(t)为sFM(t)=Acosθ(t)=20cos(2π*106t+10sin2π103t)V2）根据频率偏移的定义Δf=∣Δf(t)∣MAX=∣104cos2π*103t∣MAX=10kHz调频指数为mf=Δf/fm=104/103=10这样可以得到调频波的带宽为B ≈2(Δf+fm)=2(10+1)=22kHz3） 现调制信号频率fm 由103Hz 提高到2*103Hz 。
因频率调制时已调波频率偏移与调制信号频率无关，故这时调频信号的频率偏移仍然是 Δf=10kHz 而这时调频指数变为mf=Δf/fm=104/2*103=5这时调频信号的带宽为B ≈2(Δf+fm)=2(10+2)=24kHz由上述结果可知：由于Δf>>fm ，所以，虽然调制信号频率fm 增加了一倍，但调制信号的带宽B 变化很小。
10 根据图所示的调制信号波形，试画出DSB 波形 解：11 根据上题所求出的DSB 图形，结合书上的AM 波形图，比较它们分别通过包络检波器后的波形差别解：讨论比较：DSB 信号通过包络检波器后产生的解调信号已经严重失真，所以DSB 信号不能采用包络检波法;而AM 可采用此法恢复m(t)12某调制方框图如下，已知m(t)的频谱如下面所示。
载频w1<<w2，w1>wH，且理想低通滤波器的截止频率为w1，试求输出信号s(t)，并说明s(t)为何种一调制信号。
s2(t)=m(t)sinw1tsinw2t经过相加器后所得的s(t)即为：s(t)=s1(t)+s2(t)=m(t)[cosw1cosw2+sinw1sinw2]=m(t)cos[(w1-w2)t]由已知w1<<w2 w1>wH故：s(t)=m(t)cosw2t所以所得信号为DSB信号13已知调制信号的频谱图如图所示，载波为cos104πt，试确定该信号的单边带信号表达解：由已知的图即可得知：上边带信号为S USB(t)=1/4m(t) cos w c t-1/4m’(t)sin w c t=1/4cos(13000πt)+1/4cos(11000πt)下边带信号为S LSB(t)=1/4m(t) cos w c t+1/4m’(t) sin w c t=1/4cos(9000πt)+1/4cos(7000πt)因此可以求得m(t)的希尔伯特变换m’（t）=sin（1000πt）+sin（3000πt）=cos（1000πt-π/2）+cos（3000πt-π/2）这样即可求得调制信号m(t)=cos(1000πt)+cos(3000πt)14已知调制信号的上边带信号为S USB(t)=1/4cos(25000πt)+1/4cos(22000πt)，已知该载波为cos2*104πt求该调制信号的表达式。
