高中数学必修二点线面知识点与练习

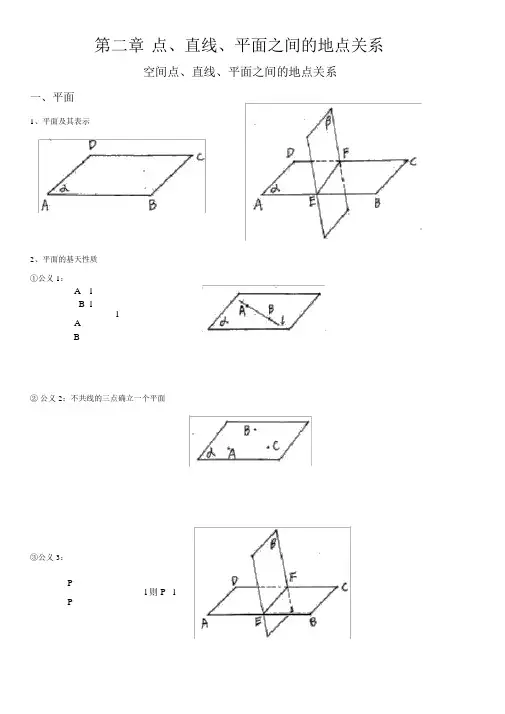
第二章点、直线、平面之间的地点关系空间点、直线、平面之间的地点关系一、平面1、平面及其表示2、平面的基天性质①公义 1：A lB llAB②公义 2：不共线的三点确立一个平面③公义 3：Pl 则 P lP二、点与面、直线地点关系1、 A1、点与平面有 2 种地点关系2、 B2、点与直线有1、 A l2 种地点关系l2、 B三、空间中直线与直线之间的地点关系1、异面直线2、直线与直线的地点关系订交共面平行异面3、公义 4 和定理公义 4：l1 Pl3l1 Pl 2l 2 Pl3定理：空间中假如两个角的两边分别对应平行，那么这两个角相等或互补。

4、求异面直线所成角的步骤：① 作：作平行线获得订交直线；② 证：证明作出的角即为所求的异面直线所成的角；③ 结构三角形求出该角。

提示： 1、作平行线常有方法有：直接平移，中位线，平行四边形。

2、异面直线所的角的范围是000 ,90。

四、空间中直线与平面之间的地点关系地点关系直线 a在平面内直线 a与平面订交直线 a与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a a IA a P图形表示五、空间中平面与平面之间的地点关系地点关系两个平面平行两个平面订交公共点没有公共点有一条公共直线符号表示P I a图形表示直线、平面平行的判断及其性质一、线面平行1、判断：ba b Pb Pa（线线平行，则线面平行）2、性质：a Pa a Pbb（线面平行，则线线平行）二、面面平行1、判断：aba b P Pa Pb P（线面平行，则面面平行）2、性质 1：PI a a PbI b（面面平行，则线面平行）性质 2：Pm Pm（面面平行，则线面平行）说明（ 1）判断直线与平面平行的方法：① 利用定义：证明直线与平面无公共点。

② 利用判断定理：从直线与直线平行等到直线与平面平行。

③ 利用面面平行的性质：两个平面平行，则此中一个平面内的直线必平行于另一个平面。

（2）证明面面平行的常用方法①利用面面平行的定义：此法一般与反证法联合。

描述：高中数学必修2(人教A版)知识点总结含同步练习题及答案第二章 点、直线、平面之间的位置关系 2.1 空间点、直线、平面之间的位置关系一、学习任务理解空间点、线、面的位置关系，会用数学语言规范地表述空间点、线、面的位置关系；了解可以作为推理依据的公理和定理，能正确地判断空间线线、线面与面面的位置关系．二、知识清单平面的概念与基本性质 点、线、面的位置关系三、知识讲解1.平面的概念与基本性质平面的概念生活中的一些物体通常呈平面形，课桌面、黑板面、海面都给我们以平面的形象．几何里所说的平面就是从这样的一些物体中抽象出来的，但是几何中的平面是没有厚度、无限延展的．平面的画法我们常常把水平的平面画成一个平行四边形，用平行四边形表示平面，平行四边形的锐角通常画为 ，且横边长等于其邻边长的 倍．如果一个平面被另一个平面遮挡住，为了增强它的立体感，我们常把被遮挡的部分用虚线画出来．平面的表示为了表示平面，常把希腊字母 等等写在代表平面的平行四边形的一个角上，如平面 、平面 ；也可以用代表平面的平行四边形的四个顶点，或者相对的两个顶点的大写英文字母作为这个平面的名称，如图中的平面可以表示为平面 、平面 或者平面 ．集合符号在立体几何中的应用以点作为元素，直线和平面都是由点构成的集合．几何中许多符号的规定都是源于将图形视为点集．例如：点 在平面 内，记作 ；点 不在平面 内，记作 ．直线 在平面 内，记作 ；直线 不在平面 内，记作 ；直线 与 相交于点 ，记作 ；平面 与平面 相交于直线 ，记作 ．平面的基本性质平面的基本性质是由三条公理描述的：公理1 如果一条直线上的两点在一个平面内，那么这条直线在此平面内．45∘2α,β,γαβABCD AC BD A αA ∈αA αA ∉αl αl ⊂αl αl ⊄αl m A l ∩m =A αβa α∩β=a A ∈l A ∈α例题：符号语言：，，且 ，．公理2 过不在一条直线上的三点，有且只有一个平面．推论1 经过一条直线和直线外一点，有且只有一个平面．推论2 经过两条相交直线，有且只有一个平面．推论3 经过两条平行直线，有且只有一个平面．公理3 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．符号语言：，且 ，且 ．空间位置关系与几何量的基础平行公理 平行于同一条直线的两条直线互相平行．等角定理 空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．A∈l B∈l A∈αB∈α⇒l⊂αP∈αP∈β⇒α∩β=l P∈l用符号语言表示下列语句．（1）点 在平面 外，点 在平面 内，直线 经过点 ，；（2） 与 交于 ， 与 交于 ．解：（1），，，．（2），．AαBαl A B平面ABD平面BCD BD平面ABC平面ADC ACa∉αB∈αA∈l B∈l平面ABD∩平面BCD=BD平面ABC∩平面ADC=AC如图所示，在四面体 中，、、、 分别是 、、、 上的点，且 ，求证 ，， 三点共线．ABCD E F G H AB AD BC CDEF∩GH=PB D P2.点、线、面的位置关系证明：因为 ，，所以 ，同理，，又，所以 ，，而 ，所以 ，即 ，， 三点共线．E ∈ABF ∈AD EF ⊂平面 ABD GH ⊂平面 BCD EF ∩GH =P P ∈平面 ABD P ∈平面 BCD 平面 ABD ∩平面 BCD =BD P ∈直线BD B D P 已知：如图，，，．求证：直线 ，， 在同一平面内．证法一：（同一法）因为 ，所以 和 确定一个平面 ．　因为 ，所以 ．又因为 ，所以 ．同理可证 ．又 ，，所以 ．因此，直线 ，， 在同一个平面内．证法二：（重合法）因为 ，所以 ， 确定一个平面 ．因为 ，所以 ， 确定一个平面 ．又因为 ，，所以 ．又 ，，所以 ．同理可证得 ，，，．所以不共线的三个点 ，， 在平面 内，又在平面 内．所以平面 和平面 重合，即直线 ，， 在同一平面内．∩=A l 1l 2∩=B l 2l 3∩=C l 1l 3l 1l 2l 3∩=A l 1l 2l 1l 2α∩=B l 2l 3B ∈l 2⊂αl 2B ∈αC ∈αB ∈l 3C ∈l 3⊂αl 3l 1l 2l 3∩=A l 1l 2l 1l 2α∩=B l 2l 3l 2l 3βA ∈l 2⊂αl 2A ∈αA ∈l 2⊂βl 2A ∈βB ∈αB ∈βC ∈αC ∈βA B C αβαβl 1l 2l 3结合空间想象回答下列问题：（1） 个平面可以分空间为______部分；（2） 个平面可以分空间为______部分；（3）正方体的各个面延伸后将空间分成______部分．解：（1），；（2），，，；（3）．对于（1）：当 个平面平行时，分成 部分；当两个面相交时，分成 部分；对于（2）：当 个平面两两平行时，分成 部分；当其中两个平面平行，和另外一个平面相交或者三个平面相交于一条直线时，分成 部分；当 个平面两两相交且交线两两平行时，分成 部分；当 个平面两两相交且交线相交于一点时，分成 部分；对于（3）：首先，将正方体的四个侧面延伸，可知将空间分成 部分，然后，将正方体的上下底面延伸可知将之前部分分成了 层，每层 部分，共 部分 ．233446782723434637389393×9=27若直线 、、 相交于一点，则这 条直线可能确定的平面有（ ）A． 个 B． 个 C．无数个 D． 个或 个解：D当 、、 三线共面时，平面只有 个；当三线不共面时，任意两条可确定一个平面，共 个．a b c 30113a b c 13描述：例题：点与平面的位置关系平面内有无数个点，平面可以看成点的集合．点 在平面 内，记作 ；点 不在平面 内，记作 ．直线与直线的位置关系空间直线与直线的位置关系共有以下两种：共面直线 在同一平面内的两条直线．更进一步，若这两条直线有且只有一个公共点，则称它们是相交直线 ，若这两条直线没有公共点，则称它们是平行直线；异面直线 不同在任何一个平面内的两条直线．直线垂直如果两条直线所成的角是直角，那么我们就说这两条直线互相垂直，记作 ．在空间，两条直线垂直包括两种情形：共面垂直和异面垂直．直线与平面的位置关系空间直线与平面的位置关系共有以下三种：直线在平面内 直线上的所有点都在平面内；直线与平面相交 直线与平面有且仅有一个公共点；直线与平面平行 直线与平面没有公共点．平面与平面的位置关系空间平面与平面的位置关系共有以下两种：平行 两个平面没有公共点，则称这两个平面平行；相交 两个平面有一条公共直线，则称这两个平面相交，此时这条公共直线称为这两个平面的交线．A αA ∈αA αA ∉αa ⊥b 如果在两个平面内分别各有一条直线，这两条直线互相平行，那么这两个平面的位置关系是（）A．平行 B．相交 C．平行或相交 D．垂直相交解：C可根据题意作图判断，如图所示，分别为两个平面平行、相交的情况 ．分别和两条异面直线都相交的两条直线的位置关系是（ ）A．相交 B．异面 C．异面或相交 D．平行解：C如图所示，可能相交，也可能异面，若两直线平行，则此两条直线确定一个平面，且原两条异面直线均在此平面内，故矛盾 ．四、课后作业 （查看更多本章节同步练习题，请到快乐学）若直线 不平行于平面 ，且 ，则（ ）A． 内的所有直线与 异面 B． 内不存在与 平行的直线 C． 内存在唯一的直线与 平行 D． 内的直线与 都相交解：B依题意，设直线 ，如图． 内的直线若经过点 ，则与直线 相交；若不经过点 ，则与直线 是异面直线，但不可能与 平行．l αl ⊄ααl αl αl αl l ∩α=A αA l A l l 答案：解析：1. 如图，在正方体 中， 是底面正方形 的中心， 是 的中点， 是 上的动点，则直线 、 的位置关系是 ．A ．平行B ．相交C ．异面垂直D ．异面不垂直C和点 确定平面 ，且 平面 ， 判定 与平面 的位置关系，只需判定直线 的位置关系即可．ABCD −A 1B 1C 1D 1O ABCD M D D 1N A 1B 1NO AM ()A 1B 1O O A 1B 1NO ⊂O A 1B 1∴MA O A 1B 1NO 、AM 答案：2. 平行六面体 中，既与 共面也与 共面的棱的条数为 A ．B ．C ．D ．C ABCD −A 1B 1C 1D 1AB C C 1()3456答案：3. 正方体 中， 、 、 分别是 、 、 的中点．那么，正方体的过 、 、 的截面图形是 A ．三角形B ．四边形C ．五边形D ．六边形D ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P Q R ()4. 下列正方体或正四面体中，，，， 分别是所在棱的中点，这四个点不共面的一个图是 P Q R S ()高考不提分，赔付1万元，关注快乐学了解详情。

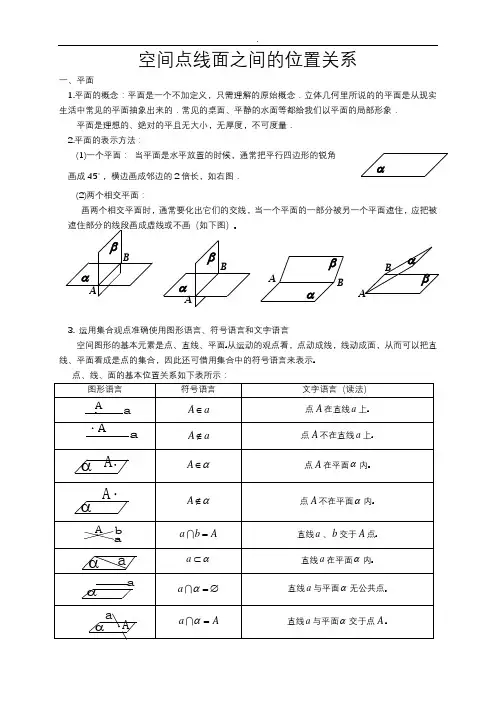
D CBA α ca b c b a //////⇒⎭⎬⎫第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系1 平面含义：平面是无限延展的2 平面的画法及表示（1）平面的画法：水平放置的平面通常画成一个平行四边形，锐角画成450，且横边画成邻边的2倍长（如图） （2）平面通常用希腊字母α、β、γ等表示，如平面α、平面β等，也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示，如平面AC 、平面ABCD 等。

3 三个公理：（1）公理1：如果一条直线上的两点在一个平面内，则这条直线在此平面内 公理1作用：判断直线是否在平面内（2）公理2：过不在一条直线上的三点，有且只有一个平面。

符号表示为：A 、B 、C 三点不共线 => 有且只有一个平面α， 使A ∈α、B ∈α、C ∈α。

公理2作用：确定一个平面的依据。

推论1：一条直线与它外一点确定一个平面。

推论2：两条平行直线确定一个平面。

推论3：两条相交直线确定一个平面。

（3）公理3：如果两个不重合的平面有一个公共点，则它们有且只有一条过该点的公共直线。

符号表示为：P ∈α∩β =>α∩β=L ，且P ∈L 公理3作用：判定两个平面是否相交的依据空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系：相交直线：同一平面内，有且只有一个公共点； 平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点。

2 公理4：平行于同一条直线的两条直线互相平行。

符号表示为：设a 、b 、c 是三条直线强调：公理4实质上是说平行具有传递性，在平面、空间这个性质都适用。

公理4作用：判断空间两条直线平行的依据。

3 等角定理：空间中如果两个角的两边分别对应平行，则这两个角相等或互补4 异面直线：① a'与b'所成的角的大小只由a 、b 的相互位置来确定，与O 的选择无关，为了简便，点O 一般取在两直线中的一条上； ② 两条异面直线所成的角θ∈(0， ]；③ 当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作a ⊥b ； ④ 两条直线互相垂直，有共面垂直与异面垂直两种情形；⑤ 计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。

§2.1点、直线、面的位置关系一、平面知识要点1. 点A 在直线上,记作A a ∈；点A 在平面α内,记作A α∈；直线a 在平面α内,记作a α⊂.2. 平面基本性质即三条公理的“文字语言”、“符号语言”、“图形语言”列推论1 经过一条直线和这条直线外的一点，有且只有一个平面； 推论2 经过两条相交直线，有且只有一个平面； 推论3 经过两条平行直线，有且只有一个平面.【例1】如果一条直线与两条平行直线都相交,那么这三条直线是否共面？ 【例2】空间四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 上的点，已知EF 和GH 交于P 点，求证：EF 、GH 、AC 三线共点.解：∵P∈EF ，EF ⊂面ABC ，∴P ∈面ABC. 同理P ∈面ADC.∵ P 在面ABC 与面ADC 的交线上，又 ∵面ABC ∩面ADC=AC ， ∴P ∈AC ，即EF 、HG 、AC 三线共点.【例3】求证：两两相交且不过同一个点的三条直线必在同一平面内.已知：直线,,AB BC CA 两两相交，交点分别为,,A B C ，求证：直线,,AB BC CA 共面. 证明：因为A ，B ，C 三点不在一条直线上，所以过A ，B ，C 三点可以确定平面α． 因为A ∈α，B ∈α，所以AB α． 同理BC α，AC α.所以AB ，BC ，CA 三直线共面．【例4】在正方体1111ABCD A B C D -中，（1）1AA 与1CC 是否在同一平面内？（2）点1,,B C D 是否在同一平面内？（3）画出平面1AC 与平面1BC D 的交线，平面1ACD 与平面1BDC 的交线. 解：（1）在正方体1111ABCD A B C D -中，∵11//AA CC ， ∴由公理2的推论可知，1AA 与1CC 可确定平面1AC ，∴1AA 与1CC 在同一平面内.（2）∵点1,,B C D 不共线，由公理3可知，点1,,B C D 可确定平面1BC D ，∴ 点1,,B C D 在同一平面内.（3）∵AC BD O = ，11D C DC E = ， ∴点O ∈平面1AC ，O ∈平面1BCD ，又1C ∈平面1AC ，1C ∈平面1BC D ， ∴ 平面1AC 平面1BC D 1OC =，同理平面1ACD 平面1BDC OE =．二、空间中直线与直线之间的位置关系 知识要点1.空间两条直线的位置关系：⎧⎧⎪⎨⎨⎩⎪⎩相交直线：同一平面内，有且只有一个公共点；共面直线平行直线：同一平面内，没有公共点；异面直线：不同在任何一个平面内，没有公共点.2. 已知两条异面直线,a b ，经过空间任一点O 作直线//,//a a b b ''，把,a b ''所成的锐角（或直角）叫异面直线,a b 所成的角（或夹角）. ,a b ''所成的角的大小与点O 的选择无关，为了简便，点O 通常取在异面直线的一条上；异面直线所成的角的范围为(0,90]︒，如果两条异面直线所成的角是直角，则叫两条异面直线垂直，记作a b ⊥. 求两条异面直线所成角的步骤可以归纳为四步：选点→平移→定角→计算.【例1】已知异面直线a 和b 所成的角为50°，P 为空间一定点，则过点P 且与a 、b 所成角都是30°的直线有且仅有（ ）.A. 1条B. 2条C. 3条D. 4条解：过P 作a '∥a ，b '∥b ，若P ∈a ，则取a 为a '，若P ∈b ，则取b 为b '．这时a '，b '相交于P 点，它们的两组对顶角分别为50°和130°. 记a '，b '所确定的平面为β，那么在平面β内，不存在与a '，b '都成30°的直线． 过点P 与a '，b '都成30°角的直线必在平面β外，这直线在平面β的射影是a '，b '所成对顶角的平分线．其中射影是50°对顶角平分线的直线有两条l 和l '，射影是130°对顶角平分线的直线不存在．故答案选B. 【例2】如图正方体1111ABCD A B C D -中，E 、F 分别为D1C1和B1C1的中点，P 、Q 分别为AC 与BD 、A1C1与EF 的交点. （1）求证：D 、B 、F 、E 四点共面；（2）若A1C 与面DBFE 交于点R ，求证：P 、Q 、R 三点共线.证明：（1）∵ 正方体1111ABCD A B C D -中，1BB //1DD ，∴BD //11B D . 又 ∵ 111B D C中，E1A 1CAE 、F 为中点， ∴ EF //1112B D . ∴ //EF BD , 即D 、B 、F 、E 四点共面.（2）∵ 1Q AC ∈平面，Q BE ∈平面，1P AC ∈平面，P BE ∈平面， ∴ 1AC BE PQ = 平面平面.又 1AC BE R = 平面， ∴ 1R AC ∈平面，R BE ∈平面， ∴ R PQ ∈. 即P 、Q 、R 三点共线【例3】已知直线a//b//c ，直线d 与a 、b 、c 分别相交于A 、B 、C ，求证：a 、b 、c 、d 四线共面.证明：因为a//b ，由公理2的推论，存在平面α，使得,a b αα⊂⊂.又因为直线d 与a 、b 、c 分别相交于A 、B 、C ，由公理1，d α⊂. 假设c α⊄，则c C α= , 在平面α内过点C 作//c b '， 因为b//c ，则//c c '，此与c c C '= 矛盾. 故直线c α⊂. 综上述，a 、b 、c 、d 四线共面.【例4】如图中，正方体ABCD —A1B1C1D1，E 、F 分别是AD 、AA1的中点.（1）求直线AB1和CC1所成的角的大小；（2）求直线AB1和EF 所成的角的大小. 解：（1）如图，连结DC1 ， ∵DC1∥AB1，∴ DC1 和CC1所成的锐角∠CC1D 就是AB1和CC1所成的角.∵ ∠CC1D=45°， ∴ AB1 和CC1所成的角是45°.（2）如图，连结DA1、A1C1， ∵ EF ∥A1D ，AB1∥DC1，∴ ∠A1DC1是直线AB1和EF 所成的角. ∵ΔA1DC1是等边三角形， ∴ ∠A1DC1=60º，即直线AB1和EF 所成的角是60º. 三、直线与平面、平面与平面位置关系 知识要点1. 直线与平面的位置关系：（1）直线在平面内（有无数个公共点）；（2）直线与平面相交（有且只有一个公共点）；（3）直线与平面平行（没有公共点）. 分别记作：l α⊂；l P α= ；//l α.2. 两平面的位置关系：平行（没有公共点）；相交（有一条公共直线）.分别记作//αβ；l αβ= .【例1】已知空间边边形ABCD 各边长与对角线都相等，求异面直线AB 和CD 所成的角的大小.解：分别取AC 、AD 、BC 的中点P 、M 、N 连接PM 、PN ，由三角形的中位线性质知PN ∥AB ，PM ∥CD ，于是∠MPN 就是异面直线AB 和CD 成的角（如图所示）.连结MN 、DN ，设AB=2， ∴PM=PN=1.而MN ⊥AD ，AM=1，得∴MN2=MP2+NP2，∴∠MPN=90°.∴异面直线AB 、CD 成90°角. 【例2】在空间四边形ABCD 中，E 、H 分别是AB 、AD 的中点，F 、G 分别是CB 、CD 的中点，若AC + BD = a ，AC ⋅BD =b ，求22EG FH +.解：四边形EFGH 是平行四边形，22EG FH +=222()EF FG +=22211()(2)22AC BD a b +=-.【例3】已知空间四边形ABCD 中，E 、H 分别是AB 、AD 的中点，F 、G 分别是BC 、CD上的点，且23CF CG CB CD ==.求证：（1）E 、F 、G 、H 四点共面；（2）三条直线EF 、GH 、AC 交于一点. 证明：（1） 在△ABD 和△CBD 中，∵ E 、H 分别是AB 和CD的中点， ∴ EH //12BD.又 ∵ 23CF CG CB CD ==， ∴ FG //23BD. ∴ EH ∥FG. 所以，E 、F 、G 、H 四点共面.A BCDE FGH。

//a α//a b点线面位置关系总复习知识梳理一、直线与平面平行 1.判定方法（1）定义法：直线与平面无公共点。

（2）判定定理：（3）其他方法：//a αββ⊂ 2.性质定理：//a abαβαβ⊂⋂=二、平面与平面平行 1.判定方法（1）定义法：两平面无公共点。

（2）判定定理：////a b a b a b Pββαα⊂⊂⋂=//αβ（3）其他方法：a a αβ⊥⊥//αβ; ////a γβγ//αβ 2.性质定理：//a bαβγαγβ⋂=⋂=三、直线与平面垂直（1）定义：如果一条直线与一个平面内的所有直线都垂直，则这条直线和这个平面垂直。

（2）判定方法 ① 用定义.//a b a b αα⊄⊂//a α//a b//a b② 判定定理:a b a cb c A bc αα⊥⊥⋂=⊂⊂a α⊥③ 推论://a a bα⊥b α⊥ （3）性质 ①a b αα⊥⊂a b ⊥ ②a b αα⊥⊥四、平面与平面垂直（1）定义：两个平面相交，如果它们所成的二面角是直线二面角，就说这两个平面互相垂直。

（2）判定定理a a αβ⊂⊥αβ⊥ （3）性质①性质定理la a lαβαβα⊥⋂=⊂⊥αβ⊥ ②lP P A A αβαβαβ⊥⋂=∈⊥垂足为A l ∈ ④lP PA αβαβαβ⊥⋂=∈⊥PA α⊂“转化思想”面面平行 线面平行 线线平行 面面垂直 线面垂直 线线垂直●求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2.在二面角的棱上任取一点O，在两半平面内分别作射线OA⊥l，OB⊥l，则∠AOB叫做二面角的平面角例1．如图，在三棱锥S-ABC中，SA⊥底面ABC，AB⊥BC，DE垂直平分SC，且分别交AC于D，交SC于E，又SA=AB，SB=BC，求以BD为棱，以BDE和BDC为面的二面角的度数。

●求线面夹角定义：斜线和它在平面内的射影的夹角叫做斜线和平面所成的角（或斜线和平面的夹角）方法：作直线上任意一点到面的垂线，与线面交点相连，利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。

1.如果一条直线上的两个点在一个平面内，那么这条直线在此平面内。

2.过不在同一条直线上的3点，有且只有一个平面。

3.如果两个不重合的平面有一个公共点，那么他们还有其他公共点，且所有这些公共点的集合是一条过这个公共点的直线。

4.经过一条直线和这条直线外一点，有且只有一个平面。

5.经过两条相交直线，有且只有一个平面。

6.经过两条平行直线，有且只有一个平面。

7.平行于同一条直线的两条直线互相平行。

8.空间中，如果两个角的两边分别对应平行，那个这两个角相等或互补。

9.连接平面内一点与平面外一点的直线，和这个平面内不经过该点的直线是异面直线。

10.平面外一条直线与平面内的一条直线平行，则这条直线和这个平面平行。

11.一个平面的两条相交直线与另一个平面平行，则这两个平面平行。

12.一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行。

13.如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

14.两个平面平行，其中一个平面内的直线必平行于另外一个平面。

15.空间中，如果两个角的两边分别对应平行，那么这两个角相等或互补。

16.一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。

17.在平面内的一条直线，如果和这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

18.如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

19..一个平面过另一平面的一条垂线，则这两个平面垂直。

20.垂直于同一个平面的两条直线平行。

20.过空间一点，作已知平面的垂线有且只有一条。

21.过空间一点，作已知直线的垂面有且只有一个。

22.两个平面垂直，则其中一个平面内垂直于交线的直线与另一个平面垂直。

描述：高中数学必修2(人教A版)知识点总结含同步练习题及答案第二章 点、直线、平面之间的位置关系 2.3 直线、平面垂直的判定及其性质一、学习任务认识和理解空间中线面垂直的有关判定定理和性质定理，能用图形语言和符号语言表述这些定理，并能证明有关性质定理；能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题．二、知识清单空间的垂直关系 点面距离三、知识讲解1.空间的垂直关系直线与平面垂直的判定如果直线 与平面 内的任意一条直线都垂直，我们就说直线 与平面 互相垂直．记作．直线 叫做平面 的垂线，平面 叫做直线 的垂面．直线与平面垂直时，它们唯一的公共点 叫做垂足．直线与平面垂直的判定定理 一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．用符号表示：，，，，．平面与平面垂直的判定定理 一个平面过另一个平面的垂线，则这两个平面垂直．用符号表示：，．l αl αl ⊥αl ααl P a b ⊂αa ∩b =P l ⊥a l ⊥b ⇒l ⊥αl ⊥αl ⊂β⇒α⊥β例题：直线与平面垂直的性质定理 垂直于同一个平面的两条直线平行．用符号表示：，．平面与平面垂直的性质定理 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．用符号来表示：，，，．a ⊥αb ⊥α⇒a ||b α⊥βα∩β=CD AB ⊂αAB ⊥CD ⇒AB ⊥β下列命题中，正确的序号是______．①若直线 与平面 内的无数条直线垂直，则 ；②若直线 与平面 内的一条直线垂直，则 ；③若直线 不垂直于平面 ，则 内没有与 垂直的直线；④若直线 不垂直于平面 ，则 内也可以有无数条直线与 垂直；⑤过一点与已知平面垂直的直线有且只有一条．解：④⑤当直线 与平面 内的无数条平行直线垂直时， 与 不一定垂直，所以①不正确；当 与 内的一条直线垂直时，不能保证 与平面 垂直，所以②不正确；当 与 不垂直时，可能与 内的无数条平行直线垂直，所以③不正确，④正确；过一点有且只有一条直线垂直于已知平面，所以⑤正确．故填④⑤．l αl ⊥αl αl ⊥αl ααl l ααl l αl αl αl αl αl α如图，三棱锥 中，，底面 的斜边为 ， 为 上一点．求证： ．证明：因为 ，，所以 ．又 ，，所以 ．又 ，所以 ．P −ABC P A ⊥平面 ABC Rt△ABC AB F P C BC ⊥AF P A ⊥平面 ABC BC ⊂平面 ABC P A ⊥BC AC ⊥BC AC ∩P A =A BC ⊥平面 P AC AF ⊂平面 P AC BC ⊥AF 如图，已知四棱锥 ，底面 是菱形，，，，点 为 的中点．求证：．P −ABCD ABCD ∠DAB =60∘P D ⊥平面 ABCD P D =AD E AB 平面P ED ⊥平面 P ABAB⊂平面P AB又 ，所以3P C⊥AC C，求点 到平面P A⊥ABCD高考不提分，赔付1万元，关注快乐学了解详情。

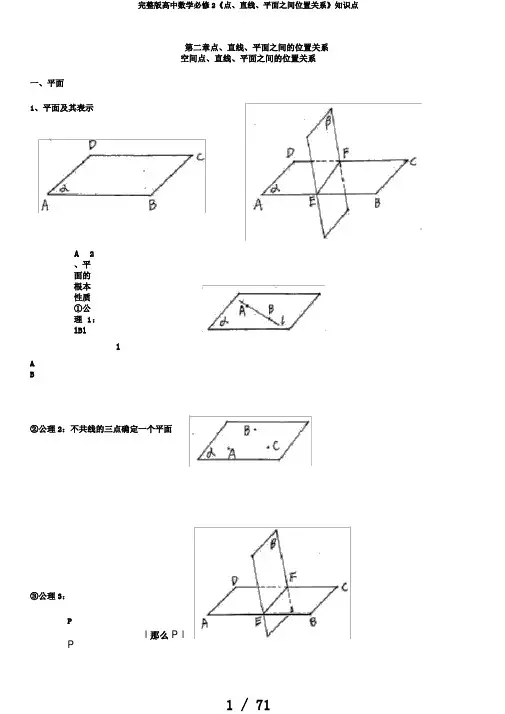
高中数学必修2《点、直线、平面之间的位置关系》知识点第二章点、直线、平面之间的位置关系一、平面及其表示平面是指在三维空间中的一个无限大的平面，可以用点和直线来表示。

平面的基本性质可以通过三条公理来描述：①公理1：如果一个点A在直线l上，另一个点B也在直线l上，且A在平面α上，那么B也在平面α上。

②公理2：如果三个不共线的点A、B、C确定一个平面α，那么这三个点必在平面α上。

③公理3：如果一个点P在平面α上，又在平面β上，那么P一定在它们的交线l上。

二、点与面、直线位置关系1、点与平面有两种位置关系：①点A在平面α上；②点B不在平面α上。

2、点与直线有两种位置关系：①点A在直线l上；②点B不在直线l上。

三、空间中直线与直线之间的位置关系1、异面直线是指不在同一平面内的两条直线。

2、直线与直线的位置关系包括相交、共面和平行三种情况。

3、公理4和定理：如果两个角的两边分别对应平行，那么这两个角相等或互补。

四、空间中直线与平面之间的位置关系直线与平面的位置关系可以分为三种情况：直线在平面内、直线与平面相交、直线与平面平行。

五、空间中平面与平面之间的位置关系平面与平面的位置关系可以分为平行和相交两种情况。

其中，平行的两个平面没有公共点，而相交的两个平面有一条公共直线。

直线、平面平行的判定及其性质直线与平面平行的判定方法有三种：利用定义、利用判定定理、利用面面平行的性质。

其中，面面平行的性质可以推导出直线与平面平行的性质。

证明面面平行的常用方法有以下几种：①利用面面平行的定义，一般与反证法结合使用；②利用判定定理；③证明两个平面垂直于同一个平面；④证明两个平面同时平行于第三个平面。

直线与平面垂直的判定方法如下：若直线l与平面α所成角α∈(0,90)，则PO⊥α，AO为___在平面α上的投影，故∠α为直线l与平面α所成角。

二面角α-l-β的平面角为∠___，其中BO⊥l，___。

线面垂直的判定方法如下：___⊥α，___α，且a∩b=A，则___⊥α。

第二章点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系一、平面1、平面及其表示A2、平面的根本性质①公理1：lBllAB②公理2：不共线的三点确定一个平面③公理3：Pl那么P lP二、点与面、直线位置关系1、A1、点与平面有2种位置关系2、B1、A l2、点与直线有2种位置关系2、B l三、空间中直线与直线之间的位置关系1、异面直线2、直线与直线的位置关系相交共面平行异面3、公理4和定理公理4：l1Pl3l1Pl2l2Pl3定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。

4、求异面直线所成角的步骤：①作：作平行线得到相交直线； ②证：证明作出的角即为所求的异面直线所成的角；③构造三角形求出该角。

提示：1、作平行线常见方法有：直接平移，中位线，平行四边形。

2、异面直线所的角的范围是 00,900。

四、空间中直线与平面之间的位置关系位置关系 直线a 在平面内 直线a 与平面相交直线a 与平面 平行 公共点 有无数个公共点 有且只有一个公共点 没有公共点 符号表示a aI A aP 图形表示 五、空间中平面与平面之间的位置关系位置关系 两个平面平行 两个平面相交公共点 没有公共点有一条公共直线 符号表示 P I a图形表示直线、平面平行的判定及其性质一、线面平行1、判定：b a bPbPa〔线线平行，那么线面平行〕2、性质：aPaP abb〔线面平行，那么线线平行〕二、面面平行1、判定：aba b P PPbP〔线面平行，那么面面平行〕2、性质1：PI a aPbI b〔面面平行，那么线面平行〕性质2：PmPm〔面面平行，那么线面平行〕说明〔1〕判定直线与平面平行的方法：①利用定义：证明直线与平面无公共点。

②利用判定定理：从直线与直线平行等到直线与平面平行。

③利用面面平行的性质：两个平面平行，那么其中一个平面内的直线必平行于另一个平面。

2〕证明面面平行的常用方法利用面面平行的定义：此法一般与反证法结合。

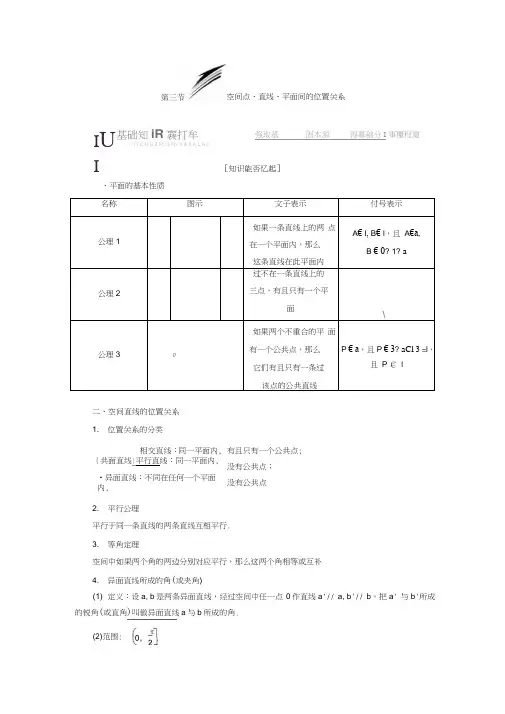
［知识能否忆起］、平面的基本性质 名称图示文子表示 付号表示公理1如果一条直线上的两 点在一个平面内，那么 这条直线在此平面内 A € l , B € l ，且 A €a,B € 0? 1? a公理2过不在一条直线上的 三点，有且只有一个平面\公理3如果两个不重合的平 面有一个公共点，那么 它们有且只有一条过该点的公共直线P € a ，且 P € 3? aCl 3 =l ，且 P € l二、空间直线的位置关系 1. 位置关系的分类相交直线：同一平面内, ｛共面直线|平行直线：同一平面内,•异面直线：不同在任何一个平面内, 2. 平行公理平行于同一条直线的两条直线互相平行. 3. 等角定理空间中如果两个角的两边分别对应平行，那么这两个角相等或互补 4. 异面直线所成的角(或夹角)(1) 定义：设a, b 是两条异面直线，经过空间中任一点 0作直线a '// a, b '// b ，把a ' 与b '所成的锐角(或直角)叫做异面直线a 与b 所成的角.I U I空间点、直线、平面间的位置关系基础知iR 襄打牟11 C H U Z H I $ H I Y A 0 A L A 0强取基 固本源 得募础分I 事覆程廈有且只有一个公共点;没有公共点；没有公共点(2)范围:三、直线与平面的位置关系/亠护¥方位置大糸图示付号表示公共点个数直线1在平面a内1? a无数个直线l与平面a相交八/l Cl a= A一个直线l与平面a平行Z / 1 〃a0个四、平面与平面的位置关系/亠护¥方位置大糸图示付号表示公共点个数两个平面平行\Aall 30个7两个平面相交aC 3= l无数个(这些公共点均在交线1上)1•三个公理的作用(1) 公理1的作用：①检验平面；②判断直线在平面内；③由直线在平面内判断直线上的点在平面内.(2) 公理2的作用：确定平面的依据，它提供了把空间问题转化为平面问题的条件.(3) 公理3的作用：①判定两平面相交；②作两相交平面的交线；③证明多点共线.2. 异面直线的有关问题(1) 判定方法：①反证法；②利用结论即过平面外一点与平面内一点的直线与平面内不过该点的直线是异面直线，如图.(2) 所成的角的求法：平移法.師吾点］学技法］得拔高分| 拿握狸度i**-平面的基本性质及应用■典题导入［例1］（2012湘潭模拟）如图所示，在正方体ABCD —A i B i C i D i中，E为AB的中点，F 为A i A的中点，求证：CE , D i F, DA三线共点.［自主解答］•EF 綊qCD i,•••直线D i F和CE必相交.设D i F n CE = P,••P Pi F 且D i F?平面AA i D i D,••P € 平面AA i D i D.又P €EC且CE?平面ABCD ,••P € 平面ABCD ,即P是平面ABCD与平面AA i D i D的公共点.而平面ABCD n平面AA i D i D = AD.••P 3D.•CE、D i F、DA三线共点.本例条件不变试证明E , C, D i, F四点共面.证明：••E, F分别是AB和AA i的中点，i•'EF 綊2A i B.又A i D i 綊B i C i 綊BC. •四边形A i D i CB为平行四边形. ••A i B CD i，从而EF CD i.•'EF与CD i确定一个平面. ••E, C i, F, D四点共面.占由题悟法i. 证明线共点问题常用的方法是：先证其中两条直线交于一点，再证交点在第三条直线上.2•证明点或线共面问题一般有以下两种途径：①首先由所给条件中的部分线（或点）确定一个平面，然后再证其余线（或点）均在这个平面内；②将所有条件分为两部分，然后分别确定平面，再证平面重合.3以题试法1. （1）（2012江•西模拟）在空间中，下列命题正确的是（）A .对边相等的四边形一定是平面图形B .四边相等的四边形- -定是平面图形C.有一组对边平行的四边形一定是平面图形D .有一组对角相等的四边形一定是平面图形⑵对于四面体ABCD，下列命题正确的是 __________ （写出所有正确命题的编号）.①相对棱AB与CD所在直线异面；②由顶点A作四面体的高，其垂足是△ BCD三条高线的交点；③若分别作△ ABC和厶ABD的边AB上的高，则这两条高所在的直线异面；④分别作三组相对棱中点的连线，所得的三条线段相交于一点.解析：（1）由“两平行直线确定一个平面”知C正确.（2）由四面体的概念可知，AB与CD所在的直线为异面直线，故①正确；由顶点A作四面体的高，只有当四面体ABCD的对棱互相垂直时,其垂足是厶BCD的三条高线的交点，故②错误；当DA = DB , CA= CB时，这两条高线共面，故③错误；设AB , BC, CD , DA的中点依次为E, F, M , N,易证四边形EFMN为平行四边形，所以EM与FN相交于一点，易证另一组对棱中点的连线也过它们的交点，故④正确.答案：（1）C （2）①④异面直线的判定由典题导入[例2] （2012金华模拟）在图中，G, N , M, H分别是正三棱柱的顶点或所在棱的中点,则表示直线GH , MN是异面直线的图形有___________ .（填上所有正确答案的序号）①②③④［自主解答］图①中，直线GH /MN ;图②中，G , H , N三点共面，但M?面GHN ,因此直线GH与MN异面；图③中，连接MG, GM /HN，因此GH与MN共面；图④中，G , M , N共面，但H?面GMN ,因此GH与MN异面.所以图②④中GH与MN异面.［答案］②④石由题悟法1•异面直线的判定常用的是反证法，先假设两条直线不是异面直线，即两条直线平行或相交，由假设的条件出发，经过严格的推理，导出矛盾，从而否定假设肯定两条直线异面. 此法在异面直线的判定中经常用到.2.客观题中，也可用下述结论：过平面外一点和平面内一点的直线，与平面内不过该点的直线是异面直线.&以题试法2. 已知m, n, I为不同的直线，a, B为不同的平面，有下面四个命题：①m, n为异面直线，过空间任一点P, —定能作一条直线I与m, n都相交.②m, n为异面直线，过空间任一点P, —定存在一个与直线m, n都平行的平面.③a丄B, aA 3= I, m? a, n? 3, m, n与I都斜交，则m与n—定不垂直；④m, n是a内两相交直线，则a与3相交的充要条件是m, n至少有一条与3相交.则四个结论中正确的个数为( )A. 1B. 2C. 3D. 4解析：选B①错误，因为过直线m存在一个与直线n平行的平面，当点P在这个平面内且不在直线m上时，就不满足结论；②错误，因为过直线m存在一个与直线n平行的平面，当点P在这个平面内时，就不满足结论；③正确，否则，若m丄n,在直线m上取一点作直线a丄I，由a丄3得a丄n.从而有n丄a,贝U n丄I :④正确.LI 典题导入［例3］ （2012大纲全国卷）已知正方体 ABCD — A 1B 1C 1D 1中，E , F 分别为BB i , CC i 的 中点，那么异面直线 AE 与D 1F 所成角的余弦值为 ___________ .［自主解答］连接DF ，则AE/DF , •••D 1FD 即为异面直线 AE 与D 1F 所成的角. 设正方体棱长为a ,则 D 1D = a , DF = ~25a , D 1F = ~25a ,… 3 ［答案］5-由题悟法求异面直线所成的角一般用平移法，步骤如下： （1） 一作：即找或作平行线，作出异面直线所成的角; ⑵二证：即证明作出的角是异面直线所成的角；（3）三求：解三角形，求出所作的角，如果求出的角是锐角或直角，则它就是要求的角, 如果求出的角是钝角，则它的补角才是要求的角.初以题试法3. （2012唐山模拟）四棱锥P — ABCD 的所有侧棱长都为.5,底面ABCD 是边长为2的 正方形，则CD 与PA 所成角的余弦值为（）D.；解析：选B 如图所示，因为四边形ABCD 为正方形，故CD // AB ,则CD 与PA 所成的角即为 AB 与FA 所成的角/ PAB ，在△ FAB 内，FB = FA = ■.5, AB = 2,利用余弦定理可知:PA 2+ AB 2- PB 2_ 5+ 4— 5 _近 2X FA X AB 2X 2八 55［小题能否全取］A. 2 *5 5B.cos / FAB =1.（教材习题改编）已知a, b是异面直线，直线c平行于直线a，那么c与b（）A .异面B.相交C.不可能平行D.不可能相交解析：选C 由已知直线c与b可能为异面直线也可能为相交直线，但不可能为平行直线，若b // c,贝U a// b.与a, b是异面直线相矛盾.2. （2012东北三校联考）下列命题正确的个数为（）①经过三点确定一个平面；②梯形可以确定一个平面；③两两相交的三条直线最多可以确定三个平面；④如果两个平面有三个公共点，则这两个平面重合.A. 0B. 1C. 2D. 3解析：选C ①④错误，②③正确.3. 已知空间中有三条线段AB, BC和CD，且/ ABC =Z BCD，那么直线AB与CD的位置关系是（）A. AB / CDB. AB与CD异面C. AB与CD相交D. AB / CD或AB与CD异面或AB与CD相交解析：选D 若三条线段共面，如果AB, BC, CD构成等腰三角形，则直线AB与CD相交，否则直线AB与CD平行；若不共面，则直线AB与CD是异面直线.4. （教材习题改编）如图所示，在正方体ABCD —A i B i C i D i中，E,F分别是AB , AD的中点，则异面直线B i C与EF所成的角的大小为解析：连接B i D i, D i C,则B i D i/EF,故ZDi B i C 为所求，又B i D i= B i C= D i C,••』i B i C= 60 °答案：60°5. （教材习题改编）平行六面体ABCD —A i B i C i D i中既与AB共面又与CC i共面的棱的条数为________ .解析：如图，与AB和CC i都相交的棱有BC;与AB相交且与CC i平行的棱有AA i,BB i；与AB平行且与CC i相交的棱有CD , C1D1,故符合条件的棱共有5条.答案：5基础MliR靈扫年J I C H U Z H D S H I YAOIRALAO［知识能否忆起］一、直线与平面平行1. 判定定理文字语言图形语言符号语言判定定理平面外一条直线与此平—面内的一条直线平行, 则直线与此平面平行—a?a、b? a b //a」^ ? a / a2.性质定理文字语言图形语言付号语言性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行a/ a '卜？ a // baCl 6= b j二、平面与平面平行直线、平面平行的判定及性质1.判定定理判定定理一个平面内的两条相交直线与另一个平面平 行，则这两个平面平行a? a 、 b? aa Ab = P » ? a// a / 3 b / 3' 32.两平面平行的性质定理文字语言图形语言付号语言性质定理如果两个平行平面同时 和第三个平面相交，那 么它们的交线平行a// 3、aA Y a * ? a // b 3A Y b J7，心/IX1.平行问题的转化关系:2.在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化， 即从“线线平行”到“线面平行”，再到“面面平行”；而在性质定理的应用中，其顺序恰好相反， 但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”.3•辅助线（面）是求证平行问题的关键，注意平面几何中位线，平行四边形及相似中有 关平行性质的应用.由典题导入[例1] （2011福建高考）如图，正方体 ABCD — A i B i C i D i 中，AB = 2, 点E 为AD 的中点，点F 在CD 上•若EF //平面ABQ ,则线段EF 的长 度等于 _______________ .线//线判定判定 ------------- 判定 -------------- 性质 |线/面—质勺面/面性质［自主解答］ 因为直线 EF //平面AB i C , EF?平面ABCD ，且平面 AB i C Q 平面ABCD = AC ,所以EF /AC.又因为点E 是DA 的中点，所以F 是DC 的中点，由中位线定理可得 EF1=2AC.又因为在正方体 ABCD — A i B i C i D i 中，AB = 2,所以AC = 2 2•所以EF = 2.［答案］,2本例条件变为“ E 是AD 中点，F , G , H , N 分别是AA i , A i D i , DD i 与D i C i 的中点,解：如图,••G N //平面AA i C i C , EG //平面 AA i C i C , 又 GN n EG = G ,•••平面EGN //平面AA i C i C.•••当M 在线段EG 上运动时，恒有 MN //平面AA i C i C.呂由题悟法解决有关线面平行、面面平行的基本问题要注意：(i)判定定理与性质定理中易忽视的条件，如线面平行的判定定理中条件线在面外易忽 视.⑵结合题意构造或绘制图形，结合图形作出判断. (3)举反例否定结论或用反证法推断命题是否正确.&以题试法i . (i)(20i2浙江高三调研)已知直线I //平面a, P € a,那么过点P 且平行于直线I 的直 线() A •只有一条，不在平面 a 内 B .有无数条，不一定在平面 a 内C .只有一条，且在平面 a 内D .有无数条，一定在平面a 内解析：选C 由直线I 与点P 可确定一个平面 3,且平面a, B 有公共点，因此它们有若M 在四边形EFGH 及其内部运动”，则M 满足什么条件时，有 MN //平面A i C i CA.一条公共直线,设该公共直线为m ,因为I // a,所以I // m ,故过点P且平行于直线I的直线只有一条，且在平面a内.(2)(2012潍坊模拟)已知m, n, l i, I2表示直线，a, B表示平面.若m? a, n? a, l i? B, 12? B IE 12= M,贝U all B的一个充分条件是()A. m l B且l i l a B • m // B且n// BC. m l B 且n l I2 D . m l l i 且n l I2解析：选D 由定理“如果一个平面内有两条相交直线分别与另一个平面平行，那么这两个平面平行”可得，由选项D可推知al B-直线与平面平行的判定与性质[例2] (2012辽宁高考)如图，直三棱柱ABC —A' B ' C', / BAC= 90° AB= AC =羽，AA' = 1,点M , N 分别为A' B 和B' C'的中点.(1) 证明：MN l 平面A' ACC ';1(2) 求三棱锥A' —MNC的体积.(锥体体积公式V = §Sh,其中S为底面面积，h为高)［自主解答］(1)证明：法一：连接AB'、AC '，因为点M , N 分别是A' B和B' C'的中点，所以点M为AB'的中点.又因为点N为B ' C'的中点,所以MN /AC'又MN?平面A' ACCAC' ?平面A' ACC',因此MN l平面A' ACC'.法二：取A' B '的中点P.连接MP.而点M, N分别为AB '与B ' C'的中点，所以MP/AA ' , PN/A ' C '.所以MP l 平面A ' ACC ' , PN l 平面A ' ACC ' •又MP n PN= P,因此平面MPN l平面A ' ACC ' •而MN?平面MPN ,因此MN //平面A ' ACC(2)法一：连接 BN ，由题意得 A ' N IB ' C '，平面 A B ' C 'Q 平面 B ' BCC '=B 'C '，所以A ' N 丄平面NBC. 又 A ' N = 1B ' C ' = 1 ,吕由题悟法利用判定定理证明线面平行的关键是找平面内与已知直线平行的直线，可先直观判断平面内是否已有，若没有，则需作出该直线，常考虑三角形的中位线、平行四边形的对边或过 已知直线作一平面找其交线.畐以题试法2. (2012淄博模拟)如图，在棱长为2的正方体 ABCD — A 1B 1C 1D 1中，E , F 分别是BD , BB 1的中点.(1) 求证：EF //平面 A 1B 1CD ; (2) 求证：EF 丄 AD 1.解：(1)在正方体ABCD — A 1B 1C 1D 1中，连接B 1D , 在平面BB 1D 内，E , F 分别为BD , BB 1的中点, ••EF BD.又•••B 1D?平面 A 1B 1CD. EF?平面 A 1B 1CD , ••EF //平面A 1B 1CD.⑵'-ABCD — A 1B 1C 1D 1 是正方体,•'AD 1 ^A 1 D , AD 1 JA 1B 1. 又 A 1D n A 1B 1 = A 1, ••AD 1 丄平面 A 1B 1D.故 V A ' - MNC = V N -A ' MC = 2V N -A ' BC = gV A '—NBC = 16.法二：V A ' -MNC = V A-NBC —V M — NBC =1V A '— NBC =••AD1I B1D.又由(1)知,EF B1D , /-EF_LAD1.平面与平面平行的判定与性质i典题导入［例3］如图，已知ABCD —A i B i C i D i是棱长为3的正方体，点E 在AA i 上，点 F 在CC i 上，G 在BB i 上，且AE = FC i = B i G= 1, H 是B i C i的中点.⑴求证：E, B, F , D i四点共面；⑵求证：平面A i GH //平面BED i F.5［自主解答］(i)在正方形AA i B i B中，'•AE = B i G= i,••BG = A i E= 2,••BG 綊A i E.•四边形A i GBE是平行四边形.•■AiG /BE.又C i F 綊B i G,•四边形C i FGB i是平行四边形.••FG 綊C i B i 綊D i A i.•四边形A i GFD i是平行四边形.• A i G 綊D i F.•D i F 綊EB.故E, B, F, D i四点共面.3⑵--H是B i C i的中点，• B i H = 2厂B i G 2又B i G= i, /B1H= 3.又EC = f,且/FCB = /GB i H = 90 ° BC 3•••△i HG s/CBF.•••启i GH = ZCFB = ZFBG.••HG /FB.••GH ?面FBED i, FB?面FBED i ,「GH //面BED i F.由⑴知A i G/BE, A i G?面FBED i, BE?面FBED i,AG //面BED i F.且HG A A i G = G ,•平面A i GH //平面BED i F.占由题悟法常用的判断面面平行的方法(1) 利用面面平行的判定定理；(2) 面面平行的传递性(all 3,训Y all Y；⑶利用线面垂直的性质(I丄a, I丄3? a// 3 .血以题试法3. (20i2北京东城二模)如图，矩形AMND所在的平面与直角梯形MBCN 所在的平面互相垂直，MB // NC , MN丄MB.(1) 求证：平面AMB //平面DNC ;(2) 若MC丄CB，求证：BC丄AC.证明：(i)因为MB /NIC , MB?平面DNC , NC?平面DNC ,所以MB //平面DNC.又因为四边形AMND为矩形，所以MA /DN.又MA?平面DNC, DN?平面DNC.所以MA //平面DNC.又MA A MB = M，且MA, MB?平面AMB ,所以平面AMB //平面DNC.(2)因为四边形AMND是矩形，所以AM丄/IN.因为平面AMND丄平面MBCN，且平面AMND A平面MBCN = MN ,所以AM丄平面MBCN.因为BC?平面MBCN ,所以AM JBC.因为MC _LBC, MC A AM = M , 所以BC丄平面AMC.因为AC? 平面AMC，所以BC JAC.[ 小题能否全取]1．（教材习题改编）下列条件中，能作为两平面平行的充分条件的是（）A •一个平面内的一条直线平行于另一个平面B .一个平面内的两条直线平行于另一个平面C. 一个平面内有无数条直线平行于另一个平面D •一个平面内任何一条直线都平行于另一个平面解析：选D 由面面平行的定义可知，一平面内所有的直线都平行于另一个平面时，两平面才能平行，故D正确.2. 已知直线a, b,平面a,则以下三个命题:①若a// b, b? a,贝U a// a;②若 a / b, a // a,贝U b // a;③若a/ a, b// a,贝U all b.其中真命题的个数是（）A. 0B. 1C. 2D. 3解析：选A 对于命题①，若a// b, b? a ,贝U应有a// a或a? a,所以①不正确;对于命题②，若a// b , a// a ,则应有b// a或b? a,因此②也不正确;对于命题③，若a//a, b // a,则应有a // b或a与b相交或a与b异面，因此③也不正确.3. （教材习题改编）若一直线上有相异三个点A , B , C到平面a的距离相等，那么直线I与平面a的位置关系是（）A . I // a B. I 丄aC. I与a相交且不垂直D. I // a或I? a解析：选D 由于I上有三个相异点到平面a的距离相等，贝U I与a可以平行，I? a时也成立.4. ___________________________________________________________ 平面a//平面3, a? a, b? 3,则直线a, b的位置关系是______________________________________________ 解析：由a//3可知，a, b的位置关系是平行或异面.答案：平行或异面5. （2012衡阳质检）在正方体ABCD —A1B1C1D1中，E是DD 1的中点，则BD i与平面ACE 的位置关系为_________解析：如图.连接AC, BD交于O点，连接OE,因为OE /BD1,而OE?平面ACE,BD1?平面ACE，所以BD1 /平面ACE.答案：平行基础知MW1 I C M U Z H I S H I Y A 0［知识能否忆起］一、直线与平面垂直1. 直线和平面垂直的定义直线I与平面a内的任意一条直线都垂直，就说直线I与平面a互相垂直.2.直线与平面垂直的判定定理及推论文字语言图形语言付号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直1心k a, b? a] a A b = O.r ? I 丄a1丄aI丄b 」推论如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直这个平面ab7 a / b、\? b丄aa丄a_直线、平面垂直的判定与性质3.直线与平面垂直的性质定理文字语言图形语言付号语言性质定理垂直于冋一个平面的两条直线平行a匚—b7a丄ab丄a€ a// b、平面与平面垂直1.平面与平面垂直的判定定理文字语言图形语言付号语言判定定理一个平面过另一个平面的垂线，则这两个平面垂直□a 丄3l丄aa j2.平面与平面垂直的性质定理文字语言图形语言付号语言性质定理a_L 3 、》？ 1丄a ad 3= a1丄a」两个平面垂直，则一个平面内垂直于父线的直线垂直于另一个平面L71•在证明线面垂直、面面垂直时，一定要注意判定定理成立的条件. 同时抓住线线、线面、面面垂直的转化关系，即:线血垂百线线垂直、一…厂：面面垂直-------- 性质---------------2•在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决，如有平面垂直时，一般要用性质定理.3•几个常用的结论：(1) 过空间任一点有且只有一条直线与已知平面垂直.(2) 过空间任一点有且只有一个平面与已知直线垂直.垂直关系的基本问题高频考点3EIB美GAOP1N K.AOI>IAN YAOLI典题导入［例1］（2012襄州模拟）若m, n为两条不重合的直线，a, B为两个不重合的平面，给出下列命题：①若m，n都平行于平面a,则m，n—定不是相交直线；②若m、n都垂直于平面a,贝U m, n—定是平行直线；③已知a, B互相垂直，m, n互相垂直，若m丄a,则n丄④m,n在平面a内的射影互相垂直，则m,n互相垂直.其中的假命题的序号是________________ .［自主解答］①显然错误，因为平面a//平面平面a内的所有直线都平行所以3内的两条相交直线可同时平行于a；②正确；如图1所示，若aCl 3= I,且n/,当m丄a时，mln,但n//3,所以③错误；如图2显然当m' Jn'时，m不垂直于n,所以④错误.［答案］①③④-由题悟法解决此类问题常用的方法有：①依据定理条件才能得出结论的，可结合符合题意的图形作出判断；②否定命题时只需举一个反例. ③寻找恰当的特殊模型（如构造长方体）进行筛选.初以题试法1. （2012长春模拟）设a, b是两条不同的直线，a, 3是两个不同的平面，则下列四个命题：①若a丄b, a丄a, b? a,贝U b // a；②若a // a, a丄3贝U a丄3；③若a丄3, a丄3,贝U a// a或a? a；④若a丄b ,a丄a, b丄3,贝U a丄3-其中正确命题的个数为()A. 1B.2C. 3D.4解析：选D对于①,由b不在平面a内知，直线b或者平行于平面a,或者与平面相交，若直线b与平面a相交，则直线b与直线a不可能垂直，这与已知"a丄b”相矛盾, 因此①正确.对于②，由 a // a知，在平面a内必存在直线a1 // a,又a丄3,所以有a j丄3, 所以a丄3,②正确.对于③，若直线a与平面a相交于点A,过点A作平面a 3的交线的垂线m,则m丄3,又a丄3,则有a / m,这与"直线a、m有公共点A”相矛盾，因此③正确.对于④，过空间一点O分别向平面a、3引垂线a1、b1 ,则有a // a1 , b / B ,又a丄b , 所以a1丄b1 ,所以a丄3,因此④正确•综上所述，其中正确命题的个数为 4.直线与平面垂直的判定与性质LI典题导入［例2］(2012广东高考)如图所示，在四棱锥P—ABCD中，AB 丄平面PAD , AB // CD, PD = AD , E 是PB 的中点，F 是DC1上的点且DF = 2AB, PH PAD中AD边上的高.(1)证明：PH丄平面ABCD ;⑵若PH = 1 , AD = 2, FC = 1,求三棱锥E—BCF的体积;(3)证EF丄平面［自主解答］(1)证明：因为AB丄平面FAD, PH?平面FAD ,所以PH JAB.因为PH为APAD中AD边上的高，所以PH 1AD.因为PH?平面ABCD , AB A AD = A, AB,AD?平面ABCD , 所以PH丄平面ABCD.连接EG.⑵如图，连接BH，取BH的中点G,因为E是PB的中点，所以EG PH ,1 1且EG = -PH = 2.因为PH丄平面ABCD , 所以EG丄平面ABCD.因为AB丄平面PAD , AD?平面PAD,所以AB丄\D.所以底面ABCD为直角梯形.所以V E-BCF = 3S Z SCF EG =1• FC AD EG =鲁.(3) 证明：取PA中点M，连接MD , ME.1 因为E是PB的中点，所以ME綊T^AB.1又因为DF綊^AB,所以ME綊DF，所以四边形MEFD是平行四边形，所以EF /MID.因为PD = AD，所以MD _LPA.因为AB丄平面PAD，所以MD 1AB.因为PA A AB = A,所以MD丄平面FAB，所以EF丄平面FAB.呂由题悟法证明直线和平面垂直的常用方法有：(1)利用判定定理.⑵利用判定定理的推论(a// b, a丄a? b丄汰⑶利用面面平行的性质(a丄a, a// 3? a± 3).(4) 利用面面垂直的性质.当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.EJ以题试法2. (2012启东模拟)如图所示，已知PA丄矩形ABCD所在平面, M , N分别是AB, PC的中点.(1) 求证：MN丄CD ;(2) 若/ PDA = 45°求证：MN丄平面PCD.证明：(1)连接AC, AN, BN,••PA丄平面ABCD , /PA1AC,1在Rt△AC 中，N 为PC 中点，••• AN = ^PC.••PA丄平面ABCD，/PAJBC,又BC _1AB,PA A AB= A,••BC 丄平面PAB./BC1PB.从而在RtAPBC中，BN为斜边PC上的中线，1「BN = ?PC.••AN = BN. •△BN为等腰三角形，又M为AB的中点，• MN _LAB,又TAB CD , AMN JCD.⑵连接PM , MC ,Vz PDA = 45 °PAAAD, A AP = AD.• •四边形ABCD 为矩形，• AD = BC,「AP = BC./?又为AB的中点，••• AM = BM.而/PAM = ZCBM = 90°• △AM 也/CBM .•'PM = CM.又N为PC的中点，• MN JPC.由⑴知，MN _LCD , PC A CD = C，/MN 丄平面PCD.面面垂直的判定与性质［例3］ (2012江苏高考)如图，在直三棱柱ABC —A i B i C i中，"B!=A i C i, D, E分别是棱BC, CC i上的点(点D不同于点C),且AD丄DE , F为B iC i的中点.求证：⑴平面ADE丄平面BCC i B i；(2)直线A i F //平面ADE.ti ［自主解答］(i)因为ABC —A i B i C i是直三棱柱，所以CC i丄平面ABC,又AD?平面ABC，所以CC i L AD.又因为AD IDE , CC i, DE?平面BCC i B i,CC i A DE = E,所以AD丄平面BCC i B i.又AD?平面ADE ,所以平面ADE丄平面BCC i B i.⑵因为A i B i= A i C i, F为B i C i的中点，所以A i F _LBi C i.因为CC i丄平面A i B i C i，且A i F?平面A i B i C i,所以CC il A i F.又因为CC i, B i C i?平面BCC i B i, CC i A B i C i= C i,所以A i F丄平面BCC i B i.由⑴知AD 丄平面BCC i B i ，所以A i F/AD. 又AD?平面ADE , A i F?平面ADE , 所以A i F //平面ADE.呂由题悟法1. 判定面面垂直的方法： （i ）面面垂直的定义.⑵面面垂直的判定定理（a 丄B, a? a a 丄2. 在已知平面垂直时，一般要用性质定理进行转化，转化为线面垂直或线线垂直. 转化方法：在一个平面内作交线的垂线， 转化为线面垂直，然后进一步转化为线线垂直.$以题试法3. （20i2泸州一模）如图，在四棱锥P — ABCD 中，底面ABCD 为 菱形，/ BAD = 60° Q 为AD 的中点.⑴若PA = PD ，求证：平面 PQB 丄平面PAD ;⑵若点M 在线段PC 上，且PM = tPC （t>0），试确定实数t 的值, 使得FA //平面MQB.解：（1）因为FA = PD , Q 为AD 的中点，所以 PQ 丄AD. 连接BD ，因为四边形 ABCD 为菱形，/ BAD = 60° 所以AB = BD. 所以BQ 丄\D.因为BQ?平面PQB , PQ?平面PQB , BQ A PQ = Q , 所以AD 丄平面PQB.因为AD?平面PAD ，所以平面 PQB 丄平面PAD.证明如下:连接AC ,设AC n BQ = O ,连接 OM •在△AOQ 与△COB 中， 因为 AD BC ,所以/OQA=ZOBC,ZOAQ = ZOCB. 所以…。

第一节空间点、直线、平面的位置关系精讲公理1:如果一条直线的两点在一个平面内，那么这条直线是所有的点都在这个平面内符号语言表示： A 三1, B 三1, Aw 很，B ： = 1 二很公理2：经过不在同一条直线上的三点，有且只有一个平面。

推论：一直线和直线外一点确定一平面；两相交直线确定一平面；两平行直线确定一平面。

公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线公理4:平行于同一条直线的两条直线互相平行1. 空间直线与直线之间的位置关系2. 空间直线与平面之间的位置关系3. 平面与平面之间的位置关系:4. 空间中的平行问题线面平行的判定定理：平面外一条直线与此平面内一条直线平行，则该直线与此平面平行。

线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交, 平面与平面平行的判定及其性质两个平面平行的判定定理1. 如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行2. 如果在两个平面内，各有两组相交直线对应平行，那么这两个平面平行。

3. 垂直于同一条直线的两个平面平行，两个平面平行的性质定理1. 如果两个平面平行，那么某一个平面内的直线与另一个平面平行。

2. 如果两个平行平面都和第三个平面相交，那么它们的交线平行。

5. 空间中的垂直问题线面垂直平面和平面垂直垂直关系的判定和性质定理线面垂直判定定理和性质定理判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面, 性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行。

面面垂直的判定定理和性质定理判定定理：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。

性质定理：如果两个平面互相垂直，那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。

点线面位置关系精炼1. 下列命题中，错误的是............................... ( )A. 平行于同一个平面的两个平面平行B. 平行于同一条直线的两个平面平行C. 一个平面与两个平行平面相交，交线平行D. —条直线与两个平行平面中的一个相交，则必与另一个相交2. 直线a,b,c及平面a , B , Y ,下列命题正确的是.................... ( )A、若a：_ a， b：_ a ,c 丄a, c丄b 贝U c丄aB、若b：_ a , allb贝U all aC 若all a , aAp =b 则allbD 、若a丄a , b 丄a 则allb3. 下列命题中正确的是.......................... ( )A. 如果一个平面内两条直线都平行于另一平面，那么这两个平面平行。

第二章：点、直线、平面之间的位置关系1、公理1：如果一条直线上两点在一个平面内，那么这条直线在此平面内。

2、公理2：过不在一条直线上的三点，有且只有一个平面。

3、公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

4、公理4：平行于同一条直线的两条直线平行.5、定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。

6、线线位置关系：平行、相交、异面。

7、线面位置关系：直线在平面内、直线和平面平行、直线和平面相交。

8、面面位置关系：平行、相交。

第二章 点、直线、平面之间的位置关系及其论证1 、公理1：如果一条直线上两点在一个平面内，那么这条直线在此平面内,,A l B ll A B ααα∈∈⎧⇒⊂⎨∈∈⎩ 公理1的作用：判断直线是否在平面内2、公理2：过不在一条直线上的三点，有且只有一个平面。

若A ，B ，C 不共线，则A ，B ，C 确定平面α推论1：过直线的直线外一点有且只有一个平面若A l ∉，则点A 和l 确定平面α推论2：过两条相交直线有且只有一个平面 若m n A = ，则,m n 确定平面α 推论3：过两条平行直线有且只有一个平面若m n ，则,m n 确定平面α 公理2及其推论的作用：确定平面；判定多边形是否为平面图形的依据。

3、公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

,P P l P l αβαβ∈∈⇒=∈ 且公理3作用：（1）判定两个平面是否相交的依据；（2）证明点共线、线共点等。

4、公理4：也叫平行公理，平行于同一条直线的两条直线平行.,a b c b a c ⇒m nαP· αL β5、定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。

,1212a a b b ''∠∠⇒∠∠ 且与方向相同＝,1212180a a b b ''∠∠⇒∠+∠︒ 且与方向相反＝作用：该定理也叫等角定理，可以用来证明空间中的两个角相等。

⎪ P ∈⎬ 第二章 点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系一、平面1、平面及其表示2、平面的基本性质①公理 1：A ∈ lB ∈ l⎫⎪ ⇒ l ⊂A ∈⎬B ∈⎪⎭②公理 2：不共线的三点确定一个平面③公理 3：P ∈⎫ ⇒⋂= l 则P ∈ l⎭⎩⎩⎩二、点与面、直线位置关系⎧1、A ∈1、点与平面有 2 种位置关系⎨2、B ∉⎧1、A ∈ l2、点与直线有 2 种位置关系 ⎨2、B ∉ l三、空间中直线与直线之间的位置关系1、异面直线2、直线与直线的位置关系⎧ ⎧相交⎪共面⎨⎨ ⎩⎪异面 3、公理 4 和定理公理 4：l 1 l 3 ⎫⇒ l l⎬ 1 2l 2 l 3 ⎭定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。

平行4、求异面直线所成角的步骤：①作：作平行线得到相交直线；②证：证明作出的角即为所求的异面直线所成的角；③构造三角形求出该角。

提示：1、作平行线常见方法有：直接平移，中位线，平行四边形。

2、异面直线所的角的范围是(00 , 900⎤⎦。

四、空间中直线与平面之间的位置关系直线a与平面相交直线a与平面平行a ⊂ a =A a五、空间中平面与平面之间的位置关系=a⎬ ⎬ ⎭ ⎬ ⎭⎭⎪直线、平面平行的判定及其性质一、线面平行1、判定：b ⊄⎫ a ⊂⎪⇒ bb a ⎪（线线平行，则线面平行）2、性质：aa ⊂⎫ ⎪⇒ a b⋂ = b ⎪（线面平行，则线线平行）二、面面平行1、判定：a ⊂⎫ b ⊂⎪ ⎪a ⋂b = P ⎬ ⇒a ⎪b ⎪⎭（线面平行，则面面平行）2、性质 1：⎫= a ⎪ ⇒ a b = b ⎪（面面平行，则线面平行）m ⊂⎬性质2：⎫⇒m⎭（面面平行，则线面平行）说明（1）判定直线与平面平行的方法：①利用定义：证明直线与平面无公共点。

②利用判定定理：从直线与直线平行等到直线与平面平行。

③利用面面平行的性质：两个平面平行，则其中一个平面内的直线必平行于另一个平面。

必修2 点线面复习姓名一、点线面的关系：直线和直线有3种关系：相交、平行、异面；直线和平面有3种关系：相交、平行、在平面内；平面和平面有2种关系：相交、平行；二、平行垂直的判定：线面平行：线平行面内一条直线————线线平行面面平行：相交直线平行面——————线线平行×2线面垂直：线垂直面内两条相交直线——线线垂直×2面面垂直：过面的垂线————————线线垂直×2三、平行垂直的性质：线面平行：线与交线平行面面平行：面面交线平行线面垂直：（1）线垂直于面内任何一直线（2）两垂线平行面面垂直：垂直交线的垂直面典型例题：1、如图，在三棱锥A-BCD中，E、F是棱AB、AD的中点求证：EF∥平面BCD2、在正方体ABCD-A 1B1C1D1中，E为边DD1的中点，O为AC和BD的交点，求证：BD1∥平面AEC3、三棱锥A-BCD中，E、F、G分别是AB、AD、AC的中点求证：平面EFG∥平面BCD4、在正方体ABCD-A1B1C1D1中，E、F为A1D1和BC的中点求证：EF∥平面ABB1A15、三棱锥A-BCD中，AB=1，AD=2，求证：AB⊥平面BCD6、三棱锥A-BCD中，AB⊥平面BCD，BC⊥CD求证：CD⊥平面ABC7、在四棱锥S-ABCD中，SD⊥平面ABCD，底面ABCD是正方形求证：AC⊥平面SBD8、ABCD和DCCD1是两个正方形，平面ABCD⊥平面DCC1D1（1）求证：AD⊥平面DCC1D1（2）求证：D1D⊥平面ABCD（3）CD⊥平面BCC1（4）AC⊥平面BDD19:、（湖北文）如图，四棱锥S＝ABCD的底面是正方形，SD⊥平面ABCD,点E是线段SD上的任意一点，求证： AC⊥BE10、（江西文）如图，在四棱锥P ABCD -中，底面ABCD 是矩形，PA ⊥平面ABCD ，M 为PD 上一点，求证：平面ABM ⊥平面A P D11、（10广州一模）如图，正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ，AE ⊥平面CDE ，求证：AB ⊥平面ADE ；12、在四面体ABCD 中，CB=CD ，AD BD ⊥，且E ，F 分别是AB ，BD 的中点， 求证（I ）直线EF D 平面AC ；（II ）EFC D ⊥平面平面BC 。