外文翻译--一个控制器使门式起重机和减摇桥精确定位

[强力推荐]翻译优秀译文中英对照一种消除震动对增量式光学编码器测量影响的方法Method for eliminating influence of vibration over measurement of incremental optical encoder本发明旨在提供一种消除震动对增量式光学编码器测量影响的方法，以解决现有技术中增量式光学编码器抗震能力差的技术问题。

该方法是在现有增量式光学编码器的基础上，将光学编码器的光电读头数量增加为四个，并将四个光电读头沿指示圆光栅盘圆周均匀安置，使各读头相对于圆心成９０度分布。

通过四个读头和ＡＤ转换电路及检相算法将四读头位置处的叠栅条纹相位解算出来，再以该四个特定位置的相位信息为基础，计算出标尺圆光栅盘震动方向和震动幅度，从而求出该震动产生的误差项并反代入光学编码器转动引起的叠栅条纹相位变化表达式，消除震动的影响。

本发明极大地降低了震动时光学编码器的检相误差，提高了存在震动时光学编码器的测量精度。

The invention aims to provide a method for eliminating the influence of vibration over the measurement of an incremental optical encoder, so as to solve the technical problem of poor anti-vibration ability of the incremental optical encoder in the prior art. The method is characterized in that on the basis of the existing incremental optical encoder, the number of photoelectric read heads of the optical encoder is increased to four; the four photoelectric read heads are evenly settled along the circumference of an indicating circular grating disc; and each read head is distributed at an angle of 90 DEG relative to a circle center. Stacked grating fringe phases in the positions of the four read heads are solved through the four read heads, an analog-digital (AD) conversion circuit and a phase detection algorithm; then the vibration direction and the vibration amplitude of a scale circular grating disc are calculated on the basis of the phase information of the four specific positions, so as to determine error terms produced during the vibration; and the vibration direction and the vibration amplitude are inversely substituted into an expression of stacked grating fringe phase changes caused by the rotation of the optical encoder, so as to eliminate the influence of the vibration. By adopting the method, phase detection errors of the optical encoder are greatly reduced during the vibration, and the measurement accuracy of the optical encoder is improved when the vibration exists.流感疫苗中的过敏原卵类粘蛋白或卵运铁蛋白定量检测Method for detecting allergen ovomucoid or ovotransferrin in influenza vaccine quantificationally本发明公开了一种流感疫苗中的过敏原卵类粘蛋白或卵运铁蛋白定量检测方法，在制备抗卵类粘蛋白或抗卵运铁蛋白单克隆抗体的基础上，经过配对抗体的筛选，建立的双抗体夹心酶联免疫吸附试验，来定量检测流感疫苗中卵类粘蛋白和卵运铁蛋白。

European Journal of Scientific ResearchISSN 1450-216X Vol.33 No.4 (2009>, pp.630-641© EuroJournals Publishing, Inc. 2009对龙门起重机系统抑制摇摆的最优跟踪控制M.A. AhmadControl and Instrumentation Research Group (COINS>,Faculty of Electrical and Electronics EngineeringUniversiti Malaysia Pahang, Lebuhraya Tun Razak26300, Kuantan, Pahang, MalaysiaE-mail:Tel: +609-5492366。

Fax: +609-5492377R.M.T. Raja IsmailControl and Instrumentation Research Group (COINS>Faculty of Electrical and Electronics EngineeringUniversiti Malaysia Pahang, Lebuhraya Tun Razak26300, Kuantan, Pahang, MalaysiaE-mail:Tel: +609-5492366。

Fax: +609-5492377M.S. RamliControl and Instrumentation Research Group (COINS>Faculty of Electrical and Electronics EngineeringUniversiti Malaysia Pahang, Lebuhraya Tun Razak26300, Kuantan, Pahang, MalaysiaE-mail:Tel: +609-5492366。

工程起重机中英文翻译对照To gain a certificate of competency for a cabin controlled bridge or gantry crane you must pass anassessment for a Bridge and gantry crane certificate conducted by an assessor registered by the Workcover Authority.Before taking the assessment you must obtain a log book and learn the competencies required to pass theassessment. Applicants must be at least 18 years old to gain a certificate.It is illegal to operate a cabin controlled bridge or gantry crane without a Bridge and gantry cranecertificate or a log book (under the supervision of a certificated driver).A cabin controlled bridge or gantry crane driver must know:●how to safely operate a bridge or gantry crane●how to detect any mechanical faults●about slinging loads,sheaves and drums,rope terminations,anchors andattachmentsIt is the responsibility of the applicant to make sure that a bridge or gantry crane of the correct class isavailable for the assessment at their workplace or has permission to use a crane at another location.If you operate this type of crane and sling loads in connection with the operation of this type of crane you will require a Dogging certificate in addition to being competent in its operation. See A guide for dogging available from the WorkCover Authority.桥梁合格证书起重机和龙门起重机为了获得一个龙门式起重机的合格证书，你必须通过操作龙门起重机进行评估，然后由劳保局注册管理局评估而得到的证书。

模糊控制式桥式起重机文摘:介绍了基于模糊控制的设计的吊车。

而不是分析复杂非线性吊车系统,该方法使用简单但有效的方法来控制起重机。

有双模糊控制器这处理反馈信息,位置的架空起重机和摆动角的负荷,抑制摇摆和加快速度当起重机运输沉重的负荷。

这种方法简化了设计过程的起重机控制器;此外,双控制器方法减少了规则数当完成模糊系统。

最后,实验结果通过起重机模型证明了该方案的有效性。

关键词:桥式起重机;模糊控制1 介绍桥式吊车系统广泛应用于工业移动沉重的货物。

因此反摇摆和位置控制已成为需求作为核心技术自动化起重机系统,能够灵活的空间自动运输。

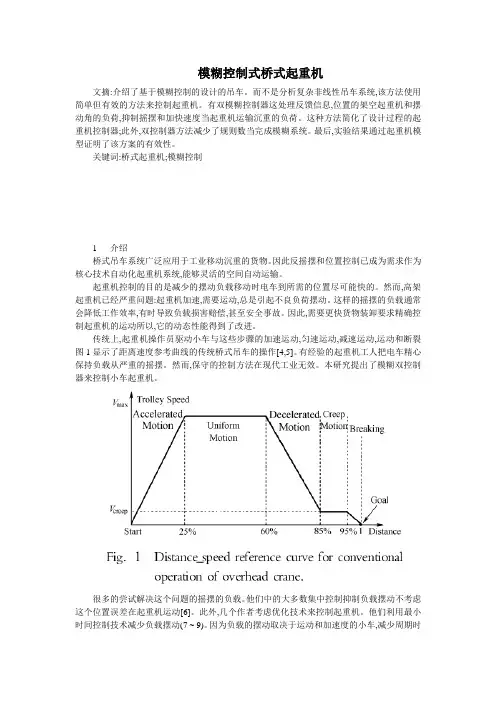
起重机控制的目的是减少的摆动负载移动时电车到所需的位置尽可能快的。

然而,高架起重机已经严重问题:起重机加速,需要运动,总是引起不良负荷摆动。

这样的摇摆的负载通常会降低工作效率,有时导致负载损害赔偿,甚至安全事故。

因此,需要更快货物装卸要求精确控制起重机的运动所以,它的动态性能得到了改进。

传统上,起重机操作员驱动小车与这些步骤的加速运动,匀速运动,减速运动,运动和断裂图1显示了距离速度参考曲线的传统桥式吊车的操作[4,5]。

有经验的起重机工人把电车精心保持负载从严重的摇摆。

然而,保守的控制方法在现代工业无效。

本研究提出了模糊双控制器来控制小车起重机。

很多的尝试解决这个问题的摇摆的负载。

他们中的大多数集中控制抑制负载摆动不考虑这个位置误差在起重机运动[6]。

此外,几个作者考虑优化技术来控制起重机。

他们利用最小时间控制技术减少负载摆动(7 ~ 9)。

因为负载的摆动取决于运动和加速度的小车,减少周期时间和减少负荷摆动部分相互冲突的需求。

除此之外,还有许多论文调查稳定性问题的控制器设计[10 ~ 12],但是这些研究缺乏实验说明了有效性。

本研究提出了一种实用的解决方案为反摇摆和精确位置控制的起重机。

这个职位的电车、旋角的负荷及其分化是应用于衍生出正确的控制输入的电车起重机。

两个模糊逻辑控制器(FLC)是用来交易单独与反馈信号,偏转角和电车位置和他们的负效应。

A controller enabling precise positioning and sway reduction inbridge and gantry cranesKhalid L. Sorensen, William Singhose, Stephen DickersonThe George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 813 Ferst Dr., MARC 257, Atlanta, GA 30332-0405, USAReceived 28 September 2005; accepted 30 March 2006Available online 5 June 2006一个控制器使门式起重机和减摇桥精确定位Khalid L. Sorensen, William Singhose, Stephen Dickerson, 乔治亚机械工程学院，乔治亚技术学院， Ferst博士813，MARC 257 ,亚特兰大，GA 30332-0405,美国，2005年9月28日收到，2006年3月30日接受，2006年6月5日可在线使用.一个控制器使门式起重机和减摇桥精确定位摘要起重机是很难精确操纵载荷的。

振荡,可以诱导成大桥或手推车的阻尼系统轻度运动,并且还对环境造成滋扰. 为解决上述两种振荡的来源,结合反馈和输入整形控制器的发展。

该控制器是由三个不同的模块组成，反馈模块的检测和定位误差补偿; 第二反馈模块侦测并拒绝振动; 使用塑料造填充的第三个模块,以减轻振荡。

一个使用精确的模型矢量驱动的交流感应马达，为典型的大型起重机, 用同一个褶分析技术,将非线性动力学起重机器分为对照设计。

在佐治亚技术学院实验10吨桥式起重机控制器。

该控制器具有良好的定位精度和性能以减少摆动.。

附录英文原文Crane Scheduling with Spatial ConstraintsAndrew Lim, Brian Rodrigues, Fei Xiao, and Yi ZhuAbstractIn this work, we examine port crane scheduling with spatial and separation constraints. Although common to most port operations, these constraints have not been previously studied. We assume that cranes cannot cross, there is a minimum distance between cranes and jobs cannot be done simultaneously. Theobjective is to find a crane-to-job matching which maximizes throughput under these constraints. We provide dynamic programming algorithms, a probabilistic tabu search and a squeaky wheel optimization heuristic for solution. Experiments show the heuristics perform well compared with optimal solutions obtained by CPLEX for small scale instances where a squeaky wheel optimization with local search approach gives good results within short times.1 IntroductionThe Port of Singapore Authority (PSA) is a large port operator located in Singapore, one of the busiest ports in the world. PSA handles 17.04 million TEU’s annually or nine percent of global container traffic in Singapore, the world’s largest transshipment hub. PSA is concerned with maximizing throughput at its port due to limited port size, high cargo transshipment volumes and limited physical facilities and equipment . Crane scheduling and work schedules are critical in port management since cranes are at the interface between land and water sections of any port, each with its own traffic lanes, intersections, and vehicle flow control systems. In this multi-channel interface we are likely to find bottlenecks where cranes and other cargo-handling equipment (forklifts, conveyors etc.) converge.Sabria and Daganzo studied port operations which focused on berthing and cargo-handling systems. In berthing, which is a widely-analyzed port activity, queuing theory has been used widely. Traffic and vehicle-flow scheduling o n land in ports has also been well studied. Danganzo studied a static crane scheduling case where cranes could move freely from hold to hold and only one crane is allowed to work on one hold at any one time.The objective was to minimize the aggregate cost of delay. In [13], container handling is modelled as ―work‖ which cranes perform at constant rates and cranes can interrupt work without loss of efficiency. This constituted an ―open shop‖ parallel and identical machines problem, where jobs consist of independent,single-stage and pre-emptable tasks. A branch- and-bound method was used to minimize delay costs for this problem. Crane scheduling has also been studied in the manufacturing environment context .Commonly-found constraints affecting crane operations are absent in studies available on the subject. Such constraints affect crane work scheduling and need to be factored into operational models. These include the basic requirement that operating cranes do not cross over each other. Also, a minimum separating distance between cranes is necessary since cranes require some spatial flexibility in performing jobs. Finally, there is a need for jobs arriving for stacking at yards to be separated in arrival time to avoid congestion.We found that operational decision-making at PSA was based largely on experience and simulation techniques. While the latter is of value, analytic models are an advantage and are not limited by experience-generated rules-of-thumbs or simulation. The object of this work is to address the need for such models which take into account common spatial and separation requirements in the scheduling cranes. This work augments Peterkofsky and Daganzo study .2 Problem DescriptionDuring the time ships are berthed, various cargo-handling equipment is used to unload cargo, mostly in the form of containers. Different types of cargo require different handling and many ports have bulk, container, dry and liquid-bulk terminals. Cargo that is containerized can be loaded and unloaded in a fewer number of moves by cranes operating directly over ship holds or by crane arms moving over holds or deck areas.Cargo stacked in yards is moved by cranes onto movers and transported for loading onto shi ps. ‖Cargo‖ here comprises containers of different capacities, which, whether in ships or in yards, are parcelled into fixed areas for access to cranes. For example, cargo placed in specific holds or deck sections on ships, or in sections within yards.Containers are unloaded from ships by quay cranes onto movers or trailers which carry them to assigned yard locations where they are loaded onto stacks by yard cranes. Containers destined for import are set aside, and restacking, if required, is carried out. In the movement of containers, sequencing is crucial because containers are stored in stacks in the ship and on the yard and lanes may be designated to specific trailers at certain times. In addition, the movement of containers involves routing and crane operations where timings may be uncertain. In fact, crane scheduling is one activity among many that determine the movement of containers. Other such activities includeberthing, yard storage, ship stowage and vehicle allocation and routing, all of which can be uncertain. Because of the uncertainty present over all activities, it is almost impossible to implement a plan over any length of time. This difficulty is present in scheduling cranes. For example, although a set of jobs may be assigned to a certain crane, it may not be possible for the crane to complete processing a job in this set onto movers once it was known that the route these movers are to take was congested. As another example, although we can specify that jobs bound for the same yard space are not unloaded from ships simultaneously, we cannot expect such containers to be unloaded at a time other than the allotted time interval, since a required resource to complete the job may become unavailable after this time, as for example, if the yard crane becomes unavailable. In view of the dynamically changing environment, a central control devises and maintains a job assignment plan that is periodically updated in order to coordinate operations, including crane scheduling. The system will allocate all jobs and resources periodically.In the port we studied, a job parcel can include a number of ships and a number of cranes together with jobs. Typically, there can be up to five ships with four to seven cranes per ship and a number of jobs depending on the size and configuration of ships. J obs have a profit value assigned to them and resources, e.g., cranes, movers, lanes etc., are assigned to each of the jobs depending on their value to the overall operations plan which aims to optimize total throughput. When an assignment plan is updated, the central system reassesses the current state of operations to regroup and reassign job parcels. Because of this, time is accommodated by constant adjustments of job parcels and assignments based on the current state of all operations. Hence, once jobs and resources are assigned for the time period no update is necessary.Jobs come in different sizes, and cranes have different handling capacities. Since we make the assumption that any crane assigned to a job completes it, the throughput or profit, for a given crane-to-job assignment, is a fixed value independent of other crane-to-job assignments.The problem is naturally represented by a bipartite graph matching problem when we take cranes and jobs to be the vertices and define the weights of connecting edges to be crane-to-job throughput. This representation is shown in Figure 1.Figure 1This matching problem is interesting because, in practice, a number of spatial constraints arise for cranes and jobs. We first introduce qualitative notions of three particularly common constraints which we call ―spatial‖ constraints since they are related to the relative posi tions of cranes and jobs. Our objective is to find a crane-to-job assignment scheme which maximizes throughput under these constraints. For reasons given above, we assume that crane-to-job assignments are performed in a given time interval, i.e., there is no temporal component in the problem. Detailed definitions will be given in the relevant sections of this paper.1. Non-crossing constraint: Cranes cannot cross over each other. This is a structural constraint on cranes and crane tracks.2. Neighborhood constraint: There is a minimum distance between cranes. This arises, for example, since cranes require flexibility in space to perform jobs and/or for safety reasons. The effect of this constraint is that neighboring jobs may be affected and may not be assignable to other cranes.3. Job-separation constraint: Certain jobs cannot be done simultaneously. For example, jobs bound for the same yard may require separation in time to avoid trailer congestion in lanes.In the following sections, we first consider these constraints separately and then simultaneously. In section 3, an O(mn) dynamic programming (DP) algorithm is given to solve the problem with only the Non-crossing constraint where m is the number of cranes and n is the number of jobs. In section 4, we use an O(m2n) dynamic programming algorithm to achieve an optimal solution for the problem with both the Non-crossing and Neighborhood constraints. In section 5, assuming all three spatial constraints, we show the problem to be NP-complete and give two heuristic approaches to solve the problem —a probabilistic tabu search and a squeaky wheel optimizationwith local search method. In section 6, we provide experimental results and compare the different approaches.3 Scheduling with the Non-Crossing Constraint3.1 The ProblemThroughout this work, C= {c1, c2, . . . , c m} is a set of cranes and J= {j1, j2, . . . , j n} a set of jobs. The order of subscripts assigned to the cranes and jobs represents their spatial (assumed linear) distribution, i.e., the neighbor of j1is j2, the neighbors of j2are j1and j3,. . . , and the neighbor of j n is j n−1, The same holds for the cranes.An m × n adjacency matrix, W , is used to represent the relationships between jobs and cranes. For each W x,y∈W , the value W x,y represents the throughput when job j y is assigned to crane c x where W x,y= 0 if job j y cannot be assigned to crane c x. The W x,y values arise from the different job sizes and crane capacities.We seek a solution set,R={(p, q )|1 ≤p≤ m, 1≤q≤n, W p,q> 0}, such that the following constraint is satisfied: For all (p1, q1), (p2, q2)∈R, p1< p2if and only if q1< q2. Viewing p’s and q’s, as subscripts in C and J respectively, we see that any crane-job assignment in R satisfies the Non-crossing Constraint.The objective is then to find a set R which maximizes ∑(p,q)∈rWp,q subject to the constraints that each job is assigned to at most one crane and each crane is assigned to at most one job.3.2 Algorithm DescriptionWe now provide a dynamic programming (DP) approach and describe how to characterize an optimal solution. DP procedures for computing values of solutions in a bottom-up way and for constructing solutions from computed information are omitted since they follow directly and are required only in implementation.3.2.1 The Structure and Value of an Optimal SolutionWe consider the cranes one by one. For each crane c x, we assign every job j y(1 ≤ y ≤ n) to it and compute the total throughput to derive a partial optimal solution P x,y which denotes the optimal value up to the step we assign job j y to crane c x. Here, it is not necessary that job j y is actually assigned to crane c x, i.e., (x, y) ∈R x,y may not hold, where R x,y is the partial solution set corresponding to the partial optimal solution P x,y.The following computes the partial optimal solution, P x,y, recursively, for the different cases:1. If x = 1 and y = 1, P1，1:= W1，12. If x = 1 and y > 1, P1,y:= max{W1，y’, P1,y-1}3. If x > 1 and y = 1, P x，1:= max{W x,1, P x-1,1 }4. If x > 1 and y > 1, P x,y:= max{P x,y-1,P x-1,y’ ,P x-1,y-1+W x,y}(1) is the basic case: If we only consider the first crane and the first job, we will assign this job to the crane if the job can be done by the crane. (2) and (3) are both special cases, i.e., when there is only one node in each part of the bipartite graph. As these are symmetrical, we need consider only (2). For crane c1and job j y, we have two choices: either, assign j y to c1, or, assign a job from {j1, . . . , j y−1}to c1. This is because at most one job can be assigned to this first crane. The throughput for the first choice is W1,y while the throughput for the second choice is P1,y−1 , which represents the maximum throughput if we assign a job among j1, j2, . . . , j y-1to crane c1. To achieve the cumulative optimal, we choose the larger of these. (4) is the general case in the DP algorithm. For c x and job j y(x > 1, y > 1), we have three choices:•Leave job j y unassigned . We are reduced to assigning cranes c1, c2, . . . , c x to jobs j1, j2, . . . , j y-1. By induction, the optimal value is then P x,y-1;•Leave crane c x unassigned . We are reduced to assigning cranes c1, c2, . . . , c x-1 to jobs j1, j2, . . . , j y. By induction, the optimal value is then P x-1,y;•Assign crane c x to job j y(or, leave both unassigned if they are not assignable to each other). In this case, the total throughput is the throughput from this assignment plus the throughput from assigning cranes c1, c2, . . . , c x-1 to jobs j1, j2, . . . , j y-1. Hence, the value is P x-1,y-1+W x,y.Taking the maximum of these throughput values, the optimal solution is then the final partial optimal solution P m,n obtained.3.2.2 A Proof of Optimal SubstructureWe provide an outline a proof that the problem defined in this section possesses optimal substructures necessary in using DP. An important property for P x,y is: P x,y≥P x’,y’,if x ≥ x’and y ≥ y’(*), which is easily verified since P x,y≥ P x,y-1 and P x,y≥ P x-1,y. We can now verify the four cases given above by induction:1. If x = 1 and y = 1, clearly P1,y = W x,1 is the only solution and must be optimal2. If (x, y)∈R’x,y, then P x,y’≤P ak-1,bk-1+W x,y. By (*), we know P x-1,y−1≥P ak-1,b-1since x − 1 ≥ ak-1, y-1 ≥ bk-1. So P x,y’≤ P x-1,y-1+W x,y. Because P x,y≥P x-1,y-1+ W x,y, we get P x,y≥ P x,y’ , which contradicts our assumption P x,y’> P x,y. Hence, P x,y is the optimal solution.We can conclude that P x,y is the optimal solution for all (x, y), 1 ≤ x ≤ m, 1 ≤ y ≤ n,3.3 The Time Complexity of the AlgorithmThe computation for every partial solution P x,y is in constant time, so the time complexity for this algorithm is O(mn).4 Scheduling with the Neighborhood Constraint4.1 The ProblemIn this problem, both the Non-crossing constraint and the Neighborhood constraint are considered. In addition to the Non-crossing constraint, we use the set S= {s1, s2, . . . , s m} to represent the Neighborhood constraint associated with the cranes. Here s x= k if crane c x performs job j y and job j z(a ≤ z ≤ b, z= y) cannot be worked on by any other crane, wh ere a = max{1, y − k}and b = min{y + k, m}. In other words, if crane c x performs job j y, the job ―interval‖ centered at y with length 2k + 1 is affected by crane c x when s x= k.We seek a solution set R = {(p, q)|1 ≤ p ≤ m, 1 ≤ q ≤ n, W p,q> 0} satisfying:1. For all (p1, q1), (p2, q2) ∈ R, p1< p2if and only if q1< q2(Non-crossing constraint)2. For all (p, q) ∈R, if 1 ≤ p’≤ m and p’= p, and a ≤ q’≤ b, where a = max{1, q − s p} and b = min{q + s p, n}, then (p’, q’) ∈R (Neighborhood constraint)Our objective is to find R that maximizes the total weight ∑(p,q)∈rWp,q where each job is assigned to at most one crane and each crane is assigned to at most one job.4.2 Algorithm DescriptionWe follow the approach in section 3.2 here.4.2.1 The Structure and Value of an Optimal SolutionWe continue to consider the cranes one by one. For each crane c x, we attempt to assign every job j y(1 ≤ y ≤ n) to it and compute the total throughput up to this step to give a partial optimal solution P x,y.Here, the partial optimal solution P x,y is cumulative and the edge inclusion (x, y) ∈R x,y may not hold. However, different from the definition used in the previous section, crane x must be assigned some job j (1 ≤ j ≤ y) for P x,y, i.e., there must be an edge (x, j) ∈R x,y, where (1 ≤ j≤ y); if there is no job in the interval [1, y] that can be assigned to crane x, then P x,y= 0. Now, we define the value of the partial optimal solution P x,y for the different cases:1. If x = 1 and y = 1, P1,1＝W1,12. If x = 1 and y > 1, P1,y:= max{W1,y,P1,y-1}3. If x > 1 and y = 1, P x,1=W x,14. If x > 1 and y > 1, P x,y:= max{P x,y-1,P i,c+W x,y}, 1 ≤ i < x, c = y− max{s x, s i} − 1.(1) is the basic case and (2) and (3) are the special cases. (2) has been explained in the previous section. (3) is different. Since we require for P x,y that crane c x must be assigned job j y, we have no choice but to assign this job to the current crane when there is only job available. The induction step in (4) is somewhat complex. In the first case, we keep job j y unassigned, so we are reduced to assigning cranes c1, c2, . . . , c x to jobs j1, j2, . . . , j y; hence, we obtain P x,y-1. In the second case, since we assigned job j y to crane c x, the Neighborhood constraint for c x must be considered. Also, we must consider the Neighborhood constraint for the cranes c1, c2, . . . , c x which are assigned to jobs. The Non-crossing constraint simplifies the computation leaving us only to check the neighborhood constraint for the ―largest label‖crane assigned and is the reason the c value is needed in the formula.The final optimal is the maximum value of all partial optimal solutions obtained,i.e., it is max{P x,y} over all (x, y), 1 ≤ x ≤ m, 1 ≤ y ≤ n.4.2.2 A Proof of Optimal SubstructureSimilar to the earlier problem, we show that this problem has an optimal substructure. As before, we use the fact that P x,y≥ P x,y’ if y ≥ y’(**). This is easy to verify since a partial optimal solution is cumulative for each crane x. As before, we have the following cases:1. If x = 1 and y = 1, clearly P1,1= W1,1is the optimal solution2. If x = 1 and y > 1, only one crane is involved, so the Neighborhood constraint does not take the effect. The proof is then as given in the previous section3. If x > 1 and y = 1, since crane c x has to be assigned a job, and there is only one job, clearly P x,1 = W x,14. If x > 1 and y > 1, P x,y= max{P x,y-1, P i,c+ W x,y}, 1 ≤ i < x, c = y−max{s x, s i} − 1. We assume there is an optimal solution P x,y0> P x,y and the solution set corresponding to P x,y’is R’x,y={(c a1, j b1), (c a2,j b2), . . . , (c ak,j bk)}. Here, we can take this set to be ordered, i.e., a1≤ a2≤ . . . ≤ a k and b1≤ b2≤ . . . ≤ b k, by virtue of the Non-crossing constraint. Noting a k= x from the definition above, there are now two possibilities for P x,y’:(a) If (x, y) ∈R’x,y, then P x,y’≤ P ak,bk, since P ak,bk is the partial optimal solution. Hence, P x,y’≤ P x,bk, since a k= x. From property (**), we know P x,y-1≥ P x,bk since y − 1 ≥ b k(job j y is unassigned). So P x,y−1 ≥ P x,y’. By the recursive definition, P x,y≥ P x,y-1. Hence, we get P x,y≥ P x,y’, which contradicts the assumption P x,y’ > P x,y. So P x,y is the optimal solution in this case(b) If (x, y ) ∈ R’x,y, then P x,y’≤ P ak-1,bk-1+W x,y, since P ak-1,bk-1is the partial optimalsolution. Obviously 1 ≤ a k-1<x, so we let i = a k-1and c = y−max{s x, s i} − 1. We know bk−1≤c since the cranes c x andc i are both assigned jobs and their Neighborhood constraints are in effect. From (**), we get P i,c≥ P i,bk-1because of c ≥ b k−1, i.e., P ak-1,c + W x,y≥ P ak-1,bk-1,+W x,y, and so P ak-1,c+W x,y≥P x,y’. From the definition P x,y= max{P x,y-1,Pi,c+W x,y}, we know P x,y≥ P x,y’ , which contradicts the assumption P x,y’> Px,y. Hence, P x,y must be the optimal solution in this caseWe conclude that P x,y is the optimal solution for all (x, y), 1 ≤ x ≤ m, 1 ≤ y ≤ n.4.3 The Time Complexity of the AlgorithmSince, for each partial solution P x,y, we take the maximum value of the partial solutions P i,c, 1 ≤ i < x, the time complexity is O.5 Scheduling with the Job Separation Constraint5.1 The ProblemWe can now study the third and most general spatial constraint —the Job-separation constraint. An n × n matrix D represents this constraint: D p,q= 1(1 ≤ i ≤ n, 1 ≤ j≤ n), when job j p and j q cannot be done simultaneously. Otherwise, the elements of D are 0. Note that D is symmetric. We seek a solution set R = {(p, q)|1 ≤ p ≤ m, 1 ≤ q ≤ n, W p,q> 0}, for which the following three conditions are satisfied:1. For all (p1, q1), (p2, q2) ∈ R, p1< p2 if and only if q1< q2(Non-crossing constraint)2. For all (p, q) ∈R, if 1 ≤ p’≤ m and p’= p, and a ≤ q’≤ b, where a = max{1, q − s p} and b = max{q + s p, n}, then (p’, q’) ∈R (Neighborhood constraint)3. For all (p, q) ∈R, if 1≤p’≤ m, and D q,q’= 1, then (p’, q’)∈R(Job-separation constraint)The objective is to find a set R which maximizes total weight ∑(p,q)∈rWp,q where each job is assigned to at most one crane and each crane is assigned to at most one job.5.2 Proof of NP-completenessTo show that this problem is NP-complete, we use the Independent Set problem which is defined as follows: Given a graph G= (V, E) and a positive integer k≤ |V |, is there a V’⊆ V such that for all u, v ∈V’, the edge (u, v) is not in E and |V’| ≥ k?In order to prove that this problem is NP-hard, we transform an arbitrary instance of the Independent Set problem to the problem in polynomial time. Assuming there are n nodes in the graph G = (V, E) of the Independent Set problem, we construct the model with n cranes and n jobs where the only edges are (1, 1), (2, 2),..., (n, n), all with weight equal to 1. The Job-separation constraint matrix D is defined as follows: For all(x, y) ∈ E, D x,y= 1, otherwise D x,y= 0, 1 ≤ x, y ≤ n. The transformation is illustrated in Figure 5 and can be achieved in polynomial time.Now we show that the Independent Set problem has a solution of size k if and only if the problem has a solution with total profit k. First, if there are k independent nodes in graph G, there must be k jobs that do not, pairwise, conflict. Since we constructed n parallel edges with weight 1, the Non-crossing constraint and Neighborhood constraint do not have any effect here. Hence, we can use k cranes to do the k jobs without violating the Job-separation constr aint with total profit k. If we now assume that there is a solution in this problem with profit k, there must be k jobs selected without violating the Job-separation constraint. There must be k nodes that are not connected by any edges and therefore a set of nodes of size k.We can verify solutions by checking crane-job assignments one by one for violation of the three constraints. Clearly, this can be done in polynomial time, so the problem is in the class NP. Since the problem has been shown to be NP-hard, it is NP-complete and, unless P = NP, there are no polynomial algorithms to solve it optimally. It would be useful therefore to develop heuristic solutions for the problem, which we do in the following sections.5.3 A Probabilistic Tabu Search ApproachTabu Search (TS) is a search procedure that iterates from one solution to another by moves in a neighborhood space with the help of an adaptive memory. Probabilistic Tabu Search (PTS) is a variant of TS, which places emphasis on randomization when compared with basic TS . The basic approach is to create move evaluations that include references to the tabu status and other relevant biases from TS strategies using penalties, modifying underlying decision criterion and selecting the next move among those neighborhood moves with different probabilities which are based on different evaluation values . In this section, we describe how it can be employed for the crane scheduling problem.5.3.1 Neighborhood StructureFrom an initial feasible solution obtained by a greedy method or a random crane-job assign－ment, the graph representation becomes almost edge ―saturated‖, i.e. we can hardly add an edge without violating the Non-crossing, Neighborhood and Job-separation constraints. We can however delete an edge from the current solution and try to add other edges until it is ―saturated‖ again. Deleting the edge which connects crane c and job j allows some cranes and jobs to become assignable. Obviously, thesecan only come from cranes and jobs which are neighbors to c and j, respectively, which do not violate the Non-crossing constraint w.r.t. all current assignments (discounting the c to j assignment). Jobs selected must also satisfy the Neighborhood and Job-separation constraints. After deleting the edge connecting c to j, we consider each neighbor of c from these feasible neighbors together with c, one by one. For each crane, we assign a probability p1for it to be selected for a job. For each selected crane, we have two types of assignments: one is a greedy assignment which selects a compatible job with the largest weight; the other is a random assignment which randomly picks one job from all the compatible jobs. Which scheme is chosen depends on yet another probability, p2.5.3.2 Tabu Search MemoryTS memory structures guide the search process. There are two kinds of memory structures. One is ―short-term memory‖, which can prevent the search from being trapped in a local optimum and the other is ―long-term m emory‖, which provides diversification and inten－sification.Short-term memory restricts the composition of new solutions generated. If an edge is deleted in a move, we forbid its addition in the next few moves; similarly, if an edge is added in a move, we forbid its deletion in the next few moves. Such a mechanism prevents the search from revisiting local optima in the short term and reduces the chance of cycling in the long term.How long a restriction is in effect depends on a tabu tenure parameter, which i dentifies the number of iterations a particular restriction remains in force . We implemented short- term memory using a recency-based memory structure as follows.future iteration values that forbid a reversal of the moves on adding edge (x, y) or deleting edge (x, y). Furthermore, let tabu add tenure and tabu delete tenure be the values of tabu tenure for these two moves. When the TS restriction is imposed, we update the recency memory by:tabu add(x, y) = iter + tabu add tenuretabu delete(x, y) = iter + tabu delete tenureWe assign positive penalties to edges in tabu status, which means they are forbidden by the recency memory.A TS restriction is overridden by aspiration if the outcome of the move under consideration is sufficiently desirable. This can be achieved by deducting a large numberfrom the total penalty.5.3.3 Move EvaluationAfter finding all neighborhood candidate moves, we evaluate these moves so that they are ready for selection. The resulting evaluation value is in two parts: the total profit and the penalties. For our crane scheduling problem, the penalties comprise: (1) Short-term memory penalties which include tabu status penalties as well as aspiration satisfaction ―penalties‖ (2) Long-term memory penalties which include transition measure and residence measure penalties and (3) Penalties for other biases.5.3.4 Probabilistic Move SelectionAfter evaluating all candidate moves, we select one move to proceed. The fundamental idea of move selection is to choose the best move, i.e., choose the move with the highest evaluation. However, we found that this greedy selection strategy is strongly biased. We therefore made adjustments using probabilities. The strategy for a probabilistic move selection is given as follows:1. Generate the candidate list and evaluate candidate moves which have described above2. Select the move from the candidate list with the highest evaluation value3. Accept the move with probability p and exit; otherwise, go to (4). Here, p is a param-eter and is set to 0.3 in the algorithm4. Remove the move from the candidate list. If the list is empty, accept the first move ofthe original candidate list and exit. Otherwise, go to (2).It is easily shown that the probability of choosing one of the best k moves is 1 − (1 − p)k, which is large even if p is not large. For example, if p is 0.25, the probability of choosing the best 5 moves is 0.763, the best 10 moves is 0.944. We can therefore choose relatively high evaluation moves while avoiding favoring those with highest evaluations always.5.4 SWO with Local Search Approach―Squeaky Wheel‖ Optimization (SWO) is a general approach to optimization and consists of a Construct-Analyze-Prioritize cycle at its core. The Analyzer will assign a numerical ‖blame‖ value to the problem elements that contribute to shortcomin gs in the current solution. The Prioritizer will modify sequences of problem elements and。

中英文对照起重机术语大全起重机（crane）moblie crane 移动式起重机truck crane 汽车式起重机wheel crane / wheeled crane 轮胎起重机crawler crane / caterpillar crane 履带吊;履带式起重机tower crane 塔吊; 塔式起重机-construction tower cranes / building tower crane 建筑塔式起重机，建筑塔机-luffing jib tower crane 动臂塔式起重机-tower jib crane 塔式挺杆起重机（含义与上同）bridge crane/traveling crane/overhead crane 桥吊；桥式吊车; 桥式起重机-electric traveling crane 电动桥式起重机（俗称行车、天车）-electric double-beam bridge crane 电动双梁桥式起重机portal crane / portal bridge crane门式起重机- semi-goliath crane 半门式起重机- semi-portal bridge crane 半龙门起重机gantry cranes 龙门起重机- rubber tyred gantry crane 轮胎式龙门吊- electric gantry crane 电动龙门式起重机- hook gantry crane 吊钩龙门吊- economical gantry crane 简单龙门起重机; 简易龙门起重机- rubber tyred container gantry crane 轮胎式集装箱龙门起重机barges / floating Cranes 船式起重机; 浮吊; 浮式起重机水上起重机boom crane 吊杆起重机; 桁梁起重机; 臂式起重机; 伸臂起重机bucket crane 料罐起重机; 吊斗起重机building crane 建筑起重机cable crane 索道起重机; 缆索起重机container crane 集装箱起重机electric crane 电动吊车; 电动起重机; 电力起重机electriomagnet crane 电磁铁起重机electric jib crane 电动单臂起重机fixed crane 固定式起重机climbing crane 爬升式起重机；攀爬式起重机fixed derrick crane 固定式动臂起重机fixed jib crane 固定式悬臂起重机flying crane helicopter 起重直升机hoist crane 起重葫芦hoisting crane 升降起重机hook type crane 钩式起重机twin hood crane 双钩吊车mobile crane 移动式吊车; 移动式起重机quay crane 码头起重机; 码头桥式起重机; 港岸起重机revolving track crane 回转式轨道起重机circular crane 旋转式吊车环形吊车roof crane 屋顶起重机transporter crane 桁架式起重机electric crane 电动吊车; 电动起重机gasoline crane 汽油起重机hydraulic crane 液力起重机; 液压起重机derrick crane 人字扒杆人字起重机-travelling derrick crane 移动式人字扒杆jib crane / cantilever crane 悬臂式起重机wall crane 壁式起重机heavy duty crane 重型起重机crane output / carrying capacity of crane / lifting capacity of crane 吊车起重能力crane load 起重机起重量; 起重机起重量crane rating 起重机定额; 起重机载重量crane radius 起重机起吊半径; 起重机伸臂活动半径; 起重机伸距craneage 吊车工时crane beam 行车梁起重机大梁crane stair 起重机楼梯hoist drive mechanism 起重机驱动机构travelling crab 起重机小车hoisting controller 起重控制器吊车控制手柄hoisting facility 起重设施lifting gear 起重装置crane (runway) girder 吊车梁crane support wall 吊车支承墙crane boom 起重机吊架; 起重架; 吊车臂; 吊车起重扒杆; 吊杆crane column 吊车柱crane hook / grab （or lift hook）（ or dolly）起重机吊钩crane jib 起重机吊杆crane bridge 起重机桥crane buffer 吊车缓冲器crane rope / crane cable起重钢绳; 起重机吊索; 吊车钢丝绳crane carriage 起重小车; 横行小车crane carrier 起重机载运车crane controller 起重控制器crane fall 起重机索crane motor / crane hoist type motor 起重机电动机crane platform 起重机平台crane rail 吊车轨，起重机轨道crane runner 吊车司机crane runway 起重机走道; 天车滑道crane weigher 吊车秤crane wheel 吊车车轮lifting tackle 起重滑车lever of crane 起重机臂hoisting tools 起重工具吊具lifting rope 吊绳起重钢丝绳起重吊装术语：hoist / load up 起升lower / load down 下降hoist slowly / load up slowly 微微起升lower slowly / load down slowly 微微下降use main hoist/use main line 使用主钩use whip hoist/use whip line 使用小钩raise boom / boom up（臂架类吊车）抬起主臂lower boom / boom down （同上）降下主臂raise boom slowly / boom up slowly（臂架类吊车）微微抬起主臂lower boom slowly / boom down slowly （同上）微微降下主臂swing （根据指挥手势、旗语或）移动摆动stop 停止Emergency stop 紧急停止Extend boom / extend hydranlic boom （汽车吊类）伸长主臂Retract boom / shorten hydranlic boom （汽车吊类）缩回主臂raise the boom and lower the load /boom up and load down （汽车吊类）抬主臂降主钩（俗称顿杆松钩）lower the boom and raise the load /boom dwon and load up （汽车吊类）降主臂起主钩（俗称趴杆起钩）turn left 向左转turn right 向右转crane output / carrying capacity of crane / lifting capacity of crane 吊车起重能力crane load 起重机起重量; 起重机起重量crane rating 起重机定额; 起重机载重量crane radius 起重机起吊半径; 起重机伸臂活动半径; 起重机伸距craneage 吊车工时crane beam 行车梁起重机大梁crane stair 起重机楼梯hoist drive mechanism 起重机驱动机构travelling crab 起重机小车hoisting controller 起重控制器吊车控制手柄hoisting facility 起重设施lifting gear 起重装置crane (runway) girder 吊车梁crane support wall 吊车支承墙crane boom 起重机吊架; 起重架; 吊车臂; 吊车起重扒杆; 吊杆crane column 吊车柱crane hook / grab （or lift hook）（ or dolly）起重机吊钩crane bridge 起重机桥crane buffer 吊车缓冲器crane rope / crane cable起重钢绳; 起重机吊索; 吊车钢丝绳crane carriage 起重小车; 横行小车crane carrier 起重机载运车crane controller 起重控制器crane fall 起重机索crane motor / crane hoist type motor 起重机电动机crane platform 起重机平台crane rail 吊车轨，起重机轨道crane runner 吊车司机crane runway 起重机走道; 天车滑道crane weigher 吊车秤crane wheel 吊车车轮crane winch 起重机绞车lifting tackle 起重滑车lever of crane 起重机臂hoisting tools 起重工具吊具lifting rope 吊绳起重钢丝绳。

NumericalControl英语翻译Numerical ControlWith China being fast to become global manufacturing center, of our country manufacturing industry in recent years develop swift and violent, numerical control is it become market competition and enterprise development new and on already to process, CAD and manufacture (CAD/CAM ) become a hot issue of the mechanical manufacturing industry.One of the most fundamental concepts in the area of advanced manufacturing technologies is numerical control (NC). Prior to the advent of NC, all machine tools were manually operated and controlled. Among the many limitations associated with manual control machine tools, perhaps none is more prominent than the limitation of operator skills. With manual control, the quality of the product is directly related to and limited to the skills of the operator. Numerical control represents the first major step away from human control of machine tools.Numerical control of machine tools is reported to have been first developed between 1947 and 1952 at the Massachusetts institute of Technology, in conjunction with the Parsons Aircraft Corporation. The development of numerical control techniques is accredited to the need for producing very accurately sized and intricately shaped parts for aircraft, principally space vehicles. Because of the complex shapes, considerable times was being spent in ensuring that the work/tool relationship was correct before machining took place; this led to long manufacturing times and hence high costs .In order to reduce costs, attempts were made to control automatically the work/tool relationship .This resulted in the development of positionalcontrol using numerical principles on a Cincinnati Hydrotel vertical mill.Numerical control means the control of machine tools and other manufacturing systems through the use of prerecorded, written symbolic instructions. Rather than operating a machine tool, an NC technician writes a program that issues operational instructions to the machine tool. For a machine tool to be numerically controlled, it must be interfaced with a device for accepting and decoding the programmed instructions, known as a readerNumerical control was developed to overcome the limitation of human operators, and it has done so. Numerical control machines are more accurate than manually operated machines, they can produce parts more uniformly, they are faster, and the long-run tooling costs are lower. The development of NC led to the development ofseveral other innovations in manufacturing technology:Electrical discharge machining.Laser cutting.Electron beam welding.Numerical control has also made machine tools more versatile than their manually operated predecessors .an NC machine tool can automatically produce a wide variety of parts, each involving an control has allowed manufacturers to undertake the production of products that would not have been feasible from an economic perspective using manually controlled machine tools and processes.Like so many advanced technologies, NC was born in the laboratories of the Massachusetts Institute of Technology. The concept of NC was developed in the early 1950s with fundingprovided by the U.S. Air Force. In its earliest stages, NC machines ere able to make straight cuts efficiently and effectively.However, curved paths were a problem because the machine tool had to be programmed to undertake a series of horizontal and vertical steps to produce a curve .the shorter the straight lines making up the steps, the smoother is the curve. Each line segment in the steps had to be calculated.This problem led to the development in 1959 of the Automatically Programmed Tools (APT) language. This is a special programming language for NC that uses statements similar to English language to define the part geometry, describe the cutting tool configuration, and specify the necessary motions. The development of the APT language was a major step forward in the further development of NC technology. The original NC systems were vastly different form those used today. The machines had hardwired logic circuits. The instructional programs were written on punched paper, which was later to be replaced by magnetic plastic tape. A tape reader was used to interpret the instructions written on the tape for the machine. Together, all of this represented a giant step forward in the control of machine tools. However, there were a number of problems with NC at this point in its development.A major problem was the fragility of the punched paper tape medium. It was common for the paper tape containing the programmed instructions to break or tear during a machining process. This problem was exacerbated by the fact that each successive time a part was produced on a machine tool, the paper tape carrying the programmed instructions had to be rerun through the reader. If it was necessary to produce 100copies of a given part, If it was also necessary to run the papertape through the reader 100separate times. Fragile paper tapes simply could not withstandthe rigors of a shop floor environment and this kind of repeated use.This led to the development of a special magnetic plastic tape. Whereas the paper tape carried the programmed instructions as a series of holes punched in the tape, the plastic tape carried the instructions as a series of magnetic dots. The plastic tape was much stronger than the paper tape, which solved the problem of frequent tearing and breakage. However, it still left two other problems.The most important of these was that it was difficult or impossible to change the instructions entered on the tape. To make even the most minor adjustments in a program of instructions, it was necessary to interrupt machining operations and make a new tape. It was also still necessary to run the tape through the reader as many times as there were parts to be produced, fortunately, computer technology became a reality and soon solved the of NC associated with punched paper and plastic tape.The development of a concept known as direct numerical control (DNC) solved the paper and plastic tape problems associated with numerical control by eliminating tape as the medium for carrying the programmed instructions. In direct numerical control, machine tools are tied, via a data transmission link, to a host computer. Programs for operating the machine tolls are stored in the host computer and fed to the machine tool as needed via the data transmission linkage. Direct numerical control represented a major step forward over punched tape and plastic tape. However, it is subject to the same limitations as alltechnologies that depend on a host computer. When the host computer goes down, the machine tools also experience downtime. This problem led to the development of computer numerical control.The development of the microprocessor allowed for the development of programmable logic controllers (PLCs) and microcomputers. These two technologies allowed for the development of computer numerical control (CNC). With CNC, each machine tool has a PLC or a microcomputer that serves the same purpose. This allows programs to be input and stored at each individual machine tool. It also allows programs to be developed off-line and downloaded at the individual machine tool. CNC solved the problems associated with downtime of the host computer, but it introduced another problem known as data management. The same program might be loaded on ten different microcomputers with no communication among them. This problem is in the process of being solved by local area net works that connect microcomputers for better data management.As application that numerical control is processed being extensive with deepening day by day, CAD and manufacture (CAD/CAM ) become a hot issue of themechanical manufacturing industry. Make by Beijing Institute of Aeronautics CAXA that Haier develop engineer rely on characteristic on " function complete , easy to learn and use " their use extensively. CAXA is used in numerical control milling machine , numerical control lathe , wire cutting machine tool and machining center ,etc. mainly. This text discusses application on the machining center of CAD/CAM system, its essence is that CAXA makes the engineer XP application on machining center.At this stage, many plants commonly used two-dimensionaldesign software for 2D design parts of the plans, and the crafts personnel / programmer at 3D concept directly to G code or apt language of NC programming. This approach applies to simple graphic processing components, linear processing, turnaround processing hardware processing and point spaces. Its programming is faster code concise. For complex geometric shapes, jig assembly complex, especially for non-Yuan camber processing, the programming method was very difficult.As a trajectory of space geometric figure and the mathematical calculation of handling large, complex process, not easily grasp and programming process, the constituent elements of the environment can not be processed geometric space relations between inspections. A knife spaces target coordinates to the geometric figure to inspect processing, precision low, not visual, and therefore, the need debugging procedures, occupancy digital machine hours, technical preparations for the cycle longer.数字控制随着中国快速成为全球制造中心，近年我国制造业发展迅猛，数控加工已经成为市场竞争和企业发展的新亮点，计算机辅助设计与制造（CAD/CAM）也成为机械制造业的一个热门话题。

1.With low-power machinery or vehicles the operator can usually apply sufficient force through a simple mechanical linkage from the pedle or handle to the stationary part of the brake. In many cases, however, this force must be multiplied by using an elaborate braking system.（P5）用低能机器或传力工具，操作者通过向踏板或把手的一个简单机械连接构件作用足够的力量到车闸固定的部分。

大多数情况，然而，用一个详细（复杂）的车闸系统使这个力量成倍增加。

2. The fundamental principle involved is the use of compressed air acting through a piston in a cylinder to set block brakes on the wheels. The action is simultaneous on the wheels of all the cars in the train. The compressed air is carried through a strong hose from car to car with couplings between cars; its release to all the separate block brake units, at the same time, is controlled by the engineer. (Braking Systems)（P5）相关的基本原理是使用压缩气体，通过气缸内的活塞将闸块压在车轮起作用。

翻译部分英文原文CONTROL OF MOBILEHYDRAULIC CRANESMarc E.MÜNZERAalborg UniversityInstitute of Energy Technology,Pontoppidanstræde 101DK-9220 Aalborg, DenmarkThe goal of the thesis described in this paper is to improve the control of mobile hydraulic cranes. The thesis is split into five parts: a requirements analysis, an analysis of the current systems and their problems, an analysis of different possibilities for system topologies, development of a new control system for the near future based on electro-hydraulic separate meter in / separate meter out valves, and finally an analysis of more advanced and complex solutions which can be applied in the more distant future. The work of the thesis will be done in coop-eration with industry so the thesis will have more of an industrial focus than a purely theoretical focus.Key words: Mobile Hydraulic Cranes, Control Strategies, Separate Meter-in/Separate Meter-out.1 INTRODUCTIONThe goal of the thesis described in this paper is to improve the control of mobile hydraulic cranes. A mobile hydraulic crane can be thought of as a large flexible mechanical structure which is moved by some sort of control system. The control system takes its input from a human operator and translates this command into the motion of actuators which move the mechanical structure.The definition of this control system is purposely left vague in order not to impose any con-straints on its design. The control system consists of actuators which move the mechanical structure, a means of controlling the actuators, a means of supplying power to the actuators,and a way of accepting inputs from the operator. It is this control system which is the target of this thesis. The goal is to analyze the requirements made on the control system and present guidelines for the design of new control systems.The thesis will be split into five parts:1.Analysis of the requirements of the control system, from the perspective of the opera-tor, the mechanical system, efficiency, stability, and safety requirements.2.Analysis of current control systems and what their problems are.3.Analysis of the different options for the control system: different types ofactuators,different types of control strategies, and different ways of organizing components.4.Presentation of a new type of control system, which is commercially implementable. A system that will meet the needs of industry in the near future.5.Analysis of more optimized systems, with higher performance, better efficiency, more flexible control, etc. This will be less commercially applicable but will be a starting point for more research.2 SECTIONS OF THE THESIS2.1Requirements Analysis of the Control System Before starting detailed work on developing new control systems, it is important to analyze what the exact demands are on the control system. The control system is influenced by many factors. For example: the mechanical structure it is controlling, the human operator, effi- ciency, stability, and industry regulations.Industry regulations are the first requirements that have to be addressed. Things like hose rupture protection and runaway load protection make a lot of demands on the control system.After regulations, stability is the next most important requirement; without stability the con-trol system can’t be used. Once stability has been assured, the performance requirements of the control system have to be set. They are determined by the mechanical structure of the crane and the human operator. The mechanical structure of a mobile hydraulic crane is a very large flexible structure which has very low natural frequencies. To prevent oscillations it is necessary to keep the speed of the control system below this natural frequency or to develop a control system which can increase this frequency. The human operator also imposes limits on the control system. If the control system is too slow or too fast then it is impossible for a human operator to give it proper inputs. And finally, once the regulations have been met, sta-bility is assured, and the performance is at the right level, the power efficiency of the control system has to be optimized.2.2Analysis of Current Control SystemsBefore designing a new control system it is good to analyze the current control systems to find out what their problems are. Current control systems are mainly hydraulic and can suffer from three main problems:1.Instability2.High cost3.Inefficiency2.2.1InstabilityInstability is a serious problem as it can cause injury to human operators or damage to equip-ment. When a system becomes unstable it usually starts to oscillate violently. To avoid insta-bility in current systems, the designers either sacrifice certain functions which are desirable,or add complexity and cost. For example, in the crane shown in Figure 1, it would be desir-able to have control over the speed. But due to the safety system that cranes are required to have, standard speed control is not stable. To add speed control requires a more complex and more expensive mechanical system.The parameters of a hydraulic system, such as temperature or load force, also affect stability.A system that is stable with one set of parameters might be unstable with another set. To ensure stability over the entire operating range of the system, performance must sometimes be sacrificed at one end of the parameter range.2.2.2High costCurrent systems are purely hydraulic-mechanical, so if the user wants a certain function, the user buys a certain hydraulic-mechanical component. Because most users have different requirements, there are many different variations of the same basic component. This means that many specialized components must be manufactured rather than one standard product.This drives up the cost of components.2.2.3InefficiencyOne form of inefficiency in current systems is due to the link between the flows of the two ports of the cylinder. This is because most valves use a single spool to control the flow in both ports. Because of this link, it is impossible to set the pressure levels in the two sides of the cylinder independently. Therefore, the outlet side will develop a back pressure which acts in opposition to the direction of travel, which increases the pressure required on the inlet side to maintain motion. Since the force generated by the actuator is proportional to the pressure dif- ference between the two sides, the actual pressures in the cylinder don't affect the action of the cylinder. For example, the action of the cylinder for 0psi/600 psi would be the same as 1000psi/1600psi. However, in the second case, the power supply would have to supply much more power. This extra power is wasted.2.3Different Options for Control SystemsCurrent control systems use hydraulic actuators with directional/proportional valves to control the movement. However there are many different options for controlling a cylinder. Options range from new high performance electro-hydraulic valves, to separate meter in / separate meter out (SMISMO) valves, to hydraulic bus systems, to intelligent actuators with built in power supplies, to pump based control strategies. These systems all have advantages and dis-advantages which need to be analyzed if the most optimum solution is to be chosen.2.4 Near Future SolutionIt is expected that even if it is proven that a completely new system topology is the optimum configuration, the crane manufacturers and component manufacturers will not accept the new technology overnight. This will most likely take time, so an interim solution will be devel-oped.This solution will be made up of micro computer controlled Separate Meter In / Separate Meter Out (SMISMO) valves (Elfving,Palmberg 1997;Jansson,Palmberg, 1990;Mattila,Virvalo 1997). SMISMO valves will make it possible to implement new control strategies which are more efficient and stable. The micro computer will make it possible to introduce flexibility to valves. Variants can be programmed in software. This eliminates the need to manufacture hundreds of different variants. The crane manufacturer will be able to choose the exact functions he wants in his valve, while the component manufacturer will have to manu-facture only one valve. This willlower the cost, even though the performance will have increased.2.5 Analysis of Higher Performance SolutionsThis analysis will depend on the results of the analysis of different topologies. If it is shown that pump based control is to be the way of the future for example, then analysis will be per-formed in this area. Another area which will also be explored, is tool position control.3 LABORATORY FACILITIESAs the focus of this thesis is on developing control strategies that can be implemented on commercial machinery, much emphasis will be placed on experimental results. Experimental results will be obtained from two systems. The first, a simple one degree of freedom crane,was designed as an experimental platform. The second is a real crane which was donated to the University by Højbjerg Maskinfabrik (HMF) a Danish crane manufacturer. Refer to Figure 1.Figure 1 Experimental Systems in Laboratory.Left: One DOF crane model. Right: Real Mobile Hydraulic Crane As there are currently no commercially available separate meter-in/separate meter-out valves,two separate valves will be used instead. A sample circuit of onecylinder is shown in Figure2. The control algorithms which control the valves, will be programmed on a Digital Signal Processor (DSP)/Pentium dual processor system. The DSP will run the control code and the Pentium will do diagnostics and provide a graphical userinterface.Figure 2 Separate Meter In / Separate Meter Out Setup4 CURRENT WORK4.1 Flow Control by Direct Actuation of the SpoolMost flow control valves on the market today work with a pressure compensator (Andersen;Ayres 1997). The pressure compensator keeps a constant pressure drop across the main spool of the valve, which keeps the flow constant. However, the addition of a pressure compensator makes the valve more complicated than a simple single spool valve. Another way of doing flow control is to measure the pressure drop across the valve and adjust the spool position to account for this (Backé; Feigel 1990). This is not a new idea but has not been implemented commercially because of the high cost of pressure transducers and micro controllers. How-ever, with the current drop in cost of micro controllers and pressure transducers this idea is now commercially feasible.The concept is very simple, spool position is calculated from the Bernoulli equation using the pressure drop across the spool and a reference flow.Even though this is a simple equation, it is not easy to implement. The accuracy of the flow control is dependent on the precision of the position sensors and of the pressure transducers.Noise on the pressure or the position signals can cause stability problems. Filtering the noise,introduces delays in the control which can also affectstability. In addition the Bernoulli equation is not followed exactly over the entire operating range of the valve, so it may be nec-essary to store the valve characteristics as a data table or develop a more complex equation.4.2 Cylinder Control StrategyTo control a hydraulic cylinder, the strategy has to be able to handle four different situations depending on the directions of the load and the velocity of the cylinder. Refer to Figure 3 The control strategies that have appeared in the literature are usually quite complex and depend on measurements of the cylinder position and velocity (Elfving,Palmberg 1997;Mattila;Virvalo 1997). They are also based on rather complex control algorithms. It is the goal of this thesis to start with a control strategy which is based on simple PI controllers and makes no demands for position and velocity of the cylinder. The performance of this system will be lower than a complex control strategy, but it may be easier to implement commercially because it has no need for special sensors and is easier to understand for the average engineer.Figure 3 Different Situations in Crane OperationAnother feature which needs to be acknowledged when designing a control strategy, is thetype of valve used. Mobile hydraulic valves demand low leakage and since most mobilevalves are spool valves, they usually have large overlaps. In addition, to make the cost of thevalve acceptable to industry, the actuation stage on the spool is usually quite slow. This com-bination of large overlap and slow actuation makes it hard to implement many of the strate-gies that have been presented. Pressure control especially becomes difficult when there is an overlap and a slow actuator.One example of a new strategy which is simple and robust is described as follows. Flow con-trol is implemented on the inlet side and pressure control is implemented on the outlet side.The flow control is based on the Bernoulli equation. Pressure control is done by a PI control-ler which maintains a low constant pressure toincrease the efficiency and prevent cavitation.To work around large overlaps and slow actuation stage, the pressure controller only does meter out control. This means that if the controller wi shes to raise the pressure, it can’t add flow to the cylinder, it can only decrease the opening of the meter out port. The benefit of this is that the only time that the spool has to cross the zero position is when the operator wishes to change the direction of motion of the cylinder. For the case where the load force and the velocity are in the same direction, this strategy has to be modified. In this case, the pressure reference of the pressure controller at the outlet is increased to a value which opposes the load force. The pressure reference is increased when it is noticed that the pressure of the inlet side is dropping. The pressure reference is also controlled by a PI controller. A schematic model of the controller system for the load lowering case is shown in Figure 4.At the time of writing this paper the initial experimental tests had been performed on the real crane shown in Figure 1 . Stability was not achieved because the crane is equipped with a load holding valve. However, the load holding valve will be replaced with a pilot operated check valve, which should make it possible to stabilize the system. In current systems, the load holding valve serves two functions, load holding and runaway load protection. Due to the use of a SMISMO valve setup, the runaway load protection is built into the control strategy,therefore the only function which is necessary for the load holding valve to perform is load holding. A pilot operated check valve will be able to do this, without adding complex dynamics which upset the stability of the system.Figure 4 Controller Strategy for Lowering of Load5 CONCLUSIONEven though not much experimental work has been finished, a good start has been made and initial tests have been promising. The outline of the thesis has been developed and organized in a logical manner. The work is split into five parts, requirements analysis, analysis of cur-rent systems, analysis of different topologies, development of a near future solution, and development of a more optimum solution.At the end of the thesis, the control of mobile hydraulic cranes will have been improved.6 ACKNOWLEDGEMENTSThis project is being funded in part by Danfoss Fluid Power A/S. The author would also like to thank Højbjerg Maskinfabrik (HMF) A/S for the donation of the test crane.7 REFERENCESAndersen, B. R.; Ayres, J. L. (1997). Load Sensing Directional Valves, Current Technology and Future Development, The Fifth Scandinavian International Conference on Fluid PowerBacké, W.; Feigel, H. (1990). Neue Möglichkeiten Beim Elektrohydraulischen Load-Sens-ing, O+P Ölhydraulik und Pneumatik 34Elfving, M.; Palmberg, J. O. (1997). Distributed Control of Fluid Power Actuators -Experimental Verification of a Decoupled Chamber Pressure Controlled Cylinder, 4th Inter-national Conference on Fluid PowerJansson, A.; Palmberg, J. O. (1990). Separate Controls of Meter-in and Meter-Out Orifices in Mobile Hydraulic Systems, International Off-Highway and Powerplant Congress and ExpositionMattila, J.;Virvalo, T. (1997). Computed Force Control of Hydraulic Manipulators, 5th Scandinavian International Conference On Fluid Power中文译文控制移动液压起重机Marc E. MÜNZER奥尔堡大学能源技术研究所Pontoppidanstræde 101丹麦奥尔堡DK-9220Email: mmun@iet.auc.dk在这篇论文中论题描述的目的是改进控制移动液压起重机。