黄昆版固体物理习题课_03

《固体物理学》习题解答黄昆 原著 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=（3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= （4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证：六方密排堆积结构中633.1)38(a c 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

第三章习题参考解答3.1已知一维单原子链，其中第j 个格波，在第n 个格点引起的位移μnj 为：δj 为任意位相因子。

并已知在较高温度下每个格波的平均能量为kT ，具体计算每个原子的平方平均位移。

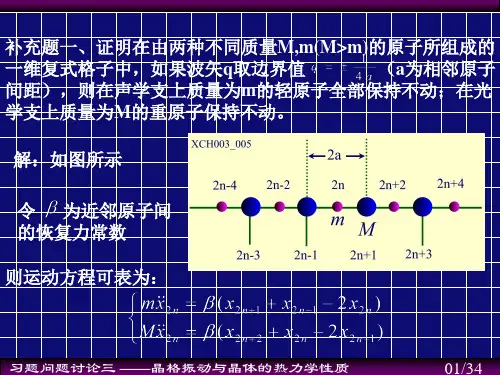
)sin(j j j j nj naq t δωαμ++=21)(sin 102=++⎰dt q n t T j j j Tδαω根据=2nj μ22221)(sin j j j j j q n t αδαωα=++解：其中T =2π/ωj 为振动周期，所以：格波的平均动能：∑∙=n njm E 221μN m j j 2241ωα=一维单原子链可以认为是经典的简谐运动，因此有：)(cos 21222j j j j n j q n t m δαωωα++=∑平均动能=平均势能= 格波平均能量=kT 2121其中：M =ρL其中振幅222j j Nm kT ωα=得：kT N m E j j 214122==ωα所以有：22221jj nj Nm kT ωαμ==所以，每个原子的平方平均位移：∑∑∑===222121j j njn Nm kT ωαμμ其中：M =ρL3.2 讨论N个原胞的一维双原子链(相邻原子间距为a)，其2N个格波解，当M=m时与一维单原子链结果一一对应。

解：质量为M的原子位于2n-1，2n+1，2n+3……。

质量为m的原子位于2n，2n+2，2n+4 ……。

牛顿运动方程体系有N个原胞，有2N个独立的方程方程的解：A,B有非零解可以得到：两种不同的格波的色散关系为：对应一个q有两支格波：一支声学波和一支光学波，总的格波数目为2N。

当M=m时,色散关系简化为：长波极限情况下与一维单原子晶格格波的色散关系一致3.3质量相同两种原子形成一维双原子链，最近邻原子间的力常数交错等于c和10c，令两种原子的质量相等，并且最近邻间距是a/2，试求在k=0和k=π/a处的ω(k)。

并粗略。

画出色散关系。

《固体物理学》部分习题解答1.3 证明：体心立方晶格的倒格子是面心立方；面心立方晶格的倒格子是体心立方 。

解 由倒格子定义2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 1231232a a b a a a π⨯=⋅⨯体心立方格子原胞基矢123(),(),()222a a a a i j k a i j k a i j k =-++=-+=-+倒格子基矢231123022()()22a a a ab i j k i j k a a a v ππ⨯==⋅-+⨯+-⋅⨯202()()4a i j k i j k v π=⋅-+⨯+-2()j k a π=+ 同理31212322()a a b i k a a a aππ⨯==+⋅⨯32()b i j a π=+ 可见由123,,b b b为基矢构成的格子为面心立方格子面心立方格子原胞基矢123()/2()/2()/2a a j k a a k i a a i j =+=+=+倒格子基矢2311232a a b a a a π⨯=⋅⨯ 12()b i j k a π=-++ 同理22()b i j k a π=-+ 32()b i j k a π=-+可见由123,,b b b为基矢构成的格子为体心立方格子1.4 证明倒格子原胞的体积为03(2)v π，其中0v 为正格子原胞体积证 倒格子基矢2311232a a b a a a π⨯=⋅⨯3121232a a b a a a π⨯=⋅⨯1231232a a b a a a π⨯=⋅⨯倒格子体积*0123()v b b b =⋅⨯3*23311230(2)()()()v a a a a a a v π=⨯⋅⨯⨯⨯ 3*00(2)v v π=1.5 证明：倒格子矢量112233G hb h b h b =++垂直于密勒指数为123()hh h 的晶面系。

黄昆版固体物理学课后答案《固体物理学》习题解答黄坤原著韩汝琦改编（陈志远答案，仅供参考）第一章晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n和小球体积v所得到的小球总体积nv与晶体原胞体积vc之比，即：晶体原胞的空间利用率，x?（1）对于简立方结构：（见教材p2图1-1）nvvc43？r、 vc=a3，n=134343？RR33∴十、0.526a38r3a=2r，v=（2）对于体心立方：晶胞的体对角线bg=3a?4r?a?n=2,vc=a343x32？∴十、434? r2？？r33330.688a3433（R）3（3）对于面心立方：单元面对角线BC=2A？4r，？A.22rn=4，vc=a3444??r34??r3233x0.74336a(22r)（4）对于六角密排：a=2r晶胞面积：s=6?s?abo?6?晶胞的体积：v=s?c?a?asin60332a=223328a?a?32a3?242r323n=1212?11?2??3=6个6246??r323x0.7436242r（5）对于金刚石结构，晶胞的体对角线bg=3a?4?2r?a?8r3n=8,vc=a3一448??r38??r33?33x0.346a3833r33c81。

2.测试：在六角形紧密堆积结构中？()1/2? 一点六三三a3证明：在六角密堆积结构中，第一层硬球a、b、o的中心联线形成一个边长a=2r 的正三角形，第二层硬球n位于球abo所围间隙的正上方并与这三个球相切，于是：na=nb=no=a=2r.也就是说，图中的Nabo形成一个正四面体1.3、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

A.a1？2（j？k）A.证明了：（1）面心立方的法向晶格基向量（固体物理的原胞基向量）：？a2？（i？k）2aa3?2(i?j)??2(a2?a3)由倒格子基矢的定义：b1??0,aa1?(a2?a3)?,2a,2a,20,a,2a?i,2aa3a???，a2?a3?,242a0,2?j,0,a,2?kaa2(?i?j?k)240?4a2???2?b1?2??3?(?i?j?k)?(?i?j? k)a4a？2.b2？（I？J？K）a类似地：2即面心立方的倒格子基矢与体心立方的正格基矢相同。

PART ONE 填空问题Q01_01_001 原胞中有p 个原子。

那么在晶体中有3支声学波和33p −支光学波？Q01_01_002 按结构划分，晶体可分为7大晶系, 共14布喇菲格子?Q01_01_004 面心立方原胞的体积为314a Ω=；其第一布里渊区的体积为334(2)*a πΩ= Q01_01_005 体心立方原胞的体积为32a Ω=；第一布里渊区的体积为332(2)*a πΩ= Q01_01_006 对于立方晶系，有简单立方、体心立方和面心立方三种布喇菲格子。

Q01_01_007 金刚石晶体是复式格子，由两个面心立方结构的子晶格沿空间对角线位移 1／4 的长度套构而成，晶胞中有8个碳原子。

Q01_01_008 原胞是最小的晶格重复单元。

对于布喇菲格子，原胞只包含1个原子；Q01_01_009 晶面有规则、对称配置的固体，具有长程有序特点的固体称为晶体；在凝结过程中不经过结晶（即有序化）的阶段，原子的排列为长程无序的固体称为非晶体。

由晶粒组成的固体，称为多晶。

Q01_01_010 由完全相同的一种原子构成的格子，格子中只有一个原子，称为布喇菲格子。

满足ij j i b a πδ2=⋅G G ⎩⎨⎧≠===)(0)(2j i j i π 关系的1b G ,2b G ,3b G 为基矢，由322211b h b h b h G h K K K K ++=构成的格子，称作倒格子。

由若干个布喇菲格子相套而成的格子，叫做复式格子。

其原胞中有两个以上的原子。

Q01_03_001 由N 个原胞构成的晶体，原胞中有l 个原子，晶体共有3lN 个独立振动的正则频率。

Q01_03_002 声子的角频率为ω，声子的能量和动量表示为ω=和q K =。

Q01_03_003 光学波声子又可以分为纵光学波声子和横光学波声子，它们分别被称为极化声子和电磁声子Q01_03_004 一维复式原子链振动中，在布里渊区中心和边界，声学波的频率为 ⎪⎩⎪⎨⎧→±==0,02,)2(211q a q M πβω；光学波的频率⎪⎪⎩⎪⎪⎨⎧±=→=a q m q 2)2(0)2(21212πβµβωQ01_04_001 金属的线度为L ，一维运动的自由电子波函数ikx e Lx 1)(=ψ；能量m k E 222==；波矢的取值Ln k π2= Q01_04_002 电子在三维周期性晶格中波函数方程的解具有()()ik r kr e u r k ψ⋅=K K K K K K 形式？式中()k u r K K 在晶格平移下保持不变。

《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r 8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 31.2、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…1.3、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩由倒格子基矢的定义：1232()b a a π=⨯Ω31230,,22(),0,224,,022a aa a a a a a a a Ω=⋅⨯==，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++ 同理可得：232()2()b i j k ab i j k aππ=-+=+-即面心立方的倒格子基矢与体心立方的正格基矢相同。

黄昆固体物理习题-第三章晶体的热性质第三章习题参考解答3.1已知⼀维单原⼦链，其中第j 个格波，在第n 个格点引起的位移µnj 为：δj 为任意位相因⼦。

并已知在较⾼温度下每个格波的平均能量为kT ，具体计算每个原⼦的平⽅平均位移。

)sin(j j j j nj naq t δωαµ++=21)(sin 12=++?dt q n t Tj j j Tδαω根据=2njµ22221)(sin jj j j jq n t αδαωα=++解：其中T =2π/ωj 为振动周期，所以：格波的平均动能：∑?=n njm E 221µN m j j 2241ωα=⼀维单原⼦链可以认为是经典的简谐运动，因此有：)(cos 21222j j j j nj q n t m δαωωα++=∑平均动能=平均势能= 格波平均能量=kT2121其中：M =ρL其中振幅222jjNm kT ωα=得：kT N m E j j 214122==ωα所以有：22221jj njNm kT ωαµ==所以，每个原⼦的平⽅平均位移：∑∑∑===222121jj njn Nm kT ωαµµ其中：M =ρL3.2 讨论N个原胞的⼀维双原⼦链(相邻原⼦间距为a)，其2N个格波解，当M=m时与⼀维单原⼦链结果⼀⼀对应。

解：质量为M的原⼦位于2n-1，2n+1，2n+3……。

质量为m的原⼦位于2n，2n+2，2n+4 ……。

⽜顿运动⽅程体系有N个原胞，有2N个独⽴的⽅程⽅程的解：A,B有⾮零解可以得到：两种不同的格波的⾊散关系为：对应⼀个q有两⽀格波：⼀⽀声学波和⼀⽀光学波，总的格波数⽬为2N。

当M=m时,⾊散关系简化为：长波极限情况下与⼀维单原⼦晶格格波的⾊散关系⼀致3.3质量相同两种原⼦形成⼀维双原⼦链，最近邻原⼦间的⼒常数交错等于c和10c，令两种原⼦的质量相等，并且最近邻间距是a/2，试求在k=0和k=π/a处的ω(k)。

《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是：NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r 同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。

PART ONE 填空问题Q01_01_001 原胞中有p 个原子。

那么在晶体中有3支声学波和33p −支光学波？Q01_01_002 按结构划分，晶体可分为7大晶系, 共14布喇菲格子?Q01_01_004 面心立方原胞的体积为314a Ω=；其第一布里渊区的体积为334(2)*a πΩ= Q01_01_005 体心立方原胞的体积为32a Ω=；第一布里渊区的体积为332(2)*a πΩ= Q01_01_006 对于立方晶系，有简单立方、体心立方和面心立方三种布喇菲格子。

Q01_01_007 金刚石晶体是复式格子，由两个面心立方结构的子晶格沿空间对角线位移 1／4 的长度套构而成，晶胞中有8个碳原子。

Q01_01_008 原胞是最小的晶格重复单元。

对于布喇菲格子，原胞只包含1个原子；Q01_01_009 晶面有规则、对称配置的固体，具有长程有序特点的固体称为晶体；在凝结过程中不经过结晶（即有序化）的阶段，原子的排列为长程无序的固体称为非晶体。

由晶粒组成的固体，称为多晶。

Q01_01_010 由完全相同的一种原子构成的格子，格子中只有一个原子，称为布喇菲格子。

满足ij j i b a πδ2=⋅G G ⎩⎨⎧≠===)(0)(2j i j i π 关系的1b G ,2b G ,3b G 为基矢，由322211b h b h b h G h K K K K ++=构成的格子，称作倒格子。

由若干个布喇菲格子相套而成的格子，叫做复式格子。

其原胞中有两个以上的原子。

Q01_03_001 由N 个原胞构成的晶体，原胞中有l 个原子，晶体共有3lN 个独立振动的正则频率。

Q01_03_002 声子的角频率为ω，声子的能量和动量表示为ω=和q K =。

Q01_03_003 光学波声子又可以分为纵光学波声子和横光学波声子，它们分别被称为极化声子和电磁声子Q01_03_004 一维复式原子链振动中，在布里渊区中心和边界，声学波的频率为 ⎪⎩⎪⎨⎧→±==0,02,)2(211q a q M πβω；光学波的频率⎪⎪⎩⎪⎪⎨⎧±=→=a q m q 2)2(0)2(21212πβµβωQ01_04_001 金属的线度为L ，一维运动的自由电子波函数ikx e Lx 1)(=ψ；能量m k E 222==；波矢的取值Ln k π2= Q01_04_002 电子在三维周期性晶格中波函数方程的解具有()()ik r kr e u r k ψ⋅=K K K K K K 形式？式中()k u r K K 在晶格平移下保持不变。

《固体物理学》习题解答黄昆 原著 韩汝琦改编第一章 晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π=（2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯=（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个74.062r224r 346x 33≈π=π⨯= （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

《固体物理学》习题解答黄昆 原著 韩汝琦改编 （陈志远解答，仅供参考）、第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= ;n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= （4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 /74.062r224r 346x 33≈π=π⨯=（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

203_11 晶格的热传导非简谐效应 —— 简谐近似下，原子之间的作用力与原子的位移成正比晶格的原子振动可以描述成为一系列线性独立的谐振子 ——声子—— 声子之间不发生作用，因而不能交换能量晶体中，某种声子一旦被激发出来，其数目就一直保持不变，它既不能把能量传递给其它频率的声子，也不能处于热平衡分布状态。

原来处于非平衡状态的系统永远不能变成平衡系统 —— 与实际物理过程不相符此外理想晶体的声子态是稳态，携带热流的声子一旦建立起来，就不随时间变化，热流将永不衰减，晶体的导热率为无穷大 —— 和实际物理过程不相符原子间的相互作用力并非严格地与原子的位移成正比。

当考虑到原子的相互作用势能泰勒级数展开中含有高次项，晶格的原子振动就不能描述成为一系列严格线性独立的谐振子。

如果原子的位移还相当小，可将高次项看成微扰。

由于微扰项的存在，这些振子不再是相互独立的，相互间要发生作用，则声子与声子之间发生能量交换。

如果开始时只存在某种频率的声子，由于声子间的互作用，这种频率的声子转换成另一种频率的声子，即一种频率的声子要湮灭．而另一种频率的声子会产生。

经过一定的弛豫时间后，各种声子的分布就能达到热平衡。

这些高次项 —— 使晶格振动达到热平衡的最主要原因两个声子通过非简谐项的作用，产生第三个声子，可以看成是两个声子碰撞，变成为第三个声子。

物理图像 —— 一个声子的存在将在晶体中引起周期性的弹性应变，由于非简谐项的影响，晶体的弹性模量不是常数，而受到弹性应变的调制，由于弹性模量的变化，将使第二个声子受到散射而产生第三个声子。

声子之间的相互作用，必须遵守能量守恒定律和动量守恒定律。

设两个相互碰撞的声子的频率和波矢分别为：112,,q andq ωωK K 第三个声子的频率和波矢为：33,q ωK三个声子之间满足：123123()()a q q q b ωωω+=⎧⎨+=⎩===K K K —— 晶格中的波矢具有平移周期性，波矢q K 和波矢h q K +KK 描写的振动状态完全一样 所以存在关系： 123()nq q q G c +=+K K K K 满足：关系的两个声子的碰撞过程 123123()()a q q q b ωωω+=⎧⎨+=⎩===K K K N 过程（正常过程）—— Normal Process满足：关系的两个声子的碰撞过程123123()()n a q q q G c ωωω+=⎧⎨+=−+⎩===K K K K U 过程（叫倒逆过程） —— Umklapp Process如果在晶体中存在温度梯度：dT dx能流密度：dT j dxθκ=− —— 单位时间内通过单位面积的热能 κ —— 晶体的导热系数存在温度梯度时，“声子气体”的密度分布是不均匀的。

PART ONE 填空问题Q01_01_001 原胞中有p 个原子。

那么在晶体中有3支声学波和33p −支光学波？Q01_01_002 按结构划分，晶体可分为7大晶系, 共14布喇菲格子?Q01_01_004 面心立方原胞的体积为314a Ω=；其第一布里渊区的体积为334(2)*a πΩ= Q01_01_005 体心立方原胞的体积为32a Ω=；第一布里渊区的体积为332(2)*a πΩ= Q01_01_006 对于立方晶系，有简单立方、体心立方和面心立方三种布喇菲格子。

Q01_01_007 金刚石晶体是复式格子，由两个面心立方结构的子晶格沿空间对角线位移 1／4 的长度套构而成，晶胞中有8个碳原子。

Q01_01_008 原胞是最小的晶格重复单元。

对于布喇菲格子，原胞只包含1个原子；Q01_01_009 晶面有规则、对称配置的固体，具有长程有序特点的固体称为晶体；在凝结过程中不经过结晶（即有序化）的阶段，原子的排列为长程无序的固体称为非晶体。

由晶粒组成的固体，称为多晶。

Q01_01_010 由完全相同的一种原子构成的格子，格子中只有一个原子，称为布喇菲格子。

满足ij j i b a πδ2=⋅G G ⎩⎨⎧≠===)(0)(2j i j i π 关系的1b G ,2b G ,3b G 为基矢，由322211b h b h b h G h K K K K ++=构成的格子，称作倒格子。

由若干个布喇菲格子相套而成的格子，叫做复式格子。

其原胞中有两个以上的原子。

Q01_03_001 由N 个原胞构成的晶体，原胞中有l 个原子，晶体共有3lN 个独立振动的正则频率。

Q01_03_002 声子的角频率为ω，声子的能量和动量表示为ω=和q K =。

Q01_03_003 光学波声子又可以分为纵光学波声子和横光学波声子，它们分别被称为极化声子和电磁声子Q01_03_004 一维复式原子链振动中，在布里渊区中心和边界，声学波的频率为 ⎪⎩⎪⎨⎧→±==0,02,)2(211q a q M πβω；光学波的频率⎪⎪⎩⎪⎪⎨⎧±=→=a q m q 2)2(0)2(21212πβµβωQ01_04_001 金属的线度为L ，一维运动的自由电子波函数ikx e Lx 1)(=ψ；能量m k E 222==；波矢的取值Ln k π2= Q01_04_002 电子在三维周期性晶格中波函数方程的解具有()()ik r kr e u r k ψ⋅=K K K K K K 形式？式中()k u r K K 在晶格平移下保持不变。