吉林大学 研究生 数值计算方法期末考试 样卷
- 格式:doc
- 大小:259.00 KB
- 文档页数:12

数值分析期末试题及答案试题一:1. 简答题(共10分)a) 什么是数值分析?它的主要应用领域是什么?b) 请简要解释迭代法和直接法在数值计算中的区别。
2. 填空题(共10分)a) 欧拉方法是一种______型的数值解法。
b) 二分法是一种______法则。
c) 梯形法则是一种______型的数值积分方法。
3. 计算题(共80分)将以下函数进行数值求解:a) 通过使用二分法求解方程 f(x) = x^3 - 4x - 9 = 0 的近似解。
b) 利用欧拉方法求解微分方程 dy/dx = x^2 + 2x + 1, y(0) = 1 在 x = 1 处的解。
c) 使用梯形法则计算积分∫[0, π/4] sin(x) dx 的近似值。
试题二:1. 简答题(共10分)a) 请解释什么是舍入误差,并描述它在数值计算中的影响。
b) 请解释牛顿插值多项式的概念及其应用。
2. 填空题(共10分)a) 数值稳定性通过______号检查。
b) 龙格-库塔法是一种______计算方法。
c) 零点的迭代法在本质上是将方程______转化为______方程。
3. 计算题(共80分)使用牛顿插值多项式进行以下计算:a) 已知插值节点 (-2, 1), (-1, 1), (0, 2), (1, 4),求在 x = 0.5 处的插值多项式值。
b) 已知插值节点 (0, 1), (1, 2), (3, 7),求插值多项式,并计算在 x = 2 处的值。
c) 使用 4 阶龙格-库塔法求解微分方程 dy/dx = x^2 + 1, y(0) = 1。
答案:试题一:1. a) 数值分析是研究使用数值方法解决数学问题的一门学科。
它的主要应用领域包括数值微积分、数值代数、插值和逼近、求解非线性方程、数值积分和数值解微分方程等。
b) 迭代法和直接法是数值计算中常用的两种方法。
迭代法通过反复迭代逼近解,直到满足所需精度为止;而直接法则通过一系列代数运算直接得到解。

研究生数值计算方法期末考试题一、 单项选择题(每小题2分,共10分)1、2ln =0.69314718…,用0.69314作为2ln 的近似值,它有( )位有效数字。
A .3B . 4C . 5D .62、用二分法求解非线性方程012=--x x 的正根,在初始区间是[0,2]的情况下,若要求误差小于0.05,那么需要二分( )次即可满足要求。
A .3B .4C .5D .63、线性多步法的一般公式∑∑=-=--++=r k r k k n k k n k n y b h y a y 01'1中,若( )成立时,则该公式是隐式公式。
A . 01=-bB .01≠-bC .00=aD .00≠a4、已知n =3时,科特斯系数83=83=81=323130)()()(,,C C C ,那么)(33C =( )。
A. 21 B.1 C.81 D.0 5、用选主元的方法解线性方程组A =,是为了( )。
A . 提高计算速度B .减少舍入误差C . 减少相对误差D .减少计算量二、 填空题(每小题3分,共18分)1、设)0(1)(≠+=n nx x f n ,则],...,,[10n x x x f = 。
2、设矩阵⎥⎦⎤⎢⎣⎡=2011A ,则矩阵A 的2-范数是 。
3、数值积分的龙贝格算法(公式)是通过对 公式的修正得到的。
4、若)(x s 是],[b a 上的分段m 次多项式,且 ,则称)(x s 是],[b a 上的m 次样条函数。
5、设3)(3-=x x f ,则其牛顿法求根的迭代公式为 。
6、设矩阵A 的特征值均可大体估计,且满足n n λλλλ>≥≥>-121 ,现用反幂法求n λ,为加速迭代采用原点平移策略,即B=A-pE ,则参数p 的最佳选择为 。
三、计算题(每小题10分,共40分)1、某矩形场地的长、宽分别为20m 和10m ,假设其绝对误差界均为0.2m ,求该矩形场地的周长及面积的相对误差界。

数值计算方法期末考试题Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】一、单项选择题(每小题3分,共15分)1. 和分别作为π的近似数具有( )和( )位有效数字. A .4和3 B .3和2 C .3和4 D .4和42. 已知求积公式()()211211()(2)636f x dx f Af f ≈++⎰,则A =( )A . 16B .13C .12D .233. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足( )A .()00l x =0,()110l x =B .()00l x =0,()111l x =C .()00l x =1,()111l x = D .()00l x =1,()111l x =4. 设求方程()0f x =的根的牛顿法收敛,则它具有( )敛速。
A .超线性B .平方C .线性D .三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩作第一次消元后得到的第3个方程( ).A .232x x -+= B .232 1.5 3.5x x -+=C .2323x x -+= D .230.5 1.5x x -=-单项选择题答案二、填空题(每小题3分,共15分)1. 设TX )4,3,2(-=, 则=1||||X ,2||||X = .2. 一阶均差()01,f x x =3. 已知3n =时,科茨系数()()()33301213,88C C C ===,那么()33C = 4. 因为方程()420x f x x =-+=在区间[]1,2上满足 ,所以()0f x =在区间内有根。
5. 取步长0.1h =,用欧拉法解初值问题()211y y yx y ⎧'=+⎪⎨⎪=⎩的计算公式 .填空题答案1. 9和292.()()0101f x f x x x --3. 184.()()120f f <5. ()1200.11.1,0,1,210.11k k y y k k y +⎧⎛⎫⎪ ⎪=+⎪ ⎪=+⎨⎝⎭⎪=⎪⎩三、计算题(每题15分,共60分)1. 已知函数211y x =+的一组数据:求分段线性插值函数,并计算()1.5f 的近似值.计算题1.答案1. 解[]0,1x ∈,()1010.510.50110x x L x x --=⨯+⨯=--- []1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为2. 已知线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩(1) 写出雅可比迭代公式、高斯-塞德尔迭代公式; (2) 对于初始值()()0,0,0X =,应用雅可比迭代公式、高斯-塞德尔迭代公式分别计算()1X (保留小数点后五位数字).计算题2.答案1.解 原方程组同解变形为 1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩ 雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m = 高斯-塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m = 用雅可比迭代公式得()()10.72000,0.83000,0.84000X = 用高斯-塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间的近似根 (1)请指出为什么初值应取2 (2)请用牛顿法求出近似根,精确到.计算题3.答案4. 写出梯形公式和辛卜生公式,并用来分别计算积分101dx x +⎰.计算题4.答案确定下列求积公式中的待定系数,并证明确定后的求积公式具有3次代数精确度证明题答案1. 设2.3149541...x *=,取5位有效数字,则所得的近似值x= .2.设一阶差商 ()()()21122114,321f x f x f x x x x --===---,()()()322332615,422f x f x f x x x x --===--则二阶差商()123,,______f x x x =3. 设(2,3,1)TX =--, 则2||||X = ,=∞||||X 。

吉林大学《数值分析》2017-2018学年第一学期期末试卷一、 单项选择题(每小题3分,共15分)1. 以下误差限公式不正确的是( ) A .()()(1212)x x x εεε−=−x B. ()()()1212x x x x εεε+=+C .()()()122112x x x x x x εε=+ε D. ()()22x x x εε=2. 步长为的等距节点的插值型求积公式,当h 2n =时的牛顿-科茨求积公式为( ) A .()()()2bahf x dx f a f b ≈+⎡⎤⎣⎦∫B .()()()432bah a b f x dx f a f f b ⎡+⎛⎞≈++⎜⎟⎢⎥⎝⎠⎣⎦∫⎤ C .()()()32bah a b f x dx f a f f b ⎡+⎛⎞≈++⎜⎟⎢⎥⎝⎠⎣⎦∫⎤ D .()()3442bah b a a b f x dx f a f a f f a ⎡−+⎛⎞⎛⎞⎛≈+++++⎜⎟⎜⎟⎜⎢⎥⎝⎠⎝⎠⎝⎣⎦∫4b a −⎤⎞⎟⎠3. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足( ) A .=0, B . ()00l x ()110l x =()00l x =0,()111l x = C .=1,()00l x ()111l x = D . ()00l x =1,()111l x =4. 用二分法求方程在区间()0f x =[],a b 上的根,若给定误差限ε,则计算二分次数的公式是( ) n ≥ A .ln()ln 1ln 2b a ε−++ B.ln()ln 1ln 2b a ε−+− C. ln()ln 1ln 2b a ε−−+ D.ln()ln 1ln 2b a ε−−− 5. 若用列主元消去法求解下列线性方程组,其主元必定在系数矩阵主对角线上的方程组是( )A . B.123123123104025261x x x x x x x x x −+=⎧⎪−+=⎨⎪−+=−⎩123123123315226x x x x x x x x x −+=⎧⎪01−−+=⎨⎪++=−⎩ C. D.12312312322526x x x x x x x x x −+=⎧⎪−−+=⎨⎪++=⎩01012312312310402501x x x x x x x x x −+=⎧⎪−+=⎨⎪−+=−⎩二、 填空题(每小题3分,共15分)6. 数x ∗=2.1972246···的六位有效数字的近似数的绝对误差限是 。

2022年吉林大学计算机科学与技术专业《数据结构与算法》科目期末试卷A(有答案)一、选择题1、用有向无环图描述表达式(A+B)*((A+B)//A),至少需要顶点的数目为()。
A.5B.6C.8D.92、下列排序算法中,占用辅助空间最多的是()。
A.归并排序B.快速排序C.希尔排序D.堆排序3、若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算,则利用()存储方式最节省时间。
A.顺序表B.双链表C.带头结点的双循环链表D.单循环链表4、最大容量为n的循环队列,队尾指针是rear,队头:front,则队空的条件是()。
A.(rear+1)MOD n=frontB.rear=frontC.rear+1=frontD.(rear-1)MOD n=front5、向一个栈顶指针为h的带头结点的链栈中插入指针s所指的结点时,应执行()。
A.h->next=sB.s->next=hC.s->next=h;h->next=sD.s->next=h-next;h->next=s6、循环队列放在一维数组A中,end1指向队头元素,end2指向队尾元素的后一个位置。
假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。
初始时为空,下列判断队空和队满的条件中,正确的是()。
A.队空:end1==end2;队满:end1==(end2+1)mod MB.队空:end1==end2;队满:end2==(end1+1)mod (M-1)C.队空:end2==(end1+1)mod M;队满:end1==(end2+1) mod MD.队空:end1==(end2+1)mod M;队满:end2==(end1+1) mod (M-1)7、排序过程中,对尚未确定最终位置的所有元素进行一遍处理称为一趟排序。
下列排序方法中,每一趟排序结束时都至少能够确定一个元素最终位置的方法是()。

数值方法期末考试题及答案一、选择题(每题2分,共20分)1. 在数值分析中,下列哪个算法用于求解线性方程组?A. 快速傅里叶变换B. 高斯消元法C. 牛顿法D. 辛普森积分法答案:B2. 插值和逼近的主要区别是什么?A. 插值点必须在数据点上B. 逼近点可以不在数据点上C. 插值是线性的,逼近是非线性的D. 插值是多项式,逼近是函数答案:A3. 以下哪个是数值稳定性好的算法?A. 直接迭代法B. 雅可比迭代法C. 高斯-塞德尔迭代法D. 松弛法答案:C4. 牛顿-拉弗森方法用于求解什么类型的方程?A. 线性方程B. 非线性方程C. 微分方程D. 积分方程答案:B5. 以下哪个是数值积分方法?A. 欧拉方法B. 辛普森方法C. 拉格朗日插值D. 牛顿法答案:B...(此处省略其他选择题)二、简答题(每题10分,共30分)1. 解释什么是病态问题,并给出一个例子。
答案:病态问题是指那些微小的输入变化会导致输出结果产生巨大变化的问题。
例如,在数值分析中,求解线性方程组时,如果系数矩阵的条件数很大,那么该问题就被认为是病态的。
这意味着即使输入数据只有微小的误差,也会导致解的误差非常大。
2. 描述数值微分和数值积分的区别。
答案:数值微分是估计函数在某点的导数,而数值积分是估计函数在某个区间上的积分。
数值微分通常涉及到差分,例如前向差分、后向差分和中心差分等。
数值积分则涉及到数值积分方法,如梯形法则、辛普森法则等。
3. 解释什么是条件数,并说明它在数值分析中的重要性。
答案:条件数是一个量度,用来衡量问题的敏感性,即输入数据的微小变化会导致输出结果多大的变化。
在数值分析中,一个条件数较小的问题被认为是良态的,因为这意味着问题对输入数据的微小变化不敏感。
相反,条件数较大的问题被认为是病态的,需要特别小心处理,以避免数值误差的累积。
三、计算题(每题25分,共50分)1. 给定线性方程组:\[\begin{align*}4x + y - 2z &= 6 \\2x - y + 3z &= -1 \\-2x + 3y + z &= 4\end{align*}\]使用高斯消元法求解该方程组,并给出解。

标准适用数值计算方法试题一、填空(共 20 分,每题 2 分)1、设,取5位有效数字,则所得的近似值x=_____.2、设一阶差商,则二阶差商3、数值微分中,已知等距节点的函数值则由三点的求导公式,有4、求方程的近似根,用迭代公式,取初始值,那么5、解初始值问题近似解的梯形公式是6、,则A的谱半径=,A的=7、设,则=和=8、若线性代数方程组AX=b 的系数矩阵 A 为严格对角占优阵,则雅可比迭代和高斯 - 塞德尔迭代都 _____9、解常微分方程初值问题的欧拉(Euler )方法的局部截断偏差为_____10、设,当时,必有分解式,此中L为下三角阵,当其对角线元素足条件时,这类分解是独一的。
标准适用二、计算题(共 60 分,每题 15 分)1、设(1)试求在上的三次Hermite插值多项式H(x)使知足H( x)以升幂形式给出。
(2)写出余项的表达式2、已知的足,怎样利用结构一个收的迭代函数,使0, 1⋯收?3、试确立常数 A, B, C和,使得数值积分公式有尽可能高的代数精度。
试问所得的数值积分公式代数精度是多少?它能否为Gauss型的?4、推常微分方程的初值问题的数值解公式:三、证明题1、设(1)写出解的 Newton 迭代格式(2)证明此迭代格式是线性收敛的2、R=I - CA,假如,明:(1)A、C 都是非奇怪的矩阵(2)参照答案:一、填空题1、2、3、4、5、6、7、8、收敛9、O(h)10、二、计算题1、1、(1)(2)2、由,可得因故故, k=0,1, ⋯收。
3、,数求公式拥有 5 次代数精准度,它是Gauss型的4、数分方法结构数解公式:方程在区上分,得,步 h, 分用 Simpson 求公式得因此得数解公式:三、明1、明:( 1)因,故,由Newton迭代公式:n=0,1, ⋯得, n=0,1, ⋯( 2)因迭代函数,而,又,故此迭代格式是性收的。
2、明:( 1)因,因此I–R非奇怪,因I–R=CA,因此C,A都是非奇怪矩(2)故有( 2.1 )因 CA=I–R,因此 C=( I – R) A-1,即 A-1 =(I –R)-1 C-1-1又 RA =A –C,故由(里用到了教材98 引理的)移得(2.2)合( 2.1 )、 (2.2) 两式,得模拟试题一、填空题(每空 2 分,共 20 分)1、解非线性方程f(x)=0的牛顿迭代法拥有_______收敛2、迭代过程(k=1,2, ⋯)收的充要条件是___3、已知数 e=2.718281828...,取近似值 x=2.7182,那麽 x 拥有的有效数字是___4、高斯 -- 塞尔德迭代法解线性方程组的迭代格式中求______________5、经过四个互异节点的插值多项式p(x), 只需知足_______,则 p(x) 是不超出二次的多项式6、对于 n+1 个节点的插值求积公式起码拥有___次代数精度 .7、插值型求积公式的求积系数之和___8、, 为使 A 可分解为 A=LL T,此中L为对角线元素为正的下三角形, a 的取值范围_9、若则矩阵A的谱半径(A)=___10 、解常微分方程初值问题的梯形格式是___阶方法二、计算题(每题15 分,共 60 分)1、用列主元消去法解线性方程组2、已知y=f(x)的数据以下x023f (x)132求二次插值多项式及 f ( 2.5 )3、用牛顿法导出计算的公式,并计算,要求迭代偏差不超出。

数值计算方法期末考试题集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#一、单项选择题(每小题3分,共15分)1. 和分别作为π的近似数具有( )和( )位有效数字. A .4和3 B .3和2 C .3和4 D .4和42. 已知求积公式()()211211()(2)636f x dx f Af f ≈++⎰,则A =( )A . 16B .13C .12D .233. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足( )A .()00l x =0,()110l x =B .()00l x =0,()111l x =C .()00l x =1,()111l x = D .()00l x =1,()111l x =4. 设求方程()0f x =的根的牛顿法收敛,则它具有( )敛速。
A .超线性B .平方C .线性D .三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩作第一次消元后得到的第3个方程( ).A .232x x -+= B .232 1.5 3.5x x -+=C .2323x x -+= D .230.5 1.5x x -=-单项选择题答案二、填空题(每小题3分,共15分)1. 设TX )4,3,2(-=, 则=1||||X ,2||||X = .2. 一阶均差()01,f x x =????? ???????????????3. 已知3n =时,科茨系数()()()33301213,88C C C ===,那么()33C =???????????? 4. 因为方程()420x f x x =-+=在区间[]1,2上满足??????????????? ?,所以()0f x =在区间内有根。
5. 取步长0.1h =,用欧拉法解初值问题()211y y yx y ⎧'=+⎪⎨⎪=⎩的计算公式????????????????????? .填空题答案1.?????? 9和292.??????()()0101f x f x x x --?3.?????? 18 4.??????()()120f f <5.?????? ()1200.11.1,0,1,210.11k k y y k k y +⎧⎛⎫⎪ ⎪=+⎪ ⎪=+⎨⎝⎭⎪=⎪⎩三、计算题(每题15分,共1. 已知函数211y x =+的一组数据:求分段线性插值函数,并计算()1.5f 的近似值.计算题1.答案1.?????? 解[]0,1x ∈,()1010.510.50110x x L x x --=⨯+⨯=---??????????[]1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为2. 已知线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩(1)?????? 写出雅可比迭代公式、高斯-塞德尔迭代公式; (2)?????? 对于初始值()()0,0,0X =,应用雅可比迭代公式、高斯-塞德尔迭代公式分别计算()1X(保留小数点后五位数字).计算题2.答案1.解 原方程组同解变形为 1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m =高斯-塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩?(0,1...)m =用雅可比迭代公式得()()10.72000,0.83000,0.84000X =用高斯-塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间的近似根(1)请指出为什么初值应取2 (2)请用牛顿法求出近似根,精确到.计算题3.答案4. 写出梯形公式和辛卜生公式,并用来分别计算积分101dx x +⎰.计算题4.答案确定下列求积公式中的待定系数,并证明确定后的求积公式具有3次代数精确度证明题答案证明:求积公式中含有三个待定系数,即101,,A A A -,将()21,,f x x x =分别代入求积公式,并令其左右相等,得得1113A A h -==,043hA =。

期末考试试卷(A 卷)2007学年第二学期 考试科目: 数值分析 考试时间:120 分钟学号 姓名 年级专业一、判断题(每小题2分,共10分)1. 用计算机求1000100011n n=∑时,应按照n 从小到大的顺序相加。
( )2. 为了减少误差,进行计算。
( )3. 用数值微分公式中求导数值时,步长越小计算就越精确。
( )4. 采用龙格-库塔法求解常微分方程的初值问题时,公式阶数越高,数值解越精确。
( )5. 用迭代法解线性方程组时,迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关,与常数项无关。
( )二、填空题(每空2分,共36分)1. 已知数a 的有效数为0.01,则它的绝对误差限为________,相对误差限为_________.2. 设1010021,5,1301A x -⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦则1A =_____,2x =______,Ax ∞=_____.3. 已知53()245,f x x x x =+-则[1,1,0]f -= ,[3,2,1,1,2,3]f ---= .4. 为使求积公式11231()((0)f x dx A f A f A f -≈++⎰的代数精度尽量高,应使1A = ,2A = ,3A = ,此时公式具有 次的代数精度。
5. n 阶方阵A 的谱半径()A ρ与它的任意一种范数A 的关系是 .6. 用迭代法解线性方程组AX B =时,使迭代公式(1)()(0,1,2,)k k XMX N k +=+=K 产生的向量序列{}()k X收敛的充分必要条件是 .7. 使用消元法解线性方程组AX B =时,系数矩阵A 可以分解为下三角矩阵L 和上三角矩阵U 的乘积,即.A LU = 若采用高斯消元法解AX B =,其中4221A -⎡⎤=⎢⎥⎣⎦,则L =_______________,U =______________;若使用克劳特消元法解AX B =,则11u =____;若使用平方根方法解AX B =,则11l 与11u 的大小关系为_____(选填:>,<,=,不一定)。
1.已知ln(2.0)=0.6931;ln(2.2)=0.7885,ln(2.3)=0.8329,试用线性插值和抛物插值计算.ln2.1的值并估计误差2.已知x=0,2,3,5对应的函数值分别为y=1,3,2,5.试求三次多项式的插值3. 分别求满足习题1和习题2 中插值条件的Newton插值(1)(2)3()1(2)(2)(3)310N x x x x x x x=+--+--4.给出函数f(x)的数表如下,求四次Newton插值多项式,并由此计算f(0.596)的值解:5.已知函数y=sinx的数表如下,分别用前插和后插公式计算sin0.57891的值6.求最小二乘拟合一次、二次和三次多项式,拟合如下数据并画出数据点以及拟合函数的图形。
(a)(b)7.试分别确定用复化梯形、辛浦生和中矩形求积公式计算积分214dxx+⎰所需的步长h,使得精度达到5 10-。
8.求A、B使求积公式⎰-+-++-≈11)]21()21([)]1()1([)(f f B f f A dx x f 的代数精度尽量高,并求其代数精度;利用此公式求⎰=211dxx I (保留四位小数)。
9.已知分别用拉格朗日插值法和牛顿插值法求)(x f 的三次插值多项式)(3x P ,并求)2(f 的近似值(保留四位小数)。
10.已知求)(x f 的二次拟合曲线)(2x p ,并求)0(f '的近似值。
11.已知x sin 区间[0.4,0.8]的函数表如用二次插值求63891.0sin 的近似值,如何选择节点才能使误差最小?并求该近似值。
12. 利用矩阵的LU 分解法解方程组⎪⎩⎪⎨⎧=++=++=++2053182521432321321321x x x x x x x x x 。
13.已知下列实验数据试按最小二乘原理求一次多项式拟合以上数据。
14. 取节点1,5.0,021===x x x ,求函数xx f -=e )(在区间[0,1]上的二次插值多项式)(2x P ,并估计误差。

吉林大学《数值分析》2020-2021学年第二学期期末试卷一、选择题(每题2分,共20分)1、舍入误差是()产生的误差。
(A)只取有限位数(B)模型准确值与用数值方法求得的准确值(C)观察与测量(D)数学模型准确值与实际值2、3.141580是π的有()位有效数字的近似值。
(A)6(B)5(C)4(D)73、设f (-1)=1,f (0)=3,f (2)=4,则抛物插值多项式中x 2的系数为()。
(A)–0.5(B)0.5(C)2(D)-24、三点的高斯求积公式的代数精度为()。
(A)2(B)5(C)3(D)45、在牛顿-柯特斯求积公式:⎰∑=-≈bani i n i x f C a b dx x f 0)()()()(中,当系数)(n i C 是负值时,公式的稳定性不能保证,所以实际应用中,当()时的牛顿-柯特斯求积公式不使用。
(A)8≥n (B)7≥n (C)10≥n (D)6≥n 6、Jacobi 迭代法解方程组b x =A 的必要条件是()。
(A)A 的各阶顺序主子式不为零(B)1)(<A ρ(C)ni a ii ,,2,1,0 =≠(D)1≤A的Newton 迭代格式为()(A)132k k k x x x +=+(B)1322k k k x x x +=+(C)122k k kx x x +=+(D)133k k kx x x +=+8、已知方程3250x x --=在2x =附近有根,下列迭代格式中在02x =不收敛的是()(A)1k x +=(B)1k x +=(C)315k k k x x x +=--(D)3122532k k k x x x ++=-9、若用二阶中点公式)),(2,2(1n n n n n n y x f hy h x hf y y +++=+求解初值问题1)0(,2=-='y y y ,试问为保证该公式绝对稳定,步长h 的取值范围为()。
(A)10≤<h (B)10≤≤h (C)10<<h (D)10<≤h 10、设A =⎛⎝ ⎫⎭⎪5443,则=∞A ()。
数值计算方法期末试题及答案研究生数值计算方法期末试题及答案、单项选择题(每小题2分,共10分)1 _51. 在下列四个数中,有一个数具有4位有效数字,且其绝对误差限为10 ,则2该数是()A0.001523B0.15230C0.01523D 1.523002.设方阵A可逆,且其n个特征值满足:「「2 -…「n,则A"1的主特征值是( )11A—B.1'nC■■■ -1 或■■ -n D 1 1'或''1 ' n_ (k 1)3.设有迭代公式X二Bx f。
若IIBII > 1, 则该迭代公式()A必收敛B必发散C 可能收敛也可能发散4. 常微分方程的数值方法,求出的结果是()A 解函数B近似解函数C 解函数值D近似解函数值5. 反幕法中构造向量序列时,要用到解线性方程组的()A 追赶法B LU分解法C 雅可比迭代法D咼斯一塞德尔迭代法填空题(每小题4分,共20分)X2 X3 =41 . 设有方程组X1 -2X2 3x^1 , 则可构造高斯一塞德尔迭代公式为2捲 - x2x3 = 0计算题(每小题 10分,共50 分)设f (x) = x - 2x 4若在[-1 , 0]上构造其二次最佳均方逼近多项式,请写出相应的法方程。
设有方程组x 1 2x 2 - 2x 3 = 1 X 1 X 2 X 3 二 1 2x 1 2x 2 x 3 = 1试确定常数 A , B , C 及「,使求积公式1f (x)dx =Af (-:)Bf(0) Cf (:) -1为高斯求积公式。
5?设有向量x = ( 2,1,2)T ,试构造初等反射阵 H ,使H x = ( 3,0,0)丁。
四?证明题(每小题 10分,共20分)1.设有迭代公式X k1xk -,试证明该公式在x^4邻近是2阶收敛的,并2X k -3- -10 1 12.设 A =-2 1 -1,则-11 1 _A::设y^x 2y 2, y(0) = 1,则相应的显尤拉公式为y . .1二2设 f (x)二 ax 1, g (x) = x 。
一、构造次数不超过三次的多项式P3(X),使满足:P 3(0)= 1;P3(1)=0;P 3′(0)=P3′(1)=0。
(10分)解:p3(x)=2x3-3x2+1.二、设f(xi )=i(i=0,1,2),构造二次式p2(x),使满足:p2(xi)=f(xi)(i=0,1,2) (10分)解:三、设节点xi=i(i=0,1,2,3),f(0)=1,f(1)=0,f(2)=-7,f(3)=26,构造次数不超过3次的多项式p3(x),满足p3(xi)=f(xi),i=0,1,2,3 (10分)解:四、对于上题的问题,构造Newton插值多项式。
(10分)五、构造三次多项式P3(X)满足:P3(0)= P3(1)=0,P3′(0)=P3′(1)=1。
(10分)解:六、在第五题的插值条件上,另加上p 4(2)=1,试用构造满足插值条件的四次插值多项式。
(10分) 解:P 4(x)=1-2x-3x(x-1)-x(x-1)(x-1)(x-2)七、利用Doolittle 分解法解方程组Ax=b 即解方程组12341231521917334319174262113x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ (10分) 解:用公式八、基于迭代原理证明22...22+++= (10分) 解:九、构造二次多项式2()x p 满足:'010222()1;()0;()1p p p x x x === (10分) 解:p 2(x )=-x 2+x+1.十、构造一个收敛的迭代法求解方程3210x x --=在[1.3,1.6]内的实根。
合理选择一个初值,迭代一步,求出1x 。
(10分) 解:f(x)=x ³-x ²-1f'(x)=3x ²-2x则x(n+1)=x n -(x n ³-x n ²-1)/(3x n ²-2x n )所以x 0=1.3则x 1≈1.4996删除:远程教育复学科的教学和研究工作有利于总结我国远程教育的实践经验并进行理论概括和创新,开创开放与远程教育的中国模式和中国学派,为世界制远程教育的繁荣和发展作出我们的贡献;有利于借鉴世界各国远程教育的实践经验和理论研究成果,使我国远程教育学科理论研究和教学的起点高、成效快;同时,将有利于更好百地以理论指导教育决策。
期末考试试卷( A 卷)2007 学年第二学期 考试科目: 数值分析 考试时间: 120 分钟学号 姓名 年级专业100011. 用计算机求11000时,应按照 n 从小到大的顺序相加。
n1n2. 为了减少误差 ,应将表达式 2001 1999 改写为 2进行计算。
( )2001 19993. 用数值微分公式中求导数值时,步长越小计算就越精确。
( )4. 采用龙格-库塔法求解常微分方程的初值问题时, 公式阶数越高,数值解越精确。
( )5. 用迭代法解线性方程组时, 迭代能否收敛与初始向量的选择、 系数矩阵及其演变方式有关,与常数项无关。
( ) 二、填空每空 2 分,共 36 分)1. 已知数 a 的有效数为 0.01 ,则它的绝对误差限为 _______ ,相对误差限为 _1 0 1 02. 设 A0 2 1 ,x 5 ,则 A 1____________________________ _, x 2 ______ ,Ax1 3 0 13. 已知 f (x) 2x 54x 35x,则 f[ 1,1,0] , f[ 3, 2, 1,1,2,3] .14. 为使求积公式 f (x)dx A 1f ( 3) A 2f (0) A 3f ( 3)的代数精度尽量高,应使13 3A 1 , A 2 , A 3,此时公式具有 次的代数精度。
5. n 阶方阵 A 的谱半径 ( A)与它的任意一种范数 A 的关系是 .6. 用迭代法解线性方程组 AX B 时,使迭代公式 X (k 1)MX (k)N (k 0,1,2,K )产 生的向量序列X (k)收敛的充分必要条件是 .7. 使用消元法解线性方程组AX B时,系数矩阵A可以分解为下三角矩阵L 和上三角矩阵U 的乘积,即A LU. 若采用高斯消元法解AX B,其中A 4 2,则21L ___________ ,U ____________ ;若使用克劳特消元法解AX B ,则u11 _______ ;若使用平方根方法解AX B,则l11与u11的大小关系为(选填:>,<,=,不一定)。
一、单项选择题〔每题3分,共15分〕1. 3.142和3.141分别作为π的近似数具有〔〕和〔〕位有效数字. A .4和3 B .3和2C .3和4D .4和42. 求积公式()()211211()(2)636f x dx f Af f ≈++⎰,那么A =〔〕A .16B .13C .12D .233. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足〔 〕A .()00l x =0,()110l x = B .()00l x =0,()111l x =C .()00l x =1,()111l x = D .()00l x =1,()111l x =4. 设求方程()0f x =的根的牛顿法收敛,那么它具有〔 〕敛速。
A .超线性B .平方C .线性D .三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩ 作第一次消元后得到的第3个方程〔 〕.A .232x x -+= B .232 1.5 3.5x x -+=C .2323x x -+= D .230.5 1.5x x -=-单项选择题答案1.A2.D3.D4.C5.B二、填空题〔每题3分,共15分〕1. 设TX )4,3,2(-=, 那么=1||||X ,2||||X = .2. 一阶均差()01,f x x =3. 3n =时,科茨系数()()()33301213,88C C C ===,那么()33C = 4. 因为方程()420x f x x =-+=在区间[]1,2上满足 ,所以()0f x =在区间有根。
5. 取步长0.1h =,用欧拉法解初值问题()211yy yx y ⎧'=+⎪⎨⎪=⎩的计算公式 .填空题答案5. ()1200.11.1,0,1,210.11k k y y k k y +⎧⎛⎫⎪ ⎪=+⎪ ⎪=+⎨⎝⎭⎪=⎪⎩三、计算题〔每题15分,共60分〕1. 函数211y x =+的一组数据:求分段线性插值函数,并计算()1.5f 的近似值.计算题1.答案1. 解[]0,1x ∈,()1010.510.50110x x L x x --=⨯+⨯=---[]1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为()[][]10.50,10.80.31,2x x L x x x ⎧-∈⎪=⎨-∈⎪⎩()1.50.80.3 1.50.35L =-⨯=2. 线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩〔1〕 写出雅可比迭代公式、高斯-塞德尔迭代公式;〔2〕 对于初始值()()0,0,0X =,应用雅可比迭代公式、高斯-塞德尔迭代公式分别计算()1X〔保存小数点后五位数字〕.计算题2.答案1.解 原方程组同解变形为 1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m =高斯-塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩ (0,1...)m =用雅可比迭代公式得()()10.72000,0.83000,0.84000X =用高斯-塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间的近似根 〔1〕请指出为什么初值应取2?〔2〕请用牛顿法求出近似根,准确到0.0001.计算题3.答案3. 解()331f x x x =--,()130f =-<,()210f =>()233f x x '=-,()12f x x''=,()2240f =>,故取2x =作初始值4. 写出梯形公式和辛卜生公式,并用来分别计算积分111dxx+⎰.计算题4.答案四、证明题〔此题10分〕确定以下求积公式中的待定系数,并证明确定后的求积公式具有3次代数准确度()()()()1010hhf x dx A f h A f A f h --=-++⎰证明题答案1. 设2.3149541...x *=,取5位有效数字,那么所得的近似值x= .2.设一阶差商()()()21122114,321f x f x f x x x x --===---,()()()322332615,422f x f x f x x x x --===--那么二阶差商()123,,______f x x x =3. 设(2,3,1)TX =--, 那么2||||X = ,=∞||||X 。
吉林大学《数值分析》2019-2020学年第一学期期末试卷一、单项选择题(每小题3分,共15分) 1. 已知近似值1x ,2x ,则()12,x x ()=A. ()()2112x x x x +B. ()()12x x +C. ()()1122x x x x +D. ()()12x x2. 已知求积公式()()211211()(6362)f x dx f Af f ≈++∫,则A =( ) A . 16 B. 13 C. 12 D. 233. 已知,则化为2112A ⎡⎤=⎢⎣⎦⎥A 为对角阵的平面旋转变换角θ=( ) A .6πB.4πC.3πD.2π4. 设求方程()0f x =的根的切线法收敛,则它具有( )敛速。
A . 线性 B. 超越性 C. 平方 D. 三次5. 改进欧拉法的局部截断误差为( )A . B. ()5O h ()4O h C. ()3O h D. ()2O h二、填空题(每小题3分,共15分)1. π的近似值3.1428是准确到 近似值。
2. 满足()a a f x x =,()b b x x =,()c f c f x x =的拉格朗日插值余项为 。
3. 用列主元法解方程组时,已知第2列主元为()142a 则()142a = 。
4.乘幂法师求实方阵 的一种迭代方法。
5. 欧拉法的绝对稳定实区间为 。
三、计算题(每小题12分,共60分) 1. 用已知函数表x 0 1 2y 1 2 5求抛物插值多项式,并求1()2f 的近似值。
2. 用紧凑格式解方程组 123410114130141x x x −⎡⎤⎡⎤⎢⎥⎢⎥−−=⎢⎥⎢⎥⎢⎥⎢⎥−⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎤⎥3. 已知方程组123210113110121x x x ⎡⎤⎡⎤⎡⎢⎥⎢⎥⎢=−⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎣⎦⎣⎦⎣⎥⎥⎦) (1) 证明高斯-塞德尔法收敛;(2)写出高斯-塞德尔法迭代公式; (3) 取初始值,求出()(00,0,0TX=()1X4. 用复化辛卜公式计算积分4n =1011dx x +∫,并估计误差。
《数值计算方法》期末考试试卷附答案一、选择题(每小题4分,共20分)1. 误差根据来源可以分为四类,分别是( )A. 模型误差、观测误差、方法误差、舍入误差;B. 模型误差、测量误差、方法误差、截断误差;C. 模型误差、实验误差、方法误差、截断误差;D. 模型误差、建模误差、截断误差、舍入误差。
2. 若132)(356++-=x x x x f ,则其六阶差商=]3,,3,3,3[6210 f ( ) A. 0; B. 1; C. 2; D. 3 。
3. 数值求积公式中的Simpson 公式的代数精度为 ( ) A. 0; B. 1; C. 2; D. 3 。
4. 若线性方程组Ax = b 的系数矩阵A 为严格对角占优矩阵,则解方程组的Jacobi 迭代法和Gauss-Seidel 迭代法 ( ) A. 都发散; B. 都收敛C. Jacobi 迭代法收敛,Gauss-Seidel 迭代法发散;D. Jacobi 迭代法发散,Gauss-Seidel 迭代法收敛。
5. 对于试验方程y y λ=',Euler 方法的绝对稳定区间为( )A. 02≤≤-h ;B. 0785.2≤≤-h ;C. 02≤≤-h λ;D.0785.2≤≤-h λ ;二、填空题(共6空,每空5分,共30分)1. 已知⎪⎪⎭⎫⎝⎛--='-=4321,)2,1(A x ,则=2x ,=1Ax ,=2A2. 已知3)9(,2)4(==f f ,则 f (x )的线性插值多项式为 ,且用线性插值可得f (7)= 。
3. 要使20的近似值的相对误差界小于0.1%,应至少取 位有效数字。
三、计算题(共2小题,每小题15分,共30分)利用下面数据表,1. 用复化梯形公式计算积分dxxfI)(6.28.1⎰=的近似值;2. 用复化Simpson公式计算积分dxxfI)(6.28.1⎰=的近似值。
(要求计算结果保留到小数点后六位). (14分)四、已知矩阵⎪⎪⎪⎭⎫⎝⎛=1256144412A,求矩阵A的Doolittle分解。
1.已知
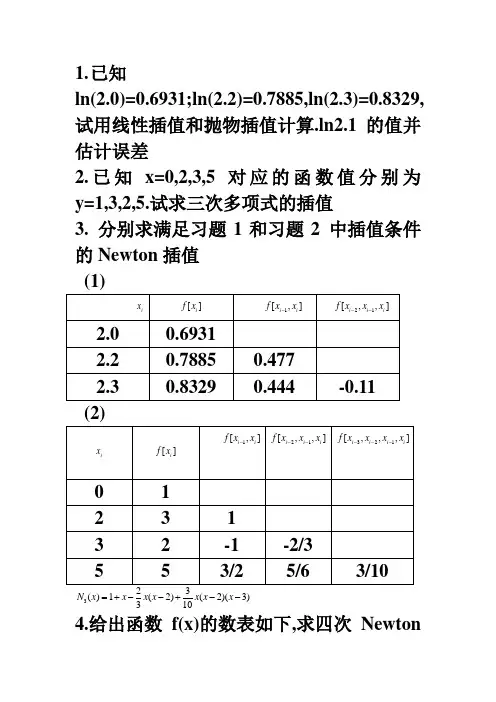
ln(2.0)=0.6931;ln(2.2)=0.7885,ln( 2.3)=0.8329,试用线性插值和抛物插值计算.ln2.1的值并估计误差
2.已知x=0,2,3,5对应的函数值分别为y=1,3,2,5.试求三次多项式的插值
3. 分别求满足习题1和习题2 中插值条件的Newton插值
(1)
x
]
i
(2)
1,]
i i x x -
3()1(2)(2)(3)
310
N x x x x x x x =+--+--4.给出函数f(x)的数表如下,求四次
Newton 插值多项式,并由此计算f(0.596)的值 解:
5.已知函数y=sinx的数表如下,分别用前插和后插公式计算sin0.57891的值
6.求最小二乘拟合一次、二次和三次多项式,拟合如下数据并画出数据点以及拟合函数的图形。
(a)
(b)
73
7.试分别确定用复化梯形、辛浦生和中
矩形求积公式计算积分2
014dx x +⎰所需的步
长h ,使得精度达到5
10
-。
8.求A 、B 使求积公式
⎰-+-++-≈1
1)]
21
()21([)]1()1([)(f f B f f A dx x f 的代数精度尽量高,并求其代数精度;利用此公式求⎰
=2
1
1dx
x I (保留四位小数)。
9.已知
5
4
分别用拉格朗日插值法和牛顿插值法求)(x f的三次插值多项式)(3x P,并求)2(f的近似值(保留四位小数)。
10.已知
2
5
求)(x f的二次拟合曲线)(2x
p,并求)0(f 的近似值。
[0.4,0.8]的函数表
11.已知x sin区间
如用二次插值求63891.0sin 的近似值,如何选择节点才能使误差最小?并求该近似值。
12. 利用矩阵的LU 分解法解方程组
⎪⎩⎪
⎨⎧=++=++=++20
53182521432321321321x x x x x x x x x 。
13.已知下列实验数据
试按最小二乘原理求一次多项式拟合以上数据。
14. 取节点1,5.0,02
1
===x x x ,求函数x
x f -=e )(在区间[0,1]上的二次插值多项式)(2
x P ,并估计误差。
15. 数值积分公式形如
⎰'+'++=≈1
)1()0()1()0()()(f D f C Bf Af x S dx x xf 试
确定参数D C B A ,,,使公式代数精度尽量高;(2)设]1,0[)(4
C x f ∈,推导余项公式
⎰-=1
)
()()(x S dx x xf x R ,并估计误差。
16. 已知数值积分公式为:
)]
()0([)]()0([2)(''20
h f f h h f f h
dx x f h
-++≈⎰
λ,试确
定积分公式中的参数λ,使其代数精确度尽
量高,并指出其代数精确度的次数。
17. 以100,121,144为插值节点,用插值法计算115的近似值,并利用余项估计误差。
用Newton 插值方法:差分表:
18用复化Simpson 公式计算积分
()⎰=1
0sin dx x x I 的近似值,要求误差限为
5
105.0-⨯。
19. 取5个等距节点 ,分别用复化梯形公式和复化辛普生公式计算积分
2
201
12+⎰dx x 的近似值(保留4位小数)。
20.确定求积公式
()()(1
1158059f x dx f
f f -⎡
⎤
≈++⎣⎦
⎰
的代数精度,它是Gauss 公式吗? 21·. 给出x x f ln )(=的数值表用线性插值及二次插值计算54.0ln 的近似值。
22.给出
900,cos ≤≤x x 的函数表,步长
)60/1(1='=h ,若函数具有5位有效数字,研究用线性插值求x cos 近似值时的总误差界。
23. 求一个次数不高于4次的多项式)(x P ,使它满足0)0()0(='=P P ,1)1()1(='=P P ,1)2(=P 。
24.. 给定数据表:5,4,3,2,1=i ,
求4次牛顿插值多项式,并写出插值余项。
25.如下表给定函数:4,3,2,1,0=i ,
42
试计算出此列表函数的差分表,并利用牛顿向前插值公式给出它的插值多项式。
26. 用最小二乘法求一个形如2bx
=的
y+
a
经验公式,使它与下列数据相拟合,并求均方误差。
27.观测物体的曲线运动,得出以下数据:
5
1
28. 单原子波函数的形式为bx
ae
y -=,试按照最小二乘法决定参数a
和b ,已知数据如下:
29. 分别用梯形公式和辛普森公式计算下列积分:
(1)⎰+10
2
4dx
x
x ;
30. 用矩阵的直接三角分解法求解方程组:⎪⎪⎪
⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛7173530103421101002014321x x x x 。