大题
- 格式:docx
- 大小:1.29 MB
- 文档页数:46

高考数学大题小题答题套路1500字高考数学大题小题答题套路:在高考数学考试中,大题小题占据了很大的比重。
为了在有限的时间内高效地完成这些题目,我们需要一些答题套路。
下面给出一些常用的答题套路,希望对你备考有所帮助。
一、解决问题的基本步骤无论是解决大题还是小题,解决问题的基本步骤是一样的:分析问题、解决问题。
1. 分析问题:仔细阅读题目,抓住关键信息,理清问题的逻辑关系,确定解题思路。
2. 解决问题:有了解题思路后,可以进行具体的计算或推理,得出结果并给出明确的解答。
二、选择题的解题技巧1. 理清题意:仔细阅读题目,理解题意是解题的第一步。
特别是一些复杂的题目,一定要抓住问题的关键信息。
2. 排除干扰项:在选择题中,往往有一些干扰项,可以通过排除法找到正确的答案。
把每个选项都带入题目中计算,排除那些肯定不符合条件的选项,就可以找到正确答案。
3. 注意选项的表达方式:有时候,选项可能用其他的方式来表达,需要注意一些等价变形或近义词的替代。
三、填空题的解题技巧1. 尝试不同的方法:填空题有时候可以用多种方法解答,尝试不同的方法可以提高解题的灵活性。
2. 合理估算:填空题往往要进行一些复杂的计算,合理估算可以减少计算量,提高解题速度。
可以先进行一些粗略的估算,然后再进行具体的计算。
3. 利用已知条件:在填空题中,利用已知条件进行推导是非常重要的。
根据已知条件和题目要求,进行推理和计算。
四、解答题的解题技巧1. 分析问题:仔细阅读题目,并理清题目的逻辑关系,确定解题思路和步骤。
2. 给出合理的假设:解答题有时候需要做一些合理的假设,可以简化问题,提高解题的效率。
3. 使用合适的公式或定理:解答题一般需要使用一些公式或定理,熟练掌握并合理运用可以快速解决问题。
4. 画图辅助解答:对于一些几何题,可以通过画图来辅助解答。
画出具体的图形,可以更直观地理解问题,找到解决方法。
总结:以上是解决高考数学大题小题的一些常用答题套路。

离散数学试题一(A 卷答案)一、(10分)证明⌝(A ∨B )→⌝(P ∨Q ),P ,(B →A )∨⌝P A 。
二、(10分)甲、乙、丙、丁4个人有且仅有2个人参加围棋优胜比赛。
关于谁参加竞赛,下列4种判断都是正确的:(1)甲和乙只有一人参加;(2)丙参加,丁必参加;(3)乙或丁至多参加一人;(4)丁不参加,甲也不会参加。
请推出哪两个人参加了围棋比赛。
三、(10分)指出下列推理中,在哪些步骤上有错误?为什么?给出正确的推理形式。
(1)∀x (P (x )→Q (x )) P(2)P (y )→Q (y ) T (1),US(3)∃xP (x ) P(4)P (y ) T (3),ES(5)Q (y ) T (2)(4),I(6)∃xQ (x ) T (5),EG四、(10分)设A ={a ,b ,c},试给出A 上的一个二元关系R ,使其同时不满足自反性、反自反性、五、(15分)设函数g :A →B ,f :B →C ,(1)若f g 是满射,则f 是满射。
(2)若f g 是单射,则g 是单射。
六、(15分)设R 是集合A 上的一个具有传递和自反性质的关系,T 是A 上的关系,使得<a ,b >∈T ⇔<a ,b >∈R 且<b ,a >∈R ,证明T 是一个等价关系。
七、(15分)若<G ,*>是群,H 是G 的非空子集,则<H ,*>是<G ,*>的子群⇔对任意的a 、b ∈H 有a *b -1∈H 。
八、(15分)(1)若无向图G 中只有两个奇数度结点,则这两个结点一定是连通的。
(2)若有向图G 中只有两个奇数度结点,它们一个可达另一个结点或互相可达吗?离散数学试题一(B 卷答案)一、(15分)设计一盏电灯的开关电路,要求受3个开关A 、B 、C 的控制:当且仅当A 和C 同时关闭或B 和C 同时关闭时灯亮。
设F 表示灯亮。

新高考数学大题6大题型
新高考数学大题常见的6大题型包括:
1.三角函数题型:涉及三角函数的画图、性质、三角恒等变换、和与差公式等。
2.向量题型:强调向量的工具性,主要涉及平面向量的背景,以及正弦定理、余弦定理、解三角形等内容。
3.数列题型:考察等差数列和等比数列的通项公式、求和公式以及相关性质。
4.不等式题型:包括不等式的证明、求解和实际应用等。
5.解析几何题型:考察直线、圆、椭圆、双曲线等图形的位置关系和数量关系。
6.函数与导数题型:主要涉及函数的单调性、奇偶性、周期性等性质,以及导数的计算和应用。
在高考数学大题中,这些题型可能会以综合题的形式出现,注重知识的交汇性和实际应用。
因此,考生需要掌握各部分内容的本质和联系,能够综合运用各种数学知识和思想方法来解决实际问题。

历史大题答题模板一、选择题。
1. ()是中国古代四大发明之一。
A. 火药。
B. 指南针。
C. 印刷术。
D. 水车。
2. 下列哪位历史人物是中国古代的伟大思想家?A. 孔子。
B. 秦始皇。
C. 刘备。
D. 孙权。
3. 下列哪位是中国古代的著名诗人?A. 李白。
B. 孟浩然。
C. 苏轼。
D. 杜甫。
4. 以下哪个朝代是中国历史上的第一个封建王朝?A. 夏朝。
B. 商朝。
C. 周朝。
D. 秦朝。
5. 中国古代的“春秋战国”时期是指哪个历史时期?A. 公元前770年至公元前476年。
B. 公元前475年至公元前221年。
C. 公元前220年至公元前206年。
D. 公元前205年至公元前220年。
二、填空题。
1. 《史记》是中国古代著名历史学家司马迁的代表作,共分为()篇。
2. 中国古代的四大发明包括了火药、()、印刷术和指南针。
3. 《庄子》是中国古代著名的()哲学家的代表作。
4. 中国古代的“春秋战国”时期是中国古代历史上政治、军事、文化变革最为激烈的时期,也是中国古代封建社会的()时期。
三、简答题。
1. 请简要介绍中国古代的四大发明。
2. 请简要介绍中国古代的“春秋战国”时期的历史背景及其特点。
3. 请简要介绍中国古代的“春秋战国”时期的主要政治、军事、文化变革。
四、论述题。
1. 论述中国古代的四大发明对世界的影响。
2. 论述中国古代的“春秋战国”时期对中国历史的影响和意义。
五、综合题。
根据你对中国古代历史的了解,结合上述题目,自行设计一道综合题,并进行解答。
以上就是历史大题答题模板的内容,希望对您有所帮助。

数学高考大题题型归纳数学作为学科有其独特性,而数学高考大题题型也有其千篇一律的特点,从性质、类型到解题的方法,这些特点都非常明显,值得对它们进行归纳,以便更加深入的理解和研究。
本文将从高考大题题型的形式、性质、类型及解题方法等多方面进行归纳,为读者全方位了解数学高考大题题型提供参考。
一、高考大题题型的形式高考大题题型的形式主要分为单选题和多项选择题。
单选题要求考生从一组答案中选择一个正确的答案,多项选择题要求考生从多个答案中选择一个或多个正确的答案,此外还有填空题、填表题等。
此外,还有计算题、解答题等,都是大题题型的组成部分。
二、高考大题题型的性质数学高考大题题型的性质主要有几种:(1)实质性题型,这类题型主要考查考生对相关知识的理解,考生需要准确的分析答案;(2)应用性题型,这类题型主要考查考生的解题能力,考生需要结合实际情况进行答题;(3)推理性题型,这类题型主要考查考生对数据分析、解决问题的能力,考生需要积极思考、综合数据来解答;(4)综合性题型,这类题型的试题形式比较复杂,考生要在多个细节问题中系统解决。
三、高考大题题型的类型数学高考大题题型的类型主要包括:(1)函数的概念和特征:函数的概念包括定义域、值域、图形、增减性判断等;(2)函数的求值:定义域、值域、函数值、一次函数的识别、函数的最值;(3)函数独特性质:偶函数、奇函数、可导函数、反函数等;(4)函数的图形:抛物线、曲线、双曲线、圆等;(5)数列:数列的类型、数列的极限等;(6)空间几何:几何图形的构造、平面图形的三视图、空间图形的性质等;(7)行列式:行列式的性质、行列式的基本运算等;(8)矩阵:矩阵的类型、矩阵的运算等;(9)不等式:图解法、代数法、套路法等;(10)概率概念:概率概念的理解、概率的计算和应用等。
四、高考大题题型的解题方法数学高考大题题型的解题方法也有几种:(1)熟记法:这种方法建立在熟练掌握基本知识的基础上,是考生在解决大题题型的最基本的尝试;(2)抽象解题法:这种方法一般用于多变量函数问题,要求考生在理解题目的基础上,对所求问题进行抽象化,将其表示成函数知识中解决问题的方法;(3)思维法:这种方法也称为综合运用方法,是从不同知识点中选择合适的知识,合理运用,从而解决复杂大题题型的最佳方式;(4)技巧法:这种方法是指在解决特定问题时,使用特定的计算方法或技巧,可以更快的解题。

1、有一连续信号x a(t)=cos(2πft+φ),式中,f=20 Hz, φ=π/2。
(1)求出x a(t)的周期;(2)用采样间隔T=0.02 s对x a(t)进行采样,试写出采样信号的表达式;(3)写出对应的时域离散信号(序列)x(n)的表达式,并求出x(n)的周期。
2、有一连续信号x a(t)=sin(2πft+φ),式中,f=20 Hz, φ=π/3。
(1)求出x a(t)的周期;(2)用采样间隔T=0.02 s对x a(t)进行采样,试写出采样信号的表达式;(3)写出对应的时域离散信号(序列)x(n)的表达式,并求出x(n)的周期。
3、有一连续信号x a(t)=sin(2πft+φ) ,式中,f=50 Hz, φ=π/8,选采样频率Fs=200 Hz ;(1)求出x a(t)的周期;(2)试写出采样信号的表达式;(3)写出对应的时域离散信号(序列)x(n)的表达式,并求出x(n)的周期。
4.已知求X(ejω)的傅里叶反变换x(n)。
5.设(1)求x(n)的傅里叶变换;(2)将x(n)以4为周期进行周期延拓,形成周期序列,画出x(n)和的波形;(3)求的离散傅里叶级数6. 设下图所示的序列x(n)的FT用X(ejω)表示,不直接求出X(ej ω),完成下列运算:8. 设序列x(n)的FT用X(ejω)表示,不直接求出X(ejω),完成下列运算:9.已知分别求:(1)收敛域0.5<|z|<2对应的原序列x(n);(2)收敛域|z|>2对应的原序列x(n)。
(3)求出对应X(z)的各种可能的序列表达式。
10.已知,求出对应X(z)的各种可能的序列表达式。
11.已知,求出对应X(z)的各种可能的序列表达式。
12.设系统由下面差分方程描述:y(n)=y(n-1)+y(n-2)+x(n-1) (1)求系统的系统函数H(z),并画出极零点分布图;(2)限定系统是因果的,写出H(z)的收敛域,并求出其单位脉冲响应h(n);(3)限定系统是稳定的,写出H(z)的收敛域,并求出其单位脉冲响应h(n)13.设系统由下面差分方程描述:(1)求系统的系统函数H(z),并画出极零点分布图;(2)限定系统是因果的,写出H(z)的收敛域,并求出其单位脉冲响应h(n);(3)限定系统是稳定的,写出H(z)的收敛域,并求出其单位脉冲响应h(n)。

高考历史的大题题型高考历史的大题题型1、叙述型。
叙述型是从历史的角度归纳和综合历史事件(或历史现象)的过程(原因、经过、结果)或历史人物主要的活动。
设问往往要求考生根据材料并结合所学知识回答或者是直接从材料中提炼论点回答。
题目中一般含有“简述”、“叙述”、“概述”、“试述”等提示语,回答时要紧紧围绕事件或者人物的主要活动,把散见于教材中的内容根据要求进行整理,注重考查对教材知识的再认再现和归纳总结。
2、综合型。
综合型是把分散在教材不同章节、不同国度、不同历史时期但又有某种联系的历史内容融合在一起进行综合考查,它既便于考查学科知识之间的系统联系,又注重考查多层次、多角度分析、解决问题的思维能力。
从解答方法上看,多运用两种或两种以上的解答方法解题,是叙述、论证、分析、比较等的综合体。
这种题型的突出特点是内容跨度大,能力要求高。
3、说明型。
说明型非选择题是对事物的本质或者对事物(事件)进行分析说明。
设问中往往包含有“试分析、试说明、表明、体现了、反映出”等词语。
这种题型主要考查考生把握事物的本质和规律并作出正确阐释的能力和多层次、多角度分析、解决问题的思维能力。
4、比较型。
比较型是将有某种关联的两个或两个以上的历史事件(现象、人物)放在一起进行对比分析。
按照不同的标准,可以划分为单项比较与综合比较、横向比较与纵向比较、求同比较与求异比较、定性比较与定量比较四大类。
这种题型主要考查考生多层次、多角度分析、解决问题的思维能力。
5、评述型。
评述型是对历史事件(现象)和历史人物,依据马克思主义的基本原理进行阐释、评判和估价,得出符合实际的理性认识。
这种题型的一般要求是对历史事件(现象)和历史人物的活动,进行综合归纳,概要叙述,再依据当时的具体条件,给予历史唯物主义的评价。
把不同要求的评述结合在一起,又可以分为:评价与叙述相结合成为评述型题;与论证相结合成为评论型题;与分析相结合形成评析型题。
题目的提示语一般有“评述”、“试评”、“评价”、“评论”、“评析”等。

大题答题技巧大题答题技巧1第一印象很重要以下6点虽然只是皮毛,但是最基础的就是最有用的,也是最容易被忽略的。
第一印象是整体上阅卷老师对试卷的直观感觉,很重要。
如果卷面做到了以下6点,在“可给分可不给分的情况,从宽给分”的中高考评分原则下,你得分的机会就很大了~1、卷面清洁,这是最基本的要求。
2、书写工整,字迹清晰。
3、在规定的答题区域答题,否则做无用功。
4、表述是要根据分值思考要点,尽量细分,用分号或①②③④等符号清楚表述。
5、语言要简洁,答中要害。
6、语言表述要规范,尽量用专业术语。
2给阅卷老师美的享受漂亮的答卷可以给阅卷老师美的享受,让老师保持愉悦的心情批改你的试卷,可以让双方都满意哦~只要记住两点:1、可以写得不漂亮。
2、一定要能看清楚。
记住,你是参加考试,不是书法比赛!!!以下是为大家找来的采访实录学姐我去年参加的高考,感悟颇深,在此说点经验来分享。
在高考之前的N个月,我们的语文老师一直要求我们写这样一种字,宽度与作文纸的格子基本一样,而高度只有作文纸格子的三分之二,而且居中,就是基本连成一横行,但是行与行之间距离很大,高考是电脑阅卷,这种字体被我们学校视为“高分字体”。
写起来我感觉很别扭,但是,在投影上一看,真的很可观,它不要求你的字漂亮,有体,可以遮盖你写字的一大部分缺点。
老师从电脑阅卷的经验来看,这么几点:1、写楷书,也就是说尽量不要连笔。
2、字要写得稍大。
3、需要一大段文字时,写之前要排版。
如果你平时字写得丑,卷面糟糕,那么你写字一定要写得慢,考前可以找几个题目,强迫自己慢慢的写字,一笔一划地写字。
放心,写字的速度跟完成整张试卷的速度一点关系都没有,答题速度只取决于你对知识点的掌握程度,和你思考的速度。
3成为自己的阅卷老师要想在会做的情况下拿全分,不会做的`情况下偷点分,阅卷老师的心思你可以猜哦!出招一:字儿太多,只看评分点吧每小题的答案都会依题意设置若干个评分点,只有按规定的评分细则答出采分点才给分。

高考物理大题题型常见题型一:共点力平衡应用力的平衡条件解题是高考命题的热点,有时还同时考查对物体进行受力分析以及力的合成与分解,对此问题的考查不是在选择题中出现,就是在计算题中出现,是高考必考的知识点。
常见题型二:热力学定律高考常把物体内能的变化与热力学第一定律结合起来考查,特别是把气体状态变化过程中内能变化的分析作为热点进行考查。
常见题型三:分子动理论、气体实验定律高考对分子动理论考查的内容包括:分子动理论的基本观点和实验依据、阿伏加德罗常数、气体分子运动速率的统计分布、温度是分子平均动能的标志、内能等。
考查分子动理论的试题为选择题,难度中等或偏易。
高考对本知识点的考查一般是状态变化过程中p、V、T 其中一个状态参量不变的情况,因此,处理这类问题要注意选取研究对象,明确状态变化过程。
常见题型四:电磁感应电磁感应中经常涉及磁感应强度、磁通量、感应电动势、感应电流等随时间(或位移)变化的图象。
解答的基本方法是:根据题述的电磁感应物理过程或磁通量(磁感应强度)的变化情况,运用法拉第电磁感应定律和楞次定律(或右手定则)判断出感应电动势和感应电流随时间或位移的变化情况,得出图象。
高考关于电磁感应与图象的试题难度中等偏难。
常见题型五:运动学(直线运动和曲线运动)重点考查的内容有:平抛运动的规律及其研究方法,圆周运动的角度、线速度、向心加速度,做圆周运动的物体的受力与运动的关系;同时还可以与带电粒子的电磁场的运动等知识进行综合考查。
重点考查的方法有运动的合成与分解,竖直平面内的圆周运动应掌握最高点和最低点的处理方法。
常见题型六、近代物理初步重点考查的有光电效应及方程、能级与光谱、核反应方程及规律(衰变、裂变和聚变等)、质能方程及核能、相关物理学史等内容,有的试题还以与现代科学技术有着密切联系的近代物理为背景来考查.原子物理的重点知识涉及知识面较广泛,但由于内容较少,“考课本”、“不回避陈题”是本专题知识考查的一大特点.另外本专题知识可与其他部分知识结合,这样结合的选择题或计算题有一定难度,还可与生产、生活、前沿科技相联系(如反物质、中微子、介子等).命题人会考虑创新情景以考查这部分内容,所以对这部分内容要引起高度重视。

高考数学大题6大题型高考是中国学生最重要的考试,大家都在努力备考。
在高考数学考题中,除了小节练习,大家最难搞定的当属大题,其实数学大题有六类型,就是选择题、填空题、解答题、计算题、证明题、应用题。
一、选择题择题有多个选项,围绕着一个话题写出,考生要从中选择一个正确的答案可以称之为选择题。
它的题干具体形式可以有一到五个选项,每一个选项都以字母A、B、C、D、E、F标注,比如“下列有关命题可正确无误地表述为()。
”生在选择时要把握好主要考点,弄清材料,多加思索,把握大意,按情理加以选择。
二、填空题空题就是把题目中间某些词语空白出来,然后由考生来填写正确的单词或数字,它的考点有可能和出题者想考查的知识点不同,所以填空题考生在填空的时候要注意理清出题者的思路,再仔细阅读四周的文字,仔细分析出题者的意图,从而把握好填空内容。
三、解答题答题是指题干中出现有关求解问题的说明,要求考生给出解题步骤,表示解法思路,同时要求列出有效解题过程,即解答题。
解答题的答题方法一般有两种,一种是按题目的设置来求解,即先分析问题,获得有效数据,根据有效数据再据此求解;另一种是先列出有效的解题方法,给出一定的公式或者表示,从而求解出解析方法。
、计算题算题要求考生结合提出材料,进行一定数量的计算,算出所求结果或者近似结果,这类性质的题目就是计算题。
计算题的正确答案比较容易确定,所以在考试中它也是重要的一种题型。
计算题的解答方法一般有两种,一是按照数学规律进行,即分析题目中出现的数学关系,然后运用规律获得解答;另一种是技巧性的,即分析题目的条件及要求,恰当的运用数学的算法实现所要求的计算结果。
五、证明题明题就是要求考生针对某一命题,给出一定的证明方法,使得命题的论证正确性得以明确,即把几个数学结论按照一定顺序,通过运用数学表达式或者数学原理,对原有命题进行论证,最终使其得以证明,这样出题者便可以问一些有关证明的题目,考生就要针对这一证明题目给出有效的论证方法,使其论证正确性得以明确。
数学高考大题及答案
1. 某班有60名学生,其中30名学生喜欢篮球,20名学生喜
欢足球,10名学生既喜欢篮球又喜欢足球。
问至少有多少名
学生不喜欢篮球也不喜欢足球?
答案:10名。
2. 甲、乙两地相距500公里,两车从甲乙同时出发相向而行,甲车每小时行驶60公里,乙车每小时行驶80公里,问两车相遇需要多少时间?
答案:4小时。
3. 若正方形ABCD的边长为x,且矩形EFGH的长为x+4,宽
为x-6,则矩形的周长是正方形周长的几倍?
答案:矩形的周长是正方形周长的2倍。
4. 已知函数f(x)满足f(x+1)-3f(x)+2=0,且f(0)=4,求f(3)的值。
答案:f(3)的值为-10。
5. 已知集合A={5, 6, 7, 8},集合B={7, 8, 9},求A与B的交集、并集以及A-B的差集。
答案:交集为{7, 8},并集为{5, 6, 7, 8, 9},差集为{5, 6}。
6. 某数列中,第一项为1,从第二项开始,每项都比前一项大
2,求该数列的第10项。
答案:第10项为19。
综合知识测试题
在我们的日常生活中,综合知识是我们所需的一种重要能力。
它包括了各种不同领域的知识,涵盖了自然科学、社会科学、文化艺术等方面。
为了检验你的综合知识水平,以下是一些综合知识测试题,希望能够帮助你进一步拓宽知识面,提升自己的综合知识水平。
题目一:自然科学
1. 在太阳系中,最大的行星是什么?
2. 什么是光年?
3. 地球上最高的山峰是哪座山?
4. 人体中最大的器官是什么?
5. 水的沸点是多少摄氏度?
题目二:社会科学
1. 世界上第一个民主国家是哪个?
2. 《资本论》是哪位思想家的著作?
3. 什么是国际货币基金组织(IMF)?
4. 亚洲四小龙是指哪四个国家?
5. 世界上第一个宪法是哪个国家制定的?
题目三:文化艺术
1. 莎士比亚是哪个国家的作家?
2. 蒙娜丽莎是哪位画家的作品?
3. 著名音乐剧《猫》的创作人是谁?
4. 著名小说《基督山伯爵》的作者是谁?
5. 古代中国四大发明分别是什么?
以上是一些综合知识测试题,希望能够对你的综合知识水平有所帮助。
请你仔细思考每个题目,并尽可能写出你的答案。
完成后,你可以对照参考答案进行自我检测,看看自己的综合知识水平如何。
希望这次测试能够让你更加了解自己,发现知识盲点,并努力提升自己的综合知识水平。
(字数:397)。
高考数学大题考什么内容作为教育专家,我们需要关注全国各地高考的信息,并就此撰写有关文章。
本文将从高考数学大题考什么内容这一话题出发,讨论一些与高考相关的话题,并提出五个建议。
一、高考数学大题考什么内容?高考数学大题是高考数学试卷的重头戏,是考生综合应用数学知识和能力的体现。
根据各省份的高考数学试卷,我们可以总结出以下几点:1. 考察综合应用能力高考数学大题通常有多个小问,每个小问的难度不同,需要考生综合应用数学知识和能力进行解答。
例如,某个小问需要用到概率、函数、微积分等多个知识点,考生需要对这些知识点进行整合运用。
2. 考察解题思路和方法高考数学大题不仅考察考生的计算能力,还考察他们的解题思路和方法。
对于同样的问题,考生可能会有不同的解题思路和方法,但只有正确的解题思路和方法才能得到正确的答案。
3. 考察实际应用能力高考数学大题经常与实际问题相关,要求考生将数学知识应用于实际问题中。
例如,某个问题需要考生计算某种物质的浓度,这就需要考生对浓度的概念有所了解,并将其应用于实际问题中。
二、高考数学大题与学生学习的关系高考数学大题的考查范围十分广泛,需要考生有扎实的数学基础和综合应用能力。
因此,高考数学大题与学生平时的学习密切相关。
以下是与高考数学大题相关的一些话题:1. 如何提高数学综合应用能力?提高数学综合应用能力需要注意以下几点:(1)积累数学知识:数学知识是综合应用的基础,只有掌握了足够的数学知识,才能进行综合应用。
(2)加强练习:只有通过不断的练习,才能提高数学综合应用能力。
(3)学会整合知识:数学知识是相互联系的,要将不同的数学知识整合运用,才能更好地解决问题。
2. 如何提高解题思路和方法?提高解题思路和方法需要注意以下几点:(1)学会分析问题:分析问题是解题的第一步,只有正确地分析问题,才能找到正确的解题思路和方法。
(2)掌握解题方法:数学中有很多不同的解题方法,要根据不同的问题选择不同的解题方法。
2020年西工大附中数学一模25题25.(12分)问题提出:(1)如图①,已知在边长为10的等边△ABC中,点D在边BC上,BD=6,连接AD,则△ACD的面积为;问题探究:(2)如图②,已知在边长为6的正方形ABCD中,点E在边BC上,点F在边CD上,且∠EAF=45°.若EF=5,求△AEF的面积;问题解决:(3)如图③是某座城市延康大道的一部分,因自来水抢修需在AB=4米,AD=6米的矩形ABCD区域内开挖一个△AEF的工作面,其中E、F分别在BC、CD边上(不与B、C、D重合),且∠EAF=45°,为了减少对该路段的拥堵影响,要求△AEF面积最小,那么是否存在一个面积最小的△AEF?若存在,请求出△AEF面积的最小值;若不存在,请说明理由.25.问题发现(1)如图①,△ABC为边长为2的等边三角形,D是AB边上一点且CD平分△ABC的面积,则线段CD的长度为;问题探究(2)如图②,▱ABCD中,AB=6,BC=8,∠B=60°点M在AD上,点N在BC上,若MN平分平行四边形ABCD的面积,且MN最短,请你画出符合要求的线段MM,并求出此时MN与AM的长度.问题解决(3)如图③,某公园的一块空地由三条道路围成,即线段AB、BC、,已知AB=160米,BC=120米,∠ABC=90°,的圆心在AB边上,现规划在空地上种植草坪,并从的中点P修一条直路PM(点M在AB上).请问是否存在PM,使得PM平分该空地的面积?若存在,请求出此时AM的长度;若不存在,请说明理由.(1)如图①,在△ABC中,∠ACB=90°,AC=b,BC=a,点E是AC的中点,点F 在BC边上,将△ECF沿着EF折叠后得到△EPF,连接BP并使得BP最小,请画出符合题意的点P;问题探究:(2)如图②,已知在△ABC和△EBD中,∠ACB=∠BDE=90°,AC=BC=4,BD =DE=2,连接CE,点F是CE的中点,连接AF,求AF的最大值.问题解决:(3)西安大明宫遗址公园是世界文化遗产,全国重点文物保护单位,为了丰富同学们的课外学习生活,培养同学们的探究实践能力,周末光明中学的张老师在家委会的协助下,带领全班同学去大明宫开展研学活动.在公园开设的一处沙地考古模拟场地上,同学们参加了一次模拟考古游戏.张老师为同学们现场设计了一个四边形ABCD的活动区域,如图③所示,其中BD为一条工作人员通道,同学们的入口设在点A处,AD⊥BD,AD ∥BC,∠DCB=60°,AB=2米.在上述条件下,小明想把宝物藏在距入口A尽可能远的C处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出AC的最大值及此时△BCD区域的面积,如果不能,请说明理由.(1)如图①,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,将△ABC绕点C 顺时针旋转,得到△A′B′C,当点B落在AB边上时,连接AA′,AA'的长为;问题探究:(2)如图②,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=75°,BC=2,CD=4,求四边形ABCD的面积;问题解决:(3)如图③,四边形ABCD是某农业观光园的部分平面示意图,其中∠A=∠B=90°,∠ADC=135°,AD=3千米,BC=(6+6)米,AB边上的点E为休息区,AE=3千米,BE=6千米,两条观光小路EH和EF(小路宽度不计,F在BC边上,H在CD边上)拟将这个园区分成三个区域,用来种植不同的蔬菜,根据实际需要,∠HEF =75°,并且要求四边形EFCH的面积尽可能大,那么是否存在满足条件的四边形EFCH?若存在,请求出四边形EFCH的面积的最大值;若不存在,请说明理由.(1)如图1,AB是⊙O的弦,直线L交⊙O于点C,在直线L上找一点P,使得∠APB <∠ACB,请画出满足条件的一个∠APB.问题探究(2)如图2,已知射线OM、ON,OM⊥ON,点A、B在射线ON上,点P是射线OM上一动点,AB=6,OB=2,当∠APB最大时,请求出此时OP的长.问题解决(3)如图3,某公园准备修建一室外儿童游乐园,地面道路ON边的AB段为儿童游乐园的入口,安全管理部门准备在与地面道路ON夹角为∠NOM的射线OM方向上确定一点P,并架设横杆PQ,使得PQ∥AB且PQ=3m,在点Q处安装一摄像头,对入口段AB实施监控(点A、B、O、P、Q、M、N在同一平面内).已知OA=8m,AB=m,tan∠MON=.调研发现,当∠AQB最大时监控效果最好.请问能否找到一个点P,从而确定点Q,使得∠AQB达到最大?如果存在,请确定点P的位置,并求出此时sin∠AQB的值;如果不存在,请说明理由.(1)如图①,已知△ABC,请在直线AB上方平面内画出使∠APB=∠C的所有点P.问题探究(2)如图②,扇形AOB的半径OA=12,的长为4π,四边形OEFG为其内接平行四边形,其中E在OB上,G在OA上,F在AB上,EF∥OG,OE∥FG,求▱OEFG 周长的最大值.问题解决(3)南岭国家植物园准备在十一国庆节前后举办花卉展,如图③是一块半圆形的展览用地,O为圆心,半圆的直径AB为200米,工作人员计划在半圆内划分出一个四边形ABCD,在四边形ABCD内部种植新培育的都金香,其中C,D两点在半圆上,且CD=100米,AD、AB、BC,CD为四条观赏小道(不计宽度),半圆内其它部分为草地,为观赏方便,请问能否设计四条小道的总长(即AB+BC+CD+AD)最长且四边形ABCD的面积尽可能大?如果能,请计算四边形ABCD面积的最大值;如果不能,请说明理由.(1)如图①,四边形ABCD中,AB=4,∠ABC=90°,对角线AC与BD交于点O,且O为AC的中点,∠ACB=30°,则点A到BD的距离为,点C到BD的距离为.问题探究:(2)如图②,四边形ABCD中,∠A+∠B=90°,AD=8,BC=6,点E和F分别是边CD和AB的中点,求线段EF的长.问题解决:(3)农业科技干部小王在下乡扶贫工作中,准备帮乡亲们在一块四边形的试验田中修建一条灌溉渠道.如图③是小王记录在笔记本上的试验田缩略图,其中AB=8cm,BC=cm,CD=cm,∠B=∠C=90°,点E和F分别是边BC与CD上的两个观测点,且CE=cm,CF=1cm.现要求在AB边上选取一点M,从点M处修一条笔直的水渠MN(点N在四边形ABCD的另一条边上),使点E和F到MN的距离相等,并且MN平分四边形ABCD的面积.小王又考虑到为了节约成本,想同时让MN的长度尽可能小.请问小王能否找到满足上述条件的点M?如果能,求出此时MN的长度;如果不能,请说明理由.(1)如图,在四边形ABCD中,AD∥BC,若AD=2,BC=6,AD与BC之间的距离为4,则四边形ABCD的面积为;问题探究(2)如图,在四边形ABCD中,AD∥BC.若AD=2,BC=6,对角线AC⊥BD,求四边形ABCD的最大面积;问题解决(3)随着社会的多元化发展,研学观光园走进了我们的生活.如图③所示的四边形ABCD 为某研学观光园的规划设计图,他们打算分为两个区域,其中一个区域为观光采摘区,如△ABD所示,要求建在一条笔直的公路AB的旁边;另一个区域为研学探究区,如△BDC所示,要求满足∠BDC=60°.从实用和美观的角度还要求AD∥BC,且AD:BC =1:3.已知AB=4km,那么是否存在这样的面积最大的四边形ABCD?若存在,请你求出这个最大值;若不存在,说明理由.2020年西工大附中数学九模25题25.(12分)问题提出:一组对角相等,另一组对角不相等的四边形叫做“等对角四边形”.如图①:四边形ABCD 中,若∠A=∠C,∠B≠∠D,则四边形ABCD是“等对角四边形”.(1)如果四边形ABCD满足AB=CD,AD=BC,则四边形ABCD(填“是”或“不是”或“不确定是”)“等对角四边形”.问题探究:(2)如图②,“等对角四边形”ABCD中,BC=CD,AB=12,AD=16,∠B+∠D=180°,求对角线AC的长.问题解决:(3)游山玩水是人们喜爱的一项户外运动,但过度的旅游开发会对环境及动植物的多样性产生影响.如图③,△ABC所在区域是某地著名的“黄花岭”风景区示意图,点B位置是国家珍稀动植物核心保护区,其中∠C=90°,BC=6km,AC=8km,该地旅游部门为科学合理开发此风景区旅游资源,计划在景区外围D点建一个“岭南山庄”度假村,据实际情况,规划局要求:四边形ABCD是一个“等对角四边形”(∠BCD≠∠BAD),核心区B与山庄D之间要尽可能远,并且四边形ABCD区域的面积要控制在56km2以内.请问BD是否存在最大值,规划局的要求能否实现?如果能,请求出BD的最大值及此时四边形ABCD的面积;如果不能,请说明理由.未完待续……。
2.9假设某一城市上方的空气为一长宽均为100 km 、高为1.0 km 的空箱模型。
干净的空气以4 m/s 的流速从一边流入。
假设某种空气污染物以10.0 kg/s 的总排放速率进入空箱,其降解反应速率常数为0.20h -1。
假设完全混合,(1)求稳态情况下的污染物浓度;(2)假设风速突然降低为1m/s ,估计2h 以后污染物的浓度。
解:(1)设稳态下污染物的浓度为ρ 则由质量衡算得10.0kg/s -(0.20/3600)×ρ×100×100×1×109 m 3/s -4×100×1×106ρm 3/s =0解之得 ρ=1.05× 10-2mg/m 3(2)设空箱的长宽均为L ,高度为h ,质量流量为q m ,风速为u 。
根据质量衡算方程 12mtm m d q q k V d ρ--=有 ()22tmd q uLh k L h L h d ρρρ--= 带入已知量,分离变量并积分,得 23600-6-501.0510t 10 6.610d d ρρρ-⨯=-⨯⎰⎰积分有ρ=1.15×10-2mg/m 33.7 水在20℃下层流流过内径为13mm 、长为3m 的管道。
若流经该管段的压降为21N/m 2。
求距管中心5mm 处的流速为多少?又当管中心速度为0.1m/s 时,压降为多少?解:设水的黏度μ=1.0×10-3Pa.s ,管道中水流平均流速为u m 根据平均流速的定义得:402020d d 18d =8d ff v m p r p q l u r A r lπμπμ=-=- 所以 28m f u lp r μ∆=-代入数值得 21N/m 2=8×1.0×10-3Pa·s×u m ×3m/(13mm/2)2 解之得 u m =3.7×10-2m/s又有 u max =2 u m所以 u =2u m [1-(r/r 0)2](1)当r =5mm ,且r 0=6.5mm ,代入上式得 u =0.03m/s(2)u max =2 u mΔp f ’= u max ’/ u max ·Δp f =0.1/0.074×21N/m =28.38N/m4.10在套管换热器中用冷水将100℃的热水冷却到50℃,热水的质量流量为3500kg/h 。
【高中历史】7种大题题型汇总
以下是高中历史中的7种大题题型及其解题方法:
1. 背景型大题:这类题目主要考察学生对历史事件背景的了解和分析。
回答这类题目时,学生需要先分析题干给出的历史事件,然后根据历史事件发生的背景来推断原因和影响。
2. 影响型大题:这类题目主要考察学生对历史事件影响的了解和分析。
回答这类题目时,学生需要先分析题干给出的历史事件,然后根据历史事件发生的影响来推断其对当时社会、政治、经济等方面的影响。
3. 特点型大题:这类题目主要考察学生对历史事件特点的了解和分析。
回答这类题目时,学生需要先分析题干给出的历史事件,然后根据历史事件的特点来推断其与其他历史事件的异同点。
4. 原因型大题:这类题目主要考察学生对历史事件原因的了解和分析。
回答这类题目时,学生需要先分析题干给出的历史事件,然后根据历史事件发生的原因来推断其背景和动因。
5. 对比型大题:这类题目主要考察学生对两个或多个历史事件的了解和对比分析。
回答这类题目时,学生需要先分析题干中给出的两个或多个历史事件,然后根据这些事件的异同点来进行对比和评价。
6. 观点型大题:这类题目主要考察学生对历史事件和人物的看法和评价。
回答这类题目时,学生需要先分析题干中的人物或事件,然后根据自己的观点来阐述对它们的看法和评价。
7. 综合型大题:这类题目主要考察学生对多个历史事件的了解和综合分析。
回答这类题目时,学生需要先分析题干中给出的多个历史事件,然后根据这些事件之间的联系和影响来进行综合分析和评价。
希望这些信息能帮助学生更好地备考高中历史考试。
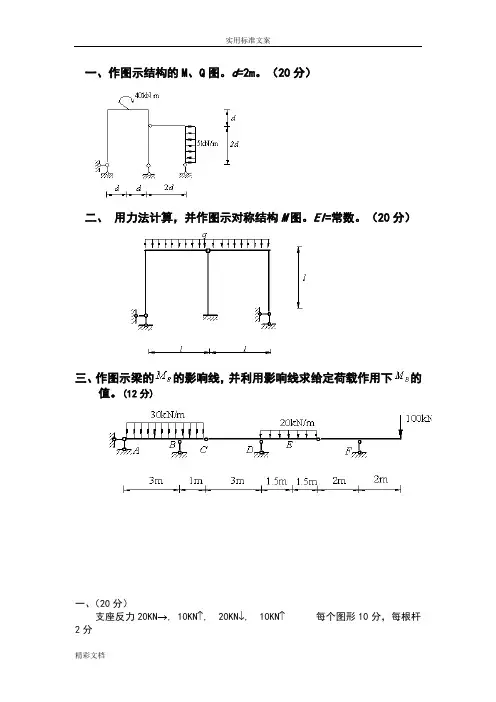
一、 计算题:1. 用剪力分配法计算题37图a 所示单层厂房排架结构各柱的柱顶剪力。
已知W =11.0kN ,q 1=1.0kN/m,q 2=0.5kN/m.(提示:支反力系数C 11=0.4,见题37图b(1);Δu 1=2Δu 2,见题1图b(2)、(3)) 。
2. 牛腿尺寸及承受的设计荷载如图示,采用Ⅱ级钢(f y =310N/mm 2),a s =35mm,试计算纵向受拉钢筋面积A s =?(提示:A s =yh y v f Fh f a F 2.185.00 )3. 某单层厂房排架结构及风载体型系数如图所示。
基本风压W O=0.4kN/m3,柱顶标高+11.8m,室外天然地坪标高为-0.3m,排架间距B=6m,求作用在排架柱顶处的风荷载设计值W。
(提示:距地面10m处,μz=1.0;距地面15m处,μz=1.14;其他高度μz按内插法取值)4. 单层厂房柱下独立基础平面尺寸如图示。
柱边基础高度为600mm ,均布地基净反力设计值为200kN/m 2,试计算沿柱边I -I 剖面基础底板抗弯钢筋的截面面积。
(提示:a sI =40mm,f y =310N/mm 2,M I =241p n (b-h c )2 (2l +b c ),A sI ..=0I y I h 0.9f M )5. 排架计算简图如图所示,A 、B 柱截面形状和尺寸均相同,水平荷载T =10kN 作用于A 柱,试用剪力分配法求A 柱弯矩图。
(提示:柱顶不动铰支座反力R =0.35T )6. 某钢筋混凝土单层厂房排架如图所示,上柱高3m ,下柱高9m ;作用于柱顶的水平集中力p=40kN ;作用于柱A 、柱C 下柱顶部的弯矩M A =M C =60kN ·m(作用方向如图所示);A 、B 、C 柱的抗剪刚度比值为K A ∶K B ∶K C =1∶2∶1;试用剪力分配法画出B 柱的弯矩图。
7. 钢筋混凝土牛腿如图所示。
作用在牛腿顶部的竖向压力设计值为100kN ,水平拉力设计值为120kN ,试计算牛腿的水平纵向受拉钢筋A S ,并画出其布置示意图。
(提示:yh 0y v S f F1.2h 0.85f a F A +=,f y =300N/mm 2,a s =35mm ;无需验证a 的适用范围)8. 某单跨单层厂房,柱距6m,设计时考虑两台桥式吊车,其最大轮压标准值分别为165kN和115kN,吊车位置及影响线如图所示。
试计算影响线中的y2、y3及支座竖向反力最大设计值D max。
(提示:两台吊车的荷载折减系数β=0.9,吊车荷载的分项系数γQ=1.4)9. 牛腿尺寸和按荷载效应标准组合计算的竖向力及水平拉力如图示。
牛腿宽度为600mm ,混凝土抗拉强度标准值为2.2N /mm 2;取裂缝控制系数为0.65,a s =35mm ,试判断该牛腿截面尺寸是否合理。
(提示:F vk ≤β[1-0.5vkhkF F ]0tk h a 5.0bh f)10. 某单层厂房柱下独立基础如图示,作用在基础顶面的轴向压力标准值N k =870kN ,弯矩标准值M k =310kN·m ,剪力标准值V k =21kN ;地基承载力特征值(已修正)f a =200kN /m 2;基础埋置深度d=1.5m ;设基础及其上土的重力密度的平均值为γm =20kN /m 3;基础底面尺寸为b×l =3.0×2.0m 。
试校核地基承载力是否足够?11. 某排架计算简图如图所示。
已知W k =3kN ,q lk =2.5kN/m ,q 2k =1.5kN /m ;A 、B 柱截面形状和尺寸均相同,试用剪力分配法求A 柱在图示荷载作用下的柱底弯矩。
(提示:均布荷载作用下柱顶不动铰支座反力R=C l1·q·H ,C ll =0.4)12. 某单层厂房柱牛腿顶部作用的竖向力设计值为500kN ,水平拉力设计值为150kN ,竖向力至下柱边缘的水平距离为500mm ,牛腿与下柱交接处的垂直截面有效高度为850mm ,钢筋设计强度为300N/mm 2。
试计算牛腿纵向受拉钢筋的面积。
(提示:yh 0y v s f F2.1h f 85.0a F A +=)13.单层单跨排架计算简图如图所示。
A 、B 柱截面形状和尺寸相同,作用在牛腿顶面的弯矩:M max =86kN ·m ,M min =32kN ·m 。
试用剪力分配法求B 柱在图示荷载作用下的弯矩图。
(提示:弯矩作用在牛腿顶面时,柱顶不动铰支座反力R=HMC 3,C 3=1.1)14. 柱子牛腿如图所示。
已知竖向力设计值F v =300kN ,水平拉力设计值F h =60kN ,采用钢筋为HRB335(f y =300N/mm 2)。
试计算牛腿的纵向受力钢筋面积。
(提示:a s =60mm ;A=;f F1.2h 0.85f a F yh 0y v +当a<0.3h 0时,取a=0.3h 0)15. 某轴心受压柱,采用柱下独立基础,剖面如题图所示。
基础顶面轴向压力标准值N k =720kN ,修正后的地基承载力特征值f a =200kN/m 2,基础埋置深度d=1.5m ,设基础及其以上土的重力密度平均值3m 20kN/m γ=。
试推导基础底面面积A的计算公式并确定基础底面尺寸(提示:设底面为正方形)。
16. 单层厂房排架结构如题39图a所示,吊车横向水平刹车力为50kN。
试用剪力分配法计算各柱的柱顶剪力。
(提示:反力系数C5A=0.68,C5B=0.70,见题39图b(1)、b(2);Δu1=1.25Δu2,见题39图b(3)、b(4))。
17.柱下独立基础如题37图所示。
基础顶面作用的轴向压力N k=700kN,弯矩M k=200kN·m,剪力V k=25kN,修正后的地基承载力特征值f a=200kN/m2,已知基础底面尺寸b=3m,l=2m,基础埋置深度d=1.5m,基础高度h=1.0m,基础及以上土的重力密度平均值 m=20kN/m3。
试验算地基承载力是否满足要求。
18.两跨等高排架结构的计算简图如题39图所示。
已知排架柱总高度为11m,上柱高为3.3m;W=2.5kN,q l=2kN/m,q2=1.2kN/m,A、B、C柱抗侧刚度之比为1∶1.2∶1。
试用剪力分配法求B柱在图示荷载作用下的柱底弯矩。
(提示:柱顶不动铰支座反力R=C11qH,C11=0.35)19.柱子牛腿如题36图所示。
已知纵向受拉钢筋面积为631mm2,f y=300N/mm2,水平拉力设计值为75kN。
试计算该牛腿所能承受的竖向力设计值。
20.排架计算简图如题40图所示。
已知W=10kN ,M=100kN·m 。
试用剪力分配法求B 柱弯矩图。
(提示:弯矩作用在牛腿顶面,柱顶不动铰支座反力R=C 3HM ,C 3=1.2)21.排架计算简图如题36图所示,A 柱与B 柱的形状和尺寸相同。
M max =84kN ·m ,M min =40kN ·m ,P=8kN 。
试用剪力分配法求B 柱的弯矩图。
(提示:柱顶不动铰支座反力R=37.1C ,C HM33=)22.钢筋混凝土牛腿如题38图所示,牛腿宽度为400mm ,采用C30混凝土(抗拉强度标准值为2.01N/mm 2),作用于牛腿顶部的竖向荷载标准值为150kN ,水平荷载标准值为70kN ,裂缝控制系数取0.65。
试验算牛腿截面是否满足斜裂缝控制条件。
(提示:00tk vk hk vk s h 5.0bh f F F 5.01F ,mm 40α+⎪⎪⎭⎫ ⎝⎛-β≤=α)23. 某单层厂房排架结构及风荷载体型系数如图所示。
基本风压w0=0.35kN/m2,柱顶标高+12.00m,室外天然地坪标高-0.30m,排架间距B=6.0m。
求作用在排架柱A及柱B上的均布风荷载设计值q A及q B。
(提示:距离地面10m处,μ=1.0;距离地面15m处,zμ=1.14;其他高度zμz按内插法取值。
)25.两跨等高排架结构计算简图如题39图所示。
排架总高13.1m,上柱高3.9m,q1=1.5kN/m,q2=0.75kN/m,A、B、C三柱抗侧刚度之比为1∶1.7∶1。
试用剪力分配法求A柱的上柱下端截面的弯矩值。
(提示:柱顶不动铰支座反力R=C11qH,C11=0.34)26.某单层单跨工业厂房排架结构,跨度18m,柱距6m,厂房内设有1台吊车,吊车的最大轮压标准值为P max,k=110kN,最小轮压标准值为P min,k=30kN,大车轮距为4.5m。
试画出吊车梁支座反力影响线,并计算作用在排架柱上的吊车竖向荷载设计值D max、D min。
(提示:4.1=γ)Q27.某牛腿尺寸及承受的设计荷载如题40图所示。
已知作用在牛腿顶部的竖向力设计值为640kN ,水平拉力设计值为100kN ,采用HRB400级钢(f y =360N/mm 2),a s =50mm 。
试计算牛腿顶部所需配置的纵向受拉钢筋面积A s 。
(提示:当a <0.3h 0时,取a =0.3h 0;A s =yh 0y v 2.185.0f Fh f a F )(未注明单位:mm)28.如题38图所示的单跨单层厂房结构,A 、B 柱抗侧移刚度相同,作用有两台300/50kN 中级工作制吊车。
已知:作用在排架柱上的吊车竖向荷载设计值D max =480kN ,D min =90kN ,偏心距e =0.45m 。
试求当D max 作用于A 柱时,各柱顶的剪力。
(提示:柱顶不动铰支座反力R=C·M/H,C=1.256)29.如题40图所示的单层厂房柱下独立柱基,上部结构传至基础顶面的轴向压力标准值N k=800kN,弯矩标准值M k=250kN·m,基础梁传至基础顶面的竖向荷载标准值N wk=40kN,e w=0.35m修正后的地基承载力特征值f a=200kN/m2,埋深d=1.5m,设基础及其上部土的重力密度的平均值为 m=20kN/m3,基础底面尺寸b×l=3.5×2.5m。
试验算地基承载力是否满足要求?30.某单层单跨厂房排架结构如题39图所示。
A 柱与B 柱尺寸相同,在牛腿顶面上分别作用有M max =104kN ·m 及M min =58kN ·m 的力矩,吊车横向水平刹车力为T=30kN 。
试用剪力分配法计算各柱的柱顶剪力。
(提示:柱顶不动铰支座支力3535, 1.30,0.70MR C TC C C H=+==)31.某轴心受压柱下扩展基础如题40图所示。
地基净反力p J =l80kN /m 2,采用HPB235级钢筋,f y =210N /mm 2,a s =70mm 。