2019人教版数学七年级上册第四章几何图形初步43 角同步练习题含答案语文

人教版初一数学七年级上册第4章几何图形初步 4.3 角同步训练卷及答案人教版初一数学七年级上册第4章几何图形初步 4.3 角同步训练卷1. 下列说法中，正确的有( )①小于90°的角是锐角；②等于90°的角是直角；③大于90°的角是钝角；④平角等于180°；⑤周角等于360°.A．5个 B．4个 C．3个 D．2个2．下列各角中是钝角的是( )A.15周角 B.23平角 C.14周角 D.23直角3．如果两个角的和等于180°，那么这两个角可以都是( )A．锐角 B．钝角 C．直角 D．平角4．如图，射线OC，OD分别在∠AOB的内部、外部，下列结论错误的是( ) A．∠AOB<∠AOD B．∠BOC<∠AOBC．∠COD>∠AOD D．∠AOB>∠AOC5. 下列说法错误的是( )A．∠AOB的顶点是OB．∠AOB的边是两条射线C．射线BO，射线AO分别是表示∠AOB的两边D．∠AOB与∠BOA表示同一个角6．下列图中，能用∠1，∠AOB，∠O三种方法表示同一个角的是( )7. 一个角是70°18′，则这个角等于( )A．70.18° B．70.3° C．70.018° D．70.03°8. 如图所示，下列说法中，正确的是( )A．∠BAC和∠DAE不是同一个角 B．∠ABC和∠ACB是同一个角1---10 CBCCC BBDBD11. 2 2 9012. 81 486013. 60 114. 30°15. 100°16. (1) 解：∠ABD ，∠ABC ，∠DBC(2) 解：∠AED ，∠ADE ，∠BED ，∠CED ，∠BDE ，∠CDE17. 解：(1)∠A ＝30°，∠B ＝90°，∠BCD ＝150°，∠D ＝45°，∠AED ＝135°(2)∠A ＜∠D ＜∠B ＜∠AED ＜∠BCD18. 解：∠EOF ＝∠COE －∠COF ＝60°，因为OF 平分∠AOE ，所以∠AOE ＝2∠EOF ＝120°，所以∠BOE ＝∠AOB －∠AOE ＝60°19. 解：设∠COD 的度数为x ，则∠AOC ＝2x ，所以∠AOD ＝3x ，∠BOD ＝180°－3x ，因为OE 平分∠BOD ，所以∠DOE ＝12∠BOD ＝12(180°－3x)，由∠COE ＝∠COD ＋∠DOE 得77°＝x ＋12(180°－3x)，解得x ＝26°，即∠COD 的度数是26° 20. 解：公园在学校的南偏东25°方向上，医院在学校的北偏东30°方向上，商场在学校的北偏西60°的方向上。

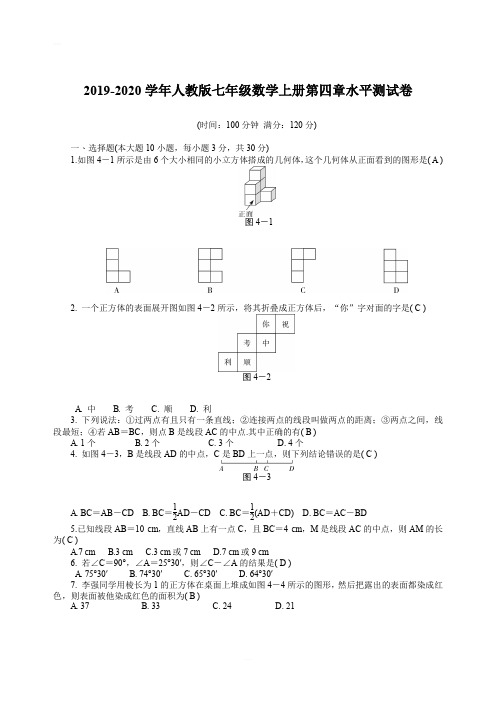
2019-2020学年人教版七年级数学上册第四章水平测试卷(时间：100分钟 满分：120分)一、选择题(本大题10小题，每小题3分，共30分)1.如图4－1所示是由6个大小相同的小立方体搭成的几何体，这个几何体从正面看到的图形是( A )图4－12. 一个正方体的表面展开图如图4－2所示，将其折叠成正方体后，“你”字对面的字是( C )图4－2A . 中B . 考C . 顺D . 利3. 下列说法：①过两点有且只有一条直线；②连接两点的线段叫做两点的距离；③两点之间，线段最短；④若AB ＝BC ，则点B 是线段AC 的中点.其中正确的有( B )A . 1个B . 2个C . 3个D . 4个4. 如图4－3，B 是线段AD 的中点，C 是BD 上一点，则下列结论错误的是( C )图4－3A . BC ＝AB －CD B . BC ＝12AD －CD C . BC ＝12(AD ＋CD) D . BC ＝AC －BD5.已知线段AB ＝10 cm ，直线AB 上有一点C ，且BC ＝4 cm ，M 是线段AC 的中点，则AM 的长为( C )A .7 cmB .3 cmC .3 cm 或7 cmD .7 cm 或9 cm 6. 若∠C ＝90°，∠A ＝25°30′，则∠C －∠A 的结果是( D ) A . 75°30′ B . 74°30′ C . 65°30′ D . 64°30′7. 李强同学用棱长为1的正方体在桌面上堆成如图4－4所示的图形，然后把露出的表面都染成红色，则表面被他染成红色的面积为( B )A . 37B . 33C . 24 D. 21图4－4图4－58. 如图4－5，在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为( C )A. 69°B. 111°C. 141°D. 159°9. 如果∠1与∠2互补，∠2与∠3互余，那么∠1与∠3的关系是( C )A. ∠1＝∠3B. ∠1＝180°－∠3C. ∠1＝90°＋∠3D. 以上都不对10.一副三角板按图4－6所示方式摆放，且∠1的度数比∠2的度数小20°，则∠1的度数为( A )图4－6A.35°B.30°C.25°D.20°二、填空题(本大题6小题，每小题4分，共24分)11.若∠1＝30°28′，则∠1的余角等于59°32′ .12. 如图4－7，从甲村到乙村共有三条路，小明选择第②条路最近，所用的数学知识为两点之间，线段最短.图4－7图4－813.如图4－8所示是由若干个大小相同的小正方体所搭成的几何体从三个方向看到的图形，则搭成这个几何体的小正方体的个数是7 个.14. 如果∠α与∠β互补，且∠α：∠β＝5：4，那么∠α＝100°，∠β＝80° .15.延长线段AB到C，使BC＝4，若AB＝8，则线段AC的长为12 .16. 32.48°＝32 度28 分48 秒.教与学广东学导练数学七年级上册配人教版第四章水平测试卷第2页(共4页)三、解答题(一)(本大题3小题，每小题6分，共18分)17. 计算：(1)48°39′＋67°31′；(2)78°－47°34′56″；(3)22°16′×5.解：原式＝116°10′.解：原式＝30°25′4″.解：原式＝111°20′.18. 如图4－9，已知A，B，C，D四点，根据下列语句画图.(1)画直线AB；(2)连接AC，BD，相交于点O；(3)画射线AD，BC，交于点P.图4－9答图4－1解：(1)如答图4－1，直线AB即为所求.(2)如答图4－1，线段AC，BD，点O即为所求.(3)如答图4－1，射线AD，BC，点P即为所求.19. 一个角的补角和这个角的余角的2倍互为补角，求这个角的度数.解：设这个角为x°，则这个角的余角为(90－x)°，补角为(180－x)°. 则有(180－x)＋2(90－x)＝180.解得x＝60.答：这个角的度数为60°.四、解答题(二)(本大题3小题，每小题7分，共21分)20. 如图4－10，OD是∠AOB的平分线，OE是∠BOC的平分线，且∠AOC＝130°，求∠DOE的度数.图4－10解：因为OD 是∠AOB 的平分线，OE 是∠BOC 的平分线，且∠AOC ＝130°， 所以∠AOD ＝∠BOD ，∠BOE ＝∠COE.所以∠DOE ＝12∠AOC ＝65°.21.如图4－11所示是由5个相同的小正方体搭成的几何体，已知小正方体的棱长为1.图4－11(1)在网格中画出从三个方向看这个几何体得到的图形； (2)求出这个几何体的表面积(含底面积). 解：(1)如答图4－2.答图4－2(2)这个几何体的表面积为2×(4＋4＋3)＝22.22.如图4－12，已知线段A B .(1)作图：延长线段AB 到点C ，使AC ＝3AB ；(2)在(1)所画图中，若AB ＝1 cm ，D 为AB 的中点，E 为AC 的中点，求DE 的长.图4－12解：(1)如答图4－3.答图4－3(2)因为AB ＝1 cm ，D 为AB 的中点，所以AD ＝0.5 cm . 因为AC ＝3AB ，所以AC ＝3 cm .因为E 为AC 的中点，所以AE ＝1.5 cm . 所以DE ＝AE －AD ＝1 cm.五、解答题(三)(本大题3小题，每小题9分，共27分)23. 一个几何体由若干个相同的小正方体组成，如图4－13是从上面看得到的图形，其中每个小正方形中的数字代表该位置小正方体的个数，请画出该几何体从正面和从左面看得到的图形.图4－13解：从正面看和从左面看得到的图形如答图4－4.答图4－424.如图4－14，已知线段AB.(1)请用尺规按下列要求作图：①延长线段AB到C，使BC＝AB，②延长线段BA到D，使AD＝AC(不写画法，但要保留画图痕迹)；(2)请直接回答线段BD与线段AC长度之间的大小关系；(3)如果AB＝2 cm，请求出线段BD和CD的长度.图4－14解：(1)如答图4－5，BC，AD即为所求.答图4－5(2)由答图4－5可得，BD＞AC.(3)因为AB＝2 cm，所以AC＝2AB＝4 cm.所以AD＝4 cm.所以BD＝4＋2＝6(cm).所以CD＝2AD＝8 cm.25. 如图4－15，已知∠AOM与∠MOB互为余角，且∠BOC＝30°，OM平分∠AOC，ON平分∠BOC.(1)求∠MON的度数；(2)如果已知中∠AOB＝80°，其他条件不变，求∠MON的度数；(3)如果已知中∠BOC＝60°，其他条件不变，求∠MON的度数；(4)从(1)(2)(3)中你能发现什么规律？图4－15 解：(1)因为OM 平分∠AOC ，所以∠MOC ＝12∠AOC.又ON 平分∠BOC ，所以∠NOC ＝12∠BOC.所以∠MON ＝∠MOC －∠NOC ＝12∠AOC －12∠BOC ＝12∠AOB.而∠AOB ＝90°，所以∠MON ＝45°.(2)当∠AOB ＝80°，其他条件不变时，∠MON ＝12×80°＝40°.(3)当∠BOC ＝60°，其他条件不变时，∠MON ＝45°. (4)分析(1)(2)(3)的结果和(1)的解答过程可知，∠MON 的大小总等于∠AOB 的一半，而与锐角∠BOC 的大小无关。

2019年人教版七年级上册数学《第4章几何图形初步》单元测试卷一．选择题（共10小题）1．如图，一个有盖的圆柱形玻璃杯中装有半杯水，若任意放置这个水杯，则水面的形状不可能是（）A．B．C．D．2．如图所示的花瓶中，（）的表面，可以看作由所给的平面图形绕虚线旋转一周形成的．A．B．C．D．3．一个棱柱有18条棱，那么它的底面一定是（）A．十八边形B．八边形C．六边形D．四边形4．10个棱长为1的正方体木块堆成如图所示的形状，则它的表面积是（）A．30B．34C．36D．485．如图，三个大小相同的长方形拼在一起组成一个大长方形，把第二个长方形平均分成2份；再把第3个长方形平均分成3份，那么图中阴影部分是大长方形面积的（）A．B．C．D．6．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．7．如图，依据尺规作图的痕迹，计算∠α＝（）A．56°B．68°C．28°D．34°8．如图，点C在∠AOB的边OB上，用尺规作出了∠BCN＝∠AOC，作图痕迹中，弧FG是（）A．以点C为圆心，OD为半径的弧B．以点C为圆心，DM为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DM为半径的弧9．如图，在△ABC中，∠C＝90°，∠CAB＝50°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（）A．40°B．55°C．65°D．75°10．用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（）A．B．C．D．二．填空题（共5小题）11．若一个棱柱有十个顶点，且所有侧棱长的和为30cm，则每条侧棱长为cm．12．长方形绕其一边旋转一周形成的几何体是，直角三角板绕其一直角边旋转一周形成的几何体是．13．一个多面体的面数为6，棱数是12，则其顶点数为．14．如图，依据尺规作图的痕迹，计算∠α＝°．15．下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程：已知：直线l和l外一点P．（如图1）求作：直线l的垂线，使它经过点P．作法：如图2（1）在直线l上任取两点A，B；（2）分别以点A，B为圆心，AP，BP长为半径作弧，两弧相交于点Q；（3）作直线PQ．所以直线PQ就是所求的垂线．请回答：该作图的依据是．三．解答题（共4小题）16．（1）下面这些基本图形和你很熟悉，试一试在括号里写出它们的名称．（）（）（）（）（）（2）将这些几何体分类，并写出分类的理由．17．已知长方形的长为4cm．宽为3cm，将其绕它的一边所在的直线旋转一周，得到一个几何体，（1）求此几何体的体积；（2）求此几何体的表面积．（结果保留π）18．如图，已知点D为OB上的一点，按下列要求进行作图．（1）作∠AOB的平分线OC；（2）在OC上取一点P，使得OP＝a；（3）爱动脑筋的小刚经过仔细观察后，进行如下操作：在边OA上取一点E，使得PE＝PD，这时他发现∠OEP与∠ODP之间存在一定的数量关系，请写出∠OEP与∠ODP的数量关系，并说明理由．19．如图，已知△ABC，按要求作图．（1）过点A作BC的垂线段AD；（2）过C作AB、AC的垂线分别交AB于点E、F；（3）AB＝15，BC＝7，AC＝20，AD＝12，求点C到线段AB的距离．2019年人教版七年级上册数学《第4章几何图形初步》单元测试卷参考答案与试题解析一．选择题（共10小题）1．如图，一个有盖的圆柱形玻璃杯中装有半杯水，若任意放置这个水杯，则水面的形状不可能是（）A．B．C．D．【分析】根据圆柱体的截面图形可得．【解答】解：将这杯水斜着放可得到A选项的形状，将水杯倒着放可得到B选项的形状，将水杯正着放可得到D选项的形状，不能得到三角形的形状，故选：C．【点评】本题主要考查认识几何体，解题的关键是掌握圆柱体的截面形状．2．如图所示的花瓶中，（）的表面，可以看作由所给的平面图形绕虚线旋转一周形成的．A．B．C．D．【分析】根据面动成体，可得答案．【解答】解：由题意，得图形与B的图形相符，故选：B．【点评】本题考查了点、线、面、体，培养学生的观察能力和空间想象能力．3．一个棱柱有18条棱，那么它的底面一定是（）A．十八边形B．八边形C．六边形D．四边形【分析】根据欧拉公式简单多面体的顶点数V、面数F及棱数E间的关系是V+F﹣E＝2，然后把棱数18代入进行讨论即可求解．【解答】解：根据欧拉公式有：V+F﹣E＝2，∵E＝18，∴V+F＝2+18＝20，①当棱柱是四棱柱时，V＝8，F＝6，V+F＝14，②当棱柱是五棱柱时，V＝10，F＝7，V+F＝17，③当棱柱是六棱柱时，V＝12，F＝8，V+F＝20，∴有18条棱的棱柱是六棱柱，它的底面是六边形．故选：C．【点评】考查了欧拉公式的应用，需要对棱柱的顶点数与面数的关系有全面的认识并熟记欧拉公式方可进行解答．4．10个棱长为1的正方体木块堆成如图所示的形状，则它的表面积是（）A．30B．34C．36D．48【分析】如图所示：第一层露出5个面；第二层露出4×2+2个面；第三层露出4×2+3+2×1+2；底面6个面．【解答】解：根据以上分析露出的面积＝5+4×2+2+4×2+3+2×1+2+6＝36．故选：C．【点评】本题关键是要注意立体图形的各个面，每个面能看到的正方形，结合作答．5．如图，三个大小相同的长方形拼在一起组成一个大长方形，把第二个长方形平均分成2份；再把第3个长方形平均分成3份，那么图中阴影部分是大长方形面积的（）A ．B ．C ．D ．【分析】三个大小相同的长方形拼在一起，组成一个大长方形，把第二个长方形平均分成2份，则其中一份就是一个长方形的，再把第三个长方形平均分成3份，则其中2份就是一个小长方形的，所以阴影部分的面积等于一个小长方形的+＝，又因为一个小长方形占大长方形的，所以阴影部分的面积等于大长方形的×＝，据此即可解答． 【解答】解：阴影部分的面积是大长方形面积的：（+）×，＝×，＝，答：图中阴影部分的面积是大长方形面积的． 故选：D ．【点评】此题重点考查学生看图计算的能力，注意把阴影部分转化为大长方形面积的几分之几． 6．如图，过△ABC 的顶点A ，作BC 边上的高，以下作法正确的是（ ）A ．B ．C ．D ．【分析】根据三角形高线的定义：过三角形的顶点向对边引垂线，顶点和垂足之间的线段叫做三角形的高线解答【解答】解：∵四个选项中只有AD⊥BC，∴C正确．故选：C．【点评】本题考查的是作图﹣基本作图，熟记三角形高线的定义是解题的关键．7．如图，依据尺规作图的痕迹，计算∠α＝（）A．56°B．68°C．28°D．34°【分析】先根据矩形的性质得出AD∥BC，故可得出∠DAC的度数，由角平分线的定义求出∠EAF 的度数，再由EF是线段AC的垂直平分线得出∠AEF的度数，根据三角形内角和定理得出∠AFE 的度数，进而可得出结论．【解答】解：∵四边形ABCD是矩形，∴AD∥BC，∴∠DAC＝∠ACB＝68°．∵由作法可知，AF是∠DAC的平分线，∴∠EAF＝∠DAC＝34°．∵由作法可知，EF是线段AC的垂直平分线，∴∠AEF＝90°，∴∠AFE＝90°﹣34°＝56°，∴∠α＝56°．故选：A．【点评】本题考查的是作图﹣基本作图，熟知角平分线及线段垂直平分线的作法是解答此题的关键．8．如图，点C在∠AOB的边OB上，用尺规作出了∠BCN＝∠AOC，作图痕迹中，弧FG是（）A．以点C为圆心，OD为半径的弧B．以点C为圆心，DM为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DM为半径的弧【分析】运用作一个角等于已知角可得答案．【解答】解：根据作一个角等于已知角可得弧FG是以点E为圆心，DM为半径的弧．故选：D．【点评】本题主要考查了作图﹣基本作图，解题的关键是熟习作一个角等于已知角的方法．9．如图，在△ABC中，∠C＝90°，∠CAB＝50°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（）A．40°B．55°C．65°D．75°【分析】根据角平分线的作法可得AG是∠CAB的角平分线，然后再根据角平分线的性质可得∠CAD＝∠CAB＝25°，然后再根据直角三角形的性质可得∠CDA＝90°﹣25°＝65°．【解答】解：根据作图方法可得AG是∠CAB的角平分线，∵∠CAB＝50°，∴∠CAD＝∠CAB＝25°，∵∠C＝90°，∴∠CDA＝90°﹣25°＝65°，故选：C．【点评】此题主要考查了基本作图，关键是掌握角平分线的作法，以及直角三角形的性质．关键是掌握直角三角形两锐角互余．10．用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（）A．B．C．D．【分析】根据过直线外一点作已知直线的垂线作图即可求解．【解答】解：A、根据垂径定理作图的方法可知，CD是Rt△ABC斜边AB上的高线，不符合题意；B、根据直径所对的圆周角是直角的方法可知，CD是Rt△ABC斜边AB上的高线，不符合题意；C、根据相交两圆的公共弦的性质可知，CD是Rt△ABC斜边AB上的高线，不符合题意；D、无法证明CD是Rt△ABC斜边AB上的高线，符合题意．故选：D．【点评】此题考查了作图﹣基本作图，关键是熟练掌握作过直线外一点作已知直线的垂线的方法．二．填空题（共5小题）11．若一个棱柱有十个顶点，且所有侧棱长的和为30cm，则每条侧棱长为6cm．【分析】根据棱柱顶点的个数确定出是五棱柱，然后根据棱柱的每一条侧棱都相等列式求解即可．【解答】解：∵棱柱共有10个顶点，∴该棱柱是五棱柱，∵所有的侧棱长的和是30cm，∴每条侧棱长为30÷5＝6cm．故答案为：6．【点评】本题考查了认识立体图形，主要利用了棱柱顶点的个数与棱数的关系，比较简单．12．长方形绕其一边旋转一周形成的几何体是圆柱，直角三角板绕其一直角边旋转一周形成的几何体是圆锥．【分析】根据面动成体的原理即可解．【解答】解：长方形绕它的一边旋转一周可形成圆柱，直角三角形绕它的直角边旋转一周可形成圆锥．故答案为圆柱，圆锥．【点评】解决本题的关键是掌握各种面动成体的特征．13．一个多面体的面数为6，棱数是12，则其顶点数为8．【分析】因为多面体的面数为6，棱数是12，故多面体为四棱柱．【解答】解：根据四棱柱的概念，有8个顶点．故答案为8．【点评】本题考查的棱柱的定义，关键点在于：棱柱的面与面相交成棱，棱与棱相交成点．14．如图，依据尺规作图的痕迹，计算∠α＝56°．【分析】先根据矩形的性质得出AD∥BC，故可得出∠DAC的度数，由角平分线的定义求出∠EAF 的度数，再由EF是线段AC的垂直平分线得出∠AEF的度数，根据三角形内角和定理得出∠AFE 的度数，进而可得出结论．【解答】解：∵四边形ABCD是矩形，∴AD∥BC，∴∠DAC＝∠ACB＝68°．∵由作法可知，AF是∠DAC的平分线，∴∠EAF＝∠DAC＝34°．∵由作法可知，EF是线段AC的垂直平分线，∴∠AEF＝90°，∴∠AFE＝90°﹣34°＝56°，∴∠α＝56°．故答案为：56．【点评】本题考查的是作图﹣基本作图，熟知角平分线及线段垂直平分线的作法是解答此题的关键．15．下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程：已知：直线l和l外一点P．（如图1）求作：直线l的垂线，使它经过点P．作法：如图2（1）在直线l上任取两点A，B；（2）分别以点A，B为圆心，AP，BP长为半径作弧，两弧相交于点Q；（3）作直线PQ．所以直线PQ就是所求的垂线．请回答：该作图的依据是到线段两个端点的距离相等的点在线段的垂直平分线上（A、B都在线段PQ的垂直平分线上）．【分析】只要证明直线AB是线段PQ的垂直平分线即可．【解答】解：到线段两个端点的距离相等的点在线段的垂直平分线上（A、B都在线段PQ的垂直平分线上），理由：如图，∵PA＝AQ，PB＝QB，∴点A、点B在线段PQ的垂直平分线上，∴直线AB垂直平分线段PQ，∴PQ⊥AB．【点评】本题考查作图﹣基本作图，解题的关键是理解到线段两个端点的距离相等的点在线段的垂直平分线上，属于中考常考题型．三．解答题（共4小题）16．（1）下面这些基本图形和你很熟悉，试一试在括号里写出它们的名称．（）（）（）（）（）（2）将这些几何体分类，并写出分类的理由．【分析】（1）针对立体图形的特征，直接填写它们的名称即可．（2）可以按柱体、锥体和球进行分类，也可以按平面和曲面进行分类，方法不同，答案不同，只要合理即可．【解答】解：（1）从左向右依次是：球、圆柱、圆锥、长方体、三棱柱．（2）观察图形，按柱、锥、球划分，则有圆柱、长方体、三棱柱为柱体；圆锥为锥体；球为球体．【点评】本题考查了立体图形的认识和几何体的分类．熟记常见立体图形的特征是解决此类问题的关键．几何体的分类，从图形形状可以分为柱体、锥体和球三种，注意结合实际几何体的特征进行分类．17．已知长方形的长为4cm．宽为3cm，将其绕它的一边所在的直线旋转一周，得到一个几何体，（1）求此几何体的体积；（2）求此几何体的表面积．（结果保留π）【分析】（1）旋转后的几何体是圆柱体，先确定出圆柱的底面半径和高，再根据圆柱的体积公式计算即可求解；（2）根据圆柱的表面积公式计算即可求解．【解答】解：长方形绕一边旋转一周，得圆柱．（1）情况①：π×32×4＝36π（cm3）；情况②：π×42×3＝48π（cm3）；（2）情况①：π×3×2×4+π×32×2＝24π+18π＝42π（cm2）；情况②：π×4×2×3+π×42×2＝24π+32π＝56π（cm2）．【点评】本题主要考查的是点、线、面、体，根据图形确定出圆柱的底面半径和高的长是解题的关键．18．如图，已知点D为OB上的一点，按下列要求进行作图．（1）作∠AOB的平分线OC；（2）在OC上取一点P，使得OP＝a；（3）爱动脑筋的小刚经过仔细观察后，进行如下操作：在边OA上取一点E，使得PE＝PD，这时他发现∠OEP与∠ODP之间存在一定的数量关系，请写出∠OEP与∠ODP的数量关系，并说明理由．【分析】（1）以点O为圆心，以任意长为半径画弧与∠AOB的两边分别相交，再以两交点为圆心，以大于两交点之间的距离的一半为半径画弧，相交于一点，过这一点与O作射线OC即可；（2）在OC上取一点P，使得OP＝a；（3）以O为圆心，以OD为半径作弧，交OA于E2，连接PE2，作PM⊥OA于M，PN⊥OB于N，根据角平分线上的点到角的两边的距离相等可得PM＝PN，利用HL证明△E2PM≌△DPN，得出∠OE2P＝∠ODP，再根据平角的定义即可求解．【解答】解：（1）如图，OC即为所求；（2）如图，OP＝a；（3）∠OEP＝∠ODP或∠OEP+∠ODP＝180°．理由是：以O为圆心，以OD为半径作弧，交OA于E2，连接PE2，作PM⊥OA于M，PN⊥OB于N，则PM＝PN．在△E2PM和△DPN中，，∴△E2PM≌△DPN（HL），∴∠OE2P＝∠ODP；以P为圆心，以PD为半径作弧，交OA于另一点E1，连接PE1，则此点E1也符合条件PD＝PE1，∵PE2＝PE1＝PD，∴∠PE2E1＝∠PE1E2，∵∠OE1P+∠E2E1P＝180°，∵∠OE2P＝∠ODP，∴∠OE1P+∠ODP＝180°，∴∠OEP与∠ODP所有可能的数量关系是：∠OEP＝∠ODP或∠OEP+∠ODP＝180°．【点评】本题主要考查了角平分线的作法，作一个角等于已知角，过直线外一点作已知直线的垂线，都是基本作图，需要熟练掌握，另外还考查了角平分线上的点到角的两边的距离相等的性质，30°角所对的直角边等于斜边的一半的性质．19．如图，已知△ABC，按要求作图．（1）过点A作BC的垂线段AD；（2）过C作AB、AC的垂线分别交AB于点E、F；（3）AB＝15，BC＝7，AC＝20，AD＝12，求点C到线段AB的距离．【分析】（1）、（2）根据几何语言作图；（3）利用三角形面积公式得到•AB•CE＝•BC•AD，然后把AB＝15，BC＝7，AD＝12代入计算可求出CE．【解答】解：（1）如图，AD为所作；（2）如图，CE、CF为所作；＝•AB•CE＝•BC•AD，（3）∵S△ABC∴CE＝＝＝，即点C到线段AB的距离为．【点评】本题考查了作图﹣基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．。

人教版数学七年级上册第4章4.1几何图形同步练习一、单选题（共10题；共20分）1、一个几何体的边面全部展开后铺在平面上，不可能是（）A、一个三角形B、一个圆C、三个正方形D、一个小圆和半个大圆2、下列图形中，是棱锥展开图的是（）A、B、C、D、3、下列图形是四棱柱的侧面展开图的是（）A、B、C、D、4、将选项中的四个正方体分别展开后，所得的平面展开图与如图不同的是（）A、B、C、D、5、如图是一个正方体的表面展开图，这个正方体可能是（）A、B、C、D、6、一个几何体的展开图如图所示，这个几何体是（）A、棱柱B、棱锥C、圆锥D、圆柱7、将一个正方体的表面沿某些棱剪开，展成一个平面图形，至少要剪开（）条棱．A、3B、5C、7D、98、在下面的图形中，不可能是正方体的表面展开图的是（）A、B、C、D、9、如图所示的正方体，如果把它展开，可以得到（）A、B、C、D、10、下列四个图形中是如图展形图的立体图的是（）A、B、C、D、二、填空题（共3题；共4分）11、一个棱锥的棱数是24，则这个棱锥的面数是________．12、如图中的几何体有________个面，面面相交成________线．13、如图是棱长为2cm的正方体，过相邻三条棱的中点截取一个小正方体，则剩下部分的表面积为________cm2．三、计算题（共4题；共20分）14、一个长方形的两边分别是2cm、3cm，若将这个长方形绕一边所在直线旋转一周后是一个什么几何体？请求出这个几何体的底面积和侧面积．15、已知有一个长为5cm，宽为3cm的长方形，若以这个长方形的一边所在的直线为轴，将它旋转一周，你能求出所得的几何体的表面积吗？16、有一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱．现在有一个长为6cm，宽为5cm的长方形，分别绕它的长、宽所在直线旋转一周，得到不同的圆柱，它们的体积分别是多大？17、我们知道，将一个长方形绕它的一边旋转一周得到的几何体是圆柱，现有一个长是5cm，宽是3cm的长方形，分别绕它的长和宽所在的直线旋转一周，得到不同的圆柱几何体，分别求出它们的体积．四、解答题（共3题；共15分）18、请你用式子表示如图所示的长方体形无盖纸盒的容积（纸盒厚度忽略不计）和表面积．这些式子是整式吗？如果是，请你分别指出它们是单项式，还是多项式．19、将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现在有一个长为4厘米，宽为3厘米的长方形，分别绕它的长、宽所在的直线旋转一周，得到不同的圆柱体，它们的体积分别是多大？20、如图所示为一个正方体截去两个角后的立体图形，如果照这样截取正方体的八个角，则新的几何体的棱有多少条？请说明你的理由．答案解析部分一、单选题1、【答案】B【考点】几何体的展开图【解析】【解答】解：正四面体展开是个3角形；顶角为90度，底角为45度的两个正三棱锥对起来的那个6面体展开可以是3个正方形；一个圆锥展开可以是一个小圆+半个大圆．故选B．【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．2、【答案】C【考点】几何体的展开图【解析】【解答】解：A、是三棱柱的展开图，故此选项错误； B、是一个平面图形，故此选项错误；C、是棱锥的展开图，故此选项正确；D、是圆柱的展开图，故此选项错误．故选：C．【分析】根据图形结合所学的几何体的形状得出即可．3、【答案】A【考点】几何体的展开图【解析】【解答】解：由分析知：四棱柱的侧面展开图是四个矩形组成的图形．故选：A．【分析】根据四棱柱的侧面展开图是矩形图进行解答即可．4、【答案】B【考点】几何体的展开图【解析】【解答】解：观察图形可知，将选项中的四个正方体分别展开后，所得的平面展开图与如图不同的选项B．故选：B．【分析】立体图形的侧面展开图，体现了平面图形与立体图形的联系．立体图形问题可以转化为平面图形问题解决．5、【答案】B【考点】几何体的展开图【解析】【解答】解：由题意，得四个小正方形组合成一个正方体的面，是阴影，是空白，故选：B．【分析】根据展开图折叠成几何体，四个小正方形组合成一个正方体的面，可得答案．6、【答案】B【考点】几何体的展开图【解析】【解答】解：圆锥的侧面展开图是扇形，底面是圆，故选：B．【分析】根据圆锥的展开图，可得答案．7、【答案】C【考点】几何体的展开图【解析】【解答】解：∵正方体有6个表面，12条棱，要展成一个平面图形必须5条棱连接，∴至少要剪开12﹣5=7条棱，故选：C．【分析】根据正方体的棱的条数以及展开后平面之间应有棱连着，即可得出答案．8、【答案】B【考点】几何体的展开图【解析】【解答】解：由四棱柱四个侧面和上下两个底面的特征可知，A，C，D选项可以拼成一个正方体，而B选项，上底面不可能有两个，故不是正方体的展开图．故选：B．【分析】由平面图形的折叠及正方体的展开图解题．9、【答案】D【考点】几何体的展开图【解析】【解答】解：如图所示的正方体，如果把它展开，可以得到．故选：D．【分析】根据题干，3个黑色图形经过1个顶点，由此可以判断选项D是这个正方体的展开图．10、【答案】A【考点】几何体的展开图【解析】【解答】解：因为含小黑正方形的面不能与含大黑正方形的面相邻，两个小黑正方形不能在同一行，所以B，C不是左边展形图的立体图；两个小黑正方形在大黑正方形的对面”，那么A图中，正好是大黑正方形在上面，那么小黑正方形就在底面，A符合；故选：A．【分析】因为含小黑正方形的面不能与含大黑正方形的面相邻，两个小黑正方形不能在同一行，据此判断．二、填空题11、【答案】13【考点】认识立体图形【解析】【解答】解：由题意，得侧棱=底棱=12，棱锥是十二棱锥，十二棱锥有十二个侧面，一个底面，故答案为：13．【分析】根据棱锥的侧棱与底棱相等，可得棱锥，根据棱锥的特征，可得答案．12、【答案】3；曲【考点】认识立体图形【解析】【解答】解：图中的几何体叫做圆台，它是由3个面围成的，面与面相交所成的线是曲线．故答案为：3, 曲．【分析】由圆台的概念和特征即可解．图中的几何体叫做圆台，它是由3个面围成的，面与面相交所成的线是曲线．13、【答案】24【考点】几何体的表面积，截一个几何体【解析】【解答】解：过相邻三条棱的中点截取一个小正方体，则剩下部分的表面积为2×2×6=24cm2．故答案为：24．【分析】由于是在正方体的顶点上截取一个小正方体，去掉小正方形的三个面的面积，同时又多出小正方形的三个面的面积，表面积没变，由此求得答案即可．三、计算题14、【答案】解：这个长方形绕一边所在直线旋转一周后是圆柱．当2cm是底面半径时，圆柱的底面积是πr2=22π=4π（cm2），圆柱的侧面积是2πrh=2π×2×3=12π（cm2）；当3cm是底面半径时，圆柱的底面积是πr2=32π=9π（cm2），圆柱的侧面积是2πrh=2π×3×2=12π（cm2）．【考点】点、线、面、体，有理数的乘法【解析】【分析】根据长方形绕一边旋转一周，可得圆柱．分类讨论：2cm是底面半径，3cm是底面半径，根据圆的面积公式，可得圆柱的底面积，根据圆柱的侧面积公式，可得答案．15、【答案】几何体的表面积为48πcm2或80πcm2．【考点】认识立体图形，点、线、面、体，几何体的表面积【解析】【解答】当以5cm的边为轴旋转一周时，圆柱的表面积=2×π×32+2π×3×5=18π+30π=48πcm2；当以3cm的边为轴旋转一周时，圆柱的表面积=2×π×52+2π×5×3=50π+30π=80πcm2．所以答案为：几何体的表面积为48πcm2或80πcm2．【分析】以5cm的边为轴旋转一周得到的是一个底面半径为3cm，高为5cm的圆柱；以3cm边为轴旋转一周得到的是一个底面半径为5cm，高为3cm的圆柱．16、【答案】解：绕长所在的直线旋转一周得到圆柱体积为：π×52×6=150π（cm3）；绕宽所在的直线旋转一周得到圆柱体积为：π×62×5=180π（cm3）．答：它们的体积分别是150π（cm3）和180π（cm3）．【考点】点、线、面、体，有理数的乘方【解析】【分析】根据圆柱体的体积=底面积×高求解，注意底面半径和高互换得圆柱体的两种情况．17、【答案】【解答】解：分两种情况：①绕长所在的直线旋转一周得到圆柱体积为：π×32×5=45π（cm3）；②绕宽所在的直线旋转一周得到圆柱体积为：π×52×3=75π（cm3）．故它们的体积分别为45πcm3或75πcm3．【考点】点、线、面、体【解析】【分析】根据圆柱体的体积=底面积×高求解，注意底面半径和高互换得圆柱体的两种情况．四、解答题18、【答案】解：根据题意得：长方体的体积为abc；表面积为ab+2（ac+bc），体积结果为单项式；表面积结果为多项式【考点】单项式，多项式，几何体的表面积【解析】【分析】根据长方体的体积=长×宽×高，表面积等于2（长×宽+长×高+宽×高），列出关系式即可做出判断．19、【答案】解：绕长所在的直线旋转一周得到圆柱体积为：π×32×4=36πcm3．绕宽所在的直线旋转一周得到圆柱体积：π×42×3=48πcm3【考点】点、线、面、体【解析】【分析】圆柱体的体积=底面积×高，注意底面半径和高互换得圆柱体的两种情况．20、【答案】解：∵一个正方体有12条棱，一个角上裁出3条棱，即8个角共3×8条棱，∴12+3×8=36条．故新的几何体的棱有36条【考点】截一个几何体【解析】【分析】一个正方体有12条棱，一个角上裁出3条棱，即8个角共3×8条棱，相加即可．2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．如图所示，已知∠AOC=∠BOD=80°，∠BOC=30°，则∠AOD的度数为( )A.160°B.110°C.130°D.140°2．如图，直线与相交于点，平分，且，则的度数为（）A. B. C. D.3．如图，C，D，E是线段AB的四等分点，下列等式不正确的是（）A．AB＝4AC B．CE＝12AB C．AE＝34AB D．AD＝12CB4．如图，电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动，电子蚂蚁P从点A出发，以个单位长度/秒的速度绕正方形作顺时针运动，电子蚂蚁Q从点A出发，以个单位长度/秒的速度绕正方形作逆时针运动，则它们第2017次相遇在（）A.点AB.点BC.点CD.点D5．如图，两个面积分别为35，23的图形叠放在一起，两个阴影部分的面积分别为a，b(n>6)，则a-b的值为（）A.6B.8C.9D.126．下列计算正确的是（ ）A ．x 2+x 2=x 4B ．(x ﹣y)2=x 2﹣y 2C ．(﹣x)2•x 3=x 5D ．(x 2y)3=x 6y 7．请通过计算推测32018的个位数是（ ）A ．1B ．3C ．7D ．98．已知|m －2|＋(n －1)2＝0，则关于x 的方程2m ＋x ＝n 的解是( )A.x ＝－4B.x ＝－3C.x ＝－2D.x ＝－19．若x=-3是方程2（x-m ）=6的解，则m 的值为（ ）A.6B.6-C.12D.12-10．一个有理数的平方等于它本身,那么这个有理数是( )A ．0B ．1C ．±1 D．0或111．5的相反数是（ ） A.15B.5C.15-D.﹣512．2322...233 (3)m n ⨯⨯⨯+++个个＝（ ） A.23n m B.m 23n C.32m n D.23m n二、填空题 13．已知△ABC 的高AD 于AB 、AC 的夹角分别是60°和20°，则∠BAC 的度数是_____________．14．在直角三角形中，一个锐角比另一个锐角的3倍还多10，则较小的锐角度数是_______．15．若代数式 4x 8- 与 3x 22+ 的值互为相反数，则x 的值是____.16．如图，数轴上点A 、B 、C 所对应的数分别为a 、b 、c ，化简|a|+|c ﹣b|﹣|a+b ﹣c|=__．17．将图1中的正方形剪开得到图2，图2中共有4个正方形，将图2中一个正方形剪开得到图3，图3中共有7个正方形，将图3中一个正方形剪开得到图4，图4中共有10个正方形⋯⋯如此下去，则图2019中共有正方形的个数为______．18．如图所示,有一个盛有水的圆柱体玻璃容器,它的底面半径为10cm,容器内水的高度为12cm,将一根半径为2cm的玻璃棒垂直插入水中后,容器里的水升高了_____cm.19．-24=________.20．若a和b是互为相反数，则a+b=_______三、解答题21．王老师到市场买菜，发现如果把10千克的菜放到秤上，指示盘上的指针转了180°，如图．第二天王老师就给同学们出了两个问题：(1)如果把0.6千克的菜放在秤上，指针转过多少角度？(2)如果指针转了7°12′，这些菜有多少千克？22．已知O为直线AB上的一点，∠COE是直角，OF平分∠AOE．（1）如图1，若∠COF=34°，则∠BOE=______；（2）如图1，若∠BOE=80°，则∠COF=______；（3）若∠COF=m°，则∠BOE=______度；∠BOE与∠COF的数量关系为______．（4）当∠COE绕点O逆时针旋转到如图2的位置时，（3）中∠BOE与∠COF的数量关系是否仍然成立？请说明理由．23．下面是马小哈同学做的一道题：解方程：212134 x x-+=-解：①去分母，得 4（2x﹣1）=1﹣3（x+2）②去括号，得 8x﹣4=1﹣3x﹣6③移项，得8x+3x=1﹣6+4④合并同类项，得 11x=﹣1⑤系数化为1，得x=-111， （1）上面的解题过程中最早出现错误的步骤是（填代号） （2）请在本题右边正确的解方程：x-12224x x -+=-． 24．解方程或计算:(1)30564x x --= (2)13142x xx ---=- (3)3425203+3542︒'⨯︒''' (4) 220161416(2)(1)2-+÷-⨯--25．已知多项式A 、B ，其中 ，某同学在计算A+B 时，由于粗心把A+B 看成了A-B 求得结果为，请你算出A+B 的正确结果。

4.3.3 余角和补角能力提升1.如图,A,O,B三点在一条直线上,已知∠AOD=25°,∠COD=90°,则∠BOC的度数为()A.25°B.85°C.115°D.155°2.如果∠AOB+∠BOC=90°,∠BOC+∠COD=90°,那么∠AOB与∠COD的关系是()A.互余B.互补C.相等D.不能确定3.如图,点O在直线AB上,∠COB=∠DOE=90°,则图中相等的角的对数是()A.3B.4C.5D.74.如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是() A.右转80°B.左转80°C.右转100°D.左转100°5.在直线AB上任取一点O,过点O作射线OC,OD,使∠COD=90°,当∠AOC=30°时,∠BOD的大小是()A.60°B.120°C.60°或90°D.60°或120°6.如图,将两块三角板的直角顶点重合后叠放在一起,若∠1=40°,则∠2=.7.如图,射线OP表示的方向是.8.如图,桌面上平放着一块三角板和一把直尺,小明将三角板的直角顶点紧靠直尺的边缘,他发现无论是将三角板绕直角顶点旋转,还是将三角板沿直尺平移,∠1与∠2的和总是保持不变,则∠1与∠2的和是度.9.学校、电影院、公园在平面图上的标点分别为A,B,C,如果电影院在学校的正东方向上,公园在学校的南偏西25°的方向上,那么平面图上的∠CAB=度.10.互余的两个角的度数之比为3∶7,则这两个角的度数分别是多少?11.如图,一只蚂蚁从点O出发,沿北偏东45°的方向爬行2.5 cm,碰到障碍物(记作B)后折向北偏西60°的方向爬行3 cm(此时位置记作点C).(1)画出蚂蚁的爬行路线;(2)求出∠OBC的度数.注:如图,,∠1=∠2★12.如图所示,已知O是直线AB上一点,∠AOE=∠FOD=90°,OB平分∠COD,图中与∠DOE互余的角有哪些?与∠DOE互补的角有哪些?并说明理由.创新应用★13.按如图所示的方法折纸,然后回答问题:(1)∠2是多少度的角?为什么?(2)∠1与∠3有何关系?(3)∠1与∠AEC,∠3和∠BEF分别有何关系?★14.根据互余和互补的定义知,20°角的补角为160°,余角为70°,160°-70°=90°;25°角的补角为155°,余角为65°,155°-65°=90°;50°角的补角为130°,余角为40°,130°-40°=90°;75°角的补角为105°,余角为15°,105°-15°=90°……观察以上几组数据,你能得到什么结论?写出你的结论.参考答案能力提升1.C因为∠AOC=∠COD-∠AOD=90°-25°=65°,所以∠BOC=180°-∠AOC=180°-65°=115°.2.C3.C因为∠COB=90°,所以∠AOC=180°-∠BOC=180°-90°=90°,所以∠AOC=∠BOC=∠DOE;因为∠BOD+∠COD=∠EOC+∠COD=90°,所以∠EOC=∠BOD;因为∠AOE+∠EOC=∠COD+∠EOC=90°,所以∠AOE=∠COD,共5对.4.A如图,∠ECF=20°,∠FCD=60°,要从BC方向转向CD方向,需转过的角为∠ECD=∠ECF+∠FCD=20°+60°=80°,即右转80°.5.D根据题意画图为如图①和图②,在图①中∠BOD的度数是60°,在图②中∠BOD的度数是120°,所以∠BOD的度数是60°或120°.6.40°7.南偏西62°8.90由图形知∠1,∠2与直角三角板的直角形成一个平角,所以无论是将三角板绕直角顶点旋转,还是将三角板沿直尺平移,形成的始终是一个平角.所以∠1与∠2的和是90度.9.11510.解:设这两个角的度数分别为3x°,7x°,由题意,得3x°+7x°=90°,解得x°=9°,3x°=27°,7x°=63°.答:这两个角的度数分别是27°,63°.11.解:(1)如图.(2)∠OBC=90°-60°+90°-45°=75°.12.解:与∠DOE互余的角有∠EOF,∠BOD,∠BOC;与∠DOE互补的角有∠BOF,∠COE.理由:∠DOE+∠EOF=90°,∠DOE+∠BOD=∠BOE=180°-∠AOE=90°,∠DOE+∠BOC=∠DOE+∠BOD=90°,∠DOE+∠BOF=∠AOF+∠BOF=180°,∠DOE+∠COE=∠DOE+∠BOF=180°.创新应用13.解:(1)∠2=90°.因为折叠,则∠1与∠3的和与∠2相等,而这三个角加起来,正好是平角∠BEC,所以∠2=×180°=90°.(2)因为∠1与∠3组成的大角和∠2相等,且三个角加起来恰好是一个平角,所以∠1+∠3=90°.所以∠1与∠3互余.(3)因为∠1与∠AEC的和为180°,∠3与∠BEF的和为180°,所以∠1与∠AEC互补,∠3与∠BEF互补.14.解:设一个角的度数为x°,则补角为(180-x)°,它的余角为(90-x)°.因为180-x-(90-x)=90,所以一个角的补角比它的余角大90°.。

人教版数学七年级上册第四章几何图形初步 4.3 角同步练习题含答案人教版数学七年级上册第四章几何图形初步 4.3 角同步练习题1. 下列说法错误的是( )A．∠AOB的顶点是OB．∠AOB的边是两条射线C．射线BO，射线AO分别是表示∠AOB的两边D．∠AOB与∠BOA表示同一个角2．下列图中，能用∠1，∠AOB，∠O三种方法表示同一个角的是( )3. 54.27°可化为( )A．54°16′26″ B．54°28′ C．54°16′15″ D．54°16′12″4. 一个角是70°18′，则这个角等于( )A．70.18° B．70.3° C．70.018° D．70.03°5. 如图，下列说法错误的是( )A．OA的方向是北偏东40° B．OB的方向是北偏西75°C．OC的方向是西南方向 D．OD的方向是南偏东40°6. 如图，∠1＋∠2等于( )A．60° B．90° C．110° D．180°7. 如图所示，下列说法中，正确的是( )A．∠BAC和∠DAE不是同一个角 B．∠ABC和∠ACB是同一个角C．∠ADE可以用∠D表示 D．∠ABC可以用∠B表示8. 如图所示，在此图中小于平角的角的个数是( )A．9 B．8 C．7 D．69. 北京时间上午8：30时，时钟上时针和分针之间的夹角(小于平角)是( ) A．85° B．75° C．70° D．60°14. 60 115. 12016. 35° 55°17. (1) 解：∠ABD，∠ABC，∠DBC(2) 解：∠AED，∠ADE，∠BED，∠CED，∠BDE，∠CDE18. 解：公园在学校的南偏东25°方向上，医院在学校的北偏东30°方向上，商场在学校的北偏西60°的方向上19. 解：66个点拨：画1条、2条、3条、4条……射线，可得3个、6个、10个、15个……锐角，即画n条射线，可得（n＋1）（n＋2）2个锐角。

人教版2019—2020学年度七年级数学上册第四章《几何图形初步》测试题及答案（满分：100分 答题时间：60分钟）温馨提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！―、选择题(每题3分,共30分）1. 根据下列线段的长度,能判断,,C A B 三点不在同一条直线上的是( )A.8AB =,8BC =,8AC =B.10AB =,8BC =, 18.9AC =C.8,11,10AB BC AC ===D.7.5,14, 6.5AB BC AC === 2. 下列说法中正确的是( ) A.两点之间,直线最短B.线段MN 就是,M N 两点间的距离C.在连接两点的所有线中,最短的连线的长度就是这两点间的距离D.从武汉到北京,火车行驶的路程就是武汉到北京的距离 3. 下列图形中,与其他三个不同类的是( )4. 如图,下列说法正确的是( ) A.图中共有5条线段B.直线AB 与直线AC 是同一条直线C.射线与射线是同一条射线D.点O 在直线上5. 平面内四条直线最少有a 个交点,最多有b 个交点,则a b +=( ) A.6 B.4 C.2 D.O6. 已知α∠的余角是2317'38''︒,β∠的补角是11317'38''︒,那么α∠和β∠的大小关系是( )A. αβ∠>∠B.αβ∠=∠C. αβ∠<∠D.不能确定7. 如图,点C 是线段AB 上一点,点M 是AC 的中点,点N 是BC 的中点,如果MC 比NC 长2cm,那么AC 比BC 长( )A.1cmB.2cmC.4cmD.6cm8. 能由如图所示的平面图形折叠而成的立体图形是（ ）9. 如图,某工厂有三个住宅区,各区分别住有职工30人,15人,10人,且这三点在一条大道上(,,A B C 三点在同一直线上）,已知AB =300米,BC =600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )A.点AB.点BC.AB 之间D.BC 之间 10. 下列时刻,时针与分针的夹角为直角的是( ) A.3时30分 B.9时30分 C.8时55分 D.3时36011分 二、填空题(每题3分,共18分）11.如图,从甲村到乙村共有三条路线,小明选择路线②最近,请用数学知识解释原因:_______.12.如图,O 为直线AB 上一点,已知140,OD ∠=︒平分B O C ∠,则AOD ∠=_______13. 一个角的补角等于它的余角的6倍,则这个角的度数为________.14. 如图,点,,A O B 在同一条直线上,射线OD 平分BOC ∠,射线OE 在AOC ∠的内部,且90DOE ∠=︒,写出图中所有互为余角的角______________：15.如图,线段AB 表示一根对折以后的绳子,现从P 处把绳子剪断,剪断后的各段绳子中最长的一段为 10 cm,若12AP PB =,则这条绳子的原长为_______cm.16.如图,平面内90,,AOB COD COE BOE OF ∠=∠=︒∠=∠平分AOD ∠给出以下结论：①AOE DOE ∠=∠; ②180AOD COB ∠+∠=︒;③90COB AOD ∠-∠=︒;④180COE BOF ∠+∠=︒.其中正确的是_______.(填序号）三、解答题(共52分）17. (8分)如图,射线OA 的方向是北偏东15°,射线OB 的方向是北偏西40°, AOB AOC ∠=∠,射线OD 是OB 的反向延长线.(1)试确定射线OC 的方向; (2)求COD ∠度数;(3)若射线平分COD ∠,求AOE ∠的度数.18. (8分)如图,,,OB OC OD 是三条射线,OB 平分AOC ∠,且AOE ∠是平角,由这些条件能否得到结论90BOD ∠=︒？若能,请说明理由;若不能,请你补充一个条件,并说明你的理由.19. (8)如图,线段AB 上有一点D ,点C 为线段DB 的中点,点D 分线段AC 为1:3的两部分,若9CD =cm,则AB 的长为多少？20. (8分)已知110EOC ∠=︒,将角的一边OE 绕点O 旋转,使终止位置9OD =cm 和起始位置OE 成一条直线,以点O 为中心将OC 顺时针方向旋转到OA ,使COA DOC ∠=∠,过点O 作COA ∠的平分线OB . (1)借助量角器、直尺补全图形; (2)求BOE ∠的度数.21. (10)以直线上一点O 为端点作射线OC ,使60BOC ∠=︒,将一个直角三角形的直角顶点放在点O 处.(90DOE ∠=︒）(1)如图1,若直角三角板DOE 的一边OD 放在射线OB 上,则COE ∠=_______︒;(2)如图2,将直角三角板DOE 绕点O 逆时针方向转动到某个位置,若OE 五恰好平分AOC ∠,请说明OD 所在射线是BOC ∠的平分线;(3)如图3,当三角板DOE 绕点O 逆时针旋转到某个位置时,若恰好15COD AOE ∠=∠,求BOD ∠的度数.22. (10分)如图,M 是线段AB 上一定点,点C 从点M 出发以1cm/s 的速度沿线段MA 向左运动,同时点D 从点B 出发,以3cm/s 的速度沿线段BA 似向左运动.(点C 在线段AM 上,点D 在线段BM 上） (1)若AB =10cm,点,C D 运动了2s,则AC MD +=_______; (2)若点,C D 运动时,总有3MD AC =,则AM =_______AB ; (3)在(2)的条件下,N 是直线AB 上一点,且AN BN MN -=,求MNAB的值.第四章综合能力检测卷1. B2. C3. C4. B5. A6. B7. C8. D9. A 10. D 11.两点之间,线段最短12.110︒【解析】因为140∠=︒,所以180118040140BOC ∠=︒-∠=︒-︒=︒,因为OD 平分B O∠,所以1702COD BOC ∠=∠=︒,所以1704AO D C O D∠=∠+∠=︒+︒=︒. 13. 72°【解析】设这个角的度数为x ︒,则它的补角为180x ︒-︒,余角为90x ︒-︒,由题意,得()180690x x -=-,解得72x =故这个角的度数为72°.14. 1∠与3∠,1∠与4∠,2∠与3∠,2∠与4∠【解析】因为90DOE ∠=︒,所以2∠+3∠=90︒,1∠+4∠=90︒.因为OD 平分BOC ∠,所以1∠=2∠,所以乙1+3∠=90︒. 2∠+4∠=90︒.故题图中所有互为余角的角为1∠与3∠,1∠与4∠,2∠与3∠,2∠与4∠.15.15或30【解析】当PB 的2倍最长时,得PB=5cm,AP=12PB=2.5cm,AB=AP+PB=7.5cm,所以这条绳子的原长为2AB=15cm;当AP 的2倍最长时,得AP=5cm,因为AP=12PB,所以PB=2AP=10cm,所以PB=2AP=10cm,所以AB=AP+PB=15cm,所以这条绳子的原长为2AB=30cm.综上,这条绳子的原长为15cm 或30cm.16.①②④【解析】因为90AOB COD ∠=∠=︒,所以A O C B O D ∠=∠,又COE BOE∠=∠所以A O E∠=∠,故①正确;9090180AOD COB AOD AOC AOB ∠+∠=∠+∠+∠=︒+︒=︒,故②正确;90COB AOD AOC AOD ∠-∠=∠+︒-∠,因为AOC ∠与AOD ∠的数量关系不确定,所以COB AOD ∠-∠不一定等于90︒,故③不正确;因为OF 平分AOD∠,所以A O F ∠=∠,又AOE DOE∠=,所以180AOF AOE DOF DOE ∠+∠=∠+∠=︒,即点,,F O E 共线,因为COE BOE ∠=∠,所以180COE BOF ∠+∠=︒,故④正确.故正确的结论是①②④.17. 【解析】(1)因为射线0B 的方向是北偏西40︒,射线的方向是北偏东15︒,所以40NOB ∠=︒,15NOA ∠=︒,所以55AOB NOB NOA ∠=∠+=︒.因为A OB A O ∠=∠,所以55AOC ∠=︒,所以70NOC NOA AOC ∠=∠+∠=︒,所以射线OC 的方向是北偏东70︒.(2)因为55AOB ∠=︒,AOC AOB ∠=∠,所以ABOC=110BOC ∠=︒.因为射线OD 是OB的反向延长线,所以180BOD ∠=︒.所以18011CO D BO D B O C ∠=∠-∠=︒-︒=︒. (3)因为70COD ∠=︒,OE 平分COD ∠,所以35COE ∠=︒.55AOC ∠=︒,所以553590AOE AOC COE ∠=∠+∠=︒+︒=︒. 18【解析】不能,需要添加条件: OD 平分COE ∠.理由如下：因为OD 平分COE ∠,OB 平分AOC ∠, 所以11,22BOC AOC COD COE ∠=∠∠=∠,因为AOE ∠是平角,所以180AOC COE AOE ∠+∠=∠=︒, 所以90BOC COD ∠+∠=︒, 又BOC BOC COD ∠=∠+∠, 所以90BOD ∠=︒.19. 【解析】因为点C 为线段DB 的中点,CD=9cm,所以BD=2CD=18cm.因为点D 分线段AC 为1:3的两部分,所以AD=13CD=3cm,所以AB=AD+BD=18+3=21(cm).20. 【解析】(1)补全图形如图所示.(2)因为110EOC ∠=︒,所以70DOC ∠=︒.因为C O A D O C ∠=∠,所以70COA ∠=︒,因为OB 是COA ∠的平分线,所以35COB ∠=︒,所以75BOE EOC COB ∠=∠-∠=︒.21. 【解析】(1)30因为,90,60BOE COE BOC BOE BOC ∠=∠+∠∠=︒∠=︒,所以30COE ∠=︒.(2)因为OE 平分AOC ∠,所以12COE AOE AOC ∠=∠=∠.因为90EOD ∠=︒,所以90AOE DOB ∠+∠=︒,所以COD DOB ∠=∠,所以OD 所在射线是BOC ∠的平分线. (3)设COD x ∠=︒,则5AOE x ∠=︒,①当三角形OED 抑在如图1的位置时,有61806090x =--,解得5x =,则60565BOD ∠=︒+︒=︒;②当三角形OED 在如图2的位置时,有590120x x +-=,解得7.5x =.则607.552.5BOD ∠=︒-︒=︒.综上,65BOD ∠=︒或52.5︒. 22. 【解析】(1)2cm (2)14(3)当点N 在线段AB 上时,如图1,因为,AN BN MN AN AM MN -=-=,所以14BN AM AB ==,所以12MN AB =,所以MN AB =,所以1MN AB =. 综上,12MN AB =或1.。

4.3角同步练习一、单选题1.若∠α的余角是30°，则∠α的补角的度数是（）A. 60°B. 120°C. 150°D. 90°【答案】B【解析】：∵∠α的余角是30°，∴∠α的补角=30°+90°=120°．故选B．【分析】根据同一个角的补角比余角大90°列式计算即可得解．2.将两块直角三角板的直角顶点重合，如图所示，若∠AOD=128°，则∠BOC的度数是（）A. 45°B. 52°C. 60°D. 50°【答案】B【解析】：∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣128°=52°．故选B．【分析】根据∠BOC=∠AOB+∠COD﹣∠AOD，即可求解．3.如果一个角的度数为20°16′，那么它的余角的度数为（）A. 159°44′B. 69°16′C. 70°54′D. 69°44′【答案】D【解析】：依题意得：90°﹣20°16'=69°44′．故选：D．【分析】根据“和为90度的两个角互为余角，1°=60′，1′=60″”进行计算即可．4.一副三角板按如图方式摆放，且∠1的度数比∠2的度数大54°，则∠1=（）A. 72°B. 70°C. 54°D. 18°【答案】A【解析】：由题意得，，解得∠1=72°，∠2=18°．故选：A．【分析】根据题意结合图形列出方程组，解方程组即可．5.下列说法中正确的是（）A. 一个角的补角一定是钝角B. ∠A的补角与∠A的余角的差一定等于直角C. 互补的两个角不可能相等D. 若∠A+∠B+∠C=90°，则∠A+∠B是∠C的余角【答案】B【解析】：A、一个角的补角一定是钝角，说法错误；B、∠A的补角与∠A的余角的差一定等于直角，说法正确；C、互补的两个角不可能相等，说法错误；D、若∠A+∠B+∠C=90°，则∠A+∠B是∠C的余角，说法错误；故选：B．【分析】根据余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角分别进行分析即可．6.时钟显示为9：30时，时针与分针所夹角度是（）A. 90°B. 100°C. 105°D. 110°【答案】C【解析】：9：30时，时针与分针所夹角度是30× =105°，故选：C．【分析】根据时针与分针相距的份数乘以每份的度数，可得答案．7.如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC：∠EOD=1：2，则∠BOD等于（）A. 30°B. 36°C. 45°D. 72°【答案】A【解析】：∵∠EOC：∠EOD=1：2，∴∠EOC=180°× =60°，∵OA平分∠EOC，∴∠AOC= ∠EOC= ×60°=30°，∴∠BOD=∠AOC=30°．故选：A．【分析】根据邻补角的定义求出∠EOC，再根据角平分线的定义求出∠AOC，然后根据对顶角相等解答．8.下列说法：①平角就是一条直线；②直线比射线线长；③平面内三条互不重合的直线的公共点个数有0个、1个、2个或3个；④连接两点的线段叫两点之间的距离；⑤两条射线组成的图形叫做角；⑥一条射线把一个角分成两个角，这条射线是这个角的角平分线，其中正确的有（）A. 0个B. 1个C. 2个D. 3个【答案】B【解析】：①平角就是一条直线，不符合题意；②直线比射线线长，错误；③平面内三条互不重合的直线的公共点个数有0个、1个、2个或3个，符合题意；④连接两点的线段叫两点之间的距离，不符合题意；⑤两条射线组成的图形叫做角，不符合题意；⑥一条射线把一个角分成两个角，这条射线是这个角的角平分线，不符合题意；其中正确的有1个．故答案为：B．【分析】由角的定义可知平角就是一条直线是错误的；直线、射线没有长度；连接两点的线段的长度叫两点之间的距离；有公共端点的两条射线组成的图形叫做角；一条射线把一个角分成相等的两个角，这条射线是这个角的角平分线.二、填空题9.计算34°25′×3＋35°42′=________【答案】138°57′【解析】：34°25′×3＋35°42′=102°75′＋35°42′=137°117′=138°57′【分析】角的换算单位是1°=60′，1′=60″；由角的和差计算出结果.10.一个角的余角的3倍比它的补角的2倍少120°，则这个角的度数为________．【答案】30°【解析】：设这个角是x°，根据题意，得3（90﹣x）=2（180﹣x）﹣120，解得x=30．即这个角的度数为30°．故答案为：30°．【分析】若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．结合已知条件列方程求解．11.如图，直线AB⊥OE，则图中互余的角有________对．【答案】两【解析】：∵直线AB⊥OE，∴∠BOE=90°，∵∠BOD=∠AOC，∴图中互余的角有∠BOD和∠DOE，∠DOE和∠AOC，一共两对．故答案为：两．【分析】根据互余两角的和为90°，再根据图形以及已知条件即可得出结果．12.如图，∠AOC=30°35′15″，∠BOC=80°15′28″，OC平分∠AOD，那么∠BOD等于________．【答案】49°40′13″【解析】：∵∠AOC=30°35′15″，OC平分∠AOD，∴∠COD=30°35′15″，又∵∠BOC=80°15′28″，∴∠BOD=∠BOC﹣∠DOC=80°15′28″﹣30°35′15″=49°40′13″．故答案为：49°40′13″．【分析】先根据角平分线的定义，得到∠AOC=∠COD，再根据∠BOD=∠BOC﹣∠DOC进行计算即可．13.如图，OA的方向是北偏东15°，OB的方向是北偏西40°，若∠AOC=∠AOB且∠AOC，∠AOB在OA的异侧，则OC的方向是________．【答案】北偏东70°【解析】：如图，，∵∠BOD=40°,∠AOD=15°，∴∠AOC=∠AOB=∠AOD+BOD=55°，∴∠COD=∠AOC+∠AOD=15+55=70°，故答案为：北偏东70°.【分析】根据题意∠AOC、∠AOB在OA的异侧，由图可知∠AOB的度数，再由∠AOC=∠AOB，求出∠COD=∠AOC+∠AOD的度数，得到OC的方向.14.如图所示，直线AB交CD于点O，OE平分∠BOD，OF平分∠COB，∠AOD：∠EOD=4：1，则∠AOF=________．【答案】120°【解析】：∵OE平分∠BOD，∴∠DOB=2∠EOD，∵∠AOD:∠EOD=4:1，∵∠AOD+∠BOD=180°，∴∠EOD=30°，∴∠BOE=30°，∵OE平分∠BOD,OF平分∠COB,∠BOD+∠COB=180°，∴∠BOF=90°−30°=60°，∴∠AOF=180°−∠BOF=180°−60°=120°.【分析】根据角平分线的定义和∠AOD：∠EOD=4：1，求出∠EOD、∠BOE的度数；再由邻补角的平分线互相垂直，求出∠BOF的度数，得到∠AOF的度数.三、解答题15.已知∠α=76°，∠β=41°31′，求：（1）∠β的余角；（2）∠α的2倍与∠β的的差．【答案】（1）解：∠β的余角=90°﹣∠β=90°﹣41°31′=48°29′（2）解：∵∠α=76°，∠β=41°31′，∴2∠α﹣∠β=2×76° ×41°31′=152°﹣20°45′30″=131°14′30″【解析】【分析】由两角之和是90°，两角互为余角；求出∠β的余角；由题意得到角的和差倍分，求出它们的差.16.如图，AB是一条直线，如果∠1=65°15′，∠2=78°30′，求∠3的度数．【答案】解：∵∠1=65°15′，∠2=78°30′，∴∠3=180°﹣∠1﹣∠2=180°﹣65°15′﹣78°30′=36°15′【解析】【分析】由平角是180°，得到∠3=180°﹣∠1﹣∠2；再把∠1、∠2的度数代入，求出∠3的度数．17.如图所示，直线AB、CD、EF交于点O，OG平分∠BOF，且CD⊥EF，∠AOE=70°，求∠DOG的度数．【答案】解：∵∠AOE=70°，∴∠BOF=∠AOE=70°，又∵OG平分∠BOF，∴∠GOF= ∠BOF=35°，又∵CD⊥EF，∴∠EOD=90°，∴∠DOG=180°﹣∠GOF﹣∠EOD=180°﹣35°﹣90°=55°【解析】【分析】求出∠BOF，根据角平分线求出∠GOF，求出∠EOD，代入∠DOG=180°﹣∠GOF﹣∠EOD求出即可．18.如图所示，在△ABC中，AE、BF是角平分线，它们相交于点O，AD是高，∠BAC=54°，∠C=66°，求∠DAC、∠BOA的度数．【答案】解：∵AD是高，∴∠ADC=90° ，∵∠C=66°，∴∠DAC=180°﹣90°﹣66°=24°∵∠BAC=54°，∠C=66°，AE是角平分线，∴∠B AO=27°，∠ABC=60°∵BF是∠ABC的角平分线，∴∠ABO=30°，∴∠BOA=180°﹣∠BAO﹣∠ABO=123°.【解析】【分析】由高的定义得到∠ADC=90° ，再由角平分线的定义和三角形内角和定理，求出∠DAC、∠BOA的度数．。