第7章麦克斯韦方程组
- 格式:doc
- 大小:406.00 KB
- 文档页数:13


第7章 麦克斯韦方程组● 静止电荷和运动电荷都可以激发电场-库伦定律。
● 运动电荷还可以激发磁场-比萨定律。
● 变化的磁场可以激发电场-法拉第定律。
● 变化电场可以激发磁场-麦克斯韦假设。
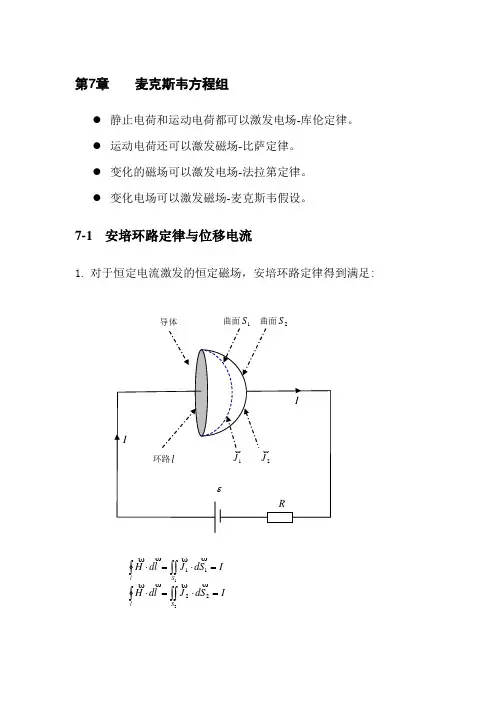
7-1 安培环路定律与位移电流1. 对于恒定电流激发的恒定磁场,安培环路定律得到满足:I S d J l d H S l=⋅=⋅⎰⎰⎰111IS d J l d H S l=⋅=⋅⎰⎰⎰222曲面S曲面S2. 对于时变电流激发的时变磁场,安培环路定律出现矛盾IS d J l d H S l=⋅=⋅⎰⎰⎰1110222=⋅=⋅⎰⎰⎰S lS d J l d H3. 引入位移电流概念,对于时变电流激发的时变磁场,消除安培环 路定律出现的矛盾。
电流连续性定律:⎰⎰⎰⎰⎰∂∂-=⋅VSdVtS d J ρ⎰⎰⎰⎰⎰⎰∂∂-=⋅+⋅-22122211S S S dS tS d J S d J σ⎰⎰⋅=111S S d J I0222=⋅⎰⎰S S d J⎰⎰⎰⎰⋅=3222S S dSD dS σ⎰⎰⎰⎰⎰⎰⋅∂∂=⋅∂∂=⋅=3312211S S S dS tD dS D tS d J I● 位移电流密度和位移电流定义:tD J D ∂∂=⎰⎰⎰⎰⋅∂∂=⋅=3222S S D D dS tD S d J I● 用位移电流表述电流连续性定律:IS d J dS tD S d J I S S S D D =⋅=⋅∂∂=⋅=⎰⎰⎰⎰⎰⎰1321122DS D S S I S d J dS tD S d J I =⋅=⋅∂∂=⋅=⎰⎰⎰⎰⎰⎰2312211● 无矛盾的安培环路定律IS d J l d H S l=⋅=⋅⎰⎰⎰111II S d J l d H D S D l==⋅=⋅⎰⎰⎰224. 无论在恒定情况还是时变情况下安培环路定律都成立● 安培环路定律()()∑⎰⎰⎰+=⋅+=⋅DSD lI I S d J J l d H或⎰⎰⎰⎰⎰⋅∂∂+⋅=⋅SSlS d tD S d J l d H● 安培环路定律说明电流可以激发磁场,变化的电场也可以激发磁场。





第三章 麦克斯韦方程第一章我们已提到电磁场可以用以下四个场量描述,它们是:E (r , t )——电场强度 (伏特/米,V /m )D (r , t )——电通量密度或电位移(库仑/米2,C /m 2) H (r , t )——磁场强度(安培/米,A /m )B (r , t )——磁感应强度或磁通量密度(韦伯/米2,Wb /m 2)这四个量都是矢量,都是时间坐标t 和空间矢径r 的函数。
这些场量在我们周围总是存在的,有来自太阳和其它星球的场,也有来自闪电的场。
传播电视的无线电波、激光则是用人工方法产生的场。
本章主要讨论电磁运动服从的基本方程——麦克斯韦方程。
需要指出的是,麦克斯韦方程不是从几个公理推导出来的,而是根据科学实验总结出来的电磁运动基本规律。
麦克斯韦方程是正确的,因为宏观世界电磁运动都遵循麦克斯韦方程。
本章分别讨论积分形式、微分形式的麦克斯韦方程以及用复矢量表示的时谐场的麦克斯韦方程。
与讨论电荷守恒定律与物质的本构关系。
麦克斯韦方程描述源产生的场,而场对源的作用由洛仑兹力方程描述。
洛仑兹力方程在讨论。
讨论坡印廷定理,它表示电磁运动满足能量守恒关系。
简要介绍唯一性定理、镜像定理、等效原理、磁流和磁荷以及互易定理。
积分与微分形式的麦克斯韦方程本节根据基本电磁现象以及对实验规律的总结,得出积分形式的麦克斯韦方程组,然后利用散度定理与斯托克斯定理,又从积分形式的麦克斯韦方程组得到微分形式的麦克斯韦方程组。
从库仑定理到高斯定理根据库仑定理,真空中带电量q 的质点对周围试验电荷q 1的作用可以看作点电荷q 激发的电场E 对试验电荷q 1的作用,点电荷q 激发的电场强度E 为0r E 204rq πε=(V /m )()式中电场强度E 的单位为V /m ,电量q 的单位为库仑(C ),()m F /10854.8120-⨯=ε,为真空介电常数,r 为点电荷q 到试验电荷q 1之间距离,用米(m )做单位,r 0表示由q 指向q 1的单位矢量。



《电磁学Mawell》课件一、教学内容本节课我们将深入探讨《电磁学Mawell》这本教材的第七章“麦克斯韦方程组”。
具体内容包括:对麦克斯韦方程组的推导和解释,重点掌握方程组中各个方程的含义及其在电磁场中的应用;学习电磁波的基本概念,探究电磁波的传播特性。
二、教学目标1. 理解并掌握麦克斯韦方程组,了解各个方程的含义及其在电磁场中的应用。
2. 学习电磁波的基本概念,掌握电磁波的传播特性。
3. 培养学生的科学思维能力和解决问题的能力。
三、教学难点与重点教学难点:麦克斯韦方程组的推导和理解,电磁波的传播特性。
教学重点:麦克斯韦方程组的应用,电磁波的基本概念。
四、教具与学具准备1. 教具:多媒体课件,板擦,黑板。
2. 学具:教材,《电磁学Mawell》第七章,笔记本,文具。
五、教学过程1. 导入:通过展示一个实践情景,如电磁波的传播现象,引发学生对本节课的兴趣。
2. 新课内容讲解:a. 麦克斯韦方程组的推导,解释各个方程的含义。
b. 举例说明麦克斯韦方程组在电磁场中的应用。
c. 介绍电磁波的基本概念,探究电磁波的传播特性。
3. 例题讲解:讲解一道关于麦克斯韦方程组的典型例题,让学生掌握解题方法。
4. 随堂练习:让学生独立完成几道练习题,巩固所学知识。
六、板书设计1. 黑板左侧:麦克斯韦方程组及其含义。
2. 黑板右侧:电磁波的基本概念和传播特性。
3. 中间部分:例题讲解和随堂练习。
七、作业设计1. 作业题目:a. 解释麦克斯韦方程组中各个方程的含义。
b. 证明电磁波的传播速度等于光速。
c. 分析一个实践问题,运用麦克斯韦方程组进行解答。
2. 答案:见附件。
八、课后反思及拓展延伸1. 反思:对本节课的教学过程进行反思,找出不足之处,进行改进。
2. 拓展延伸:鼓励学生阅读相关资料,深入了解电磁学的发展历程,提高学生的科学素养。
重点和难点解析1. 麦克斯韦方程组的推导和理解。
2. 电磁波的传播特性。
3. 教学过程中的实践情景引入、例题讲解和随堂练习。
第7章 导行电磁波前面我们讨论了电磁波在无界空间的传播以及电磁波对平面分界面的反射与透射现象。
在这一章中我们将讨论电磁波在有界空间的传播,即导波系统中的电磁波。
所谓导波系统是指引导电磁波沿一定方向传播的装置,被引导的电磁波称为导行波。
常见的导波系统有规则金属波导(如矩形波导、圆波导)、传输线(如平行双线、同轴线)和表面波波导(如微带线),图7.0.1给出了一些常见的导波系统。
导波系统中电磁波的传输问题属于电磁场边值问题,即在给定边界条件下解电磁波动方程,这时我们可以得到导波系统中的电磁场分布和电磁波的传播特性。
在这一章中,将用该方法讨论矩形波导、圆波导和同轴线中的电磁波传播问题以及谐振腔中的场分布及相关参数。
然而,当边界比较复杂时,用这种方法得到解析解就很困难,这时如果是双导体(或多导体)导波系统且传播的电磁波频率不太高,就可以引入分布参数,用“电路”中的电压和电流等效前面波导中的电场和磁场,这种方法称为“等效传输线”法。
这一章我们还将用该方法讨论平行双线和同轴线中波的传播特性。
7.1导行电磁波概论任意截面的均匀导波系统如图7.1.1所示。
为讨论简单又不失一般性,可作如下假设: (1)波导的横截面沿z 方向是均匀的,即导波内的电场和磁场分布只与坐标x ,y 有关,与坐标z 无关。
(2)构成波导壁的导体是理想导体,即σ=∞。
(3)波导内填充的媒质为理想介质,即0σ=,且各向同性。
(4)所讨论的区域内没有源分布,即0ρ=0=J 。
a 矩形波导b 圆柱形波导c 同轴线传输线d 双线传输线e 微带线图7.0.1 常见的几种导波系统(5)波导内的电磁场是时谐场,角频率为ω。
设波导中电磁波沿+z 方向传播,对于角频率为ω的时谐场,由假设条件(1)和(2)可将其电磁场量表示为()()()(),,,,,,,z z x y z x y e x y z x y e γγ--==E E H H (7.1.1)式中γ称为传播常数,表征导波系统中电磁场的传播特性。
一、判断题(请分别在正确或错误的命题前面括号中打“√”或“×”)第一章静电场的基本规律()1、等势面上任意两点之间移动电荷,电场力所做的功为零.()2、等势面上场强处处为零.()3、等势面上任意两点的电势是相等()4、电场线方向即为场强方向()5、若高斯面内没有自由电荷,则高斯面上各点的电场强度为零.()6、在静电场中,沿电场线方向,电势一定下降.()6、在静电场中,沿电场线方向,电势越来越低.()7、《电磁学》教材在静电场部分讲述了的二个叠加原理()8、《电磁学》教材在静电场部分只讲述了场强叠加原理和电势叠加原理.()9、在静电场中,电场线是实际存在的曲线.()10、任何电荷的相互作用都是通过电场来传递的.()11、只有静电场具有某种对称性时,才能用静电场的环路定理求解.()12、只有静电场具有某种对称性时,才能用静电场的高斯定理求解..()13、任何两条电场线都不可能相交.()14、静止电荷之间的的相互作用不需要任何媒介.()15、电场强度大的地方电势高,电势高的地方电场强度也一定大.第二章有导体时的静电场()1、处于外电场中的中性导体或带电导体,达静电平衡时,导体处处无电荷分布.()2、处于外电场中的带电导体,达静电平衡时,导体处处无电荷分布.()3、处于外电场中的带电导体,达静电平衡时,导体内部无电荷分布。
()4、凡接地导体其表面必处处无电荷.()5、空腔导体内的带电体在腔外产生的场强一定为零.()6、由于静电感应,在导体表面的不同区域出现异号电荷时,导体不再是等势体,导体表面也不是等势面.()7、空腔导体内的带电体在腔外产生的场强为零.()8、导体达到静电平衡时,导体内部场强处处为零,导体是等势体,导体表面是等势面.()9、处于外电场中的导体,达到静电平衡时,导体内部的场强和电势都处处为零.()10、孤立导体球接地后,表面电荷密度处处为零.第三章静电场中的电介质()1、极化电荷与自由电荷按同样规律激发电场.()2、极化电荷与自由电荷各以不同规律激发电场.( )3、由0S d q ⋅=⎰⎰D S 可知,电位移矢量D 仅与自由电荷有关.( )4、描述电介质极化程度的物理量有位移极化、取向极化、极化强度.( )5、极化强度是描述电介质极化程度的物理量.( )6、极化电荷体密度和极化电荷面密度均与极化强度有关.( )7、自由电荷可以迁移,而极化电荷不能迁移.第四章 恒定电流和电路( )1、不含源支路的电流必从高电势流向低电势.( )2、若一复杂电路共有n 个节点,则只有 (1-n )个节点方程是独立的.( )3、在任何电路中,电功等于焦耳热.( )4、电源内部非静电力起主导作用;在外电路中,没有非静电力.( )5、在恒定电流电路中,电源内部非静电力起主导作用,在外电路中电场力起主导作用. ( )6、在恒定电流电路中,电荷守恒定律不成立.( )7、在恒定电流电路中,非静电力总是存在于整个回路之中,即整个回路中的非静电力大小均不为零.( )8、电流连续性方程是电荷守恒定律的数学表述.( )9、电源的作用是将其他形式的能量转化为电能.( )10、在闭合电路中,外电路的电阻越大,电源输出的功率越大.( )11、支路电流为零时,该支路两端电压烽为零.第五章 恒定电流的磁场( )1、任意形状通电导线的磁场,磁感应线都是闭合曲线.( )2、电场线与磁感应线一样,都不是电场或磁场中实际存在的曲线.( )3、电场和磁场都是抽象的东西,不是客观存在的物质.( )4、电场和磁场都不是客观存在的物质.( )5、电场和磁场虽然看不见摸不着的,但是客观存在的物质.( )6、运动电荷在电磁场中所受的作用力称为洛伦兹力.载流导线在磁场中所受的作用力称为安培力.安培力是洛伦兹力的一种宏观表现.( )7、只有磁场具有某种对称性时,才能用安培环路定理来求解.( )8、磁场对置于其中的电荷都有磁力的作用.( )9、B 的高斯定理0S d ⋅=⎰⎰B S ,H 的环路定理0L d I ⋅=⎰H l ,B 与H 的关系μ=B H ,对非铁磁质和铁磁质均成立.第六章 电磁感应与暂态过程( )1、感应电动势包括动生电动势、感生电动势、自感电动势、互感电动势等.( )2、动生电动势与感生电动势有相同的非静电力.( )4、感应电流的磁通总是阻碍引起感应电流的磁通变化.( )5、感应电流的磁通总是与引起感应电流的磁通相同.( )6、感生电场与库仑电场一样,也是由电荷激发的.( )7、感生电场与库仑电场都是由电荷激发的.( )8、感生电场的电场线与库仑电场的电场线一样,都是从正电荷出发,终止于负电荷. ( )9、动生电动势的非静电力是洛伦兹力.( )10、当电流减小时,自感电动势方向与电流方向相反.( )11、自感电动势所反抗的是电流的变化,而不是电流本身.( )12、楞次定律不符合能量守恒定律.( )13、变压器和电机的铁心用互相绝缘的很薄的矽钢片叠压而成,是为了减小涡流、降低损耗. ( )12、日光灯的镇流器、变压器都是应用自感的例子.( )13、日光灯的镇流器、变压器都是互感器件.第七章 磁介质( )1、B 的高斯定理0S d ⋅=⎰⎰B S ,H 的环路定理0Ld I ⋅=⎰H l ,B 与H 的关系μ=B H ,对非铁磁质和铁磁质均成立.( )2、所有磁介质都具有抗磁性.( )3、所有磁介质都具有顺磁性.( )4、顺磁性存在于分子固有磁矩不为零的媒质.( )5、磁介质分为顺磁质、抗磁质和铁磁质.( )6、磁化强度是描述磁介质磁化程度的物理量.( )7、电介质中有极化电荷与自由电荷之分,磁介质中有磁化电流与传导电流之分. ( )8、铁磁质具有高μ值、非线性、磁滞的特点.第九章 时变电磁场和电磁波( )1、位移电流和传导电流都按相同的规律激发磁场,并都产生焦耳热.( )2、偶极振子辐射的电磁场,其近区场和远区场均具有波的性质.( )3、位移电流和传导电流激发的磁场的磁感应线都是闭合曲线.( )4、麦克斯韦由麦克斯韦方程组预言了电磁波的存在,并指出光波也是电磁波. ( )5、电磁波是麦克斯韦提出,赫兹通过实验证实的.( )6、位移电流实质就是变化的电场.综合( )1、电场线与磁感应线一样,都是用来形象地描述电场或磁场的曲线.( )1、电场线与磁感应线一样,都是电场或磁场中实际存在的曲线.( )2、任何磁的相互作用都是通过磁场来传递的;任何电的相互作用都是通过电场来传递的.二、填空题第一章 静电场的基本规律1、在一对等量异种电荷Q ±相距为r ,连线中点的电势为 (取无限远为参考点).把单位正点电荷从该中点沿任意路径移至无限远处,则电场力对该点电荷所做的功为 .2、在边长为a 的正方体中心放置一点电荷q ,则通过该正方体一个侧面的E 通量为 .3、《电磁学》在第一章中讲述了 个叠加原理,它们分别是 .4、在静电场中,电场力作功与路径 关,静电场是 场(填保守力或非保守力),故 引入势的概念.4、静电场是保守力场,电场力做功只取决于运动的 位置,与路径 关.5、半径为0.3m 的球面,带有正电C 6105.4-⨯,距球心0.5m 处的电场强度的大小为 ,电势为 .(计算结果保留π和0ε)6、静电场是由 激发的.静电场的三个叠加原理分别是 、 、 .7、在均匀电场中,有一半径为R 的半球面,电场强度E 与半球面的轴线平行(如图1所示),那么通过半球面的E 通量是 (取球面外法线为正).8、如图2所示,在封闭球面S 内A 点和B 点分别放置+ q 和- q 电荷,O 为球心,且A O = O B =a ,则O 点的场强0E = ,封闭球面S 的电通量d S ⋅⎰⎰E S = . 9、在静电场的基本规律中,库仑定律在MKSA 制中的表达式为 ,电场强度的定义式为 .10、电量分别为q 与q -的两个点电荷相距为d ,两点电荷连线中点处的电势为 (取图1 图 2无限远处电势为零),电场强度的大小 和方向 .第二章 有导体时的静电场1、真空中有一半径为R 、所带电荷量为Q 的导体球,则空间任一点的能量密度为2、一平行板电容器的电容为C ,将它接在电压为U 的电源上充电后断开电源,然后将两极板距离d 从拉到2d ,这时极板间场强的大小为 ,电势差等于 .3、带正电的导体A 右边放一个中性导体B ,则在B 的两端出现感应电荷.若将B 左端接地,流入地面的是 电荷;若将B 右端接地,流入地面的是 电荷.3、带负电的导体A 右边放一个中性导体B ,则在B 的两端出现感应电荷.若将B 左端接地,流入地面的是 电荷;若将B 右端接地,流入地面的是 电荷.4、一个孤立导体,当它带有电荷q 而电势为U 时,则定义该导体的电容为C = 。
第七章电磁感应变化电磁场思考题7-1感应电动势与感应电流哪一个更能反映电磁感应现象的本质?答:感应电动势。
7-2 直流电流表中线圈的框架是闭合的铝框架,为什么?灵敏电流计的线圈处于永磁体的磁场中,通入电流线圈就发生偏转。
切断电流后线圈在回复原来位置前总要来回摆动好多次。
这时如果用导线把线圈的两个接头短路,则摆动会马上停止。
这是什么缘故?答:用导线把线圈的两个接头短路,线圈中产生感应电流,因此线圈在磁场中受到一力偶矩的作用,阻碍线圈运动,使线圈很快停下来。
7-3让一块磁铁在一根很长的铅直铜管内落下,若不计空气阻力,试描述磁铁的运动情况,并说明理由。
答:当磁铁在金属管中时,金属管内感应感生电流,由楞次定律可知,感生电流的方向,总是使它所激发的磁场去阻止引起感应电流的原磁通量的变化,即:阻碍磁铁相对金属管的运动。
磁铁在金属管内除重力外,受到向上的磁力,向下的加速度减小,速度增大,相应磁力增大。
当磁力等于重力时,磁铁作匀速向下运动,达到动态平衡。
7-4用金属丝绕制的标准电阻是无自感的,怎样绕制才能达到自感系数为零的目的?答:如果回路周围不存在铁磁质,自感L的数值将与电流无关,仅由回路的几何性质、匝数以及周围磁介质的磁导率所决定。
把一条金属丝接成双线绕制,就能得到自感系数为零的线圈。
做纯电阻用的电阻器都是这样绕制的。
7-5 举例说明磁能是贮藏在磁场中的。
7-6如果电路中通有强电流,当你突然拉开闸刀断电时,就会有火花跳过闸刀。
试解释这一现象。
答:当突然拉开通有强电流电路中的刀闸而断电时,电路中电流迅速减小,电流的变化率很大,因而在电路中会产生很大的自感电动势。
此电动势可以把刀闸两端间的空气击穿,因而在刀闸处会有大的火花跳过。
7-7 变化的电场所产生的磁场,是否一定随时间而变化?变化的磁场所产生的电场,是否也一定随时间而变化?7-8 试比较传导电流与位移电流。
答:位移电流具有磁效应-与传导电流相同。
两者不同之处:产生机理不同,传导电流是电荷定向运动形成的,位移电流是变化的电场产生的;存在条件不同,传导电流需要导体,位移电流不需要导体,可以存在于真空中、导体中、介质中;位移电流没有热效应,传导电流产生焦耳热。
第7章 麦克斯韦方程组● 静止电荷和运动电荷都可以激发电场-库伦定律。
● 运动电荷还可以激发磁场-比萨定律。
● 变化的磁场可以激发电场-法拉第定律。
● 变化电场可以激发磁场-麦克斯韦假设。
7-1 安培环路定律与位移电流1. 对于恒定电流激发的恒定磁场,安培环路定律得到满足:I S d J l d H S l=⋅=⋅⎰⎰⎰111I S d J l d H S l=⋅=⋅⎰⎰⎰222曲面S曲面S2. 对于时变电流激发的时变磁场,安培环路定律出现矛盾I S d J l d H S l=⋅=⋅⎰⎰⎰1110222=⋅=⋅⎰⎰⎰S lS d J l d H3. 引入位移电流概念,对于时变电流激发的时变磁场,消除安培环 路定律出现的矛盾。
电流连续性定律:⎰⎰⎰⎰⎰∂∂-=⋅V SdV t S d J ρ ⎰⎰⎰⎰⎰⎰∂∂-=⋅+⋅-22122211S S S dS t S d J S d J σ⎰⎰⋅=111S S d J I0222=⋅⎰⎰S S d J⎰⎰⎰⎰⋅=3222S S dS D dSσ⎰⎰⎰⎰⎰⎰⋅∂∂=⋅∂∂=⋅=3312211S S S dS t DdS D t S d J I● 位移电流密度和位移电流定义:tD J D ∂∂=⎰⎰⎰⎰⋅∂∂=⋅=3222S S D D dS t DS d J I● 用位移电流表述电流连续性定律:I S d J dS t DS d J I S S S D D =⋅=⋅∂∂=⋅=⎰⎰⎰⎰⎰⎰1321122D S D S S I S d J dS t DS d J I =⋅=⋅∂∂=⋅=⎰⎰⎰⎰⎰⎰2312211● 无矛盾的安培环路定律I S d J l d H S l=⋅=⋅⎰⎰⎰111I I S d J l d H D S D l==⋅=⋅⎰⎰⎰224. 无论在恒定情况还是时变情况下安培环路定律都成立● 安培环路定律()()∑⎰⎰⎰+=⋅+=⋅D SD lI I S d J J l d H或⎰⎰⎰⎰⎰⋅∂∂+⋅=⋅SS l S d t D S d J l d H● 安培环路定律说明电流可以激发磁场,变化的电场也可以激发磁场。
7-2 麦克斯韦方程组1. 电荷和变化的磁场可以激发电场:● 电场的高斯定理:由库仑定律得到∑⎰⎰⎰⎰⎰==⋅q dV S d D VSρ● 电场的环路定理:由库仑定律和电磁感应定律得到⎰⎰⎰⋅∂∂-=⋅Sl S d t B l d E● 辅助方程:由电介质的极化效应得到P E D+=0ε2. 电流(运动电荷)和变化电场可以激发磁场:● 磁场的高斯定理:由毕萨定律得到0=⋅⎰⎰SS d B● 磁场的安培环路定理:由毕萨定律和麦克斯韦位移假设得到()∑⎰⎰⎰⎰⎰+=⋅∂∂+⋅=⋅D SS l I I S d t D S d J l d H● 辅助方程:由磁介质的磁化效应得到M H B00μμ+=3. 麦克斯韦方程组的积分形式:⎰⎰⎰⎰⎰=⋅VS dV S d D ρ⎰⎰⎰⋅∂∂-=⋅S l S d t B l d E0=⋅⎰⎰SS d B⎰⎰⎰⎰⎰⋅∂∂+⋅=⋅SS l S d t D S d J l d HPE D +=0ε MH B 00μμ+=4. 麦克斯韦方程组的微分形式:引入数学定律⎰⎰⎰⎰⎰⎰⎰⎰=⋅∇=⋅VVSdV dV D S d D ρ()⎰⎰⎰⎰⎰⋅∂∂-=⋅⨯∇=⋅SS l S d t B S d E l d E⎰⎰⎰⎰⎰⎰⎰⎰=⋅∇=⋅VVSdV dV B S d B 0()⎰⎰⎰⎰⎰⋅⎪⎪⎭⎫ ⎝⎛∂∂+=⋅⨯∇=⋅S S l S d t D J S d H l d HPE D+=0ε MH B 00μμ+=麦克斯韦方程组的微分形式ρ=⋅∇DtB E ∂∂-=⨯∇0=⋅∇BtD J H ∂∂+=⨯∇PE D +=0ε MH B 00μμ+=7-3 麦克斯韦方程组与电磁场的物质性1. 电磁场对电荷作用的力密度:单位体积的电荷所受的电磁场力[]B v E f ⨯+=ρ2. 电磁场的能量密度:单位体积中的电磁场能量22121c B H D E w m ρ=⋅+⋅=3. 电磁场的能流密度:单位时间内垂直流过单位面积的电磁场能量H E S ⨯=4. 电磁场的动量密度:单位体积中电磁场的能量5. 根据麦克斯韦方程组,可证明电磁场与电荷系统的能量守恒定律()⎰⎰⎰⎰⎰⎰⎰⎰∂∂-⋅-=⋅VSVwdV t S d S dV v ftwS v f ∂∂-⋅-∇=⋅ 0=∂∂+⋅∇+⋅tw S v f6. 电磁场的动量密度:单位体积中电磁场的动量2u S H E B D g=⨯=⨯=εμ,εμ1=u ,001με=c7. 电磁场的动量流密度:单位时间内垂直流过单位面积电磁场动量⎪⎭⎫ ⎝⎛⋅+⋅+--=B H D E IB H D E T 2121ˆˆ 8. 根据麦克斯韦方程组,可证明电磁场与电荷系统的动量守恒定律⎰⎰⎰⎰⎰⎰⎰⎰∂∂-⋅-=V SV dV g t S d T dV ft g T f ∂∂-⋅-∇= 0=∂∂+⋅∇+tgT f9. 根据麦克斯韦方程组,可以证明电荷守恒定律(电流连续性定律)t J ∂∂-=⋅∇ρ0=∂∂+⋅∇tJ ρ7-4 麦克斯韦方程组与电磁波1. 根据麦克斯韦方程组,可得空间中的电磁波动方程。
● 电磁波动方程012222=∂∂-∇E tu E012222=∂∂-∇B tu Brr cu μεεμ==1● 真空中的平面电磁波()r k t E E⋅-⋅=ωcos 0()r k t B B⋅-⋅=ωcos 0λπω2==ckk B E ˆˆˆ00=⨯ 0ˆˆ00=⋅B E cE B =● 赫兹通过实验证实了电磁波的存在,也就证明了麦克斯韦方程组的正确性,也就是麦克斯韦的位移电流假设是正确的。
2. 电磁场的势● 电磁场的标量势ϕ的矢量势AAt E ∂∂--∇=ϕ A B⨯∇=● 根据麦克斯韦方程组,可得标量势ϕ和矢量势A的波动方程 ✧ 库仑规范下的电磁势方程J tu A t u A μϕ-=∇∂∂-∂∂-∇2222211ερϕ-=∇2 库仑规范:0=⋅∇Arr cu μεεμ==1✧ 洛伦兹规范下的电磁势方程-达朗伯方程ερϕϕ-=∂∂-∇22221tuJ A tu Aμ-=∂∂-∇22221洛伦兹规范:012=∂∂+⋅∇ϕtu Arr cu μεεμ==17-5 电磁场的统一性和电场与磁场的相对性1. 坐标系K '相对坐标系K 以速度v 做匀速直线运动。
● 在坐标系K '中,时空为:t z y x '''',,,;电磁场为:B E '',.● 在坐标系K 中,时空为:t z y x ,,,;电磁场为:B E,.2. 麦克斯韦方程组具有不变性(遵循相对性原理):● 在坐标系K '中:ρ'='⋅∇'Dt B E '∂'∂-='⨯∇'0='⋅∇'Bt D J H '∂'∂+'='⨯∇'P E D '+'=' 0ε M H B '+'=' 00μμ● 在坐标系K 中:ρ=⋅∇Dt B E ∂∂-=⨯∇0=⋅∇Bt D J H ∂∂+=⨯∇PE D +=0ε MH B 00μμ+=3. 洛伦兹坐标变换()vt x x -='γy y ='z z ='⎪⎭⎫ ⎝⎛-='x c v t t 2γ()t v x x '+'=γy y '=z z '=⎪⎭⎫ ⎝⎛'-'=x c v t t 2γ211⎪⎭⎫ ⎝⎛-=c v γ4. 电磁场变换x xE E ='()z y y vB E E -='γ, ()y z zvB E E +='γx xB B ='⎪⎭⎫ ⎝⎛+='z y y E c v B B 2γ ⎪⎭⎫ ⎝⎛-='y z zE c v B B 2γxx E E '= ()z y y B v E E '+'=γ,()y z z B v E E '-'=γxx B B '= ⎪⎭⎫⎝⎛'-'=z y y E c v B B 2γ ⎪⎭⎫ ⎝⎛'+'=y z z E c v B B 2γ 5. 以速度v 在x 方向运动的点电荷的电磁场。
● 高速时()()[]23222204z y vt x vt x q E x ++--=γπεγ()[]23222204zy vt x qyE y ++-=γπεγ()[]23222204z y vt x qzE z ++-=γπεγ0=x Bz y E cv B 2-= y z E c v B 2=● 低速时()()[]2322204zy vt x vt x q E x ++--=πε()[]2322204z y vt x qyE y ++-=πε()[]2322204z y vt x qzE z ++-=πε0=x Bz y E cv B 2-= y z E c v B 2=或304r rqE πε=,库仑定律 3024r r qv E cv B ⨯=⨯=πμ,毕萨定律7-6 习题14-1,14-2,14-3,14-7。