下载文档原格式
第六章 一阶电路◆ 重点：1． 电路微分方程的建立 2． 三要素法 3．阶跃响应◆ 难点：1． 冲激函数与冲激响应的求取 2．有跃变时的动态电路分析 含有动态元件（电容或电感等储能元件）的电路称为动态电路。
回忆储能元件的伏安关系为导数（积分）关系，因此根据克希霍夫定律列写出的电路方程为微积分方程。
所谓“一阶”、“二阶”电路是指电路方程为一阶或二阶微分方程的电路。
本章只讨论一阶电路，其中涉及一些基本概念，为进一步学习第十五章打下基础。
6.1 求解动态电路的方法6.1.1 求解动态电路的基本步骤在介绍本章其他具体内容之前，我们首先给出求解动态电路的基本步骤。
1．分析电路情况，得出待求电量的初始值； 2．根据克希霍夫定律列写电路方程； 3．解微分方程，得出待求量。
由上述步骤可见，无论电路的阶数如何，初始值的求取、电路方程的列写和微分方程的求解是解决动态电路的关键。
6.2.1 一阶微分方程的求解一、一阶微分方程的解的分析初始条件为)()0()()(t f t t f δ=δ的非齐次线性微分方程Bw Ax dtdx=- 的解)(t x 由两部分组成：)()()(t x t x t x p h +=。
其中)(t x h 为原方程对应的齐次方程的通解，)(t x p 为非齐次方程的一个特解。
二、)(t x h 的求解由齐次方程的特征方程，求出特征根p ，直接写出齐次方程的解pt h Ke t x =)(，根据初始值解得其中的待定系数K ，即可得出其通解。
三、)(t x p 的求解根据输入函数的形式假定特解的形式，不同的输入函数特解形式如下表。
由这些形式的特解代入原微分方程使用待定系数法，确定出方程中的常数Q 等。
四、一阶微分方程的解的求取)()()()(t x Ke t x t x t x p ptp h +=+=将初始条件00)(X t x =代入该式：000)()(0X t x Ke t x p pt =+=由此可以确定常数K ，从而得出非齐次方程的解。
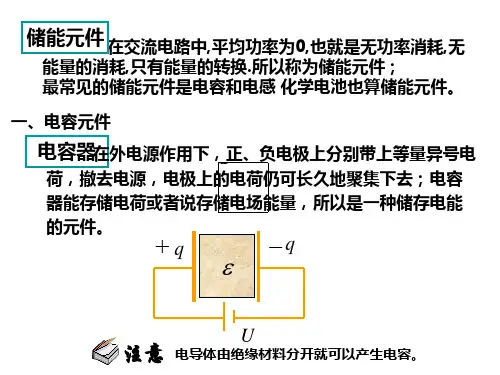
第六章储能元件一、线性电容元件(capacitor)C ＋_i u 1. 线性电容元件定义（库伏特性）+q-q q /Cu /V图5.1-1 线性时不变电容元件在外电源作用下，电容器两极板上分别带上等量异号电荷，撤去电源，板上电荷仍可长久地集聚下去，其特性可用u ～q 平面上的一条曲线来描述，称为库伏特性。
电荷量q 与其端电压的关系为)()(t Cu t q 电容器是一种能储存电荷或者说储存电场能量的部件。
线性电容元件就是反映这种物理现象的电路模型。
(5.1-1)式中C 是电容元件的参数，称为电容元件的电容量，单位为法拉(F)。
C 是一个正实常数。
电容元件简称为电容，其符号C 既表示元件的参数，也表示电容元件。
2. 伏安特性（VCR ，voltage current relation ）在电路分析中，关心的是元件的VCR 。
若电容端电压u 与通过的电流i 采用关联参考方向，如图5.1-1(a )所示，则有dt du C dt dq i ==（5.1-2）这是伏安特性的微分形式。
（1）伏安特性的微分形式：上式表明：1)任何时刻，通过电容元件的电流与该时刻的电压变化率成正比，与u的大小无关，称为动态元件。
如果电容两端加直流电压，则i=0，电容元件相当于开路。
故电容元件有隔断直流的作用。
2)在实际电路中，通过电容的电流i总是为有限值，这意味着d u/d t必须为有限值，也就是说，电容两端电压u必定是时间t的连续函数，而不能跃变。
这从数学上可以很好地理解，当函数的导数为有限值时，其函数必定连续。
将式(5.1-2)改写为dt t i Ct du )(1)(=可见，电容有“记忆”电流的作用，称为记忆元件。
（而电阻元件的电压仅与该瞬时的电流值有关，是无记忆元件，称为即时元件。
）（5.1-3)对上式从-∞到t 进行积分，并设u (-∞)=0，得1()()tu t i d C ξξ-∞=⎰（2）伏安特性的积分形式：设t 0为初始时刻。
