浙江大学2014年数学分析考研试题
- 格式:pdf
- 大小:302.90 KB
- 文档页数:2


2014年全国硕士研究生入学统一考试数学(二)试题及答案解析一、选择题:1~8小题,每小题4分,共32分。
下列每题给出的四个选项中,只有一个选项是符合题目要求的,请将所选项前的字母填在答题纸指定位置上。
(1)当x →0+时,若1ln (12),(1-cos )x x αα+均是比x 高阶的无穷小,则α的取值范围是( ) (A )),(∞+2 (B )(1,2) (C )),(121 (D ))(210, 【答案】B【解析】当x →0+时,∵()()ln12~2x x αα+,111211(1cos )~()()22x x ααα-=·2x α ,∴由2111 2.ααα>>⇔<<且(2)下列曲线有渐近线的是( )(A ).sin x x y += (B ).sin 2x x y +=(C ).1sin x x y += (D )21sin .y x x=+【答案】C【解析】1sin()11lim lim lim(1sin )1x x x x f x x a x x x x→∞→∞→∞+===+= 11lim[()]lim[sin ]lim sin 0x x x b f x ax x x x x→∞→∞→∞=-=+-==∴y=x 是y=x +1sin x的斜渐近线注:渐近线有3种:水平、垂直、斜渐近线。
本题中(A)(B)(D)都没有渐近线,(C)只有一条斜渐近线。
(3)设函数()f x 具有2阶导数,()()()()011g x f x f x =-+,则在区间[0,1]上( )(A)当0f x '≥()时,()()f x g x ≥.(B)当0f x '≥()时,()()f x g x ≤ (C)当0f ''≥时,()()f x g x ≥.(D)当0f ''≥时,()()f x g x ≤【答案】D【解析】方法1:(利用函数的凹凸性)当() 0f x "≥时,()f x 是凹函数,而()g x 是连接()()0,0f 与()1,1f ()的直线段,如右图 故()()f xg x ≤方法2:(利用函数的单调性)()()()h x g x f x =-令,则(0)(1)0h h ==,由洛尔定理知,(0,1)()0,h ξξ'∃∈=,使若()0f x ''≥,则()0,()h x h x '''≤单调递减, 当(0,)x ξ∈时,()()0h x h ξ''≥=,()h x 单调递增,()(0)0,g(x)()h x h f x ≥=≥即; 当(,1)x ξ∈时,()()0h x h ξ''≤=,()h x 单调递减,()(1)0,g(x)()h x h f x ≥=≥即;注:当0f x '≥()时,只能说明()f x 是单调增加的,但增加的方式可能是以凸的形式,也可能是以凹的形式,若是前者,则()()f x g x ≥,此时(A)成立,如()f x x =;若是后者,则()()f x g x ≤,此时(B)成立,如2()f x x =.(4)曲线⎪⎩⎪⎨⎧++=+=,t t y ,t x 14722上对应1t =的点处的曲率半径是( )(A ).5010 (B ).10010 (C ).1010 (D ).105 【答案】C【解析】令()27x t t ϕ==+ ()241y t t t ψ==++则2,()2t t t ϕϕ'''=()=; ()24t t ψ'=+ ()2t ψ"=当t =1时,(1)2,(1)2(1)6,(1)2ϕϕψψ''''''====则332222|2226|811010(26)40K ⨯-⨯===+,曲率半径11010.K ρ== (5)设函数()arctan f x x =,若)()(ξf x x f '=,则22limx xξ→=( )(A )1. (B ).32 (C ).21(D ).31【答案】D【解析】由()()arctan , f x x f x ==()xf ξ'得21arctan 1x x ξ=⋅+ ()3322222|||()()()()|1[()()]y t t t t K y t t ϕψϕψϕψ''''''''-=='''++2arctan arctan x x x ξ-=,222232000011arctan arctan 11lim lim lim lim arctan 33x x x x x x x xx x x x xx ξ→→→→---+∴==== (6)设函数()u x y ,在有界闭区域D 上连续,在D 的内部具有2阶连续偏导数,且满足0022222=∂∂+∂∂≠∂∂∂yux u y x u 及,则( ) (A )()u x y ,的最大值和最小值都在D 的边界上取得. (B )()u x y ,的最大值和最小值都在D 的内部取得.(C )()u x y ,的最大值在D 的内部取得,最小值在D 的边界上取得. (D )()u x y ,的最小值在D 的内部取得,最大值在D 的边界上取得. 【答案】A【解析】A=22u x ∂∂,B=2u x y∂∂∂,C=22u y ∂∂,22200 0B A C AC B A B ≠+=-=--<,,,∴D 内部无极值.(7)行列式=dc dc b a ba 00000000( )(A )2()ad bc - (B )2()ad bc --(C )2222a dbc - (D)2222b c a d -【答案】B【解析】41440000004(1)00(1)00000000a ba b a ba bc bd a c d c d c dc d++-+-按第行展开 32212(1)(1)()()()()()a b a b c b d a c dc dad bc bc ad ad bc ad bc bc ad ad bc ++=-⋅-+⋅⋅-=-⋅--=--=--注:此题按其它行或列展开计算都可以。




2014年浙江专升本(高等数学)真题试卷(题后含答案及解析) 题型有:1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.当x→x0时,若f(x)存在极限,g(x)不存在极限,则下列结论正确的是( )A.当x→x0时,f(x)g(x)必定存在极限B.当x→x0时,f(x)g(x)必定不存在极限C.当x→x0时,f(x)g(x)若存在极限,则此极限必为零D.当x→x0时,f(x)g(x)可能存在极限,也可能不存在极限正确答案:D解析:极限运算法则,可以举反例,若f(x)=x2,g(x)=lnx,则f(x)= x2=0,g(x)=lnx=-∞,但f(x).g(x)=x2lnx=0;若f(x)=2,g(x)=sin=2,不存在,但f(x).g(x)=不存在;可见选项D正确.2.曲线y=x3-3x上切线平行于x轴的点是( )A.(0,0)B.(1,2)C.(一1,2)D.(0,2)正确答案:C解析:由导数几何意义可知,k切=y′(x0)=3—3=0,所以切点坐标为(1,一2)或(一1,2),即选项C正确.3.函数f(x)=(x2—x一2)|x3一x|的不可导点个数是( )A.3B.2C.1D.0正确答案:B解析:导数定义,f′(0)=所以f′-(0)==2,f′+(0)==-2所以函数f(x)在x=0处不可导;同理,f′(1)=所以f′-(1)=一(x2一x—2)|x(x+1)|=4.f′+(1)=(x2一x—2)|x(x+1)|=-4,所以函数f(x)在x=1处不可导;f′(-1)==(x-2)|x3-x|=0,所以函数f(x)在x=-1处可导;综上可知,函数f(x)共有2个不可导点,选项B正确.4.若f(x=sin(t一x)dt,则f(x)= ( )A.-sinxB.-1+cosxC.sinxD.0正确答案:A解析:变限函数求导数,因为sin(t一x)dt sinudu,所以sin(t—x)dt=sinudu=0一sin(一x).(一1)=-sim,可见选项A正确.5.微分方程y′+的通解是( )A.arctanx+CB.(arctanx+C)C.arctanx+CD.+arctanx+C正确答案:B解析:一阶线性微分方程,由通解公式可得y=e-∫p(x)dx[∫Q(x).e∫p(x)dxdx+C]=.elnxdx+C]=(arctanx+C),可见选项B正确.填空题6.设f(x)在(-∞,+∞)上连续,且f(2)=3,则=___________.正确答案:9解析:利用连续性求极限,=3f(2)=9 7.设f(x)=,则f[f(x)]=___________.正确答案:解析:求复合函数的表达式,f[f(x)]=f[f(x)]=8.曲线y=xln(e+)(x>0)的渐近线方程是___________.正确答案:y=x+解析:计算斜渐近线,设直线y=ax+b为所求曲线的渐近线,则a==lne=1,b=所以,斜渐近线为y=x+.9.设y=ln,则y′|x=0=___________.正确答案:-1解析:求导函数,因为y=ln[ln(1一x)一ln(1+x)]所以y′=,故y′(0)=-1.10.曲线y=(x>0)的拐点是___________.正确答案:()解析:求曲线的拐点,当x>0时,y′=令y″=0,得x=,所以拐点为().11.由曲线y=x和y=x2所围成的平面图形的面积是___________.正确答案:解析:据题意画图,求所围平面图形的面积S=(x—x2)dx=(x2一12.将函数f(x)=sin2x展开成x的幂级数为___________.正确答案:,x∈(一∞,+∞)解析:麦克劳林展式,f(x)=sin2x=cos2x,又因cosx=x2n,x∈(一∞,+∞),所以cos2x=(2x)2n即f(x)=,x∈(一∞,+∞).13.设(a×b).c=1,则[(a+b)×(b+c)].(c+a)=___________.正确答案:2解析:混合积,向量积运算法则,在混合积计算中,如有两向量相同,则混合积为0.因此,[(a+b)×(b+c)].(c+a)=[a×(b+c)+b×(b+c)]=[a×b+a×c+b×b+b ×c].(c+a)=[a×b+a×c+b×c].(c+a)=(a×b).c+(a×b).a+(a×c).c+(a×c).a+(b×c).c+(b×c).a=(a×b).c-(b×c).a=2(a×b).c=214.微分方程(1+x)ydx+(1一y)xdy=0的通解为___________.正确答案:ln|xy|+x-y+C=0,C为任意常数解析:可分离变量的微分方程,(1+x)ydx+(1一y)xdx=0x+ln|x+C=y—ln|y|,即通解为y=x+ln|xy|+C,C为任意常数.15.设二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=C1ex+C1e2x,那么非齐次y″+ay′+by=1满足的条件y(0)=2,y′(0)=-1的解为___________.正确答案:y=4ex-解析:求二阶线性常系数非齐次方程的通解,特征方程为r2+ar+b=0,r1=1,r2=2即(r-1)(r-2)=0,r2-3r+2=0,故a=-3,b=2.所以原微分方程为y″一3y′+2y=1,由于λ=0不是特征方程的根,取k=0,因此,设特解y*=A,则(y*)′=0,(y*)″=0,代入可得A=,所以y*=,所以y″一3y′+2y=1的通解为y=C1ex+C2e2x+,再由y(0)=2,y′(0)=-1,可得C1=4,C2=,故满足初始条件的特解为y=4ex-解答题解答时应写出推理、演算步骤。

2014年考研数学(二)试题答案速查一、选择题(1)B (2)C (3)D (4)C (5)D (6)A (7)B (8)A 二、填空题(9)3π8 (10)1 (11)1(d d )2x y −+ (12)2ππ2y x =−+ (13)2011 (14)]2,2[−三、解答题 (15)21. (16)(1)1y =为极大值,(1)0y −=为极小值. (17)34−. (18)22111()e e 444u u y f u u −⎛⎫==−− ⎪⎝⎭.(19)略. (20)1. (21)5π2πln24−. (22)(Ⅰ)T(1,2,3,1)ξ=−.(Ⅱ)123123123123261123212134313k k k k k k k k k k k k −−−−⎛⎫⎪−+−++ ⎪=⎪−+−++⎪⎝⎭B ,123,,k k k 为任意常数.(23)略.2014年全国硕士研究生入学统一考试数学(二)参考答案一、选择题:1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项是符合题目要求的.请将所选项前的字母填在答题纸...指定位置上. (1)【答案】B.【解答】由定义02lim )2(lim )21(ln lim 1000===+−→→→ααααx xx x x x x x ,所以10,1αα−>>.当+→0x 时,ααα1212~)cos 1(x x −是比x 的高阶无穷小,所以210,2αα−><.故选择B.(2)【答案】C.【解答】C 选项,11sinsinlimlim1lim 1,x x x x x x a x x→∞→∞→∞+==+= 11lim[sin ]limsin 0x x b x x x x→∞→∞=+−==,所以x x y 1sin +=存在斜渐近线y x =,故选择C.(3)【答案】D.【解答】令)()1()1)(0()()()(x f x f x f x f x g x F −+−=−=,则0)1()0(==F F ,)()(),()1()0()(x f x F x f f f x F ''−='''−+−='.若()0,f x ''则()0,()F x F x ''在]1,0[上是凸的,又0)1()0(==F F ,故当]1,0[∈x 上时,()0F x ,从而()()g x f x ,故选择D.(4)【答案】C.【解答】22111122d 24d 3,1d 2d 2t t t t y t y t x t x t ====−+====−, 10101,)91(1)1(23232==+='+''=KR y y K ,故选择C. (5)【答案】D. 【解答】因,11)()(2ξξ+='=f x x f 所以)()(2x f x f x −=ξ,313111limarctan arctan lim )()(limlim220202022=+−=−=−=→→→→x x x x xx x f x x f x x x x x x ξ,故选择D. (6)【答案】A.【解答】记C A B yuC y x u B x u A ,,0,,,22222≠∂∂=∂∂∂=∂∂=互为相反数,故20AC B −<. 由于闭区域上连续函数必有极值,所以),(y x u 在D 内无极值,则极值在边界上取得.故选择A. (7)【答案】B.【解答】00000000a b abc d cd=0000000000000000c d c d a b a b c d d c a b b a −=2()c d d cad bc a b b a=⋅=−−. 故选择B.(8)【答案】A.【解答】132312310()(,,)01k ,l k l ⎛⎫⎪++= ⎪ ⎪⎝⎭ααααααα,记1323()k ,l =++A αααα,123(,,)=B ααα,1001k l ⎛⎫⎪= ⎪ ⎪⎝⎭C . 若123,,ααα线性无关,则()()()2r r r ===A BC C ,故1323k ,l ++αααα线性无关,所以13k +αα,23l +αα线性无关是向量组123,,ααα线性无关的必要条件;反之,未必成立,例如取3=α0,12,αα线性无关,虽然13k +αα,23l +αα线性无关,123,,ααα却线性相关,故选A.二、填空题:9~14小题,每小题4分,共24分.请将答案写在答题纸...指定位置上. (9)【答案】3π8. 【解答】1122111113πd d arctan 25(1)4228x x x x x x −∞−∞+===−∞++++⎰⎰. (10)【答案】1.【解答】由于]2,0[),1(2)(∈−='x x x f ,所以]2,0[,)1()(2∈+−=x C x x f ,又)(x f 为奇函数,故0)0(=f ,代入方程可得1−=C ,故]2,0[,1)1()(2∈−−=x x x f ,又)(x f 是周期为4的奇函数,则1)1()1()81()7(=−=−=+−=f f f f . (11)【答案】1(d d )2x y −+. 【解答】对方程两边同时对y x ,求偏导数得22e 210,e (22)20,yzyz z z y x x z z z y y y y ∂∂⎧⋅⋅++=⎪∂∂⎪⎨∂∂⎪+++=∂∂⎪⎩当21==y x 时,0=z ,故21,21)21,21()21,21(−=∂∂−=∂∂yz x z ,故11(,)221d (d d )2zx y =−+.(12)【答案】2ππ2y x =−+. 【解答】由直角坐标和极坐标的关系cos cos ,sin sin ,x r y r θθθθθθ==⎧⎨==⎩于是ππ(,)(,)22r θ=对应于π(,)(0,)2x y =,切线斜率d d cos sin d d d cos sin d yy x x θθθθθθθθ+==−, 所以π(0,)2d 2d πy x=−,从而切线方程为2ππ2y x =−+. (13)【答案】2011. 【解答】质心坐标为1010()d ()d x x x x x xρρ=⎰⎰,而11205()d (21)d 3x x x x x ρ=−++=⎰⎰,1120011()d (21)d 12x x x x x x x ρ=−++=⎰⎰,所以2011351211==x . (14)【答案】]2,2[−.【解答】3231222132142),,(x x x ax x x x x x f ++−==232232231)4()2()(x a x x ax x −+−−+,由于二次型的负惯性指数为1,故240a −,故22a −.三、解答题:15~23小题,共94分.解答应写出文字说明、证明过程或演算步骤.请将答案写在答题纸...指定位置上. (15)(本题满分10分)解:11221122(e 1)d (e 1)d limlim 11ln(1)xx t tx x t t t t t t x x x x→+∞→+∞⎡⎤⎡⎤−−−−⎢⎥⎢⎥⎣⎦⎣⎦=+⋅⎰⎰12201e 1lim [(e 1)]limt xx t t t x x x t +→+∞→=−−=−−00e 11lim lim 222t t t t t t ++→→−===.(16)(本题满分10分)解:由y y y x '−='+122得,221)1(x y y −='+ ① 此时方程为可分离变量,通解为C x x y y +−=+333131,由0)2(=y 得32=C ; 由①可得2211)(y x x y +−=',当0)(='x y 时,1±=x ,且有 0)(,1;0)(,11;0)(,1<'>>'<<−<'−<x y x x y x x y x ,所以)(x y 在1−=x 处取得极小值,在1=x 取得极大值,且1)1(,0)1(==−y y , 故)(x y 的极限值为0,极大值为1. (17)(本题满分10分)解:如图因为D 关于x y =对称,由轮换对称性质,则22sin(π)d d Dx x y x y x y ++⎰⎰22sin(π)d d D y x y x y x y +=+⎰⎰ 所以,22sin(π)d d Dx x y I x y x y +=+⎰⎰22()sin(π)1d d 2D x y x y x y x y++=+⎰⎰ yxO12221x y +=224x y +=221sin(π)d d 2D x y x y =+⎰⎰π220113d sin πd 24r r r θ=⋅=−⎰⎰.(18)(本题满分10分) 解:由(e cos )x z f y =可得(e cos )e cos ,(e cos )(e sin )x x x x z zf y y f y y x y∂∂''=⋅=⋅−∂∂, 22(e cos )e cos e cos (e cos )e cos x x x x xz f y y y f y y x ∂'''=⋅⋅+⋅∂,22(e cos )(e sin )(e sin )(e cos )(e cos )x x x x xz f y y y f y y y ∂'''=⋅−⋅−+⋅−∂.由22222(4e cos )e x xz z z y x y∂∂+=+∂∂,并把以上式子代入得 22(e cos )e[4(e cos )e cos ]e xxx x x f y f y y ''⋅=+,即 (e cos )4(e cos )e cos x x xf y f y y ''−=,令 e cos xu y =得 ()4()f u f u u ''−= ① 特征方程为 042=−λ,特征根为2λ=±,通解2212e e uu y C C −=+.设方程①的特解b au y +=*,代入方程 得1,04a b =−=,特解为*4u y =−, 则原方程的通解为22121()ee 4uu y f u C C u −==+−,由0)0(,0)0(='=f f 得1211,1616C C ==−,则方程为22111()e e 444u u y f u u −⎛⎫==−− ⎪⎝⎭.(19)(本题满分10分) 证:(Ⅰ)由积分中值定理()d ()(),[,]xag t t g x a a x ξξ=−∈⎰,因为0()1g x ,故0()(),0()d ()xag x a x a g t t x a ξ−−−⎰;(Ⅱ)()d ()()()d ()d ua ua g t t aaF u f x g x x f x x +⎰=−⎰⎰令,()()()(()d )()u aF u f u g u f a g t t g u '=−+⋅⎰()[()(()d )]uag u f u f a g t t =−+⎰,由(Ⅰ)知0()d (),()d uuaag t t u a a a g t t u −+⎰⎰,由于)(x f 单调增加,则()(()d )0uaf u f ag t t −+⎰,所以()0,()F u F u '单调不减,则()()0F u F a =, 取b u =得()0F b ,即所证结论成立.(20)(本题满分11分)解:因为12(),()112x xf x f x x x==++,3()13x f x x =+,…,由数学归纳法可得()1n xf x nx =+,所以1100()d d 1n n x S f x x x nx==+⎰⎰, 111000d 1()d d 11ln(1)11n n nx x nS n f x x x n nx nx n===−=−+++⎰⎰⎰,从而可知lim 1n n nS →∞=.(21)(本题满分11分) 解:因为)1(2+=∂∂y yf,所以)(),(2),(2x x y y y x f ϕϕ其中++=为待定函数. 又因为2(,)(1)(2)ln f y y y y y =+−−,则()(2)ln y y y ϕ=−−,从而x x y x x y y y x f ln )2()1(ln )2(12),(22−−+=−−++=,所以0),(=y x f 对应的方程为2(1)(2)ln ,(12)y x x x +=−, 其所围图形绕直线1−=y 旋转所成旋转体的体积为222221111π(1)d π(2)ln d π2ln d πln d V y x x x x x x x x x =+=−=−⎰⎰⎰⎰π352π(2ln 21)(4ln 2)(2ln 2)π224=−−−=−.(22)(本题满分11分)解:(Ⅰ)对矩阵A 作初等行变换,可得123410010111010212030013−−⎛⎫⎛⎫ ⎪ ⎪=−→− ⎪ ⎪ ⎪ ⎪−−⎝⎭⎝⎭A ,则方程组=Ax 0的一个基础解系为T)1,3,2,1(−=ξ. (Ⅱ)对矩阵()AE 作初等行变换,有12341001234100()0111010011101012030010431101−−−−⎛⎫⎛⎫⎪ ⎪=−→− ⎪ ⎪ ⎪ ⎪−−−⎝⎭⎝⎭A E123410010012610111010010213100131410013141−−−⎛⎫⎛⎫ ⎪ ⎪→−→−−− ⎪ ⎪ ⎪ ⎪−−−−−−⎝⎭⎝⎭. 记T3T 2T 1)1,0,0(,)0,1,0(,)0,0,1(===e e e ,则1e x A =的通解为T1111T1),31,21,2()0,1,1,2(k k k k ξk x +−+−−=−−+=, 2e x A =的通解为T2222T2),34,23,6()0,4,3,6(k k k k k x +−+−−=−−+=ξ, 3e x A =的通解为T3333T3),31,21,1()0,1,1,1(k k k k k x ++−−=−+=ξ,所以,123123123123261123212134313k k k k k k k k k k k k −−−−⎛⎫⎪−+−++ ⎪=⎪−+−++⎪⎝⎭B ,123,,k k k 为任意常数.(23)(本题满分11分)证:不妨设111111111⎛⎫ ⎪⎪= ⎪⎪⎝⎭A ,00100200B n ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭,则, ()()111...111...111...111 (1)..................11...111...1n n n λλλλλλλλλ−−−−−−−−−−−−==−=−−−−−−E A ,特征值为1210,n n n λλλλ−=====,()10...10 (2).........00...n n n λλλλλλ−−−−==−−E B ,特征值为1210,n n n λλλλ−=====,因为矩阵A 为对称阵,所以必可以对角化,相似于矩阵00n ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭Λ; 对于矩阵B ,当0λ=时,(0)()1r r −==E B B ,所以矩阵B 对应于特征值0有1n −个线性无关的特征向量,所以矩阵B 可以对角化为00n ⎛⎫⎪⎪= ⎪ ⎪⎝⎭Λ,所以二者相似.。

浙大数学分析考研真题浙大数学分析考研真题数学分析是数学的基础学科之一,也是考研数学科目中的重要部分。
浙江大学的数学分析考研真题一直备受考生关注。
本文将从历年的浙大数学分析考研真题中选取一些典型题目进行分析和讨论,以帮助考生更好地理解和应对这一科目。
第一道题目是2018年浙大数学分析考研真题中的一道选择题。
题目要求考生判断函数序列$f_n(x)=\frac{nx}{1+n^2x^2}$在区间$(0,1)$上的一致收敛性。
这是一个经典的一致收敛性问题,需要考生熟练掌握一致收敛的定义和判断方法。
通过计算函数序列的极限函数,可以发现该函数序列在区间$(0,1)$上一致收敛于零函数。
这道题目考查了考生对一致收敛的理解和运用能力。
接下来是2019年浙大数学分析考研真题中的一道计算题。
题目给出一个积分$\int_0^1\frac{x^3}{(1+x^2)^2}dx$,要求考生计算该积分的值。
这是一个典型的定积分计算题,需要考生熟练掌握定积分的计算方法和技巧。
通过变量代换或部分分式分解等方法,可以将该积分化简为简单的有理函数积分,最终得到积分的精确值。
这道题目考查了考生对定积分计算的掌握程度。
第三道题目是2020年浙大数学分析考研真题中的一道证明题。
题目要求考生证明函数$f(x)=\frac{x}{1+x}$在区间$(0,+\infty)$上是严格单调递增的。
这是一个典型的函数单调性证明题,需要考生运用导数的定义和性质进行证明。
通过计算函数的导数,可以得到导函数$f'(x)=\frac{1}{(1+x)^2}$,由导函数的正负性可以证明原函数在区间$(0,+\infty)$上是严格单调递增的。
这道题目考查了考生对函数单调性证明的能力。
最后是2021年浙大数学分析考研真题中的一道应用题。
题目给出一个函数$f(x)=\frac{1}{x}$,要求考生求出该函数在区间$(1,+\infty)$上的最小值。
这是一个典型的最值问题,需要考生熟练掌握最值的求解方法和技巧。
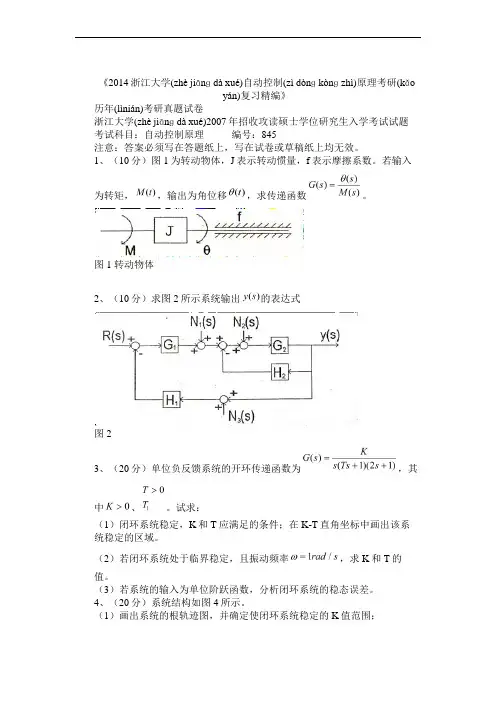
《2014浙江大学(zhè jiānɡ dà xué)自动控制(zì dònɡ kònɡ zhì)原理考研(kǎoyán)复习精编》历年(lìnián)考研真题试卷浙江大学(zhè jiānɡ dà xué)2007年招收攻读硕士学位研究生入学考试试题考试科目:自动控制原理编号:845注意:答案必须写在答题纸上,写在试卷或草稿纸上均无效。
1、(10分)图1为转动物体,J表示转动惯量,f表示摩擦系数。
若输入为转矩,,输出为角位移,求传递函数。
图1 转动物体2、(10分)求图2所示系统输出的表达式图23、(20分)单位负反馈系统的开环传递函数为,其中、。
试求:(1)闭环系统稳定,K和T应满足的条件;在K-T直角坐标中画出该系统稳定的区域。
(2)若闭环系统处于临界稳定,且振动频率,求K和T的值。
(3)若系统的输入为单位阶跃函数,分析闭环系统的稳态误差。
4、(20分)系统结构如图4所示。
(1)画出系统的根轨迹图,并确定使闭环系统稳定的K值范围;(2)若已知闭环系统的一个极点为,试确定闭环传递函数。
图45、(10分)系统(xìtǒng)动态方框图及开环对数频率特性见图5,求、、、的值。
图56、(10分)已知单位(dānwèi)负反馈系统开环频率特性的极坐标如图6所示,图示曲线(qūxiàn)的开环放大倍数K=500,右半s平面(píngmiàn)内的开环极点P=0,试求:(1)图示系统是否(shì fǒu)稳定,为什么?(2)确定使系统稳定的K值范围。
图67、(10分)是非题(若你认为正确,则在题号后打√,否则打×,每题1分)(1)经过状态反馈后的系统,其能控能观性均不发生改变。
()(2)若一个可观的n维动态系统其输出矩阵的秩为m,则可设计m维的降维观测器。

2014年全国硕士研究生入学统一考试数学二试题一、选择题:1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合 题目要求的,请将所选项前的字母填在答题纸...指定位置上. 1、当0x +→时,若ln (12)x α+,1(1cos )x α-均是比x 高阶的无穷小,则α的取值范围是( )(A )(2,)+∞ (B )(1,2) (C )1(,1)2 (D )1(0,)2【答案】B【考点】等价无穷小、高阶无穷小 【详解】当0x +→时,ln (12)~(2)x x αα+,1121(1cos )~2x x αα⎛⎫-⎪⎝⎭因为它们都是比x 高阶的无穷小,故12,1>>αα,即21<<α2、下列曲线中有渐近线的是( )(A )sin y x x =+ (B )2sin y x x =+ (C )1sin y x x =+ (D )21sin y x x=+ 【答案】C【考点】函数的渐近线 【详解】对于选项A , lim(sin )x x x →∞+ 不存在,因此没有水平渐近线,同理可知,选项A 没有铅直渐近线, 而sinxlimlimx x y x x x→∞→∞+=不存在,因此选项A 中的函数没有斜渐近线; 对于选项B 和D ,我们同理可知,对应的函数没有渐近线;对于C 选项,1siny x x=+.由于1sin lim lim1x x x yx x x→∞→∞+==,又()1lim 1limsin0x x y x x →∞→∞-⋅==.所以1sin y x x=+存在斜渐近线y x =.故选C.(4)设函数()f x 具有2阶导数,()(0)(1)(1)g x f x f x =-+,则在区间[0,1]内( ) (A )当()0f x '≥时,()()f x g x ≥ (B )当()0f x '≥时,()()f x g x ≤ (C )当()0f x ''≥时,()()f x g x ≥ (D )当()0f x ''≥时,()()f x g x ≤ 【答案】D【考点】函数单调性的判别、函数图形的凹凸性 【详解】 【解法一】令)()()(x f x g x F -=则)()1()0()(x f f f x F '-+-='由拉格朗日中值定理知,存在)1,0(∈ξ,使得)()()01()0()1(ξξf f f f '='-=- 即0)(='ξF又因为)()(x f x F ''-=''若()0f x ''≥,则()0F x ''≤,所以)(x F '单调递减, 当(0,),()0,()x F x F x ξ'∈>单调递增, 当(,1),()0,()x F x F x ξ'∈<单调递减,又0)1(.0)0(==F F ,所以()0F x ≥,即()()f x g x ≤,故选D 【解法二】令2()f x x =,则函数()f x 具有2阶导数,且()0f x ''≥所以()(0)(1)(1)g x f x f x x =-+= 当]1,0[∈x 时,()()f x g x ≤,故选D4、曲线227,41x t y t t ⎧=+⎪⎨=++⎪⎩上对应于1t =的点处的曲率半径是( ) (A(B(C)(D)【答案】C【考点】参数方程求导、曲率及曲率半径 【详解】2223212133222233222242222(24)8(2)2(2)3,1"1(1')(13)1(13)10t t dy dy t dt dx dx tdtt t d y t dx t t dy d y dx dx y k y R k==+==⋅-+-==∴==-∴==++∴==+==Q5、设函数()arctan f x x =,若()()f x xf ξ'=,则22limx x ξ→=( )(A )1 (B )23 (C )12(D )13【答案】D【考点】函数求导、函数求极限 【详解】2()arctan 11f x x x x ξ==+Q.2arctan arctan x xx ξ-∴=.22230arctan arctan limlimlim rctan x x x x x x xx x a x x ξ→→→--∴==⋅22222001111limlim 33(1)3x x x x x x x →→-+===+. 6、设函数(,)u x y 在有界闭区域D 上连续,在D 的内部具有2阶连续偏导数,且满足20ux y ∂≠∂∂及22220u ux y ∂∂+=∂∂,则( ) (A )(,)u x y 的最大值和最小值都在D 的边界上取得 (B )(,)u x y 的最大值和最小值都在D 的内部取得(C )(,)u x y 的最大值在D 的内部取得,(,)u x y 的最小值在D 的边界上取得 (D )(,)u x y 的最小值在D 的内部取得,(,)u x y 的最大值在D 的边界上取得 【答案】A【考点】二元函数极值的充分条件 【详解】因为22220u u x y ∂∂+=∂∂,故22u A x ∂=∂与22uC y∂=∂异号.又20u B x y ∂=≠∂∂, 则20AC B -<,所以函数(,)u x y 在区域D 内没有极值.又连续函数在有界闭区域内有最大值和最小值,故最大值和最小值在D 的边界点取到.7、行列式0000000ab a bcd c d=( )(A )2()ad bc - (B )2()ad bc --(C )2222a d b c - (D )2222b c a d - 【答案】B【考点】分块矩阵的行列式运算、行列式的性质、行列式按行(列)展开定理 【详解】 【解法一】132320000000000000000000000()()()a b b a b a a b a b d c c c r r c dd c a b c dc dc db a a b bc ad ad bc ad bc d c c d↔-↔=⋅=--=--故选B 【解法二】2141332320a 0000000(1)0(1)00000(1)(1)()()b a b c d c d a ba ba c dc bd c d a b a ba d cbcd c da b a b adbc c d c da b bc ad c d ad bc ++++=⨯-+⨯-=-⨯⨯--⨯⨯-=-+=-=--8、设123,,ααα为3维向量,则对任意常数,k l ,向量组1323,k l αααα++线性无关是向量组123,,ααα线性无关的( )(A )必要非充分条件 (B )充分非必要条件 (C )充分必要条件(D )既非充分也非必要条件 【答案】A【考点】向量组的线性相关性 【详解】1231132231122123121213231323123123+k )()0++k )00+k ++k +100=0=1=0000l l k l l l αααλααλααλαλαλλαλλλλαααααααααααααα++=+=⇒==+=⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭已知,,无关设(即(从而,无关反之,若,无关,不一定有,,无关例如,,,二、填空题:9~14小题,每小题4分,共24分.请将答案写在答题纸...指定位置上. 9、12125dx x x -∞=++⎰ .【答案】π83【考点】无穷限的反常积分 【详解】()11221211125141111221()21113arctan |[()]222428dx dx x x x xd x x πππ-∞-∞-∞-∞=+++++=+++==--=⎰⎰⎰ 10、设)(x f 是周期为4的可导奇函数,且]2,0[),1(2)(∈-='x x x f ,则=)7(f【答案】1【考点】一阶微分方程、周期函数【详解】()22'2(1)[0,2]()2()(0)00()2[0,2]()4(7)(3)(1)(1)(12)1f x x x f x x x c f x f c f x x x x f x f f f f =-∈∴=-+∴=∴=∴=-∈∴==-=-=--=Q 又是奇函数的周期为11、设(,)z z x y =是由方程22274yzex y z +++=确定的函数,则11(,)22dz = . 【答案】)(21dy dx +-【考点】隐函数求偏导、全微分 【详解】221111(,)(,)222211(,)2211,022,(2)20(22)2011,221()2yzyz x y z x y z z e y x x x z z e z y y y y z z x y dz dx dy ===∂∂⎧⋅++=⎪∂∂⎪⎨∂∂⎪+++=∂∂⎪⎩∂∂=-=-∂∂=-+当时,代入方程解得方程两边对分别求偏导得,解得:故12、曲线L 的极坐标方程是r θ=,则L 在点(,)(,)22r ππθ=处的切线的直角坐标方程是 . 【答案】22ππ+-=x y【考点】参数方程求导、极坐标与直角坐标的转化、切线方程 【详解】把极坐标方程化为直角坐标方程令cos cos sin sin x r y r θθθθθθ==⎧⎨==⎩2sin cos cos sin 1022012cos 02sin 22()(0)222dy dy d dx dx d dy dxx y y x y x πθθθθθθθθθπππθθπθπθθππππ=+==-+⋅==--⋅==⎧⎪=⎨==⎪⎩-=--=-+则当时,则切线方程为:化简为: 13、一根长为1的细棒位于x 轴的区间[0,1]上,若其线密度2()21x x x ρ=-++,则该细棒的质心坐标x = . 【答案】2011 【考点】质心坐标 【详解】质心横坐标公式:⎰⎰=b aba dxx dx x x x )()(ρρ 所以:43212123201121()(21)4320111201(21)()30x x x x x x dx x x x dx x x x -++-++===-++-++⎰⎰14、设二次型22123121323(,,)24f x x x x x ax x x x =-++的负惯性指数为1,则a 的取值范围是 .【答案】]2,2[-【考点】二次型的规范形、矩阵的特征值、配方法化二次型为标准形 【详解】 【解法一】二次型对应的系数矩阵为:O a a ≠⎪⎪⎪⎭⎫ ⎝⎛-0221001,记特征值为321,,λλλ则0011)(321=+-==++A tr λλλ,即特征值必有正有负,共3种情况; 因二次型的负惯性指数为⇔1特征值1负2正或1负1正1零;0402210012≤+-=-⇔a aa ,即]2,2[-∈a【解法二】221231213232222221133223322221323322221232(,,)2424()(2)(4)(4)140[2,2]f x x x x x ax x x x x ax x a x x x x a x x ax x x a x y y a y a a =-++=++-+-=+--+-=-+--≥∈-若负惯性指数为,则,三、解答题:15~23小题,共94分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤. 15、(本题满分10分)求极限1212[(1)]lim1ln(1)xtx t e t dt x x→+∞--+⎰【考点】函数求极限、变限积分函数求导、等价无穷小、洛必达法则 【详解】111221221122200((1))((1))(1)1limlimlim lim (1)111ln(1)1111lim lim 22xxttxx x x x x t t t t t e t dtt e t dtx e x x e xx x x xe t e t x t t ++→+∞→+∞→+∞→+∞→→------===--+⋅---===⎰⎰令16、(本题满分10分)已知函数()y y x =满足微分方程221x y y y ''+=-,且(2)0y =,求()y x 的极大值与极小值.【考点】微分方程、函数的极值 【详解】22222222333322'1'1'1(1)(1),(1)(1)11332(2)031123331'0,11(,1),'0,(11),'0,(1+),'0,x y y y x y y y dy x dx y dy x dx y y x x c y c y y x x x y x y x y x y x y +=--∴=+∴+=-+=-∴+=-+=∴=∴+=-+-===±+∈-∞-<∈->∈∞<⎰⎰Q 积分得又 令得时函数单调递减,时函数单调递增,时函数单调递减所以函11(1)0,(1)1()1,0x x y y y x =-=-==数在时取得极小值,在时取得极大值由函数方程解得:故:的极大值是极小值是17、(本题满分10分)设平面区域{}22(,)14,0,0D x y x y x y =≤+≤≥≥,计算D.【考点】二重积分的计算、轮换对称性 【详解】积分区域D 关于y x =对称,利用轮对称行,121sin(2D D D Ddxdy ==+=⎰⎰222011221111sin()d cos()2411cos()|cos()d 44113244d r r r rd r r r r r πθππππ==-=-+=--=-⎰⎰⎰⎰18、(本题满分10分)设函数()f u 具有2阶连续导数,(cos )xz f e y =满足22222(4cos )x x z z z e y e x y∂∂+=+∂∂.若(0)0f =,(0)0f '=,求()f u 的表达式.【考点】多元函数求偏导、二阶常系数非齐次线性微分方程【详解】 令y e u xcos =xx x xx x x xx x xe u uf y e u f y e u f e y e z yzx z y e u f y e u f y z y e u f y z y e u f y e u f x z y e u f x z 222222222222222222])(4[sin )(cos )()cos 4(cos )(sin )(),sin ()(cos )(cos )(,cos )(+=⋅''+⋅''∴+=∂∂+∂∂⋅'-⋅''=∂∂-⋅'=∂∂⋅'+⋅''=∂∂⋅'=∂∂∴Θ 即:u u f u f =-'')(4)(对应的齐次微分方程的特征方程为:042=-r 解得:2,221-==r r故齐次微分方程的通解为:u u e C e C u f 2221)(-+=设b au u f +=)(*,则0)(,)(**="='u f a u f ,代入微分方程解得:0,41=-=b a ,即u u f 41)(*-= 故u e C e C u f xx 41)(2221-+=-所以uu u u e C e C u f e C e C u f 2221222144)(,4122)(--+=''--='因为(0)0f =,(0)0f '=,代入解得:161,16121-==C C所以22111()16164x x f u e e u -=--19、(本题满分10分)设函数()f x ,()g x 在区间[,]a b 上连续,且()f x 单调增加,0()1g x ≤≤. 证明:(Ⅰ)(I )a x dt t g xa-≤≤⎰)(0,],[b a x ∈;(II )⎰⎰⎰≤+badtt g a abadx x g x f dx x f )()()()(【考点】定积分中值定理、不等式的证明 【详解】(I )【解法一】因为函数)(x g 在区间],[b a 上连续,且1)(0≤≤x g . 所以⎰⎰⎰≤≤xax axadt dt t g dt 1)(0即a x dt t g x a-≤≤⎰)(0【解法二】由定积分中值定理知:存在),(b a ∈ξ,使得)()()(ξg a x dt t g xa-=⎰,又因为],[b a x ∈时1)(0≤≤x g , 所以)()()(0a x g a x -≤-≤ξ 即a x dt t g xa-≤≤⎰)(0【解法三】[][]11111222222()()()0'()()0(),()0()()'()()10()1'()0()()0,()0xaxa h x g t dth a h x g x h x x a b h x h x g t dt x ah x g x g x h x h x h a x a b h x ===≥∴∴∈≥=-+=-≤≤∴≤∴=∴∈≤⎰⎰Q 单调增加当时,单调减少,又当时,(II )令()()()()()xa xa g t dt aaF x f u g u du f u du +⎰=-⎰⎰()'()()()[()]()()[()]()I (),()()[()]'()0()0()0()()()ba xxaa x axa ba g t dt a aF x f x g x f a g t dt g x f x f a g t dt g x a g t dt a x a x f x f x f a g t dt F x F x F a F b f x g x dx f x dx+⎡⎤∴=-+⋅=-+⎢⎥⎣⎦+≤+-=∴≥+∴≥∴=∴≥⎰≥⎰⎰⎰⎰⎰⎰由()知又单调增加单调增加又()即20、(本题满分11分) 设函数()1xf x x=+,[0,1]x ∈.定义数列 1()()f x f x =,21()(())f x f f x =,L ,1()(())n n f x f f x -=,L记n S 是由曲线()n y f x =,直线1x =及x 轴所围平面图形的面积,求极限lim n n nS →∞.【考点】定积分求面积、函数求极限 【详解】1213222(),()()11()(())121112()(())13112(),[0,1]111()0(1)(1)()(0)=0()0[0,1]n n n n n xf x f x f x xxxx f x f f x x x x xxx f x f f x x x x xf x x nxnx nx f x nx nx f x f f x x ==++∴===++++∴===+++=∈++-'==>++∴∴≥∈Q Q Q 由归纳法知:单调递增,,1120021111=(1)=ln(1)1111ln(1)lim lim [ln(1)]1lim ln(1)11lim 1lim 11n n n n n x x x S dx dx n nx n nx n nn nS n n n n nx xx →∞→∞→∞→∞→∞∴=--++++=-+=-+=-=-=+⎰⎰21、(本题满分11分) 已知函数(,)f x y 满足2(1)fy y∂=+∂,且2(,)(1)(2)ln f y y y y y =+--.求曲线(,)0f x y =所围图形绕直线1y =-旋转所成旋转体的体积. 【考点】偏积分、隐函数、旋转体的体积 【详解】由函数(,)f x y 满足2(1)fy y∂=+∂可知:)(2),(2x y y y x f ϕ++= 又22(,)2()(1)(2)ln f y y y y y y y y ϕ=++=+-- 所以()1(2)ln y y y ϕ=--所以x x y x x y y x y y y x f ln )2()1(ln )2(12)(2),(222--+=--++=++=ϕ 令1+=y z ,则(,)0f x y =对应的曲线方程为:x x z ln )2(2-=,定义域为]2,1[则曲线(,)0f x y =所围图形绕直线1y =-旋转,即x x z ln )2(2-=绕0=z 旋转,所成的旋转体体积πππππ)452ln 2()412(ln )212()212(ln ln )2(212221221212-=⎥⎦⎤⎢⎣⎡---=-=-==⎰⎰⎰x x x x x x x xd xdxx dx z V x22、(本题满分11分)设E A ,302111104321⎪⎪⎪⎭⎫⎝⎛----=为3阶单位矩阵.(I )求方程组0=Ax 的一个基础解系; (II )求满足E AB =的所有矩阵B . 【考点】解线性方程组 【详解】1234100()011101012030011205412301021310013141100126101021310013141A E --⎛⎫ ⎪=- ⎪⎪-⎝⎭--⎛⎫ ⎪→--- ⎪ ⎪--⎝⎭-⎛⎫ ⎪→--- ⎪ ⎪---⎝⎭M M M M M M M M M M (I ) 方程组0=Ax 的同解方程组为⎪⎪⎩⎪⎪⎨⎧===-=4443424132x x x x xx x x ,即基础解系为⎪⎪⎪⎪⎪⎭⎫⎝⎛-1321(II )⎪⎪⎪⎭⎫ ⎝⎛=001Ax 的同解方程组为:⎪⎪⎩⎪⎪⎨⎧+=-=-=+-=01312244434241x x x x x x x x ,即通解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-011213211k⎪⎪⎪⎭⎫ ⎝⎛=010Ax 的同解方程组为:⎪⎪⎩⎪⎪⎨⎧+=-=-=+-=04332644434241x x x x x x x x ,即通解为⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-043613212k⎪⎪⎪⎭⎫ ⎝⎛=100Ax 的同解方程组为:⎪⎪⎩⎪⎪⎨⎧+=+=+=--=01312144434241x x x x x x x x ,即通解为⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-011113213k ,123123123123261212321313431k k k k k k B k k k k k k -+-+--⎛⎫⎪--+ ⎪∴= ⎪--+ ⎪⎝⎭,321,,k k k 为任意常数23、(本题满分11分)证明:n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111ΛM O M M ΛΛ与⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100ΛM M M ΛΛ相似. 【考点】矩阵的特征值、相似对角化 【详解】设⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦L L L L L L L111111111A ,⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦L L L L L L L L0001000200n B 因为1)(,1)(==B r A r所以A 的特征值为:n A tr n n ======-)(,0121λλλλΛB 的特征值为:n B tr n n =='='=='='-)(,0121λλλλΛ 关于A 的特征值0,因为1)()()0(==-=-A r A r A E r ,故有1-n 个线性无关的特征向量,即A 必可相似对角化于⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00O同理,关于B 的特征值0,因为1)()()0(==-=-B r B r B E r ,故有1-n 个线性无关的特征向量,即B 必可相似对角化于⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00O由相似矩阵的传递性可知,A 与B 相似.。
2014考研数学一真题及答案详解2014年全国硕士研究生入学考试数学一真题及答案详解Part A1. 设f(x) = sinx + cosx (0 ≤ x ≤ π),则f '(x) = _____解析:f(x) = sinx + cosx,则f '(x) = cosx - sinx 当x ∈ [0, π]时,cosx ≥ 0 且sinx ≥ 0,所以f '(x) = cosx - sinx ≥ 0答案:cosx - sinx2. 已知函数f(x) = sinx + cosx,定义在[0, π]上,则f(x)在[0, π]上的最大值为____,最小值为____。
解析:f(x)在[0, π]上的最大值和最小值分别为f(π/4)和f(π/4 + π)。
f(π/4) = sin(π/4) + cos(π/4) = √2f(π/4 + π) = sin(π/4 + π) + cos(π/4 + π) = -√2答案:最大值为√2,最小值为-√23. 设向量a = 2i - 3j + k,b = i + j + 2k,则向量a与向量b的夹角为____°。
解析:向量a与向量b的夹角cosθ为cosθ = (a·b)/(|a||b|) = (2 - 3 + 2)/(√4 + 9 + 1)√6 = 1/√6故θ = arccos(1/√6)答案:θ ≈ 32.5°4. 已知向量a,b,其大小分别为3和4,且它们的夹角为60°。
则向量a + b的大小为____。
解析:根据余弦定理,a + b的大小为|a + b|² = |a|² + |b|² + 2|a||b|cosθ = 9 + 16 + 2×3×4×1/2 = 25故|a + b| = √25 = 5答案:55. 设函数y = f(x)在点x = a处可导,且f '(a) > 0,则以下哪个极限一定存在?()(A) lim[x→a]f(x)/x(B) lim[x→a]f(x)(C) lim[x→a](f(x))^2(D) lim[x→a]f(x) - f(a)解析:由可导性可知,右导数和左导数存在且相等,则有lim[x→a]f(x)/x = lim[x→a](f(x) - f(a))/(x -a)×(x - a)/x = f '(a)×1 = f '(a)lim[x→a]f(x) = f(a)lim[x→a](f(x))^2 = (lim[x→a]f(x))² = (f(a))²lim[x→a]f(x) - f(a) = lim[x→a](f(x) - f(a)) = f '(a)×(a - a) = 0故正确选项为:(A) lim[x→a]f(x)/x答案:(A)6. 设函数y = x³ + px + q,则当p = 0 时,y = x³+ q有两个零点,一个为0,另一个为____。
2014年全国硕士研究生入学统一考试数学二试题一、选择题:1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合 题目要求的,请将所选项前的字母填在答题纸...指定位置上. 1、当0x +→时,若ln (12)x α+,1(1cos )x α-均是比x 高阶的无穷小,则α的取值范围是( )(A )(2,)+∞ (B )(1,2) (C )1(,1)2 (D )1(0,)2【答案】B【考点】等价无穷小、高阶无穷小 【详解】当0x +→时,ln (12)~(2)x x αα+,1121(1cos )~2x x αα⎛⎫-⎪⎝⎭因为它们都是比x 高阶的无穷小,故12,1>>αα,即21<<α2、下列曲线中有渐近线的是( )(A )sin y x x =+ (B )2sin y x x =+ (C )1sin y x x =+ (D )21sin y x x=+ 【答案】C【考点】函数的渐近线 【详解】 关于C 选项:()1sinlimlim 11lim limsin 01sin x x x x x yx k x x y x xy x y xx→∞→∞→∞→∞+===-==∴=+=存在斜渐近线 3、设函数()f x 具有2阶导数,()(0)(1)(1)g x f x f x =-+,则在区间[0,1]内( ) (A )当()0f x '≥时,()()f x g x ≥(B )当()0f x '≥时,()()f x g x ≤ (C )当()0f x ''≤时,()()f x g x ≥ (D )当()0f x ''≤时,()()f x g x ≤ 【答案】C【考点】函数单调性的判别 【详解】 【解法一】令)()()(x f x g x F -=则)()1()0()(x f f f x F '-+-='由拉格朗日中值定理知,存在)1,0(∈ξ,使得)()()01()0()1(ξξf f f f '='-=- 即0)(='ξF又因为)()(x f x F ''-=''若0)(≤''x f ,则0)(≥''x F ,所以)(x F '单调递增, 当)(,0)(),,0(x F x F x <'∈ξ单调递减, 当)(,0)(),1,(x F x F x >'∈ξ单调递增,又0)1(.0)0(==F F ,所以0)(≤x F ,即()()f x g x ≥,故选C 【解法二】令2)(x x f -=,则函数()f x 具有2阶导数,且0)(≤''x f 所以()(0)(1)(1)g x f x f x x =-+=- 当]1,0[∈x 时,()()f x g x ≥,故选C4、曲线227,41x t y t t ⎧=+⎪⎨=++⎪⎩上对应于1t =的点处的曲率半径是( ) (A(B(C)(D)【答案】C【考点】参数方程求导、曲率及曲率半径 【详解】2223212133222233222242222(24)8(2)2(2)3,1"1(1')(13)1(13)10t t dy dy t dt dx dx tdtt t d y t dx t t dy d y dx dx y k y R k==+==⋅-+-==∴==-∴==++∴==+==Q5、设函数()arctan f x x =,若()()f x xf ξ'=,则22limx xξ→=( )(A )1 (B )23 (C )12(D )13【答案】D【考点】函数求导、函数求极限 【详解】2()arctan 11f x x x x ξ==+Q. 2arctan arctan x xx ξ-∴=.22230arctan arctan limlimlim rctan x x x x x x xx x a x x ξ→→→--∴==⋅22222001111limlim 33(1)3x x x x x x x →→-+===+. 6、设函数(,)u x y 在有界闭区域D 上连续,在D 的内部具有2阶连续偏导数,且满足20ux y ∂≠∂∂及22220u ux y ∂∂+=∂∂,则( ) (A )(,)u x y 的最大值和最小值都在D 的边界上取得 (B )(,)u x y 的最大值和最小值都在D 的内部取得(C )(,)u x y 的最大值在D 的内部取得,(,)u x y 的最小值在D 的边界上取得 (D )(,)u x y 的最小值在D 的内部取得,(,)u x y 的最大值在D 的边界上取得 【答案】A【考点】二元函数极值的充分条件 【详解】因为22220u u x y ∂∂+=∂∂,故22u A x ∂=∂与22uC y∂=∂异号.又20u B x y ∂=≠∂∂, 则20AC B -<,所以函数(,)u x y 在区域D 内没有极值.又连续函数在有界闭区域内有最大值和最小值,故最大值和最小值在D 的边界点取到.7、行列式0000000ab a bcd c d=( )(A )2()ad bc - (B )2()ad bc -- (C )2222a dbc - (D )2222b c a d - 【答案】B【考点】分块矩阵的行列式运算、行列式的性质、行列式按行(列)展开定理【解法一】132320000000000000000000000()()()a b b a b a a b a b d c c c r r c dd c a b c dc dc db a a b bc ad ad bc ad bc d c c d↔-↔=⋅=--=--故选B 【解法二】2141332320a 0000000(1)0(1)00000(1)(1)()()b a b c d c d a ba ba c dc bd c d a b a ba d cbcd c da b a b adbc c d c da bbc ad c dad bc ++++=⨯-+⨯-=-⨯⨯--⨯⨯-=-+=-=--8、设123,,ααα为3维向量,则对任意常数,k l ,向量组1323,k l αααα++线性无关是向量组123,,ααα线性无关的( )(A )必要非充分条件 (B )充分非必要条件 (C )充分必要条件(D )既非充分也非必要条件【考点】向量组的线性相关性 【详解】1231132231122123121213231323123123+k )()0++k )00+k ++k +100=0=1=0000l l k l l l αααλααλααλαλαλλαλλλλαααααααααααααα++=+=⇒==+=⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭已知,,无关设(即(从而,无关反之,若,无关,不一定有,,无关例如,,,二、填空题:9~14小题,每小题4分,共24分.请将答案写在答题纸...指定位置上. 9、12125dx x x -∞=++⎰ .【答案】π83【考点】无穷限的反常积分 【详解】()11122111113arctan |[()]2522242814x dx dx x x x πππ-∞-∞-∞+===--=++++⎰⎰ 10、设)(x f 是周期为4的可导奇函数,且]2,0[),1(2)(∈-='x x x f ,则=)7(f【答案】1【考点】一阶微分方程、周期函数 【详解】()22'2(1)[0,2]()2()(0)00()2[0,2]()4(7)(3)(1)(1)(12)1f x x x f x x x c f x f c f x x x x f x f f f f =-∈∴=-+∴=∴=∴=-∈∴==-=-=--=Q 又是奇函数的周期为11、设(,)z z x y =是由方程22274yzex y z +++=确定的函数,则11(,)22dz = . 【答案】)(21dy dx +-【考点】隐函数求偏导、全微分 【详解】221111(,)(,)222211(,)2211,022,(2)20(22)2011,221()2yzyz x y z x y z z e y x x x z z e z y y y y z z x y dz dx dy ===∂∂⎧⋅++=⎪∂∂⎪⎨∂∂⎪+++=∂∂⎪⎩∂∂=-=-∂∂=-+当时,代入方程解得方程两边对分别求偏导得,解得:故12、曲线L 的极坐标方程是r θ=,则L 在点(,)(,)22r ππθ=处的切线的直角坐标方程是 . 【答案】22ππ+-=x y【考点】参数方程求导、极坐标与直角坐标的转化、切线方程 【详解】把极坐标方程化为直角坐标方程令cos cos sin sin x r y r θθθθθθ==⎧⎨==⎩2sin cos cos sin 1022012cos 02sin 22()(0)222dy dy d dx dx d dy dxx y y x y x πθθθθθθθθθπππθθπθπθθππππ=+==-+⋅==--⋅==⎧⎪=⎨==⎪⎩-=--=-+则当时,则切线方程为:化简为: 13、一根长为1的细棒位于x 轴的区间[0,1]上,若其线密度2()21x x x ρ=-++,则该细棒的质心坐标x = . 【答案】2011 【考点】质心坐标 【详解】质心横坐标公式:⎰⎰=b aba dxx dx x x x )()(ρρ 所以:43212123201121()(21)4320111201(21)()30x x x x x x dx x x x dx x x x -++-++===-++-++⎰⎰14、设二次型22123121323(,,)24f x x x x x ax x x x =-++的负惯性指数为1,则a 的取值范围是 .【答案】]2,2[-【考点】二次型的规范形、矩阵的特征值、配方法化二次型为标准形 【详解】 【解法一】二次型对应的系数矩阵为:O a a ≠⎪⎪⎪⎭⎫ ⎝⎛-0221001,记特征值为321,,λλλ则0011)(321=+-==++A tr λλλ,即特征值必有正有负,共3种情况; 故二次型的负惯性指数为⇔1特征值1负2正或1负1正1零;0402210012≤+-=-⇔a aa ,即]2,2[-∈a【解法二】221231213232222221133223322221323322221232(,,)2424()(2)(4)(4)140[2,2]f x x x x x ax x x x x ax x a x x x x a x x ax x x a x y y a y a a =-++=++-+-=+--+-=-+--≥∈-若负惯性指数为,则,三、解答题:15~23小题,共94分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤. 15、(本题满分10分)求极限1212[(1)]lim1ln(1)xtx t e t dt x x→+∞--+⎰【考点】函数求极限、变限积分函数求导、等价无穷小、洛必达法则 【详解】1112212211222((1))((1))(1)1limlimlim lim (1)111ln(1)1111lim lim 22xxttxx x x x x t t x x t e t dtt e t dtx e x x e xx x x xe t e t x t t →∞→∞→∞→∞→∞→∞------===--+⋅---===⎰⎰令16、(本题满分10分)已知函数()y y x =满足微分方程221x y y y ''+=-,且(2)0y =,求()y x 的极大值与极小值.【考点】微分方程、函数的极值 【详解】22222222333322'1'1'1(1)(1),(1)(1)11332(2)031123331'0,11(,1),'0,(11),'0,(1+),'0,x y y y x y y y dy x dx y dy x dx y y x x c y c y y x x x y x y x y x y x y +=--∴=+∴+=-+=-∴+=-+=∴=∴+=-+-===±+∈-∞-<∈->∈∞<⎰⎰Q 积分得又 令得时函数单调递减,时函数单调递增,时函数单调递减所以函11(1)0,(1)1()1,0x x y y y x =-=-==数在时取得极小值,在时取得极大值由函数方程解得:故:的极大值是极小值是17、(本题满分10分)设平面区域{}22(,)14,0,0D x y x y x y =≤+≤≥≥,计算D.【考点】二重积分的计算、轮换对称性 【详解】积分区域D 关于y x =对称,利用轮对称行,121sin(2D D D Ddxdy ==+=⎰⎰222011221111sin()d cos()2411cos()|cos()d 44113244d r r r rd r r r r r πθππππ==-=-+=--=-⎰⎰⎰⎰18、(本题满分10分)设函数()f u 具有2阶连续导数,(cos )xz f e y =满足22222(4cos )x x z z z e y e x y∂∂+=+∂∂.若(0)0f =,(0)0f '=,求()f u 的表达式.【考点】多元函数求偏导、二阶常系数非齐次线性微分方程【详解】 令y e u xcos =xx x xx x x xx x xe u uf y e u f y e u f e y e z yzx z y e u f y e u f y z y e u f y z y e u f y e u f x z y e u f x z 222222222222222222])(4[sin )(cos )()cos 4(cos )(sin )(),sin ()(cos )(cos )(,cos )(+=⋅''+⋅''∴+=∂∂+∂∂⋅'-⋅''=∂∂-⋅'=∂∂⋅'+⋅''=∂∂⋅'=∂∂∴Θ 即:u u f u f =-'')(4)(对应的齐次微分方程的特征方程为:042=-r 解得:2,221-==r r故齐次微分方程的通解为:u u e C e C u f 2221)(-+=设b au u f +=)(*,则0)(,)(**="='u f a u f ,代入微分方程解得:0,41=-=b a ,即u u f 41)(*-= 故u e C e C u f xx 41)(2221-+=-所以uu u u e C e C u f e C e C u f 2221222144)(,4122)(--+=''--='因为(0)0f =,(0)0f '=,代入解得:161,16121-==C C所以22111()16164x x f u e e u -=--19、(本题满分10分)设函数()f x ,()g x 在区间[,]a b 上连续,且()f x 单调增加,0()1g x ≤≤. 证明:(Ⅰ)(I )a x dt t g xa-≤≤⎰)(0,],[b a x ∈;(II )⎰⎰⎰≤+badtt g a abadx x g x f dx x f )()()()(【考点】定积分中值定理、不等式的证明 【详解】(I )【解法一】因为函数)(x g 在区间],[b a 上连续,且1)(0≤≤x g . 所以⎰⎰⎰≤≤xax axadt dt t g dt 1)(0即a x dt t g x a-≤≤⎰)(0【解法二】由定积分中值定理知:存在),(b a ∈ξ,使得)()()(ξg a x dt t g xa-=⎰,又因为],[b a x ∈时1)(0≤≤x g , 所以)()()(0a x g a x -≤-≤ξ 即a x dt t g xa-≤≤⎰)(0【解法三】[][]11111222222()()()0'()()0(),()0()()'()()10()1'()0()()0,()0xaxa h x g t dth a h x g x h x x a b h x h x g t dt x ah x g x g x h x h x h a x a b h x ===≥∴∴∈≥=-+=-≤≤∴≤∴=∴∈≤⎰⎰Q 单调不减当时,单调不增又当时,(II )令()()()()()xa xa g t dt aaF x f u g u du f u du +⎰=-⎰⎰()'()()()[()]()()[()]()I (),()()[()]'()0()0()0()()()ba xxaa x axa ba g t dt a aF x f x g x f a g t dt g x f x f a g t dt g x a g t dt a x a x f x f x f a g t dt F x F x F a F b f x g x dx f x dx+⎡⎤∴=-+⋅=-+⎢⎥⎣⎦+≤+-=∴≥+∴≥∴=∴≥⎰≥⎰⎰⎰⎰⎰⎰由()知又单调增加单调不减又()即20、(本题满分11分) 设函数()1xf x x=+,[0,1]x ∈.定义数列 1()()f x f x =,21()(())f x f f x =,L ,1()(())n n f x f f x -=,L记n S 是由曲线()n y f x =,直线1x =及x 轴所围平面图形的面积,求极限lim n n nS →∞.【考点】定积分求面积、函数求极限 【详解】1213222(),()()11()(())121112()(())13112(),[0,1]111()0(1)(1)()(0)=0()0[0,1]n n n n n xf x f x f x xxxx f x f f x x x x xxx f x f f x x x x xf x x nxnx nx f x nx nx f x f f x x ==++∴===++++∴===+++=∈++-'==>++∴∴≥∈Q Q Q 由归纳法知:单调递增,,1120021111=(1)=ln(1)1111ln(1)lim lim [ln(1)]1lim ln(1)11lim 1lim 11n n n n n x x x S dx dx n nx n nx n nn nS n n n n nx xx →∞→∞→∞→∞→∞∴=--++++=-+=-+=-=-=+⎰⎰21、(本题满分11分) 已知函数(,)f x y 满足2(1)fy y∂=+∂,且2(,)(1)(2)ln f y y y y y =+--.求曲线(,)0f x y =所围图形绕直线1y =-旋转所成旋转体的体积. 【考点】偏积分、隐函数、旋转体的体积 【详解】由函数(,)f x y 满足2(1)fy y∂=+∂可知:)(2),(2x y y y x f ϕ++= 又22(,)2()(1)(2)ln f y y y y y y y y ϕ=++=+-- 所以()1(2)ln y y y ϕ=--所以x x y x x y y x y y y x f ln )2()1(ln )2(12)(2),(222--+=--++=++=ϕ 令1+=y z ,则(,)0f x y =对应的曲线方程为:x x z ln )2(2-=,定义域为]2,1[则曲线(,)0f x y =所围图形绕直线1y =-旋转,即x x z ln )2(2-=绕0=z 旋转,所成的旋转体体积πππππ)452ln 2()412(ln )212()212(ln ln )2(212221221212-=⎥⎦⎤⎢⎣⎡---=-=-==⎰⎰⎰x x x x x x x xd xdxx dx z V x22、(本题满分11分)设E A ,302111104321⎪⎪⎪⎭⎫⎝⎛----=为3阶单位矩阵.(I )求方程组0=Ax 的一个基础解系; (II )求满足E AB =的所有矩阵B . 【考点】解线性方程组 【详解】1234100()011101012030011205412301021310013141100126101021310013141A E --⎛⎫ ⎪=- ⎪⎪-⎝⎭--⎛⎫ ⎪→--- ⎪ ⎪--⎝⎭-⎛⎫ ⎪→--- ⎪ ⎪---⎝⎭M M M M M M M M M M (I ) 方程组0=Ax 的同解方程组为⎪⎪⎩⎪⎪⎨⎧===-=4443424132x x x x xx x x ,即基础解系为⎪⎪⎪⎪⎪⎭⎫⎝⎛-1321(II )⎪⎪⎪⎭⎫ ⎝⎛=001Ax 的同解方程组为:⎪⎪⎩⎪⎪⎨⎧+=-=-=+-=01312244434241x x x x x x x x ,即通解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-011213211k⎪⎪⎪⎭⎫ ⎝⎛=010Ax 的同解方程组为:⎪⎪⎩⎪⎪⎨⎧+=-=-=+-=04332644434241x x x x x x x x ,即通解为⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-043613212k⎪⎪⎪⎭⎫ ⎝⎛=100Ax 的同解方程组为:⎪⎪⎩⎪⎪⎨⎧+=+=+=--=01312144434241x x x x x x x x ,即通解为⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-011113213k ,123123123123261212321313431k k k k k k B k k k k k k -+-+--⎛⎫⎪--+ ⎪∴= ⎪--+ ⎪⎝⎭,321,,k k k 为任意常数23、(本题满分11分)证明:n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111ΛM O M M ΛΛ与⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100ΛM M M ΛΛ相似. 【考点】矩阵的特征值、相似对角化 【详解】设⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦L L L L L L L111111111A ,⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦L L L L L L L L0001000200n B 因为1)(,1)(==B r A r所以A 的特征值为:n A tr n n ======-)(,0121λλλλΛB 的特征值为:n B tr n n =='='=='='-)(,0121λλλλΛ 关于A 的0特征值,因为1)()()0(==-=-A r A r A E r ,故有1-n 个线性无关的特征向量,即A 必可相似对角化于⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00O同理,关于B 的0特征值,因为1)()()0(==-=-B r B r B E r ,故有1-n 个线性无关的特征向量,即B 必可相似对角化于⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00O由相似矩阵的传递性可知,A 与B 相似.。