短期生产函数与成本曲线图

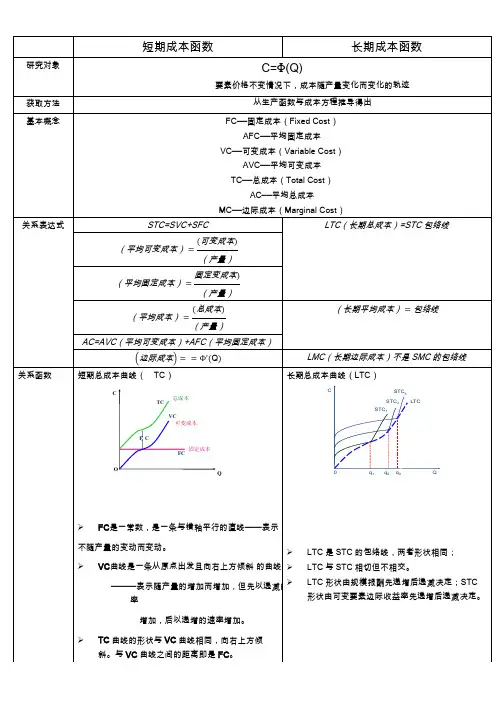
短期总成本曲线（TC ）FC 是一常数，是一条与横轴平行的直线——表示不随产量的变动而变动。

VC 曲线是一条从原点出发且向右上方倾斜 的曲线。

———表示随产量的增加而增加，但先以递减的速率增加，后以递增的速率增加。

TC 曲线的形状与VC 曲线相同，向右上方倾斜。

与VC 曲线之间的距离即是FC 。

COFCVCTCF C总成本可变成本固定成本Q短期平均成本曲线（）固定不变的FC 随产量的增加，其与产量的比值越来越小，即为AFC 。

AC 、AVC 随产量的增加而趋向接近。

AC 、AVC 间的垂直距离就是AFC 。

长期平均成本线（）LAC 与SAC 的联系LAC 是SAC 的包络线，都呈U 形；当且仅当LAC 处于最低点，唯一对应的SAC 也在最低点与其相切。

LAC 与SAC 的区别 LAC 最低点：最佳工厂规模； SAC 最低点：最优产出率短期边际成本曲线（）TC （VC ）曲线上点的切线的斜率就是MC （即导数）。

边际成本的变化引起和决定总成本和平均成本的变化。

长期边际成曲线（）长期边际成本曲线并不是短期边际成本曲线的包络线。

长期边际成本曲线上的任一点总是与某一特定短期边际成本曲线相交，交点所代表的产量即是LAC 与SAC 相切之点相应的产量。

O CAFCA VC AC短期平均成本平均固定成本QOCMC 短期边际成本曲线QQCq 1SAC 1qSAC 2SAC 3LACq 2q 3q 2aQLACSAC1SAC2SAC3EHQ1 Q2 Q3CSMC1SMC2SMC3LMCWelcome To Download !!!欢迎您的下载，资料仅供参考！。

之阳早格格创做近期死产启初时，由于可变果素相对付于没有成变果素加进量而行明隐缺累，所以边沿酬报是递加的，即减少一单位可变果素处事的加进所死产的边沿产量是递加的，减少一个工人死产的产出大于往日工人死产的产出，由于新删劳能源是企业减少产出的成原，所以1单位产出所需减少的工人人数缩小了，即那一阶段减少一单位产量所需的边沿成原是递减的.果此正在该阶段，处事的边沿产量降高，边沿成原递减.由于总产量上各面的斜率是边沿产量，所以总产量以递加的速度减少，共理，总成原上各面的斜率是边沿成原，所以总成原直线以递减的速度减少.随着可变死产果素的持绝减少，由于所有产品的死产历程中，可变果素战没有成变果素之间皆有一个最好协共比率，当超出那个临界面后，边沿酬报递减顺序爆收效率，也即减少一单位可变果素加进所戴去的边沿产量是递近期死产函数战近期成原函数之间的对付应闭系Q O减的（总产量直线以递减的速度减少），反过去道，1单位产出所需要的处事人数减少了，由于处事是企业的成原开销，所以每减少一单位产量所需要的边沿成原减少了.果此，边沿产量直线下落，共时，边沿成原递减.从图中可瞅出边沿量战仄衡量的闭系：只消边沿量大于仄衡量，仄衡量往降高；反之，只消边沿量小于仄衡量，仄衡量下落.另一种要领，用数教要领道明：()()Q L Q w QQ L w Q TVC AVC 1⋅=⋅== 即上式反映了仄衡产量取仄衡可形成原的闭系：最先，AP L 取AVC 成反比.当AP L 递减时，AVC 递加；当AP L 递加时，AVC 递减；当AP L 达到最大值时，AVC 最小.果此AP L 直线的顶面对付应AVC 直线的最矮面.第两，由于产量直线中MP L 直线取AP L 直线正在AP L 直线的顶面相接，所以MC 直线正在AVC 直线的最矮面取其相接.边沿产量取边沿成原：又果为：()Q dL dQ MPL = 所以：LMP w MC 1⋅=从推导的截止不妨瞅出，边沿成原MC 取边沿产量MP L也成反比闭系.由于MP L直线先降高，而后下落，所以MC直线先下落，而后降高；且MC直线的最矮面对付应MP L直线的顶面.从上式中可瞅出，死产函数取成原函数存留对付奇闭系，不妨由死产函数推导出成原函数.分离MP取MC的闭系可知：当TP L直线以递加的速度降高时，TC直线战TVC 直线以递减的速度降高；当TP L直线以递减的速度降高时，TC直线战TVC直线以递加的速度降高；TP L直线上的拐面对付应TC直线战TVC直线上的拐面.。

短期临盆开端时,因为可变要素相对于不成变要素投入量而言显著缺少,所以边沿酬报是递增的,即增长一单位可变要素劳动的投入所临盆的边沿产量是递增的,增长一个工人临盆的产出大于以前工人临盆的产出,因为新增劳动力是企业增长产出的成本,所以1单位产出所需增长的工人人数削减了,即这一阶段增长一单位产量所需的边沿成本是递减的.是以在该阶段,劳动的边沿产量上升,边沿成本递减.因为总产量上各点的斜率是边沿产量,所以总产量以递增的速度增长,同理,总成本上各点的斜率是边沿成本,所以总成本曲线以递减的速度增长. 跟着可变临盆要素的中断增长,因为任何产品的临盆进程中,可变要素和不成变要素之间都有一个最佳合营比例,当超出这个临短期临盆函数和短期成本函数之间的对应关系QO界点后,边沿酬报递减纪律产生感化,也即增长一单位可变要素投入所带来的边沿产量是递减的（总产量曲线以递减的速度增长）,反过来说,1单位产出所须要的劳动听数增长了,因为劳动是企业的成本支出,所以每增长一单位产量所须要的边沿成本增长了.是以,边沿产量曲线降低,同时,边沿成本递减.从图中可看出边沿量和平均量的关系：只要边沿量大于平均量,平均量往上升;反之,只要边沿量小于平均量,平均量降低.另一种办法,用数学办法证实：()()Q L Q w QQ L w Q TVC AVC 1⋅=⋅== 即上式反应了平均产量与平均可变成本的关系：起首,AP L 与AVC 成反比.当AP L 递减时,AVC 递增;当AP L 递增时,AVC 递减;当AP L 达到最大值时,AVC 最小.是以AP L 曲线的极点对应AVC 曲线的最低点.第二,因为产量曲线中MP L 曲线与AP L 曲线在AP L 曲线的极点订交,所以MC 曲线在AVC 曲线的最低点与其订交.边沿产量与边沿成本：又因为：()Q dL dQ MPL = 所以：LMP w MC 1⋅= 从推导的成果可以看出,边沿成本MC 与边沿产量MP L 也成反比关系.因为MP L 曲线先上升,然后降低,所以MC 曲线先降低,然后上升;且MC 曲线的最低点对应MP L 曲线的极点.从上式中可看出,临盆函数与成本函数消失对偶关系,可以由临盆函数推导出成本函数.联合MP与MC的关系可知：当TP L曲线以递增的速度上升时,TC曲线和TVC曲线以递减的速度上升;当TP L曲线以递减的速度上升时,TC曲线和TVC曲线以递增的速度上升;TP L曲线上的拐点对应TC曲线和TVC曲线上的拐点.。

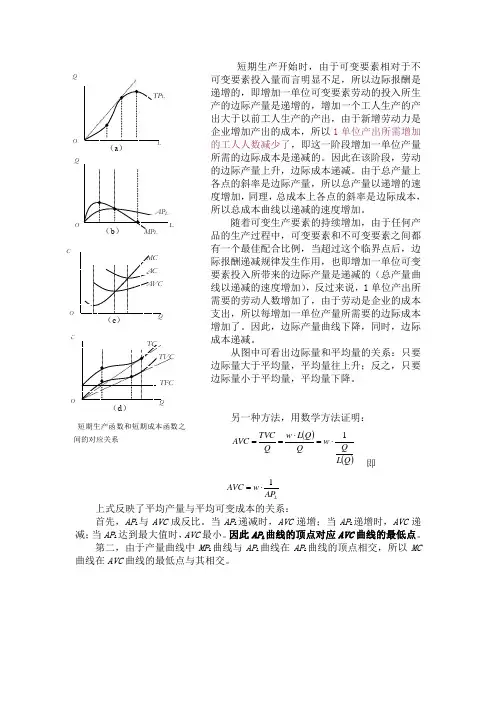
短期生产开始时，由于可变要素相对于不可变要素投入量而言明显不足，所以边际报酬是递增的，即增加一单位可变要素劳动的投入所生产的边际产量是递增的，增加一个工人生产的产出大于以前工人生产的产出，由于新增劳动力是企业增加产出的成本，所以1单位产出所需增加的工人人数减少了，即这一阶段增加一单位产量所需的边际成本是递减的。

因此在该阶段，劳动的边际产量上升，边际成本递减。

由于总产量上各点的斜率是边际产量，所以总产量以递增的速度增加，同理，总成本上各点的斜率是边际成本，所以总成本曲线以递减的速度增加。

随着可变生产要素的持续增加，由于任何产品的生产过程中，可变要素和不可变要素之间都有一个最佳配合比例，当超过这个临界点后，边际报酬递减规律发生作用，也即增加一单位可变要素投入所带来的边际产量是递减的（总产量曲线以递减的速度增加），反过来说，1单位产出所需要的劳动人数增加了，由于劳动是企业的成本支出，所以每增加一单位产量所需要的边际成本增加了。

因此，边际产量曲线下降，同时，边际成本递减。

从图中可看出边际量和平均量的关系：只要边际量大于平均量，平均量往上升；反之，只要边际量小于平均量，平均量下降。

另一种方法，用数学方法证明：()()Q L Q w QQ L w Q TVC AVC 1⋅=⋅== 即L AP w AVC 1⋅= 上式反映了平均产量与平均可变成本的关系： 首先，AP L 与AVC 成反比。

当AP L 递减时，AVC 递增；当AP L 递增时，AVC 递减；当AP L 达到最大值时，AVC 最小。

因此AP L 曲线的顶点对应AVC 曲线的最低点。

第二，由于产量曲线中MP L 曲线与AP L 曲线在AP L 曲线的顶点相交，所以MC 曲线在AVC 曲线的最低点与其相交。

短期生产函数和短期成本函数之间的对应关系 Q O边际产量与边际成本：()()dQ k r Q L w d dQ dTC MC ⋅+⋅== ()0+⋅=dQ Q dL w又因为： ()Q dL dQ MP L =所以： LMP w MC 1⋅= 从推导的结果可以看出，边际成本MC 与边际产量MP L 也成反比关系。

之迟辟智美创作短时间生产开始时，由于可变要素相对不成变要素投入量而言明显缺乏，所以边缘酬谢是递增的，即增加一单元可变要素劳动的投入所生产的边缘产量是递增的，增加一个工人生产的产出年夜于以前工人生产的产出，由于新增劳动力是企业增加产出的本钱，所以1单元产出所需增加的工人人数减少了，即这一阶段增加一单元产量所需的边缘本钱是递加的.因此在该阶段，劳动的边缘产量上升，边缘本钱递加.由于总产量上各点的斜率是边缘产量，所以总产量以递增的速度增加，同理，总本钱上各点的斜率是边缘本钱，所以总本钱曲线以递加的速度增加.随着可变生产要素的继续增加，由于任何产物的生产过程中，可变要素和不成变要素之间都有一个最佳配合比例，当超越这个临界点后，边缘酬谢递加规律发生作用，也即增加一单元可变要素投入所带来的边缘产量是递加的短时间生产函数和短时间本钱函数之间的对应关系Q O（总产量曲线以递加的速度增加），反过来说，1单元产出所需要的劳动听数增加了，由于劳动是企业的本钱支出，所以每增加一单元产量所需要的边缘本钱增加了.因此，边缘产量曲线下降，同时，边缘本钱递加.从图中可看出边缘量和平均量的关系：只要边缘量年夜于平均量，平均量往上升；反之，只要边缘量小于平均量，平均量下降.另一种方法，用数学方法证明：()()Q L Q w QQ L w Q TVC AVC 1⋅=⋅== 即上式反映了平均产量与平均可酿本钱的关系：首先，AP L 与AVC 成反比.当AP L 递加时，AVC 递增；当AP L 递增时，AVC 递加；当AP L 到达最年夜值时，AVC 最小.因此AP L 曲线的极点对应AVC 曲线的最低点.第二，由于产量曲线中MP L 曲线与AP L 曲线在AP L 曲线的极点相交，所以MC 曲线在AVC 曲线的最低点与其相交.边缘产量与边缘本钱：又因为：()Q dL dQ MPL = 所以：L MP w MC 1⋅=从推导的结果可以看出，边缘本钱MC 与边缘产量MP L 也成反比关系.由于MP L 曲线先上升，然后下降，所以MC曲线先下降，然后上升；且MC曲线的最低点对应MP L 曲线的极点.从上式中可看出，生产函数与本钱函数存在对偶关系，可以由生产函数推导出本钱函数.结合MP与MC的关系可知：当TP L曲线以递增的速度上升时，TC曲线和TVC 曲线以递加的速度上升；当TP L曲线以递加的速度上升时，TC曲线和TVC曲线以递增的速度上升；TP L曲线上的拐点对应TC曲线和TVC曲线上的拐点.。

短期总成本曲线总不变成本（TFC）：厂商在短期内为生产一定数量的产品对不变生产要素所支付的总成本。

短期内不变要素投入量是固定的，所以总不变成本为常数。

总可变成本（TVC）：厂商在短期内为生产一定数量的产品对可变生产要素所支付的总成本。

TVC = TVC（Q）总成本（TC）：厂商在短期内为生产一定数量的产品对全部生产要素所支付的总成本。

TC（Q）= TFC + TVC（Q）平均不变成本（AFC ）：厂商在短期内平均每生产一单位产品所消耗的不变成本。

()QTFCQ AFC =平均可变成本（AVC ）：厂商在短期内平均每生产一单位产品所消耗的可变成本。

()()QQ TVC Q AVC =平均总成本（AC ）：厂商在短期内平均每生产一单位产品所消耗的全部成本。

()()()()Q AVCQ AFCQQTC Q AC +==边际成本（MC ）：厂商在短期内增加一单位产量时所增加的总成本。

()()()()QTCQQTC Q MC QQ TC Q MC Q d d lim0=∆∆=∆∆=→∆MC 是TC 曲线上点的斜率。

拐点短期成本曲线由总成本曲线到平均成本曲线和边际成本曲线由TFC曲线到AFC曲线某一产量水平上的AFC值等于连接原点到TFC曲线相应点的直线的斜率。

某一产量水平上的AVC值等于连接原点到TVC曲线相应点的直线的斜率。

由TVC曲线到AVC曲线某一产量水平上的AC值等于连接原点到TC曲线相应点的直线的斜率。

由TC曲线到AC曲线某一产量水平上的MC值等于TC曲线和TVC曲线上点的斜率。

由TC曲线和TVC曲线到MC曲线。

短期总产量曲线和短期总成本曲线的关系由厂商短期生产函数出发，可以得到相应的短期成本函数，而且，由厂商的短期总产量曲线出发，也可以得到相应的短期总成本曲线。

下面，我们来进行具体的分析与推导。

假定厂商在短期内使用劳动和资本这两种要素生产一种产品，其中，劳动投入量是可变的，资本投入量是固定的，则短期生产函数为：),(K L f Q = (1)(1)式表示：在资本投入量固定的前提下，可变要素劳动投入量L 和产量Q 之间存在着相互依存的对应的关系。

这种关系可以理解为：厂商可以通过对劳动投入量的调整来实现不同的产量水平。

也可以反过来理解为：厂商根据不同的产量水平的要求，来确定相应的劳动的投入量。

根据后一种理解，且假定要素市场上劳动的价格ω和资本的价格r 是给定的，则可以用下式来表示厂商在每一产量水平上的短期总成本：K r Q L Q STC ⋅+⋅=)()(ω (2)式中，)(Q L ⋅ω为可变成本部分；K r ⋅为固定成本部分，两部分之和构成厂商的短期总成本，STC 是短期总成本的英文缩写。

如果以由)(Q φ表示可变成本)(Q L ⋅ω，以b 表示固定成本K r ⋅，则短期总成本函数可以写成以下形式：b Q Q STC +=)()(φ (3)至此，我们由(1)式的短期生产函数出发，写出了相应的短期总成本函数。

显然，短期总成本是产量的函数。

进一步地，利用(2)式可以很方便地由厂商的短期总产量曲线求得相应的短期总成本曲线。

其具体做法如下：以短期总产量曲线图为例，在图中的总产量L TP 曲线上，找到与每一个总产量相对应的可变要素劳动投人量L ，再用所得到的L 去乘已知的劳动价格ω(在此假定2=ω)，便可得到每一总产量水平的可变成本)(Q L ⋅ω。

将这种总产量与可变成本之间的对应关系描绘在平面坐标图中，即可得到短期可变成本曲线，如下图所示。

图中的横轴Q 代表产量，纵轴C 代表成本，由原点出发的曲线)(Q L ⋅ω就是短期可变成本曲线。