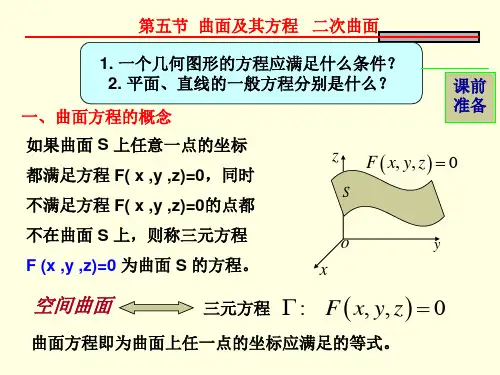
七-5第五节曲面及其方程
- 格式：ppt
- 大小：131.52 KB
- 文档页数：22
下载文档原格式
合集下载
2021研究生考试-高等数学考点解读及习题特训
点马的去心邻域，记作。（凡，肉，即
） U(Pc,,8) = {<x,y)IO < �（x-x0 问y-yo )2 ＜δ
(1）内点 (2）外点 (3）边界点 开集，闭集，连通集，区域，闭区域，有界集，无界集．
二、多元函数的概念
二元函数：设D是 R2 的一个非空子集，称映射 f:D →R为定义在D上的二元函数，通
no
＋ 飞．，， z
在 xOy 面上的投影方程．
y 求 ｛匕 的 交 线 C
案 UA抽
zx＝ ． fl4111、
y 2 － 叮／缸
nu
－y叫／－
AU
在古I) 例4设一 个立体由上半球面 z＝ 乒三亨利恍而 z＝
所围成，求它在 xOy
而上的投i；在．
答案
zx rlll〈lll
2 －
E
VJ
、，．
＝ AU
【旋转曲面方程求法】
IF(x,y)=O
( 1)坐标面上的曲线｛ I z=v
绕x轴旋转的曲面方程为 F(x，土石可？°）＝0;
绕y轴的旋转曲面方程为 F（±乒亏豆，y)=O.
I F(x,y,z) = 0,
Ix= /(z),
l lY (2）空间曲线｛ G(x,y,z) = 0, 绕z轴旋转的曲面方程，先从方程组中解出｛
xα 面上的投影．
习题10.求旋转抛物面 z=r+y(O 三z 三4）在三坐标面上的投影．
习题参考答案
习题1【答案】 x+y-3z-4=0. 习题2【答案】 9y-z-2=0. 习题3【答案】一x-一-20－＝一y一-3 2一＝一z-一1 4－．
习题4【答案】 Sx- 9y- 22z -59 = 0.
lf(x,y)-AI < e
） U(Pc,,8) = {<x,y)IO < �（x-x0 问y-yo )2 ＜δ
(1）内点 (2）外点 (3）边界点 开集，闭集，连通集，区域，闭区域，有界集，无界集．
二、多元函数的概念
二元函数：设D是 R2 的一个非空子集，称映射 f:D →R为定义在D上的二元函数，通
no
＋ 飞．，， z
在 xOy 面上的投影方程．
y 求 ｛匕 的 交 线 C
案 UA抽
zx＝ ． fl4111、
y 2 － 叮／缸
nu
－y叫／－
AU
在古I) 例4设一 个立体由上半球面 z＝ 乒三亨利恍而 z＝
所围成，求它在 xOy
而上的投i；在．
答案
zx rlll〈lll
2 －
E
VJ
、，．
＝ AU
【旋转曲面方程求法】
IF(x,y)=O
( 1)坐标面上的曲线｛ I z=v
绕x轴旋转的曲面方程为 F(x，土石可？°）＝0;
绕y轴的旋转曲面方程为 F（±乒亏豆，y)=O.
I F(x,y,z) = 0,
Ix= /(z),
l lY (2）空间曲线｛ G(x,y,z) = 0, 绕z轴旋转的曲面方程，先从方程组中解出｛
xα 面上的投影．
习题10.求旋转抛物面 z=r+y(O 三z 三4）在三坐标面上的投影．
习题参考答案
习题1【答案】 x+y-3z-4=0. 习题2【答案】 9y-z-2=0. 习题3【答案】一x-一-20－＝一y一-3 2一＝一z-一1 4－．
习题4【答案】 Sx- 9y- 22z -59 = 0.
lf(x,y)-AI < e
高等数学(下)教案曲面及其方程
高等数学(下)教案曲面及其方程教学目标：1. 理解曲面的概念，掌握曲面的基本性质。
2. 学习曲面的方程表示方法，掌握常见曲面的方程。
3. 能够利用曲面方程进行曲面的绘制和分析。
教学内容：一、曲面的概念与基本性质1. 曲面的定义2. 曲面的基本性质2.1 曲面的导数2.2 曲面的切线和法线2.3 曲面的曲率2.4 曲面的切平面和法平面二、曲面的方程表示方法1. 参数方程表示法2.1 参数方程的定义2.2 参数方程的求导和积分2. 普通方程表示法2.1 普通方程的定义2.2 普通方程的求导和积分3. 柱面和二次曲面的方程3.1 柱面的方程3.2 二次曲面的方程三、常见曲面的方程1. 圆锥面的方程2. 椭圆面的方程3. 双曲面的方程4. 抛物面的方程5. 直纹面的方程四、曲面的绘制和分析1. 利用参数方程绘制曲面2. 利用普通方程绘制曲面3. 曲面的切线和法线分析4. 曲面的曲率分析5. 曲面的切平面和法平面分析教学方法：1. 采用多媒体教学，通过图形和动画展示曲面的形状和性质。
2. 通过例题讲解和练习，使学生掌握曲面方程的求解和分析方法。
3. 引导学生运用曲面方程解决实际问题，提高学生的应用能力。
教学评价：1. 课堂讲解和练习的参与度。
2. 学生对曲面方程的掌握程度。
3. 学生能够运用曲面方程进行曲面的绘制和分析。
教学资源：1. 教学PPT和动画演示。
2. 曲面方程的相关教材和参考书。
3. 计算机软件进行曲面的绘制和分析。
六、曲面的切平面和法线1. 切平面的定义与性质6.1 切平面的定义6.2 切平面的性质2. 法线的定义与性质6.3 法线的定义6.4 法线的性质3. 切平面和法线的求法6.5 切平面和法线的求法七、曲面的曲率1. 曲率的定义与性质7.1 曲率的定义7.2 曲率的性质2. 曲率的计算7.3 曲率的计算方法3. 曲面的弯曲程度分析7.4 曲面的弯曲程度分析八、曲面的绘制与分析实例1. 实例一：圆锥面的绘制与分析8.1 圆锥面的参数方程8.2 圆锥面的普通方程8.3 圆锥面的切平面和法线分析2. 实例二：椭圆面的绘制与分析8.4 椭圆面的参数方程8.5 椭圆面的普通方程8.6 椭圆面的切平面和法线分析3. 实例三：双曲面的绘制与分析8.7 双曲面的参数方程8.8 双曲面的普通方程8.9 双曲面的切平面和法线分析九、曲面在实际问题中的应用1. 曲面在工程中的应用9.1 曲面在机械设计中的应用9.2 曲面在建筑设计中的应用2. 曲面在自然科学中的应用9.3 曲面在光学中的应用9.4 曲面在声学中的应用十、复习与练习1. 复习本章内容10.1 复习曲面的概念与基本性质10.2 复习曲面的方程表示方法10.3 复习常见曲面的方程2. 课堂练习10.4 完成课堂练习题3. 课后作业10.5 布置课后作业教学方法：1. 采用案例教学法，通过具体实例讲解曲面的绘制与分析方法。
曲面及其方程
锥面上任意两点之间的曲线相交于一点，锥顶是锥面的顶点。
02
曲面的方程
曲面方程的定义
曲面方程是描述曲面上的点与三维空间中某点的关系，它可以通过几何图形或方程的形式来表示。
曲面方程的概念与性质
曲面方程的性质
曲面方程的性质取决于曲面的形状和特性，例如对称性、连续性、光滑性等。
曲面方程的变量
曲面方程通常由两个或三个变量构成，这些变量可以是坐标系中的x、y、z值或其他参数。
曲面在航空航天中的应用
THANKS
谢谢您的观看
短程线
曲面上的测地线与短程线
04
曲面的分类与性质
定义
性质
方程
平面的性质与特征
定义
球面是一种以定点为中心，半径为定长的封闭曲面。
性质
球面的法线与半径垂直，且通过球心的法线有两个。
方程
球面的方程通常采用球心坐标和半径表示，即(x - h)2 + (y - k)2 + (z - l)2 = r2，其中(h, k, l)是球心的坐标，r是球的半径。
在机械设计中，曲面可以用来创建平滑、流线型的形状，同时还可以实现功能性的要求，例如引导气流、提供结构强度等。
曲面可以由专业的CAD软件创建，这些软件通常提供了丰富的曲面功能，例如拉伸、旋转、扫描等操作。
03
曲面在建筑设计中还可以用来解决物理问题，例如引导光线、遮阳、排水等。
曲面在建筑设计中的应用
01
在建筑设计中，曲面被广泛应用于创造富有艺术感和流动感的建筑外形。
02
通过使用曲面，建筑师可以创造出平滑的建筑立面，以及具有自然形态的室内空间。
在航空航天领域，曲面被广泛应用于飞机和火箭的设计中。
曲面可以用来创建平滑、符合空气动力学的机身外形，同时还可以实现高效的空气动力学性能。
02
曲面的方程
曲面方程的定义
曲面方程是描述曲面上的点与三维空间中某点的关系，它可以通过几何图形或方程的形式来表示。
曲面方程的概念与性质
曲面方程的性质
曲面方程的性质取决于曲面的形状和特性，例如对称性、连续性、光滑性等。
曲面方程的变量
曲面方程通常由两个或三个变量构成，这些变量可以是坐标系中的x、y、z值或其他参数。
曲面在航空航天中的应用
THANKS
谢谢您的观看
短程线
曲面上的测地线与短程线
04
曲面的分类与性质
定义
性质
方程
平面的性质与特征
定义
球面是一种以定点为中心，半径为定长的封闭曲面。
性质
球面的法线与半径垂直，且通过球心的法线有两个。
方程
球面的方程通常采用球心坐标和半径表示，即(x - h)2 + (y - k)2 + (z - l)2 = r2，其中(h, k, l)是球心的坐标，r是球的半径。
在机械设计中，曲面可以用来创建平滑、流线型的形状，同时还可以实现功能性的要求，例如引导气流、提供结构强度等。
曲面可以由专业的CAD软件创建，这些软件通常提供了丰富的曲面功能，例如拉伸、旋转、扫描等操作。
03
曲面在建筑设计中还可以用来解决物理问题，例如引导光线、遮阳、排水等。
曲面在建筑设计中的应用
01
在建筑设计中，曲面被广泛应用于创造富有艺术感和流动感的建筑外形。
02
通过使用曲面，建筑师可以创造出平滑的建筑立面，以及具有自然形态的室内空间。
在航空航天领域，曲面被广泛应用于飞机和火箭的设计中。
曲面可以用来创建平滑、符合空气动力学的机身外形，同时还可以实现高效的空气动力学性能。
高等数学上册第七章第五节 曲面及其方程
0z 3
在
yOz面上的投影
z
3y2 ,
xOy面上的圆 x 2 y 2 R2
叫做它的准线，平行于 z 轴的直线 l 叫做它的母线。 其实在 yOz 面内的一条直线: y R, 绕z轴旋转而成的旋转
曲面就是该圆柱面,则圆柱面方程为: x 2 y 2 R. 即
x2 y2 R2.
9
P11
定义: 平行于定直线并沿定曲线C平行移动的直线 l形成的轨迹
方程 Fx, y 0, 在空间 z
Fx, y 0,
直角坐标系中表示：
o 母线平行于 z 轴的柱面,
其准线是 xOy 面上的曲线
y
C : Fx, y 0.
x
C
方程 Gx,z 0, 在空间
直角坐标系中表示：
方程中缺哪个字母，母线 平行于相应的轴。
母线平行于 y轴的柱面, 其准线是 xOz 面上的曲线
1
在空间解析几何中关于曲面的研究,有下列两个基本问题: (1) 已知曲面点的几何轨迹，求曲面的方程； (2) 已知曲面的方程，求这方程所表示的曲面的形状。
1、球面方程
例1 建立球心在 M 0 x0 , y0 , z0 ,
半径为 R 的球面 S 的方程.
解：Mx, y, z S M0M R
M0 M x x0 2 y y0 2 z z0 2 ,
xz 0
o
x
y
12
小 结：
1.曲面的概念
2.球面方程 x x0 2 y y0 2 z z0 2 R2
3.平面方程 Ax By Cz D 0 作业:习题7-5
4.旋转曲面
作业纸P50
设 C : f y, z 0 yoz面
下次交P49-50
同济版高等数学第六版课件第八章第五节曲面及其方程
制造领域，如汽车、航空和船舶制造等。
直纹曲面在建筑设计中的应用
总结词
设计曲面建筑外观
VS
详细描述
直纹曲面方程在建筑设计中用于描述复杂 的曲面结构。通过直纹曲面，建筑师可以 创造出独特且富有艺术感的建筑外观。直 纹曲面在建筑设计中的广泛应用，不仅提 高了建筑的审美价值，也为建筑师提供了 更多的创作空间。
方程
锥面的方程通常表示为 x^2 + y^2 = r^2(z)，其中 (x, y) 是平面上的点，r 是锥顶到平面的距离，z 是锥面的参数。
性质
锥面是一个非对称的曲面，在锥顶处曲率为无穷大。
旋转曲面
定义
旋转曲面是由一条平面曲线绕 一条直线旋转一周所形成的曲
面。
方程
旋转曲面的方程通常表示为 x = x(t), y = y(t), z = z(t)，其 中 t 是参数，x(t), y(t), z(t) 是
非标准曲面
定义
01
非标准曲面是指不符合常规形式的曲面，如参数曲面、隐式曲
面等。
性质
02
非标准曲面具有一些特殊的几何性质，如曲率、法向量等，这
些性质有助于理解曲面的几何结构。
应用
03
非标准曲面在计算机图形学、计算几何等领域有广泛的应用，
如动画设计、虚拟现实、游戏开发等。
曲面的微分性质
定义
曲面的微分性质是指曲面在局部的几何性质，如切线、法线、曲率 等。
给定的平面曲线。
性质
旋转曲面是一个具有旋转对称 性的曲面，其曲率随旋转角度
而变化。
直纹曲面
定义
直纹曲面是由一条直线按一定方式移动所形成的曲面 。
方程
直纹曲面的方程通常表示为 z = f(x, y)，其中 f(x, y) 是给定的函数，(x, y) 是平面上的点。
直纹曲面在建筑设计中的应用
总结词
设计曲面建筑外观
VS
详细描述
直纹曲面方程在建筑设计中用于描述复杂 的曲面结构。通过直纹曲面，建筑师可以 创造出独特且富有艺术感的建筑外观。直 纹曲面在建筑设计中的广泛应用，不仅提 高了建筑的审美价值，也为建筑师提供了 更多的创作空间。
方程
锥面的方程通常表示为 x^2 + y^2 = r^2(z)，其中 (x, y) 是平面上的点，r 是锥顶到平面的距离，z 是锥面的参数。
性质
锥面是一个非对称的曲面，在锥顶处曲率为无穷大。
旋转曲面
定义
旋转曲面是由一条平面曲线绕 一条直线旋转一周所形成的曲
面。
方程
旋转曲面的方程通常表示为 x = x(t), y = y(t), z = z(t)，其 中 t 是参数，x(t), y(t), z(t) 是
非标准曲面
定义
01
非标准曲面是指不符合常规形式的曲面，如参数曲面、隐式曲
面等。
性质
02
非标准曲面具有一些特殊的几何性质，如曲率、法向量等，这
些性质有助于理解曲面的几何结构。
应用
03
非标准曲面在计算机图形学、计算几何等领域有广泛的应用，
如动画设计、虚拟现实、游戏开发等。
曲面的微分性质
定义
曲面的微分性质是指曲面在局部的几何性质，如切线、法线、曲率 等。
给定的平面曲线。
性质
旋转曲面是一个具有旋转对称 性的曲面，其曲率随旋转角度
而变化。
直纹曲面
定义
直纹曲面是由一条直线按一定方式移动所形成的曲面 。
方程
直纹曲面的方程通常表示为 z = f(x, y)，其中 f(x, y) 是给定的函数，(x, y) 是平面上的点。
第五节曲面及其方程
第五节 曲面及其方程 二次曲面
1. 一个几何图形的方程应满足什么条件？ 2. 平面、直线的一般方程分别是什么？
一、曲面方程的概念
课前 准备
如果曲面 S 上任意一点的坐标 都满足方程 F( x ,y ,z)=0，同时 不满足方程 F( x ,y ,z)=0的点都
z F x, y, z 0
S
不在曲面 S 上，则称三元方程
x x0 2 y y0 2 z z0 2 R z
即 x x0 2 y y0 2 z z0 2 R2
——称为球面方程的标准形式。 o
M M0
y
x
2、旋转曲面
一平面曲线绕着该平面内一定直线L旋转一周而成的曲面
叫做旋转曲面，其中定直线L叫做旋转曲面的轴。 z
如：XOY面内的椭圆
过点M作垂直于x轴的平面, 交x轴于点Q，交曲线C于点P，则有
Q x,0,0, Px, y1,0, QM PQ ,
M
o
y
Q
x
•
P
C
小结旋转曲面方程的规律
1 xoy面内的曲线
f
x,
y
0 ,
z 0
绕x轴旋转而成旋转曲面的方程为 f x, y2 z2 0；
绕y轴旋转而成旋转曲面的方程为 f x2 z2 , y 0.
转曲面、母线平行于坐标轴的柱面等曲面方程 的建立方法
Exercises
1. P192 1，3，4 2. 复习第一章
柱面
返回
返回
返回
返回
x2 a2
y2 b2
1
绕Y轴旋转一周而形成的曲面。
XOY面内的曲线C： f x, y 0 绕Y轴旋转
z 0
x
o
1. 一个几何图形的方程应满足什么条件？ 2. 平面、直线的一般方程分别是什么？
一、曲面方程的概念
课前 准备
如果曲面 S 上任意一点的坐标 都满足方程 F( x ,y ,z)=0，同时 不满足方程 F( x ,y ,z)=0的点都
z F x, y, z 0
S
不在曲面 S 上，则称三元方程
x x0 2 y y0 2 z z0 2 R z
即 x x0 2 y y0 2 z z0 2 R2
——称为球面方程的标准形式。 o
M M0
y
x
2、旋转曲面
一平面曲线绕着该平面内一定直线L旋转一周而成的曲面
叫做旋转曲面，其中定直线L叫做旋转曲面的轴。 z
如：XOY面内的椭圆
过点M作垂直于x轴的平面, 交x轴于点Q，交曲线C于点P，则有
Q x,0,0, Px, y1,0, QM PQ ,
M
o
y
Q
x
•
P
C
小结旋转曲面方程的规律
1 xoy面内的曲线
f
x,
y
0 ,
z 0
绕x轴旋转而成旋转曲面的方程为 f x, y2 z2 0；
绕y轴旋转而成旋转曲面的方程为 f x2 z2 , y 0.
转曲面、母线平行于坐标轴的柱面等曲面方程 的建立方法
Exercises
1. P192 1，3，4 2. 复习第一章
柱面
返回
返回
返回
返回
x2 a2
y2 b2
1
绕Y轴旋转一周而形成的曲面。
XOY面内的曲线C： f x, y 0 绕Y轴旋转
z 0
x
o
高等数学-几种常见的二次曲面
母线 平行于 z 轴;
准线 xoy 面上的曲线 l1.
方程 G( y, z) 0 表示柱面,
母线 平行于 x 轴;
准线 yoz 面上的曲线 l2.
方程 H (z, x) 0 表示柱面,
y x l1
x z l3
z l2 y
母线 平行于 y 轴;
x
准线 xoz 面上的曲线 l3.
y
9
注:柱面方程与坐标面上的曲线方程容易混淆,应该
例如 :
11
下面我们重点讨论母线在坐标面,旋转轴是坐标轴 的旋转曲面.
建立yoz面上曲线C 绕 z 轴旋转所成曲面的方程:
给定 yoz 面上曲线 C: f ( y, z) 0
z
若点 M1(0, y1, z1) C, 则有 f ( y1, z1) 0
当绕 z 轴旋转时, 该点转到
求旋转曲面方程C时，平面
z oy
27
z
4. 椭圆锥面
z
x2 a2
y2 b2
z2
( a, b 为正数)
在平面 z t 上的截痕为椭圆
x2 (at)2
y2 (bt)2
1,
zt
①
xx
o yy
在平面 x＝0 或 y＝0 上的截痕为过原点的两直线 .
可以证明, 椭圆①上任一点与原点的连线均在曲面上. (椭圆锥面也可由圆锥面经 x 或 y 方向的伸缩变换
绕 y 轴旋转时得旋转曲面方程:
o
f ( y, x2 z2 ) 0
y
例3. 旋转抛物面
x
特点:母线C为抛物线,旋转轴L为抛物线的对称轴。
例如:将yoz平面上的抛物线C: z2 2 py
绕 y 轴旋转一周所产生的抛物面为:
高等数学(下) 第5讲 理论-2课时
2x 3z 6 表示平面：
z
y o xz
交
2
线
o
y
为：
oy
3 x
x
z a2 x2 y2
例2
方程组
(
x
a )2 2
y2
a2 表示怎样的曲线？ 4
解 z a2 x2 y2
表示上半球面,
(x
a )2
y2
a
2
表示圆柱面,
2
4
交线如图：
例3
曲线
一、空间曲线的一般方程
空间曲线C可看作空间两曲面的交线.
F ( x, y, z) 0 S1
G(x, y,z) 0 S2
空间曲线的一般方程 x
z
S1
S2
C
o
y
例1
方程组
x2
y2 1 表示怎样的曲线？
2x 3z 6
z
解 x2 y2 1 表示母线
平行于z轴的圆柱面：
o
y
x
3. 双曲柱面（一支）
y2 x2 1
z
b2 a2
b
o
y
x
六、空间区域简图
例1 由曲面 z 6 x2 y2 与 z x2 y2 围成一个 空间区域, 试作出它的简图.
例2 由曲面 x 0, y 0, z 0, x y 1, y2 z2 1 围 成一个空间区域(在第I卦限部分), 试作出它的简图.
定义3 平行于某定直线的直线L并沿定曲线 C 移动 所 形成的轨迹叫做柱面.
下面我们来分析一下方程
在空间表示怎样的曲面 .
z
y o xz
交
2
线
o
y
为：
oy
3 x
x
z a2 x2 y2
例2
方程组
(
x
a )2 2
y2
a2 表示怎样的曲线？ 4
解 z a2 x2 y2
表示上半球面,
(x
a )2
y2
a
2
表示圆柱面,
2
4
交线如图：
例3
曲线
一、空间曲线的一般方程
空间曲线C可看作空间两曲面的交线.
F ( x, y, z) 0 S1
G(x, y,z) 0 S2
空间曲线的一般方程 x
z
S1
S2
C
o
y
例1
方程组
x2
y2 1 表示怎样的曲线？
2x 3z 6
z
解 x2 y2 1 表示母线
平行于z轴的圆柱面：
o
y
x
3. 双曲柱面（一支）
y2 x2 1
z
b2 a2
b
o
y
x
六、空间区域简图
例1 由曲面 z 6 x2 y2 与 z x2 y2 围成一个 空间区域, 试作出它的简图.
例2 由曲面 x 0, y 0, z 0, x y 1, y2 z2 1 围 成一个空间区域(在第I卦限部分), 试作出它的简图.
定义3 平行于某定直线的直线L并沿定曲线 C 移动 所 形成的轨迹叫做柱面.
下面我们来分析一下方程
在空间表示怎样的曲面 .
高数讲义第五节 曲面及其方程(二)
椭球面也可由下面方法伸缩变形而来
（1）将球面 x2 y2 z2 a2
沿 z 轴方向伸缩 c 倍：z a z, 得旋转椭球面：
a
c
x2
y2
a2 c2
z2
a2,
或
x2 a2
y2向伸缩 b 倍： y a y,
a
b
即得椭球面：
x2 a2
y2 b2
z2 c2
x2 a2
y2 b2
z
其图形不可由旋转曲面伸缩变形而来
可用截痕法讨论其图形的形状。
（三）双曲面
（1）单叶双曲面
x2 a2
y2 b2
z2 c2
1
可由旋转单叶双曲面伸缩变形得到
（2）双叶双曲面
x2 a2
y2 b2
z2 c2
1
可由旋转双叶双曲 面伸缩变形得到
（四）椭圆锥面
x2 a2
y2 b2
z2
又称二次锥面
倍而得到平面曲线 C´ ， 则 C´ 的平面方程为：
F(x, y) 0
结论1：将平面曲线 C ：F ( x , y ) = 0 沿 y 轴方向伸缩
倍而得到平面曲线C´ ， 则 C´ 的平面方程为：
F(x, y) 0
结论2：将平面曲线C ：F ( x , y ) = 0 沿 x 轴方向伸缩
倍而得到平面曲线C´ ， 则 C´ 的平面方程为：
第五节 曲面及其方程（2）
四、二次曲面
了解一般空间曲面形状的两种常用方法： （1）截痕法
用坐标面和平行于坐标面的平面与曲面 相截，考察其交线（即截痕）的形状，然后 加以综合，从而了解曲面的全貌．
例4 方程 解 根据题意有
的图形是怎样的？
《曲面及方程》课件
7. 曲面的切向量与切线方程
⇢⇠
8. 曲面的法向向量与法线方程⇑⇓
9. 曲面的曲率及主曲率
10. 可视化表示曲面
11. 曲面的翻转与旋转
12. 曲面的投影与裁剪⇩⇧
13. 三维曲面的交点⚡
14. 曲面的梯度、散度、旋度⚙️
15. 曲面的高斯曲率与平均曲率⚖️
16. 曲面的最小曲面与最小旋
转曲面
17. 曲面的拓扑结构
18. 曲面的曲线包络与曲面包络⭕
19. 曲面的偏微分方程
20. 曲面的应用与发展趋势
《曲面及方程》PPT课件
从曲面的定义和特点开始，逐步深入探讨曲面的方程表示、参数化曲面以及
其切平面、法向量等概念，包括曲面的曲率、可视化表示以及应用与发展趋
势。
1. 什么是曲面？
2. 曲面的分类及特点✨
3. 曲面的方程表示
4. 参数化曲面的定义及优点
ห้องสมุดไป่ตู้
5. 常见的参数化曲面
6. 曲面的切平面与法向量⏩⏪
同济版高等数学第六版课件第八章第五节曲面及其方程
曲面的应用领域
物理学：研究曲面形状对 物理现象的影响
计算机图形学：用于创建 三维模型和动画
地质学：用于描述地球表 面的形态
生物学：用于研究生物体 的表面结构
工程学：用于设计各种曲 面形状的物体，如汽车车 身、飞机机翼等
数学：用于研究曲面的性 质和结构，以及解决相关 的数学问题
06
曲面方程的解题技 巧与注意事项
同济版高等数学第 六版课件第八章第 五节曲面及其方程
单击此处添加副标题
汇报人：PPT
目录
添加目录项标题 曲面方程的求解方法 曲面方程的拓展知识
曲面及其方程的基本概念
曲面方程的应用实例 曲面方程的解题技巧与注 意事项
01
添加章节标题
02
曲面及其方程的基 本概念
曲面的定义和分类
曲面的定义：曲面是连续但不光滑的二维图形，由一条或多条曲线组成
04
曲面方程的应用实 例
球面方程的应用
定义：球面方程是描述球面形状的数学方程 应用实例1：计算球面上的点到球心的距离 应用实例2：确定球面上点的坐标 应用实例3：绘制球面图形
柱面方程的应用
定义：柱面方程是 平面与空间直线或 平面相交形成的曲 面
应用实例1：在计 算机图形学中，柱 面方程可以用来描 述三维图形的旋转 和扭曲
总结：通过对解题思路的总结，可以更好地掌握曲面方程的解题技巧 和注意事项，提高解题效率。
感谢观看
汇报人：PPT
解题技巧
熟练掌握曲面方 程的基本形式和 性质
灵活运用代数运 算技巧，简化方 程
掌握常见的曲面 方程的解题方法
注意方程的适用 范围和限制条件
注意事项
理解曲面方程的 基本概念和性质
曲面及其方程
z
l o o x M(x, y, 0) y
xoy面上的圆 x2 + y2 = R2 叫做柱面的准线. 平行于 z 轴的直线 L 叫做柱面的母线.
(1) 定义: 平行于定直线并沿定曲线C移动 直线 L 形成的轨迹叫做柱面. 定曲线C叫做柱面的准线. 动直线 L 叫做柱面的母线.
例2: 方程 y2 =2x 表示.母线平行于 z 轴的柱面, 它的准线是xoy面上的抛物线y2 =2x,该柱 面叫做抛物柱面. z y
y2 =2x
o
x
例2: 方程 x−y = 0表示. 母线平行于 z 轴的柱面, 它的准线是xoy面上 的直线x−y = 0, 所以它是过z轴的平面.
z
o x
y x−y = 0
(2) 母线平行于坐标轴的柱面方程. 1° 方程F (x, y) =0 表示: 母线平行于 z 轴的柱面, 准线为xoy面上的曲线 C: F (x, y) = 0 . 2° 方程F (x, z) =0 表示: 母线平行于 y 轴的柱面, 准线为xoz面上的曲线 C: F (x, z) = 0 . 3° 方程F (y, z) =0 表示: 母线平行于 x 轴的柱面, 准线为yoz面上的曲线 C: F (y, z) = 0 .
y
那末, 方程F (x, y, z) =0叫做曲面S的方程, 而曲面S 叫做方程F (x, y, z) =0的图形.
二、几种常见曲面的方程. 几种常见曲面的方程.
M
1. 球面 考虑球心为M0(x0, y0, z0), 半径为R的球面. 对于球面上任 一点M(x, y, z), 都有|M M0|2 =R2. 即: (x− x0)2 + (y − y0)2 + (z − z0)2 = R2 称方程(1)为球面的标准方程. 特别: 当球心在原点O(0, 0, 0)时, 球面方程: x2 + y2 + z2 =43; y 2 )
l o o x M(x, y, 0) y
xoy面上的圆 x2 + y2 = R2 叫做柱面的准线. 平行于 z 轴的直线 L 叫做柱面的母线.
(1) 定义: 平行于定直线并沿定曲线C移动 直线 L 形成的轨迹叫做柱面. 定曲线C叫做柱面的准线. 动直线 L 叫做柱面的母线.
例2: 方程 y2 =2x 表示.母线平行于 z 轴的柱面, 它的准线是xoy面上的抛物线y2 =2x,该柱 面叫做抛物柱面. z y
y2 =2x
o
x
例2: 方程 x−y = 0表示. 母线平行于 z 轴的柱面, 它的准线是xoy面上 的直线x−y = 0, 所以它是过z轴的平面.
z
o x
y x−y = 0
(2) 母线平行于坐标轴的柱面方程. 1° 方程F (x, y) =0 表示: 母线平行于 z 轴的柱面, 准线为xoy面上的曲线 C: F (x, y) = 0 . 2° 方程F (x, z) =0 表示: 母线平行于 y 轴的柱面, 准线为xoz面上的曲线 C: F (x, z) = 0 . 3° 方程F (y, z) =0 表示: 母线平行于 x 轴的柱面, 准线为yoz面上的曲线 C: F (y, z) = 0 .
y
那末, 方程F (x, y, z) =0叫做曲面S的方程, 而曲面S 叫做方程F (x, y, z) =0的图形.
二、几种常见曲面的方程. 几种常见曲面的方程.
M
1. 球面 考虑球心为M0(x0, y0, z0), 半径为R的球面. 对于球面上任 一点M(x, y, z), 都有|M M0|2 =R2. 即: (x− x0)2 + (y − y0)2 + (z − z0)2 = R2 称方程(1)为球面的标准方程. 特别: 当球心在原点O(0, 0, 0)时, 球面方程: x2 + y2 + z2 =43; y 2 )
第五节 曲面及其方程(导学答案)
第五节 曲面及其方程（导学解答）一、相关知识1．证明如果2220a b c d ++->，那么由方程2222220x y z ax by cz d ++++++= 给出的曲面是一球面，求出球心坐标和半径.证明：原方程可化为：222222()()()x a y b z c a b c d +++++=++-即2222(())(())(())x a y b z c --+--+--=， ∴该曲面为一球面，球心坐标为(,,)a b c ---2．已知椭球面方程2222221x y z a b c++=()c a b <<，试求过x 轴且与椭球面的交线是圆的平面.解：不妨设过x 轴的平面z ky =，它与椭球面的交线为222222221x c b k y a b c z ky ⎧++=⎪⎨⎪=⎩，如果该交线是圆，则圆心为原点，又因交线关于x 轴对称并且(,0,0)a ±在这条交线上，故该圆可看成以原点为球心，a 为半径的球与平面z ky =的交线，即222221x k y a a z ky ⎧++⎪⎨⎪=⎩，比较上述两个方程组得2222222()()c b a k b a c -=-，0=. 二、曲面的有关问题1．在空间直角坐标系中，球心在),,(0000z y x P 半径为R 的球面上的点),,(z y x P 满足什么条件？答：点(,,)P x y z 满足2222000()()()x x y y z z R -+-+-=.2．在空间直角坐标系中，满足条件122=+y x 的点),,(z y x P 的集合构成一个什么图形？答：满足122=+y x 的点),,(z y x P 构成了一个以z 轴为对称轴，到对称轴距离为1的圆柱面.3．怎么定义一般曲面的方程？答：若曲面C 上的点的坐标都满足方程(,,)0F x y z =，而不在曲面C 上的点的坐标都不满足方程(,,)0F x y z =，则称方程(,,)0F x y z =为曲面C 的方程.4．二次曲面方程及其分类；答：对于不含交叉项的二次曲面方程：222123142434442220x y z a x a y a z a λλλ++++++=，通过坐标变换可化为下列简单方程之一：222123123(1):0,0;x y z d λλλλλλ+++=≠(1.1)0.d ≠123(1.1.1),,λλλ同号但与d 异号，它表示椭球面.123(1.1.2),,λλλ与d 同号,它表示虚椭球面.(1.1.3)d 与123,,λλλ中的一个同号，它表示单叶双曲面.(1.1.4)d 与123,,λλλ中的两个同号，它表示双叶双曲面.(2)0d =.(1.2.1)123,,λλλ同号，它表示一个点.\(1.2.2)123,,λλλ不全同号，它表示二次锥面.221234(2)20.x y a z d λλ+++=120.λλ≠34(2.1)0.a ≠12(2.1.1),λλ同号，它表示椭圆抛物面.12(2.1.2),λλ异号，它表示双曲抛物面.34(2.2)0.a =12(2.2.1),λλ同号，但与d 异号，它表示椭圆柱面.12(2.2.2),λλ与d 同号，它表示虚椭圆柱面.12(2.2.3),λλ同号，但0d =,它表示一对相交于一条实直线的虚平面. 12(2.2.4),λλ异号，且0d ≠.它表示双曲柱面.12(2.2.5),λλ异号，但0d =，它表示一对相交平面.212434(3)220x a y a z d λ+++=.2434(3.1),a a 中至少有一个不为0，它表示抛物柱面.2434(3.2)0a a ==.1(3.2.1)λ与d 异号，它表示一对平行平面.1(3.2.1)λ与d 同号，它表示一对虚的平行平面.(3.2.3)0d =,它表示一对重合平面.5．求一条平面曲线绕固定轴旋转所得到的曲面S 的方程。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
成过程:
播放
柱面举例
z
z
y2 2x
o
y
o
x
x
抛物柱面
平面
y
y x
从柱面方程看柱面的特征：
只含 x, y 而缺z 的方程F ( x, y) 0 ，在
空间直角坐标系中表示母线平行于z 轴的柱
面，其准线为 xoy面上曲线C（.其他类推）
y2 z2
实 例
b2 c2 1 椭圆柱面 // x轴
x2 a2
y2 b2
1
双曲柱面
// z轴
x2 2 pz 抛物柱面 // y 轴
四、小结
曲面方程的概念 F ( x, y, z) 0. 旋转曲面的概念及求法. 柱面的概念(母线、准线).
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形？
(1) x 2;
(2) x2 y2 4;
第五节 曲面及其方程
一、曲面方程的概念
曲面的实例： 水桶的表面、台灯的罩子面等． 曲面在空间解析几何中被看成是点的几何轨迹． 曲面方程的定义：
如果曲面S 与三元方程F ( x, y, z) 0有下述关系： （1）曲面S 上任一点的坐标都满足方程； （2）不在曲面S 上的点的坐标都不满足方程； 那么，方程F ( x, y, z) 0 就叫做曲面S 的方程， 而曲面S 就叫做方程的图形．
将 z z1 , y1 x2 y2 代入
f ( y1, z1 ) 0
将 z z1, y1 x2 y2 代入 f ( y1, z1 ) 0
得方程 f x2 y2 , z 0,
yoz 坐标面上的已知曲线 f ( y, z) 0绕z 轴旋
转一周的旋转曲面方程.
二、旋转曲面
定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋
转曲面.
这条定直线叫旋转
曲面的轴．
播放
旋转过程中的特征：
如图 设 M ( x, y, z),
(1) z z1
（2）点M 到z 轴的距离
z
d M1(0, y1, z1)
M f ( y,z) 0
o
y
d x2 y2 | y1 | x
特殊地：球心在原点时方程为 x2 y2 z2 R2
例 2 求与原点O 及M0 (2,3,4)的距离之比为1 : 2 的
点的全体所组成的曲面方程.
解 设M( x, y, z)是曲面上任一点，
根据题意有 | MO | 1 , | MM0 | 2
x2 y2 z2
1
,
x 22 y 32 z 42 2
(3) y x 1.
思考题解答
方程
平面解析几何中 空间解析几何中
x2
平行于y 轴的直线 平行于 yoz 面的平面
圆心在(0,0) ，
x2 y2 4
半径为2 的圆
以z 轴为中心轴的圆柱面
y x 1 斜率为1的直线 平行于z 轴的平面
练习题
一、填空题：
1、与Z 轴和点 A(1 , 3 ,1) 等距离的点的轨迹方程是
x2 a2
y2
z2 c2
1
椭 球 面
（3）抛物线 y2 2 pz 绕z 轴； x 0
x2 y2 2 pz 旋转抛物面
三、柱面
定义 平行于定直线并沿定曲线 C 移动的直线 L 所形成的曲面称为柱面.
这条定曲线 C叫 柱面的准线， 动直线 叫L 柱 面的母线.
观察柱面的形
当平面z c 上下移动时，
c
得到一系列圆
o
y
圆心在(1,2,c)，半径为 1 c x
半径随c 的增大而增大. 图形上不封顶，下封底．
以上几例表明研究空间曲面有两个基本问题： （1）已知曲面作为点的轨迹时，求曲面方程．
（讨论旋转曲面） （2）已知坐标间的关系式，研究曲面形状．
（讨论柱面、二次曲面）
以下给出几例常见的曲面.
例 1 建立球心在点M0 ( x0 , y0 , z0 )、半径为R
的球面方程.
解 设M( x, y, z)是球面上任一点，
根据题意有 | MM0 | R
x x0 2 y y0 2 z z0 2 R 所求方程为 x x0 2 y y0 2 z z0 2 R2
_____________；
2、以点O(2 ,2 , 1)为球心，且通过坐标原点的球面
x2 a2
z c
2 2
1分别绕x
轴和z 轴；
绕x 轴旋转
x2 a2
y2 c2
z2
Hale Waihona Puke 1旋 转绕z 轴旋转
x2 a2
y2
z2 c2
1
双 曲 面
y2 （2）椭圆 a 2
z2 c2
1绕y
轴和z
轴；
x 0
绕 y 轴旋转
y2 a2
x2 c2
z2
1
旋 转
绕z 轴旋转
角．试建立顶点在坐标原点，旋转轴为z 轴，半顶
角为 的圆锥面方程．
z
解 yoz面上直线方程为 z y cot
圆锥面方程
z x2 y2 cot x
M1(0, y1, z1 )
o
y
M( x, y, z)
例6 将下列各曲线绕对应的轴旋转一周，求 生成的旋转曲面的方程．
（1）双曲线
同理： yoz 坐标面上的已知曲线 f ( y, z) 0 绕 y 轴旋转一周的旋转曲面方程为
f y, x2 z2 0.
例 5 直线L绕另一条与L相交的直线旋转一周，
所得旋转曲面叫圆锥面．两直线的交点叫圆锥面的
顶点，两直线的夹角
0
2
叫圆锥面的半顶
所求方程为
x
22
y
12
z
42
116 .
3
3 9
例 3 已知A(1,2,3)，B(2,1,4)，求线段AB 的
垂直平分面的方程.
解 设M( x, y, z)是所求平面上任一点， 根据题意有 | MA || MB |,
x 12 y 22 z 32
x 22 y 12 z 42 ,
化简得所求方程 2x 6 y 2z 7 0.
例4 方程 z ( x 1)2 ( y 2)2 1的图形是怎样的？
解 根据题意有 z 1
z
用平面z c 去截图形得圆：
( x 1)2 ( y 2)2 1 c (c 1)