小学数学思维导图 全

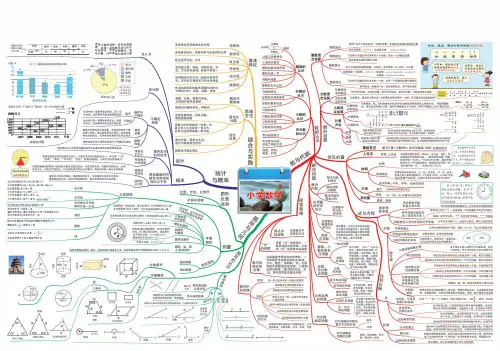
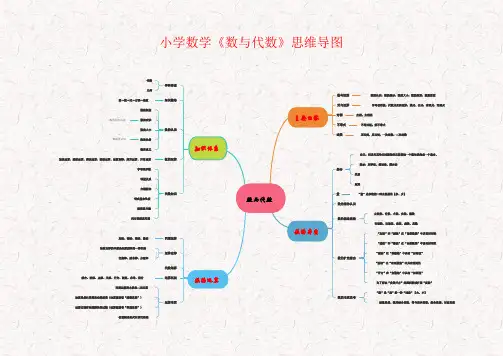
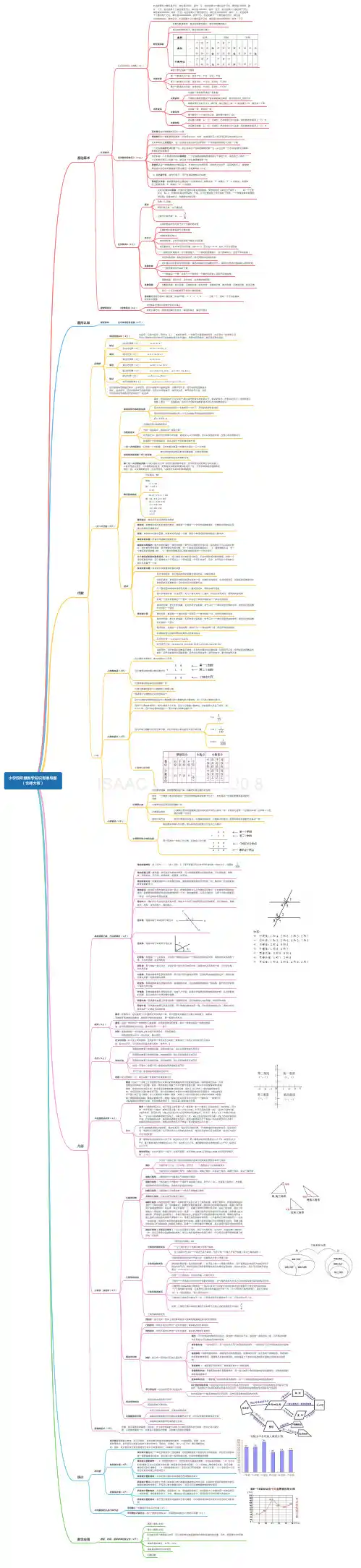
小学数学《数与代数》思维导图

数与代数 数的本质

数的运算 四则运算

运算定律 代数运算

知识体系 学科体系 知识脉络

集合 量 数的整体认识 “量”是事物的一种自然属性【多、少】

数的概念建构

运算拓展 运算本质

数的扩充缘由

数的本质思考

数的认识 数的运算 代数知识

代数 几何 量→数→式→方程→函数 数的概念 数的表示 数的大小 数的性质 数的意义 数的初步认识

数的再认识 加法运算、减法运算、乘法运算、除法运算、运算定律、乘方运算、开方运算 字母表示数 等量关系 方程概念 等式基本性质 解简易方程 列方程解应用题

定义：把具有某种共同属性的元素看做一个整体就构成一个集合。 表示：列举法、描述法、图示法 关系 运算

自然数、分数、小数、负数、整数 有理数、无理数、实数、虚数、复数 “加法”和“减法”在“自然数集”中具有封闭性 “减法”和“除法”在“自然数集”中没有封闭性 “减法”在“整数集”中具有“封闭性” “除法”在“有理数集”中具有封闭性 “开方”在“实数集”中具有“封闭性” 为了解决“负数开方”问题把数域扩到“复数” “数”是“量”的一种“抽象”【大、小】 抽象思想、数形结合思想、符号表示思想、集合思想、对应思想

加法、减法、乘法、除法 运算定律的本质是运算规律的一种归纳 交换律、结合律、分配率

乘方、阶乘、点乘、叉乘、开方、极限、求导、积分 四则运算的本质是二元运算 运算是量化思想的必然结果（运算蕴涵着“建模思想”） 运算过程即问题解决的过程（运算蕴涵着“推理思想”） 位值制是竖式计算的基础

主要内容 数与运算 式与运算 方程 不等式 函数

数的认识；数的表示；数的大小；数的运算；数量的估 字母表示数；代数式及其运算；整式、分式；有理式、无理式 方程；方程组 不等式组；解不等式 正比例、反比例；一次函数、二次函数

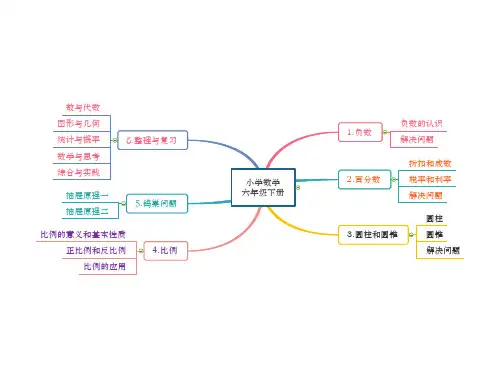
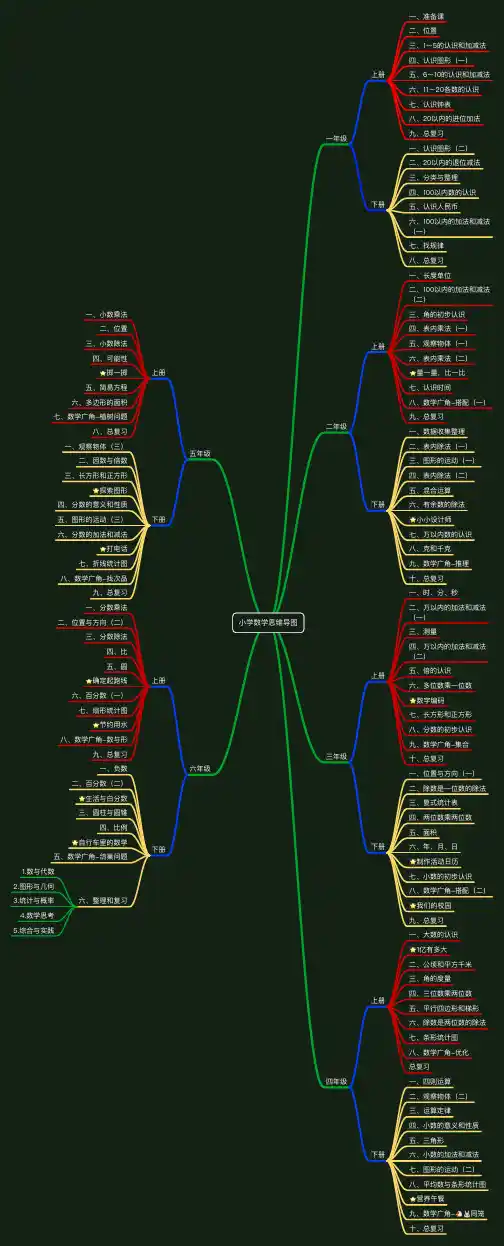
⼩小学数学思维导图⼀一年年级上册⼀一、准备课⼆二、位置三、1～5的认识和加减法四、认识图形（⼀一）五、6～10的认识和加减法六、11～20各数的认识七、认识钟表⼋八、20以内的进位加法九、总复习下册⼀一、认识图形（⼆二）⼆二、20以内的退位减法三、分类与整理理四、100以内数的认识五、认识⼈人⺠民币六、100以内的加法和减法（⼀一）七、找规律律⼋八、总复习⼆二年年级上册⼀一、⻓长度单位⼆二、100以内的加法和减法（⼆二）三、⻆角的初步认识四、表内乘法（⼀一）五、观察物体（⼀一）六、表内乘法（⼆二）量量⼀一量量，⽐比⼀一⽐比七、认识时间⼋八、数学⼴广⻆角-搭配（⼀一）九、总复习下册⼀一、数据收集整理理⼆二、表内除法（⼀一）三、图形的运动（⼀一）四、表内除法（⼆二）五、混合运算六、有余数的除法⼩小⼩小设计师七、万以内数的认识⼋八、克和千克九、数学⼴广⻆角-推理理⼗十、总复习三年年级上册⼀一、时、分、秒⼆二、万以内的加法和减法（⼀一）三、测量量四、万以内的加法和减法（⼆二）五、倍的认识六、多位数乘⼀一位数数字编码七、⻓长⽅方形和正⽅方形⼋八、分数的初步认识九、数学⼴广⻆角-集合⼗十、总复习下册⼀一、位置与⽅方向（⼀一）⼆二、除数是⼀一位数的除法三、复式统计表四、两位数乘两位数五、⾯面积六、年年、⽉月、⽇日制作活动⽇日历七、⼩小数的初步认识⼋八、数学⼴广⻆角-搭配（⼆二）我们的校园九、总复习四年年级上册⼀一、⼤大数的认识1亿有多⼤大⼆二、公顷和平⽅方千⽶米三、⻆角的度量量四、三位数乘两位数五、平⾏行行四边形和梯形六、除数是两位数的除法七、条形统计图⼋八、数学⼴广⻆角-优化总复习下册⼀一、四则运算⼆二、观察物体（⼆二）三、运算定律律四、⼩小数的意义和性质五、三⻆角形六、⼩小数的加法和减法七、图形的运动（⼆二）⼋八、平均数与条形统计图营养午餐九、数学⼴广⻆角-同笼⼗十、总复习六年年级上册⼀一、分数乘法⼆二、位置与⽅方向（⼆二）三、分数除法四、⽐比五、圆确定起跑线六、百分数（⼀一）七、扇形统计图节约⽤用⽔水⼋八、数学⼴广⻆角-数与形九、总复习下册⼀一、负数⼆二、百分数（⼆二）⽣生活与⽩白分数三、圆柱与圆锥四、⽐比例例⾃自⾏行行⻋车⾥里里的数学五、数学⼴广⻆角-鸽巢问题六、整理理和复习1.数与代数2.图形与⼏几何3.统计与概率4.数学思考5.综合与实践五年年级上册⼀一、⼩小数乘法⼆二、位置三、⼩小数除法四、可能性掷⼀一掷五、简易易⽅方程六、多边形的⾯面积七、数学⼴广⻆角-植树问题⼋八、总复习下册⼀一、观察物体（三）⼆二、因数与倍数三、⻓长⽅方形和正⽅方形探索图形四、分数的意义和性质五、图形的运动（三）六、分数的加法和减法打电话七、折线统计图⼋八、数学⼴广⻆角-找次品九、总复习。

超实用小学数学思维导图，让孩子快速掌握因数和倍数！
了解什么是因数，什么是倍数，以及数字的因数与倍数的范围最大值最小值。

对2、3、5这类比较特殊的数字，分别观察数字倍数的特征规律。

特别地，根据是否为2的倍数，可将数字划分为奇数和偶数。

质数的特征是只含1和本身两个因数，而合数除了1和本身之外还存在其他的因数。

其中1既不是质数也不是合数，最小的质数是2，最小的合数是4。

对于a×b=c（其中a,b,c都是不为0的整数），那么称a 和b都是c的因数，c是a、b的倍数，倍数和因数是相互依存的关系，不能单独的谈论谁是因数，谁是倍数。

因数针对的是非0的自然数，其数量是有限的，最小的为1，最大的为它本身。

非0整数的倍数有无限多个，最小的倍数是数字本身，数字的倍数可以无限大，不存在某个具体的最大倍数。

2、3、5的倍数有独特的特征，2的倍数个位上是0、2、4、6、8， 5的倍数个位上一般是0或5，而各个位上的数的和是3的倍数，那么这个数也是3的倍数。

根据数字是否是2的倍数，可将数字分为偶数和奇数，0是最小的偶数，1是最小的奇数。

质数的特征是只有1和它本身两个因数，而合数除了1和它本身之外还存在其他的因数。

最小的质数是2，最小的合数是4，其中1既不是质数也不是合数。

---。

右边起第五个数位是万位，单位是10000，读作：万，右边起第六个数位是十万位，单位是100000，读
作：十万，右边起第七个数位是百万位，单位是1000000，读作：百万，右边起第八个数位是千万位，
单位是10000000，读作：千万，右边起第九个数位是亿位，单位是100000000，读作：亿，右边起第
十个数位是十亿位，单位是1000000000，读作十亿，右边起第十一个数位是百亿位，单位是
10000000000，读作百亿，右边起第十二个数位是千亿位，单位是100000000000，读作：千亿
先将数字相乘，按照整数乘法计算，再确定积的小数点的位置
两角有一个公共顶点，而且两个角的两边是另一个角两边的反向延长线，具有这样关系的两个
两个角有一条公共边，它们的另一边互为反向延长线，具有这样关系的两个角，互为邻补角，
两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样
边形；两组对边分别相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形
度的平行四边形，正方形是四条边相等的长方形
时间单。