自由落体运动例题及习题

高三物理自由落体运动试题答案及解析1.在真空中，将苹果和羽毛同时从同一高度由静止释放，下列频闪照片中符合事实的是：【答案】C【解析】在真空中，轻重物体下落的一样快，故选项AB错误；又因为自由落体运动是匀加速运动，每经过相同时间，间隔越来越大，故选项C正确，D错误。

【考点】自由落体运动2.一个同学在研究小球自由落体运动时，用频闪照相连续记录下小球的位置如图所示。

已知闪光周期为s，测得x1=7.68cm，x3=12.00cm，用上述数据通过计算可得小球运动的加速度约为_______m/s2，图中x2约为________cm。

（结果保留3位有效数字）【答案】 9.72, 9.84【解析】根据可以得出，从而求出物体运动的加速度．同理可以根据，.【考点】测定匀变速直线运动的加速度3.若从砖墙前的某高处使一个石子由静止自由落下，用照相机拍摄石子在空中的照片如图所示，由于石子的运动，它在照片上留下了一条模糊的径迹AB。

已知该照相机的曝光时间为0.015s，每块砖的平均厚度为6cm，这个石子大约是从距离位置A多高处自由落下A．1m B．3m C．5m D．7m【答案】.B【解析】石子在曝光时间内的平均速度为可近似将此速度看成是石子到A点时的瞬间速度，取g=10m/s2,根据v2-0=2gh ，解得：h=3.2m，选项B正确。

【考点】自由落体运动的规律.4.（18分）如图甲所示，平行金属导轨竖直放置，导轨间距为L＝1m，上端接有电阻R1＝3，下端接有电阻R2＝6，虚线OO′下方是垂直于导轨平面的匀强磁场．现将质量m＝0.1 kg、电阻不计的金属杆ab，从OO′上方某处垂直导轨由静止释放，杆下落0.2 m过程中始终与导轨保持良好接触，加速度a与下落距离h的关系图象如图乙所示. 求：（1）磁感应强度B；（2）杆下落0.2 m过程中通过金属杆的电荷量q.【答案】 (1) 2 T (2) 0.15 C【解析】(1)由图象知，杆自由下落距离是0.05 m，当地重力加速度g＝10 m/s2，则杆进入磁场时的速度（2分）由乙图象知，杆进入磁场时加速度a＝－g＝－10 m/s2 （1分）＝ma （2分）由牛顿第二定律得mg－F安回路中的电动势E＝BLv （1分）杆中的电流I＝（1分）＝（2分）R并＝BIL＝（1分）F安得B＝＝2 T （1分）(2)杆在磁场中运动产生的平均感应电动势（2分）杆中的平均电流（2分）通过杆的电荷量（2分）通过杆的电荷量q＝0.15 C （1分）【考点】本题考查落体运动的规律、牛顿运动定律以及电磁感应现象中的相关计算等。

自由落体运动典型例题 [例1]从离地500m的空中自由落下一个小球，取g= 10m/s2，求： （1）经过多少时间落到地面； （2）从开始落下的时刻起，在第1s内的位移、最后1s内的位移； （3）落下一半时间的位移.[例2] 一个物体从H高处自由落下，经过最后196m所用的时间是4s，求物体下落H高所用的总时间T和高度H是多少？取g=9.8m/s2，空气阻力不计.[例3] 气球下挂一重物，以v0=10m/s匀速上升，当到达离地高h=175m处时，悬挂重物的绳子突然断裂，那么重物经多少时间落到地面？落地的速度多大？空气阻力不计，取g=10m/s2.[例4] 如图所示，A、B两棒长均为 L=1m，A的下端和 B的上端相距s=20m.若 A、B同时运动，A做自由落体、 B做竖直上抛，初速度v0=40m/s，求： （1） A、 B两棒何时相遇；（2） 从相遇开始到分离所需的时间.[例5] A、B两球，A从距地面高度为h处自由下落，同时将B球从地面以初速v0竖直上抛，两球沿同一竖直线运动.试求以下两种情况下，B球初速度v0的取值范围： ①B球在上升过程中与A球相遇；　②B球在下落过程中与A球相遇.　1. 对物体运动的描述，以下说法正确的是（ ）A. 加速度变化的运动可以是直线运动B. 加速度不变的运动一定是直线运动C. 加速度减小的运动是减速运动，加速度增加的运动是加速运动D. 当运动物体的加速度改变时，速度也同时改变，因此向右运动的物体，有向左的加速度时，运动方向立即向左。

2. 甲乙两物体均做直线运动，其速度——时间图象如图所示，则下列说法正确的是（）A. 甲、乙两物体相向运动B. 甲、乙两物体都做匀变速直线运动C. 时刻两物相遇D. 时刻两物体相遇3. 一小球从4m高处落下，反弹后1m高处被接住，这一过程中小球的位移及路程分别是（）A. 5m、5mB. 3m、5mC. 3m、4mD. 1m、4m4. 一个做直线运动的物体，某时刻速度大小是，那么这个物体（）①在这一时刻前0.1s内的位移一定是1m；②从这一时刻起1s内的位移一定是1m③从这一时刻起，10s内的位移可能有50m；④如从这一时刻起开始匀速运动，那么它继续通过1000m路程，所需时间一定是100s以上说法正确的是（）A. ①②B. ①④C. ③④D. ②④5. 一辆车以速度v行驶了的路程，接着以的速度跑完了余下的路程，若全程的平均速度是，则速度v的大小为（）A. B. C. D.6. 一质点沿直线运动，在t时间内的位移为S，它在位移中点处速度为，在一半时间的速度为，则和的关系叙述，不正确的是（）A. 当质点做匀加速直线运动时，B. 当质点做匀减速直线运动时，C. 当质点做匀速直线运动时，D. 当质点做匀减速直线运动时，7. 一个运动员在百米赛跑中，测得他在50米处的瞬时速度是9m/s，12秒末到终点时的瞬时速度为11m/s，则全程内的平均速度大小为（）A. 9m/sB. 10m/sC. 11m/sD. 8.33m/s8. A、B、C三点在同一直线上，一个质点自A点从静止开始做匀加速直线运动，经过B点时速度为，到C点时速度为，则AB与BC两段距离之比为（）A. B. 1:2 C. 1:3 D.9. 如图所示，质点做匀加速运动，由A点到C点，在A点的速度为，在AC中点B的速度，在C点的速度，假若在AB段加速度为，在BC段的加速度为，而且。

匀变速直线运动的特例 自由落体运动【基础知识】一、自由落体运动：1、定义：2、运动性质:初速度为 加速度为 的 运动.3、运动规律：由于其初速度为零，公式可简化为v t = h = v t 2 =2gh二、竖直上抛运动：1、定义：2、运动性质:初速度为v 0，加速度为 －g 的 运动.3、处理方法：⑴ 将竖直上抛运动全过程分为上升和下降两个阶段来处理。

上升阶段为初速度为v 0，加速度为 －g 的 运动，下降阶段为 。

要注意两个阶段运动的对称性。

⑵ 将竖直上抛运动全过程视为 的运动4、两个推论： ①上升的最大高度gv h m 220= ②上升最大高度所需的时间gv t m 0= 5、特殊规律：由于下落过程是上升过程的逆过程,所以物体在通过同一段高度位置时，上升速度与下落速度大小 ,物体在通过同一段高度过程中，上升时间与下落时间 。

1．关于自由落体运动的加速度,下列说法中正确的是（ ）A 、重的物体下落的加速度大B 、同一地点,轻、重物体下落的加速度一样大C 、这个加速度在地球上任何地方都一样大D 、这个加速度在地球赤道比在地球北极大2。

自由落体运动在任何两个相邻的1s 内，位移的增量为 ［ ]A 。

1mB 。

5m C.10m D 。

不能确定3.甲物体的重量比乙物体大5倍,甲从H 高处自由落下，乙从2H 高处与甲物体同时自由落下，在它们落地之前,下列说法中正确的是 [ ］A 。

两物体下落过程中,在同一时刻甲的速度比乙的速度大B 。

下落1s 末，它们的速度相同C 。

各自下落1m 时，它们的速度相同D.下落过程中甲的加速度比乙的加速度大4.甲、乙两物体分别从10m和20m高处同时自由落下，不计空气阻力，下面描述正确的是［]A。

落地时甲的速度是乙的1/2B。

落地的时间甲是乙的2倍C。

下落1s时甲的速度与乙的速度相同D。

甲、乙两物体在最后1s内下落的高度相等5.长为5m的竖直杆下端距离一竖直隧道口为5m,若这个隧道长也为5m，让这根杆自由下落,它通过隧道的时间为［］6。

自由落体运动典型例题：例1 从离地500m 的空中自由落下一个小球，取g= 10m/s 2，求：（1）经过多少时间落到地面；（2）从开始落下的时刻起，在第1s 内的位移、最后1s 内的位移；解析 由h=500m 和运动时间，根据位移公式可直接算出落地时间、第1s 内位移和落下一半时间的位移．最后1s 内的位移是下落总位移和前（n —1）s 下落位移之差．[]1h =12解（）由，得落地时间：×gt t h g s s 2225001010===（2）第1s 内的位移：h gt m 112212121015===×× 因为从开始运动起前9s 内的位移为： h gt m m 99221212109405===×× 所以最后1s 内的位移为：h 10=h-h 9=500m-405m=95m（3）落下一半时间即t'=5s ，其位移为h gt m m 5212121025125==='×× 说明 根据初速为零的匀加速运动位移的特点，由第1s 内的位移h 1=5m ，可直接用比例关系求出最后1s 内的位移，即h 1∶h 10=1∶19∴ h 10=19h 1=19×5m=95m同理，若把下落全程的时间分成相等的两段，则每一段内通过的位移之比：h t/2∶h t =12∶22=1∶4∴×h h m m t t /21414500125=== 例2 一个物体从H 高处自由落下，经过最后196m 所用的时间是4s ，求物体下落H 高所用的总时间T 和高度H 是多少？取g=9．8m/s 2，空气阻力不计．解析 根据题意画出小球的运动示意图（图1）其中t=4s ， h=196m ．解 方法1根据自由落体公式H gT H h g T t =-=-121222，(). 式（1）减去式（2），得h gTt gt =-122， ∴，×××，××T h gt gts H gT m m =+=+====121961298169842712129872401222..... 方法2 利用匀变速运动平均速度的性质由题意得最后4s 内的平均速度为v h t m s m s ===196449//. 因为在匀变速运动中，某段时间中的平均速度等于中点时刻的速度，所以下落至最后2s 时的瞬时速度为v v m s t '/.==49由速度公式得下落至最后2s 的时间t v g s s t ''.===49985， ∴××T t t s s s H gT m m =+=+====' (254271212)987240122 方法3 利用v －t 图象画出这个物体自由下落的v-t 图，如图2所示．开始下落后经时间（T —t ）和T 后的速度分别为g （T-t ）、 gT ． 图线的AB 段与t 轴间的面积表示在时间t 内下落的高度h ．。

自由落体运动练习1. 关于自由落体运动的加速度g ，下列说法正确的是：( )A ．同一地点的物体，无论轻重g 值一样大；B ．重的物体g 值大；C ．g 值在地面任何地方都一样大；D ．g 值在赤道处大于两极处。

2. 以下对物体做自由落体运动的说法正确的是：( )A ．物体开始下落时，速度为零，加速度也为零；B ．物体下落过程中，速度增大加速度保持不变；C ．物体下落过程中，速度和加速度同时增大；D ．物体下落过程中，速度的变化是个恒量。

3. 一个铁钉和一块小海棉从同一高处同时下落，总是铁钉先落地，这是因为：( )A ．铁钉比海棉重；B ．铁钉比海棉密度大；C ．海棉受到的空气阻力影响大；D ．海棉的体积大。

4．甲物体从高处自由下落一段时间后，乙物体从同一位置自由下落。

若以甲为参考系，则乙物体的运动状态是（甲乙均未着地前）：( )A ．相对静止；B ．向上做匀变速直线运动；C ．向下做匀速直线运动；D ．向上做匀速直线运动。

5. 自由下落的物体，自起点开始依次下落三段相等位移所用的时间的比是：( )A ．1：3：5；B ．1：4：9；C ．3:2:1；D ．1：)23(:)12(--。

6. 在深为8米的井口某处水滴每隔一定时间落下，当第五滴刚离开井口时，第一滴水正好落下，那么，这时第2滴水离进底的高度是：( )A ．2m ；B ．2.5m ；C ．2.9m ；D ．3.5m 。

7. 一小球从距地面为H 高处下落，下落H/4时的速度是落地的速度的：( )A ．1/2；B ．1/3；C ．1/4；D ．1/5。

8. 自由下落的物体，它下落一半高度所用的时间和全程所用的时间之比是：( )A ．1/2；B ．2；C ．22； D ．2。

9. 球A 和球B 先后由同一高度自由下落，B 比A 迟0.5s ，g = 10m/s 2，A 、B 均在下落时，以下判断正确的是：( )A ．A 相对B 作v = 5m/s 向下的自由落体运动； B ．B 相对A 作v = 5m/s 向上的竖直上抛运动；C ．B 相对A 作v = 5m/s 向下的匀速直线运动；D ．A 相对B 作v = 5m/s 向下的匀速直线运动。

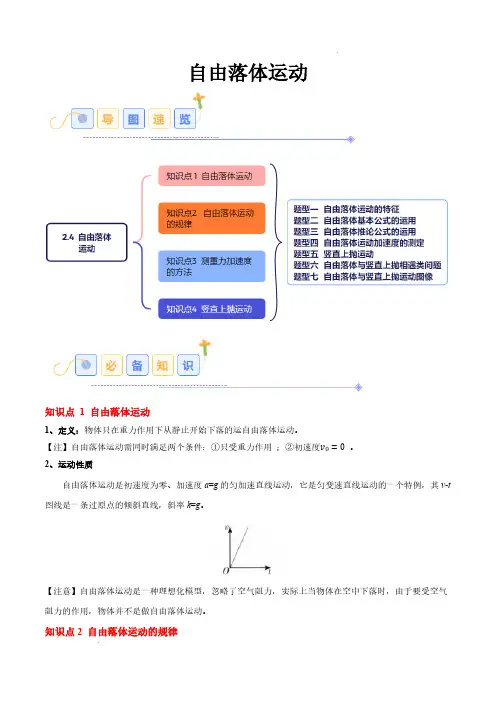
自由落体运动知识点 1 自由落体运动1、定义：物体只在重力作用下从静止开始下落的运自由落体运动。

【注】自由落体运动需同时满足两个条件：①只受重力作用；②初速度v0=0。

2、运动性质自由落体运动是初速度为零、加速度a=g的匀加速直线运动，它是匀变速直线运动的一个特例，其v-t 图线是一条过原点的倾斜直线，斜率k=g。

【注意】自由落体运动是一种理想化模型，忽略了空气阻力，实际上当物体在空中下落时，由于要受空气阻力的作用，物体并不是做自由落体运动。

知识点2 自由落体运动的规律1、重力加速度①定义：在同一地点，一切物体自由下落的加速度都相同，这个加速度叫自由落体加速度，又叫重力加速度，通常用g表示。

②方向：总是竖直向下。

③大小：在地球的不同地点，g的大小一般不相同，从赤道到两极，一般随着纬度的增大而增大，从海平面到高山，一般随着海拔高度的增大而减小。

计算中g一般取9.8m/s2，近似计算时，取10 m/s2。

2、自由落体运动的规律初速度为零的匀加速直线运动的公式及匀变速直线运动的相关推论式对自由落体运动都适用。

①基本公式速度公式：v t=g t位移公式：ℎ=12g t2速度与位移的关系式：v2t=2gℎ②推论平均速度：v=v t2=v2连续相等时间间隔T内下落的高度差：∆ℎ=g T2知识点3 测重力加速度的方法1、打点计时器法①利用如图1所示装置，让重物自由下落，利用打点计时器打出点迹清晰的纸带。

②对纸带上计数点间的距离h进行测量，利用g=ℎn―ℎn+1T2求出重力加速度。

2、频闪照相机法频闪照相机可以每间隔相等的时间拍摄一次，利用频闪照相机可追踪记录做自由落体运动的物体在各个时刻的位置，根据匀变速直线运动的推论∆ℎ=g T2可求出重力加速度g=∆ℎT2。

3、滴水法在水龙头正下方放一个盘，让水一滴一滴地滴下，使第1滴水碰到盘的瞬间第2滴水正好从水龙头口开始下落，依次持续下去。

用刻度尺测出水龙头口距盘面的高度h ，再测出每滴水下落的时间T ，其方法是：当听到某一滴水滴落在盘上的同时，开启停表开始计时，之后每落到盘上一滴水依次数1，2，3，…，当数到n 时按下停表停止计时，每一滴水滴下落的时间为T =tn ―1，由ℎ=12g T 2得g =2（n―1）2ℎt2。

自由落体运动(基础)小试身手: 一个物体从20m高的地方自由下落，到达地面时的速度多大？下落最后1s内的位移多大？（g取）练习题；1、某物体做自由落体运动，它在1s内，2s内，3s内位移之比它在第1s内，第2s内，第3s内位移之比s．2s末，3s末的速度之比2、物体从距地面高度为H处开始做自由落体运动，物体下落到地面时的速度大小为，当其速度等于着地时速度的时，物体距地面的高度为．3、做自由落体运动的物体，通过某一点时的速度为19.6m/s，这时物体下落高度是多少？物体下落了多长时间？4、一个物体从楼顶下落，在到达地面前最后1s内下落的高度为楼高的，求楼高？（）5、物体做自由落体运动，3s末落地，求出发点的高度？物体的平均速度？经过中间位置时的瞬时速度？（g取）6.一小钢珠由塔顶静止开始释放，最初的3秒内的位移为S1，最后3秒内的位移为S2，若S2—S1=6米，求塔高为多少？(g=10m/s2)自由落体运动(提高)小试身手: 一个做自由落体运动的物体落至地面前最后一秒钟内通过的路程是全程的一半，求它落到地面所需的时间。

练习题1、一石块从楼房阳台边缘向下做自由落体运动, 到达地面, 把它在空中运动的时间分为相等的三段, 如果它在第一段时间内的位移是 1.2m, 那么它在第三段时间内的位移是( )(A) 1.2m (B) 3.6m (C) 6.0m (D) 10.8m2、一个物体从某一高度做自由落体运动, 已知它第一秒内的位移恰为它最后一秒内位移的一半, g 取10m/s 2, 则它开始下落时距地面的高度为： ( )(A) 5m (B) 11.25m (C) 20m (D) 31.25m3、物体自楼顶处自由落下(不计空气阻力), 落到地面的速度为v ． 在此过程中, 物体从楼顶落到楼高一半处所经历的时间为： ( )(A) v/2 (B) v/(2g) (C) )2/(2g v (D) )2/()22(g v4、一物体从16 m 高的A 处自由落下，它经过B 点时的速率是落地时速率 的3 / 4 ，则B 点离地的高度为____ m 。

自由落体运动例题习题例1：一个物体从20m高的地方自由下落，到达地面时的速度多大？下落最后1s内的位移多大？（g取10m/s²）分析与解答：根据自由落体运动公式可得物体到达地面时的速度为：v = √(2gh) = √(2×10×20) ≈ 20m/s根据位移公式可得物体下落的时间t为：t = √(2h/g) = √(2×20/10) = 2s据题意最后1s以前物体下落的时间为1s，其位移为：s = vt - (1/2)gt² = 20×1 - (1/2)×10×1² = 10m例2：一只小球自屋檐自由下落，在窗口处撞击地面，求窗口的顶端距屋檐多少米？（取g内通过高度为h的窗口选题角度：考查自由落体运动位移与时间有关计算．解析1：设窗顶距离屋檐为x，则小球自屋檐到窗口的时间为：t1 = √(2h/g)小球从屋檐落至速度为v的位置历时为：t2 = v/g小球从窗口落地所用的时间为：t3 = √(2(h-x)/g)根据自由落体运动位移公式可得：h = (1/2)gt1² = (1/2)gt3² + vt2 + x代入t1、t2、t3的表达式，得：x = (1/2)g(t1² - t3²) - vt2代入已知数据，得：x = (1/2)×10×(2 - 2√(1 - x/h)) - 0×√(2h/g)化XXX：x = h(1 - √(1 - x/h))解析2：球经过窗口过程的中间时刻的瞬时速度为：v = √(2gh)设从屋檐落至速度为v的位置历时为t，则小球从屋檐到达窗口所用的时间为：t1 = t - t2根据自由落体运动位移公式可得：h = (1/2)gt² = (1/2)g(t1+t2)² + vt2 + x代入t1、t2的表达式，得：h = (1/2)g(t-t2+t2)² + vt2 + x化XXX：x = h - (1/2)gt² + vt2代入已知数据，得：x = h - 10 + 0 = h - 10综上可知，窗口的顶端距屋檐的距离为h-10米。

高一物理自由落体运动试题答案及解析1.(13分)某跳伞运动员做低空跳伞表演.他离开飞机后先做自由落体运动，直到距离地面125m处打开降落伞.伞张开后，他以14.3m/s2的加速度做匀减速运动，到达地面时速度为5m/s.求：（1）伞张开时运动员的速度；（2）运动员离开飞机时离地面的高度；（3）设跳伞运动员及伞的总质量为80kg，求跳伞运动员下落过程中运动员和降落伞整体所受的阻力.(g=10m/s2)【答案】（1）60m/s （2）305m （3）1944N【解析】⑴设伞张开时运动员的速度为v，对运动员减速过程应用(2分)(2分)⑵从运动员离开飞机到打开降落伞运动员做自由落体运动，下落的高度为h1由v2=2gh1(2分)得： (2分)运动员离开飞机时离地面的高度为H=h1+h2=180m+125m=305m (1分)⑶跳伞运动员下落过程中运动员和降落伞整体受重力及空气阻力由牛顿第二定律：mg－Ff=ma (2分)则：Ff=m(g－a)=80×(10+14.3)N=1944N (2分)【考点】本题考查运动学关系、自由落体运动和牛顿第二定律。

2.如图甲所示，两位同学根据课本提示的方法，利用自由落体运动做反应时间的测量。

如图乙所示，A点是开始时受测人手指的位置，B点是结束时受测人手指的位置，则受测人的反应时间大致为：A．0.6s B．0.5s C．0.4s D．0.3s【答案】D【解析】由图可知，在受测人的反应时间内直尺下落的高度为：，由自由落体运动规律得：，解之得：，故选D。

【考点】本题考查自由落体运动规律，意在考查考生灵活运用自由落体运动规律处理实际问题的能力。

3.（7分）小张利用高中学过的物理知识探测“深井”的深度。

他向“深井”丢下一块石块（有安全措施），同伴记录时间，经1.0秒，听到石块落底的声音。

若不计石块的初速度和声音回传时间的影响，重力加速度取10m/s2，试估算“深井”的深度。

【答案】5m【解析】可将石块的运动看成自由落体运动（3分）则由 h=gt2/2（2分）得“深井”估计深度为H估=5m（2分）【考点】自由落体运动4.让一轻一重两个石块同时从同一高处自由下落，空气阻力忽略不计，关于两石块的运动情况，下列说法正确的是()A．重的石块落得快，先着地B．在着地前的任一时刻，两石块具有相同的位移C．在着地前的任一时刻，两石块具有相同的速度D．两石块在下落这段时间内的平均速度相等【答案】BCD【解析】因忽略空气阻力，所以两石块都做自由落体运动，又从同一高度下落，运动性质和过程完全相同，所以不仅同时落地，而且任意时刻，丙石块所处高度、速度都相同，下落时间和位移相同，所以平均速度相同，所以选项A错误，BCD正确；【考点】自由落体运动5.(16分)两个物体用长L＝9.8 m的细绳连接在一起，从同一高度以1 s的时间差先后自由下落，当绳子拉紧时，第二个物体下落的时间是多少? （g取9.8 m/s2，并且物体的高度足够高）【答案】0.5s【解析】设当绳子拉紧时，第二个物体下落的时间为t，则第二个物体下落的高度为：①此时第一个物体下落的高度为：②其中h1－h2＝L③①②③式联立得，t＝0.5 s．【考点】本题考查自由落体运动。

高考物理-自由落体运动（含答案）-专题练习一、选择题1、一个铁钉与一根鸡毛同时从同一高度下落，总是铁钉先落地，这是因为最终的原因是（ ）A ．铁钉比鸡毛重．铁钉比鸡毛重B ．铁钉比鸡毛密度大．铁钉比鸡毛密度大C ．鸡毛受到的空气阻力大．鸡毛受到的空气阻力大D ．铁钉下落的加速度比鸡毛下落的加速度大．铁钉下落的加速度比鸡毛下落的加速度大2、一名宇航员在某星球上完成自由落体运动实验，让一个质量为2 kg 的小球从一定的高度自由下落，测得在第5 s 内的位移是18 m ，则（，则（，则（ ） A ．物体在2 s 末的速度是20 m/s B ．物体在第5 s 内的平均速度是3.6 m/s C ．物体在第2 s 内的位移是20 m D ．物体在5 s 内的位移是50m. m.3、某人在静止的湖面上竖直上抛一小铁球，小铁球上升到最高点后自由下落，穿过湖水并陷入湖底的淤泥中一段深度，不计空气阻力，取向上为正方向，在下面4个vt 图象中，最能反映小铁球运动过程的是（ ）94、甲、乙两物体，甲的质量为4kg 4kg，乙的质量为，乙的质量为2kg 2kg，不计空气阻力，甲从，不计空气阻力，甲从20m 高处自由落下，1s 后乙从同样高处自由落下，此后，在两物体落地之前，下列说法中正确的是后乙从同样高处自由落下，此后，在两物体落地之前，下列说法中正确的是( ( ( ) A.A.同一时刻甲的速度大同一时刻甲的速度大同一时刻甲的速度大 B.B.同一时刻两物体的速度相同同一时刻两物体的速度相同同一时刻两物体的速度相同C.C.两物体从起点各自下落两物体从起点各自下落1m 时的速度是相同的时的速度是相同的D.D.落地之前甲和乙的高度之差不断增大落地之前甲和乙的高度之差不断增大落地之前甲和乙的高度之差不断增大5、从某一高度相隔3s 先后自由释放两小球甲和乙，不计空气阻力，则它们在空中任意时刻（ ） A ．两球间速度之差越来越大．两球间速度之差越来越大 B ．两球速度之差始终保持不变．两球速度之差始终保持不变C ．两球间距离始终保持不变．两球间距离始终保持不变D ．乙至少需要6s 以上的时间才能追上甲以上的时间才能追上甲6、一个物体从H 高处自由下落，经时间t 落地，则它下落时，它下落的高度为（时，它下落的高度为（ ）A ．B ．C ．D ．7、一个物体做自由落体运动，取g=10m/s 2，则在物体下落的过程中（ ） ①物体第2s 末的速度为20m/s 20m/s②物体第2s 内的平均速度为10m/s 10m/s③物体前2s 内下落的高度为20m 20m④物体第2s 内下落的高度是10m 10m．．A ． ①②①②B ． ③④③④C ． ①③①③D D ． ②④②④8、钢球A 自塔顶自由落下2米时，钢球B 自离塔顶6米距离处自由落下，两钢球同时到达地面，不计空气阻力，则塔高为（不计空气阻力，则塔高为（ ）A ． 24mB ． 16mC ． 12mD ． 8m9、做自由落体运动的甲、乙两物体所受的重力之比为2：1，下落高度之比为l ：2，则，则 A ．下落时间之比是1：2 2 B ．落地速度之比是．落地速度之比是1：1C ．落地速度之比是1：D ．下落过程中的加速度之比是2：11010、．某物体做自由落体运动，从起点起向下将其分成三段，使物体通过三段位移的时间之比为、．某物体做自由落体运动，从起点起向下将其分成三段，使物体通过三段位移的时间之比为1∶2∶3，则此三段位移之比是，则此三段位移之比是( ( ( )A ．1∶1∶1 1 B．1∶3∶5 C ．1∶4∶9 9D ．1∶8∶27二、多项选择1111、关于自由落体运动、关于自由落体运动、关于自由落体运动((g ＝10 m/s 2)，下列说法中正确的是，下列说法中正确的是( ( ( ) A ．它是竖直向下，v 0＝0、a ＝g 的匀加速直线运动的匀加速直线运动 B ．在开始连续的三个1 s 内通过的位移之比是1∶3∶5 C ．在开始连续的三个1 s 末的速度大小之比是1∶2∶3D ．从开始运动到距下落点5 m 、10 m 、15 m 所经历的时间之比为1∶2∶31212、一石块从、一石块从30m 高处开始做自由落体运动，（高处开始做自由落体运动，（g=10m/s g=10m/s 2，取竖直向下为正方向）则石块下落后（ ）A ．第1s 内的位移为5m 5mB ．第3s 末的速度为30m/s 30m/sC ．第2s 内的平均速度为10m/s 10m/sD ．3s 内的平均速度为10m/s 1313、、自由落体运动的物体，先后经过空中M,N 两点时的速度分别为1和2。

高一物理《自由落体运动》专项练习（A）一、选择题1.甲物体的重力是乙物体的3倍，它们在同一高度处同时自由下落，则下列说法中正确的是 ( C )A.甲比乙先着地B.甲比乙的加速度大C.甲、乙同时着地D.无法确定谁先着地2.关于自由落体运动，下列说法正确的是( AC)A.某段时间的平均速度等于初速度与末速度和的一半B.某段位移的平均速度等于初速度与末速度和的一半C.在任何相等时间内速度变化相同D.在任何相等时间内位移变化相同3.自由落体运动在任何两个相邻的1s内，位移的增量为( C )A.1mB.5mC.10mD.不能确定4.甲物体的重量比乙物体大5倍，甲从H高处自由落下，乙从2H高处与甲物体同时自由落下，在它们落地之前，下列说法中正确的是 ( BC )A.两物体下落过程中，在同一时刻甲的速度比乙的速度大B.下落1s末，它们的速度相同C.各自下落1m时，它们的速度相同D.下落过程中甲的加速度比乙的加速度大5从地面竖直上抛一物体A，同时在离地面某一高度处有另一物体B自由落下，两物体在空中同时到达同一高度时速率都为v，则下列说法中正确的是( AC )A．物体A上抛的初速度和物体B落地时速度的大小相等，都是2v；B．物体A、B在空中运动的时间相等；C．物体A能上升的最大高度和B开始下落时的高度相同；D．两物体在空中同时达到同一个高度处一定是B物体开始下落时高度的中点．6.长为5m的竖直杆下端距离一竖直隧道口为5m，若这个隧道长也为5m，让这根杆自由下落，它通过隧道的时间为( B )7.图1所示的各v－t图象能正确反映自由落体运动过程的是 ( BD )8.甲、乙两物体分别从10m和20m高处同时自由落下，不计空气阻力，下面描述正确的是 (C)A.落地时甲的速度是乙的1/2B.落地的时间甲是乙的2倍C.下落1s时甲的速度与乙的速度相同D.甲、乙两物体在最后1s内下落的高度相等9．关于自由落体运动，下列说法正确的是（ AC ）A．自由落体运动是竖直方向的匀加速直线运动B．竖直方向的位移只要满足x1:x2:x3…=1：4：9…的运动就是自由落体C．自由落体运动在开始连续的三个2 s 内的路程之比为1：3：5D．自由落体运动在开始连续的三个1 s 末的速度之比为1：3：5二、填空题9.从高h 处自由下落的物体，落到地面所用的时间是t=_____，落地时的速度v=______，物体落下 h/3时和落下全程时的速度之比是______，各自所经历的时间之比是______.10.自由下落的物体在头ts 内，头 2ts 内和头 3ts 内下落的高度之比是______；在第 1个ts 内、第2个ts 内、第3个ts 内下落的高度之比又是______.11.物体从高270m 处自由下落，把它运动的总时间分成相等的3段，则这3段时间内下落的高度分别为______m 、______m 和______m ；若把下落的总高度分成相等的三段，则物体依次下落这3段高度所用的时间之比为____________.12.一物体从45m 高处自由下落，在最后1s 通过的高度是______s ，最后1s 的初速度是______m/s ，最后 1s 内的平均速度是______m/s 。

1、取一根长2 m左右的细线，5个铁垫圈和一个金属盘。

在线的一端系上第一个垫圈，隔12 cm再系一个，以后每两个垫圈之间的距离分别为36 cm、60 cm、84 cm，如图3所示，站在椅子上，向上提起线的另一端，让线自由垂下，且第一个垫圈紧靠放在地面上的金属盘内。

松手后开始计时，若不计空气阻力，则第2、3、4、5各垫圈( )图3A．落到盘上的声音时间间隔越来越大B．落到盘上的声音时间间隔相等C．依次落到盘上的速率关系为1∶∶∶2D．依次落到盘上的时间关系为1∶(－1)∶(－)∶(2－)2、为了研究蹦床运动员跃起的高度，可在弹性网上安装压力传感器，利用传感器记录运动员运动过程中对弹性网的压力大小，并由计算机作出压力—时间图象（如图所示）。

运动员在空中运动时可视为质点，则可依据传感器描绘的F—t图象估算出运动员跃起的最大高度为（g取10m/s2）A．1.5m B．1.8m C．5.0mD．7.2m3、甲、乙两物体质量之比为m甲∶m乙 = 5∶1，甲从高H处自由落下的同时乙从2H处自由落下，不计空气阻力，以下说法错误的是（）A．在下落过程中，同一时刻二者速度相等B．甲落地时，乙距地面的高度为HC．甲落地时，乙的速度的大小为D．甲、乙在空中运动的时间之比为1∶24、小球从靠近竖直砖墙的某位置由静止释放，用频闪方法拍摄的小球位置如图中1、2、3和4所示。

已知连续两次闪光的时间间隔均为T，每块砖的厚度为d。

由此可知小球A．下落过程中的加速度大小约为B．经过位置3时的瞬时速度大小约为C．经过位置4时的瞬时速度大小约为D．从位置1到4过程中的平均速度大小约为5、在地质、地震、勘探、气象和地球物理等领域的研究中，需要精确的重力加速度g值，g值可由实验精确测定。

近年来测g值的一种方法叫“对称自由下落法”，它是将测g归于测长度和时间，以稳定的氦氖激光的波长为长度标准，用光学干涉的方法测距离，以铷原子钟或其他手段测时间，能将g值测得很准，具体做法是：将真空长直管沿竖直方向放置，自其中O点向上抛小球又落至原处的时间为T2，在小球运动过程中经过比O点高H的P点，小球离开P点至又回到P点所用的时间为T1，测得T1 、T2和H，可求得g等于A． B． C． D．6、在反恐演习中，中国特种兵进行了飞行跳伞表演。

自由落体运动典型例题[例1]从离地500m的空中自由落下一个小球，取g= 10m/s2，求：（1）通过量少时刻落到地面；（2）从开始落下的时刻起，在第1s内的位移、最后1s内的位移；（3）落下一半时刻的位移.[分析]由h=500m和运动时刻，依照位移公式可直接算出落地时刻、第1s内位移和落下一半时刻的位移.最后1s内的位移是下落总位移和前（n—1）s下落位移之差.（2）第1s内的位移：因为从开始运动起前9s内的位移为：因此最后1s内的位移为：h10=h-h9=500m-405m=95m（3）落下一半时刻即t'=5s，其位移为[说明]依照初速为零的匀加速运动位移的特点，由第1s内的位移h1=5m，可直接用比例关系求出最后1s内的位移，即h1∶h10=1∶19∴ h10=19h1=19×5m=95m同理，假设把下落全程的时刻分成相等的两段，那么每一段内通过的位移之比：h t/2∶h t=12∶22=1∶4[例2]一个物体从H高处自由落下，通过最后196m所用的时刻是4s，求物体下落H高所用的总时刻T和高度H是多少？取g=s2，空气阻力不计.[分析]依照题意画出小球的运动示用意（图1）其中t=4s， h=196m.[解]方式1 依照自由落体公式式（1）减去式（2），得方式2 利用匀变速运动平均速度的性质由题意得最后4s内的平均速度为因为在匀变速运动中，某段时刻中的平均速度等于中点时刻的速度，因此下落至最后2s时的瞬时速度为由速度公式得下落至最后2s的时刻方式3 利用v－t图象画出那个物体自由下落的v-t 图，如图2所示.开始下掉队经时刻（T—t）和T后的速度别离为g（T-t）、gT. 图线的AB段与t轴间的面积表示在时刻t内下落的高度h.。

由[例3]气球下挂一重物，以v0=10m/s匀速上升，当抵达离地高h=175m处时，悬挂重物的绳索突然断裂，那么重物经多少时刻落到地面？落地的速度多大？空气阻力不计，取g=10m/s2.[分析]那个地址的研究对象是重物，原先它随气球以速度v0匀速上升.绳索突然断裂后，重物可不能当即下降，将维持原先的速度做竖直上抛运动，直至最高点后再自由下落.[解]方式1 分成上升时期和下落时期两进程考虑绳索断裂后重物可继续上升的时刻和上升的高度别离为故重物离地面的最大高度为H=h+h1=175m＋5m=180m.重物从最高处自由下落，落地时刻和落地速度别离为v t=gt2=10×6m/s=60m/s.因此从绳索突然断裂到重物落地共需时刻t=t1＋t2=1s＋6s=7s.方式2 从统一的匀减速运动考虑从绳索断裂开始计时，经时刻t最后物体落至抛出点下方，规定初速方向为正方向，那么物体在时刻t内的位移h= -175m.由位移公式或 t2-2t-35=0，取合明白得，得 t=7s.因此重物的落地速度为v t=v0-gt=10m/s-10×7m/s= -60m/s.其负号表示方向向下，与初速方向相反.[说明]从统一的匀减速运动考虑，比分段计算方便得多，只是在应历时，需注意位移、速度等物理量的方向，那个物体从绳索断裂到落地进程中的v-t图如下图.[例4]如下图，A、B两棒长均为 L=1m，A的下端和 B的上端相距 s=20m.若 A、B同时运动，A做自由落体、B做竖直上抛，初速度v0=40m/s，求：（1） A、 B两棒何时相遇；（2）从相遇开始到分离所需的时刻.[分析]那个地址有两个研究对象：A棒和B棒，同时别离做不同的运动.相遇时两棒位移大小之和等于s.从相碰到分离两棒位移大小之和等于2L.[解]（1）设经时刻t两棒相遇，由得（2）从相遇开始到两棒分离的进程中，A棒做初速不等于零的匀加速运动，B棒做匀减速运动.设那个“擦肩而过”的时刻为△t，由式中v A=gt，v B=v0-gt.代入后得[说明]上面是从地面参考系所观看到的两个物体的运动情形列式计算的，比较麻烦.在第（2）小题中，还常容易误以为从相遇开始A棒仍做自由落体运动而造成错误.由于竖直上抛运动能够看成一个向上的匀速运动和一个自由落体的合运动，因此，若是以A棒为参照物，即从A棒上去观看B棒，B棒向上做着速度为v0的匀速运动，于是当即可得（1）两棒相遇时刻（2）两棒从相碰到分离的时刻[例6] A、B两球，A从距地面高度为h处自由下落，同时将B球从地面以初速v0竖直上抛，两球沿同一竖直线运动.试求以下两种情形下，B球初速度v0的取值范围：①B球在上升进程中与A球相遇；②B球在下落进程中与A球相遇.[分析]此题考察两个物体两种运动特点，和它们之间彼此联系.解答时对特殊状态——临界点的分析是关键的.解决此题时，画出运动示用意，找准关系，运用规律求解即得.[解]B球做竖直上抛运动（全进程中）：由于 AB相遇不时刻相等t1=t2=t，且h1+h2=ht∴ t=h/v0设B球上升到最大高度时，与球A相遇，如图1，B球上升到最大高度时刻为v0/g.由此可知，要使AB在B球上升进程中与A相遇，只要v0/g≥t即可.B球就会在上升时与A球相遇，，如图2是AB还能相遇的最小速度，因此要知足在下落中相遇，需知足[说明]（1）此题要成立时刻和位移关系，同时，依照题设条件.寻觅临界点，此题的临界点在B球上，即B 球达最大高度和B球落地时，成立速度与时刻的关系.（2）值得说明的是，复杂的运动很难在分析时成立物理图景，方法是对每一个物体运动进程认真分析以后，据各自运动特点成立联系.。

高三物理自由落体运动试题答案及解析1.(18分)如图所示，竖直平面内有无限长、不计电阻的两组平行光滑金属导轨，宽度均为L=0.5m，上方连接一个阻值R=1Ω的定值电阻，虚线下方的区域内存在磁感应强度B=2T的匀强磁场．完全相同的两根金属杆1和2靠在导轨上，金属杆与导轨等宽且与导轨接触良好，电阻均为r=0.5Ω．将金属杆1固定在磁场的上边缘（仍在此磁场内），金属杆2从磁场边界上方h=0.8m处由静止释放，进入磁场后恰作匀速运动．(g取10m/s2)求：（1）金属杆的质量m为多大？（2）若金属杆2从磁场边界上方h1=0.2m处由静止释放，进入磁场经过一段时间后开始匀速运动．在此过程中整个回路产生了1.4J的电热，则此过程中流过电阻R的电量q为多少？（3）金属杆2仍然从离开磁场边界h1=0.2m处由静止释放，在金属杆2进入磁场的同时由静止释放金属杆1，两金属杆运动了一段时间后均达到稳定状态，试求两根金属杆各自的最大速度．（已知两个电动势分别为E1、E2不同的电源串联时，电路中总的电动势E=E1+E2．）【答案】0.2kg 0.65c v1=1m/s，v2=3m/s【解析】（1）金属杆2进入磁场前做自由落体运动，vm==m/s=4m/s （1分）金属杆2进入磁场后受两个力平衡：mg=BIL，（1分）且 E=BLvm（1分）（1分）解得m===0.2kg （2分）金属杆2从下落到再次匀速运动的过程中，能量守恒（设金属杆2在磁场内下降h2）：mg(h1+h2)=+Q（2分）（2分）解得h2=1=……=1.3m（1分）金属杆2进入磁场到匀速运动的过程中，，，q=（3分）解得q=c=0.65c （1分）（3）金属杆2刚进入磁场时的速度v==m/s=2m/s释放金属杆1后，两杆受力情况相同，且都向下加速，合力等于零时速度即最大。

mg=BIL，且， E1=BLv1，E2=BLv2整理得到：v1+ v2=（2分）代入数据得v1+ v2="4" m/s因为两个金属杆任何时刻受力情况相同，因此任何时刻两者的加速度也都相同，在相同时间内速度的增量也必相同，即：v 1-0 =v2- v （3分）代入数据得v2= v1+2 （画出v-t图，找到两者速度差值(v2-v1)恒为2m/s的，同样给分）联立求得：v1=1m/s，v2=3m/s （2分）【考点】本题考查自由落体运动、功能关系、感应电动势。

1、取一根长2 m左右的细线，5个铁垫圈和一个金属盘。

在线的一端系上第一个垫圈，隔12 cm再系一个，以后每两个垫圈之间的距离分别为36 cm、60 cm、84 cm，如图3所示，站在椅子上，向上提起线的另一端，让线自由垂下，且第一个垫圈紧靠放在地面上的金属盘内。

松手后开始计时，若不计空气阻力，则第2、3、4、5各垫圈( )图3A．落到盘上的声音时间间隔越来越大B．落到盘上的声音时间间隔相等C．依次落到盘上的速率关系为1∶∶∶2D．依次落到盘上的时间关系为1∶(－1)∶(－)∶(2－)2、为了研究蹦床运动员跃起的高度，可在弹性网上安装压力传感器，利用传感器记录运动员运动过程中对弹性网的压力大小，并由计算机作出压力—时间图象（如图所示）。

运动员在空中运动时可视为质点，则可依据传感器描绘的F—t图象估算出运动员跃起的最大高度为（g取10m/s2）A．1.5m B．1.8m C．5.0mD．7.2m3、甲、乙两物体质量之比为m甲∶m乙 = 5∶1，甲从高H处自由落下的同时乙从2H处自由落下，不计空气阻力，以下说法错误的是（）A．在下落过程中，同一时刻二者速度相等B．甲落地时，乙距地面的高度为HC．甲落地时，乙的速度的大小为D．甲、乙在空中运动的时间之比为1∶24、小球从靠近竖直砖墙的某位置由静止释放，用频闪方法拍摄的小球位置如图中1、2、3和4所示。

已知连续两次闪光的时间间隔均为T，每块砖的厚度为d。

由此可知小球A．下落过程中的加速度大小约为B．经过位置3时的瞬时速度大小约为C．经过位置4时的瞬时速度大小约为D．从位置1到4过程中的平均速度大小约为5、在地质、地震、勘探、气象和地球物理等领域的研究中，需要精确的重力加速度g值，g值可由实验精确测定。

近年来测g值的一种方法叫“对称自由下落法”，它是将测g归于测长度和时间，以稳定的氦氖激光的波长为长度标准，用光学干涉的方法测距离，以铷原子钟或其他手段测时间，能将g值测得很准，具体做法是：将真空长直管沿竖直方向放置，自其中O点向上抛小球又落至原处的时间为T2，在小球运动过程中经过比O点高H的P点，小球离开P点至又回到P点所用的时间为T1，测得T1 、T2和H，可求得g等于A． B． C． D．6、在反恐演习中，中国特种兵进行了飞行跳伞表演。

高二物理自由落体运动试题答案及解析1. 如图所示，桌面离地面的高度是0.8m ，坐标系原点定在桌面上，向上方向为坐标轴的正方向。

从桌边与桌面相平处的A 点自由释放一个小球，经过一段时间落到地面，设小球下落的加速度大小是10m/s 2。

则从释放到落地，小球的A ．位移是0.8mB ．位移是－0.8mC ．运动时间是0.2sD ．落地速度是－4m/s【答案】D【解析】BD 解析：位移x ＝－0.8m ，方向竖直向下，选项A 错误，选项B 正确；由得：t ＝0.4s ，选项C 错误；v ＝（－g ）t ＝－4m/s ，选项D 正确。

【考点】本题考查自由落体运动的规律及对位移、速度矢量性的理解运用。

2. 如图所示，在地面上的A 点将一质量为m=2kg 的装有少量炸药物块以初速度v 0＝10 m/s,抛射角α=60°斜向右上方抛出，当物块恰好到达最高点时爆炸成质量相等的两块，其中一物块的速度v ="12" m/s,方向水平向右，(不计空气阻力，炸药的质量可忽略不计。

假设爆炸前后物块的总质量不变)求（1）另一物块的速度v ； （2）爆炸时释放的能量E ；【答案】（1）2m/s ，方向水平向左；（2）49J【解析】试题分析:（1）规定水平向右为正方向，爆炸的瞬间，内力远大于外力，在水平方向上动量守恒．mv 0cosα=(m/2)v 1+(m/2)v 2 解得：v 2=-2m/s （2）爆炸前的动能E k0==25J 爆炸后的动能E k =+=74J爆炸时释放的能量E=74J-25J=49J 【考点】动量守恒定律；自由落体运动3. 一观察者发现，每隔一定时间有一个水滴自8 m 高处的屋檐落下，而且看到第五滴水刚要离开屋檐时，第一滴水正好落到地面，那么这时第二滴水离地的高度是 【答案】3.5m【解析】 根据题意，已有四滴水滴在空中下落，第一滴刚落地， 而每滴水之间的等时间间隔的，那么从上到下间距之比1：3：5：7，则第二滴水离地的高度是是整个高度的，即3.5m 。

适用文档自由落体运动典型例题[ 例 1] 从离地 500m的空中自由落下一个小球，取g= 10m/s 2，求：（1）经过多少时间落到地面；（2）从开始落下的时辰起，在第1s 内的位移、最后 1s 内的位移；（3）落下一半时间的位移 .[ 剖析 ] 由 h=500m和运动时间，依据位移公式可直接算出落地时间、第1s 内位移和落下一半时间的位移. 最后 1s 内的位移是着落总位移和前（n—1） s 着落位移之差 .（2）第 1s 内的位移：因为从开始运动起前9s 内的位移为：所以最后 1s 内的位移为：h=h-h =500m-405m=95m（3）落下一半时间即t'=5s ，其位移为[ 说明 ] 依据初速为零的匀加快运动位移的特色，由第1s 内的位移 h1=5m，可直接用比率关系求出最后1s 内的位移，即h1∶ h10=1∶ 19∴h 10=19h1=19× 5m=95m同理，若把着落全程的时间分红相等的两段，则每一段内经过的位移之比：h t/2∶ h t =12∶ 22=1∶ 4[ 例 2] 一个物体从 H 高处自由落下，经过最后 196m所用的时间是 4s，求物体着落 H 高所用的总时间 T 和高度 H 是多少？取 g=9.8m/s 2，空气阻力不计 .[ 剖析 ]依据题意画出小球的运动表示图（图1）此中 t=4s ， h=196m.[ 解] 方法 1 依据自由落体公式式（ 1）减去式（ 2），得方法 2 利用匀变速运动均匀速度的性质由题意得最后4s 内的均匀速度为因为在匀变速运动中，某段时间中的均匀速度等于中点时辰的速度，所以着落至最后 2s 时的刹时速度为由速度公式得着落至最后 2s 的时间方法 3 利用 v－ t 图象画出这个物体自由着落的 v-t 图，如图 2 所示 . 开始着落伍经时间（ T— t ）和 T 后的速度分别为 g（ T-t ）、 gT. 图线的 AB 段与 t 轴间的面积表示在时间 t 内着落的高度 h. 。

自由落体运动典型例题!iedtxx(`stylebkzd',`1101P03.htm')[例1]从离地500m的空中自由落下一个小球，取g=10m/s2，求：（1）经过多少时间落到地面；（2）从开始落下的时刻起，在第1s内的位移、最后1s内的位移；（3）落下一半时间的位移.[分析]由h=500m和运动时间，根据位移公式可直接算出落地时间、第1s内位移和落下一半时间的位移.最后1s内的位移是下落总位移和前（n—1）s下落位移之差.（2）第1s内的位移：因为从开始运动起前9s内的位移为：所以最后1s内的位移为：h10=h-h9=500m-405m=95m（3）落下一半时间即t'=5s，其位移为[说明]根据初速为零的匀加速运动位移的特点，由第1s内的位移h1=5m，可直接用比例关系求出最后1s内的位移，即h1∶h10=1∶19∴h10=19h1=19×5m=95m同理，若把下落全程的时间分成相等的两段，则每一段内通过的位移之比：ht/2∶ht=12∶22=1∶4[例2]一个物体从H高处自由落下，经过最后196m所用的时间是4s，求物体下落H 高所用的总时间T和高度H是多少？取g=9.8m/s2，空气阻力不计.[分析]根据题意画出小球的运动示意图（图1）其中t=4s，h=196m.[解]方法1根据自由落体公式式（1）减去式（2），得方法2利用匀变速运动平均速度的性质由题意得最后4s内的平均速度为因为在匀变速运动中，某段时间中的平均速度等于中点时刻的速度，所以下落至最后2s时的瞬时速度为由速度公式得下落至最后2s的时间方法3利用v－t图象画出这个物体自由下落的v-t图，如图2所示.开始下落后经时间（T—t）和T后的速度分别为g（T-t）、gT.图线的AB段与t轴间的面积表示在时间t内下落的高度h.。

由[例3]气球下挂一重物，以v0=10m/s匀速上升，当到达离地高h=175m处时，悬挂重物的绳子突然断裂，那么重物经多少时间落到地面？落地的速度多大？空气阻力不计，取g=10m/s2.[分析]这里的研究对象是重物，原来它随气球以速度v0匀速上升.绳子突然断裂后，重物不会立即下降，将保持原来的速度做竖直上抛运动，直至最高点后再自由下落. [解]方法1分成上升阶段和下落阶段两过程考虑绳子断裂后重物可继续上升的时间和上升的高度分别为故重物离地面的最大高度为H=h+h1=175m＋5m=180m.重物从最高处自由下落，落地时间和落地速度分别为vt=gt2=10×6m/s=60m/s.所以从绳子突然断裂到重物落地共需时间t=t1＋t2=1s＋6s=7s.方法2从统一的匀减速运动考虑从绳子断裂开始计时，经时间t最后物体落至抛出点下方，规定初速方向为正方向，则物体在时间t内的位移h=-175m.由位移公式或t2-2t-35=0，取合理解，得t=7s.所以重物的落地速度为vt=v0-gt=10m/s-10×7m/s=-60m/s.其负号表示方向向下，与初速方向相反.[说明]从统一的匀减速运动考虑，比分段计算方便得多，只是在应用时，需注意位移、速度等物理量的方向，这个物体从绳子断裂到落地过程中的v-t图如图所示.[例4]如图所示，A、B两棒长均为L=1m，A的下端和B的上端相距s=20m.若A、B 同时运动，A做自由落体、B做竖直上抛，初速度v0=40m/s，求：（1）A、B两棒何时相遇；从相遇开始到分离所需的时间.[分析]这里有两个研究对象：A棒和B棒，同时分别做不同的运动.相遇时两棒位移大小之和等于s.从相遇到分离两棒位移大小之和等于2L.[解]（1）设经时间t两棒相遇，由得（2）从相遇开始到两棒分离的过程中，A棒做初速不等于零的匀加速运动，B棒做匀减速运动.设这个“擦肩而过”的时间为△t，由式中vA=gt，vB=v0-gt.代入后得[说明]上面是从地面参考系所观察到的两个物体的运动情况列式计算的，比较麻烦.在第（2）小题中，还常容易误认为从相遇开始A棒仍做自由落体运动而造成错误. 由于竖直上抛运动可以看成一个向上的匀速运动和一个自由落体的合运动，因此，如果以A棒为参照物，即从A棒上去观察B棒，B棒向上做着速度为v0的匀速运动，于是立即可得（1）两棒相遇时间（2）两棒从相遇到分离的时间!iedtxx(`stylebkzd',`1101P03.htm')[例6]A、B两球，A从距地面高度为h处自由下落，同时将B球从地面以初速v0竖直上抛，两球沿同一竖直线运动.试求以下两种情况下，B球初速度v0的取值范围：①B球在上升过程中与A球相遇；②B球在下落过程中与A球相遇.[分析]本题考察两个物体两种运动特点，以及它们之间相互联系.解答时对特殊状态——临界点的分析是关键的.解决本题时，画出运动示意图，找准关系，运用规律求解即得.[解]B球做竖直上抛运动（全过程中）：由于AB相遇时时间相等t1=t2=t，且h1+h2=h∴t=h/v0设B球上升到最大高度时，与球A相遇，如图1，B球上升到最大高度时间为v0/g.由此可知，要使AB在B球上升过程中与A相遇，只要v0/g≥t即可.B球就会在上升时与A球相遇，，如图2是AB还能相遇的最小速度，所以要满足在下落中相遇，需满足[说明]（1）本题要建立时间和位移关系，同时，根据题设条件.寻找临界点，本题的临界点在B球上，即B球达最大高度和B球落地时，建立速度与时间的关系. （2）值得说明的是，复杂的运动很难在分析时建立物理图景，办法是对每个物体运动过程仔细分析以后，据各自运动特点建立联系.。

自由落体运动练习题及答案解析LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】(本栏目内容，在学生用书中以活页形式分册装订！) 1．下图所示的各图象中能正确反映自由落体运动过程的是(设向上为正方向)() 解析：自由落体运动是初速度为0的匀加速直线运动，v＝gt，其v－t图象是一条倾斜直线．因取向上为正方向，故只有C对．答案： C2．伽利略认为自由落体运动应该是最简单的变速运动，即它的速度是均匀变化的，速度的均匀变化意味着()A．速度与时间成正比B．速度与位移成正比C．速度与时间的二次方成正比D．位移与时间的二次方成正比解析：伽利略认为速度的均匀增加意味着速度与时间成正比，又从数学上推导出位移与时间的二次方成正比．答案：AD3．物体从某一高度自由落下，到达地面时的速度与在一半高度时的速度之比是()∶2∶1C．2∶1 D．4∶1解析：由v2＝2gh知v＝2gh，所以v1∶v2＝2∶1.答案： B4．17世纪意大利科学家伽利略在研究落体运动的规律时，做了着名的斜面实验，其中应用到的物理思想方法属于()A．等效替代B．实验归纳C．理想实验D．控制变量【解题流程】▏斜面实验→自由落体运动规律→理想实验，C项正确答案： C5．关于重力加速度的说法不正确的是()A．重力加速度g是标量，只有大小没有方向，通常计算中g取 m/s2B．在地球上不同的地方，g值的大小不同，但它们相差不是很大C．在地球上同一地点，一切物体在自由落体运动中的加速度都相同D．在地球上的同一地方，离地面高度越大重力加速度g越小解析：首先重力加速度是矢量，方向竖直向下，与重力的方向相同，在地球的表面，不同的地方，g值的大小略有不同，但都在 m/s2左右，在地球表面同一地点，g 的值都相同，但随着高度的增大，g的值逐渐变小．答案： A6．一石块从高度为H处自由下落，当速度达到落地速度的一半时，它的下落距离等于()答案： B7．两物体在不同高度自由下落，同时落地，第一个物体下落时间为t ，第二个物体下落时间为t /2，当第二个物体开始下落时，两物体相距( )A ．gt 2B ．3gt 2/8C ．3gt 2/4D ．gt 2/4解析： 当第二个物体开始下落时，第一个物体已下落t 2时间，此时离地高度h 1＝12gt 2－12g ⎝ ⎛⎭⎪⎫t 22；第二个物体下落时的高度h 2＝12g ⎝ ⎛⎭⎪⎫t 22，则待求距离Δh ＝h 1－h 2 ＝12gt 2－2×12g ⎝ ⎛⎭⎪⎫t 22＝gt 24. 答案： D8．小球从空中自由下落，与水平地面相碰后弹到空中某高度，其v －t 图象如下图所示，则由图可知(g ＝10 m/s 2)以下说法正确的是( )A ．小球下落的最大速度为5 m/sB ．第一次反弹初速度的大小为3 m/sC ．小球能弹起的最大高度 mD ．小球能弹起的最大高度 m答案： ABC9．从某高处释放一粒小石子，经过1 s 从同一地点再释放另一粒小石子，不计空气阻力，则在它们落地之前的任一时刻( )A ．两粒石子间的距离将保持不变，速度之差保持不变B ．两粒石子间的距离将不断增大，速度之差保持不变C ．两粒石子间的距离将不断增大，速度之差也越来越大D ．两粒石子间的距离将不断减小，速度之差也越来越小解析： 当第一个石子运动的时间为t 时，第二个石子运动的时间为(t －1)．h 1＝12gt 2①v 1＝gt ②h 2＝12g (t －1)2③v 2＝g (t －1)④由①③得：Δh ＝gt －12g由②④得：Δv ＝g因此，Δh 随t 增大，Δv 不变，B 选项正确．答案： B10. 如右图所示，A 、B 两小球用长为L 的细线连接悬挂在空中，A 距湖面高度为H ，释放小球，让它们自由落下，测得它们落水声相差Δt .如果球A 距湖面的高度H 减小，则Δt 将( )A ．增大B ．不变C ．减小D ．无法判断解析： B 落水时，A 、B 的速度为v ＝2gH －L ，A 再落水时有L ＝v Δt ＋12g Δt 2.由两式可知H 减小，v 变小，则Δt 增大．答案： A11．从离地面80 m 的空中自由落下一个小球，取g ＝10 m/s 2，求：(1)经过多长时间落到地面；(2)自开始下落时计时，在第1 s 内和最后1 s 内的位移；(3)下落时间为总时间的一半时的位移．解析： (1)由h ＝12gt 2得，下落总时间为t ＝2h g ＝2×8010 s ＝4 s.(2)小球第1 s 内的位移为h 1＝12gt 21＝12×10×12 m ＝5 m 小球前3 s 内的位移为h 3＝12gt 23＝12×10×32 m ＝45 m 小球从第3 s 末到第4 s 末的位移，即最后1 s 内的位移为h 4＝h －h 3＝80 m －45 m ＝35 m.(3)小球下落时间的一半为t ′＝t 2＝2 s这段时间内的位移为h ′＝12gt ′2＝12×10×22 m ＝20 m.答案： (1)4 s (2)5 m 35 m (3)20 m12．跳水是一项优美的水上运动，如图所示是2008年北京奥运会跳水比赛中小将陈若琳和王鑫在跳台上腾空而起的英姿．运动员从离出水面10 m 的跳台向上跃起，举双臂直体离开台面，重心(此时其重心位于从手到脚全长的中点)升高 m 达到最高点．落水时身体竖直，手先入水(在此过程中运动员水平方向的运动忽略不计)，从离开跳台到手触水面，他可用于完成空中动作的时间是多长(不计重力，g 取10 m/s 2)解析： 把运动员看成一个质点，把上升阶段看成自由落体运动的逆运动，根据对称性原理，运动员上升的时间t 1等于做自由落体运动下落 m 所用的时间，t 1＝2h 1g ＝2×10 s ＝ s.下降过程，自由落体，t 2＝2h 2g ＝2×10 s ≈ s. 从离开跳台到手触水面，运动员可用于完成空中动作的时间t ＝t 1＋t 2＝ s.答案： s。