数理方程试题-定稿

数理方程练习题（1）一、填空题1．二阶线性偏微分方程xx xy yy x y Au Bu C u D u Eu Fu G +++++=（其中各系数均为x 和y 的函数）在某一区域的性质由式子：24B AC -的取值情况决定，取值为正对应的是（双曲）型，取值为负对应的是（椭圆）型，取值为零对应的是（抛物）型。

2．在实际中广泛应用的三个典型的数学物理方程：第一个叫（弦自由横振动），表达式为（2tt xx u a B u =），属于（双曲）型；第二个叫（热传导），表达式为（ 2t xx u a B u =），属于（椭圆）型；第三个叫（拉普拉斯方程和泊松方程），表达式为（0x x y yu u+=，(,)xx yy u u x y ρ+=-），属于（椭圆）型；二、选择题1．下列泛定方程中，属于非线性方程的是［ B ］(A) 260t xx u u xt u ++=；(B) sin i t tt xx u u u e ω-+=； (C) ()220y xxxxy u x yuu +++=； (D) 340t x xx u u u ++=；2. 下列泛定方程中，肯定属于椭圆型的是［ D ］(A)0xx yy u xyu +=； (B) 22x xx xy yy x u xyu y u e -+=；(C)0xx xy yy u u xu +-=； (D)()()()22sin sin 2cos xx xy yy x u x u x u x ++=； 3. 定解问题()()()()()()2,0,00,,0,0,,0tt xx x x t u a u t x lu t u l t u x x u x xφ?=><<?==??==?的形式解可写成［ D ］(A) ()01,coscos2n n a n at n x u x t a ll ππ∞==+∑(B) ()001,coscosn n n at n x u x t a b t a llππ∞==++∑(C) ()0,cos sin cos n nn n at n at n x u x t a b l l l πππ∞=?=+∑(D) ()001,cos sin cos n n n n at n at n x u x t a b t a b l llπππ∞=??=+++??∑ 4. 若非齐次边界条件为12(0,)(),(,)()x u t t u l t t μμ==，则辅助函数可取［C ］(A) ()()12(,)W x t t x t μμ=+； (B) ()()21(,)W x t t x t μμ=+；(C) ()()()12(,)W x t x l t t μμ=-+； (D) ()()()21(,)W x t x l t t μμ=-+；三、求解下列问题（1）2,0,tt xx u a u t x =>-∞<<∞ ，其中a 为常数。

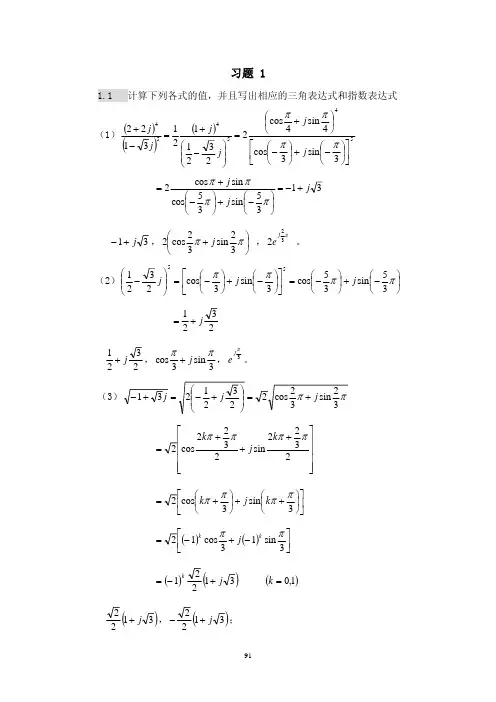
一、填空题1．二阶线性偏微分方程xx xy yy x y Au Bu C u D u Eu Fu G +++++=（其中各系数均为x 和y 的函数）在某一区域的性质由式子：24B AC -的取值情况决定，取值为正对应的是（ 双曲 ）型，取值为负对应的是（ 椭圆）型，取值为零对应的是（ 抛物 ）型。

2．在实际中广泛应用的三个典型的数学物理方程：第一个叫（ 弦自由横振动 ），表达式为（2tt xx u a B u =），属于（双曲）型； 第二个叫（ 热传导 ），表达式为（ 2t xx u a B u =），属于（ 椭圆 ）型； 第三个叫（拉普拉斯方程和泊松方程），表达式为（0x x y yu u+=，(,)xx yy u u x y ρ+=-），属于（椭圆）型；二、选择题1．下列泛定方程中，属于非线性方程的是［ B ］(A) 260t xx u u xt u ++=； (B) sin i t tt xx u u u e ω-+=； (C) ()220y xxxxy u x yuu +++=； (D) 340t x xx u u u ++=；2. 下列泛定方程中，肯定属于椭圆型的是［ D ］(A)0xx yy u xyu +=； (B) 22x xx xy yy x u xyu y u e -+=；(C)0xx xy yy u u xu +-=； (D)()()()22sin sin 2cos xx xy yy x u x u x u x ++=； 3. 定解问题()()()()()()2,0,00,,0,0,,0tt xx x x t u a u t x lu t u l t u x x u x xϕφ⎧=><<⎪==⎨⎪==⎩的形式解可写成［ D ］(A) ()01,coscos2n n a n at n x u x t a ll ππ∞==+∑(B) ()001,coscosn n n at n x u x t a b t a llππ∞==++∑(C) ()0,cos sin cos n nn n at n at n x u x t a b l l l πππ∞=⎡⎤=+⎢⎥⎣⎦∑(D) ()001,cos sin cos n n n n at n at n xu x t a b t a b l llπππ∞=⎡⎤=+++⎢⎥⎣⎦∑ 4. 若非齐次边界条件为12(0,)(),(,)()x u t t u l t t μμ==，则辅助函数可取［C ］ (A) ()()12(,)W x t t x t μμ=+； (B) ()()21(,)W x t t x t μμ=+； (C) ()()()12(,)W x t x l t t μμ=-+； (D) ()()()21(,)W x t x l t t μμ=-+；三、求解下列问题（1）2,0,tt xx u a u t x =>-∞<<∞ ，其中a 为常数。

南昌航空大学2009—2010 学年第二学期期末考试课程名称：数 理 方 程 闭 卷 A （B ）卷 分钟一、 解答题（共40 分）1、 当n 为正整数时，讨论()n J x 的收敛范围。

（5分）2、解一维热传导方程，其初始条件及边界条件为：0t u x ==，0x u x=∂=∂，0x lu x=∂=∂ （10分）3、有一均匀杆，只要杆中任一小段有纵向位移或速度，必导致邻段的压缩或伸长， 这种伸缩传开去，就有纵波沿着杆传播。

试推导杆的纵振动方程。

（10分）4、写出01(),(),()n J x J x J x （n 是正整数）的级数表示式的前5项。

（15分）二、计算题（共60分）1、求方程：22,1,0ux y x y x y∂=>>∂∂，满足边界条件： 20y u x ==，1cos x u y ==的解。

（10分）2、就下列初始条件及边界条件解弦振动方程：(,0)0,0u x x l =≤≤；(,0)(),0u x x l x x l t∂=-≤≤∂； (0,)(,)0,0u t u l t t ==> （15分）3、试确定下列定解问题：22200(),0,0,,,0,(),0x x l t u ua f x x l t t x u A u B t u g x x l ===⎧∂∂=+<<>⎪∂∂⎪⎪==>⎨⎪=≤≤⎪⎪⎩（15分） 解的一般形式。

4、（20分）求下列柯西问题：22222200280,0,3,0,y y u u uy x x x y y u u x x y ==⎧∂∂∂+-=>-∞<<+∞⎪∂∂∂∂⎪⎨∂⎪==-∞<<+∞⎪∂⎩的解。

（20分）。

数学物理方程与特殊函数09级试题选讲一、求解定解问题22200,0,(0,0)x x lt u u a t x u u x l t xx u x ===춶=ﶶﶶï==<<>í¶¶ïï=ïî)()(),(t T x X t x u =)()()()(2t T x X a t T x X ¢¢=¢22)()()()(b -=¢¢=¢x X x X t T a t T 0>b 设，代入原方程得，则)()(22=+¢t T a t T b 0)()(2=+¢¢x X x X b 则，0x x lu u xx==¶¶==¶¶'(0)'()0X X l Þ==又因为得固有值问题2()()0'(0)'()0X x X x X X l b ¢¢ì+=í==î22)(ln pb =()cos 0,1,2,n n n xX x A n lp ==则固有值固有函数，数学物理方程与特殊函数09级试题选讲)()()(2=+¢t T la n t T p 2()()n a tl n T t C ep -Þ=2()01(,)cosn a tln n n x u x t C C elp p ¥-==+å从而0t ux==有因为01cosnn n x x C C lp ¥==+å所以220022[(1)1]cos 12n ln l n x l C x dx l l nl C xdx lp p --====òò2()2212(1)1(,)cos 2n a ntln l l n xu x t enlp p p¥-=--=+å数学物理方程与特殊函数09级试题选讲二、求解定解问题2222,,0(),0(),0(0)(0)t x t x u ut x t t t x ux x u x x =-=춶=-<<>ﶶïï=F £íï=Y ³ïïF =Y î解：特征变换为x t x tx h =-ìí=+î2u x h¶=¶¶原方程化为12()()u f f x h =+则它的通解为00(),()()(),()()2222t xt x ux u x u u h x x h x h x h=-====F =Y +-Þ=F =F =Y =Y 又因为数学物理方程与特殊函数09级试题选讲1212(0)()()2()(0)()2f f f f h h xx +=Y +=F 2112()()(0)2()()(0)2f f f f h h x x ì=Y -ïïÞíï=F -ïî12()()((0)(0))22()()(0)22u f f x t x tx h=F +Y -+-+=F +Y -F 则它的解为三、求解定解问题)0,(,0,3,03202022222>+¥<<-¥ïïïîïïíì=¶¶==¶¶-¶¶¶+¶¶==y x y ux u y uy x u x u y y 解：原方程的特征方程为22()23()0dy dydx dx --=13C x y +=2C x y +-=，则特征线为3x y x yx h =-ìí=+î特征变换20ux h¶=¶¶原方程化为12()()u f f x h =+则它的通解为数学物理方程与特殊函数09级试题选讲12(,)(3)()u x y f x y f x y =-++即203,y y u ux y==¶==¶又因为21212(3)()3(3)()0f x f x xf x f x ì+=í¢¢-+=î则可得C x x f¢-=2149)3(C x x f ¢+=2243)(C x x f¢-=2141)(222234)(34)3(),(yx y x y x y x u +=++-=22()()C Du vv u u v d v u ds n n s ¶¶Ñ-Ñ=-¶¶òòò 四、证明平面上的格林公式其中n 为曲线的外法线向量。

工程数学一、 (10分)填空题1、初始位移为)(x ϕ,初始速度为)(x ψ的无界弦的自由振动可表述为定解问题:⎪⎩⎪⎨⎧==>+∞<<∞-===).(),(0,,002x u x u t x u a u t t t xx tt ψϕ 2、为使定解问题⎪⎪⎩⎪⎪⎨⎧=======0,00002t lx x x xxt u u u u u a u (0u 为常数)中的边界条件齐次化,而设)(),(),(x w t x v t x u +=,则可选=)(x w xu 03、方程0=xyu 的通解为)()(),(y G x F y x u +=4.只有初始条件而无边界条件的定解问题,称为柯西问题、5.方程y x u xy 2=满足条件1cos ),0(,)0,(2-==y y u x x u 的特解为1cos 61),(223-++=y x y x y x u 二、 (10分)判断方程02=+yy xx u y u的类型,并化成标准形式.解:因为)0(02≠<-=∆y y ,所以除x 轴外方程处处就是椭圆型的。

……2分它的特征方程就是 022=+⎪⎭⎫⎝⎛y dx dy ……5分即iy dxdy±= 特征线为 21ln ,ln c ix y c ix y =+=-作变换:⎩⎨⎧==x yηξln ……7分求偏导数⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-====)(112ξξξξηηηu u y u u y u u u u u yy y xx x 将二阶偏导数代入原方程,便可得到标准形式ξηηξξu u u =+ ……10分三、 (10分)求解初值问题⎪⎩⎪⎨⎧==>+∞<<∞-===x u x u t x u u t t t xx tt cos ,0,,4020解:x x x x a cos )(,)(,22===ψϕ利用达朗贝尔公式⎰+-+-++=atx atx d a at x at x t x u ξξψϕϕ)(21)]()([21),( ……5分得)]2sin()2[sin(414cos 41])2()2[(21),(222222t x t x t x d t x t x t x u tx tx --+-+=+-++=⎰+-ξξt x t x 2sin cos 21422++= ……10分四、 (15分)用分离变量法解定解问题⎪⎪⎩⎪⎪⎨⎧====><<=====.0,0|,00,0,0002t t t l x x x x xx tt u x u u u t l x u a u 解 先求满足方程与边界条件的解、设解为)()(),(t T x X t x u = ……2分代入方程得)()()()(2t T x X a t T x X ''=''除以)()(2t T x X a 有λ-=''='')()()()(2t T a t T x X x X得到两个常微分方程0)()(=+''x X x X λ ……3分0)()(2=+''t T a t T λ ……4分由边界条件得0)()(,0)()0(='='t T l X t T X 由0)(≠t T ,得0)(,0)0(='='l X X ……5分 于就是固有值问题为⎩⎨⎧='='=+''0)(,0)0(,0)()(l X X x x X λ解之得一系列固有值Λ,2,1,0,)(2===n ln n πλλ 相应的固有函数为x ln x X n πcos)(= ……8分 再解方程 0)()()(2=+''t T l a n t T π,通解为t lan D t l a n C t T n n n ππsin cos )(+= ……10分利用解的叠加原理,可得满足方程与边界条件的级数形式解∑∞=+=1cos )sin cos(),(n n n x ln t l a n D t l a n C t x u πππ ……12分 由初始条件0|0==t t u ,得0=n D , ……13分 由得,0x u t == ∑∞==1cos n n x ln C x π其中⎰==l l xdx l C 0021⎰=--==l nn n n l dx l n x l C 02,2,1],1)1[()(2cos 1Λππ ……14分 将n n D C ,代入),(t x u 得定解问题解∑∞=--+=122cos cos 1)1(22),(n n x l n t l a n n l l t x u πππ……15分 五、 (15分)解非齐次方程的混合问题⎪⎪⎩⎪⎪⎨⎧≤≤=≥==><<+====πππx u t u u t x x u u t x x xx t 0.00,0,00,0,00 解 先确定固有函数)(x X n 、令)()(),(t T x X t x u =代入相应的齐次方程与齐次边界条件得固有值问题⎩⎨⎧===+''0)(,0)0(0)()(πλX X x X x X 固有函数为 Λ,2,1,sin )(==n nx x X n ……5分设解为∑∞==1sin )(),(n n nx t T t x u (1) ……7分其中)(t T n 就是待定函数、显然),(t x u 满足边界条件、为确定函数)(t T n ,先将方程中的非齐次项展为固有函数级数 ∑∞==1sin )(n n nxt f x (2) ……8分其中nnxdx x t f n n 2)1(sin 2)(10+-=⋅=⎰ππ……9分再将(1),(2)代入方程得∑∞=+=⎥⎦⎤⎢⎣⎡--+'1120sin 2)1()()(n n n n nx n t T n t T比较系数,有Λ,2,1,2)1()()(12=-=+'+n nt T n t T n n n ……10分由初始条件得0sin )0(1=∑∞=n n nx T所以0)0(=n T ……11分解初值问题⎪⎩⎪⎨⎧=-=+''+,0)0(2)1()()(12nn n n T n t T n t T 得)1(2)1()(231tn n n e n t T -+--=……14分 将)(t T n 代入级数(1),得定解问题的解、nx e n t x u n tn n sin )1()1(2),(1312∑∞=-+--= ……15分 六、 (15分)用积分变换法解无界杆热传导问题⎪⎩⎪⎨⎧=>+∞<<∞-==).(0,,02x u t x u a u t xx t ϕ 本题所用公式:ta x ta eta eF 22224121][---=πλ解 对x 作傅氏变换,记=),(~t uλ F )],([t x u =)(~λϕF )]([x ϕ ……2分 对方程与初始条件关于x 取傅氏变换,有⎪⎩⎪⎨⎧=-==)(~~~~022λϕλt u u a dtu d ……7分 解常微分方程的初值问题,得t a et u 22)(~),(~λλϕλ-= ……10分 再对),(~t uλ进行傅氏逆变换得 =),(t x u F])(~[221t a e λλϕ-- ……13分 ta x eta x 22421)(-*=πϕ⎰∞+∞---=ξξϕπξd et ata x 224)()(21 ……15分七、 (15分)用静电源像法求解上半平面0>y 的狄利克雷问题⎪⎩⎪⎨⎧=>=+=).(|0,00x f u y u u y yy xx解 先求格林函数,由电学知在上半平面0>y 的点),(000y x M 处置单位负电荷,在0M 关于x 轴的对称点),(001y x M -处置单位正电荷,则它与0M 产生的电势在x 轴上 互相抵消,因此上半平面0>y 的格林函数为)1ln 1(ln 21),(100MM MM r r M M G -=π[][]}{20202020)()(ln )()ln(41y y x x y y x x ++---+--=π……7分 下面求==∂∂-=∂∂y y yG nG0)()()(2)()()(2412020020200=⎥⎦⎤⎢⎣⎡++-+--+--=y y y x x y y y y x x y y π2200)(1y x x y +-⋅-=π ……10分 所以dx y x x x f y dl n Guy x u ⎰⎰+∞∞-Γ+-=∂∂-=220000)(1)(),(π……15分 八、 (10分)证明调与方程的狄利克雷内问题的解如果存在,则必就是唯一的,而且连续地依赖于所给的边界条件f .证明:假设有两个调与函数),,(1z y x u 与),,(2z y x u ,它们在有界区域Ω的边界Γ上完全相同,则它们的差21u u u -=在Ω中也满足方程0=∆u ,且0|=Γu 。

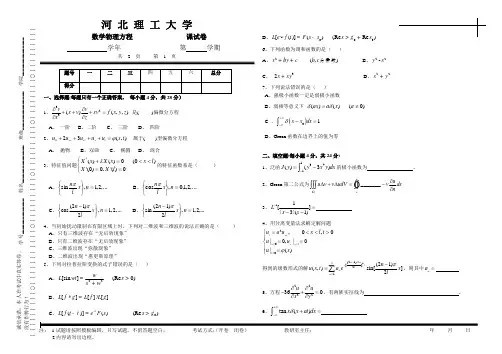
第一章定义和方程类型1、34233(,,)v v v xyv g x y z x x y z∂∂∂+++=∂∂∂∂ 是( D )偏微分方程 A 、 一阶 B 、二阶 C 、 三阶 D 、 四阶 1、22(,,)vxy v g x y z z∂+=∂ 是( A )偏微分方程 A 、 一阶 B 、二阶 C 、 三阶 D 、 四阶1、33232(,,)v v vv xyv g x y z x x y z ∂∂∂+++=∂∂∂∂ 是( C )偏微分方程A 、 一阶B 、二阶C 、 三阶D 、 四阶 2、2(,)txx u a u f x t -= (其中0>a ) 属于( A )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合 2、2(,)ttxx u a u x t ϕ-= (其中0>a ) 属于( B )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合2、22(,,)tt xx u a u x y t ϕ+= (其中0>a ) 属于( C )型偏微分方程 A 、 抛物 B 、双曲 C 、 椭圆 D 、 混合 2、(,)xx yy u u f x y += (其中(,)u u x y =) 属于( C )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合 4、下列方程是非线性偏微分方程的是（ A ）A 22()()sin u u x x y 抖+=抖 B (,)u uf x y x y抖+=抖 C 22(,)(,)cos u ua x tb x t x x t抖+=抖 D 3433(,,)v v v g x y z x x y z ∂∂∂++=∂∂∂∂ 7、下列方程是非齐次方程的是（ A ）A(,)(,)0u uxy f x y f x y x y 抖+=?抖， B 2,0t xx u a u a =?C 22(,)(,)0u u a x t b x t x t 抖+=抖 D 34330v v v x x y z ∂∂∂++=∂∂∂∂3、在用分离变量法求解定解问题200,0,0|0,|0|()t xx x x x l t u a u x l t u u u x ϕ===⎧=<<>⎪==⎨⎪=⎩时，得到的固有函数系为( D ) A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x ln π B 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n π C 、{},...2,1,sin =n x n π D 、 ,...2,1,2)12(sin =⎭⎬⎫⎩⎨⎧-n x ln π 3、在用分离变量法求解定解问题⎪⎩⎪⎨⎧====><<=====)(|),(|0|,0|0,0,0002x u x u u u t l x u a u t t t l x x x x xx tt ψϕ时，得到的固有函数系为( B )A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x l n πB 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n πC 、(21)cos ,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭ D 、 ,...2,1,2)12(sin =⎭⎬⎫⎩⎨⎧-n x l n π3、在用分离变量法求解定解问题⎪⎩⎪⎨⎧===><<====)(|0|,0|0,0,002x u u u t l x u a u t l x x xx t ϕ时，得到的固有函数系为( A )A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x l n π B 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n πC 、(21)cos,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭ D 、,...2,1,2)12(sin=⎭⎬⎫⎩⎨⎧-n x l n π7、给出未知函数 u 在区域Ω的边界Γ上的值0,),,(|≥Γ∈=Γt M t M u μ 的边界条件，称为第( A )类边界条件。

第一部分分离变量法一、(1) 求解特征值问题(2) 验证函数系关于内积正交,并求范数二、用分离变量法求解定解问题的解的表达式,写出具体的分离变量过程、进一步,当时,求与时的值、三、(方程非齐次的情形)求定解问题四、(边界非齐次的情形)求定解问题五、(Possion方程)求定解问题六、求定解问题:注意:1、考试只考四种边界条件,即还有以下三种:2)3)4)2、以上均为抛物型方程,还可以考双曲型方程(相应的初值条件变为两个)与椭圆型方程(无初值条件);3、考试中除特别要求(如以上的第二题)外,不要求必须用分离变量法、特征函数法等方法求解,您可以自己选择方法(如上面的第三题)可以用Laplace 变换求解。

第二部分 积分变换法一、请用下面三种方法求解无穷限波动问题()()2222200,, 0,,t t u u a x t t x u x x u x x t ϕψ==⎧∂∂=-∞<<∞>⎪∂∂⎪⎪=-∞<<∞⎨⎪∂⎪=-∞<<∞∂⎪⎩(1) 用积分变换法推导达朗贝尔公式(2) 用特征线法推导达朗贝尔公式 (3) 用降维法推导达朗贝尔公式二、用积分变换法求解定解问题22301,1, 0,1cos ,0y x u x y x y x y u x x u y y ==⎧∂=>>⎪∂∂⎪⎪=≥⎨⎪=>⎪⎪⎩注意:只考应用Fourier 变换与Laplace 变换求解方程的问题第三部分 特征线问题一、判断方程的类型、二、从达朗贝尔公式出发,证明在无界弦问题中(1) 若初始位移()x ϕ与初始速度()x ψ为奇函数,则(),00u t = (2) 若初始位移()x ϕ与初始速度()x ψ为偶函数,则(),00x u t = 三、请用下列方法求解定解问题(1) 用特征线法求解 (2) 用积分变换法求解第四部分 Legendre 多项式一、将()2f x x =在区间()1,1-内展成勒让德多项式的级数二、在半径为1的球内求调与函数,使1321cos r u θ==+(提示:边界条件仅与θ有关,解也同样)第五部分 Green 函数20、证明:()()0lim x x εεδρ→=(弱),其中 ()1,20,x x x εερεε⎧<⎪=⎨⎪≥⎩21、证明:()sin limN Nxx Nxδ→+∞=(弱) 22、证明:当时,弱收敛于23、求()()0x δξξπ-<<在()0,π上的余弦级数,并证明该级数若收敛于()x δξ- 24、求()()0x δξξπ-<<在()0,π上的正弦级数,并证明该级数若收敛于()x δξ-。

数理方程试题一．判断题（每题2分）.1. 2u u x y x y x+=是非线性偏微分方程.( )2. 绝对可积函数一定可做Fourier 积分变化.( )3. ()(1) 1.n n F x n Legendre F =是次正交多项式，则 ( )4. (,)0xy f x y =的解是调和函数.( )5. **12u u 已知,是线性偏微分方程(,)xx yy u u f x y +=的解，则**12u u -是0u ?= 的解.( )二．填空题（每题2分）.1. ()sin t xx yy u u u xt -+= 是____________型偏微分方程.2. 内部无热源的半径为R 的圆形薄板,内部稳态温度分布，当边界上温度为()t φ时，试建立方程的定解问题________________________.3. 2x 的Legendre 正交多项式的分解形式为__________________.4.某无界弦做自由振动,此弦的初始位移为()x φ,初始速度为()a x φ-,则弦振动规律为______________________________.5. []()____________.at m L e t s = 三．求解定解问题（12分）20sin ;0,0;0.t xx xx xx lt u a u A t u u u ω===-====四．用积分变换方法求解以下微分方程（每题12分，共24分）（1）1,0,0;1,1.xy x y u x y uy u===>>=+=（2） 00230, 1.tt t y y y e y y =='''+-='==五．某半无界弦的端点是自由的，初始位移为零，初始速度为cos x ，求弦的自由振动规律。

（12分）六．设有长为a ，宽为b 的矩形薄板，两侧面绝热，有三边的温度为零，另一边的温度分布为x ，内部没有热源，求稳定状态时板内的温度分布。

数理方程练习题一（2009研）1. 设(,)u u x y =，求二阶线性方程20ux y∂=∂∂ 的一般解。

解 先把所给方程改写为()0ux y∂∂=∂∂ 2分 两边对x 积分，得()0()()u udx dx y y y x yϕϕ∂∂∂==+=∂∂∂⎰⎰ 4分 这里， ()y ϕ是任意函数。

再两边对y 积分，得方程的一般解为y()()()()uu dy y dy f x f x g y yϕ∂==+=+∂⎰⎰ 6分 这里，(),()f x g y 是任意两个一次可微函数。

2. 设u f = 满足Laplace 方程22220u u x y ∂∂∂∂+=求函数u.解: ,.r x r y r x r x r ∂∂===∂∂ ''(),().u x u y f r f r x r y r∂∂⇒==∂∂ 3分 因此有222'''223222'''223()()()()u x y f r f r x r ru y x f r f r y r r ∂=+∂∂=+∂ 3分 原方程化为:'''1()()0f r f r r+= 2分 故有:1212()ln r u f r c c c c ==+= 2分例1 求Cauchy 问题22000(,)(0,)cos tt xx t t t u a u x t u x u x x ==⎧-=∈⨯∞⎪⎨==∈⎪⎩R R的解．解 由定理3.1得22222()()1u(x, t)cos 221cos sin x atx atx at x at d a x a t x ataξξ+-++-=+=++⎰例2 求解Cauchy 问题200cos (,)(0,)cos 010tt xx t t t u a u t x x t x x u x u x ==⎧-=∈⨯∞⎪≥⎧⎨==⎨⎪<⎩⎩R解 由公式错误！未找到引用源。

第一部分分离变量法一、(1) 求解特征值问题(2) 验证函数系关于内积正交，并求范数二、用分离变量法求解定解问题的解的表达式，写出具体的分离变量过程. 进一步，当时，求和时的值.三、（方程非齐次的情形）求定解问题四、（边界非齐次的情形）求定解问题五、（Possion方程）求定解问题六、求定解问题：注意：1、考试只考四种边界条件，即还有以下三种：2)3)4)2、以上均为抛物型方程，还可以考双曲型方程（相应的初值条件变为两个）和椭圆型方程（无初值条件）；3、考试中除特别要求（如以上的第二题）外，不要求必须用分离变量法、特征函数法等方法求解，你可以自己选择方法（如上面的第三题）可以用Laplace 变换求解。

第二部分 积分变换法一、请用下面三种方法求解无穷限波动问题()()2222200,, 0,,t t u u a x t t x u x x u x x t ϕψ==⎧∂∂=-∞<<∞>⎪∂∂⎪⎪=-∞<<∞⎨⎪∂⎪=-∞<<∞∂⎪⎩ (1) 用积分变换法推导达朗贝尔公式(2) 用特征线法推导达朗贝尔公式 (3) 用降维法推导达朗贝尔公式二、用积分变换法求解定解问题22301,1, 0,1cos ,0y x u x y x y x y u x x u y y ==⎧∂=>>⎪∂∂⎪⎪=≥⎨⎪=>⎪⎪⎩注意：只考应用Fourier 变换和Laplace 变换求解方程的问题第三部分 特征线问题一、判断方程的类型.二、从达朗贝尔公式出发，证明在无界弦问题中(1) 若初始位移()x ϕ和初始速度()x ψ为奇函数，则(),00u t = (2) 若初始位移()x ϕ和初始速度()x ψ为偶函数，则(),00x u t = 三、请用下列方法求解定解问题(1) 用特征线法求解 (2) 用积分变换法求解第四部分 Legendre 多项式一、将()2f x x =在区间()1,1-内展成勒让德多项式的级数二、在半径为1的球内求调和函数，使1321cos r u θ==+（提示：边界条件仅与θ有关，解也同样）第五部分 Green 函数20、证明：()()0lim x x εεδρ→=（弱），其中 ()1,20,x x x εερεε⎧<⎪=⎨⎪≥⎩21、证明：()sin limN Nxx Nxδ→+∞=（弱） 22、证明：当时，弱收敛于23、求()()0x δξξπ-<<在()0,π上的余弦级数，并证明该级数若收敛于()x δξ- 24、求()()0x δξξπ-<<在()0,π上的正弦级数，并证明该级数若收敛于()x δξ-赠送相关资料考试答题的技巧拿到试卷之后，可以总体上浏览一下，根据以前积累的考试经验，大致估计一下试卷中每部分应该分配的时间。