内准圆的性质

沪教版初三数学知识点归纳圆★重点★①圆的重要性质;②直线与圆、圆与圆的位置关系;③与圆有关的角的定理;④与圆有关的比例线段定理。

☆内容提要☆一、圆的根本性质1.圆的定义(两种)2.有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。

3.“三点定圆”定理4.垂径定理及其推论5.“等对等”定理及其推论6.与圆有关的角：⑴圆心角定义(等对等定理)⑵圆周角定义(圆周角定理，与圆心角的关系)⑶弦切角定义(弦切角定理)二、直线和圆的位置关系1.切线的性质(重点)2.切线的判定定理(重点)3.切线长定理三、圆换圆的位置关系1.五种位置关系及判定与性质：(重点：相切)2.相切(交)两圆连心线的性质定理3.两圆的公切线：⑴定义⑵性质四、与圆有关的比例线段1.相交弦定理2.切割线定理五、与和正多边形1.圆的内接、外切多边形(三角形、四边形)2.三角形的外接圆、内切圆及性质3.圆的外切四边形、内接四边形的性质4.正多边形及计算中心角：初中数学复习提纲内角的一半：初中数学复习提纲(右图)(解Rt△OAM可求出相关元素,初中数学复习提纲、初中数学复习提纲等)六、一组计算公式1.圆周长公式2.圆面积公式3.扇形面积公式4.弧长公式5.弓形面积的计算（方法）6.圆柱、圆锥的侧面绽开图及相关计算九年级上册数学单元学问点第一章证明一、等腰三角形1、定义：有两边相等的三角形是等腰三角形。

2、性质：1.等腰三角形的两个底角相等(简写成“等边对等角”)2.等腰三角形的顶角的平分线，底边上的中线，底边上的高的重合(“三线合一”)3.等腰三角形的两底角的平分线相等。

(两条腰上的中线相等，两条腰上的高相等)4.等腰三角形底边上的垂直平分线上的点到两条腰的距离相等。

5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(可用等面积法证)7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴3、判定：在同一三角形中，有两个角相等的三角形是等腰三角形(简称：等角对等边)。

双曲线焦点三角形内切圆的性质及应用
双曲线焦点三角形内切圆是一种特殊的圆，由三个焦点所确定。

它的性质主要有以下几点：
一、它的半径等于双曲线的离心率。

因为双曲线焦点三角形的三
条边都穿过双曲线的两个焦点，使得双曲线的离心率也就等于内切圆
的半径。

二、它的圆心介于双曲线的两个焦点之间。

因为双曲线的两个焦
点被视为双曲线的中心，而内切圆的圆心处于中心和焦点之间，所以
双曲线焦点三角形内切圆的圆心就位于双曲线的两个焦点之间。

三、它的圆心和焦点构成正方形。

由此可见，双曲线焦点三角形
内切圆的圆心和双曲线的两个焦点构成正方形，而这个正方形被称为“双曲线矩形”，其中圆心到每个双曲线焦点的距离均相等。

双曲线焦点三角形内切圆的应用非常广泛，它可以用于绘制复杂
的曲线，用来拟合物体的形状，也可以用来求解几何学问题，特别是
工程中的测量问题。

此外，由于双曲线焦点三角形内切圆的特殊性质，它也可以应用于电子设备的紧密结构设计，增强机械设备的稳定性和
精度。

总之，双曲线焦点三角形内切圆是一种有用的几何工具，它具有
多种性质和应用，可以用来解决各种工程和几何问题，广泛应用于精
密仪器的设计及检测上。

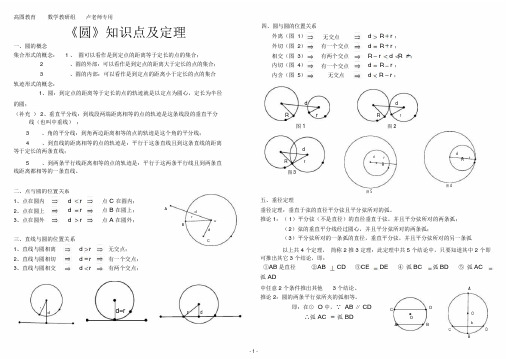
高图教育数学教研组卢老师专用《圆》知识点及定理一、圆的概念集合形式的概念： 1 、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充） 2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；四、圆与圆的位置关系外离（图 1）无交点d R r ；外切（图 2）有一个交点d R r ；相交（图 3）有两个交点R r d R r ；内切（图 4）有一个交点d R r ；内含（图 5）无交点d R r ；d dR r R r图 1图 23、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

dR r图3d rRdR图4r二、点与圆的位置关系1、点在圆内d r点 C 在圆内；2、点在圆上d r点 B 在圆上；A d3、点在圆外d r点 A 在圆外；r OBd三、直线与圆的位置关系C1、直线与圆相离d r无交点；2、直线与圆相切d r有一个交点；3、直线与圆相交d r有两个交点；rd d=r r d图 5五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论 1：（ 1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共 4 个定理，简称 2 推 3 定理：此定理中共 5 个结论中，只要知道其中 2 个即可推出其它 3 个结论，即：①AB是直径②AB CD③CE DE④ 弧BC弧BD⑤ 弧AC弧 AD中任意 2 个条件推出其他 3 个结论。

圆的基本性质是初中数学九年级下学期第一章第一节的内容．需要掌握点与圆的位置关系，理解圆心角、弧、弦、弦心距的概念和掌握它们之间的关系，重点是这四者关系的灵活运用，以及垂径定理及其推论的应用．1、圆的概念圆：平面上到一个定点的距离等于定长的所有点所成的图形．圆心：以上概念中的“定点”；以点O为圆心的圆称为“圆O”，记作O．半径：联结圆心和圆上任意一点的线段；以上概念中的“定长”是圆的半径长．2、点与圆的位置关系设一个圆的半径长为R，点P到圆心的距离为d，则有以下结论：当点P在圆外时，d > R；当点P在圆上时，d = R；当点P在圆内时，0d R≤<．反之亦然．3、相关定理：不在同一直线上的三个点确定一个圆．三角形的三个顶点确定一个圆．经过一个三角形各顶点的圆叫做这个三角形的外接圆，外接圆的圆心叫做这个三角形的外心；这个三角形叫做这个圆的内接三角形．如果一个圆经过一个多边形的各顶点，那么这个圆叫做这个多边形的外接圆，这个多边形叫做这个圆的内接多边形．圆的基本性质内容分析知识结构模块一：圆的确定知识精讲ABCD O【例1】 在平面直角坐标系内，A （3-，tan30-︒），B （2a a，0），A 的半径为4，试说明点B 与A 的位置关系．【难度】★ 【答案】点B 在A 外．【解析】由题意得33A ⎛⎫-- ⎪ ⎪⎝⎭，，()10B ，，所以()22373313AB ⎛⎫=--+-= ⎪ ⎪⎝⎭， 因为4AB >，所以点B 在A 外．【总结】本题考察了点与圆的位置关系，设一个圆的半径长为R ，点P 到圆心的距离为 d ，则有以下结论：当点P 在圆外时，d > R ；当点P 在圆上时，d = R ；当点P 在 圆内时，0d R ≤<．反之亦然．【例2】 过一个点可以画______个圆，过两个点可以画______个圆，过三个点可以画______个圆．【难度】★【答案】无数；无数；一或零．【解析】不共线的三点才可以确定一个圆．【总结】本题考察了圆的确定，不共线的三点可以确定一个圆．【例3】 已知，如图，在O 中，AB 、BC 为弦，OC 交AB 于点D ．求证：（1）ODB OBD ∠>∠；（2）ODB OBC ∠>∠．【难度】★ 【答案】详见解析．【解析】（1）∵OA OB =，∴OAB OBA ∠=∠，∵ODB OAB AOD ∠=∠+∠，∴ODB OBA AOD ∠=∠+∠，∴ODB OBD ∠>∠．（2）∵OC OB =，∴OBC OCB ∠=∠，∵ODB OCB DBC ∠=∠+∠，∴ODB OBC DBC ∠=∠+∠，∴ODB OBC ∠>∠．【总结】本题考查了圆的性质，利用外角是解决问题的关键．例题解析【例4】 如图，O 的半径为15，O 到直线l 的距离OH = 9，A 、B 、C 为直线l 上的三个点，AH = 9，BH = 12，CH = 15，请分别说明点A 、B 、C 与O 的位置关系．【难度】★★【答案】A 在O 内；B 在O 上；C 在O 外． 【解析】连接OP ，∵15OP =，9OH =，∴2212PH OP OH =-=，∵9AH HP =<，∴A 在O 内； ∵12BH HP ==，∴B 在O 上； ∵12CH HP =<，∴C 在O 外．【总结】本题考查了点与圆的位置关系．【例5】 若A （a ，27-）在以点B （35-，27-）为圆心，37为半径的圆上，求a 的值．【难度】★★ 【答案】2或72-．【解析】∵A 点在B 上，∴37BA =，即()()2235272737a ++-+=，解得12a =，272a =-．【总结】本题考查了点与圆的位置关系，注意此题有两种解．【例6】 如图，作出AB 所在圆的圆心，并补全整个圆． 【难度】★★ 【答案】如图所示．【解析】在AB 上任意作两条弦，分别做两条弦的垂直平分线，两垂直平分线的交点即为圆心．【总结】本题考查了不共线三点定圆的作法．HOlP【例7】 如图，CD 是半圆的直径，O 是圆心，E 是半圆上一点，且45EOD ∠=︒，A 是DC 延长线上一点，AE 与半圆交于B ，若AB = OC ，求EAD ∠的度数．【难度】★★★ 【答案】15EAD ∠=︒．【解析】∵AB OC =，OC OB =，∴AB OB =，∴EAD BOA ∠=∠， ∴2OBE BOA EAD EAD ∠=∠+∠=∠，∵OB OE =，∴E OBE ∠=∠，∴2OEB EAD ∠=∠， ∵345EOD OEA EAD EAD ∠=∠+∠=∠=︒， ∴15EAD ∠=︒．【总结】本题考查了同一个圆中半径处处相等及三角形外角的应用．【例8】 已知，如图，AB 是O 的直径，半径OC AB ⊥，过OC 的中点D 作EF // AB ．求证：12ABE CBE ∠=∠．【难度】★★★ 【答案】详见解析． 【解析】连接OE ，∵OC AB ⊥，EF //AB ， ∴OC EF ⊥，OBE DEB ∠=∠，∵OB OE =，∴OBE OEB ∠=∠，∴OBE OEB DEB ∠=∠=∠，∵D 为OC 的中点，∴1122OD OC OE ==，∴30OED ∠=︒，∴1152ABE OED ∠=∠=︒，∴451530CBE CBO ABE ∠=∠-∠=︒-︒=︒，∴12ABE CBE ∠=∠．【总结】本题主要考查了等腰三角形的性质以及直角三角形性质的综合运用．AB CDEOABC D E F O【例9】已知：AB是O的直径，点P是OA上任意一点，点C是O上任意一点．≤≤．求证：PA PC PB【难度】★★★【答案】详见解析．==，【解析】当P与O重合时，可得PA PC PB当P与O不重合时，连接OC，则OA = OC = OB，=-=-<，∴PA OA OP OC OP PC=+=+>，PB OP OB OP OC PC≤≤．综上可知PA PC PB【总结】本题考查了圆中半径处处相等，并利用三角形的三边关系解决问题．A BCO1、 圆心角、弧、弦、弦心距的概念圆心角：以圆心为顶点的角叫做圆心角； 弧：圆上任意两点之间的部分叫做圆弧，简称弧；弦：连接圆上任意两点的线段叫做弦，过圆心的弦就是直径； 弦心距：圆心到弦的距离叫做弦心距． 2、 半圆、优弧、劣弧半圆：圆的任意一条直径的两个端点将圆分成两条弧，每一条弧都叫做半圆． 优弧：大于半圆的弧叫做优弧． 劣弧：小于半圆的弧叫做劣弧．如图，以A 、C 为端点的劣弧记作AC ，读作“弧AC ”； 以A 、C 为端点的优弧记作ABC ，读作“弧ABC ”． 3、 等弧和等圆能够重合的两条弧称为等弧，或者说这两条弧相等．若AB 与''A B 是等弧，记作''AB A B ．半径相等的两个圆一定能够重合，我们把半径相等的两个圆称为等圆． 4、 圆心角、弧、弦、弦心距之间关系的定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．5、 圆心角、弧、弦、弦心距之间关系的定理的推论在同圆或等圆中，如果两个圆心角、两条劣弧（或优弧）、两条弦、两条弦的弦心距得到的四组量中有一组量相等，那么它们所对应的其余三组量也分别相等．模块二：圆心角、弧、弦、弦心距之间的关系知识精讲ABCO【例10】 下列命题中真命题的个数是（ ）① 相等的圆心角所对的弧也相等；② 在同圆中，如果两条弦相等，那么所对的弧也相等； ③ A 、B 是O 上任意两点，则AO + BO 等于O 的直径长； ④ 三角形的外心到三角形三边的距离相等． A ．1个B ．2个C ．3个D ．4个【难度】★ 【答案】A ．【解析】① 需说明是在同圆或等圆中，故①错误；② 一条弦对两条弧，所以需要说明是优弧还是劣弧，故②错误； ③ 易知AO 、BO 均为圆的半径，所以AO BO +为直径，故③正确； ④ 三角形的外心到三角形三个顶点的距离相等，故④错误．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【例11】 一条弦把圆分成1 : 3两部分，则弦所对的圆心角为______°． 【难度】★ 【答案】90．【解析】∵一条弦把圆分成1 : 3两部分，∴整个圆分为四等分，则劣弧的度数为360490︒÷=︒， ∴弦所对的圆心角为90︒．【总结】本题考查了同圆中圆心角、弧、弦、弦心距之间的关系．【例12】 如图，在O 中，AB AC =，70B ∠=︒，则BAC ∠=______． 【难度】★ 【答案】40︒．【解析】∵在O 中，AB AC =，∴C B ∠=∠，∵70B ∠=︒，∴18040BAC B C ∠=︒-∠-∠=︒．【总结】本题主要考查等腰三角形的性质以及三角形内角和定理的应用．例题解析ABCDO【例13】 如图，已知O 的半径是6，30BOD ∠=︒，BD BC =，CD =______．【难度】★★ 【答案】6．【解析】∵BD BC =，30BOD ∠=︒，∴30BOD BOC ∠=∠=︒，∴60COD ∠=︒，∵OC OD =，∴OCD ∆是等边三角形， ∴6CD =．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理的应用．【例14】 如图，1O 和2O 是等圆，P 是12O O 的中点，过点P 作直线AD 交1O 于点A 、B ，交2O 于点C 、D ．求证：AB = CD ．【难度】★★ 【答案】详见解析．【解析】作1O E AB ⊥于E ，2O F CD ⊥于F ，∵P 是12O O 的中点，∴1PEO ∆≌2PFO ∆，∴12O E O F =， ∵1O 和2O 是等圆，∴AB CD =．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理的应用．【例15】 已知，如图，AB 、CD 是O 的直径，弦AE // CD ，联结CE 、BC ．求证：BC = CE ． 【难度】★★ 【答案】详见解析．【解析】∵OA OE =，∴A OEA ∠=∠，∵AE //CD ，∴BOC A ∠=∠，EOC OEA ∠=∠， ∴BOC EOC ∠=∠，∴BC CE =．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理的应用．FABCDPEA BCDEOOABC【例16】 如图，O 是ABC ∆的外接圆，AO 平分BAC ∠，AOB BOC ∠=∠，判断ABC∆的形状，并说明理由．【难度】★★ 【答案】等边三角形．【解析】∵AO 平分BAC ∠，∴BAO CAO ∠=∠，∵OA OC OB ==，∴ABO BAO CAO ACO ∠=∠=∠=∠， ∴AOB AOC ∠=∠，∵AOB BOC ∠=∠，∴AOB AOC BOC ∠=∠=∠， ∴AB BC CA ==，∴ABC ∆是等边三角形．【总结】本题考查同圆中相等的圆心角所对的弦相等．【例17】 已知，如图，AB 是O 直径，M 、N 分别是AO 、BO 的中点，CM AB ⊥，DN AB ⊥．求证：AC BD =．【难度】★★★ 【答案】详见解析．【解析】连接OC 、OD ，则OC OD =，∵M 、N 分别是AO 、BO 的中点，∴OM ON =， ∵CM AB ⊥，DN AB ⊥，∴OCM ∆≌ODN ∆， ∴COM DON ∠=∠，∴AC BD =．【总结】本题考查了同圆中相等的圆心角所对的弧相等．【例18】 如图，以点O 为圆心的圆弧上依次有四个点A 、B 、C 、D ，且AOB COD ∠=∠．求证：四边形ABCD 是等腰梯形．【难度】★★★ 【答案】详见解析． 【解析】连接AC 、BD ，∵AOB COD ∠=∠，∴AB CD =，∵12ACB AOB ∠=∠，12CAD COD ∠=∠，∴ACB CAD ∠=∠，∴AD ∥BC ，∴四边形ABCD 是等腰梯形．【总结】本题综合性较强，主要考查了同一条弦所对的圆周角和圆心角的关系，老师可以选择性的讲解．ABCDO NM OABCD1、 垂径定理如果圆的一条直径垂直于一条弦，那么这条直径平分这条弦，并且平分这条弦所对的弧． 2、 相关结论（1）如果圆的直径平分弦（这条弦不是直径），那么这条直径垂直于这条弦，并且平分这条弦所对的弧．（2）如果圆的直径平分弧，那么这条直径就垂直平分这条弧所对的弦． （3）如果一条直线是弦的垂直平分线，那么这条直线经过圆心，并且平分这条弦所对的弧．（4）如果一条直线平分弦和弦所对的一条弧，那么这条直线经过圆心，并且垂直于这条弦．（5）如果一条直线垂直于弦，并且平分弦所对的一条弧，那么这条直线经过圆心，并且平分这条弦．总结：在圆中，对于某一条直线“经过圆心”、“垂直于弦”、“平分弦”、“平分弦所对的弧”这四组关系中，如果有两组关系成立，那么其余两组关系也成立．【例19】 O 的直径为10，圆心O 到弦AB 的距离OM 的长为3，则弦AB 的长为______． 【难度】★ 【答案】8．【解析】∵O 的直径为10，∴5OB =，∵OM AB ⊥，∴OM 平分AB ， ∴224BM OB OM =-=，∴28AB BM ==． 【总结】本题考查了垂径定理的运用．模块三：垂径定理知识精讲例题解析ABCDE F O【例20】 在半径为2的O 中，弦AB 的长为22，则弦AB 所对的圆心角AOB ∠=____°． 【难度】★ 【答案】90．【解析】作OD AB ⊥于D ，则2AD BD ==，∵2OB =，∴222OD OB BD =-=，∴45BOD ∠=︒，∴90AOB ∠=︒．【总结】本题考查了垂径定理的运用．【例21】 如图，O 是ABC ∆的外接圆，圆心O 在这个三角形的高CD 上，点E 和点F分别是边AC 和BC 的中点． 求证：四边形CEDF 是菱形．【难度】★★ 【答案】详见解析．【解析】∵CD AB ⊥，且CD 过圆心，∴AD BD =，∴CA CB =，∵点E 和点F 分别是边AC 和BC 的中点，∴12CE AC =，12DE AC =，12CF BC =，12DF BC =，∴CE DE DF CF ===，∴四边形CEDF 是菱形．【总结】本题考查了垂径定理的运用即菱形的判定．【例22】 如图，一根横截面为圆形的输水管道，阴影部分为有水部分，此时水面宽AB为0.6米，污水深CD 为0.1米，求圆形的下水管道的直径．【难度】★★ 【答案】1米．【解析】连接OB ，设圆半径为R ，则0.1OD R =-， 10.32BD AB ==，由222OD BD OB +=得()2220.10.3R R -+=，解得0.5R =， 所以下水管道的直径为1米．【总结】本题考查了垂径定理以及勾股定理的综合运用．A BD O【例23】 如图，在O 中，弦CD 、EF 的延长线相交于点P ，G 、H 分别是CD 、EF 的中点，GH 与PC 、PE 分别相交于Q 、R 两点，试判断PQR ∆的形状，并证明所得到的结论．【难度】★★ 【答案】等腰三角形． 【解析】连接OG 、OH ，∵G 、H 分别是CD 、EF 的中点， ∴OG CD ⊥，OH EF ⊥，∵OH OG =，∴H G ∠=∠，∴GQC HRE ∠=∠，∴PQR PRQ ∠=∠， ∴PQR ∆是等腰三角形．【总结】本题考查了垂径定理的运用．【例24】 如图，P 是O 的弦AB 的中点，PC OA ⊥，垂足为C ，求证：PA PB AC AO =． 【难度】★★ 【答案】详见解析．【解析】连接OP ，∵P 是O 的弦AB 的中点，∴OP AB ⊥，∵PC OA ⊥，∴ACP ∆∽APO ∆，∴PA AOAC PA =，∵PA PB =， ∴PA AOAC PB=，即PA PB AC AO =． 【总结】本题考查了垂径定与相似三角形的综合运用．CDEFG O PQROP ABCABCDH O【例25】 位于本市浦东临港新城的滴水湖是圆形人工湖．为测量该湖的半径，小智和小方沿湖边选取A 、B 、C 三根木柱，使得A 、B 之间的距离与A 、C 之间的距离相等，并测得BC 长240米，A 到BC 的距离为5米，如图所示．请你帮他们求出滴水湖的半径．【难度】★★ 【答案】1442.5米．【解析】连接OA 交BC 于D 点，连接OC ，∵A 、B 之间的距离与A 、C 之间的距离相等， ∴OA BC ⊥，BD DC =，设半径为R ，则5OD R =-，120DC =，由222OD DC OC +=，∴()2225120R R -+=，解得：1442.5R =， 所以滴水湖的半径为1442．5米．【总结】本题考查了垂径定理的运用．【例26】 如图，弦CD 垂直于O 的直径AB ，垂足为H ，且22CD =，3BD =，则AB 的长为_______．【难度】★★ 【答案】3．【解析】由题意得2DH =，221BH DB DH =-=，设半径为R ，则1OH R =-，由222OD OH HD =+，∴()()22212R R =-+，解得32R =，∴23AB R ==．【总结】本题考查了垂径定理的运用．BCOD【例27】 已知O 的半径4r =，AB 、CD 为O 的两条弦，AB 、CD 的长分别是方程()24341630x x -++=的两根，其中AB > CD ，且AB // CD ，求AB 与CD 间的距离．【难度】★★★【答案】232+或232-．【解析】∵()24341630x x -++=，解得：143x =，24x =．∵AB >CD ，∴43AB =，4CD =，当AB 、CD 圆心同侧时，作OE AB ⊥于E ，并延长交CD 于F ，∵AB // CD ，∴OF ⊥CD ，∴222OE OB BE =-=，2223OF OD DF =-=， ∴232EF OF OE =-=-，当AB 、CD 圆心两侧时，同理可得232EF OF OE =+=+， ∴AB 与CD 间的距离是232+或232-．【总结】本题考查了垂径定理的运用，做题的关键是要分情况讨论．【例28】 已知，如图，1O 与2O 交于A 、B ，过A 的直线分别交1O 与2O 于M 、N ，C 是MN 的中点，P 是12O O 的中点． 求证：PA PC =．【难度】★★★ 【答案】详见解析．【解析】作1O E AM ⊥，2O F AN ⊥，作PH MN ⊥于H ，则12////O E PH O F ，且E 、F 分别为AM 、AN 的中点，∴12AE AF EF MN +==，∵C 是MN 的中点，∴12NC MN =，∴EF NC =，∴EC FN AF ==，∵P 是12O O 的中点，∴EH FH =， ∴HC HA =，∴PA PC =．【总结】本题考查了垂径定理的运用．ABCP N ME FH【例29】 如图，已知四边形ABCD 外接圆O 的半径为2，对角线AC 与BD 的交点为E ，AE = EC ，2AB AE =，且23BD =，求四边形ABCD 的面积．【难度】★★★ 【答案】23．【解析】∵AE EC =，2AB AE =，∴222AB AE AE AC ==⋅，∴AB AE AC AB=，又EAB BAC ∠=∠，∴ABE ∆∽ACB ∆， ∴ABE ACB ∠=∠，∵ADB ACB ∠=∠，∴ABE ADB ∠=∠，∴AB AD =， 连接AO 交BD 于H ，连接BO ，∵AB AD =，∴AO BD ⊥，∴3BH DH ==， ∵2OB =，∴1OH =，∴1AH =，∴132ABD S BD AH ∆=⋅⋅=，∵E 为AC 中点，∴ABE CBE S S ∆∆=，ADE CDE S S ∆∆=，即ABD CBD S S ∆∆=， ∴223ABD ABCD S S ∆==四边形， ∴四边形ABCD 的面积是23．【总结】本题考查了垂径定理的运用及图形的分割，综合性较强，解题时注意认真观察．A BC DE OH【例30】 如图，在半径为2的扇形AOB 中，90AOB ∠=︒，点C 是弧AB 上的一个动点（不与点A 、B 重合），OD BC ⊥，OE AC ⊥，垂足分别为D 、E ．（1）在DOE ∆中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由．（2）设BD = x ，DOE ∆的面积为y ，求y 关于x 的函数关系式，并写出它的定义域．【难度】★★★【答案】（1）DE 长度不变，2DE =；（2）()2244024x x x y x -+-=<<．【解析】（1）连接AB ，∴2222AB OA OB =+=，∵OD BC ⊥，OE AC ⊥， ∴D 、E 分别为BC 、AC 中点，∴122DE AB ==．（2）作DF OE ⊥于F ，由（1）易得1452DOE AOB ∠=∠=︒，由题意得24OD x =-，∴28222ODx DF OF -===，2222EF DE EF x =-=， ∴28222x xOE OF EF -+=+=，∴()221440224x x x y DF OE x -+-=⋅⋅=<<．【总结】本题考查了垂径定理、勾股定理及中位线定理的综合运用，综合性较强．OABCDEFABCDEO【习题1】已知O 半径为5，若点P 不在O 上，则线段OP 的取值范围为_______________．【难度】★【答案】05OP ≤<或5OP >．【解析】∵点P 不在O 上，∴当点P 在O 内时，05OP ≤<；当点P 在O 外时， 5OP >，综上可知05OP ≤<或5OP >． 【总结】本题考查了点与圆的位置关系．【习题2】 如图，AB 是直径，BC CD DE ==，40BOC ∠=︒，则AOE ∠=_____．【难度】★ 【答案】60︒．【解析】∵BC CD DE ==，∴BOC COD DOE ∠=∠=∠， ∵40BOC ∠=︒，∴180360AOE BOC ∠=︒-∠=︒． 【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【习题3】如图，为方便三个村庄居民子女的上学问题，上级镇政府决定在A 、B 、C 三个村庄旁边造一所学校，要求它到各村庄的距离相等，请你在图中画出学校的位置．（保留作图痕迹）【难度】★ 【答案】如图所示．【解析】作线段AB 、AC 的中垂线的交点P 即为学校位置． 【总结】本题考查了不共线的三点可以确定一个圆．随堂检测A BC D EFOAB CD E O【习题4】如图，AB CD =，OE AB ⊥，OF CD ⊥，25OEF ∠=︒，求EOF ∠的度数．【难度】★★【答案】130︒．【解析】∵AB CD =，OE AB ⊥，OF CD ⊥，∴OE OF =，∴OEF OFE ∠=∠，∵25OEF ∠=︒， ∴1801802130EOF OEF OFE OEF ∠=︒-∠-∠=︒-∠=︒．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【习题5】如图，在ABC ∆中，90B ∠=︒，60A ∠=︒，以点B 为圆心，AB 为半径画圆，交AC 于点D ，交BC 于点E ．求证：（1）2AD DE =；（2）D 是AC 的中点．【难度】★★ 【答案】详见解析．【解析】（1）连接BD ，∵BA BD =，60A ∠=︒，∴ABD ∆是等边三角形，∴60ABD ∠=︒，∵90B ∠=︒，∴30DBC ∠=︒，∴2ABD DBC ∠=∠， ∴2AD DE =；（2）由（1）得60ADB ∠=︒，DB DA =，∵ADB DBC C ∠=∠+∠，∴30C ∠=︒，∴DB DC =，∴DA DC =， ∴D 是AC 的中点．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【习题6】如图，AB 为O 直径，E 为BC 的中点，OE 交BC 于点D ，BD = 3，AB =10，则AC =______．【难度】★★ 【答案】8．【解析】∵AB 为O 直径，E 为BC 的中点，∴OD BC ⊥，BD CD =，∴224OD OB BD =-=， ∵OA OB =，∴28AC OD ==．【总结】本题考查了垂径定理及三角形中位线．AB CD ECDEFO【习题7】 如图，一条公路的转弯处是一段圆弧（即图中的CD ），点O 是CD 的圆心，其中CD = 600米，E 为CD 上一点，且OE CD ⊥，垂足为F ，EF = 90米，求这段弯路的半径．【难度】★★ 【答案】545米．【解析】∵点O 是CD 的圆心，OE CD ⊥，∴13002DF CD ==，设O 的半径为R ，则90OF R =-，由222OD OF FD =+得()22290300R R =-+，解得545R =， ∴这段弯路的半径为545米．【总结】本题考查了垂径定理的应用．【习题8】如图，在ABC ∆中，70A ∠=︒，O 截ABC ∆的三边所得的弦长都相等，求BOC ∠的度数．【难度】★★★ 【答案】125︒．【解析】作OE AB ⊥、OF BC ⊥、OG AC ⊥，∵O 截ABC ∆的三边所得的弦长都相等， ∴OE OF OG ==，∴OB 平分ABC ∠，OC 平分ACB ∠， ∵70A ∠=︒，∴110ABC ACB ∠+∠=︒，∴115522OBC OCB ABC ACB ∠+∠=∠+∠=︒，∴18055125BOC ∠=︒-︒=︒．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理、角平分线的逆定理及三角形的内角和．ABCOEFG【习题9】 已知，如图，ABC ∆是等边三角形，AB 是O 的直径，AE EF FB ==，CE 、CF 交AB 于点M 、N ． 求证：AM = MN = NB ．【难度】★★★ 【答案】详见解析． 【解析】连接OE 、OF ，∵AE EF FB ==，∴60AOE EOF FOB ∠=∠=∠=︒， ∵ABC ∆是等边三角形，∴CAO AOE ∠=∠，∴OE //AC ，∴OM OEMA AC=． ∵AC BC =，O 是AB 中点， ∴1302ACO ACB ∠=∠=，∴12OA AC =，∴12OE AC =．∴2AM OM =，∴23AM OA =，13OM OA =， 同理23BN OB =，13ON OB =，∵OA OB =，∴23OM ON OA +=，∴AM MN NB ==．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理及平分线分线段成比例．【习题10】 如图，AB 为O 的直径，CD 为弦，过点C 、D 分别作CN CD ⊥、DM CD ⊥，分别交AB 于点N 、M ，请问图中的AN 与BM 是否相等，说明理由．【难度】★★★【答案】AN 与BM 相等． 【解析】作OH CD ⊥交CD 于H ，则CH DH =，∵CN CD ⊥、DM CD ⊥， ∴CN ∥OH ∥DM ，∴ON OM =， ∵OA OB =，∴OA ON OB OM -=-， ∴AB BM =．【总结】本题考查了垂径定理及梯形的中位线．ABCDON M HABCE FN MO【作业1】在下列命题中，正确的个数是（ ） ① 圆心角相等，则它们所对的弦必相等；② 经过线段的两个端点及线段所在直线外一点可以确定一个圆； ③ 直径平分弦，则必垂直于弦；④ 如果同圆中，两条弦互相平分，那么这两条弦都是直径． A ．0个B ．1个C ．2个D ．3个【难度】★ 【答案】B ．【解析】① 需说明是在同圆或等圆中，故①错误；② 不共线的三点可以确定一个圆，故②正确； ③ 直径平分非直径的弦，则必垂直于弦，故③错误； ④ 如果同圆中，直径垂直于弦，则必然平分弦，故④错误．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理及垂径定理．【作业2】在ABC ∆中，90C ∠=︒，D 、E 分别是AB 、AC 的中点，AC = 7，BC = 4．若以点C 为圆心，BC 为半径作圆，判断点D 、E 与C 的位置关系．【难度】★【答案】点D 在C 外；点E 在C 内．【解析】∵AC = 7，BC = 4，90C ∠=︒，∴2265AB AC BC =+=，∵4C R =，1652DC AB R ==>，∴点D 在C 外； 1722EC AC R ==<，∴点E 在C 内． 【总结】本题考查了点与圆的位置关系．课后作业【作业3】已知直线a 和直线外两点A 、B ，经过A 、B 作一圆，使它的圆心在直线a上．【难度】★ 【答案】如图所示．【解析】作线段AB 的中垂线于直线a 的交点P 即为圆心． 【总结】本题考查了线段的垂直平分线的作法．【作业4】已知O 外一点A 和圆上的点最大距离为23厘米，最小距离为10厘米，则O 的半径为______厘米．【难度】★★【答案】132．【解析】点A 与圆心的连心线所在的直线与圆的交点即为点A 到圆上的最大距离和最小距离，所以半径()13231022R =-÷=厘米．【总结】本题考查了点与圆的位置关系．【作业5】 如图，在O 中，2AB BC =，试确定AB 与2BC 的大小关系．【难度】★★ 【答案】2AB BC <．【解析】取AB 中点E ，∵2AB BC =，∴AE EB BC ==，∵AE EB AB +>， ∴2AB BC <．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．AB COE【作业6】如图，矩形ABCD 与圆心在AB 上的O 交于点G 、B 、F 、E ，GB = 8厘米，AG = 1厘米，DE = 2厘米，则EF = ______厘米．【难度】★★ 【答案】6．【解析】连接OE ，作OH DC ⊥于H 点，∵GB = 8厘米，AG = 1厘米，DE = 2厘米， ∴4OE =厘米，3EH =厘米， ∴26EF EH ==厘米．【总结】本题考查了垂径定理的应用．【作业7】已知点A （1，0），B （4，0），P 是经过A 、B 两点的一个动圆，当P与y 轴相交，且在y 轴上两交点的距离为3时，求圆心P 的坐标．【难度】★★【答案】5522⎛⎫ ⎪⎝⎭，或5522⎛⎫- ⎪⎝⎭，．【解析】设()P x y ，∵P 是经过A 、B 两点的一个动圆，∴P 在线段AB 的中垂线上，∵A （1，0），B （4，0），∴52x =且P 在x 轴上两交点的距离为3，∵P 与y 轴相交，且在y 轴上两交点的距离为3， ∴P 在x 轴上与y 轴上截得的两条弦相等．∴x y =，∴52y =±，∴P 点坐标为5522⎛⎫ ⎪⎝⎭，或5522⎛⎫- ⎪⎝⎭，． 【总结】本题考查了垂径定理的应用．OABCD EF GHOP ABC【作业8】 已知，如图，在O 中，弦AB 的长是半径OA 的3倍，C 为AB 的中点，AB 、OC 相交于P ．求证：四边形OACB 为菱形．【难度】★★★ 【答案】详见解析．【解析】∵C 为AB 的中点，∴OC AB ⊥，AP PB =，∵弦AB 的长是半径OA 的3倍，∴32AP AO =，∴30PAO ∠=︒， ∴1122PO OA OC ==，即OP PC =，∵AP BP =，OC AB ⊥，∴四边形OACB 为菱形．【总结】本题考查了垂径定理的应用及菱形的判定．【作业9】已知：过圆O 内一点P 作弦AB 、CD ，且AB = CD ，在BD 上取两点E 、F ，且BE DF =．求证：直线PO 是EF 的垂直平分线．【难度】★★★ 【答案】详见解析．【解析】作OM AB ⊥，ON CD ⊥，∵AB = CD ，∴OM ON =，BM DN =， ∴POM ∆≌PON ∆，∴PM PN =，∴PB PD =，∵OB OD =，PO PO =，∴OPB ∆≌OPD ∆， ∴POB POD ∠=∠，∵BE DF =，∴BOE DOF ∠=∠， ∴POE POF ∠=∠，∴EOH FOH ∠=∠，∵OE OF =， ∴直线PO 是EF 的垂直平分线．【总结】本题考查了垂径定理及圆心角、弧、弦、弦心距之间关系的定理的综合应用．ABC D EFOPM NH【作业10】 如图，1O 与2O 交于A 、B ，M 为12O O 的中点，过点A 作EF AM ⊥分别交1O 与2O 于点E 、F ．若1290O AO ∠=︒，1212AO AO O O m ==（2m ≥），求EF 的长．【难度】★★★ 【答案】4．【解析】作1O C AE ⊥于C 点，并延长与2O A 的延长线交于G 点，作2O D AF ⊥于D 点，∵EF AM ⊥，M 为12O O 的中点，∴AC AD =，∴2O AD ∆≌GAC ∆，∴2AG AO =，∵1290O AO ∠=︒，∴1O AC ∆∽1O GA ∆，∴11O A AG O G AC ⋅=⋅， ∴121O A AO O G AC ⋅=⋅，∵1212AO AO O O m ==，∴121O O O G AC =⋅，∵1290O AO ∠=︒，2AG AO =，∴121O O O G =， ∴1AC =，∴44EF AC ==．【总结】本题考查了垂径定理及相似三角形性质的综合应用．ABEFMGC D。

高三数学知识点内接圆内接圆是指一个圆与多边形的所有边都相切，且圆心与多边形的每个顶点都在一条直线上。

在高三数学中，内接圆是一个重要的几何概念，涉及到许多相关的知识点。

本文将介绍内接圆在高三数学中的应用和相关概念。

一、内接圆的定义和性质内接圆的定义是指一个圆与多边形的所有边都相切，且圆心与多边形的每个顶点都在一条直线上。

内接圆有以下重要性质：1. 内接圆的圆心与多边形的重心、垂心和外心共线；2. 内接圆的半径等于多边形的内接圆半径；3. 内接圆的半径等于半周长除以多边形的边数；4. 内接圆与多边形的边相切，切点分别是多边形的顶点。

二、内接圆的应用内接圆在高三数学中有广泛的应用，涉及到以下几个重要的知识点：1. 内接圆的性质在三角形的几何证明中具有重要作用。

例如，利用内接圆的性质可以证明三角形的垂心、重心、外心共线；2. 内接圆与三角形的面积关系。

根据内接圆的性质，可以得到三角形面积的简洁表达式，减少计算量；3. 内接圆在解决数学问题中的应用。

例如，利用内接圆的特性可以解决最优化问题，如最大面积、最短路径等；4. 内接圆与圆的切线。

内接圆与多边形的边相切，如果一条直线同时是内接圆与外接圆的切线，则该直线必然是多边形的一个对称轴。

三、内接圆的相关概念在高三数学中，内接圆还涉及到以下几个相关的概念：1. 外接圆：一个圆与多边形的所有顶点都在圆上；2. 内接多边形：一个多边形的内接圆与该多边形的边相切；3. 外接多边形：一个多边形的外接圆与该多边形的顶点相切；4. 近似多边形：一个多边形的内接圆半径与外接圆半径之差很小；5. 多边形的内切圆半径与外接圆半径的比值：内接圆半径与外接圆半径的比值越接近1，证明多边形越接近于正多边形。

结论在高三数学中，内接圆是一个重要的几何概念，具有许多重要的性质和应用。

了解和熟练掌握内接圆的定义、性质和相关的概念，对于解决几何问题和证明定理有着重要的意义。

同时，通过对内接圆的深入研究，可以提高数学思维能力和解决问题的能力。

已知莱洛三角形内接圆形的半径-概述说明以及解释1.引言1.1 概述莱洛三角形是指一个内心在三角形内部的特殊三角形。

内接圆形是指与三角形的三条边都相切的圆形。

而本文的目的是研究已知莱洛三角形内接圆形的半径。

在数学几何领域，研究内接圆形的性质一直是一个重要的课题。

通过分析三角形的特点和内接圆形的特性，我们可以推导出莱洛三角形内接圆形的半径的表达式。

在本文的正文部分，我们将首先介绍莱洛三角形的定义，包括其内心的特点以及与三角形的边的关系。

接着，我们将详细定义内接圆形，并讨论其与三角形边的相切关系。

最重要的是，我们将推导出已知莱洛三角形内接圆形的半径的方法。

通过运用几何定律和三角函数，我们将给出内接圆形半径与莱洛三角形边长的关系式，并通过实例来说明具体的计算步骤。

本文的结论部分将总结已知莱洛三角形内接圆形的半径对于解决相关数学问题的重要性。

我们将探讨该结论对进一步研究和应用的潜在影响，并给出对未来研究方向的展望。

通过本文的研究，我们可以更深入地理解莱洛三角形和内接圆形的性质，并为解决与此相关的数学问题提供了一种有效的方法。

同时，我们也希望能够吸引更多数学爱好者和专业研究者对于这一领域进行更深入的探索。

1.2文章结构1.2 文章结构本文将按照以下顺序展开讨论已知莱洛三角形内接圆形的半径的推导过程：首先，我们将介绍莱洛三角形的定义，包括其特征和性质。

莱洛三角形是指一个具有特殊定位的三角形，它的顶点分别位于一个普通三角形的三条边上。

我们将深入探讨莱洛三角形的性质，为后面的推导奠定基础。

接下来，我们将给出内接圆形的定义及其与莱洛三角形的关联。

内接圆形是指一个圆形，它的圆心位于三角形内部，且与三角形的三边均相切。

我们将详细解释内接圆形的性质，并说明它与莱洛三角形的共同特点。

然后，我们将展示如何通过已知莱洛三角形内接圆形的半径来推导出内接圆的直接计算方法。

我们将引入一些数学定理和公式，以帮助读者理解推导过程。

同时，我们还会提供详细的计算步骤和实例，以加深读者对推导过程的理解。

中考总复习：圆的有关概念、性质与圆有关的位置关系—知识讲解（基础）责编：常春芳【考纲要求】1. 圆的基本性质和位置关系是中考考查的重点，但圆中复杂证明及两圆位置关系中证明会有下降趋势，不会有太复杂的大题出现；2.中考试题中将更侧重于具体问题中考查圆的定义及点与圆的位置关系，对应用、创新、开放探究型题目，会根据当前的政治形势、新闻背景和实际生活去命题，进一步体现数学来源于生活，又应用于生活．【知识网络】【考点梳理】考点一、圆的有关概念及性质1．圆的有关概念圆、圆心、半径、等圆；弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧；三角形的外接圆、三角形的内切圆、三角形的外心、三角形的内心、圆心角、圆周角．要点诠释：等弧：在同圆或等圆中，能够互相重合的弧叫做等弧．2．圆的对称性圆是轴对称图形，任何一条直径所在直线都是它的对称轴，圆有无数条对称轴；圆是以圆心为对称中心的中心对称图形；圆具有旋转不变性．3．圆的确定不在同一直线上的三个点确定一个圆．要点诠释：圆心确定圆的位置，半径确定圆的大小．4．垂直于弦的直径垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论 平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．要点诠释：在图中(1)直径CD ，(2)CD ⊥AB ，(3)AM ＝MB ，(4)C C A B =，(5)AD BD =．若上述5个条件有2个成立，则另外3个也成立．因此，垂径定理也称“五二三定理”．即知二推三． 注意：(1)(3)作条件时，应限制AB 不能为直径．5．圆心角、弧、弦之间的关系定理 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．推论 在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量也相等． 6．圆周角圆周角定理 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半． 推论1 在同圆或等圆中，相等的圆周角所对的弧也相等．推论2 半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径． 要点诠释：圆周角性质的前提是在同圆或等圆中．考点二、与圆有关的位置关系 1．点和圆的位置关系设⊙O 的半径为r ，点P 到圆心的距离OP ＝d ，则有：点P 在圆外⇔d ＞r ； 点P 在圆上⇔d ＝r ； 点P 在圆内⇔d ＜r ． 要点诠释：圆的确定：①过一点的圆有无数个，如图所示．②过两点A 、B 的圆有无数个，如图所示．③经过在同一直线上的三点不能作圆．④不在同一直线上的三点确定一个圆．如图所示．2．直线和圆的位置关系（1）切线的判定切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线．(会过圆上一点画圆的切线)（2）切线的性质切线的性质定理圆的切线垂直于过切点的半径．（3）切线长和切线长定理切线长经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长．切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．要点诠释：直线l是⊙O的切线，必须符合两个条件：①直线l经过⊙O上的一点A；②OA⊥l．3．圆和圆的位置关系(1)基本概念两圆相离、相切、外离、外切、相交、内切、内含的定义．(2)请看下表：要点诠释：①相切包括内切和外切，相离包括外离和内含．其中相切和相交是重点． ②同心圆是内含的特殊情况．③圆与圆的位置关系可以从两个圆的相对运动来理解． ④“R-r ”时，要特别注意，R ＞r ．【典型例题】类型一、圆的性质及垂径定理的应用【高清课堂：圆的有关概念、性质及与圆有关的位置关系 ID:412074 经典例题1】1．已知：如图所示，在⊙O 中，弦AB 的中点为C ，过点C 的半径为OD ．(1)若AB ＝OC ＝1，求CD 的长； (2)若半径OD ＝R ，∠AOB ＝120°，求CD 的长.【思路点拨】如图所示，一般的，若∠AOB ＝2n °，OD ⊥AB 于C ，OA ＝R ，OC ＝h ，则AB ＝2R ·sin n °＝2n ·tan n °＝CD ＝R －h ；AD 的长180n Rπ=． 【答案与解析】解：∵半径OD 经过弦AB 的中点C ， ∴半径OD ⊥AB ．(1)∵AB＝AC＝BC∵OC＝1，由勾股定理得OA＝2．∴CD＝OD－OC＝OA－OC＝1，即CD＝1.(2)∵OD⊥AB，OA＝OB，∴∠AOD＝∠BOD．∴∠AOB＝120°，∴∠AOC＝60°．∵OC＝OA·cos∠AOC＝OA·cos60°＝12 R，∴1122CD OD OC R R R =-=-=．【总结升华】圆的半径、弦长的一半、弦心距三条线段组成一个直角三角形，其中一个锐角为弦所对圆心角的一半，可充分利用它们的关系解决有关垂径定理的计算问题．举一反三：【变式】在足球比赛场上，甲、乙两名队员互相配合向对方球门进攻，当甲带球冲到A点时，乙已跟随冲到B点(如图所示)，此时甲是自己直接射门好还是迅速将球回传给乙，让乙射门好呢?(不考虑其他因素)【答案】解：过M、N、B三点作圆，显然A点在圆外，设MA交圆于C，则∠MAN＜∠MCN．而∠MCN＝∠MBN，∴∠MAN＜∠MBN．因此在B点射门较好．即甲应迅速将球回传给乙，让乙射门．2．（2015•大庆模拟）已知AB是⊙O的直径，C是圆周上的动点，P是弧AC的中点．（1）如图1，求证：OP∥BC；（2）如图2，PC交AB于D，当△ODC是等腰三角形时，求∠A的度数．【思路点拨】（1）连结AC，延长PO交AC于H，如图1，由P是弧AC的中点，根据垂径定理得PH⊥AC，再根据圆周角定理，由AB是⊙O的直径得∠ACB=90°，然后根据OP∥BC；（2）如图2，根据圆心角、弧、弦的关系，以及三角形内角和等推论证来求得∠A的度数.【答案与解析】（1）证明：连结AC，延长PO交AC于H，如图1，∵P是弧AB的中点，∴PH⊥AC，∵AB是⊙O的直径，∴∠ACB=90°，∴BC⊥AC，∴OP∥BC；（2）解：如图2，∵P是弧AC的中点，∴PA=PC，∴∠PAC=∠PCA，∵OA=OC，∴∠OAC=∠OCA，∴∠PAO=∠PCO，当DO=DC，设∠DCO=x，则∠DOC=x，∠PAO=x，∴∠OPC=∠OCP=x，∠PDO=2x，∵∠OPA=∠PAO=x，∴∠POD=2x，在△POD中，x+2x+2x=180°，解得x=36°，即∠PAO=36°，当CO=CD，设∠DCO=x，则∠OPC=x，∠PAO=x，∴∠POD=2x，∴∠ODC=∠POD+∠OPC=3x，∵CD=CO，∴∠DOC=∠ODC=3x，在△POC中，x+x+5x=180°，解得x=（）°，即∠PAO=（）°．综上所述，∠A的度数为36°或（）°．【总结升华】本题考查了圆周角定理及其推论同时考查了等腰三角形的性质、垂径定理和三角形内角和定理．举一反三：【变式】（2015•温州模拟）如图，在Rt△ABC中，∠ACB=90°，AC=5，CB=12，AD是△ABC的角平分线，过A、C、D三点的圆与斜边AB交于点E，连接DE．（1）求BE的长；（2）求△ACD外接圆的半径．【答案】解：（1）∵∠ACB=90°，且∠ACB为圆O的圆周角（已知），∴AD为圆O的直径（90°的圆周角所对的弦为圆的直径），∴∠AED=90°（直径所对的圆周角为直角），又AD是△ABC的角平分线（已知），∴∠CAD=∠EAD（角平分线定义），∴CD=DE（在同圆或等圆中，相等的圆周角所对的弦相等），在Rt△ACD和Rt△AED中，，∴Rt△ACD≌Rt△AED（HL），∴AC=AE（全等三角形的对应边相等）；∵△ABC为直角三角形，且AC=5，CB=12，∴根据勾股定理得：AB==13，∴BE=13﹣AC=13﹣5=8；（2）由（1）得到∠AED=90°，则有∠BED=90°，设CD=DE=x，则DB=BC﹣CD=12﹣x，EB=AB﹣AE=AB﹣AC=13﹣5=8，在Rt△BED中，根据勾股定理得：BD2=BE2+ED2，即（12﹣x）2=x2+82，解得：x=，∴CD=，又AC=5，△ACD为直角三角形，∴根据勾股定理得：AD==，根据AD是△ACD外接圆直径，∴△ACD外接圆的半径为：×=．类型二、圆的切线判定与性质的应用3．如图所示，AB＝AC，O是BC的中点，⊙O与AB相切于点D，求证：AC与⊙O相切．【思路点拨】AC与⊙O有无公共点在已知条件中没有说明，因此只能过点O向AC作垂线段OE，长等于⊙O的半径，则垂足E必在⊙O上，从而AC与⊙O相切．【答案与解析】证明：连接OD，作OE⊥AC，垂足为E，连结OA．∵AB与⊙O相切于点D，∴OD⊥AB．∵AB＝AC，OB＝OC，∴∠1＝∠2，∴OE＝OD．∵OD为⊙O半径，∴AC与⊙O相切．【总结升华】如果已知直线经过圆上一点，那么连半径，证垂直；如果已知直线与圆是否有公共点在条件中并没有给出，那么作垂直，证半径．举一反三：【变式】如图所示，在Rt△ABC中，∠C＝90°，BC＝a，AC＝b，AB＝c．求△ABC的内切圆的半径．【答案】解：设△ABC的内切圆与三边的切点分别为D、E、F，根据切线长定理可得：AE ＝AF ，BF ＝BD ，CD ＝CE ，而AE+CE ＝b ，CD+BD ＝a ，AF+BF ＝c ， 可求2a b cCE +-=． 连接OE 、OD ，易证OE ＝CE ．即直角三角形的内切圆半径2a b cr +-=．4．如图所示，已知：△ABC 内接于⊙O ，点D 在OC 的延长线上，1sin 2B =，∠D ＝30°． (1)求证：AD 是⊙O 的切线； (2)若AC ＝6，求AD 的长．【思路点拨】（1）连接OA ，根据圆周角定理求出∠O 的度数，根据三角形的内角和定理求出∠OAD ，根据切线的判定推出即可；（2）得出等边三角形AOC ，求出OA ，根据勾股定理求出AD 的长即可． 【答案与解析】(1)证明：连接OA ，∵1sin 2B =，∴∠B ＝30°． ∵∠AOC ＝2∠B ，∴∠AOC ＝60°． ∵∠D ＝30°，∴∠OAD ＝180°－∠D －∠AOD ＝90°． ∴AD 是⊙O 的切线．(2)解：∵OA ＝OC ，∠AOC ＝60°，∴△AOC是等边三角形，∴OA＝AC＝6．∵∠OAD＝90°，∠D＝30°，∴AD＝【总结升华】证明直线是圆的切线的方法：①有半径，证垂直；②有垂直，证半径．举一反三：【变式】如图所示，半径OA⊥OB，P是OB延长线上一点，PA交⊙O于D，过D作⊙O的切线交PO于C 点，求证：PC＝CD．【答案】证明：连接OD．∵CE切⊙O于D，∴OD⊥CE．∴∠2+∠3＝90°．∵OA⊥OB，∴∠P+∠A＝90°．∵OD＝OA，∴∠3＝∠A．．∴∠P＝∠2．又∵∠1＝∠2，∴∠P＝∠1．∴PC＝CD．类型三、切线的性质与等腰三角形、勾股定理综合运用5．已知AB是⊙O的直径，点P是AB延长线上的一个动点，过P作⊙O的切线，切点为C，∠APC 的平分线交AC于点D，求∠CDP的度数.【思路点拨】连接OC，根据题意，可知OC⊥PC，∠CPD+∠DPA+∠A+∠ACO=90°，可推出∠DPA+∠A=45°，即∠CDP=45°．【答案与解析】解：连接OC，∵OC=OA，，PD平分∠APC，∴∠CPD=∠DPA，∠A=∠ACO，∵PC为⊙O的切线，∴OC⊥PC，∵∠CPD+∠DPA+∠A+∠ACO=90°，∴∠DPA+∠A=45°，即∠CDP=45°．【总结升华】本题主要考查切线的性质、等边三角形的性质、角平分线的性质、外角的性质，解题的关键在于做好辅助线构建直角三角形，求证∠CPD+∠DPA+∠A+∠ACO=90°，即可求出∠CDP=45°．【高清课堂：圆的有关概念、性质及与圆有关的位置关系 ID:412074 经典例题3】6．如图所示，AB是⊙O的直径，AF是⊙O的弦，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF于点D，交AB的延长线于点C．(1)求证：CD是⊙O的切线；(2)若DE＝4，sinC＝35，求AE的长．【思路点拨】构造半径、半弦、弦心距的直角三角形．【答案与解析】解：(1)证明：连接OE，BF，交于点G，则BF⊥AF，BF∥CD．∵OA＝OE，∴∠OAE＝∠OEA．∵∠OAE＝∠FAE，∴∠OEA＝∠FAE．∴OE∥AF，∵AF⊥DE，∴OE⊥CD．∴CD为⊙O的切线．(2)解：∵ BF∥DE，OE∥AF，∠D＝90°，∴四边形DEGF为矩形．∴BF＝2GF＝2DE＝8．∵BF∥CD，∴∠C＝∠ABF．可求得OA＝OB＝5，OG＝3．∴DF＝EG＝2，AF＝AB·sinC＝6．∴AD＝8，AE=【总结升华】(1)通过挖掘图形的性质，将分散的条件sinC＝35，DE＝4，集中到一个直角三角形中，使问题最终得到解决；(2)本题第(2)问还可以适当改变后进行变式训练，如改为：若DF＝2，sinC＝35，求AE的长；(3)第(2)问还可以过O作OM⊥AF于M后得OM＝DE＝4，sin∠AOM＝sinC＝35加以解决.。

关于圆的所有定理1．圆是以圆心为对称中心的中心对称图形；围绕圆心旋转任意一个角度α,都能够与原来的重合．2.顶点在圆心的角叫做圆心角．圆心到弦的距离叫做弦心距．圆幂定理（相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理）切线长定理（从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角）垂径定理（垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧）圆周角定理弦切角定理（定义弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半. (弦切角就是切线与弦所夹的角））3．在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等．4．在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等．5．把整个圆周等分成360份,每一份弧是1°的弧．圆心角的度数和它所对的弧的度数相等．6.圆是中心对称图形,即圆绕其对称中心(圆心)旋转180°后能够与原来图形重合,这一性质不难理解．圆和其他中心对称图形不同,它还具有旋转不变性,即围绕圆心旋转任意一个角度,都能够与原来的图形重合．7.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧8.（1）平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧（2）弦的垂直平分线经过圆心,并且平分弦所对的两条弧（3）平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧9.圆的两条平行弦所夹的弧相等10.(1)一条弧所对的圆周角等于它所对的圆心角的一半.(2)同弧或等弧所对的圆周角相等；同圆或等圆中,相等的圆周角所对的弧也相等.(3)半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径.(4)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.11.(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.(2)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(3)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(4)弦的垂直平分线经过圆心,并且平分弦所对的两条弦.(5)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.(6)圆的两条平行弦所夹的弧度数相等.12.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴．垂直于弦的直径平分这条弦,并且平分弦所对的两条弧．13.平分弦(不是直径)的直径垂直与弦,并且平分弦所对的两条弧.14.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距也相等.15.在同圆或等圆中,相等的弦所对的弧相等,所对的圆心角相等,所对的弦的弦心距也相等.16.同一个弧有无数个相对的圆周角.17.弧的比等于弧所对的圆心角的比.18.圆的内接四边形的对角互补或相等.19.不在同一条直线上的三个点能确定一个圆.20.直径是圆中最长的弦.21.一条弦把一个圆分成一个优弧和一个劣弧.。

如果别人思考数学的真理像我一样深入持久，他也会找到我的发现。

——高斯圆的有关性质⎧⎪⎪⎨⎪⎪⎩垂径定理弧、弦、圆心角的关系圆的有关性质圆周角定理及推论圆内接四边形的性质 知识点1 垂径定理①弦和直径：(1)弦：连接圆上任意两点的线段叫做弦.(2)直径：经过圆心的弦叫做直径。

直径等于半径的两倍。

②弧：(1) 弧：圆上任意两点间的部分叫做圆弧，简称弧，用符号⌒表示，以A,B 为端点的的弧记作AB ⌒,读作弧AB. (2)半圆、优弧、劣弧：圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。

大于半圆的弧叫做优弧，优弧大于180º用三个字母表示，如ACB .小于半圆的弧叫做劣弧，如AB 。

（3）等弧：在同圆或者等圆中能够相互重合的弧是等弧，度数或者长度相等的弧不一定是等弧。

③弦心距：（1）圆心到弦的距离叫做弦心距。

（2）圆心角、弧、弦、弦心距之间的相等关系：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的圆心角也相等，所对弦的弦心距也相等。

四者有一个相等，则其他三个都相等。

圆心到弦的垂线段的长度称为这条弦的弦心距。

④圆的性质：(1)旋转不变性：圆是旋转对称图形，绕圆心旋转任一角度都和原来图形重合；圆是中心对称图形，对称中心是圆心．在同圆或等圆中，两个圆心角，两条弧，两条弦，两条弦心距，这四组量中的任意一组相等，那么它所对应的其他各组分别相等．(2)轴对称：圆是轴对称图形，直径所在的直线是它的对称轴。

⑤垂径定理及推论：(1)垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．(2)平分弦（此弦不能是直径）的直径垂直于弦，并且平分弦所对的两条弧．(3)弦的垂直平分线过圆心，且平分弦对的两条弧．(4)平分一条弦所对的两条弧的直线过圆心，且垂直平分此弦．(5)平行弦夹的弧相等．⑥同心圆与等圆（1）同心圆：圆心相同，半径不相等的两个圆叫做同心圆。

如图一，半径为r1与半径为r2的⊙O叫做同心圆。

2016年春季初三数学学案圆一、学习目标1、熟记并运用圆内定理2、学会圆内等角的表示或者找角的关系3、学会运用圆内定理与三角形、四边形等性质一起结合使用。

二、知识点总结 知识点一 圆内定理1、一个基本思路：圆→等腰三角形→等腰、等角、三线合一2、三个基本概念：（同圆或者等圆中）弦、弧、圆心角【一等即三等】 【★注意：弦等不能得到圆周角相等】3、四大定理：（1）圆周角定理：在同圆或等圆中：①同弧或等弧所对的圆周角相等②都等于这条弧所对圆心角的一半【六字真言→_→隐藏条件：角 找 弧，弧 找 角】（2）半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

【直 径 → 90°】 （3）圆内接四边形的对角互补【→_→隐藏条件：外 角 等 于 内 对 角】例1、（2014年质检）如图9，⊙O 是△ABC 的外接圆，D 是︵ACB 的中点，DE ∥BC 交AC 的延长线于点E ，若AE=10，∠ACB=60°，求BC 的长．基础练习（★）：1．（一中第一次月考）如图，BC CD DE ==，已知AB 是圆O 的直径，40BOC ∠=，那么AOE ∠=( ) A ．40︒ B ．60︒ C ．80︒ D ．120︒ 2．（一模）如图，O 是ABC ∆的外接圆，100BOC ∠=︒，则A ∠的度数为第3题图9OEDC BAC O图2B AE D O图8CBA3．（双十月考、外国语期中）如图，O 是ABC ∆的外接圆，若40OCB ∠=︒，则A ∠= 。

4．（莲花月考）如图，四个边长为2的小正方形拼成一个大正方形，A 、B 、O 是小正方形顶点，O 的半径为2，P 是O 上的点，且位于右上方的小正方形内，则APB ∠等于（ ）A ．30︒B ．45︒C ．60︒D ．90︒5．（湖滨期中）如图，ABC ∆为O 内接三角形，AB 为O 的直径，点D 在O 上，68ADC ∙∠=，则BAC ∠的度数为 ．6．（莲花月考）圆的弦长与它的半径相等，则该弦所对的圆周角的度数是（ ）A ．30︒B ．150︒C ．30︒或150︒D ．60︒7、（厦门中考）如图2，在⊙O 中，︵AB ＝︵AC ，∠A ＝30°，则∠B ＝_________A ．150°B ．75°C ．60°D ．15°8、（九上质检）如图，在⊙O 中，弦AC 和BD 相交于点E ，︵AB ＝︵BC ＝︵CD .若∠BEC ＝110°，则∠BDC 的度数是A . 35°B . 45°C .55°D . 70° 9、（同安一模）如图P ，在圆内接四边形ABCD 中，若∠C =80°，则∠A 等于( )A ．120°B ．100°C ．80°D ．90°10、（2014年厦门质检） 如图2，A 、B 、C 是⊙O 上的三个点，若∠AOC ＝110°，则∠ABC ＝ °.11、（厦门中考）如图8，已知A ，B ，C ，D 是⊙O 上的四点，延长DC ，AB 相交于点E ．若BC ＝BE ．求证：△ADE 是等腰三角形.图1OE DCBA 图2O CBA图P12、如图，等边△ABC 内接于⊙O ，P 是弧AB 上任一点（点P 不与点A 、B 重合），连AP 、BP ，过点C 作CM ∥BP 交PA 的延长线于点M ．求证：△ACM ≌△BCP ；中等练习（★★）：1、（★★）如图，090AOB ∠=，C 、D 是AB 的三等分点，AB 分别交OC 、OD 于点E 、F ，求证AE=BF=CD2、（一中一模）（★★）如图7，已知A ，B ，C ，D 是⊙O 四点，E 是AD 上，连接BE 交AD 于Q ，若∠AQE=∠EDC ，∠CQD=∠E ，求证：AQ=BC 。

双曲线的蒙日圆和内准圆1. 引言双曲线是数学中的一种重要曲线，具有许多独特的性质和应用。

在双曲线的研究中，蒙日圆和内准圆是两个重要概念。

本文将详细介绍双曲线、蒙日圆和内准圆的定义、性质以及它们在数学和物理中的应用。

2. 双曲线双曲线是由一个平面上满足一定条件的点集构成的曲线。

它可以通过焦点和直角双曲线方程来定义。

对于一个给定的焦点F和直角双曲线方程x 2a2−y2b2=1，其中a和b是正实数，满足a>b，所有满足方程的点构成了一个双曲线。

双曲线有许多重要性质，例如： - 双曲线有两个分支，分别称为左支和右支； - 双曲线与x轴、y轴都有渐近线； - 双曲线关于原点对称等。

3. 蒙日圆蒙日圆是与给定的双曲线相切于其两个焦点的圆。

具体来说，对于一个给定的双曲线和其焦点F1、F2，蒙日圆是与F1、F2分别相切于两个点P1、P2，并且与双曲线相切于这两个点的圆。

蒙日圆有以下性质： - 蒙日圆与双曲线外公切于两个点； - 蒙日圆与双曲线内公切于无穷远处。

蒙日圆在数学中有广泛的应用。

例如，在几何光学中，蒙日圆可以用来描述光线在折射或反射过程中的路径。

此外，蒙日圆还可以用来计算双曲线的离心率等重要参数。

4. 内准圆内准圆是与给定的双曲线内公切于一点，并且与该双曲线外公切于无穷远处的圆。

具体来说，对于一个给定的双曲线和其焦点F1、F2，内准圆是与焦点连线上某一点P相交，并且与该焦点连线垂直，并且与双曲线外公切于无穷远处的圆。

内准圆的性质如下： - 内准圆与双曲线内公切于一点； - 内准圆与双曲线外公切于无穷远处。

内准圆在数学和物理中都有重要的应用。

例如，在电磁场分析中，内准圆可以用来描述电荷分布和电场强度之间的关系。

此外，在天体力学中，内准圆可以用来描述行星轨道之间的相对位置。

5. 结论蒙日圆和内准圆是双曲线研究中的两个重要概念。

蒙日圆是与双曲线相切于其焦点的圆，而内准圆是与双曲线内公切于一点，并且与该双曲线外公切于无穷远处的圆。

椭圆的外准圆和内准圆公式推导过程首先，我们来定义一下什么是外准圆和内准圆。

设定椭圆的长轴长为2a，短轴长为2b，焦距为2c，离心率为e。

外准圆是一个与椭圆相切的圆，它的半径等于椭圆的离心率乘以椭圆的长轴半径，即R = ae。

内准圆也是一个与椭圆相切的圆，它的半径等于椭圆的离心率减去1后再乘以椭圆的长轴半径，即r=a(e-1)。

接下来，我们来推导一下外准圆的公式。

假设外准圆的圆心位于原点O，半径为R，我们需要证明椭圆的焦点F与外准圆的切点P、圆心O和长轴的交点M共线。

首先，我们知道，椭圆的焦距为2c，离心率为e，椭圆的方程为：(x^2/a^2)+(y^2/b^2)=1椭圆的焦点坐标可以表示为F(c,0)和F'(-c,0)。

设圆心O的坐标为O(0,0)，外准圆上的切点P的坐标为P(x,y)。

由于P点位于外准圆上，根据圆的标准方程，得到P点满足的方程为：x^2+y^2=R^2由于P点位于椭圆上，根据椭圆的方程，得到P点满足的方程为：(x^2/a^2)+(y^2/b^2)=1联立以上两个方程，我们可以解得：x^2=R^2-y^2代入椭圆的方程，得到一个关于y的方程：(R^2-y^2)/a^2+(y^2/b^2)=1化简得：(R^2-y^2)b^2+y^2a^2=a^2b^2整理可得：R^2b^2-y^2b^2+y^2a^2-a^2b^2=0把R = ae代入，得到：a^2e^2b^2-y^2b^2+y^2a^2-a^2b^2=0进一步化简，得到：(a^2e^2-a^2)b^2=(b^2-a^2)y^2或者：y^2=[(1-e^2)/(b^2-a^2)](b^2-a^2)考虑到同一位置的y坐标是相等的，我们约定y=a(e-1)。

将y的值代入得到：[(1-e^2)/(b^2-a^2)](b^2-a^2)=(a(e-1))^2化简得到：[(1-e^2)/(b^2-a^2)]=(e-1)^2整理得到：e^2-(2e-1)b^2+a^2=0利用二次根公式解得e，得到：e=b^2/(b^2-a^2)将e带入即可得到：R=a(b^2/(b^2-a^2))化简得到：R = ab^2/(b^2 - a^2)因此，外准圆的半径R为ab^2/(b^2 - a^2)，这就是外准圆的公式。

内准圆证明
设f， g满足：|1、
证明：证明用逆向思维法。

考虑到下面问题都可转化为等积变形。

2、内准圆的面积证明：内准圆的周长=16n，内准圆半径=5n=5m，内准圆面积=2πm2=π200m^2=200π（ 2m^2），根据三角形内切圆的面积计算公式，我们得出中垂线上的阴影部分的面积=√
2*5n*5m^2-(200πm^2-5m^2)^2=8m^2（实际上根据中垂线上部分的面积=外切圆的面积-内切圆的面积，我们可以看出
m^2=8m^2-5m^2-200m^2-500π），得出中垂线上部分的面积为8m^2。

即证明结束。

3、中垂线定理证明：垂足分别为O、 P、 Q、 R、 S、 T、 U、V、 W，过O做水平直线L=y=mx（ x为内准圆半径），过P做水平直线L=y=ky（ x为内准圆半径），过Q做水平直线L=y=ky-1（ x为内准圆半径），过R做水平直线L=y=l（ x为内准圆半径），过S做水平直线L=y=kx（ x为内准圆半径），过U做水平直线L=y=-x（ x为内准圆半径），过V做水平直线L=y=-kx-1（ x为内准圆半径）。

，过D做水平直线L=y=kx-1（ x为内准圆半径），过E做水平直线L=y=kx-1（ x为内准圆半径），过F做水平直线L=y=kx-1（ x为内准圆半径），过G做水平直线L=y=kx-1（ x为内准圆半径），过H 做水平直线L=y=kx-1（ x为内准圆半径）。

那么在阴影部分的面积等于内准圆面积+3*2*5n*5m^2-(200πm^2-5m^2)^2-8m^2，阴影部分的面积=4m^2=8m^2。

即证明完毕。

内准圆证明
内准圆是一种特殊的圆，它的定义是：在一个多边形内部，经过多边形所有顶点的圆叫做内准圆。

下面是证明内准圆存在的方法：
1.利用奇偶性
由于内准圆经过所有顶点，因此其半径为所有顶点到圆心的距离的最大值。

假设多边形有奇数个顶点，则所有顶点到圆心的距离的奇偶性必定不同，因此内准圆必定存在。

2.利用四边形的性质
对于四边形来说，可以将其分成两个互不相交的三角形。

先考虑三角形的内准圆，可以将其看成是三条边的中线的交点，连接三角形顶点的圆心。

而四边形的内准圆就是两个三角形的内准圆的圆心的中点，连接四边形顶点的圆心。

3.利用图像反演
图像反演是一种将几何图形映射到另一个几何图形的方法。

假设内准圆的圆心为O，多边形的某个顶点为 A，则将多边形的所有顶点按照 O 为中心进行图像反演，得到的图形一定是一个凸包（也就是将多边形的所有边延长相交的图形）。

由于凸包的内准圆存在，因此多边形的内准圆也存在。

这三种方法都可以用来证明多边形的内准圆存在。

对于具体的求法，可以使用三角函数或者图像反演的方法来求出内准圆的圆心和半径。

注意：内准圆并不一定是多边形的最小圆覆盖，也就是说，内准圆的半径可能会比多边形的最小圆覆盖的半径要大。

椭圆的蒙日圆和内准圆
椭圆的蒙日圆和内准圆是数学中的一种必要名词：这些概念是基于点、直线、
椭圆和其他几何图形有关的，也是有关函数的重要概念。

蒙日圆是一种形状较大的椭圆，是两个坐标轴之间的离散圆，其参数为a和b，是蒙日圆的大小尺寸。

蒙日圆覆盖了一个给定椭圆的可能路径。

在任何情况下，当一个椭圆的离心率大于1时就是蒙日圆。

它的质心在坐标原点，其中所有一般点都落在椭圆轨迹上；椭圆的方程为$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$，其中a和b分别为椭圆的长短轴，而蒙日圆的椭圆方程为$x^{2}+4y^{2}=4a^{2}$。

内准圆是一种形状较小的椭圆，是一个在椭圆轨迹上满足内准圆方程
$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$的内部圆，其参数也是a和b，
长短轴为a和b，当内准圆的离心率小于1时，为内准圆；它的质心不是在原点，
而是在（0，c）点，其中c为椭圆的短半轴；内准圆的椭圆方程为
$x^{2}+4y^{2}=4a^{2}-c^{2}$。

以上所述就是椭圆的蒙日圆和内准圆，对于坐标轴中的这种几何图形，来说它
拥有着一定的意义，也是复习数学公式和概念的重要内容，在接下来的学习和使用中也会有一定帮助。

内准圆结论推导
内准圆结论是指：在一个平面图形内，若图形的所有内角均小于180°，则该图形必定可以包围一个圆。

证明：
设图形内的任意一点为O，图形的边界上的任意一点为A。

第一步：图形内所有角均小于180°，则图形内至少存在两条边，使得这两条边的夹角小于180°。

第二步：由第一步可知，图形内至少存在两条边，使得这两条边的夹角小于180°。

则在这两条边的夹角内，必定可以构造一条线段，使得这条线段的两端点分别在这两条边上。

第三步：由第二步可知，图形内存在一条线段，使得这条线段的两端点分别在图形的边界上。

设这条线段的两端点分别为A、B。

则由相似三角形的知识可知，于180°。

则在这两条边的夹角内，必定可以构造一条线段，使得这条线段的两端点分别在这两条边
上。

由第二步可知，图形内存在一条线段，使得这条线段的两端点分别在图形的边界上。

设这条线段的两端点分别为A、B。

则由相似三角形的知识可知，
$\frac{AB}{AC}=\frac{AB}{BC}$，即$AC=BC$。

由第三步可知，若存在一条线段，使得这条线段的两端点分别在图形的边界上，且这两个端点距离图形内点O相等，则可以构造一个圆，使得这个圆的圆心为O，圆的半径为这条线段的长度。

所以，证毕。

最内稳定圆轨道
最内稳定圆轨道是指在一个力场中，满足条件的轨道，使得运动体在该轨道上运动时，有最小的能量，也就是最稳定的轨道。

常见的力场有引力场、电磁场等。

在引力场中，最内稳定圆轨道是指满足条件的圆轨道，使得运动体在该轨道上运动时，有最小的能量，也就是最稳定的轨道。

常见的最内稳定圆轨道有轨道半径、轨道长度、轨道周期等参数，这些参数受到力场的影响。

例如，在引力场中，轨道半径与物体的质量和运动速度有关，轨道长度与物体的质量和运动周期有关，轨道周期与物体的质量和轨道半径有关。

最内稳定圆轨道在自然界中有广泛的应用，例如地球运行的轨道、卫星运行的轨道等。

它也广泛应用在人类的技术领域，例如航天技术、卫星通信技术等。

准圆1. 定义（1）内准圆：到对称中心张角为90°的弦，与定圆恒相切，称此定圆为曲线的内准圆； （2）外准圆：曲线上两条互相垂直的切线交点在定圆上，称此定圆为曲线的外准圆；2. 椭圆的准圆 （1）椭圆的内准圆设 OA 是椭圆 x 2a 2+y 2b 2=1 的一条中心半径其与 x 轴正半轴的夹角为 θ ，设 OB 是另一条与 x 轴正半轴的夹角为 θ+π2 的中心半径，OA ⊥OB 且A,B 的坐标分别为 (|OA |cos θ,|OA |sin θ), (|OB |cos (θ+π2),|OB |sin (θ+π2))，于是有|OA |2cos 2θa 2+|OA |2sin 2θb 2=1,|OB |2cos 2(θ+π2)a 2+|OB |2sin 2(θ+π2)b 2=11|OA |2=cos 2θa 2+sin 2θb 2,1|OB |2=sin 2θa 2+cos 2θb 2得到：1|OA|2+1|OB|2=1a2+1b 2根据勾股定理：|OA |2+|OB |2=|AB |2 过O 作 OH 垂直于 AB 于 H 根据面积公式有 |OA |∙|OB |=|OH |∙|AB | 于是有 |OH |=|OA |∙|OB ||AB ||OH |2=|OA |2|OB |2|OA |2+|OB |2 =11|OA|2+1|OB|2=11a 2+1b 2=a 2b 2a 2+b 2（定值）称 x 2+y 2=a 2b 2a 2+b 2 为椭圆 x 2a 2+y 2b 2=1 的内准圆 根据射影定理有|HA |∙|HB |=|OH |2=a 2b 2a 2+b2特别地，当 a =b =r 时，表示圆有内准圆 x 2+y 2=r 22易证：∆ABB ′是以 BB ′为底的等腰三角形，且 k OH ∙k OH′=−a 2b 2（2）椭圆的外准圆（蒙日圆）设 PA,PB 是椭圆x2a2+y2b2=1 的一组互相垂直的切线，P 的坐标为(x0,y0)设直线 PA,PB 的方程为y−y0=k(x−x0)联立方程组{x2a2+y2b2=1y−y0=k(x−x0)b2x2+a2[k(x−x0)+y0]2=a2b2(a2k2+b2)x2+2a2k(y0−kx0)x+a2(k2x02−2kx0y0+y02−b2)=0令∆4a2=a2k2(kx0−y0)2+(a2k2+b2)(k2x02−2kx0y0+y02−b2)=0 (x02−a2)k2−2x0y0k+(y02−b2)=0因为PA⊥PB所以 k1∙k2=−1k1∙k2=y02−b2x02−a2=−1x02+y02=a2+b2（定值）称 x2+y2=a2+b2为椭圆x2a2+y2b2=1 的外准圆.k OA∙k PA=k OB∙k PB=−b2a2k OA∙k OB=−b4a4特别地，当 a=b=R 时，表示圆有外准圆 x2+y2=2R2（3）椭圆外准圆的性质⚫ OP 将弦 AB 平分，AB ∥QQ′ ⚫ 椭圆上一点 A 的切线交外准圆于P,Q 两点，则 k OP ∙k OQ =−b 2a 2⚫ OM 2+ON 2=a 2+b 2推导：延长 PB 、PA 分别交外准圆于 Q 、Q ′ 连接 QQ ′，则 QQ ′ 过圆心 O,(∠QPQ’=π2) 根据切点弦的性质可知，OP 平分 AB 又因为 OP 平分 QQ ′，所以 QQ ′∥AB 根据切点弦性质有 k OP ∙k AB =−b 2a 2 则 k OP ∙k OQ =−b 2a 2MN 在椭圆上且 k OM ∙k ON =−b 2a2不妨设 M (a cos θ,b sin θ)，N (−a sin θ,b cos θ) 则 OM 2+ON 2=a 2+b 2⚫ PA ∙QA =F 1A ∙F 2A证明：如图，F 1、F 2 是椭圆 x 2a 2+y 2b 2=1 的焦点，设 A 的坐标为 (x 0,y 0) 则有：{F 1A =a +ex 0F 2A =a −ex 0F 1A ∙F 2A =(a +ex 0)(a −ex 0)=a 2−e 2x 02根据圆的相交弦定理有PA ∙QA =C 1A ∙C 2A =(R −OA )(R +OA ) =R 2−OA 2=a 2+b 2−(x 02+y 02)=a 2+b 2−(x 02+b 2−b 2a2x 02)=a 2−a 2−b 2a 2x 02=a 2−e 2x 02PA ∙QA =F 1A ∙F 2A ，证毕⚫P 到弦 AB 的距离的与 O 到弦 AB 的距离之积为定值d1d2=a2b2a2+b2证明：设 P 的坐标为(x0,y0)则弦 AB 的方程为x0xa2+y0yb2=1P 到弦 AB 的距离d1=|x022+y022−1|√x02a4+y02b4O 到弦 AB 的距离 d2=√x0 a4+y0 b4d1d2=|x02a2+y02b2−1| x02a4+y02b4因为 P 在外准圆x2+y2=a2+b2上所以y02=a2+b2−x02代入得d1d2=|x02a2+a2+b2−x02b2−1|x02a4+a2+b2−x02b4=|(1a2−1b2)x02+a2b2|(1a4−1b4)x02+a2+b2b4=|(1a2−1b2)x02+a2b2|(1a2−1b2)(1a2+1b2)x02+a2b2(1a2+1b2)=|(1a2−1b2)x02+a2b2|[(1a2−1b2)x02+a2b2](1a2+1b2)=11a2+1b2=a2b2a2+b2（定值）（4）椭圆内准圆与外准圆的关系通过伸缩变换，使得椭圆变成圆，则相应的准圆变为椭圆。