锐角三角函数第3课时

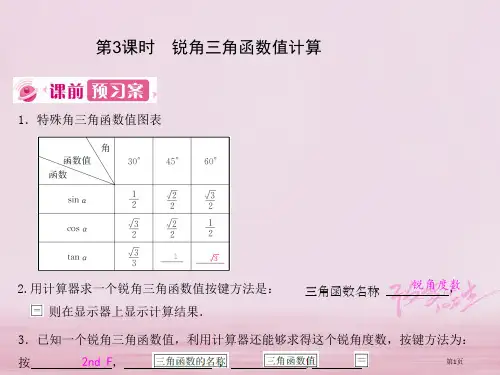
锐角三角函数（第3课时）教学目标1．通过探究三角尺的边角关系，推导并掌握特殊角（30°，45°，60°角）的正弦值、余弦值、正切值．2．会运用特殊角的锐角三角函数值进行有关计算，会根据特殊角的三角函数值判断三角形的形状或求特殊角．教学重点掌握特殊角（30°，45°，60°角）的正弦值、余弦值、正切值．教学难点会灵活运用特殊角的三角函数值解决问题．教学过程知识回顾如图，在Rt△ABC中，∠C＝90°，我们把∠A的邻边与斜边的比叫做∠A的余弦，记作cos A，即cos A＝A∠的邻边斜边＝bc；把∠A的对边与邻边的比叫做∠A的正切，记作tan A，即tan A＝AA∠∠的对边的邻边＝ab．【设计意图】回顾上节课学习的“锐角的余弦、正切”，为本节课的学习内容作铺垫．新知探究一、探究学习【问题】如图，两块三角尺中有几个不同的锐角？这几个锐角的正弦值、余弦值和正切值各是多少？【师生活动】教师引导学生思考、交流，得出：两块三角尺中有3个不同的锐角，分别是30°，45°和60°角．教师提示：设图中两块三角尺较短的边长分别为a，d，利用勾股定理和锐角三角函数的定义可以求出这些锐角三角函数值．教师先带领学生求出30°和60°角的正弦值、余弦值和正切值，再让学生独立求出45°角的正弦值、余弦值和正切值．解：如图，设BC＝a．在Rt△ABC中，∠C＝90°，∵∠A＝30°，∴AB＝2BC＝2a．由勾股定理得AC．∴sin 30°＝BCAB＝2aa＝12，cos 30°＝ACAB，tan 30°＝BCAC．∴sin 60°＝ACAB，cos 60°＝BCAB＝2aa＝12，tan 60°＝AC BC如图，设EF＝d．在Rt △DEF 中，∠F ＝90°，∵∠D ＝∠E ＝45°，∴DF ＝EF ＝d ．由勾股定理得DE ．∴sin 45°＝EFDE ，cos 45°＝DFDE 2，tan 45°＝EF DF ＝dd＝1．【新知】30°，45°，60°角的正弦值、余弦值和正切值如下表：【设计意图】让学生通过自主探索，求出特殊角的三角函数值，进一步体会锐角的度数与比值之间的对应关系，加深对锐角三角函数概念的理解，提高分析问题、解决问题的能力．二、典例精讲【例1】求下列各式的值： （1）cos 2 60°＋sin 2 60°；（2）cos 45sin 45︒︒－tan 45°．【师生活动】教师提示：sin 2 60°表示(sin 60°)2，即(sin 60°)·(sin 60°)．学生根据提示，独立完成，教师指导、讲解．【答案】解：（1）cos 2 60°＋sin 2 60°＝212⎛⎫⎪⎝⎭＋2⎝⎭＝1；（2）cos 45sin 45︒︒－tan45°＝2÷2－1＝0．【归纳】有关特殊角的三角函数值的计算，先直接写出三角函数值，将运算转化为实数的混合运算，然后根据实数的运算法则计算．【设计意图】通过例1，考察学生是否会运用特殊角的锐角三角函数值进行计算．【例2】（1）如图（1），在Rt △ABC 中，∠C ＝90°，AB ，BC A 的度数；（2）如图（2），AO 是圆锥的高，OB 是底面半径，AO ，求α的度数．【师生活动】学生小组讨论，尝试作答，教师指导、讲解，并给出提醒：当A ，B 均为锐角时，若A ≠B ，则sin A ≠sin B ，cos A ≠cos B ，tan A ≠tan B ．【答案】解：（1）∵sin A ＝BC AB ，∴∠A ＝45°．（2）∵tan α＝AOOB∴α＝60°．【归纳】由锐角三角函数值确定特殊角的一般步骤：第1步：通过边之间的关系或者其他关系得到锐角三角函数值； 第2步：根据特殊角的锐角三角函数值，确定锐角的度数．【设计意图】通过例2，让学生学会根据特殊角的三角函数值求特殊角．【例3】已知△ABC 中的∠A 与∠B 是锐角，且∠A 与∠B 满足(1－tan A )2＋sin B -＝0，试判断△ABC 的形状．【师生活动】学生小组讨论，尝试作答，教师指导、讲解．【答案】解：∵(1－tan A )2＋sin B -0，∴tan A＝1，sin B．∴∠A＝45°，∠B＝60°，∠C＝180°－45°－60°＝75°．∴△ABC是锐角三角形．【设计意图】通过例3，让学生学会根据特殊角的三角函数值判断三角形的形状．课堂小结板书设计一、特殊角的三角函数值二、应用特殊角的三角函数值判断三角形的形状或求特殊角课后作业完成教材第67页练习第1～2题．。

“自学互帮导学法”课堂教学设计
课题28.1锐角三角函数第3课时课时 1 课型复习巩固课修改意见
1.掌握三种锐角三角函数：锐角的正弦、余弦和正切。

教学目标
2.应用公式解题并感知探索过程。

教学重点锐角三角函数相关定义的理解以及根据定义计算锐角三角函数的值.
教学难点利用锐角三角函数解题
学生能背住公式，但不能准确应用，对于灵活性较大的题目，容易找不到突破口。

学情分析
学法指导引导学生自主探索去观察、交流、归纳、合作互帮。

教学过程
效果预测
修改意见教学内容教师活动学生活动
及补救措施
一、回顾思考，知识运用
二、新课讲授
三．练习巩固1.请同学们回顾上节课所学锐角三角
函数的正弦值、余弦值和正切值。

（教师巡堂，并加以评价。

）
2、活动1 思考（书上65页探究）
[.Com]
1.归纳锐角三角函数值得表格
（揭示某些规律）
2.例题讲解
1.实际运用
2.变式运用
1、学生思考，并写出公式。

2、学生思考、讨论.
1.理解并记忆。

2.运用公式解题
1.思考探索，并运用所学知识解答
2.独立思考，再小组评议。

1.归纳不太
全面，容易记
忆混淆，教师
建议图和公
式一起记忆。

四．课堂小结并反思
五．拓展与提高1.再次引导学生记忆锐角三角函数值
得表格
1.习题练习
1.回忆并再次记忆。

1.独立完成作业
参考书目板书设计
及推荐资料教学反思。

锐角三角函数（第3课时）【教学目标】1．记忆特殊角的正弦、余弦和正切的函数值，并会由一个特殊角的三角函数值说出这个角． 2．比较锐角三角函数值的大小.运用三角函数的性质计算并能熟练解题．【复习引入】1. 在Rt △ABC 中，∠C =90°，AC=2，BC=3，则cos A = ．2. 对于锐角α，总有=+αα22cos sin ． 3. 在Rt △ABC 中,∠C =90°，135sin =A ，则B sin = ． 4. 在Rt △ABC 中,∠C =90°，a ，b ，c 分别是∠A ，∠B ，∠C 的对边，若b =2a ，则tan A = ．【探究新知】三角函数角度sinα cosα tanα30° 45° 60°例1（1）cos 260°＋ sin 260°； （222(sin 451)(1cos45)︒--︒；（3）2sin45°＋ cos30°tan60°－()23-； (4) ︒-︒︒45tan 45cos 45sin1.若α=30°，则α的余角是 ，cosα= ，sinα= ，tanα= .2.计算︒-︒︒45tan 30cos 60sin = ．二、锐角三角函数的增减性：例2 （1）用不等号连接下面的式子:①cos30° cos28°; ②sin45° sin55°; ③tan60° tan50°.（2）已知∠A 为锐角,且cos A ≤21,则∠A 的取值范围是 .三、应用例3 （1）如图甲所示，在Rt △ABC 中，∠C ＝90°，AB ＝6，BC ＝3，求∠A 的度数．（2）如图乙所示，已知圆锥的高AO 等于圆锥的底面半径OB 的3倍，求∠α的度数．【巩固练习】1．等腰三角形底边与底边上的高的比是3:2，则顶角为 （ ）A ．60°B ．90°C ．120°D ．150°2．有一个角是︒30的直角三角形，斜边为cm 1，则斜边上的高为 （ ）A ．cm 41B ．cm 21C ．cm 43D ．cm 233．在ABC ∆中，︒=∠90C ，若A B ∠=∠2，则tan A 等于 （ ）4．如果∠α是等边三角形的一个内角，那么cos α的值等于 （ ）A ．21 B ．22 C ．23 D ．1 5．某市在“旧城改造”中计划把一块如图所示的三角形空地上种植某种 草皮以美化环境，已知这种草皮每平方米a 元，则购买这种草皮至少要 （ ） A ．450a 元 B ．225a 元 C ．150a 元 D ．300a 元6．计算(1)sin30°＋cos45°； (2) sin60°－tan45°；(3) 22sin45°＋sin60°－2cos45°； (4)cos60°＋tan60°；(5)sin60°＋︒-60tan 11； （6）13230sin 1+-︒；(7) (2＋1)－1＋2sin30°－8； （8）(1＋2)0－｜1－sin30°｜＋(21)-1；（9）sin60°＋︒-60tan 11； （10）2-3－(2003＋π) °－cos60°－211-；︒15020米30米。

28.1.3锐角三角函数教学设计一、教材解析本节内容是在学生已经学习了第三学段“图形的性质”中“相似三角形”和“勾股定理”的知识之后安排的，是高中数学中学习解斜三角形、三角函数、反三角函数和简单的三角方程等知识的基础。

无论是从内容上看，还是从思考问题的方法上看，掌握锐角三角函数的相关知识都是今后进行深入学习的重要准备。

研究锐角三角函数的直接基础是相似三角形的一些结论，解直角三角形主要依赖锐角三角函数和勾股定理等内容，因此相似三角形和勾股定理等是学习本章的直接基础。

本节课教科书借助于学生熟悉的两种三角尺研究特殊角的正弦、余弦和正切值，并以例题的形式介绍了已知锐角三角函数值求锐角的问题，当然这时所要求出的角都是特殊角。

教科书把求特殊角的三角函数值和已知特殊角的三角函数值求角这两个相反方向的问题安排在一起，目的是体现锐角三角函数中角与函数值之间的对应关系。

同时渗透函数思想。

基于上述分析，我把本节课的教学重点设定为：熟记30°、45°、60°角的三角函数值，能熟练计算含有30°、45°、60°角的三角函数的运算式。

二、目标和目标解析1．能推导并熟记30°、45°、60°角的三角函数值，并能根据这些值说出对应的锐角度数。

2．能熟练计算含有30°、45°、60°角的三角函数的运算式。

3.让学生经历观察、操作等过程，知道特殊三角函数值，经历锐角三角函数基本性质的探索活动，进一步发展空间观察能力，培养探索精神。

三、教学问题诊断分析无论直角三角形的大小如何，角所对的边与斜边的比总是一个常数，这种角与数之间的对应关系，以及用含有几个字母的符号 sinA 、 cosA 、 tanA 表示函数等，体现了函数的对应的思想，在本章学生首次接触到以角度为自变量的三角函数，初学者不易理解因此对学生来讲有一定的难度。

锐角三角函数教案第三课时
一、课前准备
1.复习上节课所讲内容，了解锐角三角函数；
2.查看课本、教材有关锐角三角函数的内容；
3.准备形象化的概念教学课件及相关教学资源；
二、教学主旨
本节课的主要目标是要带领学生深刻理解锐角三角函数的概念，明白
它的实际应用，形成良好的学习态度。

三、教学内容
1.锐角三角函数的概念介绍：在数学上，三角函数是一类特殊的函数，用来描述特定的物理系统的行为。

它通常以锐角的弧度为角度单位，
用来描述特定面积角度圆心角。

2.生成函数曲线：在了解了锐角三角函数的概念后，我们开始实践。

首先要把函数f(x)，即y=sinx、y=cosx、y=tanx，都可以用图像的方式生
成出来，描绘出函数曲线。

3.基本公式：了解了生成函数曲线后，就要知道它们的基本公式，比如：sinx+cosx=1，sinx+tany=1等等；
4.实际应用：在深入了解锐角三角函数的时候，不妨从实际的例子出发，比如定位、电动机、圆周率等等，将知识点应用到实践中去了解更多
有关三角函数的相关内容；
四、讨论与反思
1.通过个案的讨论，学生可以挖掘更多有关三角函数的联系，并尝试把这些知识点运用到实际例子中去；
2.让学生进行思考，分享自己在学习过程中表现最好的经验，并通过反复练习，熟悉图和表达式，以及其它一些计算锐角三角函数的工具；
3.通过思考实践的层次提高学生的思维能力，并给予学生较为详细的巩固性训练，以更进一步学习和理解锐角三角函数。

鲁教版数学九年级上册2.1《锐角三角函数》（第3课时）说课稿一. 教材分析鲁教版数学九年级上册2.1《锐角三角函数》（第3课时）这一节课，主要让学生了解锐角三角函数的概念，以及会运用锐角三角函数解决实际问题。

在教材中，通过生活实例引入锐角三角函数的概念，然后引导学生通过实验、探究、归纳等方法，掌握正弦、余弦、正切函数的定义和性质。

教材内容由浅入深，符合学生的认知规律。

二. 学情分析九年级的学生已经学习了初中阶段的三角函数知识，对函数的概念和性质有一定的了解。

但是，对于锐角三角函数的定义和应用，还需要进一步的引导和培养。

此外，学生的空间想象能力和逻辑思维能力有待提高，因此，在教学过程中，需要注重培养学生的空间想象能力和逻辑思维能力。

三. 说教学目标1.知识与技能目标：让学生了解锐角三角函数的概念，掌握正弦、余弦、正切函数的定义和性质。

2.过程与方法目标：通过实验、探究、归纳等方法，培养学生独立思考、合作交流的能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的创新精神和实践能力。

四. 说教学重难点1.教学重点：锐角三角函数的概念，正弦、余弦、正切函数的定义和性质。

2.教学难点：正弦、余弦、正切函数的性质的推导和应用。

五. 说教学方法与手段1.教学方法：采用实验、探究、归纳等教学方法，引导学生主动参与，培养学生的独立思考和合作交流能力。

2.教学手段：利用多媒体课件，直观展示锐角三角函数的定义和性质，提高学生的空间想象能力。

六. 说教学过程1.导入：通过生活实例，引导学生了解锐角三角函数的概念。

2.新课导入：介绍正弦、余弦、正切函数的定义和性质。

3.实验探究：让学生进行实验，观察和记录正弦、余弦、正切函数的变化规律。

4.归纳总结：引导学生通过实验结果，归纳出正弦、余弦、正切函数的性质。

5.应用拓展：让学生运用所学的锐角三角函数知识，解决实际问题。

七. 说板书设计板书设计如下：正弦函数：y = sin(θ)性质：1. 在锐角三角形中，正弦函数随着角度的增大而增大。