最新几个平行四边形判定的假命题

考点21多边形与平行四边形考点总结1．n 边形以及四边形的性质：(1)n 边形的内角和为(n －2)×180°(n ≥3)，外角和为360°，对角线条数为n （n －3）2．(2)四边形的内角和为360°，外角和为360°，对角线条数为 2 ．(3)正多边形的定义：各边相等、各内角也相等的多边形叫做正多边形．2．平行四边形的性质及判定：(1)性质：①平行四边形的两组对边分别平行且相等．②平行四边形的对角相等，邻角互补．③平行四边形的对角线互相平分．④平行四边形是中心对称图形．(2)判定：①定义：两组对边分别平行的四边形是平行四边形．②一组对边平行且相等的四边形是平行四边形．③两组对边分别相等的四边形是平行四边形．④两组对角分别相等的四边形是平行四边形．⑤对角线互相平分的四边形是平行四边形．3．三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半．4．在两条平行线中，一条直线上任意一点到另一条直线的距离，叫做两条平行线之间的距离．夹在两条平行线间的平行线段相等．真题演练一、单选题1．（2021·浙江衢州·中考真题）如图，在ABC 中，4AB =，5AC =，6BC =，点D ，E ，F 分别是AB ，BC ，CA 的中点，连结DE ，EF ，则四边形ADEF 的周长为（ ）A ．6B ．9C ．12D ．15【答案】B【分析】 根据中点的定义可得AD 、AF 的长，根据三角形中位线的性质可得DE 、EF 的长，即可求出四边形ADEF 的周长．【详解】∵4AB =，5AC =，6BC =，点D ，E ，F 分别是AB ，BC ，CA 的中点，∵AD =12AB =2，AF =1522AC =，DE 、EF 为∵ABC 的中位线， ∵EF =12AB =2，DE ==1522AC =， ∵四边形ADEF 的周长=2+2+5522+=9， 故选：B ．2．（2021·浙江·中考真题）如图，已知在ABC 中，90ABC ∠<︒，,AB BC BE ≠是AC 边上的中线．按下列步骤作图：①分别以点,B C 为圆心，大于线段BC 长度一半的长为半径作弧，相交于点,M N ；①过点,M N 作直线MN ，分别交BC ，BE 于点,D O ；①连结,CO DE ．则下列结论错误的是（ ）A ．OB OC =B ．BOD COD ∠=∠C ．//DE ABD ．DB DE =【答案】D【分析】 首先根据题意可知道MN 为线段BC 的中垂线，然后结合中垂线与中线的性质逐项分析即可．【详解】由题意可知，MN 为线段BC 的中垂线，∵O 为中垂线MN 上一点，∵OB =OC ，故A 正确；∵OB =OC ，∵∵OBC =∵OCB ，∵MN ∵BC ，∵∵ODB =∵ODC ，∵∵BOD =∵COD ，故B 正确；∵D 为BC 边的中点，BE 为AC 边上的中线，∵DE 为∵ABC 的中位线，∵DE ∵AB ，故C 正确；由题意可知DB =DC ，假设DB =DE 成立，则DB =DE =DC ，∵BEC =90°，而题干中只给出BE 是中线，无法保证BE 一定与AC 垂直，∵DB 不一定与DE 相等，故D 错误；故选：D ．3．（2021·浙江宁波·中考真题）如图是一个由5张纸片拼成的ABCD ，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为1S ，另两张直角三角形纸片的面积都为2S ，中间一张矩形纸片EFGH 的面积为3S ，FH 与GE 相交于点O ．当,,,AEO BFO CGO DHO 的面积相等时，下列结论一定成立的是（ ）A ．12S SB ．13S S =C ．AB AD = D ．EH GH =【答案】A【分析】 根据∵AED 和∵BCG 是等腰直角三角形，四边形ABCD 是平行四边形，四边形HEFG是矩形可得出AE =DE =BG =CG =a ， HE =GF ，GH =EF ，点O 是矩形HEFG 的中心，设AE =DE =BG =CG =a ， HE =GF = b ，GH =EF = c ，过点O 作OP ∵EF 于点P ，OQ ∵GF 于点Q ，可得出OP ，OQ 分别是∵FHE 和∵EGF 的中位线，从而可表示OP ，OQ 的长，再分别计算出1S ，2S ，3S 进行判断即可【详解】解：由题意得，∵AED 和∵BCG 是等腰直角三角形，∵45ADE DAE BCG GBC ∠=∠=∠=∠=︒∵四边形ABCD 是平行四边形，∵AD =BC ，CD =AB ，∵ADC =∵ABC ，∵BAD =∵DCB∵∵HDC =∵FBA ，∵DCH =∵BAF ，∵∵AED ∵∵CGB ，∵CDH ∵ABF∵AE =DE =BG =CG∵四边形HEFG 是矩形∵GH =EF ，HE =GF设AE =DE =BG =CG =a ， HE =GF = b ，GH =EF = c过点O 作OP ∵EF 于点P ，OQ ∵GF 于点Q ，∵OP //HE ，OQ //EF∵点O 是矩形HEFG 的对角线交点，即HF 和E G 的中点，∵OP ，OQ 分别是∵FHE 和∵EGF 的中位线， ∵1122OP HE b ==，1122OQ EF c == ∵1111()()2224BOF S BF OQ a b c a b c ∆==-⨯=- 11112224AOE S AE OP a b ab ∆==⨯= ∵BOF AOE S S ∆∆=∵11()44a b c ab -=，即ac bc ab -= 而211122AED S S AE DE a ∆===，222211111()()()()22222AFB S S AF BF a c a b a ab ac bc a ab ab a ∆===+-=-+-=-+= 所以，12S S ，故选项A 符合题意，2223=()()S HE EF a b a c a bc ab ac a ab ab a =-+=--+=+-=∵13S S ≠，故选项B 不符合题意， 而AB AD =于EH GH =都不一定成立，故,C D 都不符合题意， 故选：A 4．（2021·浙江宁波·中考真题）如图，在ABC 中，45,60,B C AD BC ∠=︒∠=︒⊥于点D ，BD =E ，F 分别为AB ，BC 的中点，则EF 的长为（ ）A B C ．1 D 【答案】C【分析】根据条件可知∵ABD 为等腰直角三角形，则BD =AD ，∵ADC 是30°、60°的直角三角形，可求出AC 长，再根据中位线定理可知EF =2AC 。

专题03《平行四边形》平行四边形以及由它衍生出来的矩形、菱形、正方形与梯形共同组成了一个和睦完美的“幸福之家”．同学们通过图形的变换与探索，对这一“家庭成员”以及相互关系进行了了解和认识，并能利用各成员的性质解决简单的问题．现在让我们再次走进这个“幸福之家”，去挖掘你所需的“宝藏”．一、思维导图二、知识回顾1. 四边形的“全家福”2. 平行四边形定义有两组______的四边形叫做平行四边形.3. 平行四边形的性质平行四边形的对边______.平行四边形的对角______.平行四边形的对角线______；平行线之间距离处处______.一组对边______的四边形是平行四边形；4. 平行四边形的判定对角线______的四边形是平行四边形.两组对角______的四边形是平行四边形.一组对边______的四边形是平行四边形.两组对边______的四边形是平行四边形.连接三角形两边中点的线段，叫做三角形的______.三角形的中位线平行于______，并且等于它的______.5. 矩形有一个角是______的平行四边形是矩形.矩形的四个内角都是______，对角线______且______；直角三角形斜边上的中线等于斜边的＿＿＿. 对角线______的平行四边形是矩形，有三个角是______的四边形是矩形.6. 菱形有一组邻边______的平行四边形，叫做菱形.菱形的四条边都______，菱形的两条对角线______，并且每一条对角线平分每一组______.四条边______的四边形是菱形.7. 正方形正方形是______的菱形；正方形是______的矩形.三、中考链接考点1：平行四边形的性质例1（2020·湖南邵阳）如图，四边形ABCD 是平行四边形，点E ，B ，D ，F 在同一条直线上，请添加一个条件使得ABE CDF △≌△，下列不正确．．．的是（ ）A ．AE CF =B ．AEB CFD ∠=∠C ．EAB FCD ∠=∠ D ．BE DF =【答案】A 【分析】根据平行四边形的性质结合全等三角形的判定，逐项进行判断即可.【解析】∵四边形ABCD 是平行四边形，∴AB=CD ，AB ∥CD ，∴∠ABD=∠BDC ，∵∠ABE+∠ABD=∠BDC+∠CDF ，∴∠ABE=∠CDF ，A.若添加AE CF =，则无法证明ABE CDF △≌△，故A 错误；B.若添加AEB CFD ∠=∠，运用AAS 可以证明ABE CDF △≌△，故选项B 正确；C.若添加EAB FCD ∠=∠，运用ASA 可以证明ABE CDF △≌△，故选项C 正确；D.若添加BE DF =，运用SAS 可以证明ABE CDF △≌△，故选项D 正确．故选：A ．【名师点睛】本题考查平行四边形的性质、全等三角形的判定和性质等知识，解题的关键是准确寻找全等三角形解决问题，属于中考常考题型．考点2：平行四边形的判定例2（2020·湖南衡阳）如图,在四边形ABCD 中,AC 与BD 相交于点O ,下列条件不能判定四边形ABCD 为平行四边形的是（ ）A ．AB ∥DC ,AB =DC B ．AB =DC ,AD =BC C ．AB ∥DC ,AD =BC D ．OA=OC ,OB =OD【答案】C【分析】根据平行四边形的判定方法逐项分析即可.【解析】A. ∵ AB ∥DC ,AB =DC ，∴四边形ABCD 是平行四边形；B. ∵ AB =DC ,AD =BC ，∴四边形ABCD 是平行四边形；C.等腰梯形ABCD 满足 AB ∥DC ,AD =BC ，但四边形ABCD 是平行四边形；D. OA=OC ,OB =OD ，∴四边形ABCD 是平行四边形；故选C.【名师点睛】本题主要考查了平行四边形的判定，平行四边形的判定方法有：①两组对边分别平行的四边形是平行四边形；②一组对边平行且相等的四边形是平行四边形；③两组对边分别相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤.两组对角分别相等的四边形是平行四边形. 考点3：三角形中位线定理例3（2020·内蒙古赤峰）如图，在△ABC 中，点D ，E 分别是边AB ，AC 的中点，点F 是线段DE 上的一点连接AF ，BF ，∠AFB =90°，且AB=8，BC= 14，则EF 的长是 （ ）A ．2B ．3C ．4D ．5【答案】B【分析】根据直角三角形的性质得到DF=4，根据BC= 14，由三角形中位线定理得到DE=7，解答即可．【解析】∵∠AFB=90°，点D 是AB 的中点，∴DF=12AB=4， ∵BC= 14，D 、E 分别是AB ，AC 的中点，∴DE=12BC=7，∴EF=DE -DF=3，故选：B 【名师点睛】本题考查了直角三角形的性质和中位线性质，掌握定理是解题的关键．考点4：矩形的性质例4（2020·贵州毕节）如图，在矩形ABCD 中，对角线AC ，BD 相交于点O ，点E ，F 分别是AO ，AD 的中点，连接EF ，若6AB cm =，8BC cm =，则EF 的长是（ ）A ．2.2cmB ．2.3cmC ．2.4cmD ．2.5cm【答案】D 【分析】由勾股定理求出BD 的长，根据矩形的性质求出OD 的长，最后根据三角形中位线定理得出EF 的长即可．【解析】∵四边形ABCD 是矩形，∴∠ABC=90°，AC=BD ，OA=OC=OD=OB ，∵6AB cm =，8BC cm =，∴10cm = ∴BD=10cm ，∴152OD BD cm ==， ∵点E ，F 分别是AO ，AD 的中点，∴115 2.522EF OD cm ==⨯=．故选：D ． 【名师点睛】本题考查矩形的性质、三角形的中位线定理等知识，解题的关键是熟练掌握基本知识． 考点5：菱形的性质例5（2020·江苏无锡）如图，在菱形ABCD 中，50B ∠=︒，点E 在CD 上，若AE AC =，则BAE ∠=__________．【答案】115°【分析】先根据菱形性质求出∠BCD ，∠ACE ，再根据AE AC =求出∠AEC ，最后根据两直线平行，同旁内角互补解题即可．【解析】四边形ABCD 是菱形，50B ∠=︒，∴AB ∥CD ，∴∠BCD=180°-∠B=130°，∠ACE=12∠BCD=65°， ∵ AE AC =，∴∠ACE=∠AEC=65°，∴∠BAE=180°-∠AEC=115°．【名师点睛】本题考查了菱形性质，等腰三角形性质，解题方法较多，根据菱形性质求解∠ACE 是解题关键．考点6：菱形的判定例6（2020·内蒙古通辽）如图，AD 是ABC 的中线，四边形ADCE 是平行四边形，增加下列条件，能判断ADCE 是菱形的是( )A ．90BAC ∠=︒B ．90DAE ∠=︒C ．AB AC =D ．AB AE =【答案】A 【分析】根据菱形的判定方法逐一分析即可.【解析】A 、若90BAC ∠=︒，则AD=BD=CD=AE ，∵四边形ADCE 是平行四边形，则此时四边形ADCE 为菱形，故选项正确；B 、若90DAE ∠=︒，则四边形ADCE 是矩形，故选项错误；C 、若AB AC =，则∠ADC=90°，则四边形ADCE 是矩形，故选项错误；D 、若AB AE =，而AB ＞AD ，则AE≠AD ，无法判断四边形ADCE 为菱形，故选项错误.故选A.【名师点睛】本题考查了菱形的判定，还涉及到平行四边形的性质，矩形的判定，等腰三角形的性质，解题的关键是掌握判定定理.考点7：正方形的性质例7（2020·内蒙古呼和浩特）如图，正方形ABCD ，G 是BC 边上任意一点（不与B 、C 重合），DE AG ⊥于点E ，//BF DE ，且交AG 于点F ．（1）求证：；（2）四边形BFDE 是否可能是平行四边形，如果可能请指出此时点G 的位置，如不可能请说明理由．AF BF EF -=【答案】（1）见解析；（2）不可能，理由见解析.【分析】（1）证明△ABF≌△DAE，从而得到AF=DE，AE=BF，可得结果；（2）若要四边形BFDE是平行四边形，则DE=BF，则∠BAF=45°，再证明∠BAF≠45°即可.【解析】（1）证明：∵正方形ABCD，∴AB=AD，∠BAF+∠DAE=90°，∵DE⊥AG，∴∠DAE+∠ADE=90°，∴∠ADE=∠BAF，BF DE，∴∠BFA=90°=∠AED，∴△ABF≌△DAE（AAS），又∵//-=-=；∴AF=DE，AE=BF，∴AF BF AF AE EF（2）不可能，理由是：如图，若要四边形BFDE是平行四边形，已知DE∥BF，则当DE=BF时，四边形BFDE为平行四边形，∵DE=AF，∴BF=AF，即此时∠BAF=45°，而点G不与B和C重合，∴∠BAF≠45°，矛盾，∴四边形BFDE不能是平行四边形.【名师点睛】本题考查了全等三角形的判定和性质，正方形的性质，平行四边形的性质，解题的关键是找到三角形全等的条件.第18章平行四边形达标检测一、选择题(每题3分,共30分)1.下列条件中，不能判定四边形为平行四边形是（）A. 一组对边平行，另一组对边相等B. 一组对边平行且相等C. 两组对边分别平行D. 对角线互相平分2.给出平面上不在同一直线上的三个点，则以此三点为顶点的平行四边形有（）A.1个B.2个C.3个D4个3. 已知□ABCD中，∠A+∠C=200°，则∠B的度数是（）A．100° B．160° C．80° D．60°4.（2020·湖南湘西）下列说法中，不正确．．．是（）A．对角线互相平分的四边形是平行四边形B．两组对角分别相等的四边形是平行四边形C．一组对边平行且相等的四边形是平行四边形D．一组对边平行另一组对边相等的四边形是平行四边形5.（2020·江苏南通）下列条件中，能判定▱ABCD是菱形的是（）A．AC＝BD B．AB⊥BC C．AD＝BD D．AC⊥BD6.如图，如果□ABCD的对角线AC和BD相交于点O，那么图中全等的三角形共有（）A.1对B.2对C.3对D.4对7.（2020·山东滨州）下列命题是假命题的是（）A．对角线互相垂直且相等的平行四边形是正方形．B．对角线互相垂直的矩形是正方形．C．对角线相等的菱形是正方形．D．对角线互相垂直平分的四边形是正方形．8.如图，矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF＝60°,则DAE等于（）A. 15°B. 30°C. 45°D. 60°9.如图，在菱形ABCD中，对角线AC=4，∠BAD=120°，则菱形ABCD的周长为（）A．20 B．18 C．16 D．1510.（2020·山东菏泽）如果顺次连接四边形的各边中点得到的四边形是矩形，那么原来四边形的对角线一定满足的条件是（ ）A ．互相平分B ．相等C ．互相垂直D ．互相垂直平分二、填空题(每题3分,共30分)11.已知在□ABCD 中，AB =14cm ，BC =16cm ，则此平行四边形的周长为 cm .12.（2020·黑龙江）如图，在四边形ABCD 中，AD//BC ，在不添加任何辅助线的情况下，请你添加一个条件____，使四边形ABCD 是平行四边形（填一个即可）．13.如图，正方形ABCD 的对线AC 、BD 相交于点O ．那么图中共有 个等腰直角三角形.14. （2020·内蒙古）如图，在平行四边形ABCD 中，2,AB ABC =∠的平分线与BCD ∠的平分线交于点E ，若点E 恰好在边AD 上，则22BE CE +的值为______．15. （2020•无锡）如图，在菱形ABCD 中，∠B ＝50°，点E 在CD 上，若AE ＝AC ，则∠BAE ＝ °．16.如图，□ABCD 中，AE 平分∠BAD ，AD =6cm,AB =9cm,则CE =________cm ．17. （2020·江苏徐州）如图，在Rt ABC ∆中，90ABC ∠=︒，D 、E 、F 分别为AB 、BC 、CA 的中点，若5BF =，则DE =_______．18. 我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形．．．．．．现有一个对角线分别为6cm 和8cm 的菱形，它的中点四边形的对角线长是 ．19. （2020·浙江金华）如图，平移图形M ，与图形N 可以拼成一个平行四边形，则图中α的度数是______°．20.如图,l 是四边形ABCD 的对称轴,如果AD ∥BC ,有下列结论: (1)AB ∥CD ;(2)AB=CD ;(3)AB ⊥BC ;(4)AO=OC .其中正确的结论是 ．(把你认为正确的结论的序号都填上)三、解答题(共60)21. （6分）（2020·山东济南）如图，在▱ABCD 中，对角线 AC ，BD 相交于点 O ，过点 O 的一条直线分别交 AD ，BC 于点 E ，F ．求证：AE=CF ．22. （6分）（2020·四川自贡）如图，在正方形中，点在边的延长线上，点在边的延长线上，且,连接和相交于点．求证： ．23. （6分）如图12, □ABCD 中,G 是CD 上一点,BG 交AD 延长线于E ,AF=CG ,∠DGE =100°.(1)试说明DF=BG ；(2)试求AFD ∠的度数.24. （6分）（2020·湖南娄底）如图，ABCD 中，2BC AB =，AB AC ⊥，分别在边BC 、AD 上的点E 与点F 关于AC 对称，连接EF 、AE 、CF 、DE ．（1）试判定四边形AECF 的形状，并说明理由；（2）求证：AE DE ⊥25. （8分）先阅读下面的题目及解题过程，再根据要求回答问题．如图，在□ABCD 中，∠BAD 的平分线与BC 边相交于点E ，∠ABC 的平分线与AD 边相交于点F ，AE 与BF 相交于O ，试说明四边形ABEF 是菱形．解：①∵四边形ABCD 是平行四边形，ABCD E BC F CD CE DF =AE BF M AE BF=A BC D 图1 ②∴AD ∥BC ，③∠ABE +∠BAF =1800，④∵AE ，BF 分别是∠BAF ，∠ABE 的平分线，⑤∴∠1=∠2=∠BAF ，∠3=∠4=∠ABE ， ⑥∴∠1+∠3=（∠BAF +∠ABE ）=900 ⑦∴∠AOB =900⑧∴AE ⊥BF⑨∴四边形ABEF 是菱形．(1)上述解题过程是 否正确？________．(2)如有错误，在第___步到第___步推理错误，应在第_____步后添加如下步骤：________．26. （8分）如图1，有一张菱形纸片ABCD ，AC ＝8，BD ＝6．（1）请沿着AC 剪一刀，把它分成两部分，把剪开的两部分分拼成一个平行四边形，在图2中用实线画出你所拼成的平行四边形；若沿着BD 剪开，请在图3中用实线画出拼成的平行四边形；并直接写出这两个平行四边形的周长．（2）沿着一条直线剪开，拼成与上述两种都不全等的平行四边形，请在图4中用实线画出拼成的平行四边形．（注：上述所画的平行四边形都不能与原菱形全等）27.（10分）（2020·四川遂宁）如图，在△ABC 中，AB ＝AC ，点D 、E 分别是线段BC 、AD 的中点，过点A 作BC 的平行线交BE 的延长线于点F ，连接CF ．（1）求证：△BDE ≌△F AE ；（2）求证：四边形ADCF 为矩形．212121 A B C D 图3 周长________ A B C D 图4 A B C D 图2周长________28.（10分）（2020·浙江嘉兴）在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF 拼在一起，使点A与点F重合，点C与点D重合（如图1），其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动．活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD（如图2），当点F与点C重合时停止平移．（思考）图2中的四边形ABDE是平行四边形吗？请说明理由．（发现）当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形（如图3）．求AF的长．活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连结OB，OE （如图4）．（探究）当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由．。

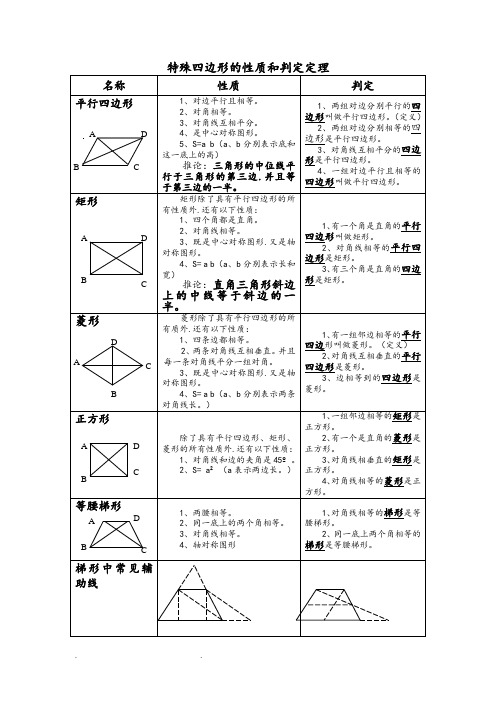
特殊四边形的性质和判定定理名称 性质判定平行四边形1、对边平行且相等。

2、对角相等。

3、对角线互相平分。

4、是中心对称图形。

5、S=a b （a 、b 分别表示底和这一底上的高）推论：三角形的中位线平行于三角形的第三边.并且等于第三边的一半。

1、两组对边分别平行的四边形叫做平行四边形。

（定义）2、两组对边分别相等的四边形是平行四边形。

3、对角线互相平分的四边形是平行四边形。

4、一组对边平行且相等的四边形叫做平行四边形。

矩形矩形除了具有平行四边形的所有性质外.还有以下性质：1、四个角都是直角。

2、对角线相等。

3、既是中心对称图形.又是轴对称图形。

4、S= a b （a 、b 分别表示长和宽）推论：直角三角形斜边上的中线等于斜边的一半。

1、有一个角是直角的平行四边形叫做矩形。

2、对角线相等的平行四边形是矩形。

3、有三个角是直角的四边形是矩形。

菱形菱形除了具有平行四边形的所有质外.还有以下性质：1、四条边都相等。

2、两条对角线互相垂直。

并且每一条对角线平分一组对角。

3、既是中心对称图形.又是轴对称图形。

4、S= a b （a 、b 分别表示两条对角线长。

）1、有一组邻边相等的平行四边形叫做菱形。

（定义）2、对角线互相垂直的平行四边形是菱形。

3、边相等到的四边形是菱形。

正方形除了具有平行四边形、矩形、菱形的所有性质外.还有以下性质： 1、对角线和边的夹角是45º。

2、S= a ²（a 表示两边长。

） 1、一组邻边相等的矩形是正方形。

2、有一个是直角的菱形是正方形。

3、对角线相垂直的矩形是正方形。

4、对角线相等的菱形是正方形。

等腰梯形1、两腰相等。

2、同一底上的两个角相等。

3、对角线相等。

4、轴对称图形1、对角线相等的梯形是等腰梯形。

2、同一底上两个角相等的梯形是等腰梯形。

梯形中常见辅助线AB CDABCDABC DABCD A BCD例1 如图.E 、F 分别为正方形ABCD 的边BC 、CD 上的一点.AM ⊥EF.垂足为M.若AM=AB.求证：EF=BE+CF例2 已知：如图.正方形ABCD 中.延长AD 到E.使DE=AD.再延长DE 到F.使DF=BD.连接BF 交CD 于Q.交CE 于P 。

中考数学平行四边形的判定经典题型精编平行四边形的判定方法有五种：①两组对边分别平行；②两组对边分别相等；③一组对边平行且相等的四边形是平行四边形；④两组对角分别相等；⑤对角线互相平分。

平行四边形性质可以用来解决许多问题，如求角的度数、线段的长度，证明角相等或互补，证明线段相等或倍分等。

还可以通过判别一个四边形为平行四边形，从而得到两直线平行，或者先判别一个四边形是平行四边形，然后再用平行四边形的特征去解决某些问题。

例1中，不能判别四边形是平行四边形的条件是两组对角分别相等的四边形。

在选项中，选B。

另一个问题是不能确定四边形ABCD是平行四边形的条件，选项中选C。

例2中，要证明四边形BEDF是平行四边形，已知AE＝CF，可以通过证明BE＝DF来得到结论。

因为ABCD是平行四边形，所以AE=CD，CF=AB。

因此，BE＝AE＋AB＝CD＋CF＝DF。

因此，四边形BEDF是平行四边形。

例3中，要证明四边形EGFH是平行四边形，可以通过证明EG∥FH和EG＝FH来得到结论。

因为G和H分别是OA和OC的中点，所以EG∥FH。

因为AC和BD是对角线，所以它们互相平分。

因此，OE＝OC和OF＝OA。

又因为G和H分别是OA和OC的中点，所以EG＝GH＝FH。

因此，四边形EGFH是平行四边形。

同步练A组中，第一题中，若OA=OC,OB=OD，则四边形ABCD是平行四边形，根据两组对边分别相等的判定方法。

第二题中，AC=BD，AB=CD=EF，CE=DF，可以得到AB∥EF和AD∥CF。

第三题中，平行四边形的三个内角的度数依次为88°，92°，92°。

因此，选项D是平行四边形。

第四题中，要证明四边形ABCD是平行四边形，可以通过证明AD∥BC和AB＝CD来得到结论。

因为AD=BC，所以∠ADE＝∠BCF。

因为AF=CE，所以∠AFE＝∠CED。

因此，四边形ADEF是平行四边形。

因为AD∥EF，所以∠AED＝∠XXX。

平行四边形的判定专项练习30题（有答案）1．如图，四边形ABCD中，AD∥BC，ED∥BF，AF=CE，求证：ABCD是平行四边形．2．如图，四边形ABCD中，∠BAC=90°，AB=11﹣x，BC=5，CD=x﹣5，AD=x﹣3，AC=4．求证：四边形ABCD为平行四边形．3．已知四边形ABCD的对角线AC与BD交于点O，现给出四个条件：①OA=OC；②AB=CD；③∠BAD=∠DCB；④AD∥BC．请你从中选择两个，推出四边形ABCD为平行四边形，并写出你的推理过程．（1）从以上4个条件中任意选取2个条件，能推出四边形ABCD是平行四边形的有（用序号表示）_________ ．（2）从（1）中选出一种情况，写出你的推理过程．4．如图，已知：点B、E、F、D在一条直线上，DF=BE，AE=CF．请从下列三个条件中选择一个合适的条件，添加到已知条件中，使四边形ABCD是平行四边形，并说明理由，供选择的三个条件（请从其中选择一个）：①AB=DC；②BC=AD；③∠AED=∠CFB．5．如图，在▱ABCD中，AC交BD于点O，点E，点F分别是OA，OC的中点，请判断线段BE，DF的位置关系和数量关系，并说明你的结论．6．如图所示，以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF，猜想：四边形ADEF 是什么四边形，试证明你的结论．7．如图，已知BE⊥AD，CF⊥AD，且BE=CF．求证：（1）AD是△ABC的中线；（2）请连接BF、CE，试判断四边形BECF是何种特殊四边形，并说明理由．8．如图，矩形ABCD的两条对角线AC和BD相交于点O，E、F是BD上的两点，且∠AEB=∠CFD．求证：四边形AECF 是平行四边形．9．如图：在四边形ABCD中，AD∥BC，AB=CD，E是BC上一点，DE=AB．求证：四边形ABED是平行四边形．10．如图，已知 AB∥DC，E是BC的中点，AE，DC的延长线交于点F；（1）求证：△ABE≌△FCE；（2）连接AC，BF．则四边形ABFC是什么特殊的四边形？请说明理由．11．等边△ABC中，点D在BC上，点E在AB上，且CD=BE，以AD为边作等边△ADF，如图．求证：四边形CDFE是平行四边形．12．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．若∠BAC=30°，EF⊥AB，垂足为F，连结DF．求证：（1）△ABC≌△EAF；（2）四边形ADFE是平行四边形．13．已知：如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点．求证：四边形DFGE是平行四边形．14．如图所示：在四边形ABCD中，AD∥BC、BC=18cm，CD=15cm，AD=10cm，AB=12cm，动点P、Q分别从A、C同时出发，点P以2cm/秒的速度由A向D运动，点Q以3cm/秒的速度由C向B运动．（1）几秒钟后，四边形ABQP为平行四边形？并求出此时四边形ABQP的周长（2）几秒钟后，四边形PDCQ为平行四边形？并求出此时四边形PDCQ的周长．15．求证：顺次连接四边形各边中点所得的四边形是平行四边形．16．△ABC中，中线BE、CF相交于O，M是BO的中点，N是CO的中点，求证：四边形MNEF是平行四边形．17．如图，AD=DB，AE=EC，FG∥AB，AG∥BC．（1）证明：△AGE≌△CFE；（2）说明四边形ABFG是平行四边形；（3）研究图中的线段DE，BF，FC之间有怎样的位置关系和数量关系．18．如图，△ABC和△ADE都是等边三角形，点D在BC边上，AB边上有一点F，且BF=DC，连接EF、EB．（1）求证：△ABE≌△ACD；（2）求证：四边形EFCD是平行四边形．19．已知在△ABC中，D、E分别是AB、AC的中点，点F在DE的延长线上，且EF=DE，图中有几个平行四边形？请说明你的理由．20．如图，在△ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．求证：四边形AFBD是平行四边形．21．如图：在四边形ABCD中，AD∥BC，E是BC的中点，BC=2AD．找出图中所有的平行四边形，并选择一个说明它是平行四边形的理由．22．求证：两组对角分别相等的四边形是平行四边形．23．已知：如图，A、B、C、D在同一条直线上，且AB=CD，AE∥DF，AE=DF．求证：四边形EBFC是平行四边形．24．如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．图中的四边形BFCE 是平行四边形吗？为什么？25．已知点E、F、G、H分别为四边形ABCD四边的中点，试问四边形EFGH的形状并说明理由．26．如图，已知四边形ABCD中AD=BC，点A、B、E在同一条直线上，且∠B=∠EAD，试说明四边形ABCD是平行四边形．27．如图，AD∥BC，ED∥BF，且AE=CF，求证：四边形ABCD是平行四边形．28．已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．29．如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．当AB≠AC时，求证：四边形ADFE为平行四边形．30．已知：在四边形ABCD中，AD∥BC，且AB=DC=5，AC=4，BC=3．求证：四边形ABCD为平行四边形．平行四边形的判定30题参考答案：1．∵AD∥BC，∴∠DAE=∠BCF，∵ED∥BF，∴∠DEF=∠BFE，∴∠AED=∠CFB，又∵AF=CE，∴AE=CF，在△ADE和△CBF中：∵∠DAE=∠BCF，∠AED=∠CFB，AE=CF，∴△ADE≌△CBF（AAS），∴AD=CB，即：AD∥CB，AD=CB，∴四边形ABCD是平行四边形，2．∵∠BAC=90°，AB=11﹣x，BC=5，AC=4．∴（11﹣x）2+42=52，解得：x1=8，x2=14＞11（舍去），当x=8时，BC=AD=5，AB=CD=3，∴四边形ABCD为平行四边形．3．（1）解：能推出四边形ABCD是平行四边形的有①④、③④；故答案是：①④、③④；（2）以①④为例进行证明．如图，在四边形ABCD中，OA=OC，AD∥BC．证明：∵AD∥BC，∴∠DAO=∠BCO．∴在△AOD与△COB中，，∴△AOD≌△COB（ASA），∴AD=BC，∴在四边形ABCD中，AD BC，∴四边形ABCD为平行四边形．4．选择①，∵DF=BE，AE=CF，AB=CD，∴△ABE≌△CDF（sss），∴∠ABE=∠CDF，∴四边形ABCD是平行四边形．5. BE=DF，BE∥DF因为ABCD是平行四边形，所以OA=OC，OB=OD，因为E，F分别是OA，OC的中点，所以OE=OF，所以BFDE是平行四边形，所以BE=DF，BE∥DF 6．四边形ADEF是平行四边形．连接ED、EF，∵△ABD、△BCE、△ACF分别是等边三角形，∴AB=BD，BC=BE，∠DBA=∠EBC=60°．∴∠DBE=∠ABC．∴△ABC≌△DBE．同理可证△ABC≌△FEC，∴AB=EF，AC=DE．∵AB=AD，AC=AF，∴AD=EF，DE=AF．∴四边形ADEF是平行四边形7．（1）∵BE⊥AD，CF⊥AD，∴∠BED=∠CFD．∵∠BDE=∠CDF，BE=CF，∴△BED≌△CFD．∴BD=CD．∴AD是△ABC的中线．（2）四边形BECF是平行四边形，由（1）得：BD=CD，ED=FD．∴四边形BECF是平行四边形8．∵四边形ABCD是矩形∴AB∥CD，AB=CD，∴∠ABE=∠CDF，又∵∠AEB=∠CFD，∴△ABE≌△CDF，∴BE=DF，又∵四边形ABCD是矩形，∴OA=OC，OB=OD，∴OB﹣BE=OD﹣DF，∴OE=OF，∴四边形AECF是平行四边形9．∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∴∠B=∠C，∵DE=AB，∴∠DEC=∠B，∴AB∥DE，∴四边形ABED是平行四边形．10．（1）证明：∵AB∥DC，∴∠1=∠2，∠FCE=∠EBA，∵E为BC中点，∴CE=BE，∵在△ABE和△FCE中，∠1=∠2，∠FCE=∠EBA，CE=BE，∴△ABE≌△FCE；（2）四边形ABFC是平行四边形；理由：由（1）知：△ABE≌△FCE，∴EF=AE，∵CE=BE，∴四边形ABFC是平行四边形11．连接BF，∵△ADF和△ABC是等边三角形，∴AF=AD=DF，AB=AC=BC，∠ABC=∠ACD=∠CAB=∠FAD=60°，∴∠FAD﹣∠EAD=∠CAB﹣∠EAD，∴∠FAB=∠CAD，在△FAB和△DAC中，∴△FAB≌△DAC（SAS），∴BF=DC，∠ABF=∠ACD=60°，∵BE=CD，∴BF=BE，∴△BFE是等边三角形，∴EF=BE=CD，在△ACD和△CBE中∵，∴△ACD≌△CBE（SAS），∴AD=CE=DF，∵EF=CD，∴四边形CDFE是平行四边形．12．（1）∵△ABE为等边三角形，EF⊥AB，∴EF为∠BEA的平分线，∠AEB=60°，AE=AB，在△ABC和△EAF中，，∴△ABC≌△EAF（AAS）；（2）∵∠BAC=30°，∠DAC=60°，∴∠DAB=90°，即DA⊥AB，∵EF⊥AB，∴AD∥EF，∵△ABC≌△EAF，∴EF=AC=AD，∴四边形ADFE是平行四边形13．在△ABC中，∵AD=BD，AE=CE，∴DE∥BC且DE=BC．在△OBC中，∵OF=FB，OG=GC，∴FG∥BC且FG=BC．∴DE∥FG，DE=FG．∴四边形DFGE为平行四边形14．（1）x秒后，四边形ABQP为平行四边形．则2x=18﹣3x，解得x=3.6．3.6秒钟后，四边形ABQP为平行四边形，此时四边形ABQP的周长是3.6×2×2+12×2=38.4cm．（2）y秒后，四边形PDCQ为平行四边形．10﹣2y=3y，解得y=2.2秒钟后，四边形PDCQ为平行四边形，此时四边形PDCQ的周长是3.6×2×2+15×2=43.2cm．15．：连接BD，∵E、F为AD，AB中点，∴FE BD．又∵G、H为BC，CD中点，∴GH BD，故GH FE．同理可证，EH FG．∴四边形FGHE是平行四边形16．∵BE，CF是△ABC的中线，∴EF∥BC且EF=BC，∵M是BO的中点，N是CO的中点，∴EF∥MN且EF=MN，∴四边形MNEF是平行四边形．17．（1）证明：∵AG∥BC（已知）∴∠G=∠EFC（两直线平行，内错角相等）∵∠AEG=∠FEC（对顶角相等），又AE=EC（已知）∴△AGE≌△CFE（AAS）；（2）说明：∵FG∥AB，AG∥BC（已知）∴四边形ABFG是平行四边形（平行四边形的定义）；（3）解：线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE=BF=FC，理由：由（1）可知△AGE≌△CFE∴AG=FC，FE=EG（全等三角形的对应边相等），∴E是FG的中点，又∵AD=DB（已知）∴DE为三角形ABC的中位线，∴DE=BC，DE∥BC，即DE∥BF，DE∥FC，由（2）可知四边形ABFG是平行四边形∴AG=BF，∴BF=FC=BC，∴DE=BF=FC，即线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE=BF=FC．18．（1）∵△ABC和△ADE都是等边三角形，∴AE=AD，AB=AC，∠EAD=∠BAC=60°，∴∠EAD﹣∠BAD=∠BAC﹣∠BAD，即：∠EAB=∠DAC，∴△ABE≌△ACD（SAS）；（2）证明：∵△ABE≌△ACD，∴BE=DC，∠EBA=∠DCA，又∵BF=DC，∴BE=BF．∵△ABC是等边三角形，∴∠DCA=60°，∴△BEF为等边三角形．∴∠EFB=60°，EF=BF∵△ABC是等边三角形，∴∠ABC=60°，∴∠ABC=∠EFB，∴EF∥BC，即EF∥DC，∴四边形EFCD是平行四边形19．平行四边形ADCF和平行四边形DBCF．理由：（1）∵D、E分别是AB、AC边的中点，∴DE∥BC ，．又∵EF=DE，∴DF=BC，∴四边形DBCF是平行四边形；（2）在四边形ADCF中，∵EF=DE，又∵E是AC边的中点，∴EA=EC，∴四边形ADCF是平行四边形20．∵E为AD中点，∴AE=DE，∵AF∥BC，∴∠AFE=∠DCE，在△AEF和△CED中∵，∴△AEF≌△CED（AAS），∴AF=DC，∵AD是△ABC的中线，∴BD=DC，∴AF=BD，即AF∥BD，AF=BD，故四边形AFBD是平行四边形21．图中有两个平行四边形：▱ABED、▱AECD．∵，∴AD=BE，∵AD∥BC，∴四边形ABED是平行四边形．22．已知：四边形ABCD，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形，证明：∵∠A=∠C，∠B=∠D，∠A+∠B+∠C+∠D=360°，∴2∠A+2∠B=360°，∴∠A+∠B=180°，∴AD∥BC，同理AB∥CD，∴四边形ABCD是平行四边形．在△ABE和△DCF中∴△ABE≌△DCF（SAS），∴EB=FC，∠ABE=∠DCF，∵∠ABE+∠EBC=180°，∠DCF+∠FCB=180°，∴∠EBC=∠FCB，∴BE∥FC，∵BE=FC，∴四边形EBFC是平行四边形24．∵CE∥BF，BD=CD，∴△BDF≌△CDE，∴BF=CE，∴四边形BFCE是平行四边形．25．四边形EFGH是平行四边形证明：连接AC、BD∵E、F、G、H分别为四边形ABCD四边的中点∴EH=BD，FG=BD，HG=AC，EF=AC∴EH=FG，EF=HG∴四边形EFGH是平行四边形．26．∵∠B=∠EAD，∴AD∥BC，∵AD=BC，∴四边形ABCD是平行四边形．27．∵AD∥BC，∴∠EAD=∠FCB，又ED∥BF，∴∠FED=∠EFB，∠AED=180°﹣∠FED，∠CFB=180°﹣∠EFB，∴∠AED=∠CFB，又已知AE=CF，∴△AED≌△CFB，∴AD=BC，∴四边形ABCD是平行四边形．28．∵AD∥BC，∴∠EAD=∠FCB，又ED∥BF，∴∠FED=∠EFB，∠AED=180°﹣∠FED，∠CFB=180°﹣∠EFB，∴∠AED=∠CFB，又已知AE=CF，∴△AED≌△CFB，∴AD=BC，∴四边形ABCD是平行四边形．29．∵△ABE、△BCF为等边三角形，∴AB=BE=AE，BC=CF=FB，∠ABE=∠CBF=60°．∴∠FBE=∠CBA，在△FBE和△CBA中，，∴△FBE≌△CBA（SAS）．∴EF=AC．又∵△ADC为等边三角形，∴CD=AD=AC．∴EF=AD．同理可得AE=DF．∴四边形AEFD是平行四边形30．∵AB=5，AC=4，BC=3∴AB2=AC2+BC2∴∠BCA=90°∵AD∥BC∴∠DAC=∠BCA=90°∵DC=5，AC=4，∴AD2=DC2﹣AC2=9∴AD=BC=3∴四边形ABCD为平行四边形．。

特殊的平⾏四边形专题（题型详细分类）要点特殊的平⾏四边形讲义知识点归纳矩形，菱形和正⽅形之间的联系如下表所⽰：四边形分类专题汇总专题⼀：特殊四边形的判定矩形菱形正⽅形性质边对边平⾏且相等对边平⾏，四边相等对边平⾏，四边相等⾓四个⾓都是直⾓对⾓相等四个⾓都是直⾓对⾓线互相平分且相等互相垂直平分，且每条对⾓线平分⼀组对⾓互相垂直平分且相等,每条对⾓线平分⼀组对⾓判定 ·有三个⾓是直⾓; ·是平⾏四边形且有⼀个⾓是直⾓; ·是平⾏四边形且两条对⾓线相等. ·四边相等的四边形；·是平⾏四边形且有⼀组邻边相等；·是平⾏四边形且两条对⾓线互相垂直。

·是矩形，且有⼀组邻边相等； ·是菱形，且有⼀个⾓是直⾓。

对称性既是轴对称图形，⼜是中⼼对称图形（1）______________ （2）______________ （3）______________ （4）______________ （5）______________2.矩形的判定⽅法：（1）______________ （2）______________ （3）______________3.菱形的判定⽅法：（1）______________ （2）______________ （3）______________4.正⽅形的判定⽅法：（1）______________ （2）______________ （3）______________5.等腰梯形的判定⽅法：（1）______________ （2）______________ （3）______________【练⼀练】⼀．选择题1．能够判定四边形ABCD是平⾏四边形的题设是（）．A．AB∥CD，AD=BC B．∠A=∠B，∠C=∠DC．AB=CD，AD=BC D．AB=AD，CB=CD2．具备下列条件的四边形中，不能确定是平⾏四边形的为（）．A．相邻的⾓互补 B．两组对⾓分别相等C．⼀组对边平⾏，另⼀组对边相等 D．对⾓线交点是两对⾓线中点3.下列条件中，能判定四边形是平⾏四边形的条件是( )A.⼀组对边平⾏，另⼀组对边相等B.⼀组对边平⾏，⼀组对⾓相等C.⼀组对边平⾏，⼀组邻⾓互补D.⼀组对边相等，⼀组邻⾓相等4．如下左图所⽰，四边形ABCD的对⾓线AC和BD相交于点O，下列判断正确的是（）．A．若AO=OC，则ABCD是平⾏四边形;B．若AC=BD，则ABCD是平⾏四边形;C．若AO=BO，CO=DO，则ABCD是平⾏四边形;D．若AO=OC，BO=OD，则ABCD是平⾏四边形5．不能判定四边形ABCD是平⾏四边形的条件是（）A．AB=CD，AD=BC B．AB∥CD，AB=CDC．AB=CD，AD∥BC D．AB∥CD，AD∥BC6.四边形ABCD的对⾓线AC，BD相交于点O，能判断它为矩形的题设是（）A．AO=CO，BO=DO B．AO=BO=CO=DOC．AB=BC，AO=CO D．AO=CO，BO=DO，AC⊥BD7.四边形ABCD的对⾓线互相平分，要使它变为矩形，需要添加的条件是（）A．AB=CD B．AD=BC C．AB=BC D．AC=BD8.在四边形ABCD中，O是对⾓线的交点，下列条件能判定这个四边形是正⽅形的是（）A、AC＝BD，AB∥CD，AB＝CDB、AD∥BC，∠A＝∠CC、AO＝BO＝CO＝DO，AC⊥BDD、AC＝CO，BO＝DO，AB＝BC9.在下列命题中，真命题是（）Ａ．两条对⾓线相等的四边形是矩形Ｂ．两条对⾓线互相垂直的四边形是菱形Ｃ．两条对⾓线互相平分的四边形是平⾏四边形Ｄ．两条对⾓线互相垂直且相等的四边形是正⽅形10.在下列命题中，正确的是（）11.如图，已知四边形ABCD 是平⾏四边形，下列结论中不正确的是（） A ．当AB=BC 时，它是菱形 B ．当AC ⊥BD 时，它是菱形C ．当∠ABC=900时，它是矩形D ．当AC=BD 时，它是正⽅形12.如图，在ABC △中，点E D F ，，分别在边AB ，BC ，CA 上，且DE CA ∥，DF BA ∥．下列四个判断中，不正确．．．的是（） A ．四边形AEDF 是平⾏四边形B ．如果90BAC ∠=o ，那么四边形AEDF 是矩形C ．如果AD 平分BAC ∠，那么四边形AEDF 是菱形D ．如果AD BC ⊥且AB AC =，那么四边形AEDF 是菱形 13.下列条件中不能判定四边形是正⽅形的条件是（）。

案例：平行四边形判定（一）设计理念：素质教育的主旨是发挥学生的主体因素，让学生自主获取知识。

因此在开始的教学引入中，要充分调动学生的情感因素，激发学生兴趣，使学生参与进来；其次本节重点中前三个判定定理的顺序与它的性质定理相对应，因此在讲授新课时，采用探索式教学模式，由学生自己动手、猜想得到命题，并去判断命题成立与否，并根据过去所学知识去验证自己的结论，比较各种方法的优劣，这样使每个学生都积极参与到教学中，同时也注意保护学生的参与积极性。

而平行四边形的判定方法较多，综合性较强，能灵活的运用判定定理证明平行四边形，是本节的难点．因此在例题讲解时，采用启发式、讨论式教学模式，根据题目中具体条件结合图形引导学生根据分析法解题程序从条件或结论出发，由学生自己去思考，去分析，充分发挥学生的主体作用，培养学生主动、积极的学习态度和有条理地思考、探究问题的能力。

教材分析：“平行四边形的判定”是初中数学中比较重要的内容。

主要体现在知识技能和思想方法两个方面。

从知识技能上讲，它既是对前面所学的全等三角形和平行四边形性质的一个回顾和延伸，又是以后学习特殊平行四边形的基础，同时它还进一步培养学生简单的推理能力和图形迁移能力；从思想方法上讲，通过平行四边形和三角形之间的相互转化，渗透了化归思想。

综上所述，本节课对培养学生的探索精神、动手能力、应用意识和抽象建模能力都有很好的作用。

教学目标：1、知识目标:（1）、经历并了解平行四边形的判别方法探索过程，使学生逐步掌握说理的基本方法。

（2）、探索并了解平行四边形的判别方法。

能根据判别方法进行有关的应用。

2、能力目标:经历观察、归纳等教学活动过程，培养学生的合作精神和有条理的思考和探究的能力。

3、情感目标：通过生动有趣的数学活动，让学生主动探索、敢于表达、乐于合作交流，进一步体验数学在生活中的应用，体验因学习而带来的快乐。

教学重点：平行四边形的判定方法重点分析：平行四边形的判定方法涉及平行四边形元素的各方面，同时它又与平行四边形的性质联系，判定一个四边形是否为平行四边形是利用平行四边形性质解决其他问题的基础，所以平行四边形的判定方法是本节的重点。

2023年中考数学备考打基础系列（特殊平行四边形的计算与证明）一、选择题。

1. 下列命题为假命题的是( )A．对角线相等的平行四边形是矩形B．对角线互相垂直的平行四边形是菱形C．有一个内角是直角的平行四边形是正方形D．有一组邻边相等的矩形是正方形2. 在下列条件中，能够判定▱ABCD为矩形的是( )A. AB＝ACB. AC⊥BDC. AB＝ADD. AC＝BD3.如图，在矩形ABCD中，已知AB＝6，∠DBC＝30°，则AC的长为( )3 B. 10 C. 12 D. 12 34.如图，在菱形ABCD中，对角线AC，BD相交于点O，点E为CD的中点．若OE＝3，则菱形ABCD的周长为( )A. 6B. 12C. 24D. 485.如图，点E在矩形ABCD的AB边上，将△ADE沿DE翻折，点A恰好落在BC边上的点F处．若CD＝3BF，BE＝4，则AD的长为( )A．9 B．12 C．15 D．186.如图，在正方形ABCD中，点O是△BCD的内心，连接BO并延长交CD于点F，则∠BFC的度数是( )A. 45°B. 60°C. 67.5°D. 75°7. 如图，菱形纸片ABCD中，∠A＝60°，P为AB中点，折叠菱形纸片ABCD，使点C的对应点C′落在DP所在的直线上，得到经过点D的折痕DE，则∠DEC＝( )A. 60°B. 65°C. 75°D. 80°8. 如图，将矩形ABCD沿EF折叠，使点B落在边AD上的点M处，点C落在点N处，已知∠DMN ＝36°，连接BM，则∠AMB的度数为( )A. 68°B. 72°C. 76°D. 85°9.如图，在边长为1的菱形ABCD中，∠ABC＝60°，动点E在AB边上(与点A，B均不重合)，点F在对角线AC上，CE与BF相交于点G，连接AG，DF.若AF＝BE，则下列结论错误的是( )A．DF＝CE B．∠BGC＝120°C．AF2＝EG·EC D．AG的最小值为22 310. 正方形ABCD的对角线相交于点O(如图①)，如果∠BOC绕点O按顺时针方向旋转，其两边分别与边AB，BC相交于点E，F(如图②)，连接EF，那么在点E由B到A的过程中，线段EF 的中点G经过的路线是( )A. 线段B. 圆弧C. 折线D. 波浪线二、填空题。