22 高二选修三第三单元题1

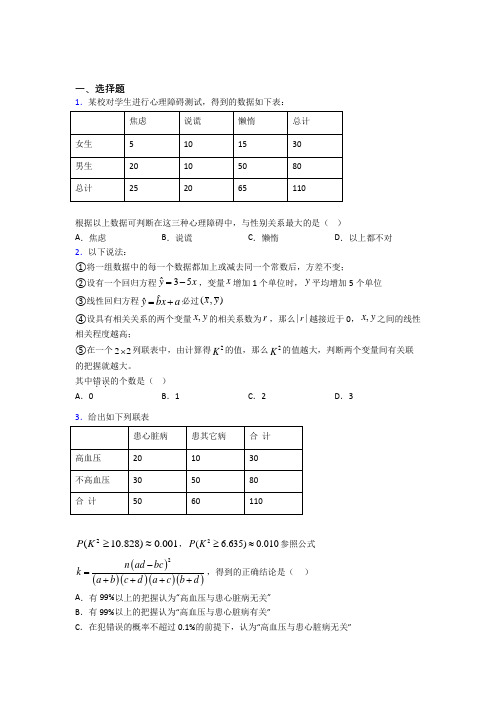
一、选择题1．某校对学生进行心理障碍测试，得到的数据如下表：根据以上数据可判断在这三种心理障碍中，与性别关系最大的是（ ） A ．焦虑 B ．说谎C ．懒惰D ．以上都不对2．以下说法：①将一组数据中的每一个数据都加上或减去同一个常数后，方差不变；②设有一个回归方程ˆ35yx =-，变量x 增加1个单位时，y 平均增加5个单位 ③线性回归方程ˆy bx a =+必过(),x y④设具有相关关系的两个变量,x y 的相关系数为r ，那么||r 越接近于0，,x y 之间的线性相关程度越高；⑤在一个22⨯列联表中，由计算得2K 的值，那么2K 的值越大，判断两个变量间有关联的把握就越大。

其中错误．．的个数是（ ） A ．0 B ．1 C ．2D ．33．给出如下列联表2(10.828)0.001P K ≥≈，2( 6.635)0.010P K ≥≈参照公式()()()()()2n ad bc k a b c d a c b d -=++++，得到的正确结论是（ ）A ．有99%以上的把握认为“高血压与患心脏病无关”B ．有99%以上的把握认为“高血压与患心脏病有关”C ．在犯错误的概率不超过0.1%的前提下，认为“高血压与患心脏病无关”D ．在犯错误的概率不超过0.1%的前提下，认为“高血压与患心脏病有关” 4．下列说法正确的是（ ）A ．在统计学中，回归分析是检验两个分类变量是否有关系的一种统计方法B ．线性回归方程对应的直线y b x a ∧∧∧=+至少经过其样本数据点中的()11,x y ，()22,x y ，()33,x y(),n n x y 一个点C ．在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高D ．在回归分析中，相关指数2R 为0.98的模型比相关指数2R 为0.80的模型拟合的效果差 5．某同学将收集到的六组数据制作成散点图如图所示，并得到其回归直线的方程为1:0.68ˆl y x a=+，计算其相关系数为1r ，相关指数为21R .经过分析确定点F 为“离群点”，把它去掉后，再利用剩下的5组数据计算得到回归直线的方程为2:0.68ˆl y bx=+，相关系数为2r ，相关指数为22R .以下结论中，不正确．．．的是A ．120,0r r >>B ．2212R R >C ．ˆ0.12a= D ．68ˆ00.b<< 6．已知下列命题：①回归直线ˆˆˆy bx a =+恒过样本点的中心(),x y ，且至少过一个样本点；②两个变量相关性越强，则相关系数r 就越接近于1； ③将一组数据的每个数据都加一个相同的常数后，方差不变；④在回归直线方程20.5ˆyx =- 中，当解释变量x 增加一个单位时，预报变量ˆy 平均减少0.5；⑤在线性回归模型中，相关指数2R 表示解释变量x 对于预报变量y 的贡献率，2R 越接近于1，表示回归效果越好；⑥对分类变量X 与Y ，它们的随机变量2K 的观测值k 来说， k 越小，“X 与Y 有关系”的把握程度越大．⑦两个模型中残差平方和越小的模型拟合的效果越好. 则正确命题的个数是（ ）A ．3B ．4C ．5D ．67．下列有关线性回归分析的六个命题： ①线性回归直线必过样本数据的中心点(),x y ；②回归直线就是散点图中经过样本数据点最多的那条直线； ③当相关性系数0r >时，两个变量正相关；④如果两个变量的相关性越强，则相关性系数r 就越接近于1；⑤残差图中残差点所在的水平带状区域越宽，则回归方程的预报精确度越高； ⑥甲、乙两个模型的2R 分别约为0.88和0.80，则模型乙的拟合效果更好. 其中真命题的个数为（ ） A ．1个B ．2个C ．3个D ．4个8．下列关于独立性检验的叙述：①常用等高条形图展示列联表数据的频率特征； ②独立性检验依据小概率原理；③样本不同，独立性检验的结论可能有差异；④对分类变量X 与Y 的随机变量2K 的观测值k 来说，k 越小，X 与Y 有关系的把握程度就越大.其中正确的个数为（ ） A ．1 B ．2C ．3D ．49．某村庄对改村内50名老年人、年轻人每年是否体检的情况进行了调查，统计数据如表所示：已知抽取的老年人、年轻人各25名.则完成上面的列联表数据错误的是( ) A ．18a =B ．19b =C ．50c d +=D ．2f e -=-10．已知,x y 的对应值表为：且,x y 线性相关，由于表格污损，y 的对应值看不到了，若6119.2ii y==∑，且线性回归直线方程为0.6y x a =+，则8x =时，y 的预报值为（ ） A ．6.1B ．22.1C ．12.6D ．3.511．研究表明某地的山高()y km 与该山的年平均气温()xC 具有相关关系，根据所采集的数据得到线性回归方程ˆ260y x =-+，则下列说法错误．．的是( ) A ．年平均气温为0时该山高估计为60km B ．该山高为72km 处的年平均气温估计为60CC ．该地的山高y 与该山的年平均气温x 的正负相关性与回归直线的斜率的估计值有关D ．该地的山高y 与该山的年平均气温x 成负相关关系 12．有下列说法：①若某商品的销售量y （件）关于销售价格x （元/件）的线性回归方程为5350y x =-+，当销售价格为10元时，销售量一定为300件；②线性回归直线y bx a =+一定过样本点中心(,)x y ；③若两个随机变量的线性相关性越强，则相关系数r 的值越接近于1；④在残差图中，残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适，与带状区域的宽度无关；⑤在线性回归模型中，相关指数2R 表示解释变量对于预报变量变化的贡献率，2R 越接近于1，表示回归的效果越好； 其中正确的结论有几个（ ） A ．1B ．2C ．3D ．413．有一散点图如图所示，在5个(,)x y 数据中去掉(3,10)D 后，下列说法正确的是（ ）A ．残差平方和变小B ．相关系数r 变小C ．相关指数2R 变小D ．解释变量x 与预报变量y 的相关性变弱二、解答题14．近年来，“双11”网购的观念逐渐深入人心.某人统计了近5年某网站“双11”当天的交易额，，统计结果如下表： 年份 2015 2016 2017 2018 2019 年份代码x12345交易额y /百亿元9 12 17 21 26r y x 留三位小数.（统计中用相关系数r 来衡量两个变量之间线性关系的强弱.若相应于变量x 的取值i x ，变量y 的观测值为i y (1i n ≤≤)，则两个变量的相关系数的计算公式为：.统计学认为，对于变量，如果[]1,0.75r -∈-，那么负相关很强;如果[]0.751r ∈，，那么正相关很强;如果(]0.75,0.30r ∈--或[)0.30,0.75r ∈，那么相关性一般;如果[]0.25,0.25r ∈-，那么相关性较弱）；（2）求出关于x 的线性y 回归方程，并预测2020年该网站“双11”当天的交易额.参考公式：121()()()ˆniii ni i x x y y bx x ==--=-∑∑，ˆˆay bx =-186043.1≈. 15．近年来，“双11”网购的观念逐渐深入人心.某人统计了近5年某网站“双11”当天的交易额，统计结果如下表： 年份 2015 2016 2017 2018 2019 年份代码x 1 2 3 4 5 交易额y /百亿元912172126y x 留三位小数.（统计中用相关系数r 来衡量两个变量之间线性关系的强弱.若相应于变量x 的取值i x ，变量y 的观测值为i y (1i n ≤≤)，则两个变量的相关系数的计算公式为：12211()()()()niii n niii i x x y y r x x y y ===--=--∑∑∑.统计学认为，对于变量,x y ，如果[]1,0.75r ∈--，那么负相关很强;如果[]0.751r ∈，，那么正相关很强;如果(]0.75,0.30r ∈--或[)0.30,0.75r ∈，那么相关性一般;如果[]0.25,0.25r ∈-，那么相关性较弱）；（2）求出y 关于x 的线性回归方程，并预测2020年该网站“双11”当天的交易额.参考公式：121()()()ˆniii ni i x x y y bx x ==--=-∑∑，ˆˆay bx =-186043.1≈. 16．某学校共有1000名学生，其中男生400人，为了解该校学生在学校的月消费情况，采取分层抽样随机抽取了100名学生进行调查，月消费金额分布在450~950之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示：将月消费金额不低于750元的学生称为“高消费群”.（1）求a 的值，并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表)；（2）现采用分层抽样的方式从月消费金额落在[550，650)，[750，850)内的两组学生中抽取10人，再从这10人中随机抽取3人，记被抽取的3名学生中属于“高消费群”的学生人数为随机变量X ，求X 的分布列及数学期望；（3）若样本中属于“高消费群”的女生有10人，完成下列22⨯列联表，并判断是否有97.5%的把握认为该校学生属于“高消费群”与“性别”有关？属于“高消费群” 不属于“高消费群” 合计男 女 合计(参考公式：2()()()()()n ad bc K a b c d a c b d -=++++，其中)n a b c d =+++2()P K k0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 2.0722.7063.8415.0246.6357.87910.82817．从某居民区随机抽取10个家庭，获得第i 个家庭的月收入i x （单位：千元）与月储蓄i y ，（单位：千元）的数据资料，算出101010102111180,20184,720ii i i i i i i i xy x y x ========∑∑∑∑，，附：线性回归方程1221ˆˆˆˆˆˆ,,ni ii nii x y nxyybx a b ay bx xnx ==-=+==--∑∑，其中,x y 为样本平均值. （1）求家庭的月储蓄y 对月收入x 的线性回归方程ˆˆˆybx a =+ ； （2）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.18．西尼罗河病毒（WNV ）是一种脑炎病毒，WNV 通常是由鸟类携带，经蚊子传播给人类．1999年8-10月，美国纽约首次爆发了WNV 脑炎流行．在治疗上目前尚未有什么特效药可用，感染者需要采取输液及呼吸系统支持性疗法，有研究表明，大剂量的利巴韦林含片可抑制WNV 的复制，抑制其对细胞的致病作用．现某药企加大了利巴韦林含片的生产，为了提高生产效率，该药企负责人收集了5组实验数据，得到利巴韦林的投入量x （千克）和利巴韦林含片产量y （百盒）的统计数据如下：由相关系数可以反映两个变量相关性的强弱，，认为变量相关性很强；||[0.3,0.75]r ∈，认为变量相关性一般；||[0,0.25]r ∈，认为变量相关性较弱．（1）计算相关系数r ，并判断变量x 、y 相关性强弱；（2）根据上表中的数据，建立y 关于x 的线性回归方程ˆˆˆybx a =+；为了使某组利巴韦林含片产量达到150百盒，估计该组应投入多少利巴韦林？ 25.69≈．参考公式：相关系数()()niix x y y r --=∑ˆˆˆybx a =+中，()()()121niii ni i x x y y b x x ==--=-∑∑，ˆˆay bx =-． 19．某中学研究性学习小组为了考察高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了50名学生.调查结果表明，在爱看课外书的24人中有18人作文水平好，另6人作文水平一般；在不爱看课外书的26人中有7人作文水平好，另19人作文水平一般.（1）试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？ 高中学生的作文水平与爱看课外书的2×2列联表爱看课外书 不爱看课外书 总计作文水平好 作文水平一般 总计（2）将其中某4名爱看课外书且作文水平好的学生分别编号为1、2、3、4，某4名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为2的倍数或3的倍数的概率.参考公22()()()()()n ad bc K a b c d a c b d -=++++其中n a b c d =+++·参考数据：()20P k k ≥0.10 0.05 0.025 0.010 0.005 0.001 0k2.7063.8415.0246.6357.87910.82820．海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg ），其频率分布直方图如下：（1）网箱产量不低于40kg 为“理想网箱”，填写下面列联表，并根据列联表判断是否有99.9%的把握认为“理想网箱”的数目与养殖方法有关：箱产量40kg <箱产量40kg ≥合计旧养殖法 新养殖法（2）已知旧养殖法100个网箱需要成本50000元，新养殖法100个网箱需要增加成本15750元，该水产品的市场价格为x 元/()15kg x ≥，根据箱产量的频率分布直方图（说明：同一组中的数据用该组区间的中间值作代表），采用哪种养殖法，请给养殖户一个较好的建议，并说明理由． 附参考公式及参考数据：()()()()()20n ad bc k a b c d a c b d -=++++21．调查某桑场采桑员和辅助工桑毛虫皮炎发病情况结果如下表：利用22⨯列联表的独立性检验估计，“患桑毛虫皮炎病与采桑”是否有关？认为两者有关系会犯错误的概率是多少？随机量变22()()()()()n ad bc K a b c d a c b d -=++++ (其中n a b c d =+++) 临界值表22．某种产品的广告费支出x 与销售额y （单位：万元）之间有对应数据：（1）求回归直线方程；（2）试预测广告费支出为10万元时，销售额多大？线性回归方程的系数公式为()()()1122211nni iiii i nniii i x y nx y x x y y b xnxx x ====---==--∑∑∑∑，a y bx =-.23．我市今年参加高考的考生是首次取消文理科后的新高考考生，新高考实行“321++”，成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况，随机调查50人（把年龄在[)15,45称为中青年，年龄在[)45,75称为中老年），并把调查结果制成下表：（1）请根据上表完成下面22⨯列联表，并判断是否有95%的把握认为对新高考的了解与年龄（中青年、中老年）有关？附：()()()()()22n ad bc K a b c d a c b d -=++++. （2）现采用分层抽样的方法从中老年人中抽取8人，再从这8人中随机抽取2人进行深入调查，求事件A ：“恰有一人年龄在[)45,55”发生的概率.24．为了解某班学生喜欢数学是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表，已知在全部50人中随机抽取1人抽到喜欢数学的学生的概率为35.（1）请将上面的列联表补充完整（不用写计算过程）；（2）能否在犯错误的概率不超过0.005的前提下认为喜欢数学与性别有关？说明你的理由；（3）现从女生中抽取2人进一步调查，设其中喜欢数学的女生人数为ξ，求ξ的分布列与期望.下面的临界表供参考：（参考公式：()()()()()22n ad bc K a b c d a cb d -=++++，其中n a bcd =+++）25．某食品店为了了解气温对销售量的影响，随机记录了该店1月份中5天的日销售量y （单位：千克）与该地当日最低气温x （单位：°C ）的数据，如下表：（1）求出y 与x 的回归方程y ＝b x +a ；（2）判断y 与x 之间是正相关还是负相关；若该地1月份某天的最低气温为6°C ，请用所求回归方程预测该店当日的营业额．附：回归方程y ＝b x +a ；中，b ＝()1221()==--∑∑ni ii nii x y nxyxn x ，a ＝y ﹣bx26．某市实施二手房新政一年多以来，为了了解新政对居民的影响，房屋管理部门调查了2018年6月至2019年6月期间购买二手房情况，首先随机抽取了其中的400名购房者，并对其购房面积m （单位：平方米，60130m ≤≤）讲行了一次统计，制成了如图1所示的频率分布直方图，接着调查了该市2018年6月至2019年6月期间当月在售二手房的均价y （单位：万元/平方米），制成了如图2所示的散点图（图中月份代码1－13分别对应2018年6月至2019年6月）（1）试估计该市市民的平均购房面积m （同一组中的数据用该组区间的中点值为代表）；（2）从该市2018年6月至2019年6月期间所有购买二手房的市民中任取3人，用频率估计概率，记这3人购房面积不低于100平方米的人数为X ，求X 的分布列与数学期望；（3）根据散点图选择ˆˆya x =+ˆˆˆln y c d x =+两个模型讲行拟合，经过数据处理得到两个回归方程，分别为ˆ0.93690.0285yx =+ˆ0.95540.0306ln y x =+，并得到一些统计量的值，如表所示：ˆ0.93690.0285yx =+ ˆ0.95540.0306ln yx =+ ()()1niii x x y y =--∑0.0054590.005886()()2211nni i i i x x y y ==--∑∑ 0.006050请利用相关系数判断哪个模型的拟合效果更好，并用拟合效果更好的模型预测2019年8月份的二手房购房均价（精确到0.001）.参考数据：ln 20.69≈，ln3 1.10≈，ln15 2.71≈3 1.73≈15 3.87≈，17 4.12≈参考公式：()()()()12211niii nni i i i x x y y r x x y y ===--=--∑∑∑【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】分别求出三种关系的观测值，比较后可得结论. 【详解】解：对于焦虑，说谎，懒惰三种心理障碍，设它们观测值分别为123,,K K K ， 由表中数据可得：()2111056025200.86330802585K ⨯⨯-⨯=≈⨯⨯⨯，()2211010702010 6.36630802090K ⨯⨯-⨯=≈⨯⨯⨯，()2311015301550 1.41030806545K ⨯⨯-⨯=≈⨯⨯⨯，因为2K 的值最大，所以说谎与性别关系最大. 故选：B. 【点睛】本题考查独立性检验的应用，考查理解能力和计算能力.2．C解析：C 【分析】根据用样本估计总体、线性回归方程、独立性检验的基本概念和基本性质，逐项判断，即可得到本题答案. 【详解】方差反映一组数据的波动大小，将一组数据中的每个数据都加上或减去同一个常数后，方差不变，故①正确；一个回归方程ˆ35yx =-，变量x 增加1个单位时，y 平均减少5个单位，故②不正确；线性回归方程ˆy bx a =+必过样本中心点，故③正确；根据线性回归分析中相关系数的定义：在线性回归分析中，相关系数为r ，||r 越接近于1，相关程度越大，故④不正确；对于观察值2K 来说，2K 越大，“x 与y 有关系”的可信程度越大，故⑤正确. 故选：C 【点睛】本题主要考查用样本估计总体、线性回归方程、独立性检验的基本思想.3．B解析：B 【分析】根据所给的列联表，利用公式求出这组数据的观测值，把观测值同临界值进行比较，即可得到结果. 【详解】由列联表中的数据可得2K 的观测值，()22110205010307.486 6.63530805060K ⨯-⨯==≥⨯⨯⨯，根据参考数据：2 6.6350.01p K ≥=，∴有10.0199%-=的把握认为高血压与患心脏病有关，即有99%的把握认为高血压与患心脏病有关,故选B. 【点睛】本题考查独立性检验的应用，属于基础题. 独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；(3) 查表比较2K 与临界值的大小关系，作统计判断.4．C解析：C 【解析】分析：首先对每个选项一一进行分析，需要明确独立性检验是检验两个分类变量是否有关系的一种统计方法，回归直线可能不过任何一个样本数据点，残差图中，残差点分布的带状区域的宽度越狭窄，其模拟精度越高，相关指数越大，拟合效果越好的结论，就可以正确选出结果.详解：对于A ，统计学中，独立性检验是检验两个分类变量是否有关系的一种统计方法，所以A 错；对于B ，线性回归方程对应的直线y b x a ∧∧∧=+可能不过任何一个样本数据点，所以B 错误；对于C ，残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高，所以C 正确；对于D ，回归分析中，相关指数2R 为0.98的模型比相关指数2R 为0.80的模型拟合的效果好，所以D 错误. 故选C.点睛：根据概率统计中变量间的相关关系，线性回归方程以及残差图与相关指数2R 的概念，对选项中的命题进行分析、判断正误即可.5．B解析：B 【分析】根据相关性的正负判断1r 和2r 的正负，根据两个模型中回归直线的拟合效果得出21R 和22R 的大小关系，将第一个模型中的样本数据中心点代入直线1l 的方程得出a 的值，由两回归直线的倾斜程度得出两回归直线的斜率大小关系． 【详解】由图可知两变量呈现正相关，故120,0r r >>，且12r r <，故2212R R <,故A 正确，B 不正确.又回归直线1:0.68ˆl y x a=+必经过样本中心点(3.5,2.5)，所以2.50.68 3.5ˆ0.12a=-⨯=，C 正确. 回归直线2:0.68ˆl y bx=+必经过样本中心点(3,2)，所以230.68ˆb =⨯+， 所以ˆ0.44b=，也可直接根据图象判断68ˆ00.b <<（比较两直线的倾斜程度），故D 正确．故选B ． 【点睛】本题考查回归分析，考查回归直线的性质、相关系数、相关指数的特点，意在考查学生对这些知识点的理解，属于中等题．6．B解析：B 【分析】由回归直线恒过样本中心点，不一定经过每一个点，可判断①；由相关系数的绝对值趋近于1，相关性越强，可判断②；由方差的性质可判断③；由线性回归直线方程的特点可判断④；相关指数R 2的大小，可判断⑤；由的随机变量K 2的观测值k 的大小可判断⑥；残差平方和越小，模型的拟合效果越好，可判断⑦． 【详解】对于①，回归直线y b x a ∧∧∧=+恒过样本点的中心（x y ，），可以不过任一个样本点，故①错误；对于②，两个变量相关性越强，则相关系数r 的绝对值就越接近于1，故②错误； 对于③，将一组数据的每个数据都加一个相同的常数后，由方差的性质可得方差不变，故③正确；对于④，在回归直线方程y ∧=2﹣0.5x 中，当解释变量x 每增加一个单位时， 预报变量y ∧平均减少0.5个单位，故④正确；对于⑤，在线性回归模型中，相关指数R 2表示解释变量x 对于预报变量y 的贡献率，R2越接近于1，表示回归效果越好，故⑤正确；对于⑥，对分类变量X与Y，它们的随机变量K2的观测值k来说，k越大，“X与Y有关系”的把握程度越大，故⑥错误；对于⑦，可用残差平方和判断模型的拟合效果，残差平方和越小，模型的拟合效果越好，故⑦正确．其中正确个数为4．故选B．【点睛】本题考查命题的真假判断，主要是线性回归直线的特点和线性相关性的强弱、样本数据的特征值和模型的拟合度，考查判断能力，属于基础题．7．B解析：B【解析】分析：根据线性回归方程的几何体特征及残差，相关指数的概论，逐一分析四个选项的正误，可得结论.详解：①线性回归直线必过样本数据中心点(),x y，故①正确；②回归直线方程在散点图中可能不经过任意样本数据点，故②错误；r>时，则两个变量正相关，故③正确；③当相关性系数0④如果两个变量的相关性越强，则相关性系数r就越接近于1或1-，故④错误；⑤残差图中残差点所在的水平带状区域越窄，回归方程的预报精确度越高，故⑤错误；⑥甲、乙两个模型的2R分别约为0.88和0.80，则模型甲的拟合效果更好，故⑥错误，真命题的个数为2，故选B.点睛：本题以命题的真假判断为截体，考查了相关关系，回归分析、残差、相关指数等知识点，意在考查对基本概念掌握的熟练程度，难度不大，属于基础题.8．C解析：C【解析】分析：根据独立性检验的定义及思想，可得结论．详解：①常用等高条形图展示列联表数据的频率特征；正确；②独立性检验依据小概率原理；正确；③样本不同，独立性检验的结论可能有差异；正确；④对分类变量X与Y的随机变量2K的观测值k来说，k越大，X与Y有关系的把握程度就越大.故④错误.故选C.点睛：本题考查了独立性检验的原理，考查了推理能力，属于基础题．9．D解析：D【解析】分析：先根据列联表列方程组，解得a,b,c,d,e,f,再判断真假.详解：因为725,625,6,7,50,50a c b d a e b f c d e f +==+==+=+=+=+=， 所以18,19,50,24,26,2a b c d e f f e ==+===-= 选D.点睛：本题考查列联表有关概念，考查基本求解能力.10．A解析：A 【分析】求出,x y ，由线性回归方程必经过点（,x y ）即得a ，代入8x =求解即可. 【详解】 由表格知，196x =， 6119.2ii y==∑3.2y ∴=，代入0.6y x a =+得：193.20.66a =⨯+， 1.3a ∴=，则回归方程为0.6 1.3y x =+， 当8x =时，0.68 1.3 6.1y =⨯+=， 故选：A ． 【点睛】本题主要考查了线性回归方程，线性回归方程的性质、应用， 属于中档题.11．B解析：B 【分析】由已知线性回归直线方程ˆ260yx =-+，可估计平均气温为60C 时该地的山高，即可得到答案． 【详解】线性回归直线方程为ˆ260yx =-+，当0x = 时ˆ60y =即年平均气温为0时该山高估计为60km ，故A 正确；当ˆ72y=时解得6x =-即山高为72km 处的年平均气温估计为6C -，故B 错误；该地的山高y 与该山的年平均气温x 的正负相关性与回归直线的斜率的估计值有关，故C 正确；由20-<，该地的山高y 与该山的年平均气温x 成负相关关系，故D 正确．故选B 【点睛】本题考查线性回归直线方程的应用，考查相关的意义，判断能力，属于基础题．12．B解析：B【分析】由最小二乘法求解回归直线和回归直线的性质可知①错误，②正确；随机变量为负相关-，③错误；残差图中带状区域越窄，拟合度时，线性相关性越强，相关系数r越接近1越高，④错误；2R越接近1，模型拟合度越高，⑤正确；由此可得结果.【详解】①当销售价格为10时，销售量的预估值为300件，但预估值与实际值未必相同，①错误；②由最小二乘法可知，回归直线必过(),x y，②正确；-，③错误；③若两个随机变量为负相关，若线性相关性越强，相关系数r越接近1④残差图中，带状区域越窄，模型拟合度越高，④错误；⑤相关指数2R越接近1，拟合度越高，则在线性回归模型中，回归效果越好，⑤正确.可知正确的结论为：②⑤，共2个本题正确选项：B【点睛】本题考查统计案例部分命题的判断，涉及到回归直线、最小二乘法、相关系数、相关指数、残差图的相关知识.13．A解析：A【分析】D后，y与x的线性相关性加强，由相关系数r，相关指数2R 由散点图可知，去掉(3,10)及残差平方和与相关性的关系得出选项.【详解】∵从散点图可分析得出：只有D点偏离直线远，去掉D点，变量x与变量y的线性相关性变强，∴相关系数变大，相关指数变大，残差的平方和变小，故选A.【点睛】该题考查的是有关三点图的问题，涉及到的知识点有利用散点图分析数据，判断相关系数，相关指数，残差的平方和的变化情况，属于简单题目.二、解答题14．（1）0.998；变量y 与x 的线性相关程度很强；（2）ˆ 4.3 4.1yx =+；29.9百亿元. 【分析】（1）直接将数据代入公式计算，即可得答案；（2）利用最小二乘法求得y 关于x 的线性回归方程为ˆ 4.3 4.1yx =+ ，再将6x =代入，即可得答案； 【详解】（1）由题意，根据表格中的数据， 可得：1(12345)35x =++++=，1(912172126)175y =++++=， 则1()()(13)(917)(53)(2617)43niii x x y y =--=--++--=∑，43.1=≈，所以()()430.99843.1niix x y y r --==≈∑ 所以变量y 与x 的线性相关程度很强. （2）由（1）可得3x =，17y =，1()()43niii x x y y =--=∑，又由2221222(13)(23)(3(3)(43)(53)1)0nii x x ==-+-+-+-+-=-∑，所以121()()43 4.30)ˆ1(niii ni i x x y y bx x ==--===-∑∑，则ˆˆ17 4.33 4.1a y bx=-=-⨯=， 可得y 关于x 的线性回归方程为ˆ 4.3 4.1y x =+ 令6x =，可得ˆ 4.36 4.129.9y=⨯+=， 即2020年该网站“双11”当天的交易额29.9百亿元. 【点睛】利用最小二乘法求回归直线方程，再利用方程进行预报值，准确计算是求解的关键.15．（1）0.998；变量y 与x 的线性相关程度很强；（2）ˆ 4.3 4.1yx =+；29.9百亿元. 【分析】（1）根据表中数据可得x 、y ，再计算出1()()niii x x y y =--∑和1()()niii x x y y =--∑，代入()()niix x y y r --=∑，得到数据与所给r 比较可得答案；（2）由（1）可得x ，y ，1()()niii x x y y =--∑，计算出21()ni i x x =-∑，代入121()()()ˆniii ni i x x y y bx x ==--=-∑∑和ˆˆay bx =-可得答案. 【详解】（1）由题意，根据表格中的数据， 可得：1(12345)35x =++++=，1(912172126)175y =++++=， 则1()()(13)(917)(53)(2617)43niii x x y y =--=--++--=∑，43.1=≈，所以()()430.99843.1niix x y y r --==≈∑， 所以变量y 与x 的线性相关程度很强. （2）由（1）可得3x =，17y =，1()()43niii x x y y =--=∑，又由2221222(13)(23)(3(3)(43)(53)1)0nii x x ==-+-+-+-+-=-∑，所以121()()43 4.30)ˆ1(niii ni i x x y y bx x ==--===-∑∑，则ˆˆ17 4.33 4.1a y bx=-=-⨯=， 可得y 关于x 的线性回归方程为ˆ 4.3 4.1y x =+， 令6x =，可得ˆ 4.36 4.129.9y=⨯+=， 即2020年该网站“双11”当天的交易额29.9百亿元. 【点睛】本题考查了变量的相关性以及回归直线方程的求解，回归分析的目的是试图通过样本数据得到真实结构参数的估计值，并要求估计结果接近真实值,要求认真计算各个数值.。

第三单元作业（1）一、选择题1．江南园林以黑白为主色调，是为了()①显示园主的富贵荣华②迎合园主追求闲适宁静的需要③与水乡风光、湿润气候融为一体④与宽阔整齐的地形、多蓝天白云的气候相辉映A．①②B．②③C．③④D．①④2．黄山奇、青城幽、峨眉秀、华山险，自然景观的美感是多方面的。

这些自然景观的构景基础是()A．地貌B．水文C．植物D．动物3．“会当凌绝顶，一览众山小”反映了泰山的()A．形象美B．色彩美C．动态美D．朦胧美4．风吹林动、流水飘烟、飞禽走兽使自然景观展示出() A．形象美B．色彩美C．动态美D．听觉美5．“雨打芭蕉”“幽林鸟语”反映了自然景观的()A．形象美B．色彩美C．动态美D．听觉美6．万里长城西起嘉峪关，东到山海关，恰似一条巨龙，跨越黄沙漫漫的戈壁，蜿蜒起伏于崇山峻岭，横贯中国的东西。

从旅游资源的审美特征看，万里长城具有()A．朦胧美B．动态美C．自然美D．人工美7．下列关于自然美和人工美的叙述，错误的是()A．自然美是自然景观在不同的条件下，呈现出的审美状态B．人工美是指能够吸引人们旅游活动，反映古今人类创造的物质文明和精神文明的事物所呈现出的审美状态C．自然美和人工美独立存在D．自然美和人工美和谐统一，构成绚丽多姿的风景美8．“两个黄鹂鸣翠柳，一行白鹭上青天。

窗含西岭千秋雪，门泊东吴万里船。

”这首诗反映了大自然的()①色彩美②动态美③声音美④形象美A．①B．①②C．①②③D．①②③④9．下列景观具有动态美和听觉美的是()A．钱塘江大潮 B．黄山云海C．云南路南石林D．武陵源群峰10．西湖“山色空蒙雨亦奇”反映了自然景观的()A．形象美B．色彩美C．动态美D．朦胧美11．“江作青罗带，山如碧玉簪”包含了自然景观的美感特征是()①形象美②色彩美③动态美④朦胧美A．①②B．②③C．③④D．①④12．“停车坐爱枫林晚，霜叶红于二月花”反映了自然景观的() A．形象美B．色彩美C．动态美D．朦胧美13．桂林山水自然景观的美学价值主要在于它的()A．形象美B．色彩美C．动态美D．听觉美14．辛弃疾词云：“明月别枝惊鹊，清风半夜鸣蝉。

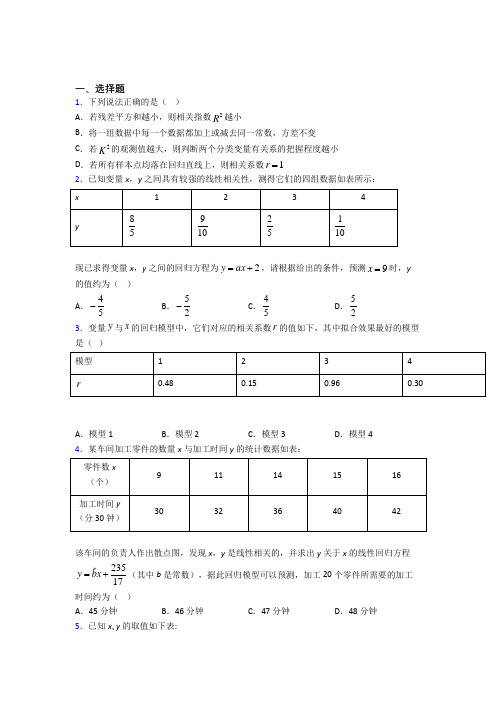
一、选择题1．下列说法正确的是（ ）A ．若残差平方和越小，则相关指数2R 越小B ．将一组数据中每一个数据都加上或减去同一常数，方差不变C ．若2K 的观测值越大，则判断两个分类变量有关系的把握程度越小D ．若所有样本点均落在回归直线上，则相关系数1r =2．已知变量x ，y 之间具有较强的线性相关性，测得它们的四组数据如表所示：现已求得变量x ，y 之间的回归方程为2y ax =+，请根据给出的条件，预测9x =时，y 的值约为（ ）A ．45-B ．52-C ．45 D ．523．变量y 与x 的回归模型中，它们对应的相关系数r 的值如下，其中拟合效果最好的模型是（ ）A ．模型1B ．模型2C ．模型3D ．模型44．某车间加工零件的数量x 与加工时间y 的统计数据如表：该车间的负责人作出散点图，发现x ，y 是线性相关的，并求出y 关于x 的线性回归方程23517=+y bx （其中b 是常数），据此回归模型可以预测，加工20个零件所需要的加工时间约为（ ） A ．45分钟 B ．46分钟 C ．47分钟 D ．48分钟 5．已知x ､y 的取值如下表:从散点图可以看出y 与x 线性相关，且回归方程0.95y x a =+，则当5x =时，估计y 的值为（ ） A ．7.1 B ．7.35C ．7.95D ．8.66．某工厂为了对新研发的一种产品进行合理定价，将该产品事先拟订的价格进行试销，得到如下数据．由表中数据求得线性回归方程ˆˆ4=-+y x a ，则15＝x 元时预测销量为（）A ．45件B ．46件C ．49件D ．50件7．下列说法中正确的是 （ ）①相关系数r 用来衡量两个变量之间线性关系的强弱， r 越接近于1，相关性越弱； ②回归直线y bx a =+一定经过样本点的中心(),x y ；③随机误差e 满足()0E e =，其方差()D e 的大小用来衡量预报的精确度； ④相关指数2R 用来刻画回归的效果， 2R 越小，说明模型的拟合效果越好. A ．①②B ．③④C ．①④D ．②③8．已知回归方程21y x =-，则该方程在样本(3,4)处的残差为（ ） A ．-1B ．1C ．2D ．59．下列命题：①在线性回归模型中，相关指数2R 表示解释变量x 对于预报变量y 的贡献率，2R 越接近于1，表示回归效果越好；②两个变量相关性越强，则相关系数的绝对值就越接近于1；③在回归直线方程0.52y x ∧=-+中，当解释变量x 每增加一个单位时，预报变量y ∧平均减少0.5个单位；④对分类变量X 与Y ，它们的随机变量2K 的观测值k 来说，k 越小，“X 与Y 有关系”的把握程度越大.其中正确命题的个数是（ ） A ．1个B ．2个C ．3个D ．4个10．由变量x 与y 相对应的一组数据()12,y 、()24,y 、()3 6,y 、()48,y 、()5 10,y 得到的线性回归方程为ˆ 1.212yx =+，则12345y y y y y ++++等于（ ） A ．88B ．90C ．92D ．9611．已知呈线性相关的变量x 与y 的部分数据如表所示：若其回归直线方程是，则（）A．5.5 B．6 C．6.5 D．712．为考察某种药物预防疾病的效果，进行动物试验，得到如下药物效果与动物试验列联表：由上述数据给出下列结论，其中正确结论的个数是（）附：22()()()()()n ad bcKa b c d a c b d-=++++；①能在犯错误的概率不超过0.05的前提下认为药物有效②不能在犯错误的概率不超过0.025的前提下认为药物有效③能在犯错误的概率不超过0.010的前提下认为药物有效④不能在犯错误的概率不超过0.005的前提下认为药物有效A．1B．2C．3D．4第II卷（非选择题）请点击修改第II卷的文字说明参考答案13．设两个变量x和y之间具有线性相关关系，它们的相关系数为r，y关于x的回归直线方程为y kx b=+，则()A．k与r的符号相同B．b与r的符号相同C．k与r的符号相反D．b与r的符号相反二、解答题14．某校从高二年级随机抽取了20名学生的数学总评成绩和物理总评成绩，记第i 位学生的成绩为(i i x y ，) (i =1，2，3...20)，其中i i x y ，分别为第i 位学生的数学总评成绩和物理总评成绩.抽取的数据列表如下( 按数学成绩降序整理):（1）根据统计学知识，当相关系数|r |≥0.8时，可视为两个变量之间高度相关.根据抽取的数据，能否说明数学总评成绩与物理总评成绩高度相关?请通过计算加以说明. 参考数据：20202022111()()485.()678.()476iiii i i i x x y y x x y y ===--=-=-=∑∑∑参考公式：相关系数12211()().()()niii n niii i x x y y r x x x y ===--=--∑∑∑（2）规定:总评成绩大于等于85分者为优秀，小于85分者为不优秀，对优秀赋分1，对不优秀赋分0，从这20名学生中随机抽取2名学生，若用X 表示这2名学生两科赋分的和，求X 的分布列和数学期望.15．从某居民区随机抽取10个家庭，获得第i 个家庭的月收入i x （单位：千元）与月储蓄i y ，（单位：千元）的数据资料，算出101010102111180,20184,720ii i i i i i i i xy x y x ========∑∑∑∑，，附：线性回归方程1221ˆˆˆˆˆˆ,,ni ii nii x y nxyybx a b ay bx xnx ==-=+==--∑∑，其中,x y 为样本平均值. （1）求家庭的月储蓄y 对月收入x 的线性回归方程ˆˆˆybx a =+ ； （2）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.16．某省即将实行新高考，不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响，对该校2018级的1000名学生进行调查，收集到相关数据如下：（1）根据以上提供的信息，完成22⨯列联表，并完善等高条形图；选物理不选物理总计数学成绩优秀数学成绩不优秀260总计6001000（2）能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关？附：22()()()()()n ad bcKa b c d a c b d-=++++临界值表：()2P K k0.100.050.0100.0050.001 0k 2.706 3.841 6.6357.87910.82817．某大学生参加社会实践活动，对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查，销售单价x和销售量y之间的一组数据如下表所示：月份123456销售单价（元）99.51010.5118（1）根据1至5月份的数据，求出y 关于x 的回归直线方程；（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元，则认为所得到的回归直线方程是理想的，试问（1）中所得到的回归直线方程是否理想？ （3）预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是2.5元/件，那么该配件的销售单价应定为多少元才能获得最大利润？（注：利润=销售收入-成本）．参考公式：回归直线方程ˆˆˆybx a =+,其中1221ˆni i i n i i x y nxy b x nx==-=-∑∑，55211392,502.5,i ii i i x yx ====∑∑18．2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出，将冰雪这个冷项目迅速炒“热”．北京某综合大学计划在一年级开设冰球课程，为了解学生对冰球运动的兴趣，随机从该校一年级学生中抽取了100人进行调查，其中女生中对冰球运动有兴趣的占23，而男生有10人表示对冰球运动没有兴趣额．（1）完成22⨯列联表，并回答能否有90%的把握认为“对冰球是否有兴趣与性别有关”？（2）已知在被调查的女生中有5名数学系的学生，其中3名对冰球有兴趣，现在从这5名学生中随机抽取3人，求至少有2人对冰球有兴趣的概率．附表：22()()()()()n ad bc K a b c d a c b d -=++++19．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：零件的个数x(个）2345加工的时间y(小时） 2.534 4.5（1）在给定的坐标系中画出表中数据的散点图；（2）求出y关于x的线性回归方程ˆˆˆy bx a=+，并在坐标系中画出回归直线；（3）试预测加工10个零件需要多少时间？(注：()()()1122211ˆn ni i i ii in ni ii ix x y y x y nxybx x x nx====---==--∑∑∑∑，ˆˆa y bx=-)20．下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据x3456y 2.534 4.5（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程ˆˆˆy bx a=+；（2）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据1求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(附:42186iix==∑，4166.5i iix y==∑，()()()1122211n ni i i ii in ni ii ix x y y x y nxybx x x nx====---==--∑∑∑∑，ˆˆa y bx=-，其中x,y为样本平均值)21．某手机企业为确定下一年度投入某种产品的研发费用，统计了近10年投入的年研发费用x千万元与年销售量y千万件的数据，得到散点图1，对数据作出如下处理：令ln i i u x =，ln i i v y =，得到相关统计量的值如图2：（1）利用散点图判断y bx a =+和dy c x =⋅()0,0c d >>哪一个更适合作为年研发费用x 和年销售量y 的回归类型（不必说明理由），并根据数据，求出y 与x 的回归方程；（2）已知企业年利润z 千万元与,x y 的关系式为27z y x e=-（其中e 为自然对数的底数），根据（1）的结果，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用？22．某市春节期间7家超市的广告费支出i x （万元）和销售额i y （万元）数据如下：超市 A B C D E F G 广告费支出i x 1 2 4 6 11 13 19 销售额i y19324044525354参数数据及公式：8x =，42y =，712794i i i x y ==∑，712708i i x ==∑，1221ˆni i nii i y n x y b nxx x ==-⋅=-∑∑，ˆˆay bx =-，ln 20.7≈. （1）若用线性回归模型拟合y 与x 的关系，求y 关于x 的线性回归方程；（2）用对数回归模型拟合y 与x 的关系，可得回归方程：ˆ12ln 22yx =+，经计算得出线性回归模型和对数模型的2R 分别约为0.75和0.97，请用2R 说明选择哪个回归模型更合适，并用此模型预测A 超市广告费支出为8万元时的销售额.23．根据教育部高考改革指导意见，广东省从2021年正式实施“312++”新的高考考试方案.为尽快了解学生的选科需求，及时调整学校人力资源配备.某校从高一学生中抽样调查了100名同学，在模拟分科选择中，一半同学（其中男生38人）选择了物理，另一半（其中男生14人）选择了历史.请完成以下22⨯列联表，并判断能否有99.9%的把握说选科与性别有关？参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++为样本容量.2()p K k ≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 k2.0722.7063.8415.0246.6357.87910.82824．某地区不同身高()x cm 的未成年男孩的体重平均值()y kg 如下表：已知ln y 与x 之间存在很强的线性相关性， （1）据此建立y 与x 之间的回归方程；（2）若体重超过相同身高男性体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高150cm 体重为45kg 的在校男生的体重是否正常？ 参考数据：()51ln 940iii x y =⋅=∑，51ln 11.5ii y==∑， 3.740.5e ≈附：对于一组数据()11,v μ，()22,v μ，…，(),n n v μ，其回归直线v bx a =+中的斜率和截距的最小二乘估计分别为1221ˆni i i nii v n vbn μμμμ==-=-∑∑，ˆˆav b μ=-. 25．某地实施乡村振兴战略，对农副产品进行深加工以提高产品附加值，已知某农产品成本为每件3元，加工后的试营销期间，对该产品的价格与销售量统计得到如下数据：（1）求销量y （件）关于单价x （元）的线性回归方程ˆˆˆybx a =+； （2）根据销量y 关于单价x 的线性回归方程，要使加工后收益P 最大，应将单价定为多少元？（产品收益=销售收入-成本）．参考公式：ˆb=()121()()ni i i ni i x x y y x x ==---∑∑=1221ni i i n i i x y nxy x nx ==--∑∑，ˆˆay bx =- 26．高一学年结束后，要对某班的50名学生进行文理分班，为了解数学对学生选择文理科是否有影响，有人对该班的分科情况做了如下的数据统计：（Ⅰ）根据数据关系，完成22⨯列联表；（Ⅱ）通过计算判断能否在犯错误的概率不超过2.5%的前提下认为数学对学生选择文理科有影响.附：22()()()()()n adbc K a b c d a c b d -=++++参考答案【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】由残差平方和越小，模型的拟合效果越好，可判断A ；由方差的性质可判断B ；由的随机变量2K 的观测值的大小可判断C ；由相关系数r 的绝对值趋近于1，相关性越强，可判断D .【详解】对于A ，可用残差平方和判断模型的拟合效果，残差平方和越小，模型的拟合效果越好，相关指数2R 越大，故A 错误；对于B ，将一组数据的每一个数据都加上或减去同一常数后，由方差的性质可得方差不变，故B 正确；对于C ，对分类变量X 与Y ，它们的随机变量2K 的观测值越大，“X 与Y 有关系”的把握程度越大，故C 错误；对于D ，若所有样本点均落在回归直线上，则相关系数1r =，故D 错误. 故选：B. 【点睛】本题考查命题的真假判断，主要是线性回归直线的特点和线性相关性的强弱、样本数据的特征值和模型的拟合度，考查判断能力，属于基础题．2．B解析：B 【分析】由已知求得x ，y ，代入2y ax =+求得a 值，则线性回归方程可求，取9x =求得y 值即可． 【详解】12342.54x +++==，1892130.7545105104y ⎛⎫=+++== ⎪⎝⎭，0.7520.52.5a -∴==-，则线性回归方程为0.52y x =-+， 取9x =，得50.5922y =-⨯+=-． 故选：B ． 【点睛】本题考查线性回归方程，明确线性回归方程恒过样本点的中心是关键，是基础题．3．C解析：C 【分析】根据相关系数的性质，r 的绝对值最大，则其拟合效果最好，进行判断即可． 【详解】线性回归分析中，相关系数为r ，r 越接近于1，相关程度越大；r 越小，相关程度越小，∵模型3的相关系数r 最大，∴模拟效果最好， 故选C ． 【点睛】本题主要考查线性回归系数的性质，在线性回归分析中，相关系数为r ，r 越接近于1，相关程度越大；r 越小，相关程度越小．4．D解析：D 【分析】求出样本数据的中心坐标(,)x y ，代入回归直线方程，求出ˆb，得到回归直线方程，然后求解加工20个零件所需要的加工时间，得到答案. 【详解】由题意，根据表中的数据，可得1(911141516)135x =++++=， 1(3032364042)365y =++++=，即样本中心点为(13,36)，将样本中心点为(13,36)代入回归方程，可得235361317b =⨯+，解得2917b =， 所以回归方程为292351717y x =+， 当20x时，292358152047.9848171717y =⨯+=≈≈（分钟）. 故选：D. 【点睛】本题主要考查了线性回归方程的求法及应用，其中解答中熟记回归直线方程经过样本中心点是解答的关键，着重考查推理与运算能力.5．B解析：B 【分析】计算2x =， 4.5y =，代入回归方程计算得到 2.6a =，再计算得到答案. 【详解】013424x +++==， 2.2 4.3 4.8 6.7 4.54y +++==，故4.50.952a =⨯+，解得2.6a =.当5x =，0.955 2.67.35y =⨯+=. 故选：B 【点睛】本题考查了回归方程的应用，意在考查学生的计算能力.6．B解析：B 【分析】计算出,x y 代入回归直线方程，求得a ，再令15x =求得预测值. 【详解】依题意 6.5,80x y ==，代入ˆˆ4=-+yx a 得80 6.54106a =+⨯=，即ˆ4106y x =-+，当15x =时，6010646y =-+=，故选B. 【点睛】本小题主要考查回归直线方程过样本中心点(),x y ，考查利用回归直线方程进行预测，属于基础题.7．D解析：D 【分析】运用相关系数、回归直线方程等知识对各个选项逐一进行分析即可 【详解】①相关系数r 用来衡量两个变量之间线性关系的强弱，r 越接近于1，相关性越强，故错误②回归直线y bx a =+一定经过样本点的中心()x y ，，故正确③随机误差e 满足()0E e =，其方差()D e 的大小用来衡量预报的精确度，故正确 ④相关指数2R 用来刻画回归的效果，2R 越大，说明模型的拟合效果越好，故错误 综上，说法正确的是②③ 故选D 【点睛】本题主要考查的是命题真假的判断，运用相关知识来进行判断，属于基础题8．A解析：A 【解析】分析：利用回归方程，计算3x =时，ˆy 的值，进而可求方程在样本()3,4处的残差． 详解：当3x =时，235ˆ1y=⨯-=， ∴方程在样本()3,4处的残差是451,-=- 故选A.点睛：本题考查线性回归方程的运用，考查学生的计算能力，属于基础题．9．C解析：C 【解析】对于①，在回归分析模型中，相关指数2R 表示解释变量x 对于预报变量y 的贡献率，2R 越接近于1，表示回归效果越好，正确，因为相关指数2R 越大，则残差平方和越小，模型的拟合效果越好，①正确．对于②两个变量相关性越强，则相关系数的绝对值就越接近于1；对于③在回归直线方程0.52y x ∧=-+中，当解释变量x 每增加一个单位时，预报变量y ∧平均减少0.5个单位；正确；对于④对分类变量X 与Y ，它们的随机变量2K 的观测值k 来说，k 越小，“X 与Y 有关系”的把握程度越大.错误，因为在对分类变量X 与Y 进行独立性检验时，随机变量2K 的观测值k 越大，则“X 与Y 相关”可信程度越大，故④错误； 故选C10．D解析：D 【分析】求出x ，代入ˆ 1.212yx =+，可得y ，则12345y y y y y ++++可求解. 【详解】由题中所给的点，可以求得24681065x ++++==，代入ˆ 1.212yx =+，可得 1.261219.2y =⨯+=， 所以12345519.296y y y y y ++++=⨯=， 故选：D. 【点睛】该题考查的是有关回归直线方程的应用，涉及到的知识点有回归直线过样本中心点，属于简单题目.11．C解析：C 【分析】 先求出5x =，245m y +=，再根据回归方程过样本中心，可求出参数m 的值. 【详解】 由题意可得2456855x ++++==，3 4.57.592455m m y +++++==，则241.0550.855m +=⨯+，解得 6.5m =. 故选：C. 【点睛】本题考查根据回归方程过样本中心求原始数据，注意不能将5x =代入回归方程求m 的值 ，属于中档题.12．B解析：B 【分析】计算出2K 的值，由此判断出正确结论的个数. 【详解】依题意()2210510302045 6.10930755055K ⨯⨯-⨯=≈⨯⨯⨯，故能在犯错误的概率不超过0.05的前提下认为药物有效, 不能在犯错误的概率不超过0.005的前提下认为药物有效,即①④结论正确，本小题选B. 【点睛】本小题主要考查22⨯列联表独立性检验，考查运算求解能力，属于基础题.13．A解析：A 【分析】根据相关系数知相关系数的性质：r 1≤，且r 越接近1，相关程度越大；且r 越接近0，相关程度越小.r 为正，表示正相关，回归直线方程上升，选出正确结果． 【详解】相关系数r 为正，表示正相关，回归直线方程上升， r 为负，表示负相关，回归直线方程下降，k ∴与r 的符号相同． 故选A ． 【点睛】本题考查用相关系数来衡量两个变量之间相关关系的方法，当相关系数为正时，表示两个变量正相关，当相关系数大于0.75时，表示两个变量有很强的线性相关关系．二、解答题14．（1）“数学学期综合成绩”与“物理学期综合成绩”高度相关；答案见解析；（2）分布列见解析，95. 【分析】（1）代入公式计算，解得0.8r >即可得解；（2）由超几何分布概率公式计算出(0)P X =、(1)P X =、(2)P X =、(3)P X =、(4)P X =，进而可得分布列，再由数学期望的公式即可得数学期望.【详解】（1）由题意，20()()ii xx y y r --==∑6260.87.515>==>=⨯=， 所以“数学学期综合成绩”与“物理学期综合成绩”高度相关； (2) 由题意得：X 的可能取值为0，1，2，3，4.，根据赋分规则可知，7人赋分为2，4人赋分为1，9个人赋分为0，所以9222036(0)190C P X C ===，49112203619(1)0C C P X C ===，2112204791609(29)C C C P X C +===，114722023810(9)C C P X C ===，27220(4)21190C P X C ===，所以X 的分布列为：所以190190190()012341901901905E X =⨯+⨯+⨯+⨯+⨯==. 【点睛】关键点点睛：解决本题的关键是对r 的值合理放缩及超几何分布的应用. 15．（1）0.30.4y x =-；（2）1.7 【分析】（1）根据数据，利用最小二乘法，即可求得y 对月收入x 的线性回归方程回归方程ˆˆyb =x ˆa +； （2）将x ＝7代入即可预测该家庭的月储蓄． 【详解】（1）由题意知，10101110,80,20ii i i n xy =====∑∑ ，80208,21010x y ∴==== ∴21082160,1064640n x y n x ⋅⋅=⨯⨯=⋅=⨯=1010211184,720i i ii i x y x ====∑∑ 由1221184160ˆ0.3720640ni ii nii x y nxybxnx ==--===--∑∑.ˆˆ20.380.4ay bx =-=-⨯=- 故所求回归方程为0.30.4y x =- （2）将7x =代入回归方程可以预测该家庭的月储蓄为0.370.4 1.7y =⨯-=（千元）. 【点睛】本题考查线性回归方程的应用，考查最小二乘法求线性回归方程，考查转化思想，属于中档题．16．（1）填表见解析，作图见解析（2）能在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关 【分析】（1）由题意计算出各组人数后即可完成列联表，进而可补全等高条形图； （2）代入公式计算出2K ，与3.841比较即可得出结论. 【详解】（1）根据题意填写列联表如下，选物理 不选物理 总计 数学成绩优秀 420 320 740 数学成绩不优秀 180 80 260 总计6004001000（2）计算222()1000(42080180320)()()()()600400740260n ad bc K a b c d a c b d -⨯⨯-⨯==++++⨯⨯⨯12.474 3.841≈>，所以能在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关. 【点睛】本题考查了独立性检验的应用，考查了计算能力，属于中档题.17．（1）ˆ3240yx =-+．. (2) 可以认为所得到的回归直线方程是理想的.(3) 该产品的销售单价定为7．5元/件时，获得的利润最大. 【解析】分析：（1）计算x 、y ，求出回归系数，写出回归直线方程；（2）根据回归直线方程，计算对应的数值，判断回归直线方程是否理想； （3）求销售利润函数W ，根据二次函数的图象与性质求最大值即可． 详解：（1）因为()()11995101051110,1110865855x =++++==++++=．．， 所以23925108325025510ˆb-⨯⨯==--⨯．．，则()ˆ8321040a =--⨯=．， 于是y 关于x 的回归直线方程为ˆ3240y x =-+．； （2）当8x =时， 32840144ˆy=-⨯+=．．，则14414045ˆ0y y -=-=<．．．， 所以可以认为所得到的回归直线方程是理想的； （3）令销售利润为W ，则()()22532403248100(25125)W x x x x x =--+=-+-<<．．．．．，因为()215321510032100802x x W x x -+⎛⎫=-+-≤⨯-= ⎪⎝⎭．．，当且仅当15x x =-+，即75x =．时， W 取最大值． 所以该产品的销售单价定为7．5元/件时，获得的利润最大． 点睛：本题考查了线性回归方程的求法与应用问题，属中档题． 18．（1）有（2）710p = 【分析】（1）根据题中数据得到列联表，然后计算出2K ，与临界值表中的数据对照后可得结论．（2）由题意得概率为古典概型，根据古典概型概率公式计算可得所求． 【详解】（1）根据已知数据得到如下列联表有兴趣 没有兴趣 合计 男 45 10 55 女 30 15 45 合计7525100由列联表中的数据可得因为，所以有90%的把握认为“对冰球是否有兴趣与性别有关”．(2)记5人中对冰球有兴趣的3人为A 、B 、C ，对冰球没有兴趣的2人为m 、n ， 则从这5人中随机抽取3人，所有可能的情况为：（A,m,n ）,（B,m,n ）,（C,m,n ）,（A,B,m ）,（A,B,n ）,（B,C,m ）,（B,C,n ）,（A,C,m ）,（A,C,n ）,（A,B,C ），共10种情况， 其中3人都对冰球有兴趣的情况有（A,B,C ），共1种，2人对冰球有兴趣的情况有（A,B,m ）,（A,B,n ）,（B,C,m ）,（B,C,n ）,（A,C,m ）,（A,C,n ），共6种，所以至少2人对冰球有兴趣的情况有7种， 因此，所求概率为710P =． 【点睛】由于独立性检验有其独特的作用，其原理不难理解和掌握，但解题时需要注意计算的准确性和判断的正确性，对独立性检验的考查多以解答题的形式出现，一般为容易题，多与概率、统计等内容综合命题．19．（1）作图见解析；（2）ˆ0.7 1.05yx =+；作图见解析；（3）8.05小时. 【分析】（1）利用描点法作图；（2）利用公式计算x ，y 及系数a ，b ，可得回归方程；（3）把10x =代入回归方程可得y 值，即为预测加工10个零件需要的时间． 【详解】解：（1）散点图如图（2）由表中数据得： 3.5x =， 3.5y =，4152.5i ii x y==∑，4215i xi ==∑，2252.54350.754435b -⨯⋅∴==-⨯⋅，3.50.7 3.5 1.05a ∴=-⨯=，ˆ0.7 1.05yx ∴=+．（3）将10x =代入回归直线方程，得ˆ0.710 1.058.05y =⨯+=， ∴预测加工10个零件需要8.05小时．【点睛】本题考查了回归分析，解答此类问题的关键是利用公式计算，计算要细心．20．（1）0.70.35y x =+；（2）19.65. 【分析】（1）由表中数据和参考公式即求线性回归方程； （2）根据（1）中的线性回归方程进行预测，即得答案. 【详解】（1）由表中数据可得3456 2.534 4.54.5, 3.544x y ++++++====. 1222441466.54 4.5 3.50.7864 4.5ˆ4i ii ii bx yxyx x ==--⨯⨯∴===-⨯-∑∑， ˆˆ 3.50.7 4.50.35ay bx =-=-⨯=. 所以线性回归方程为0.70.35y x =+.（2）由（1）知线性回归方程为0.70.35y x =+. 把100x =代入，得0.71000.3570.35y =⨯+=，所以生产100吨甲产品的生产能耗比技改前降低9070.3519.65-=吨标准煤. 【点睛】本题考查线性回归方程及其应用，属于中档题. 21．（1）d y c x =⋅更适合，13y e x =⋅；（2）2.7亿元 【分析】（1）根据散点图可直接判断回归类型d y c x =⋅更适合；对dy c x =⋅两边取对数得ln v c du =+，代入公式计算出d 、ln c 后即可得回归方程；（2）由题意1327z x x =-，求导后得出函数的单调性后即可得解. 【详解】（1）由散点图知，选择回归类型dy c x =⋅更适合，对dy c x =⋅两边取对数，得ln ln ln y c d x =+，即ln v c du =+，由表中数据得，122130.510 1.5 1.5146.510 1.5 1.53ni i i nii u v nuvd unu==--⨯⨯===-⨯⨯-∑∑，所以1ln 1.5 1.513c v du =-=-⨯=，所以c e =， 所以年研发费用x 和年销售量y 的回归方程为13y e x =⋅. （2）由（1）知1327z x x =-，求导得2391z x -'=-，令()23910z x x-'=-=，得27x =，函数1327z x x =-在()0,27上单调递增，在()27,+∞上单调递减， 所以当27x =时，年利润取最大值5.4亿元.故要使得年利润最大，预计下一年应投入2.7亿元研发费用. 【点睛】本题考查了非线性回归方程的求解和应用，考查了利用导数求函数的最值，属于中档题.22．（1） 1.7284ˆ.yx =+；（2）对数模型更合适；47.2万元. 【分析】（1）利用最小二乘法计算可得回归直线；（2）根据2R 的值，可确定对数模型更合适；将8x =代入模型求得y 即为所求结果. 【详解】（1）7121227727947842ˆ 1.7708787i i i i i y xyx x b x ==-⋅-⨯⨯===-⨯-∑∑，ˆˆ42 1.7828.4ay bx ∴=-=-⨯=， y ∴关于x 的线性回归方程为： 1.7284ˆ.y x =+.（2）0.970.75>，∴对数模型更合适.∴当广告费支出为8万元，即8x =时，销售额预测值12ln82236ln 222360.72247.2y =+=+≈⨯+=（万元）.【点睛】本题考查最小二乘法求解回归直线、相关指数的意义和预测值的求解问题；考查学生的计算和求解能力.23．列联表见解析，有99.9%的把握说选科与性别有关. 【分析】选物理的男生38人，则女士12人，选历史的男生14人，则女士36人，即可完成22⨯列联表，做出假设0H ：选科与性别没有关系，再由表中数据计算2K 的观测值，可得观测值大于10.828，所以在犯错误的概率不超过0.001的前提下认为选科与性别有关系，即有99.9%的把握有关系. 【详解】列出22⨯列联表如下：提出假设0：选科与性别没有关系.根据列联表中的数据计算2K的观测值2100(38361412)30023.0775248505013k ⨯⨯-⨯==≈⨯⨯⨯.因为10.828k ≥，所以有99.9%的把握说选科与性别有关. 【点睛】本题考查独立性检验的基本应用，属于中档题. 24．(1) 0.020.7x y e +=. (2) 正常的. 【分析】 （1）先求得x 及521ii x=∑,即可求得52215i i xx =-∑.代入线性回归方程中即可求得ˆb.再由ˆˆav b μ=-即可求得ˆa ,进而得回归方程. （2）根据回归方程及参考数据,即可求得该男生的体重,进而判断该体重是否位于平均值的1.2倍与0.8倍之间. 【详解】 （1）由已知可得80x =,()522221100671033000i i x ==⨯+++=∑∴5221533000320001000i i xx =-=-=∑又()51ln 940iii x y =⋅=∑,11.52.35v == ∴9405 2.380ˆ0.021000b-⨯⨯== ˆ 2.30.02800.7a=-⨯= 所以ln 0.020.7y x =+ ∴回归方程为：0.020.7x y e +=（2）当150x =时, 3.7ˆ40.5ye =≈, 而40.5 1.248.645⨯=>,40.50.832.445⨯=<,∴这一在校男生的体重是正常的. 【点睛】本题考查了非线性回归方程在实际问题中的应用,计算量较为复杂,需要耐心计算,属于中档题.25．（1）ˆ20200yx =-+；（2）6.5元. 【分析】（1）由题意计算平均数和回归系数，即可写出回归直线方程；（2）由题意写出收益函数P 的解析式，求出P 取最大值时对应的x 值即可． 【详解】解：（1）由题意得，x =16×（6+6.2+6.4+6.6+6.8+7）=6.5， y =16×（80+74+73+70+65+58）=70； 则()61()5 1.20.30 1.5614iii x x y y =--=------=-∑，621()0.250.090.010.010.090.250.7ii x x =-=+++++=∑；所以142007ˆ.b-==- ，() 7020 6.5200ˆˆa y bx =-=--⨯= 所以所求回归直线方程为20200ˆy x =-+． （2）由题意可得，()()()3202ˆ003P yx x x =-=-+-， 整理得P =-20（x -6.5）2+245， 当x =6.5时，P 取得最大值为245；所以要使收益达到最大，应将价格定位6.5元． 【点睛】本题考查了线性回归方程的求法与应用问题，也考查了计算与推理能力，是基础题． 26．（Ⅰ）见解析；（Ⅱ）见解析 【分析】（Ⅰ）根据题意，结合数据之间的关系，补全22⨯的列联表即可； （Ⅱ）计算观测值2K ，通过观测值表进行比较，即可得出结论. 【详解】（Ⅰ）根据数据关系，得22⨯的列联表如下：（Ⅱ）∵2250(2510510) 6.349 5.024********K ⨯-⨯=≈>⨯⨯⨯.故可以在犯错误的概率不超过2.5%的前提下认为数学对学生选择文理科有影响. 【点睛】该题考查的是有关独立性检验的问题，涉及到的知识点有补全列联表，判断能否在犯错误的概率不超过2.5%的前提下认为数学对学生选择文理科有影响，属于简单题目.。

高二物理选修3-3综合测试题答案和解析【答案】1 A2 C3 D4 D5 C6 B7 D8 A9 C10 A11 BDE12 ADE13 AD14 ABD15 BCE16 解：(i)打开K2之前,A缸内气体p A=3p0,B缸内气体p B=p0,体积均为V,温度均为T=(273+27)K=300K,打开K2后,B缸内气体(活塞上方)等温压缩,压缩后体积为V1,A缸内气体(活塞下方)等温膨胀,膨胀后体积为2V−V1,活塞上下方压强相等均为p1,则：对A缸内(活塞下方)气体：3p0V=p1(2V−V1),对B缸内(活塞上方)气体：p0V=p1V1,联立以上两式得：p1=2p0,V1=12V；即稳定时活塞上方体积为12V,压强为2p0；(ⅱ)打开K3,活塞上方与大气相连通,压强变为p0,则活塞下方气体等温膨胀,假设活塞下方气体压强可降为p0,则降为p0时活塞下方气体体积为V2,则3p0V=p0V2,得V2=3V>2V,即活塞下方气体压强不会降至p0,此时活塞将处于B气缸顶端,缸内气压为p2,3p0V=p2×2V,得p2=32p0,即稳定时活塞位于气缸最顶端；(ⅱ)缓慢加热汽缸内气体使其温度升高,等容升温过程,升温后温度为T3=(300+20)K=320K,由p2T =p3T3得：p3=1.6p0,即此时活塞下方压强为1.6p0。

答：(i)打开K2,稳定时活塞上方气体的体积为12V,压强为2p0；(ii)打开K3,稳定时位于气缸最顶端；(iii)缓慢加热汽缸内气体使其温度升高20℃,此时活塞下方气体的压强为1.6p0。

17 解：(1)初态压强P1=(76−16)cmHg末态时左右水银面的高度差为：(16−2×3)cm=10cm末状态压强为：P 2=(76−10)cmHg =66cmHg 由理想气体状态方程得：P 1V 1T 1=P 2V 2T 2解得：T 2=P 2V2P 1V 1T 1=66×2560×22×280K =350K(2)加注水银后,左右水银面的高度差为：由玻意耳定律得,P 1V 1=P 3V 3,其中P 3=76−(20−l ) 解得：l =10cm18 解：U 形管两边水银面的高度差为△ℎ=25cmA 种气体的压强为：P A1=P 0+△ℎ=75+25cmHg =100cmHgB 中为大气,设活塞产生压强为P 塞,由平衡得：P 0S +P 塞S =P A1S解得：P 塞=25cmHg闭合阀门,容器内温度降低,压强均减小且A 处降低较多,活塞下移 设此时表示A 种气体的压强为P A2=P 0−25=75−25cmHg 由理想气体状态方程得：P A1L A1S T 1=P A2L A2S T 2解得：L A2=P A1L A1T 2P A2T 1=100×50×(273−57)50×300cm =72cm >50cm假设不成立,说明U 管表示的应该是B 种气体的压强,P B2=50cmHg则A 种气体压强为：P A2=P B2+P 塞=75cmHg对A 种气体由理想气体状态方程得：P A1L A1S T 1=P A2L A2S T 2代入数据解得：L A2=48cm活塞离容器底部的高度为：L′=L A2=48cm (2)对B 中气体由理想气体状态方程得：P B1L B1ST 1=P B2L B2S T 2设整个柱形容器的高度H ,则P B1(H−L A1)ST 1=P B2(H−L A2)ST 2代入数据解得：H=75cm答：(1)此时活塞离容器底部高度L′=48cm；(2)整个柱形容器的高度H=75cm。

高二选修3化学练习册答案化学是研究物质的组成、结构、性质以及变化规律的科学。

在高二选修3化学课程中，我们深入探讨了化学反应的基本原理、有机化学的基础以及化学实验技能。

以下是高二选修3化学练习册的部分答案，供同学们参考。

一、选择题1. 以下哪种物质不是有机化合物？A. 甲烷B. 乙醇C. 尿素D. 碳酸钙答案：D2. 根据勒夏特列原理，当一个平衡系统受到外部条件的改变时，系统将如何调整自身以减弱这种改变？A. 向正反应方向移动B. 向逆反应方向移动C. 保持不变D. 随机移动答案：B二、填空题1. 有机化学反应中，取代反应是指_________。

答案：一个原子或原子团被另一个原子或原子团替换。

2. 根据化学平衡常数的定义，当一个化学反应达到平衡时，反应物和生成物的浓度比值是一个常数，这个常数被称为_________。

答案：化学平衡常数。

三、简答题1. 请简述什么是同分异构体，并给出一个例子。

答案：同分异构体是指具有相同分子式但结构不同的化合物。

例如，正丁烷和异丁烷都是C4H10的同分异构体，但它们的分子结构不同。

2. 什么是酸碱中和反应？请举例说明。

答案：酸碱中和反应是指酸和碱在一定条件下反应生成盐和水的过程。

例如，盐酸（HCl）与氢氧化钠（NaOH）反应生成氯化钠（NaCl）和水（H2O）。

四、计算题1. 已知某化学反应的平衡常数Kc=1.2×10^-5，反应物A的初始浓度为0.1M，求平衡时A的浓度。

答案：设平衡时A的浓度为x M，根据平衡常数的定义，有Kc = [A]/[B]，其中[B]为生成物的浓度。

由于反应物和生成物的摩尔比为1:1，我们可以设[B] = x M。

代入Kc的值，解得x = √(Kc *[A]_initial) = √(1.2×10^-5 * 0.1) ≈ 0.01 M。

结束语化学是一门实验性很强的学科，通过习题的练习，我们不仅能够巩固理论知识，还能够提高解决实际问题的能力。

高中物理选修33课后习题和答案以及解释第一题：习题：一个物体以 3 m/s的速度水平移动，冲破一块墙，两秒钟后，墙壁的碎片垂直抛向天空并上升了2 m。

求墙壁的高度。

解答：首先，物体在两秒钟内水平移动的距离可以用速度和时间的关系来计算：移动距离=速度×时间=3 m/s × 2 s = 6 m。

墙壁的高度可以通过求解墙壁碎片的垂直抛体运动来确定。

根据抛体运动的公式 h = v0t - 1/2gt^2，其中h为高度，v0为初速度，t为时间，g为重力加速度。

题目中已经给出了碎片上升的高度为2 m，所以可以得到方程 2 =v0 × 2 - 1/2 × 9.8 × (2^2)。

解方程可得 v0 = 2 m/s。

由于物体在冲破墙壁前以3 m/s的速度水平移动，那么碎片的初速度等于物体的速度，即v0 = 3 m/s。

因此，墙壁的高度为：高度 = 速度 ×时间 = 3 m/s × 2 s = 6 m。

答案：墙壁的高度为6米。

第二题：习题：一个质量为1 kg的物体以4 m/s的速度水平运动到达一个下降斜面，在斜面上下滑动并到达斜面底部。

斜面倾角为30°，摩擦系数为0.2。

求物体下滑的距离。

解答：首先，我们可以根据斜面的倾角来确定斜面的高度和长度的比例关系。

对于一个倾角为30°的斜面，它的高度和长度的比例关系是1：√3。

所以，斜面的高度可以表示为h = l × √3，其中h为高度，l为长度。

接下来，我们需要计算物体在斜面上受到的重力和摩擦力。

摩擦力可以通过将重力分解为斜面和垂直于斜面的两个力来计算。

首先，我们计算物体在斜面上受到的垂直于斜面的重力分量，即Fv = m × g × cosθ，其中m为质量，g为重力加速度，θ为斜面的倾角。

然后，我们计算物体在斜面上受到的平行于斜面的重力分量，即Fp = m × g × sinθ。

数学高二选修三练习题高二数学选修三练习题1. 解析几何1.1 平面与空间直线相交的情况在解析几何中，平面和空间直线的相交情况有三种：相交于一点、平行、重合。

1.2 直线与平面的位置关系一条直线与平面的位置关系有四种情况，即相交、平行、重合和垂直。

1.3 直线与平面的距离直线与平面之间的距离可以通过现场求解或公式计算得出。

2. 二次函数2.1 二次函数的图像二次函数的图像是一个开口朝上或朝下的抛物线。

2.2 二次函数的性质二次函数的性质包括单调性、最值等，可以通过导数或求解二次函数的顶点得到。

2.3 二次函数的应用二次函数可以应用于物理、经济等问题中，例如求解最值、模型拟合等。

3. 概率3.1 事件与概率概率是描述事件发生可能性的数值，可以通过实验、频率定义或几何概率等方法计算。

3.2 基本概率公式基本概率公式包括加法公式和乘法公式，可用于计算复合事件的概率。

3.3 排列组合与概率概率与排列组合密切相关，可以通过排列组合的知识解决概率问题。

4. 统计与概率4.1 统计中的常用概念统计中常用的概念包括频数、频率、平均数、中位数等，可以用于描述和分析数据集。

4.2 正态分布正态分布是一种连续型随机变量的概率分布，具有钟型对称曲线特点。

4.3 抽样与估计通过抽样和估计可以根据样本数据估计总体的参数，如均值、比例等。

5. 三角函数5.1 三角函数的定义与性质三角函数包括正弦、余弦、正切等，具有周期性和对称性等性质。

5.2 三角函数的图像与变换通过对三角函数进行平移、伸缩等变换，可以得到不同的图像。

5.3 三角函数的应用三角函数在物理、工程等领域有广泛的应用，如模拟波动、测量高度等。

总结：数学高二选修三练习题涵盖了解析几何、二次函数、概率、统计与概率以及三角函数等知识点。

对于高中数学学习者来说，通过练习这些题目可以巩固基础知识，提高解题能力。

高二化学选修3第三章测试题：晶体结构与性质第Ⅰ卷（选择题共70分）一、选择题(本题包括10小题，每小题3分，共30分。

每小题只有一个选项符合题意)．．．．1.晶体与非晶体的严格判别可采用A. 有否自范性B.有否各向同性C.有否固定熔点D.有否周期性结构2．某离子化合物的晶胞如右图所示立体结构，晶胞是整个晶体中最基本的重复单位。

阳离子位于此晶胞的中心，阴离子位于8个顶点，该离子化合物中，阴、阳离子个数比是A、1∶8B、1∶4C、1∶2D、1∶13、共价键、离子键和范德华力是构成物质粒子间的不同作用方式，下列物质中，只含有上述一种作用的是A.干冰B.氯化钠C.氢氧化钠D.碘4、石墨晶体是层状结构，在每一层内；每一个碳原于都跟其他3个碳原子相结合，如图是其晶体结构的俯视图，则图中7个六元环完全占有的碳原子数是A.10个B.18个C.24个D.14个5、关于晶体的下列说法正确的是A、在晶体中只要有阴离子就一定有阳离子B、在晶体中只要有阳离子就一定有阴离子C、原子晶体的熔点一定比金属晶体的高D、分子晶体的熔点一定比金属晶体的低6、金属的下列性质中，不能用金属的电子气理论加以解释的是A．易导电B．易导热C．有延展性D．易锈蚀7、金属能导电的原因是A.金属晶体中金属阳离子与自由电子间的相互作用较弱B．金属晶体中的自由电子在外加电场作用下可发生定向移动C．金属晶体中的金属阳离子在外加电场作用下可发生定向移动D ．金属晶体在外加电场作用下可失去电子8、由钾和氧组成的某种离子晶体中含钾的质量分数为78/126，其阴离子只有过氧离子(O 22－)和超氧离子(O 2－)两种。

在此晶体中，过氧离子和超氧离子的物质的量之比为 A. 2︰1 B. 1︰1 C . 1︰2 D. 1︰39．食盐晶体如右图所示。

在晶体中，· 表示Na +，o 表示Cl -。

已知食盐的密度为r g / cm 3，NaCl 摩尔质量M g / mol ，阿伏加德罗常数为N ，则在食盐晶体里Na +和Cl -的间距大约是A.32NMρcm B. 32N Mρcm A.32MNρcm D. 38NMρcm10、1mol 气态钠离子和1mol 气态氯离子结合生成1mol 氯化钠晶体释放出的热能为氯化钠晶体的晶格能。

统编版(2019)选择性必修3高二下学期第三单元达标检测卷历 史注意事项：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，考生务必将自己的姓名、考生号填写在答题卡上。

2、回答第Ⅰ卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在试卷上无效。

3、回答第Ⅱ卷时，将答案填写在答题卡上，写在试卷上无效。

4、考试结束，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题）本卷共24个小题，每小题2分，共48分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．“美索不达米亚历史，在很大程度上也就是来自北面的入侵者印欧人与来自南面的入侵者闪米特人为争夺这块肥沃的大河流域地区而展开长达数千年的斗争的历史。

”此观点强调了（ ） A ．人类文明的冲突 B ．古代战争的目的 C ．地理环境的影响 D ．历史形成的残酷2．为了新月地带的城市和尼罗河谷的沃野而抛弃荒凉沙漠的困苦生活，阿拉伯人勇往直前。

当时的一个阿拉伯诗人写道：“你抛弃自己的故乡，不是为了寻找天堂。

却是那面包和椰枣，把你吸引到了远方。

”由此可见，驱动阿拉伯帝国向外扩张的原因主要是（ ） A ．解决粮食问题 B ．经济利益驱使 C ．传播伊斯兰教 D ．商业活动需要3．美国亨廷顿教授的《文明的冲突与世界秩序的重建》中指出“1965年希望减少美国移民的人只占美国人口的33%，1977年占42%，1986年占49%，在1990年和1993年占61%。

90年代的民意测验持续表明60%或以上的美国公众赞同减少移民人数。

”这种现象出现的主要原因是（ ）A ．在这一时期美国人口增长过快，财政负担加重B ．大量移民与美国公众在文化和生活上的冲突扩大C ．移民增多导致美国社会贫富差距扩大，D ．美国政府推行的歧视性移民政策的影响4．截至目前，在美的非法移民已达1100万之多。

2015年，美国公布的研究报告显示，排除通胀等其他因素，1990年至2013年，没有高中文凭的美国男性收入降低了20%，仅有高中文凭的美国男性收入也降低了13%。

高二物理选修3-3模块考试试题一、单项选择题（每小题4分，共16分。

在每小题给出的四个选项中，只有一个选项正确，选对的得3分，选错或不答的得0分）13、布朗运动是说明分子运动的重要实验事实,布朗运动是指（）A、液体分子的运动B、悬浮在液体中的固体分子运动C、悬浮在液体中的固体微粒的运动D、液体分子与固体分子的共同运动14、分子间的相互作用力由引力f引和的斥力f斥两部分组成，则（）A、f斥与f引都随分子间距离增大而减小B、f斥与f引都随分子间距离增大而增大C、分子间距离增大时，f引增大，f斥减小D、分子间距离增大时，f引减小，f斥增大15、液体表面具有收缩的趋势，其原因是（）A、由于液体表面分子间距离小于液体内部分子间的距离，液面分子间表现为引力，所以液体表面具有收缩的趋势B、由于液体表面分子间的距离大于液体内部分子间的距离，液面分子间表现为引力，所以液体表面具有收缩的趋势C、由于液体表面的分子受到外部空气分子的吸引力，所以液体表面具有收缩的趋势D、因液体具有流动性，所以液体表面具有收缩的趋势16、汽车关闭发动机后恰能沿斜坡匀速下滑，在这过程中（）A、汽车的机械能守恒B、汽车的动能和势能相互转化C、机械能转化为内能，总能量守恒D、机械能和内能之间没有转化二、双项选择题（每小题6分，共30分。

在每小题给出的四个选项中，有二个选项正确，选对的得6分，选错或不答的得0分，选对但不全得3分）17、甲、乙两种薄片的表面分别涂有薄薄的一层石蜡，然后用烧热的钢针的针尖分别接触这两种薄片，接触点周围熔化了的石蜡分别形成如图所示形状。

对这两种薄片，下列说法正确的是（）A、甲的熔点一定高于乙的熔点B、甲一定是晶体C、乙一定是晶体D、甲具有各向异性，乙具有各向同性。

18、下列关于热现象的说法，正确的是（）A、对于同一种液体，饱和汽压随温度升高而增大B、自然界中进行的涉及热现象的宏观过程都具有方向性C、当两个分子间的距离为r0(平衡位置)时，分子力为零，分子势能为零。