数的认识(数的分类)
- 格式:ppt
- 大小:637.00 KB
- 文档页数:13

数的认识与理解数的分类与辨认数的认识与理解数的分类与辨认数的认识与理解对于孩子来说是数学学习的基础,也是日常生活中必不可少的技能。
通过数的分类与辨认,孩子可以准确地描述和表达数量,有助于培养他们的逻辑思维和分析能力。
下面将从数的认识与理解以及数的分类与辨认两个方面进行详细论述。
一、数的认识与理解数是描述对象数量的符号,是数学中的基本概念。
孩子初识数时,可以通过数的物质表示进行感知与认识,例如手指、计数棒、计数球等。
逐渐地,他们将会明白数是一种抽象的概念,可以用符号来表示。
数的认识与理解主要包括以下几个方面:1. 数的概念:孩子需要了解数是用来计数和比较数量大小的,以及数的基本性质,如加法、减法、乘法和除法等运算规则,通过这些基本概念的学习,孩子能够根据实际情况进行数的运算和应用。
2. 数的顺序:孩子需要学会按照顺序排列数,如1、2、3……,这可以通过数数游戏和儿歌等方式进行学习,提高他们的观察力和记忆力。
3. 数的大小比较:孩子需要学会将数进行大小比较,了解数的大小关系,如大于、小于和等于等,这可以通过实际物品的比较和游戏等方式进行学习。
二、数的分类与辨认数的分类与辨认是在数的认识与理解的基础上进行的。
孩子需要学会将不同的数进行分类,并能够准确地辨认数的类型。
下面将介绍一些常见的数的分类与辨认方法:1. 自然数:自然数是最基础的数,包括正整数和零。
孩子可以通过数数游戏和计算题等方式学习自然数,了解数字的排列规律和数的性质。
2. 整数:整数是包括正整数、零和负整数的数,孩子可以通过温故知新、拓展学习的方式来认识整数。
例如,通过观察温度计的标度和海拔高度的正负等,深入理解整数的概念和作用。
3. 分数:分数是指除法的结果,由分子和分母表示,孩子可以通过将物品进行分割和分数的比较等方式,来了解分数的用途和特点。
4. 小数:小数是包含整数部分和小数部分的数,可以用于表示不完整的数量。
例如表示身高、体重、时间等,孩子可以通过量化的方式来认识小数,了解数与实际情况的对应关系。

数的认识(一)数的分类数的分类是数学中一个基础概念,从分类来概括和进行比较,是对更深入研究和理解数数学性质的必要条件。
由于数的特点不同,因此一般分为实数、复数、有理数、无理数、自然数、整数、质数等数分类。
1.实数:实数的单位是有限的几何空间,体现在坐标系中就是点,实数就是指坐标系中所有的点,如自然数、有理数、无理数和無穷大的数都可以看作实数。
2.复数:复数就是有实数部分和虚数部分的数,在复平面上表示,舍入它们都是以实数部分为中心的点,它们总是和虚数部分搭配使用,而虚数部分永远为负,复数就是一组由实数部分、虚数部分及它们搭配组成的一组复数值。
3.有理数:有理数就是存在有理数分母的数,它包括有理数的分母可以是正数,也可以是负数,可以是整数也可以是分数,有理数比任何数位任何有限阶梯小,根据有理数的不同表示,它可以是有穷小数、无穷小数或有限小数。
4.无理数:无理数就是不能用有理数表示的数,它可以是有穷无理数,也可以是无穷无理数,通常以π 和e 为代表,5.自然数:自然数是一类有体系性(线性)规律的数字,从1 开始相继往下编号,就像是一个无止尽排成的序列,它不仅可以表示某一数量的个体,也可以用来指代人们在日常生活中所理解的数量,比如1 个猫、2 根棍子、3 个人等。
6.整数:整数是自然数、零以及负数之和,它们具有丰富的性质,诸如加法,减法,乘法,级,具有某种内在联系,大多数概念都与整数有关,即所有数学中的研究与整数有着密切的关系。
7.质数:质数是指除了1 和其本身外,不能被其他自然数整除的数,质数通常可以视为两个正整数a 和b 的乘积,如2*3=6,若6 这个数不再可以分解出其他自然数的乘积,我们就称它为质数。
质数又分为永质数,有理质数,无理质数等,它们也具有各自的特性和出现规律。

探索数字世界认识数的概念和分类数字世界中,数的概念和分类扮演着重要的角色。
数被广泛用于计量、计算、统计和表达各种现象,对我们的生活和社会发展具有重要影响。
本文将探索数字世界中数的概念和分类,以帮助读者更好地理解和应用数。
一、数的概念数是一种用于表示数量、度量、排序和比较的概念。
在数字世界中,数被用于描述和计算各种事物的属性和特征。
数的概念包括以下几个方面:1.1 数的基本属性数具有基本属性,包括整数、分数、小数、负数、正数、零等。
整数是自然数和它们的负数及零的集合,用于表示不具体大小的数量。
分数和小数用于表示部分或部分之间的比例关系。
负数和正数用于表示相对的增减。
零表示没有数量的概念。
1.2 数的符号表示在数字世界中,数通过符号来表示。
一般使用阿拉伯数字和特定的符号来表达数的概念。
阿拉伯数字包括0、1、2、3、4、5、6、7、8、9,通过不同组合可以表示不同的数值。
符号用于表示数的正负,以及数的大小关系。
1.3 数的运算规则数的概念还涉及到数的运算规则,包括加法、减法、乘法、除法等。
这些运算规则用于计算和改变数的大小和关系。
数的运算规则是数学的基础,人们通过运算规则进行数的计算和推导。
二、数的分类数的分类是根据不同属性和应用进行的。
在数字世界中,数可以根据以下几个方面进行分类:2.1 自然数自然数是最基本的数,包括0和正整数。
自然数用于计数和排序,表示数量和次序的概念。
自然数可以进行加减运算,但不能进行除法运算。
2.2 整数整数是包括自然数、负整数和零的集合。
整数用于表示相对的增减关系,可以进行加减运算和乘法运算。
整数在财务、经济、统计等领域应用广泛。
2.3 分数分数是用于表示部分或部分之间的比例关系的数。
分数由分子和分母组成,分子表示部分的数量,分母表示整体的数量。
分数可以进行加减乘除运算,用于计算比例、比率、概率等。
2.4 小数小数是用于表示数的一部分或一部分数量的数。
小数由整数部分和小数部分组成,小数部分表示小数点后的位数。

知识要点知识点1数的意义及分类过程讲解1.数的分类。
重点提示小学阶段学过的数都可以在直线上表示出来。
2.整数的意义:像…,-3,-2,-1,0,1,2,3,…这样的数统称为整数。
整数的个数是无限的。
没有最小的整数,也没有最大的整数。
3.正整数和负整数的意义:像1,2,3,4,…这样的数叫做正整数;像 -1,-2,-3,-4,…这样的数叫做负整数。
正整数和负整数的个数都是无限的,其中最小的正整数是1,最大的负整数是-1。
4.自然数的意义:在数物体个数时,用来表示物体个数的1,2,3,4,5,…叫做自然数。
一个物体也没有用0表示。
自然数的个数是无限的。
最小的自然数是0,没有最大的自然数。
自然数是整数的一部分。
重点提示0表示一个物体也没有;表示正、负数的分界;表示起点(如0刻度);计数时,0起占位作用。
(1)一个自然数有两方面的意义:一是表示事物的多少,称为基数;二是表示事物的次序,称为序数。
如“3个学生”中的“3”是基数,“第3个学生”中的“3”是序数。
(2)自然数的单位:任何非0自然数都是由若干个“一”组成的,所以“一”是自然数的单位。
5.正数和负数的意义:像+16,2000,,6.3,…这样的数叫做正数,像-16,-500,,-0.4,…这样的数叫做负数。
0既不是正数,也不是负数。
6.分数的意义:把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数。
(1)分数单位:把单位“1”平均分成若干份,表示这样一份的数就是这个分数的分数单位。
一个分数的分母是几,它的分数单位就是几分之一;分子是几,它就有几个这样的分数单位。
(注意:带分数只有化成假分数后,它的分子才能表示这个带分数含有分数单位的个数)(2)分数的分类。
真分数:分子比分母小的分数叫做真分数。
真分数小于1。
假分数:分子比分母大或分子和分母相等的分数叫做假分数。
假分数大于或等于1。
带分数是大于1的假分数的另一种表示形式。
7.百分数的意义:表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。


数的认识知识点整理一、什么是数?数是用来表示事物数量或顺序关系的抽象概念。
数在人类社会的发展中起到了重要的作用,它是计算、测量和描述事物的基础。
二、数的分类数可以分为自然数、整数、有理数和实数等几个不同的分类。
2.1 自然数自然数是最早出现的数的概念,包括了0和正整数。
自然数用来表示物体的个数或事物的顺序。
例如,1代表第一个、2代表第二个,以此类推。
2.2 整数整数是自然数的扩展,它不仅包括了自然数,还包括了负整数。
整数可以表示具有相反意义的数量,例如欠债、温度等。
2.3 有理数有理数是指可以表示为两个整数的比值的数,包括了整数和带分数。
有理数可以用来表示可量度的量,例如长度、时间、质量等。
2.4 实数实数是数的最广泛的分类,包括了所有的有理数和无理数。
实数可以用来表示点的位置、图形的大小等连续的量。
三、数的运算数的运算是对数进行加、减、乘、除等基本操作的过程。
数的运算有一定的规则和性质。
3.1 加法和减法加法是将两个数合并在一起,减法是从一个数中减去另一个数。
加法和减法是相反的运算,可以互相抵消。
3.2 乘法和除法乘法是将两个数相乘得到一个新的数,除法是将一个数分成若干份。
乘法和除法也是相反的运算,可以互相抵消。
四、数的性质数的性质描述了数在运算中的一些特点和规律。
4.1 交换律加法和乘法满足交换律,即两个数交换位置结果不变。
例如,a + b = b + a。
4.2 结合律加法和乘法满足结合律,即三个数进行运算时,先进行两个数的运算,再与第三个数进行运算结果不变。
例如,(a + b) + c = a + (b + c)。
4.3 分配律乘法对加法满足分配律,即一个数与两个数的和相乘,等于这个数与每个数分别相乘再求和。
例如,a × (b + c) = a× b + a × c。
五、数的比较数的比较是通过比较数的大小来确定它们的关系。
5.1 大于、小于和等于对于任意两个数a和b,如果a大于b,可以表示为a > b;如果a小于b,可以表示为a < b;如果a等于b,可以表示为a = b。

小学二年级数学数的认识数学是一门抽象而又有趣的学科,它在我们生活中无处不在。
对于小学二年级的孩子来说,数学的学习尤为重要,因为这是他们开始接触基础数学概念的时候。
在本文中,我们将探讨小学二年级学生对数的认识与理解。
1. 数的概念数是数学的基础,不同的数有不同的含义和用途。
在小学二年级阶段,孩子们需要从简单到复杂、从具体到抽象的认识和理解数的概念。
他们需要学会认识数字,并能够用数字表示数量、排序和比较物体的大小。
2. 数的分类数可以分为自然数、0和整数。
在小学二年级,孩子们主要学习自然数和0的概念。
自然数包括1、2、3等正整数,它们用于计数。
而0是一个特殊的数字,表示没有任何东西。
通过对自然数和0的学习,孩子们可以逐渐形成对数的概念和认识。
3. 数的运算数的运算是数学学习的核心内容之一。
在二年级阶段,孩子们开始学习简单的加法和减法。
他们需要学会通过数的运算来解决实际问题,同时也需要理解运算符号的含义和使用方法。
4. 数的比较数的比较是数学中的重要概念之一。
在小学二年级,孩子们需要学会使用“大于”、“小于”和“等于”等比较符号来比较数的大小。
通过比较数的大小,孩子们可以培养对数量关系的敏感性,并能够在实际问题中进行正确的判断和分析。
5. 数的应用数学的应用在我们的日常生活中无处不在。
在小学二年级,孩子们需要学会将数学知识应用到实际问题中。
他们可以通过数的认识和理解来解决日常生活中的计数、排序和比较等问题,提高解决问题的能力。
总结:小学二年级是孩子们接触数学的重要阶段,他们需要从简单到复杂、从具体到抽象的学习和认识数的概念。
通过对数的认识和理解,孩子们能够培养逻辑思维和分析问题的能力,为将来学习更高级的数学知识奠定基础。
数学的学习应该注重培养孩子们的兴趣和动手能力,通过实际问题的解决来提高他们的数学思维能力。
希望孩子们在小学二年级的数学学习中能够取得良好的成绩,并对数学充满热爱和兴趣。

数的认识与分类在日常生活中,我们经常接触到各种各样的数字和数值。
无论是计算购物清单上的商品总价,还是统计某个城市的人口数量,我们都需要运用数的知识和技巧。
数的认识与分类是数学学习的基础,掌握好这一基础知识对于后续数学学科的学习和应用至关重要。
一、数的基本认识1. 数的概念数是用来计数和表示数量关系的概念。
数是人们对客观事物数量的抽象和反映,它通过符号的方式来表示。
我们常见的数包括自然数、负整数、分数、小数、百分数等。
2. 数的表达方式数的表达方式有多种,在不同的情境中使用不同的表示方法。
比如,我们可以使用阿拉伯数字(例如1、2、3)或罗马数字(例如Ⅰ、Ⅱ、Ⅲ)来表示整数;使用分数形式(例如1/2、3/4)或小数形式(例如0.25、0.75)来表示部分或分数;使用百分数形式(例如50%、75%)来表示比例关系等。
二、数的分类1. 自然数自然数是最早被人们认识和使用的数,它包括0和比0大的正整数。
自然数用来计数,表示数量。
例如:1、2、3、4、5...整数包括自然数、0和负整数。
整数可以表示有向量的大小和方向。
例如:...-3、-2、-1、0、1、2、3...3. 分数分数是用来表示整体中的一部分,它由一个分子和一个分母构成,分子表示整体的一部分,分母表示整体被分成了几个等分。
例如:1/2、3/4、5/8...4. 小数小数是一种十进制分数,分母为10的正整数或10的幂次。
小数可以表示整体中更精确的一部分。
例如:0.5、0.75、0.125...5. 负数负数是小于0的整数,它表示相反的概念或方向。
负数在数轴上位于原点左侧。
例如:-1、-2、-3...6. 百分数百分数是一种特殊的分数,分母为100,分子表示相对于100的比例关系。
百分数经常用来表示比例、增减等情况。
例如:50%、75%、80%...三、数的运算了解数的分类之后,我们需要学习数的运算,即对数进行加减乘除等基本运算。
加法是将两个或多个数按照一定的规则相加得到一个和的过程。


数字的魔力认识数的分类和大小关系数字的魔力:认识数的分类和大小关系数字在我们生活中无处不在,它们是我们思考、交流和计算的基础。
数字的魔力在于它们能够帮助我们认识世界,了解事物的分类和大小关系。
本文将探讨数字的分类和大小关系,带领读者一起揭开数字的奥秘。
一、自然数与整数数字的最基本分类是自然数和整数。
自然数是指从1开始,依次往后无限延伸的数,用符号“N”表示。
自然数包括1、2、3、4等等。
当我们需要处理比自然数更小的数时,就会引入负数,形成整数集合。
整数是包括自然数和负数的数集,用符号“Z”表示。
整数集合包括-3、-2、-1、0、1、2、3等等。
整数的大小关系通过绝对值来判断,绝对值越大,整数的大小就越大。
二、有理数与无理数有理数是可以表示为两个整数的比的数,用符号“Q”表示。
有理数包括整数和分数,例如-3、0、1/2、3等等。
有理数的大小关系可以通过分数的大小关系来确定,分数的分子越大,大小越大。
与有理数相对的是无理数,它们不能被表示为两个整数的比。
无理数包括像π(圆周率)和√2(根号2)这样的数。
无理数的大小关系往往需要借助近似值来判断。
三、实数与虚数实数是包括有理数和无理数的数集,用符号“R”表示。
实数包括所有可能的数,例如整数、分数、无理数等。
实数的大小关系可以直接通过数轴上的位置来判断,数轴上靠右的数字更大。
虚数是形如a+bi的数,其中a和b是实数,i是虚数单位,定义为√(-1)。
虚数由实部和虚部组成,无法直接比较大小,因此虚数没有大小关系。
四、小数与百分数小数是指整数和分数之间的数,它们以小数点作为分隔符。
小数可以用于表示实数的一部分,例如0.5、0.25等等。
小数的大小关系可以通过数的大小和小数点后的位数来判断。
百分数是百分之一的数,用百分号“%”表示。
百分数常用于表示比例和增减情况。
百分数的大小关系可以通过比较百分数的数值大小来确定。
总结起来,数字的分类和大小关系涵盖了自然数、整数、有理数、无理数、实数、虚数、小数和百分数等多个概念。
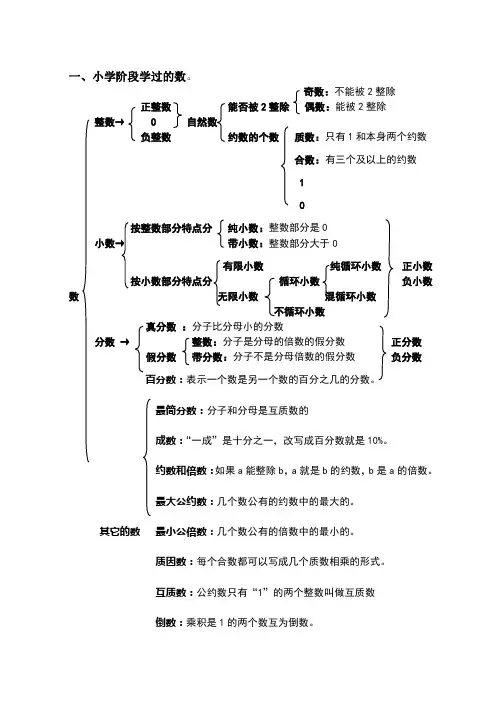
一、小学阶段学过的数。
奇数:不能被2整除正整数能否被2整除偶数:能被2整除整数→ 0 自然数负整数约数的个数质数:只有1和本身两个约数合数:有三个及以上的约数1按整数部分特点分纯小数:整数部分是0小数→带小数:整数部分大于0有限小数纯循环小数正小数按小数部分特点分循环小数负小数数无限小数混循环小数不循环小数真分数:分子比分母小的分数分数→整数:分子是分母的倍数的假分数正分数假分数带分数:分子不是分母倍数的假分数负分数百分数:表示一个数是另一个数的百分之几的分数。
最简分数:分子和分母是互质数的成数:“一成”是十分之一,改写成百分数就是10%。
约数和倍数:如果a能整除b,a就是b的约数,b是a的倍数。
最大公约数:几个数公有的约数中的最大的。
其它的数最小公倍数:几个数公有的倍数中的最小的。
质因数:每个合数都可以写成几个质数相乘的形式。
互质数:公约数只有“1”的两个整数叫做互质数倒数:乘积是1的两个数互为倒数。
2、整数和小数数位顺序表3、数的读写二、练习。
(一)、观察下面的数,然后归类。
8844.43、-1623、 40%、53、 1、-32、-3.5、 25、 0、8907 自然数: 负数: 整数: 小数: 分数: 百分数:(二)、在数轴上表示下面各数。
-121,43,3.5,-2.5, -3,1,-1(三)、填空。
1、最小的质数是(),最小的合数是()。
2、()既不是质数也不是合数。
()既不是正数也不是负数。
3、100内的质数共有()个,100内,最小质数与最小质数的和是()。
4、自然数的基本单位是(),最小的自然数是()。
5、最小的奇数是(),最小的偶数是(),最小的整数是()。
6、自然数中,最大的三位是(),最小的两位数是()。
7、分子和分母是()数的分数是最简分数。
任意两个相邻的自然数都是()数。
8、乘积是()的两个数互为倒数。
公约数只有“1”的两个数是()数。
9、一个数的约数是()的,最小的是(),是大的是()。
数的分类与分析认识数的分类和分析技巧数的分类与分析:认识数的分类和分析技巧数是我们日常生活中必不可少的概念,它们在各个领域中都发挥着重要的作用。
为了更好地理解数的本质和应用,我们需要对数进行分类和分析。
本文将介绍数的分类以及分析数的技巧,帮助读者提升对数的认识和运用能力。
一、数的分类数可以按照不同的属性进行分类,常见的数的分类包括:自然数、整数、有理数、无理数、实数和复数。
1. 自然数自然数是最基本的数的概念,包括从1开始的正整数,即:1, 2, 3, 4, ...自然数在我们的日常生活中起到了重要的作用,用于计数、排名以及描述事物的数量等。
2. 整数整数包括正整数、负整数和零,即:..., -3, -2, -1, 0, 1, 2, 3, ...整数的运算包括加法、减法、乘法和除法,广泛应用于数学、物理、经济等领域。
3. 有理数有理数是可以表示为两个整数的比值的数,包括整数和分数。
有理数可以是正数、负数或零。
有理数的加减乘除运算可以通过约分和通分来进行,用于解决实际问题,如比例、百分比以及分数运算等。
4. 无理数无理数是不能表示为两个整数的比值的数,它们的十进制表示是无限不循环的小数,如π和√2等。
无理数的运算主要依赖近似值和数列逼近,用于精确计算和实际应用,如几何、物理以及工程等领域。
5. 实数实数是包括有理数和无理数的数集,它们可以在数轴上进行表示。
实数的运算包括加法、减法、乘法和除法,是数学和科学领域中最常用的数集。
6. 复数复数由实数部分和虚数部分组成,形如a + bi的形式,其中a和b为实数,i为虚数单位。
复数在物理、工程以及信号处理等领域中有广泛应用,如电路分析、波动理论以及图像处理等。
二、数的分析技巧在处理数的问题时,我们可以运用一些分析技巧来加深对数的理解和应用。
1. 探索数的规律数的规律是数学的核心,通过对数进行观察和分析,我们可以发现其中的规律性。
例如,自然数中的偶数可以表示为2的倍数,3的倍数可以被3整除,这些规律有助于我们解决一些数学问题。
数的分类与整数的认识数是我们日常生活中经常会接触到的概念,它们被广泛应用于各个领域。
在数学中,数可以被分为不同的类型,而整数则是其中一种特殊的数。
本文将介绍数的分类,并深入探讨整数的一些基本概念和性质。
一、数的分类在数学中,数可以分为自然数、整数、有理数和实数等多个类型。
以下是对这些类型的简要介绍:1. 自然数:自然数是最简单的数。
它们从1开始,一直递增到无穷大。
自然数用符号N来表示。
2. 整数:整数是包括自然数和它们的相反数(负整数)以及零在内的数。
整数用符号Z来表示。
3. 有理数:有理数包括所有可以表示为两个整数的比值的数,即分数形式。
例如,1/2、-3/4等都是有理数。
有理数用符号Q来表示。
4. 实数:实数是包括有理数和无理数的数。
无理数是无法用有限小数或分数形式表示的数。
实数用符号R来表示。
二、整数的认识整数是数的一种重要类型,它在数学和实际应用中都有广泛的应用。
以下是关于整数的一些基本概念和性质:1. 整数的定义:整数是包括正整数、负整数和零在内的数。
用整数表示没有小数部分的数。
2. 整数的表示:整数可以用数字直接表示,如1、2、-3等。
也可以用符号Z表示,表示为Z={..., -3, -2, -1, 0, 1, 2, 3, ...}。
3. 整数的加减运算:整数的加减运算仍然是整数。
例如,1+2=3,5-4=1。
正整数加负整数时,可以看作是正整数减去绝对值较大的负整数。
4. 整数的乘除运算:整数的乘除运算仍然是整数,但是要注意负数的乘除规则。
两个负整数相乘得到正整数,一个负整数除以正整数得到负整数。
5. 整数的大小比较:对于两个整数的比较,可以直接比较它们的绝对值大小。
正整数大于负整数,正整数大于零,负整数和零的大小关系则取决于它们的绝对值。
6. 整数的应用:整数在实际应用中有许多重要的用途。
例如,我们在计算金融利息、距离的变化、温度的变化等时常会用到整数。
总结:通过了解数的分类和整数的认识,我们深入理解了数的不同类型以及整数的特点和应用。
认识各种数的分类与性质在数学中,数被分为多种不同的类型,并且每种类型都具有自己独特的性质和特点。
通过认识各种数的分类与性质,我们可以更深入地理解数的本质和数学的基础。
本文将介绍一些常见的数的分类以及它们的性质,帮助读者对数学有更全面的认识。
一、自然数自然数是最基本的数,它从1开始,依次递增,没有负数和小数部分。
自然数用来表示计数和顺序,例如1、2、3、4等。
自然数的性质包括封闭性、交换律、结合律等。
它们是整数、有理数和实数的基础。
二、整数整数包括自然数、0和自然数的负数,用来表示计数和顺序,但也可以表示欠款、亏损等。
整数的性质包括封闭性、交换律、结合律、加法逆元等。
整数是有理数和实数的基础,但不包括分数和小数。
三、有理数有理数包括整数和分数,可以用两个整数的比值表示。
有理数可以是有限小数、循环小数或者无限不循环小数。
有理数的性质包括封闭性、交换律、结合律、乘法逆元等。
有理数是实数的一部分,但不包括无理数。
四、无理数无理数是不能表示为两个整数的比值的数,其小数部分是无限不循环的。
无理数包括根号2、圆周率π等,它们无法被表示为整数或分数的形式。
无理数的性质包括无限性、无穷不循环性等。
无理数是实数的一部分,但不包括有理数。
五、实数实数包括有理数和无理数,用来表示实际的量和现实中的数量关系。
实数的性质包括封闭性、交换律、结合律、乘法逆元等。
实数是数学中最广泛使用的一类数,几乎所有的数学分支都涉及到实数。
六、复数复数是由实数和虚数构成的数,虚数定义为虚数单位i与实数的乘积。
复数可以表示平面上的向量、波动、电路等。
复数的性质包括加法封闭性、乘法封闭性、共轭性等。
复数是数学中非常重要的一类数,广泛应用于物理学、工程学和计算机科学等领域。
七、超实数超实数是在实数的基础上扩展得到的一类数,它们可以表示无限大和无限小。
超实数的性质包括无界性、孤立性等。
超实数扩展了实数系统,使得我们能够更好地处理无穷大和无穷小的概念。
数字的奥秘认识数的分类和性质数字在我们的日常生活中扮演着重要的角色,它们是我们用来计算、测量和表示数量的基本工具。
对数字的深入认识有助于我们更好地理解数学,同时也能帮助我们更好地应用数字于实际生活和工作中。
本文将探讨数字的分类和性质,帮助读者进一步认识数字的奥秘。
1. 整数整数是最基本的数字类型之一,它们包括正整数、负整数和零。
正整数是大于零的整数,负整数是小于零的整数,而零则表示没有数量。
整数在数学运算中起着重要的作用,我们可以用它们进行加减乘除等各种计算。
此外,整数还有一些特殊的性质,比如任何一个整数加上零等于它本身,任何一个整数乘以一都等于它本身等。
2. 分数分数是另一种常见的数字类型,它们由一个分子和一个分母组成,分子表示数量的一部分,分母表示整体的划分。
分数可以用于表示不完整的数量,比如将一个整体分成若干块,分子表示其中的一部分块的数量,分母表示整体块的数量。
分数也可以用于表示比例和比率,比如我们常用的百分比就是分数的一种形式。
在数学运算中,分数也扮演着重要的角色,我们可以用它们进行加减乘除等各种计算。
3. 小数小数是另一种常见的数字类型,它们由整数部分和小数部分组成,小数部分表示数量的一部分。
小数在实际生活中广泛应用,比如用于表示长度、重量、时间等连续的量值。
小数可以用十进制、百分制或其他进制进行表示。
在数学运算中,我们也可以对小数进行加减乘除等各种计算。
4. 负数负数是整数的一种特殊形式,它们表示小于零的数量。
负数在数学中扮演着重要的角色,比如在坐标系中表示方向。
负数与正数之间可以进行加减乘除等各种计算,它们之间满足一些特殊的性质,比如两个负数相加得到一个更小的负数。
5. 实数实数是包括所有有理数和无理数的数字类型。
有理数包括整数、分数和小数,它们可以用有限个整数和分数的运算得到。
无理数包括无限不循环小数和无法表示为两个整数的比例的分数,它们不能用有限个整数和分数的运算得到。
实数在数学中扮演着重要的角色,它们用于表示连续的量值,比如长度、时间、速度等。
数的认识总结分类1. 整数整数是最基本的数学概念之一,指没有小数部分且包括正整数、负整数和零的数。
整数集合用ℤ表示,可以表示为:ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}整数可以进行加法、减法和乘法运算,并且满足结合律、交换律和分配律等基本运算法则。
2. 实数实数是包括有理数和无理数的数的集合。
实数集合用ℝ表示,可以表示为:ℝ = {x | x 是有理数或 x 是无理数}有理数包括整数、分数或证书部分为有限小数的数。
无理数是指不能用分数表示的数,如π(圆周率)和√2(2的平方根)等。
实数可视为实数轴上的点,可以进行加法、减法、乘法和除法运算,并且满足实数的代数运算法则。
3. 自然数自然数是从1开始的正整数,用符号ℕ表示。
自然数在数学中是最基础的数,代表了事物的计数和编号。
自然数集合可以表示为:ℕ = {1, 2, 3, 4, 5, ...}自然数是整数和实数的一部分,可以进行加法、减法和乘法运算。
4. 质数质数是指只能被1和自身整除的正整数。
质数不包括1,最小的质数是2。
如果一个数除了1和自身以外还能被其他数整除,那么它就不是质数,而是合数。
质数在数论中有重要的地位,是许多数学问题的基础。
5. 合数合数是指除了1和自身以外还能被其他数整除的正整数。
换句话说,合数是非质数。
合数可以分解为质数的乘积,例如 12 = 2 × 2 × 3。
合数在数论和代数中有广泛的应用。
6. 分数分数是表示一个数被另一个数除而得到的结果。
分数由两个整数表示,分子和分母。
分数可以是正数、负数或零。
分数的分母不可以为0,分子可以为0。
分数可以进行加法、减法、乘法和除法运算。
7. 百分数百分数是指以100为基数的分数,表示出来的形式为百分之几。
百分数常用来表示比例、比率和增减量等。
例如,60%表示60/100,等价于3/5。
百分数可以换算为小数和普通分数。
8. 负数负数是小于零的数。