电容充电放电时间计算公式
- 格式:doc
- 大小:25.00 KB
- 文档页数:2

放电时间计算公式1. 基本公式。
- 对于电容通过电阻放电的电路,其放电时间的计算公式为t =RC×ln(V_0)/(V),其中t是放电时间,R是放电电阻(单位为欧姆Ω),C是电容(单位为法拉F),V_0是电容初始电压,V是放电过程中某一时刻的电压。
- 当电容放电到初始电压的36.8%(即V = 0.368V_0)时,此时的时间t=τ = RC,这里τ被称为时间常数。
2. 推导过程(简单理解)- 根据电容的电压 - 电流关系i = C(dv)/(dt),在放电电路中,根据欧姆定律i=(v)/(R)(这里v是电容两端电压)。
- 所以(v)/(R)=-C(dv)/(dt)(负号表示放电,电流方向与充电时相反)。
- 对这个微分方程进行求解,分离变量得到(dv)/(v)=-(1)/(RC)dt。
- 两边积分∫_V_0^V(dv)/(v)=-(1)/(RC)∫_0^tdt,解得ln(V)/(V_0)=-(t)/(RC),即t = RC×ln(V_0)/(V)。
1. 公式。
- 对于电池以恒定电流I放电,电池容量为Q(单位为安时Ah),则放电时间t=(Q)/(I)。
- 例如,一个电池容量为10Ah,以2A的恒定电流放电,那么放电时间t=(10)/(2) = 5h。
2. 注意事项。
- 实际电池放电过程中,由于电池内阻的存在,随着放电的进行,电池电压会逐渐降低,当电压降低到一定程度(例如,对于铅酸蓄电池,电压降低到终止电压时),就不能再继续放电了。
而且电池的容量也会受到放电率(电流大小)、温度等因素的影响,所以这个公式是在理想恒流放电且不考虑电池老化等其他因素的情况下的简单计算。

RC电路充放电时间的计算RC电路是由电阻(R)和电容(C)组成的电路,充放电时间是指电容器上电压从0V充电到一定电压或从一定电压放电到0V所花费的时间。
1.充电时间的计算:在RC电路中,电压(V)会通过电阻和电容器进行充电。
充电时,电容器的电压会随时间逐渐上升,直到趋于稳定。
在一个理想的RC电路中,充电时间可以通过以下公式计算:t = R * C * ln(V_batt / (V_batt - V_c))其中,t是充电时间,R是电阻的阻值,C是电容器的电容量,V_batt是电源电压,V_c是电容器上的电压。
2.放电时间的计算:在RC电路中,电容器中存储的电能会通过电阻耗散,电容器的电压会随时间逐渐下降,直到趋于0V。
在一个理想的RC电路中,放电时间可以通过以下公式计算:t = R * C * ln(V_c / V_0)其中,t是放电时间,R是电阻的阻值,C是电容器的电容量,V_c是电容器上的电压,V_0是初始电压。
需要注意的是,以上的公式是基于理想的条件得出的,实际的电路中可能存在一些非理想因素,如电路的电阻、电容等元件的精确值与理论值之间的差异,以及电池的内阻等因素。
此外,还需要注意的是,在实际的RC电路中,电容器上的电压不会严格上升到电源电压或严格下降到0V,而是逐渐接近这些值。
因此,我们可以定义充电时间为电容器上电压达到电源电压的时间的约90%。
同样,放电时间可以定义为电容器上电压从电源电压下降到初始电压的时间的约90%。
总之,充放电时间的计算可以通过RC电路的电阻、电容、电源电压和初始电压,结合以上的计算公式,得出结果。
需要注意的是,公式是基于理想条件下得出的,实际的电路中可能存在一些不可忽略的非理想因素。

超级电容充放电时间计算方法一般应用在太阳能指示灯上时, LED 都釆用之闪烁妁发光, 例如釆用一颗LED且控制每秒闪烁放电持续时间为0。
05 秒,对超级电容充电电流100mA (0.1A)下面以2。
5V / 50F在太阳能交通指示灯为例, 超级电容充电时间如下:C X dv = I X tC: 电容器额定容量;V: 电容器工作电压I:电容器充电t:电容器充电时间R: 电容器内阻dv: 工作电压差故2。
5V / 50F 超级电容充电时间为:t = ( C X V) / I= (50 X 2。
5)/ 0.1= 1250S超级电容放电时间为:C X dv — I X C X R = I X t故2.5V / 50F 超级电容从2。
5V 放到0.9V 放电时间为:t = C X (dv / I - R)= 50 X [ (2。
5 — 0.9) ]/ 0.015 — 0.02 ]= 5332S应用在LED 工作时间为5332 / 0.05 = 106640S = 29.62 hrC: 电容器额定容量(F)R: 电容器内阻(Ohm)V work: 正常工作电压(V)V min :停止工作电压(V)t :在电路中要求持续工作时间(s)I : 负载电流(A)超级电容量的计算方式:C = (Vwork + Vmin)It / (Vwork-Vmin)例:如单片机应用系统中, 应用超级电容作为後备电源,在断电後需要用超级电容维持100mA 电流,持续时间为10S,单片机停止工作电压为4.2V,那麼需要多大容量的超级电容才能保证系统正常工作?工作起始电压Vwork = 5V停止工作电压Vmin = 4。
2V工作时间t = 10S工作电源I = 0.1A那麼需要的电容容量为:C = (Vwork + Vmin)It / (Vwork-Vmin)= (5 + 4。
2)X 0。
1 X 10 / (5 X 4.2)= 1。
25F根据计算结果,可以选择5。


RC 时间常常被用于描述电路中的电压或电流变化速度。
在一个简单的RC 电路中,R 代表电阻值(单位为欧姆),C 代表电容值(单位为法拉),而RC 时间常被定义为电容充电或放电到达其初始值的时间。
计算RC 时间的公式如下:
RC 充电时间常数(τ):τ = R × C
- 电容充电时间(t):当电容充电到达63.2%(即1 - 1/e, 其中e 是自然对数的底数)所需的时间。
t = τ × ln(2)
- 电容放电时间(t):当电容放电到达36.8%(即1/e)所需的时间。
t = τ × ln(2)
请注意,这些公式是基于简化的模型,假设电路是理想的完美条件。
在实际情况下,可能还需要考虑其他因素,例如电压源的特性和导线电阻等。
此外,RC 时间在不同的领域和应用中也具有不同的含义和计算方式。
如在信号处理中,RC 时间常使用于描述带通滤波器的截止频率,其计算方式为1/(2πRC)。
因此,具体使用的场景和定义会对应有所差异。

法拉电容充电时间计算公式法拉电容,也叫超级电容,在很多电子设备和电路中都有着重要的应用。
那咱们今儿就来好好唠唠法拉电容充电时间的计算公式。
先来说说啥是法拉电容。
这玩意儿就像是一个超级大电池,能快速充放电,储存大量的电能。
比如说,在一些需要瞬间大电流的设备里,法拉电容就能派上大用场。
那它充电时间咋算呢?这就得提到一个公式:$t = RC\ln(\frac{V_0}{V_0 - V_f})$ 。
这里面的“t”就是充电时间,“R”是充电电阻,“C”是法拉电容的电容值,“V0”是充电电源的电压,“Vf”是法拉电容最终要达到的电压。
举个例子哈,有一次我在实验室里做一个小项目,要给一个 100 法拉的法拉电容充电。
充电电源的电压是5 伏,我设定最终要充到4 伏,充电电阻是 10 欧姆。
那咱们就来算算充电时间。
把数值代入公式:$t = 10×100×\ln(\frac{5}{5 - 4}) = 1000×\ln(5) ≈ 1609$ 秒。
这一算就清楚了,大概得 1609 秒才能充好。
不过实际情况中,可能会有点小偏差,因为还得考虑一些其他因素,像电路中的损耗啦,电容本身的漏电啦等等。
再比如说,在一些电动汽车的能量回收系统里,法拉电容的充电时间计算就特别重要。
要是计算不准确,就可能影响到整个系统的效率和性能。
咱们在实际应用中,还得根据具体情况灵活调整。
比如说,如果充电电阻变小了,那充电时间就会缩短;要是电容的电容值变大了,充电时间也会相应变长。
总之,法拉电容充电时间的计算虽然有公式可循,但实际操作中得综合考虑各种因素,才能让法拉电容发挥出最大的作用。
所以啊,朋友们,掌握好这个计算公式,对于咱们在电子电路方面的研究和应用,那可是相当有帮助的。
不管是搞小发明,还是做大项目,都能让咱们心里更有底,把事儿做得更漂亮!。

电容充电时间计算公式
蓄电池是日常生活中常见的一种发电设备,它能够储存电能,是众多产品的电能原料。
充电是影响蓄电池使用寿命的关键,充电时间的长短不仅直接影响到使用寿命,还会影响到蓄电池的使用效率。
因此,计算准确的充电时间是非常重要的。
电容充电时间计算公式即为: 充电时间(T)=R × C × Ln
(V1÷V2)/U;
其中,R为充电器输出电阻,C为蓄电池容量,V1为蓄电池充电初始电压,V2为蓄电池充电目标电压,U为充电器输出电压。
计算电容充电时间时,实际中会出现四种情形:
1、若V1>V2,T=0,即为0时间充满电;
2、若V1=V2,T=正无穷大,即为不能充满;
3、若V1<V2,T>0,即为可充满的时间;
4、若V1=0,T=R×C/U,即为放电时间。
电容充电时间计算公式是非常有用的,相比其他测算方式,该公式考虑了多种参数因素,准确性更高。
但是,在实际计算中,由于周围环境、蓄电池放电和充电状态等因素的影响,充电时间可能会有所延长,因此在使用这个计算公式的过程中,要根据一定的实际情况,结合实际测量数据,进行综合判断。

电容充放电时间计算硬件工程师在做一些仪表产品时,往往会面临一个“掉电保存”的问题。
例如在数显电能表中,当突然发生外部电源断电时;MCU要在断电的一刹那,运行掉电中断服务程序,把电量数据或当前工作状态存到外部的E2PROM中。
这样在下一次上电时,MCU就能从E2PROM中读取数据,或恢复断电前的工作状态。
在没有后备电池的应用中,这个动作只能通过大电容的短时间放电来完成。
如果不考虑中断服务程序中执行指令的时间,仅仅普通24C02写一页(8字节)的编程时间最大就会达10ms;电容的放电时间最起码要比这个时间长,这样我们就需要计算电容放电的持续时间。
下面给出两个例子:1、100uF的电容充上5V的电;之后用1mA恒流放电,多长时间能放干净(放到0V)?2、100uF电容用1mA恒流放电,从2.8V放电到2.2V,需要多长时间?(实际中的例子:系统总工作电流为1mA;设置单片机2.8V进入掉电中断,2.2V发生低压复位;掉电中断程序必须在这个时间区内完成对24C02的写操作)。
------------------------------------------------------------计算方法有很多,这里给出一个公式和计算过程:根据电容上的电流和电压公式:。
因为恒流放电,ic恒定,uc线性变化;上面公式可改为:,可得,这个就是电容恒流充放电计算公式。
第1题,代入C=0.1mF,Ic=1mA,电压变化=5V,可计算出放电时间=500ms。
第2题,电压变化=2.8-2.2=0.6V,其他不变,可计算出=60ms;也就是从从2.8V 放电到2.2V,需要60ms。
实际使用中如果掉电保存内容比较多,这个时间不够,那就把这个电容加大一点。
另外,电容恒流充电计算也是同样的过程。

超级电容充放电时间计算方法一般应用在太阳能指示灯上时, LED 都釆用之闪烁妁发光,例如釆用一颗LED 且控制每秒闪烁放电持续时间为0。
05 秒,对超级电容充电电流100mA (0.1A) 下面以2。
5V / 50F在太阳能交通指示灯为例, 超级电容充电时间如下:C X dv = I X tC: 电容器额定容量;V:电容器工作电压I:电容器充电t: 电容器充电时间R: 电容器内阻dv: 工作电压差故2.5V / 50F 超级电容充电时间为:t = (C X V) / I= (50 X 2。
5)/ 0.1= 1250S超级电容放电时间为:C X dv — I X C X R = I X t故2。
5V / 50F 超级电容从2。
5V 放到0。
9V 放电时间为:t = C X (dv / I — R)= 50 X [( 2.5 — 0.9)] / 0.015 — 0.02 ]= 5332S应用在LED 工作时间为5332 / 0.05 = 106640S = 29。
62 hrC: 电容器额定容量(F)R:电容器内阻(Ohm)V work:正常工作电压(V)V min : 停止工作电压(V)t : 在电路中要求持续工作时间(s)I : 负载电流(A)超级电容量的计算方式:C = (Vwork + Vmin)It / (Vwork-Vmin)例:如单片机应用系统中,应用超级电容作为後备电源,在断电後需要用超级电容维持100mA 电流,持续时间为10S,单片机停止工作电压为4。
2V,那麼需要多大容量的超级电容才能保证系统正常工作?工作起始电压Vwork = 5V停止工作电压Vmin = 4.2V工作时间t = 10S工作电源I = 0.1A那麼需要的电容容量为:C = (Vwork + Vmin)It / (Vwork—Vmin)= (5 + 4。
2)X 0.1 X 10 / (5 X 4。
2)= 1.25F根据计算结果,可以选择5.5V , 1。

rc电路电容充放电时间的计算(含计算公式)英文版RC Circuit Capacitor Charging and Discharging Time Calculation (Including Calculation Formulas)In an RC circuit, the capacitor's charging and discharging process is governed by the interaction between the resistance (R) and capacitance (C) elements. Understanding how to calculate the charging and discharging times of a capacitor in an RC circuit is crucial for analyzing and designing electronic circuits.Charging Time Calculation:When a capacitor is being charged in an RC circuit, the time taken for it to reach a particular voltage level is known as the charging time. This time can be calculated using the formula: (t_{charge} = RC \ln\left(\frac{V_{final}}{V_{initial}}\right))where:(t_{charge}) is the charging time.(R) is the resistance in the circuit.(C) is the capacitance in the circuit.(V_{final}) is the final voltage across the capacitor.(V_{initial}) is the initial voltage across the capacitor (usually 0 for a completely discharged capacitor).The natural logarithm ((\ln)) is used in this formula to account for the exponential nature of capacitor charging.Discharging Time Calculation:Similarly, when a capacitor is being discharged in an RC circuit, the time taken for it to reach a particular voltage level is known as the discharging time. This time can be calculated using the formula:(t_{discharge} = RC \ln\left(\frac{V_{initial}}{V_{final}}\right)) where:(t_{discharge}) is the discharging time.(R) and (C) have the same meanings as in the charging formula.(V_{initial}) is the initial voltage across the capacitor.(V_{final}) is the final voltage across the capacitor (usually 0 for a completely discharged capacitor).Again, the natural logarithm is used in the discharging time calculation.Conclusion:Understanding the charging and discharging time calculation formulas for capacitors in RC circuits is essential for effective circuit analysis and design. These formulas provide a quantitative understanding of how the resistance and capacitance values in an RC circuit affect the rate at which a capacitor charges or discharges. By manipulating these values, engineers can fine-tune the behavior of electronic circuits to meet specific design requirements.中文版RC电路电容充放电时间的计算(含计算公式)在RC电路中,电容器的充放电过程是由电阻(R)和电容(C)元件之间的相互作用所决定的。
电容放电计算公式
电容放电是一个常见的物理现象,在电路中起着重要作用。
它描述了电容器从充电状态到放电状态的过程。
电容放电计算公式是用来计算电容器放电过程中电荷量变化的公式。
假设我们有一个电容器,其电容量为C,带有电荷量Q。
当电容器开始放电时,电荷量会随时间的流逝而减少。
根据电容放电计算公式,我们可以计算出电荷量随时间变化的关系。
公式如下:
Q(t) = Q0 * e^(-t/RC)
其中,Q(t)表示时间t时刻的电荷量,Q0表示初始电荷量,e表示自然对数的底数,t表示时间,R表示电阻值,C表示电容值。
根据这个公式,我们可以看出电荷量随时间呈指数衰减的趋势。
当时间t趋近于无穷大时,电荷量趋近于0。
这意味着电容器最终会完全放电。
在实际应用中,电容放电计算公式可以用来预测电容器放电过程中电荷量的变化。
它在电子电路设计、电力系统分析等领域都有广泛的应用。
需要注意的是,电容放电计算公式是基于一些假设和理论模型得出的,实际情况可能会受到电容器内部电阻、外部电路条件等因素的
影响。
因此,在实际应用中,需要根据具体情况进行修正和调整。
总结一下,电容放电计算公式是用来计算电容器放电过程中电荷量变化的公式。
它可以帮助我们了解电容器放电的规律,并在实际应用中起到指导作用。
通过深入理解和应用这个公式,我们可以更好地设计和优化电子电路,提高系统的性能和稳定性。
电容恒流充电时间计算电容恒流充电时间是指在恒定电流条件下,将一个电容器充电至特定电压所需要的时间。
电容恒流充电时间的计算公式为t=RC,其中t表示充电时间,R表示电阻值,C表示电容值。
在实际应用中,电容恒流充电时间的计算是非常重要的,尤其在电子工程和电气工程领域。
下面将详细介绍电容恒流充电时间的计算方法以及相关的应用。
一、电容恒流充电时间的计算方法为了计算电容恒流充电时间,首先需要知道电容器的电容值和电阻值。
电容器的电容值可以通过产品标识或测量得到,电阻值可以通过测量或电路设计得到。
1. 根据电容值和电阻值计算RC的值,即RC=电容值×电阻值。
2. 将RC的值代入公式t=RC,即可得到电容恒流充电时间t的值。
需要注意的是,电容恒流充电时间的单位通常为秒(s),所以在计算时需要将电容值和电阻值转换为国际单位制。
二、电容恒流充电时间的应用电容恒流充电时间的应用非常广泛,特别是在电子电路设计和电气设备中。
以下是一些常见的应用场景:1. 电子电路设计中的电容充电时间计算:在设计电子电路时,需要考虑电容充电时间,以确保电路正常工作。
通过计算电容恒流充电时间,可以确定电路中电容器的充电速度和充电时间,从而保证电路的稳定性和可靠性。
2. 电池充电时间计算:在充电设备中,需要根据电池容量和充电电流来计算电池的充电时间。
通过计算电容恒流充电时间,可以确定电池的充电时间,从而确保电池能够充满并正常工作。
3. 电容器充电时间的优化:在一些应用中,需要尽可能缩短电容器的充电时间,以提高系统的响应速度和效率。
通过计算电容恒流充电时间,可以选择合适的电容值和电阻值,以达到最短的充电时间。
4. 电容器放电时间的计算:除了充电时间,电容器的放电时间也是重要的参数。
通过计算电容恒流充电时间,可以得到电容器放电的时间常数,从而确定电容器的放电速度和放电时间。
总结:电容恒流充电时间的计算是电子电路设计和电气工程中的重要内容。
RC电路充放电时间计算RC电路是由电容器C和电阻器R组成的电路,在充电和放电过程中,会出现一些特定的时间计算问题。
本文将详细介绍RC电路充放电时间的计算方法。
首先,我们来看充电过程。
在充电开始时,电容器C还未充满电,电源的电压会通过电阻R逐渐充满电容器C。
充电的时间可以用充电时间常数τ来表示,充电时间常数τ等于电容器C与电阻器R的乘积,即τ=RC。
充电时间常数τ可以表示充电过程的特性,它表示了充电过程充满63.2%电量所需的时间。
通常我们使用电容器充电至充满电量所需的时间作为充电的时间计算参考。
充电过程中,电容器充电到电源电压的约99.3%需要多长时间呢?我们可以使用逃逸指数法来计算。
假设充电电压达到电源电压的99.3%所需的时间为t1,而充电时间常数τ为RC。
那么根据逃逸指数法的定义,99.3%的电源电压是电容器充电到63.2%电量所需要的时间,即t1 = τ * ln(1/(1-0.993))。
通过这个公式,我们可以计算出电容器充电到电源电压的约99.3%所需的时间。
接下来,我们来看放电过程。
放电过程与充电过程类似,只是电容器中的电荷会逐渐流出,电容器的电压也会逐渐降低。
放电的时间也可以用放电时间常数τ来表示,放电时间常数τ仍然等于电容器C与电阻器R的乘积,即τ=RC。
放电时间常数τ可以表示放电过程的特性,它表示了电容器放电到37.0%电量所需的时间。
通常我们使用电容器放电至其初始电压的一半所需的时间作为放电的时间计算参考。
放电过程中,电容器放电到初始电压的一半需要多长时间呢?使用逃逸指数法计算,假设放电时间常数τ为RC,放电电压降到初始电压一半所需的时间为t2、根据逃逸指数法的定义,37.0%的电源电压是电容器放电到初始电压一半所需的时间,即t2 = τ * ln(1/(1-0.5))。
通过这个公式,我们可以计算出电容器放电到初始电压一半所需的时间。
在实际应用中,我们可以根据需要计算充电和放电时间,以确定电容器电压的变化情况。
电容充放电是电子电路中常见的过程之一,涉及到电容器的充电和放电过程。
以下是电容充电和放电的基本公式以及相应的曲线:**电容充电:**电容充电过程是指将电荷从电源(例如电池)传输到电容器中的过程。
在这个过程中,电荷在电容器的极板之间积累,电压逐渐上升。
电容充电的基本公式如下:1. 电流(I)与电容充电电压(V)之间的关系:$$I(t) = C \cdot \frac{dV(t)}{dt}$$其中,I(t) 是时间t 时刻的电流,C 是电容器的电容,V(t) 是时间t 时刻的电压。
这个方程表示电流与电压变化率成正比,电容越大,电流变化越缓慢。
2. 电压随时间的变化:$$V(t) = V_{\text{max}} \cdot (1 - e^{-\frac{t}{R \cdot C}})$$其中,V(t) 是时间t 时刻的电压,V_{\text{max}} 是最终电压(电容充满时的电压),R 是电路中的电阻,C 是电容。
**电容放电:**电容放电过程是指从电容器中释放储存的电荷的过程。
在这个过程中,电压逐渐下降,直到电容器完全放电。
电容放电的基本公式如下:1. 电流与电容放电电压之间的关系:$$I(t) = -C \cdot \frac{dV(t)}{dt}$$这个方程表示电流的方向与电压下降率成反比,所以电流是负数。
2. 电压随时间的变化:$$V(t) = V_0 \cdot e^{-\frac{t}{R \cdot C}}$$其中,V(t) 是时间t 时刻的电压,V_0 是初始电压,R 是电路中的电阻,C 是电容。
**电容充放电曲线:**电容充放电的曲线可以用电压随时间的变化来表示。
在电容充电过程中,电压会逐渐上升,而在电容放电过程中,电压会逐渐下降。
曲线的形状取决于电容值、电阻值、初始电压等参数。
在充电过程中,电压逐渐上升并趋近于最终电压。
在放电过程中,电压逐渐下降并趋近于零。
请注意,实际电容充放电过程可能受到电阻、内部电阻、电源电压等因素的影响,因此曲线的形状可能会有所不同。
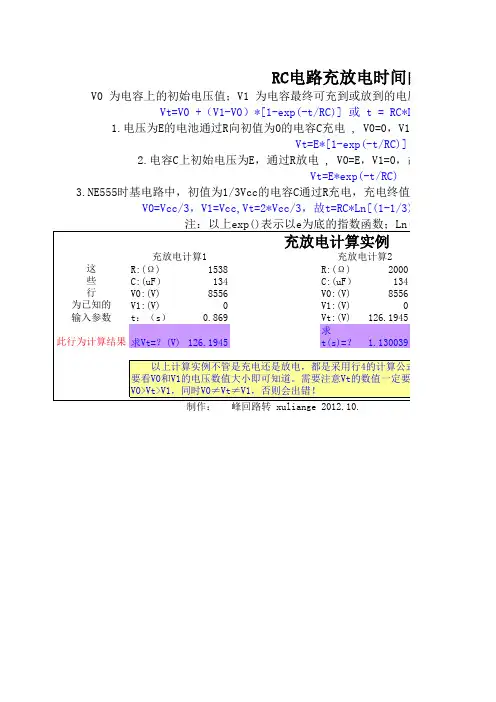
电容充电放电时间计算公式
设,V0 为电容上的初始电压值;
V1 为电容最终可充到或放到的电压值;
Vt 为t时刻电容上的电压值。
则,
Vt="V0"+(V1-V0)* [1-exp(-t/RC)]
或,
t = RC*Ln[(V1-V0)/(V1-Vt)]
例如,电压为E的电池通过R向初值为0的电容C充电
V0=0,V1=E,故充到t时刻电容上的电压为:
Vt="E"*[1-exp(-t/RC)]
再如,初始电压为E的电容C通过R放电
V0=E,V1=0,故放到t时刻电容上的电压为:
Vt="E"*exp(-t/RC)
又如,初值为1/3Vcc的电容C通过R充电,充电终值为
Vcc,问充到2/3Vcc需要的时间是多少?
V0=Vcc/3,V1=Vcc,Vt=2*Vcc/3,故
t="RC"*Ln[(1-1/3)/(1-2/3)]=RC*Ln2
=0.693RC
注:以上exp()表示以e为底的指数函数;Ln()是e为底的对数函
数