(力学)第4章(修)
- 格式：ppt
- 大小：2.09 MB
- 文档页数：58
下载文档原格式
合集下载
高中物理必修一 讲义 第4章 专题强化 动力学中的连接体问题
专题强化动力学中的连接体问题[学习目标] 1.知道什么是连接体，会用整体法和隔离法分析动力学中的连接体问题(重难点)。
2.进一步熟练应用牛顿第二定律解题(重点)。
连接体：两个或两个以上相互作用的物体组成的具有相同运动状态的整体叫连接体。
如几个物体叠放在一起，或并排放在一起，或用绳子、细杆等连在一起，在求解连接体问题时常用的方法为整体法与隔离法。
一、加速度和速度都相同的连接体问题例1如图所示，光滑水平面上A、B两物体用不可伸长的轻绳相连，用力F拉A使A、B 一起运动，A的质量为m A、B质量为m B，求A、B两物体间绳的拉力F T的大小。
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________连接体问题的解题方法1．整体法：把整个连接体系统看作一个研究对象，分析整体所受的外力，运用牛顿第二定律列方程求解。
其优点在于它不涉及系统内各物体之间的相互作用力。
2．隔离法：把系统中某一物体(或一部分)隔离出来作为一个单独的研究对象，进行受力分析，列方程求解。
其优点在于将系统内物体间相互作用的内力转化为研究对象所受的外力，容易看清单个物体(或物体的一部分)的受力情况或单个过程的运动情形。
工程力学第4章
（３） 列平衡方程，求解未知量。列力矩方程时，通常 选未知力较多的交点为矩心。
（４） 结果分析或校核。
第4章 平面任意力系
例4-2 摇臂吊车如图4-9（a）所示。横梁AB的A端为固定 铰链支座，B端用拉杆BC与立柱相连。已知梁的重力G1＝4kN, 载荷G2＝12 kN，横梁长l＝６ｍ，α＝30°，求当载荷距A端距 离x＝4 ｍ时， 拉杆BC的受力和铰支座A的约束反力。
第4章 平面任意力系
3. 平面力偶系是特殊的力系，根据力偶的性质，在基本方程 中的投影方程自然满足，所以只有一个方程，
MO (F) 0
第4章 平面任意力系
4.2.3
（１） 根据题意，选取适当的研究对象；对所选研究对 象进行受力分析并画受力图。
（２） 选取适当的直角坐标系。坐标轴应与较多的未知 反力平行或垂直。一般情况下，水平和垂直的坐标轴可以不画， 但其它特殊方向的坐标轴必须画出。
第4章 平面任意力系
（3） 该力系上述的三种简化结果，从形式上是不同的， 但都与原力系等效。所以，三种情况的简化结果是等效的。
第4章 平面任意力系
4.1.3 固定端约束
固定端约束是工程中一种常见的约束。如图4-6所示，夹紧 在卡盘上的工件（图(a)），固定在刀架上的车刀（图(b)）， 嵌入墙中的雨罩（图(c)）等都属于固定端约束。由约束的性质 可知， 固定端约束能限制物体沿任何方向的移动，也能限制物 体在约束处的转动。所以，固定端Ａ处的约束反力可用两个正
主矢FR′的大小和方向分别为：
FR' (FRx )2 (FRy )2 2002 1502 250N
tan FRy 150 0.75
FRx 200
第4章 平面任意力系
（４） 结果分析或校核。
第4章 平面任意力系
例4-2 摇臂吊车如图4-9（a）所示。横梁AB的A端为固定 铰链支座，B端用拉杆BC与立柱相连。已知梁的重力G1＝4kN, 载荷G2＝12 kN，横梁长l＝６ｍ，α＝30°，求当载荷距A端距 离x＝4 ｍ时， 拉杆BC的受力和铰支座A的约束反力。
第4章 平面任意力系
3. 平面力偶系是特殊的力系，根据力偶的性质，在基本方程 中的投影方程自然满足，所以只有一个方程，
MO (F) 0
第4章 平面任意力系
4.2.3
（１） 根据题意，选取适当的研究对象；对所选研究对 象进行受力分析并画受力图。
（２） 选取适当的直角坐标系。坐标轴应与较多的未知 反力平行或垂直。一般情况下，水平和垂直的坐标轴可以不画， 但其它特殊方向的坐标轴必须画出。
第4章 平面任意力系
（3） 该力系上述的三种简化结果，从形式上是不同的， 但都与原力系等效。所以，三种情况的简化结果是等效的。
第4章 平面任意力系
4.1.3 固定端约束
固定端约束是工程中一种常见的约束。如图4-6所示，夹紧 在卡盘上的工件（图(a)），固定在刀架上的车刀（图(b)）， 嵌入墙中的雨罩（图(c)）等都属于固定端约束。由约束的性质 可知， 固定端约束能限制物体沿任何方向的移动，也能限制物 体在约束处的转动。所以，固定端Ａ处的约束反力可用两个正
主矢FR′的大小和方向分别为：
FR' (FRx )2 (FRy )2 2002 1502 250N
tan FRy 150 0.75
FRx 200
第4章 平面任意力系
理论力学课后习题答案 第4章 运动分析基础
(b)第4章 运动分析基础4－1 小环A 套在光滑的钢丝圈上运动，钢丝圈半径为R （如图所示）。
已知小环的初速度为v 0，并且在运动过程中小环的速度和加速度成定角θ，且 0 ＜ θ ＜2π，试确定小环A 的运动规律。
解：Rv a a 2nsin ==θ，θsin 2R v a =θθtan cos d d 2tR v a tv a ===，⎰⎰=t v v t R vv 02d tan 1d 0θ t v R R v t s v 00tan tan d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0tan tan ln tan -=θθθ4－2 已知运动方程如下，试画出轨迹曲线、不同瞬时点的 1．⎪⎩⎪⎨⎧-=-=225.1324tt y tt x ， 2．⎩⎨⎧==t y t x 2cos 2sin 3解：1．由已知得 3x = 4y （1） ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动，轨迹如图（a ），其v 、a 图像从略。
2．由已知，得2arccos 213arcsin y x =化简得轨迹方程：2942x y -=（2）轨迹如图（b ），其v 、a 图像从略。
4－3 点作圆周运动，孤坐标的原点在O 点，顺钟向为孤坐标的正方向，运动方程为221Rt sπ=，式中s 以厘米计，t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时，求点的加速度在x 和y 轴上的投影。
解：Rt s v π== ，R v a π==t ，222n Rt Rv a π==y 坐标值最大的位置时：R Rt s 2212ππ==，12=∴tR a a x π==t ，R a y 2π-=4－4 滑块A ，用绳索牵引沿水平导轨滑动，绳的另一端绕在半径为r 的鼓轮上，鼓轮以匀角速度ω转动，如图所示。
理论力学教程(第四章)
静滑动摩擦力的特点
1 方向：沿接触处的公切线，
与相对滑动趋势反向；
2 大小：
3
（库仑摩擦定律）
④静摩擦系数的测定方法(倾斜法)
两种材料做成物体
和可动平面测沿下面滑
动时的 。
p
F=mgsin =fmgcos
2)、动滑动摩擦
tg f
两物体接触表面有相对运动时,沿接触面产生的切向 阻力称为动滑动摩擦力。
1)、静滑动摩擦
① 定义 两相接触物体虽有相对运动趋势，但仍保持相对静止F时，
给接触面产生的切向阻力，称为静滑动摩擦力或简称静摩 擦力。
满足
0 F Fmax (最大静摩擦力)
当 F Fmax时,则物体处于临界平衡状态
F
P Fmax f N (库仑静摩擦定律)
若物体静止，则 F P
摩擦的现象和概念
在大学物理已经讲到什么是摩擦：当物体与另一物体 沿接触面的切线方向运动或有相对运动的趋势时，在两物 体的接触面之间有阻碍它们相对运动的作用力，这种力叫 摩擦力。接触面之间的这种现象或特性叫“摩擦”。这里 来作更深入的研究，首先来看它的分类：滑动摩擦和滚动 摩擦。
滑动摩擦：相对运动为滑动或具有滑动趋势时的摩擦。
第四章 摩擦
欢迎加入湖 工大考试资
料群：
引言
前几章我们把接触表面都看成是绝对光滑的，忽略了物体 之间的摩擦，事实上完全光滑的表面是不存在的，一般情况下 都存在有摩擦。 [例]
平衡必计摩擦 3
摩擦
☆§4–1 滑动摩擦 ☆§4–2 摩擦角和自锁现象 ☆§4–3 考虑摩擦时物体的平衡问题 ☆§4–4 滚动摩阻的概念
性质：当物体静止在支承面时，支承面的总反力的偏角
理论力学-第4章
z
v
P
r
P´
r(t) r (t＋t) O y
t＋ t 瞬时: 矢径 r (t ＋ t ) 或r(t)＋ r(t) t 时间间隔内矢径的改变量, 称为点的位移 r(t)＝ r (t＋t)－r(t) 点在 t 瞬时的速度
x
r dr v lim r t 0 t dt
描述点的运动的弧坐标法
如果已知点的轨迹，则可在轨迹 上任取一点为原点，运动的点P至原 点的弧长s＝OP，并且规定：原点O 的某一侧弧长为正；另一侧为负。这 种具有确定正负号的弧长s称为P点的 弧坐标(arc coordinate of a directed curve)。弧坐标s完全确定了动点P在 轨迹上的位置。 点运动时，其弧坐标随时间而变化：
第2篇 工程运动学基础
工程运动学涉及工程运动分析的基本的概念、基 本理论和基本方法。这些内容不仅是工程运动学的基 础，而且也是工程动力学(dynamics)的基础。
运动学的研究对象是点和刚体。 工程运动学的分析方法主要是矢量方法。
第4章 运动分析基础
运动学（kinematics）研究物体在空间的位置随时间的 变化，即物体的运动，但是不涉及引起运动的原因。 物体的运动都是相对的，因此研究物体的运动必须指 明参考体和参考系。 物体运动的位移、速度和加速度都是矢量，因此研究 运动学采用矢量方法。而且，一般情形下，这些矢量的大 小和方向会随着时间的变化而变化，因而称为变矢量。变 矢量运算与常矢量有相同之处，也有不同之处。这是学习 运动学的难点。
例题2
3．确定M点的轨迹在最高点 处的曲率半径
dr ds
的速度在切线轴上的投影等于弧坐标对时间的一阶导数。
ds ＝s＝vτ dt
最新《力学》漆安慎(第二版)答案04章
力学（第二版）漆安慎习题解答第四章动能和势能第四章 动能和势能 一、基本知识小结1、功的定义式：⎰⋅=2112r r rd F A直角坐标系中：⎰⎰+==221121,,1212y x y x yxx x x dy F dx F A dx F A ，自然坐标系中：⎰=2112s s ds F A τ极坐标系中： ⎰+=2211,,12θθθθr r rrd F dr F A2、⎰⋅-=-=b ap p k r d F a E b E mv E 保势能动能)()(,212重力势能m g y y E p =)(弹簧弹性势能 2)(21)(l r k r E p -=静电势能 rQqr E p πε4)(=3、动能定理适用于惯性系、质点、质点系 ∑∑∆=+k E A A 内外4、机械能定理适用于惯性系 ∑∑+∆=+)p k E E A A （非保内外5、机械能守恒定律适用于惯性系若只有保守内力做功，则系统的机械能保持不变，C E E p k =+6、碰撞的基本公式接近速度）（分离速度（牛顿碰撞公式）动量守恒方程）e v v e v v v m v m v m v m =-=-+=+)((2010122211202101对于完全弹性碰撞 e = 1 对于完全非弹性碰撞 e = 0对于斜碰，可在球心连线方向上应用牛顿碰撞公式。
7、克尼希定理 ∑+=22'2121i i c k v m mv E绝对动能=质心动能+相对动能应用于二体问题 222121u mv E c k μ+=212121m m m m m m m +=+=μ u 为二质点相对速率二、思考题解答4.1 起重机起重重物。
问在加速上升、匀速上升、减速上升以及加速下降、匀速下降、减速下降六种情况下合力之功的正负。
又：在加速上升和匀速上升了距离h 这两种情况中，起重机吊钩对重物的拉力所做的功是否一样多？答:在加速上升、匀速上升、减速上升以及加速下降、匀速下降、减速下降六种况下合力之功的正负分别为：正、0、负、正、0、负。
理论力学
vD QD v0 QD QD v0 v0 cos QA QA
4.7 高为h,顶角为2α的圆锥在一平面上滚而不滑,如此锥体以等角速度ω 绕 Oz0轴转动,求此圆锥地面上最高点A的速度和加速度.
' .OB为圆锥的瞬时转轴 解：如图圆锥绕z0轴与z轴的角速度分别为 和 合角速度: 0 ' , 0 在x轴上, 0 cot i
I11 x2 I 22 y 2 I33 z 2 2I12 xy 2I13 xz 2I32 yz 1
使惯量积等于零的坐标轴称为惯量主轴。
惯量主轴垂直于惯量椭球面，如以惯量主轴为坐标轴，则椭球 面的方程可写为标准形式的椭球方程：
其中：
x2 y 2 z2 2 2 1 2 a b c
有几何关系A点坐标, h h OA cos 2 i 0 j sin 2 k cos cos i j k 则: v A 0 OA cot 0 0 h h cos2 0 sin 2 cos cos 2h cos j 向心加速度: 2 vA a向 k
快速陀螺应用的实际例子：炮弹的旋转，回转力矩，回转罗盘
其他、
1. 刚体转动的稳定性，
2. 刚体定轴转动时支点上的动反作用力， 3. 刚体的碰撞
第4章
刚
体
4.1 半径为r1的圆柱体P约束在水平面上运动，另一个半径为r2的圆柱体S约 束在P上运动(如图所示)。分别就下列三种情况写出体系的自由度，并选取 适当的广义坐标表示S和P的角速度:(1)P 固定不动，S在P上只滚不滑; (2)S 和P之间，P和平面之间绝对粗糙，接触点相对速度都是零;(3)S和P之间， P和平面之间绝对光滑 解：(1)以P中心O为原点， S由起始位置滚至图示位置时，经过弧长 r1 , r 经过S的角度为 1 由于P固定不动， p 0， r2 k ，而S自转角速度 则S相对P的角速度 sp d r1 r1 s ' dt r2 r2 由角速度合成： k r1 k (1 r1 ) k s sp s ' r2 r2
4.7 高为h,顶角为2α的圆锥在一平面上滚而不滑,如此锥体以等角速度ω 绕 Oz0轴转动,求此圆锥地面上最高点A的速度和加速度.
' .OB为圆锥的瞬时转轴 解：如图圆锥绕z0轴与z轴的角速度分别为 和 合角速度: 0 ' , 0 在x轴上, 0 cot i
I11 x2 I 22 y 2 I33 z 2 2I12 xy 2I13 xz 2I32 yz 1
使惯量积等于零的坐标轴称为惯量主轴。
惯量主轴垂直于惯量椭球面，如以惯量主轴为坐标轴，则椭球 面的方程可写为标准形式的椭球方程：
其中：
x2 y 2 z2 2 2 1 2 a b c
有几何关系A点坐标, h h OA cos 2 i 0 j sin 2 k cos cos i j k 则: v A 0 OA cot 0 0 h h cos2 0 sin 2 cos cos 2h cos j 向心加速度: 2 vA a向 k
快速陀螺应用的实际例子：炮弹的旋转，回转力矩，回转罗盘
其他、
1. 刚体转动的稳定性，
2. 刚体定轴转动时支点上的动反作用力， 3. 刚体的碰撞
第4章
刚
体
4.1 半径为r1的圆柱体P约束在水平面上运动，另一个半径为r2的圆柱体S约 束在P上运动(如图所示)。分别就下列三种情况写出体系的自由度，并选取 适当的广义坐标表示S和P的角速度:(1)P 固定不动，S在P上只滚不滑; (2)S 和P之间，P和平面之间绝对粗糙，接触点相对速度都是零;(3)S和P之间， P和平面之间绝对光滑 解：(1)以P中心O为原点， S由起始位置滚至图示位置时，经过弧长 r1 , r 经过S的角度为 1 由于P固定不动， p 0， r2 k ，而S自转角速度 则S相对P的角速度 sp d r1 r1 s ' dt r2 r2 由角速度合成： k r1 k (1 r1 ) k s sp s ' r2 r2
第四章 虚功原理
（1）解除约束代之以约束力，建立静力状态（k）； （2）沿所求约束力的方向给以单位位移，建立协调的位移状态（m）； （3）用“m”状态考察“k”状态的平衡条件，建立虚功方程，求解未知力。
结构力学
第4章 虚功原理
例题1
A a
试利用单位位移法求FRD 和M E。
q=F/ 2a E a B a F
解： 1、解除D支座约束代之以FRD作用，
W (外力虚功) = U (变形虚功)
虚功方程
1
平面杆系结构 虚功方程
Fk km = ∑ ∫ FNk ε m ds + ∑ ∫ FQk γ m ds + ∑ ∫ M k
s s s
ρm
ds
虚功原理适用范围：刚体体系、弹性、非弹性、线性、非线性 的变形体系均可适用。
结构力学
第4章 虚功原理
虚功原理两种应用形式：
1
s s
ρm
Fk km = ∑ ∫ FNk ε m ds + ∑ ∫ FQk γ m ds + ∑ ∫ M k
ρm
ds
FQk FQm FNk FNm M M = ∑∫ ds + ∑ ∫ λ ds + ∑ ∫ k m ds s s s EA GA EI
结构力学
第4章 虚功原理
1、虚功互等定理
Fk km FQk FQm FNk FNm MkMm = ∑∫ ds + ∑ ∫ λ ds + ∑ ∫ ds s s s EA GA EI
Mk Mk
FNk
FNk
FQ k FQ k
FQ k
FQ k
ρm
ρm
dθm
dθm
γmds
ds
εmd s
结构力学
第4章 虚功原理
例题1
A a
试利用单位位移法求FRD 和M E。
q=F/ 2a E a B a F
解： 1、解除D支座约束代之以FRD作用，
W (外力虚功) = U (变形虚功)
虚功方程
1
平面杆系结构 虚功方程
Fk km = ∑ ∫ FNk ε m ds + ∑ ∫ FQk γ m ds + ∑ ∫ M k
s s s
ρm
ds
虚功原理适用范围：刚体体系、弹性、非弹性、线性、非线性 的变形体系均可适用。
结构力学
第4章 虚功原理
虚功原理两种应用形式：
1
s s
ρm
Fk km = ∑ ∫ FNk ε m ds + ∑ ∫ FQk γ m ds + ∑ ∫ M k
ρm
ds
FQk FQm FNk FNm M M = ∑∫ ds + ∑ ∫ λ ds + ∑ ∫ k m ds s s s EA GA EI
结构力学
第4章 虚功原理
1、虚功互等定理
Fk km FQk FQm FNk FNm MkMm = ∑∫ ds + ∑ ∫ λ ds + ∑ ∫ ds s s s EA GA EI
Mk Mk
FNk
FNk
FQ k FQ k
FQ k
FQ k
ρm
ρm
dθm
dθm
γmds
ds
εmd s
工程力学 第4章 平面任意力系_2
第四章 平面任意力系
E
300
200
B C A 100
100
FEx F Ey
B FAy D W C
FAx
D W
∑F
y
= 0 FEy + FAy − W = 0 FAy = −66.7 N
第四章 平面任意力系
例：已知 DK = KD ,AB = BC =1m ,F=1732kN , Q=1000kN 处的约束力。 求：A、E 处的约束力。
A、B 连线与 轴不垂直 连线与Ox
A、B、C三点不共线 三点不共线
第四章 平面任意力系
平面平行力系平衡的条件： 平面平行力系平衡的条件
y
平面问题
∑ Fy = 0 ∑ M O ( F ) = 0
o
x
平面平行力系平衡的条件（二矩式） 平面平行力系平衡的条件（二矩式）：
∑ M A ( F ) = 0 , ∑ M B ( F ) = 0
第四章 平面任意力系
与重物的总重力为P=10kN，梁的 例4-2：已知起重电动机 与重物的总重力为 ：已知起重电动机E与重物的总重力为 ， 重力为W=5kN。已知角度θ=30º。求：钢索 和铰链 的约 。已知角度 钢索BC和铰链 和铰链A的约 重力为 。 束力， 束力，钢索受力的最大值 y
FBC FAx
F
E K
300
解：1、研究ED杆，画受力图. 研究 杆 画受力图. E D
FEx
F
FEy
F D
D
∑
W M E (F) = 0 FD ED cos 30 − F ⋅ EK = 0 FD = 1000kN
A
B
C
∑ Fx = 0
理论力学第4章
n BA
τ
aτ BA
B
aA
n BA
当ω ≠ 0 时
a
A
ω
a ≠0
n BA
α
[aB ]AB ≠ [aA]AB
当 ω = 0时
n aBA = 0 aτ ⊥ BA BA
aA
有 [ aB ] AB = [ aA ] AB
4-2 平面图形上各点的速度与加速度分析
4.2.3 投影法 已知R﹑ω﹑30°，求vB，αB。
r
A
O
vA
vO 2rω ωO = = = 2ω r r
ωO
r
ω
vA = 2rωO = 4rω
5.已知 aO ,θ , R求 α? ,
O
R
θ
vo
ao
vO = Rω
τ 对t求导 αO = Rα
aO cosθ ∴ α= R
4-2 平面图形上各点的速度与加速度分析
4-2-2 瞬心法 二. 加速度瞬心法 a)加速度瞬心Ca S上 aCa = 0
a
n CB
τ aCB
C
R
ω
aC
aB
x
①铰接，各点运动方向确定，可顺次求解； ② ωAB = 0 ,
[αA ]AB =[αB ]AB；
③投影方向的选择。
4.3 平面机构的运动分析
4-3-1 一般分析思路 2 .瓦特行星转动机构。 已知 r1 = r2 = 30 3cm
O A = 75cm,AB =150cm,ω0 = 6 (1/s) ,θ = 60o ,β = 90o 1
S
v BA
ω
vA
B
vA
A
vB = vA + vBA
τ
aτ BA
B
aA
n BA
当ω ≠ 0 时
a
A
ω
a ≠0
n BA
α
[aB ]AB ≠ [aA]AB
当 ω = 0时
n aBA = 0 aτ ⊥ BA BA
aA
有 [ aB ] AB = [ aA ] AB
4-2 平面图形上各点的速度与加速度分析
4.2.3 投影法 已知R﹑ω﹑30°，求vB，αB。
r
A
O
vA
vO 2rω ωO = = = 2ω r r
ωO
r
ω
vA = 2rωO = 4rω
5.已知 aO ,θ , R求 α? ,
O
R
θ
vo
ao
vO = Rω
τ 对t求导 αO = Rα
aO cosθ ∴ α= R
4-2 平面图形上各点的速度与加速度分析
4-2-2 瞬心法 二. 加速度瞬心法 a)加速度瞬心Ca S上 aCa = 0
a
n CB
τ aCB
C
R
ω
aC
aB
x
①铰接，各点运动方向确定，可顺次求解； ② ωAB = 0 ,
[αA ]AB =[αB ]AB；
③投影方向的选择。
4.3 平面机构的运动分析
4-3-1 一般分析思路 2 .瓦特行星转动机构。 已知 r1 = r2 = 30 3cm
O A = 75cm,AB =150cm,ω0 = 6 (1/s) ,θ = 60o ,β = 90o 1
S
v BA
ω
vA
B
vA
A
vB = vA + vBA
工程力学理论力学第4章
Fi xi F
平衡的充要条件为 主矢 R =0
主矩MO =0
所以 平面平行力系的平衡方程为：
Y 0
mO (Fi )0
一矩式
实质上是各力在x 轴上的投影 恒等于零，即 X 0 恒成立 ，所以只有两个 独立方程，只能求解两个独立 的未知数。
mA (Fi ) 0 二矩式
RB
qa 2
m a
2P
200.8 2
16 0.8
22012(
kN)
YA PqaRB 20200.81224(kN)
§4-4 物体系统的平衡、静定与超静定问题的概念
一、静定与超静定问题的概念
我们学过：
平面汇交力系 X 0 Y 0
两个独立方程，只能求两个独立 未知数。
例3. 塔式起重机翻转问题
如图所示塔式起重机的简图。已知机身重W，重 心在C处；最大的起吊重量为P。各部分的尺寸如图。 求能保证起重机不致翻转的平衡锤重Q大小。
b
Q
C e
W
a
P
A
B
dd
★ 物体系统的平衡问题
例5. 如图所示，水平梁由AB和BC两部分组成，它们
在B处用铰链相连。梁的A端固定在墙上，在C处受滚 动支座支持，该支座放在倾角为α =30°的光滑斜面 上。已知P=4KN，均布载荷q=2KN/m，尺寸如图。试求 A、B、C处约束反力。
解物系问题的一般方法：
由整体
局部（常用），由局部
整体（用较少）
[例1] 已知：OA=R, AB= l , 当OA水平时，冲压力为P 时，
求：①M=？②O点的约束反力？③AB杆内力？ ④冲头给导轨的侧压力？
理论力学第四章1解剖
相对速度 vr 牵连速度ve
4.1.3 速度合成定理
由
rM rO r xi
r yj
zk
可得
va
drM dt
rO xi yj zk xi yj zk
再由vr与ve的定义式，有速度合成定理 va vr ve
该定理表明，无论动系作何种运动，动点在某瞬时的绝 对速度等于该瞬时它的牵连速度与相对速度的矢量和。
再由ar与ae的定义式，有
aa ae ar 2(xi yj zk)
结果与动系的运动（牵连运动）特点有关
1. 牵连运动为平移
此时动系的单位矢量 i, j, k 是常矢量，即 i j k 0 ，所以
aa ae ar
牵连运动为平移时点的加速度合成定理：牵连运动 为平移时，动点在某瞬时的绝对加速度等于该瞬时它的 牵连加速度与相对加速度的矢量和。
rM r
rO xi
r yj
zk
设此瞬时动点M的牵连点为 M’，它在定系中的矢径是 rM’。有如下关系
rM rM
z
M
rM
y’
r’ k’ j’
O’
rO’
O
y
x
z’ x’ i’
1. 绝对速度va和绝对加速度aa 动点M相对定系运动的速度和加
速度称为绝对速度和绝对加速度。
va
drM dt
aa
思考题讨论
1. 图示速度分析正确吗？
2.图示速度分析正确吗？
例4-3:凸轮半径为R,沿水平面以匀速v0向右运动,求φ=600 时杆AB的速度.
B
A R
φ
解： 1.动点与动系的选择： 2.三种速度分析、作图： 3.用速度合成定理求解：
v0
①.正确地选取并明确地指出动点和动系： ．动点和动系不能在同一刚体上； ．在某一物体上，动点相对该物体的位置应是不变的点； ．动点的相对运动轨迹要清晰可辨； ．常取两物体的接触点、滑块、套筒、小环、小球等为动点。
工程力学课件 第四章 平面一般力系
第4章 平面一般力系
14
3. 力系平衡
0, MO 0 FR
FR′
O
MO
合力矩定理 平面一般力系如果有合力，则合力对该力系 作用面内任一点之矩等于力系中各分力对该点之 矩的代数和。
课程：工程力学
第4章 平面一般力系
15
证明： 如下图所示，显然有
M O ( FR ) FR d M O , M O M O ( F ), M O ( FR ) M O ( F )
课程：工程力学
第4章 平面一般力系
1
第4章 平面一般力系
前言 §4-1 力线平移定理 §4-2 平面一般力系向一点简化 §4-3 分布荷载 §4-4 平面一般力系的平衡条件
§4-5 平面平行力系的平衡条件 §4-6 物体系统的平衡问题 §4-7 滑动摩擦
课程：工程力学
第4章 平面一般力系
2
前言
平面一般力系是指位于同一平面内的诸力其作 用线既不汇交于一点，也不互相平行的力系。 工程计算中的很多实际问题都可以简化为平 面一般力系来处理。
FAx A D
B x
arctan
FA y FA x
E F
FAy
P
思考题 4-4 如果例题4-3中的荷载F可以沿AB梁移动，问： 荷载F在什么位置时杆BC所受的拉力（FT）最大？ 其值为多少？
课程：工程力学
第4章 平面一般力系
33
思考题 4-5 (1) 由右图所示的受力图，试按
M A (F ) 0 M B (F ) 0 F
22
(2) 非均布荷载：荷载集度不是常数。 如坝体所受的水压力等。
A qy y
B C
课程：工程力学
哈工大理论力学第四章
∑F =0
z
FOA sin 45 −P = 0
（拉） F = −1414N F = F = 707N OA OB OC
例4-4 已知： F, l, a,θ 求： x ( F ) , My ( F ) , Mz ( F ) M 解：把力 F 分解如图
Mx F = −F ( l + a) cosθ My F = −Fl cosθ
∑F = 0
FA = 8.66kN
例4-3 已知：P=1000N ,各杆重不计. 求：三根杆所受力. 解：各杆均为二力杆，取球铰O， 画受力图。
∑F =0 ∑F =0
x
y
FOB sin 45 − FOC sin 45 = 0
− FOB cos 45 − FOC cos 45 − FOA cos 45 = 0
空间平行力系的平衡方程
∑F = 0 ∑M
z
x
=0
பைடு நூலகம்
∑M
y
=0
2.空间约束类型举例 2.空间约束类型举例 3.空间力系平衡问题举例 3.空间力系平衡问题举例
§4–6 重 心 6
1．计算重心坐标的公式
P ⋅ xC = P ⋅ x1 + P2 ⋅ x2 + .... + Pn ⋅ xn 1 = ∑ Pi ⋅ xi
M = rBA × F
2、力偶的性质 (1） (1）力偶中两力在任意坐标轴上投影的代数和为零 . （2）力偶对任意点取矩都等于力偶矩，不因矩心的改 力偶对任意点取矩都等于力偶矩， 变而改变。 变而改变。
M O ( F , F ′) = M O ( F ) + M O ( F ′) = rA × F + rB × F ′
建筑力学(第四章)
Da a
Fx 0 :
FAx FCcon45 0
FAx FCcon45
2F
2 2
F
FAx
A
M0=Fa
C
FAy FC
B F
Fy 0 : FAy FC sin 45 F 0
FAy FC sin 45 F
2F
2 2
F
第二节 平面一般力系向作用面内任一点简化
简化中心 F1
OA
F3 C
B
F2 =
m1F'1′ F′3 O
m2
F'2′ =
m3
M0 O
FR
主矢（FR’ ）：将平面汇交力系 （F1’、F2’、 F3’ ）合成， 可得一合力FR’，这个力称为原力系的主矢。通过0点。
大小:
FR ( Fx)2 ( Fy)2 ( Fx )2 ( Fy )2
0
aa
负号说明约束反力FAX的实际方向与图中
假定方向相反。
应用举例
例4-4：求图示梁支座的
y
F
F
约束反力。已知 ：
Fy
F 2kN a 2m A
解:取梁为研究对象。
Fx
受力图如图示。建立坐标
a
a
FB
Bx
a
系，列平衡方程：
Fx 0 Fy 0
M
O
(
F
)
0
(2) 主矢、主矩均不为零 FR≠0 Ｍ0≠0 根据力的平移定理的逆过程可知，主矢FR和主矩ＭO也可
以合成为一个 合力FR。
工程力学课后答案第4章
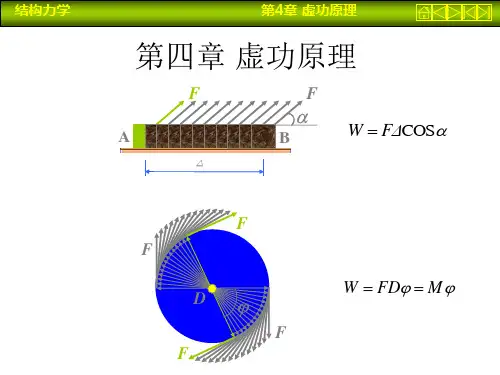
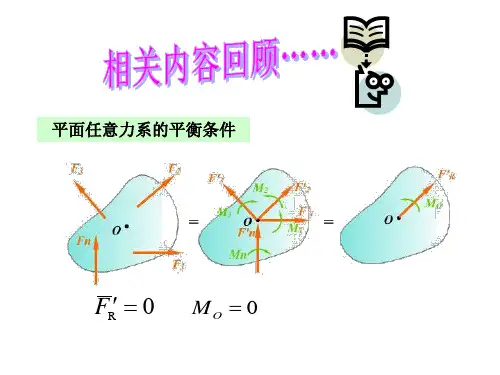
第4章影响线1.【解】 （1）图4-22（2）图4-231M 的影响线A F 的影响线SA M 的影响线C F 的影响线SC（3）图4-24（4）图4-25（1）图4-26M CF SC（2）图4-273. 【解】（1）图4-28判别60kN 和20kN 是否为临界荷载403<60+20+309 40+603>20+309所以60kN 是临界荷载40+603>20+309 40+60+203>309所以20kN 不是临界荷载C 0.752.251.751.25M CC0.250.750.5830.417F SCC0.0830.750.523F SC0.250.25M Cmax =40×0.75+60×2.25+20×1.75+30×1.25=237.5kN ·mF SCmax =40×0.75+60×0.583+20×0.417+30×0.25 =80.82kN ·mF SCmin =−60×0.083−20×0.25+30×0.583 =−9.16kN ·m判别478.5kN 是否为临界荷载03<478.5+324.5+324.59 478.53>324.5×29所以478.5kN 是临界荷载判别左边324.5kN 是否为临界荷载478.53>324.5×29 478.5+324.53>324.59所以324.5kN 不是临界荷载C2.251.88750.6875C0.750.250.25M CF SCF SCC0.750.6290.2294. 【解】 （1）图4-30①求使跨中截面C 发生最大弯矩的临界荷载 判别左边324.5kN06<324.5+324.56 324.56≥324.56所以第一个324.5kN 是临界荷载1.2m4.8m0.636m②求临界载荷的位置因为对称，右边集中力也为临界荷载，产生相同大小的跨中弯矩合力F =629kN ，所以 x =l 2−a 2=122−2.42=4.8m③求绝对最大弯矩M Cmax =478.5×2.25+324.5×1.8875+324.5×0.6875 =1912.21kN ·mF SCmax =478.5×0.75+324.5×0.629+324.5×0.229 =637.296kN ·mF SCmin =−324.5×0.25 =−81.125kN ·mM Cmax =324.5×3+324.5×0.6 =1168.2kN ·m（2）图4-31①求使跨中截面C 发生最大弯矩的临界荷载06≤120+606 1206≥60+206所以120kN 是临界荷载2m4m136m②求临界载荷的位置因为对称，右边集中力也为临界荷载，产生相同大小的跨中弯矩合力F =200kN ，因为 200∙x ′=60×4+20×8 所以 x ′=2m =a x =l2−a2=122−22=5m ，此时20kN 不在范围内重新计算合力F =120+60=180kN ，因为 180∙x ′=60×4 所以 x ′=1.333m =ax =l 2−a 2=122−1.3332=5.334m ③求绝对最大弯矩5. 【解】①自重下的弯矩图kN·mM Cmax =120×3+60×1=420kN ·m②各截面弯矩影响线及相应不利荷载的位置M 1的影响线M 2的影响线M 3的影响线单位：kN·m移动荷载下弯矩包络图③叠加①和②的弯矩图450706.7706.7450单位：kN·m0.5m0.5m。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(力学)第4章(修)
单击此处添加副标题
力的瞬时作用规律——第二章 牛顿第二定律 力对时间积累作用规律——第三章 动量定理 力对空间积累作用规律——？
E
第四章 功和能
质点受力的作用时，如果持续一段时间，质点的动 量会改变；如果质点由空间位置的变化，则力对位移的 累积（功）会使质点的能量（动能和势能）发生变化。 对功和能的研究，是经典力学中重要的组成部分。
解： AFdx
平衡时：kxm g xmg 0.1m
k
F
20cm
I. 01c0m Fkx
A100.1kxd 1 2xk2x1J
I.I1 02c0m Fmg
0 .2
A 20 .1mg m d(0 .g x 2 0 .1 )2J
AA 1A 23J
E
§4-2 动能定理
Theorem of Kinetic Energy
正 v0
f mg
解：合外力对质点所做的功等于质点动能的增量
A EkEkEk0
m gfH01 2m02 v
f mv02 mg1N 2H
E
[例]质量为M的木快静止在光滑的水平面上，质量为m、速度为 v 的子弹
沿水平方向打入木块并陷在其中，试计算相对于地面木块对子弹所做的功 W1及子弹对木块所作的功W2。 解：木块、子弹系统水平方向不受外力作用，动量守恒。
陨石落地过程中，万有引力的功
地球 O
AF dr R R hG r2M dr m GM R R hd r2 r m R G (R M h) mh
v 2GM R(Rhh)v02
E
[例]把一质量为m＝0.4 kg的物体，以初速度v 0＝20 m/s竖直向上抛出，测 得上升的最大高度H＝16 m，求空气对它的阻力f（设为恒力）等于多大？
B A F id r A i
i
结论：合力的功等于各分力沿同一路径所做功的代数和。
3.功率
功率的定义：单位时间内所做的功。即
P limAdA
t0 t dt
E
4.一对力的功
设两个质点m1和m2之间的相互作
用力为： f12——质点1受质点2的作用力； f2 1——质点2受质点1的作用力。
dr1
f12
E
[例]在如图所示系统中（滑轮质量不计，轴光滑），外力 F通过不可伸长的
绳子和倔强系数k=200N/m的轻弹簧缓慢地拉地面上的物体，物体质量
M=2Kg ,初始时弹簧为自然长度，在把绳子拉下20cm的过程中，F 所做的功
为（重力加速度g取10m/s2) [
]
( A ) 2 J( B ) 1 J( C ) 3 J( D ) 4 J( E ) 2 J0
(A)动量不守恒，动能守恒．
(B)动量守恒，动能不守恒．
(C)对地心的角动量守恒，动能不守恒．
与机械运动相联系的能量守恒定律（机械能守恒 定律），是普遍的能量守恒定律的一种特殊形式。
E
§4-1 功
Work
E
1.功的定义
功——力在位移方向上的分量与位移大小的乘积。
—位设移质元dr点受，力则为该F力，做它功d的A空表间示位为置发生一无限小的位移—
d A F td rF d rcosd AFdr
E
1.质点的动能定理
力对空间的积累（即做功）会给质点带来怎样的结果？
考虑合力的功：
过程量A A B F d r A B F td r m A B d dd v r t m v v A B vdv
即状态量 1mv来自2A12mvB2 12mvA2
AEk BEk A
2
在B点的取值
状态量 1 mv 2 2
用下质点的运动方程为 X3t4t2t3 (S)I。在0到4s的时间间隔内：
（1）力 F 的冲量大小I=
(2)力 F对质点所作的功W=
解： I F dW t F d r Fma
vdx38t3t2 dt
adv86t dt
IF d0 4 t8 6 td t 8 t 3 t20 4 16
W F d 8 6 x t v d 0 4 ( 8 t6 t ) 3 8 t 3 t 2 d 1 t 7
动能定理：合外力对质点
在A点的取值
引入动能 Ek：
所做的功等于质点动能的增量。
Ek
1mv2 2
p2 2m
功是能量传递或转化的量度。
E
[例]如图所示陨石在距地面高h处时速度为v0．忽略空气阻力，求 陨石落地的速度.令地球质量为M, 半径为R, 万有引力常量为G．
解： 根据动能定理
h v0
AEK1 2mv21 2mv0 2
E
[例]已知地球质量为M，半径为R．一质量为m的火箭从地面上升到距地面
高度为2R处．在此过程中，地球引力对火箭作的功为
___________________． 解：选择地心为原点，坐标轴如图所示
A
3R R
GMm r2 dr
GMm3R rR
O
GMm 1 1 2GMm 3R R 3R
E
[例]一个力作用在质量为1.0Kg的质点上，使之沿x轴运动。已知在此力作
设子弹打入后二者的共同运动速度为V
mvm M V
木块对子弹所做的功： （对子弹应用动能定理）
W 1 E K 子 1 2 弹 m 2 1 2 V m 2 m v 2 m M M M 2 m v 2
子弹对木块所作的功： （对木块应用动能定理）
W21 2M2V02M m2m V M22
E
[例]人造地球卫星，绕地球作椭圆轨道运动，地球在椭圆的一个焦点上，则 卫星的[ C ]
元功
注意：功是一个标量。 有正有负：
L B
当 090时， dA0； 当 9018时0， dA。0
F
dr
质点沿曲线 L从 A
到 B，整个路径上的 功为元功之和：
B A Fdr
A
A
线积分
L
E
2.合力的功
如果质点同时受到多个力的作用，计算它们等效合力
的功：
A A B F d r A B i F i d r i
f2 1
m
2
dr2
m1
这两个力的元功之和为：
d d A f1 dd 2 d rr1r A 21 f 1 df d2 d 2 ((rr r 11 2d 1 r 2 rr 2f 1)2 )f1表表d 2 1 d 示示r r 2 1 mm 21相相f1 与对对2 参d 于于r 2 照mm 12系的的ff的1 1 相相选对2 对2 (d d 取位位(r1 r无1 移移 关d 。；rr 2 2 ))
单击此处添加副标题
力的瞬时作用规律——第二章 牛顿第二定律 力对时间积累作用规律——第三章 动量定理 力对空间积累作用规律——？
E
第四章 功和能
质点受力的作用时，如果持续一段时间，质点的动 量会改变；如果质点由空间位置的变化，则力对位移的 累积（功）会使质点的能量（动能和势能）发生变化。 对功和能的研究，是经典力学中重要的组成部分。
解： AFdx
平衡时：kxm g xmg 0.1m
k
F
20cm
I. 01c0m Fkx
A100.1kxd 1 2xk2x1J
I.I1 02c0m Fmg
0 .2
A 20 .1mg m d(0 .g x 2 0 .1 )2J
AA 1A 23J
E
§4-2 动能定理
Theorem of Kinetic Energy
正 v0
f mg
解：合外力对质点所做的功等于质点动能的增量
A EkEkEk0
m gfH01 2m02 v
f mv02 mg1N 2H
E
[例]质量为M的木快静止在光滑的水平面上，质量为m、速度为 v 的子弹
沿水平方向打入木块并陷在其中，试计算相对于地面木块对子弹所做的功 W1及子弹对木块所作的功W2。 解：木块、子弹系统水平方向不受外力作用，动量守恒。
陨石落地过程中，万有引力的功
地球 O
AF dr R R hG r2M dr m GM R R hd r2 r m R G (R M h) mh
v 2GM R(Rhh)v02
E
[例]把一质量为m＝0.4 kg的物体，以初速度v 0＝20 m/s竖直向上抛出，测 得上升的最大高度H＝16 m，求空气对它的阻力f（设为恒力）等于多大？
B A F id r A i
i
结论：合力的功等于各分力沿同一路径所做功的代数和。
3.功率
功率的定义：单位时间内所做的功。即
P limAdA
t0 t dt
E
4.一对力的功
设两个质点m1和m2之间的相互作
用力为： f12——质点1受质点2的作用力； f2 1——质点2受质点1的作用力。
dr1
f12
E
[例]在如图所示系统中（滑轮质量不计，轴光滑），外力 F通过不可伸长的
绳子和倔强系数k=200N/m的轻弹簧缓慢地拉地面上的物体，物体质量
M=2Kg ,初始时弹簧为自然长度，在把绳子拉下20cm的过程中，F 所做的功
为（重力加速度g取10m/s2) [
]
( A ) 2 J( B ) 1 J( C ) 3 J( D ) 4 J( E ) 2 J0
(A)动量不守恒，动能守恒．
(B)动量守恒，动能不守恒．
(C)对地心的角动量守恒，动能不守恒．
与机械运动相联系的能量守恒定律（机械能守恒 定律），是普遍的能量守恒定律的一种特殊形式。
E
§4-1 功
Work
E
1.功的定义
功——力在位移方向上的分量与位移大小的乘积。
—位设移质元dr点受，力则为该F力，做它功d的A空表间示位为置发生一无限小的位移—
d A F td rF d rcosd AFdr
E
1.质点的动能定理
力对空间的积累（即做功）会给质点带来怎样的结果？
考虑合力的功：
过程量A A B F d r A B F td r m A B d dd v r t m v v A B vdv
即状态量 1mv来自2A12mvB2 12mvA2
AEk BEk A
2
在B点的取值
状态量 1 mv 2 2
用下质点的运动方程为 X3t4t2t3 (S)I。在0到4s的时间间隔内：
（1）力 F 的冲量大小I=
(2)力 F对质点所作的功W=
解： I F dW t F d r Fma
vdx38t3t2 dt
adv86t dt
IF d0 4 t8 6 td t 8 t 3 t20 4 16
W F d 8 6 x t v d 0 4 ( 8 t6 t ) 3 8 t 3 t 2 d 1 t 7
动能定理：合外力对质点
在A点的取值
引入动能 Ek：
所做的功等于质点动能的增量。
Ek
1mv2 2
p2 2m
功是能量传递或转化的量度。
E
[例]如图所示陨石在距地面高h处时速度为v0．忽略空气阻力，求 陨石落地的速度.令地球质量为M, 半径为R, 万有引力常量为G．
解： 根据动能定理
h v0
AEK1 2mv21 2mv0 2
E
[例]已知地球质量为M，半径为R．一质量为m的火箭从地面上升到距地面
高度为2R处．在此过程中，地球引力对火箭作的功为
___________________． 解：选择地心为原点，坐标轴如图所示
A
3R R
GMm r2 dr
GMm3R rR
O
GMm 1 1 2GMm 3R R 3R
E
[例]一个力作用在质量为1.0Kg的质点上，使之沿x轴运动。已知在此力作
设子弹打入后二者的共同运动速度为V
mvm M V
木块对子弹所做的功： （对子弹应用动能定理）
W 1 E K 子 1 2 弹 m 2 1 2 V m 2 m v 2 m M M M 2 m v 2
子弹对木块所作的功： （对木块应用动能定理）
W21 2M2V02M m2m V M22
E
[例]人造地球卫星，绕地球作椭圆轨道运动，地球在椭圆的一个焦点上，则 卫星的[ C ]
元功
注意：功是一个标量。 有正有负：
L B
当 090时， dA0； 当 9018时0， dA。0
F
dr
质点沿曲线 L从 A
到 B，整个路径上的 功为元功之和：
B A Fdr
A
A
线积分
L
E
2.合力的功
如果质点同时受到多个力的作用，计算它们等效合力
的功：
A A B F d r A B i F i d r i
f2 1
m
2
dr2
m1
这两个力的元功之和为：
d d A f1 dd 2 d rr1r A 21 f 1 df d2 d 2 ((rr r 11 2d 1 r 2 rr 2f 1)2 )f1表表d 2 1 d 示示r r 2 1 mm 21相相f1 与对对2 参d 于于r 2 照mm 12系的的ff的1 1 相相选对2 对2 (d d 取位位(r1 r无1 移移 关d 。；rr 2 2 ))