高中数学必修一基本初等函数知识点与典型例题总结精品PPT课件

基本初等函数第一讲 幂函数1、幂函数的定义一般地，形如y x α=（x ∈R ）的函数称为幂函数，其中x 是自变量，α是常数.如11234,,y x y x y x -===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数.注意：y x α=中，前面的系数为1，且没有常数项2、幂函数的图像（1）y x = （2）12y x = （3）2y x = （4）1y x -= （5）3y x =3、幂函数的性质（1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）（原因：11x=）；（2）0>α时，幂函数的图象通过原点，并且在区间),0[+∞上是增函数．特别地，当1>α时，幂函数的图象下凸；当10<<α时，幂函数的图象上凸；（3）0<α时，幂函数的图象在区间),0(+∞上是减函数．在第一象限内，当x 从右边趋向原点时，图象在y 轴右方无限地逼近y 轴正半轴，当x 趋于∞+时，图象在x 轴上方无限地逼近x 轴正半轴．分数指数幂概念 有理指数幂运算性质(0,,)r s r s a a a a r s Q +=>∈；()(0,,)r s rs a a a r s Q =>∈(0,,*,1)a m n N n >∈>且 ()(0,0,)r r r ab a b a b r Q =>>∈第二讲 指数函数1、指数（1）n 次方根的定义若x n =a ，则称x 为a 的n 次方根，“n”是方根的记号.在实数范围内，正数的奇次方根是一个正数，负数的奇次方根是一个负数，0的奇次方根是0；正数的偶次方根是两个绝对值相等符号相反的数，0的偶次方根是0，负数没有偶次方根.（2）方根的性质①当n 为奇数时，n n a =a . ②当n 为偶数时，n n a =|a |=⎩⎨⎧<-≥).0(),0(a aa a（3）分数指数幂的意义①a nm =n m a （a ＞0，m 、n 都是正整数，n ＞1）. ②an m -=nm a1=nma1（a ＞0，m 、n 都是正整数，n ＞1）.2、指数函数的定义一般地，函数xy a =（a ＞0且a ≠1）叫做指数函数，其中x 是自变量，函数的定义域为R . 说明：因为a ＞0，x 是任意一个实数时，xa 是一个确定的实数，所以函数的定义域为实数集R .n mnm a a=nmn m nm aa a1＝=-000,0xx a a x a ⎧>⎪=⎨≤⎪⎩x当时,等于若当时,无意义若a ＜0，如1(2),,8xy x x =-=1先时,对于=等等,6在实数范围内的函数值不存在. 若a =1, 11,xy == 是一个常量， 5,,3,31x x x a y x y y +===+1xx为常数,象y=2-3,y=2等等, 不符合(01)x y a a a =>≠且的形式,所以不是指数函数.3、 指数函数的图像及其性质（1）底数互为倒数的两个指数函数的图象关于y 轴对称.（2）在[,]x a b f x a 上,()=（a ＞0且a ≠1）值域是[(),()][(),()];f a f b f b f a 或 （3）若0,x f x f x x ≠≠∈则()1;()取遍所有正数当且仅当R;（4）对于指数函数()xf x a =（a ＞0且a ≠1），总有(1);f a =（5）当a ＞1时，若1x ＜2x ，则1()f x ＜2()f x ；第三讲 对数函数1、 对数（1）对数的概念一般地，若(0,1)xa N a a =>≠且，那么数x 叫做以a 为底N 的对数，记作log a x N =a 叫做对数的底数，N 叫做真数.如：24416,2log 16==则，读作2是以4为底，16的对数. 1242=，则41log 22=，读作12是以4为底2的对数. （2）指数式与对数式的关系：a b =N ⇔log a N =b （a ＞0，a ≠1，N ＞0）.两个式子表示的a 、b 、N 三个数之间的关系是一样的，并且可以互化.（3）对数运算性质:①log a （MN ）=log a M +log a N . ②log a NM =log a M －log a N . ③log a M n=n log a M .（M ＞0，N ＞0，a ＞0，a ≠1） ④对数换底公式：log b N =bNa a log log （a ＞0，a ≠1，b ＞0，b ≠1，N ＞0）. （4）两类对数① 以10为底的对数称为常用对数，10log N 常记为lg N .② 以无理数e=2.71828…为底的对数称为自然对数，log e N 常记为ln N .以后解题时，在没有指出对数的底的情况下，都是指常用对数，如100的对数等于2，即lg1002=.2、对数函数的概念一般地，我们把函数log a y x =（a ＞0且a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）． 3、对数函数的图象及其性质a <11))底数互为倒数的两个对数函数的图象关于x 轴对称.。

高一数学必修1知识点总结ppt 本文是关于高一数学必修1知识点总结ppt的内容。

下面将具体介绍每个知识点的要点和主要内容。

第一部分：函数与方程1. 函数的概念与性质函数的定义、自变量、因变量、定义域、值域、对应关系等基本概念。

函数的奇偶性、单调性、周期性等性质。

2. 二次函数二次函数的基本形式、顶点形式、根与系数的关系。

二次函数的图像、性质、最值问题等。

3. 一次函数一次函数的表达式、图像、斜率、截距等基本概念。

一次函数的平行、垂直以及两函数关系的判定方法。

第二部分：平面解析几何1. 点、直线和平面的基本概念点的坐标表示、距离公式、中点公式等基本概念。

直线的倾斜角、方向角、截距式和一般式等表示方法。

平面的法向量、点法式和一般式等表示方法。

2. 直线的位置关系与方程直线的平行、垂直判定方法。

直线与平面的位置关系判定方法。

直线的点斜式、两点式和截距式等方程的表示方法。

3. 圆的方程与性质圆的标准方程、一般方程及其应用。

圆心、半径、弦、弧、切线、切点等基本概念。

第三部分：三角函数1. 任意角与弧度制角的概念与表示方法。

弧度制的定义与换算公式。

2. 三角比的概念与性质正弦、余弦、正切等三角比的定义与性质。

三角比中的基本关系和特殊角值。

3. 三角函数图像与性质正弦函数、余弦函数、正切函数的图像与性质。

三角函数的周期性、奇偶性、单调性等特点。

第四部分：概率与统计1. 基本统计概念总体与样本、频率与频数、平均数等基本概念。

中位数、众数、四分位数等统计中常用的概念。

2. 概率的基本概念随机事件的定义、基本事件、对立事件等概念。

概率的定义与性质、加法定理与乘法定理。

3. 极限与无穷极限的概念与性质、左极限和右极限的定义。

无穷大与无穷小的概念与性质。

以上是高一数学必修1知识点总结ppt的主要内容。

通过这份ppt，同学们可以对相关知识点有一个清晰的了解，进一步提高数学学习的效果。

希望本文对你有所帮助！。

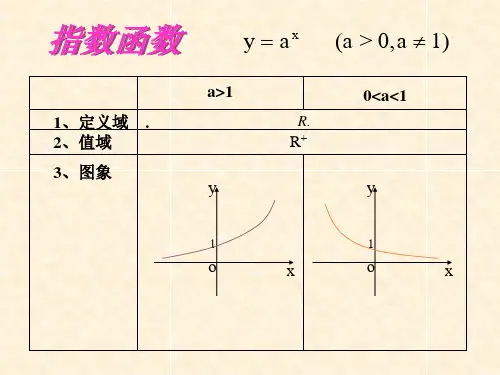
n a n；当 为偶数时，⎨-a2.1.1 指数与指数幂的运算（1）根式的概念第二章基本初等函数知识点整理〖2.1〗指数函数①如果 x n = a , a ∈ R , x ∈ R , n > 1，且 n ∈ N + ，那么 x 叫做 a 的 n 次方根．当 n 是奇数时， a 的 n 次方根用符号表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号 0；负数 a 没有 n 次方根．表示，负的 n 次方根用符号- n a 表示；0 的n 次方根是②式子na 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当 n 为奇数时， a 为任意实数；当 n 为偶数时， a ≥ 0 ．③根式的性质： ( n a )n = a ；当 n 为奇数时， = a n =| a |= ⎧a⎩(a ≥ 0) ．(a < 0)（2） 分数指数幂的概念m①正数的正分数指数幂的意义是： an= (a > 0, m , n ∈ N +, 且 n > 1) ．0 的正分数指数幂等于 0．②正数的负分a -m= ( )1 m( ) 1(a > 0, m , n ∈ N , n > 1) 注意口诀：数指数幂的意义是：nn = n m+且 ．0 的负分数指数幂没有意义．aa底数取倒数，指数取相反数．（3） 分数指数幂的运算性质① a r ⋅ a s = a r +s (a > 0, r , s ∈ R ) ② (ar )s= a rs (a > 0, r , s ∈ R ) ③ (ab )r = a r b r (a > 0, b > 0, r ∈ R )2.1.2 指数函数及其性质（4） 指数函数函数名称指数函数定义函数 y = a (a > 0且 a ≠ 1) 叫做指数函数a > 1 0 < a < 1图象y 1yOya x(0,1)xya xy 1Oy(0,1)x定义域 R值域 （0,+∞）过定点 图象过定点（0,1），即当 x=0 时，y=1．奇偶性 非奇非偶单调性在 R 上是增函数在 R 上是减函数n a n a nn a m nab〖2.2〗对数函数【2.2.1】对数与对数运算（1） 对数的定义①若 a x = N (a > 0,且a ≠ 1) ，则 x 叫做以 a 为底 N 的对数，记作 x = log a N ，其中 a 叫做底数， N 叫做真数．②负数和零没有对数．③对数式与指数式的互化： x = log a N ⇔ a x = N (a > 0, a ≠ 1, N > 0) ．（2） 几个重要的对数恒等式:log a 1 = 0 ， log a a = 1， log a a b = b ．（3） 常用对数与自然对数：常用对数： lg N ， 即log 10 N ；自然对数： ln N ， 即log e N （其中 e = 2.71828 …）．（4） 对数的运算性质如果 a > 0, a ≠ 1, M > 0, N > 0 ，那么①加法： log M + log N = log (MN )②减法： log M - log N = logMaa aaaaN③数乘： n log a M= log a M n (n ∈ R )log aN = NlogM n =nlog M (b ≠ 0, n ∈ R ) log N =log b N(b > 0,且b ≠ 1)⑤a bba⑥换底公式：alog aa ④【2.2.2】对数函数及其性质（5）对数函数函数名称对数函数定义函数y = log a x(a >0 且a≠ 1) 叫做对数函数图象a > 1 0 <a < 1yOx 1(1, 0)y log a xxyOx 1(1, 0)y logaxx定义域(0, +∞)值域R过定点图象过定点(1, 0) ，即当x = 1 时，y = 0 ．奇偶性非奇非偶单调性在(0, +∞) 上是增函数在(0, +∞) 上是减函数函数值的变化情况log a x > 0 (x > 1)log a x = 0 (x = 1)log a x < 0 (0 <x < 1)log a x < 0 (x > 1)log a x = 0 (x = 1)log a x > 0 (0 <x < 1)a 变化对图象的影响在第一象限内，a 越大图象越靠低，越靠近 x轴在第四象限内，a 越大图象越靠高，越靠近 y轴在第一象限内，a 越小图象越靠低，越靠近 x 轴在第四象限内，a 越小图象越靠高，越靠近 y 轴(6)反函数的概念设函数y =f (x) 的定义域为A ，值域为C ，从式子y =f (x) 中解出x ，得式子x =( y) ．如果对于y 在C 中的任何一个值，通过式子x =(y) ，x 在A 中都有唯一确定的值和它对应，那么式子x =(y) 表示x 是y 的函数，函数x =(y) 叫做函数y =f (x) 的反函数，记作x =f -1( y) ，习惯上改写成y =f -1(x) ．（7）反函数的求法①确定反函数的定义域，即原函数的值域；②从原函数式y =f (x) 中反解出x =f -1( y) ；③将x =f -1( y) 改写成y =f -1(x) ，并注明反函数的定义域．（8）反函数的性质q①原函数 y = f (x ) 与反函数 y = f -1(x ) 的图象关于直线 y = x 对称．②函数 y =f (x ) 的定义域、值域分别是其反函数 y = f -1(x ) 的值域、定义域．③若 P (a , b ) 在原函数 y = f (x ) 的图象上，则 P ' (b , a ) 在反函数 y =f -1(x ) 的图象上．④一般地，函数 y =f (x ) 要有反函数则它必须为单调函数．〖2.3〗幂函数（1） 幂函数的定义一般地，函数 y = x 叫做幂函数，其中 x 为自变量，是常数．（2） 幂函数的图象（3） 幂函数的性质①图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限(图象关于 y 轴对称)；是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第一象限．②过定点：所有的幂函数在(0, +∞) 都有定义，并且图象都通过点(1,1) ．③单调性：如果> 0 ，则幂函数的图象过原点，并且在[0, +∞) 上为增函数．如果< 0 ，则幂函数的图象在(0, +∞) 上为减函数，在第一象限内，图象无限接近 x 轴与 y 轴．④奇偶性：当为奇数时，幂函数为奇函数，当为偶数时，幂函数为偶函数．当= （其中 p , q 互质， p 和 pqqq ∈ Z ），若 p 为奇数 q 为奇数时，则 y = x p 是奇函数，若 p 为奇数 q 为偶数时，则 y = x p是偶函数，若 p 为偶数∆ qq 为奇数时，则 y = x p 是非奇非偶函数．⑤图象特征：幂函数 y = x , x ∈(0, +∞) ，当> 1 时，若 0 < x < 1，其图象在直线 y = x 下方，若 x > 1 ，其图象在直线 y = x 上方，当< 1时，若 0 < x < 1，其图象在直线 y = x 上方，若 x > 1 ，其图象在直线 y = x 下方．（1） 二次函数解析式的三种形式〖补充知识〗二次函数①一般式： f (x ) = ax 2 + bx + c (a ≠ 0) ②顶点式： f (x ) = a (x - h )2 + k (a ≠ 0)③两根式： f (x ) = a (x - x 1 )(x - x 2 )(a ≠ 0)（2） 求二次函数解析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式．③若已知抛物线与 x 轴有两个交点，且横线坐标已知时，选用两根式求 f (x ) 更方便．（3） 二次函数图象的性质2bb 4ac -b 2①二次函数 f (x ) = ax + bx + c (a ≠ 0) 的图象是一条抛物线，对称轴方程为 x = - , 顶点坐标是(- , )②当 a > 0 时，抛物线开口向上，函数在(-∞, -4ac - b 2b ] 上递减，在[- 2a2a b , +∞) 上递增，当 x = - b 时，2a 2a b b2a 4af min (x ) =；当 a < 0 时，抛物线开口向下，函数在(-∞, - ] 上递增，在[- , +∞) 上递减，当 4a 2a 2ax = - b时 ， f (x ) = 2amax4ac - b 2．4a③二次函数 f (x ) = ax 2 + bx + c (a ≠ 0) 当∆ = b 2 - 4ac > 0 时，图象与 x 轴有两个交点M (x ,0), M (x ,0),| M M |=| x - x |= ． 1 1 2 2 1 2 1 2 | a |（4） 一元二次方程 ax 2 + bx + c = 0(a ≠ 0) 根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整， 且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用，下面结合二次函数图象的性质， 系统地来分析一元二次方程实根的分布．设一元二次方程 ax 2 + bx + c = 0(a ≠ 0) 的两实根为 x , x ，且 x≤ x ．令 f (x ) = ax 2 + bx + c ，从以下四个1212b方面来分析此类问题：①开口方向： a②对称轴位置： x = -③判别式： ∆ ④端点函数值符号．2a（5） 二次函数 f (x ) = ax 2 + bx + c (a ≠ 0) 在闭区间[ p , q ] 上的最值b b设f (x) 在区间[ p, q] 上的最大值为M ，最小值为m ，令x0=1 ( p +q)．2（Ⅰ）当a > 0 时（开口向上）b b b b①若-<p ，则m =2af ( p) ②若p ≤-≤q ，则m =2af (-)2a③若->q ，则m =2af (q)①若-2a≤x，则M =f (q) ②- 2a >x0 ，则M =f ( p)(Ⅱ)当a < 0 时(开口向下)b b b b①若-<p ，则M =2af ( p) ②若p ≤-≤q ，则M =2af (-)2a③若->q ，则M =2af (q)①若-2a ≤x0 ，则m = f (q) ②-2a >x0 ，则m =f ( p) ．x0f (-b)2ax0f (-b)2a“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

精品文档高中数学必修1知识点总结第二章基本初等函数〖2.1〗指数函数N ，那么x 叫做a 的n 次方根•当n 是奇数时，a 的n 次方根用符号 V aa 叫做被开方数•当n 为奇数时，a 为任意实数；当n 为偶数时,③根式的性质： (n，a)na ；当n 为奇数时，a ;当n 为偶数时， n? |a|(2)分数指数幂的概念①正数的正分数指数幂的意义是：ma n (a 0, m, nN ,且n 1). 0的正分数指数幂等于0.②正数的负分数m指数幂的意义是：a71 m(2)nJ(1)m (a 0,m, n N ,且n 1). 0的负分数指数幂没有意义 .注意口诀：底a '■ a数取倒数，指数取相反数.(3)分数指数幂的运算性质rsr s① a a a (a0, r, s R)②(a r )s a rs (a0, r,s R)③(ab)r a r b r (a0,b 0,r R)2.1.2指数函数及其性质(4)指数函数2.1.1指数与指数幕的运算(1)根式的概念表示；当n 是偶数时，正数 a 的正的n 次方根用符号7a 表示，负的n 次方根用符号 na 表示；o 的n 次方根是o ；负数a 没有n 次方根.①如果 x n a, a R, x R, n 1，且 n②式子n a 叫做根式，这里n 叫做根指数,a (a 0)a (a 0)12.2〗对数函数【221】对数与对数运算(1) 对数的定义①若a x N(a 0,且a 1)，则x 叫做以a 为底N 的对数，记作x log a N ，其中a 叫做底数，N 叫做真数.【222】对数函数及其性质(5② 负数和零没有对数.③对数式与指数式的互化:x log a Na xN (a 0, a 1,N 0).(2) 几个重要的对数恒等式loga 1 0，lOg a a 1，lOgb aa(3) 常用对数与自然对数：常用对数:lg N ，即 loge 自然对数:In N ，lOg e N(其中 e 2.71828 …).(4) 对数的运算性质如果a 0, a1,M0, N那么①加法:lOg a M lOg a N log a (MN)②减法:lOg a MlOg a N③数乘:nlog a M log a M n(n R)④alOga N⑤loga bM n n log a M(b 0,n R) a b⑥换底公式：lOg aNlog b N(b 0,且 b 1) log b a设函数y f (x)的定义域为A，值域为C，从式子y f (x)中解出x，得式子x (y).如果对于y在C中的任何一个值，通过式子x (y) , x在A中都有唯一确定的值和它对应，那么式子x (y)表示x是y的函数，函数x ( y)叫做函数y f(x)的反函数，记作x f 1(y)，习惯上改写成y f 1(x).(7)反函数的求法①确定反函数的定义域，即原函数的值域；②从原函数式y f(x)中反解出x f 1(y)；1 1③将x f (y)改写成y f (x)，并注明反函数的定义域.(8)反函数的性质①原函数y f(x)与反函数y f (x)的图象关于直线y x对称.②函数y f (x)的定义域、值域分别是其反函数y f 1(x)的值域、定义域.③若P(a,b)在原函数y f (x)的图象上，贝U p'(b,a)在反函数y f 1(x)的图象上.④一般地，函数y f (x)要有反函数则它必须为单调函数.（1）幂函数的定义（2）幂函数的图象（3）幂函数的性质① 图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象•幂函数是偶函数时，图象分布在第一、二象限 （图象关于y 轴对称）；是奇函数时，图象分布在第一、三象限 （图象关于原点对称）；是非奇非偶函数时，图象只分布在第一象限 • ② 过定点：所有的幂函数在 （0,）都有定义，并且图象都通过点 （1,1） •③ 单调性：如果0，则幂函数的图象过原点，并且在 [0, ）上为增函数•如果0,则幂函数的图象在（0, ）上为减函数，在第一象限内，图象无限接近x 轴与y 轴.④奇偶性：当 为奇数时，幂函数为奇函数，当 为偶数时，幂函数为偶函数.当 —（其中p,q 互质，p 和q Z ）， P，q q若p 为奇数q 为奇数时，则yx p 是奇函数，若 p 为奇数q 为偶数时，则y x p 是偶函数，若p 为偶数q 为奇数时, q则y x p 是非奇非偶函数.⑤图象特征：幂函数 y x,x（0,），当 1时，若0 x 1,其图象在直线 y x 下方，若x 1，其图象12.3〗幕函数一般地，函数yx 叫做幂函数，其中x 为自变量,是常数.在直线y x上方，当1时，若0 x 1,其图象在直线y x上方，若x 1，其图象在直线y x下方.(1)二次函数解析式的三种形式①一般式：f (x ) ax 2 bx c(a 0)②顶点式：f(x) a(x h)2 k(a 0) ③两根式：f (x) a(x xj(x x 2)(a 0) (2) 求二次函数解析式的方法 ① 已知三个点坐标时，宜用一般式.② 已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时，常使用顶点式. ③ 若已知抛物线与 x 轴有两个交点，且横线坐标已知时，选用两根式求 f(x)更方便.(3) 二次函数图象的性质① 二次函数f(x) ax 2 bx c(a 0)的图象是一条抛物线，对称轴方程为x —,顶点坐标是( ——, ---------------- )2a 2a 4a② 当a 0时，抛物线开口向上，函数在 (，-—］上递减，在［ ——,)上递增，当x时，2a 2a 2af min (x) 4" —；当a 0时，抛物线开口向下，函数在 (， —］上递增，在［卫，)上递减，当4a 2a 2a x P 时，f max (X ) 2a4a2 2③二次函数f (x) ax bx c(a 0)当 — 4ac 0时，图象与x 轴有两个交点M 1(xi>0),M2(x2>0)>M 1M 21 |xi(4)一元二次方程ax 2 bx c 0( a 0)根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整， 且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用，下面结合二次函数图象的性质，系 统地来分析一元二次方程实根的分布.2 2 设一元二次方程ax bx c 0(a 0)的两实根为x i ,X 2，且x 1 x 2 •令f(x) ax bx c ，从以下四个方K面来分析此类问题：①开口方向：a ②对称轴位置：x —— ③判别式： ④端点函数值符号.① k < x i < X 21补充知识〗二次函数|a|2a精品文档②x i< X2 < k④k i< x i< X2< k2⑤有且仅有一个根X i (或X2)满足k i<X i (或X2) < k2f( k i)f( k2) 0，并同时考虑f( k i)=O 或f( k2)=0 这两种情况是否也符合精品文档⑥k i<X i v k2< p i< x>< p2 此结论可直接由⑤推出.（5）二次函数f（x）ax2bx c(a 0）在闭区间［p, q］上的最值设f（x）在区间［p, q］上的最大值为M ，最小值为m，令X。