第7章力复习教案教案

第2节化学反应的限度工业合成氨考纲定位要点网络1.了解化学反应的可逆性及化学平衡的建立.2.掌握化学平衡的特征。

3.理解外界条件(浓度、温度、压强、催化剂等)对化学平衡的影响，能用相关理论解释其一般规律.4.了解化学平衡的调控在生活、生产和科学研究领域中的重要作用。

可逆反应与化学平衡状态知识梳理1．可逆反应［辨易错]（1）2H2＋O22H2O为可逆反应。

（2）Pb＋PbO2＋2H2SO42PbSO4＋2H2O为可逆反应.（3）2 mol SO2和2 mol O2在一定条件下的密闭容器中发生2SO2（g)＋O2(g)2SO3(g），平衡时的O2物质的物质的量为1 mol。

()［答案](1)×(2)×（3)×2．化学平衡状态（1)概念在一定条件下可逆反应进行到一定程度时，反应物和生成物的浓度不再随时间的延长而发生变化，正反应速率和逆反应速率相等，这种状态称为化学平衡状态。

(2)建立在一定条件下，把某一可逆反应的反应物加入固定容积的密闭容器中。

反应过程如下：以上过程可用如图表示：；若开始加入生成物,从逆反应建立平衡，则v.t图像为.因此，化学平衡状态的建立可以从正反应建立，也可以从逆反应方向建立，也可以从正、逆两反应方向同时建立，即平衡建立与反应途径无关。

（3）特征注意：化学平衡状态的两种标志错误![辨易错］（1）可逆反应达到平衡时，各组分浓度不变，反应停止.(2)从正反应建立平衡的过程中，平衡前v正大于v逆。

(3)对于N2(g)＋3H2(g）2NH3（g）反应,当v正(N2）＝v逆(NH3）时反应达到平衡状态。

() (4）在相同温度下，相同容器(恒容）发生2SO2(g)＋O2(g）2SO3（g）反应，当分别向容器中充入2 mol SO2、1 mol O2与2 mol SO3平衡时,c（SO2）相同。

(）(5)一个可逆反应达到的平衡状态就是这个反应在该条件下所能达到的限度。

重力、弹力、摩擦力复习教案第一章：重力1.1 重力的概念解释重力的定义，即地球对物体产生的吸引力。

强调重力的作用是使物体朝向地心运动。

1.2 重力的大小介绍重力的大小与物体的质量成正比，与距离地心的距离成反比。

解释重力加速度的概念，并指出其值约为9.8 m/s²。

1.3 重力的方向强调重力的方向总是指向地心，即垂直向下。

讨论重力对物体的影响，如物体在自由下落时的加速度。

第二章：弹力2.1 弹力的概念解释弹力是物体由于形变而产生的力。

强调弹力的作用是使物体恢复原状。

2.2 弹力的大小介绍弹力的大小与物体的形变程度有关，遵循胡克定律。

解释弹簧常数的概念，并指出其与弹力的大小成正比。

2.3 弹力的方向强调弹力的方向总是指向物体恢复原状的方向。

讨论弹力在实际应用中的例子，如弹簧和弹性体。

第三章：摩擦力3.1 摩擦力的概念解释摩擦力是物体表面接触时产生的阻碍相对滑动的力。

强调摩擦力的作用是使物体保持静止或匀速运动。

3.2 摩擦力的大小介绍摩擦力的大小与物体表面的粗糙程度和压力有关。

解释静摩擦力和动摩擦力的概念，并指出其与摩擦力的大小有关。

3.3 摩擦力的方向强调摩擦力的方向总是与物体的运动方向相反。

讨论摩擦力在实际应用中的例子，如汽车刹车和摩擦材料。

第四章：重力、弹力、摩擦力的相互作用4.1 重力、弹力、摩擦力的合成解释在实际问题中，物体可能受到重力、弹力和摩擦力的作用。

强调需要根据物体的状态和受力情况进行合成分析。

4.2 重力、弹力、摩擦力的平衡介绍平衡状态的概念，即物体受到的合外力为零。

强调在平衡状态下，重力、弹力和摩擦力相互抵消。

4.3 重力、弹力、摩擦力的应用讨论重力、弹力和摩擦力在实际问题中的应用，如结构设计和物体运动。

强调需要综合考虑重力、弹力和摩擦力的影响，以解决实际问题。

第五章：复习题和练习5.1 复习题设计一系列关于重力、弹力和摩擦力的复习题，以巩固学生对这些概念的理解。

提供答案和解析，帮助学生巩固知识点。

第1讲电场力的性质目标要求内容要求说明1.电荷和电荷守恒定律通过实验，了解静电现象．能用原子结构模型和电荷守恒的知识分析静电现象．带电粒子在匀强电场中运动的计算2。

点电荷和库仑定律知道点电荷模型．知道两个点电荷间相互作用的规律．体会探究库仑定律过程中的科学思想和方法．3.电场和电场强度电场知道电场是一种物质．了解电场强度，体会用物理量之比定义新物理量的方法．会用电场线描述电场．实验九观察电容器的的充、放电现象场强的情况。

第1讲电场力的性质一、电荷电荷守恒定律1．元电荷、点电荷（1）元电荷：e＝1.60×10－19C，所有带电体的电荷量都是元电荷的整数倍．（2)点电荷：代表带电体的有一定电荷量的点，忽略带电体的大小、形状及电荷分布状况的理想化模型．2．电荷守恒定律(1）内容：电荷既不会创生，也不会消灭，它只能从一个物体转移到另一个物体，或者从物体的一部分转移到另一部分，在转移过程中，电荷的总量保持不变．(2)三种起电方式：摩擦起电、感应起电、接触起电．(3）带电实质：物体得失电子．(4)电荷的分配原则:两个形状、大小相同且带同种电荷的同种导体，接触后再分开，二者带等量同种电荷,若两导体原来带异种电荷，则电荷先中和，余下的电荷再平分．自测1如图1所示,两个不带电的导体A和B,用一对绝缘柱支撑使它们彼此接触．把一带正电荷的物体C置于A附近,贴在A、B下部的金属箔都张开（)图1A．此时A带正电，B带负电B．此时A带正电，B带正电C．移去C，贴在A、B下部的金属箔都闭合D．先把A和B分开,然后移去C，贴在A、B下部的金属箔都闭合答案C解析由静电感应可知，A左端带负电，B右端带正电,选项A、B错误；若移去C,A、B两端电荷中和，则贴在A、B下部的金属箔都闭合，选项C正确；先把A和B分开，然后移去C，则A、B带的电荷不能中和，故贴在A、B下部的金属箔仍张开,选项D错误．二、库仑定律1．内容真空中两个静止点电荷之间的相互作用力，与它们的电荷量的乘积成正比，与它们的距离的二次方成反比,作用力的方向在它们的连线上．2．表达式F＝k错误!，式中k＝9.0×109N·m2/C2，叫做静电力常量．3．适用条件真空中的静止点电荷．(1）在空气中，两个点电荷的作用力近似等于真空中的情况，可以直接应用公式．(2)当两个带电体间的距离远大于其本身的大小时,可以把带电体看成点电荷．4．库仑力的方向由相互作用的两个带电体决定，即同种电荷相互排斥，异种电荷相互吸引．判断正误(1）由库仑定律公式F＝k错误!可知，当r→0时，F 为无穷大．(×)（2）两个带电体之间的库仑力是一对相互作用力，大小相等,方向相反．(√)（3）库仑定律是通过实验总结出的规律．(√）三、电场、电场强度1．电场（1)定义:存在于电荷周围，能传递电荷间相互作用的一种特殊物质;（2)基本性质：对放入其中的电荷有力的作用．2．电场强度（1）定义：放入电场中某点的电荷受到的电场力F与它的电荷量q的比值．(2）定义式：E＝错误!；单位：N/C或V/m。

第2课时必备知识——化学平衡及其移动知识清单[重要概念]①可逆反应；②化学平衡状态；③化学平衡的移动[基本规律]①化学平衡状态的判断方法；②化学平衡移动原理及规律知识点1 可逆反应与化学平衡状态1．化学平衡研究的对象——可逆反应2．化学平衡状态(1)概念一定条件下的可逆反应，当反应进行到一定程度时，正反应速率和逆反应速率相等，反应物的浓度和生成物的浓度不再改变，称为“化学平衡状态”，简称化学平衡。

化学平衡是一种动态平衡。

(2)建立过程(3)平衡特点3．理解化学平衡状态判断的两种标志 (1)直接标志(2)间接标志①有气体参加的反应，气体的总压强、总体积、总物质的量不变时，若是等体积反应时，不一定达到平衡；若是不等体积反应时，达到平衡。

②气体的密度(ρ＝m （气体）V （气体） )、气体的平均相对分子质量[M ＝m （气体）n （气体）]不变时，要具体分析各表达式中的分子或分母变化情况，判断是否平衡。

③如果平衡体系中的物质有颜色，则平衡体系的颜色不变时，达到平衡。

④一定温度下，若浓度商与平衡常数相等，即Q c ＝K 时，化学反应处于平衡状态。

⑤根据化学键的断裂与形成判断，要考虑分子结构及所含共价键的数目。

[通关1] (易错排查)判断正误(1)在化学平衡建立过程中，v 正一定大于v 逆(×) (2)恒温恒容下进行的可逆反应：2SO 2(g)＋O 2(g)2SO 3(g)，当SO 3的生成速率与SO 2的消耗速率相等时，反应达到平衡状态(×)(3)在一定条件下，向密闭容器中充入1 mol N2和3 mol H2充分反应，生成2 mol NH3(×)(4)对于反应H2(g)＋Br2(g)2HBr(g)，恒温恒容下，反应体系中气体的颜色保持不变时达到平衡状态(√)(5)对于反应2NO2(g)N2O4(g)，恒温恒容下，反应体系中气体的压强保持不变时达到平衡状态(√)[通关2] (人教选修4·P32，5题改编)在一个体积固定的密闭容器中，进行的可逆反应A(s)＋3B(g)3C (g)。

2023年中考物理一轮第七章《从粒子到宇宙》复习教学案一、教学内容本节课主要复习人教版九年级物理教材第七章《从粒子到宇宙》的内容，包括：物质的组成、原子结构、元素周期表、宇宙的起源和发展、黑洞等。

二、教学目标1. 掌握物质的基本组成，了解原子结构和元素周期表的相关知识。

2. 理解宇宙的起源和发展，认识黑洞的概念。

3. 提高学生的分析问题和解决问题的能力。

三、教学难点与重点1. 教学难点：原子结构、元素周期表的理解和运用。

2. 教学重点：宇宙的起源和发展、黑洞的概念。

四、教具与学具准备1. 教具：黑板、粉笔、多媒体设备。

2. 学具：教材、笔记本、练习册。

五、教学过程1. 引入：通过一个日常生活中的实例，如水的沸腾，引出物质的基本组成。

2. 讲解：讲解原子结构，介绍原子核和电子的组成，并通过示例说明原子的稳定性。

3. 互动：提问学生关于元素周期表的知识，引导学生思考和回答。

4. 讲解：讲解元素周期表的排列规律，介绍元素周期律。

5. 练习：给出一些元素周期表的练习题，让学生课后完成。

6. 引入：通过一个关于宇宙起源的科普视频，引出宇宙的起源和发展。

7. 讲解：讲解宇宙的起源和发展，介绍大爆炸理论和宇宙的膨胀。

8. 讲解：讲解黑洞的概念，介绍黑洞的形成和特点。

9. 互动：提问学生关于宇宙和黑洞的知识，引导学生思考和回答。

六、板书设计板书设计如下：第七章从粒子到宇宙1. 物质的组成原子结构元素周期表2. 宇宙的起源和发展大爆炸理论宇宙的膨胀3. 黑洞黑洞的形成黑洞的特点七、作业设计1. 请简述原子结构和元素周期表的相关知识。

2. 请解释宇宙的起源和发展，并简要描述黑洞的概念。

作业答案：1. 原子结构：原子由原子核和电子组成，原子核由质子和中子组成，电子围绕原子核运动。

元素周期表是按照原子序数排列的化学元素表格，反映了元素的原子结构和性质。

2. 宇宙的起源和发展：宇宙起源于大约138亿年前的大爆炸，宇宙中的物质和能量从那时起开始膨胀和演化。

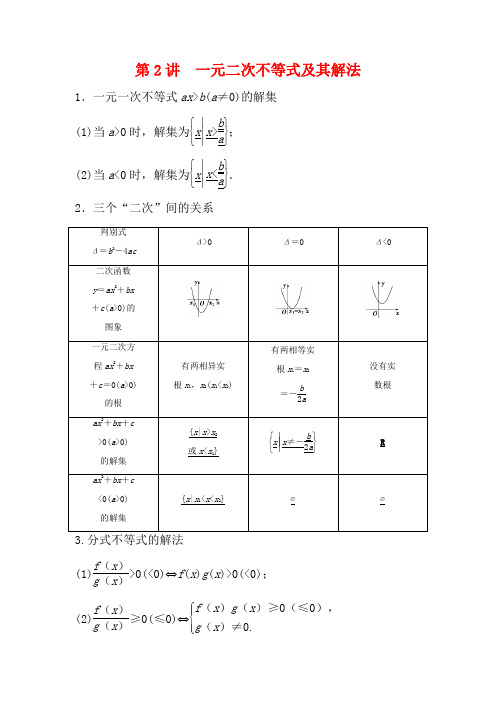
第2讲 一元二次不等式及其解法1．一元一次不等式ax >b (a ≠0)的解集 (1)当a >0时，解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x >b a ；(2)当a <0时，解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x <b a ．2．三个“二次”间的关系判别式Δ＝b 2－4acΔ>0 Δ＝0 Δ<0二次函数y ＝ax 2＋bx＋c (a >0)的 图象一元二次方 程ax 2＋bx ＋c ＝0(a >0)的根有两相异实 根x 1，x 2(x 1<x 2)有两相等实根x 1＝x 2＝－b 2a没有实 数根ax 2＋bx ＋c>0(a >0)的解集{x |x >x 2或x <x 1}⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠－b 2aRax 2＋bx ＋c<0(a >0) 的解集{x |x 1<x <x 2}∅∅(1)f （x ）g （x ）>0(<0)⇔f (x )g (x )>0(<0)；(2)f （x ）g （x ）≥0(≤0)⇔⎩⎪⎨⎪⎧f （x ）g （x ）≥0（≤0），g （x ）≠0.4．绝对值不等式的解法(1)|f (x )|>|g (x )|⇔[f (x )]2>[g (x )]2；(2)|f (x )|>g (x )⇔f (x )>g (x )或f (x )<－g (x )； (3)|f (x )|<g (x )⇔－g (x )<f (x )<g (x )．判断正误(正确的打“√”，错误的打“×”)(1)若不等式ax 2＋bx ＋c <0的解集为(x 1，x 2)，则必有a >0.( ) (2)若不等式ax 2＋bx ＋c >0的解集是(－∞，x 1)∪(x 2，＋∞)，则方程ax 2＋bx ＋c ＝0的两个根是x 1和x 2.( )(3)若方程ax 2＋bx ＋c ＝0(a ≠0)没有实数根，则不等式ax 2＋bx ＋c >0的解集为R .( )(4)不等式ax 2＋bx ＋c ≤0在R 上恒成立的条件是a <0且Δ＝b 2－4ac ≤0.( )(5)若二次函数y ＝ax 2＋bx ＋c 的图象开口向下，则不等式ax 2＋bx ＋c <0的解集一定不是空集．( )答案：(1)√ (2)√ (3)× (4)× (5)√(教材习题改编)不等式2x 2－x －3>0的解集为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪－1<x <32B.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >32或x <－1 C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪－32<x <1 D.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >1或x <－32解析：选B.2x 2－x －3>0⇒(x ＋1)(2x －3)>0， 解得x >32或x <－1.所以不等式2x 2－x －3>0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >32或x <－1. 不等式x －12x ＋1≤0的解集为( )A.⎝ ⎛⎦⎥⎤－12，1B.⎣⎢⎡⎦⎥⎤－12，1 C.⎝ ⎛⎭⎪⎫－∞，－12∪[1，＋∞)D.⎝⎛⎦⎥⎤－∞，－12∪[1，＋∞)解析：选A.由不等式x －12x ＋1≤0，可得⎩⎪⎨⎪⎧（x －1）（2x ＋1）≤0，2x ＋1≠0，解得－12<x ≤1，所以不等式的解集为⎝ ⎛⎦⎥⎤－12，1.设二次不等式ax2＋bx ＋1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－1<x <13，则ab 的值为________． 解析：由不等式ax2＋bx ＋1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－1<x <13，知a <0且ax2＋bx ＋1＝0的两根为x 1＝－1，x 2＝13，由根与系数的关系知⎩⎪⎨⎪⎧－1＋13＝－b a，－13＝1a ，所以a ＝－3，b ＝－2，ab ＝6. 答案：6若不等式x 2＋ax ＋4＜0的解集不是空集，则实数a 的取值范围是__________．解析：因为不等式x 2＋ax ＋4<0的解集不是空集， 所以Δ＝a 2－4×4>0，即a 2>16. 所以a >4或a <－4.答案：(－∞，－4)∪(4，＋∞)一元二次不等式的解法(高频考点)一元二次不等式的解法是高考的常考内容，题型多为选择题或填空题，难度为中档题．高考对一元二次不等式解法的考查主要有以下三个命题角度：(1)解不含参数的一元二次不等式； (2)解含参数的一元二次不等式；(3)已知一元二次不等式的解集求参数．[典例引领]角度一 解不含参数的一元二次不等式(1)解不等式：－x 2－2x ＋3≥0；(2)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x ，x ≥0，－x 2＋2x ，x <0，解不等式f (x )>3.【解】 (1)不等式两边同乘以－1，原不等式可化为x 2＋2x －3≤0.方程x 2＋2x －3＝0的解为x 1＝－3，x 2＝1.而y ＝x 2＋2x －3的图象开口向上，可得原不等式－x 2－2x ＋3≥0的解集是{x |－3≤x ≤1}．(2)由题意⎩⎪⎨⎪⎧x ≥0，x 2＋2x >3或⎩⎪⎨⎪⎧x <0，－x 2＋2x >3，解得x >1.故原不等式的解集为{x |x >1}．角度二 解含参数的一元二次不等式(分类讨论思想)解关于x 的不等式：12x 2－ax >a 2(a ∈R )．【解】 因为12x 2－ax >a 2，所以12x 2－ax －a 2>0，即(4x ＋a )(3x －a )>0. 令(4x ＋a )(3x －a )＝0，解得x 1＝－a 4，x 2＝a3.①当a >0时，－a 4<a3，解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <－a 4，或x >a 3；②当a ＝0时，x 2>0，解集为{x |x ∈R ，且x ≠0}；③当a <0时，－a 4>a3，解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <a 3，或x >－a 4.综上所述：当a >0时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <－a 4，或x >a 3；当a ＝0时，不等式的解集为{x |x ∈R ，且x ≠0}；当a <0时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <a 3，或x >－a 4.角度三 已知一元二次不等式的解集求参数已知不等式ax 2－bx －1>0的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪⎪－12<x <－13，则不等式x 2－bx －a ≥0的解集是________．【解析】 由题意，知－12，－13是方程ax 2－bx －1＝0的两个根，且a <0，所以⎩⎪⎨⎪⎧－12＋⎝ ⎛⎭⎪⎫－13＝b a，－12×⎝ ⎛⎭⎪⎫－13＝－1a ，解得⎩⎪⎨⎪⎧a ＝－6，b ＝5.即不等式x 2－bx －a ≥0为x 2－5x ＋6≥0， 解得x ≥3或x ≤2.【答案】 {x |x ≥3或x ≤2}(1)解一元二次不等式的方法和步骤 (2)解含参数的一元二次不等式的步骤①二次项若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为二次项系数为正的形式．②判断相应方程的根的个数，讨论判别式Δ与0的关系． ③确定无根时可直接写出解集，确定方程有两个根时，要讨论两根的大小关系，从而确定解集形式．[通关练习]1．(2018·陕西西安模拟)若集合A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x x －1≤0，B ＝{x |x 2<2x }，则A ∩B ＝( ) A ．{x |0<x <1} B ．{x |0≤x <1} C ．{x |0<x ≤1} D ．{x |0≤x ≤1}解析：选A.因为A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x x －1≤0＝{x |0≤x <1}， B ＝{x |x 2<2x }＝{x |0<x <2}，所以A ∩B ＝{x |0<x <1}，故选A.2．(2018·广东清远一中模拟)关于x 的不等式ax －b <0的解集是(1，＋∞)，则关于x 的不等式(ax ＋b )(x －3)>0的解集是( ) A ．(－∞，－1)∪(3，＋∞) B ．(1，3)C ．(－1，3)D ．(－∞，1)∪(3，＋∞)解析：选C.关于x 的不等式ax －b <0的解集是(1，＋∞)，即不等式ax <b 的解集是(1，＋∞)，所以a ＝b <0，所以不等式(ax ＋b )(x －3)>0可化为(x ＋1)(x －3)<0，解得－1<x <3，所以所求解集是(－1，3)．故选C.3．不等式0<x 2－x －2≤4的解集为________．解析：原不等式等价于⎩⎪⎨⎪⎧x 2－x －2>0，x 2－x －2≤4，即⎩⎪⎨⎪⎧x 2－x －2>0，x 2－x －6≤0，即⎩⎪⎨⎪⎧（x －2）（x ＋1）>0，（x －3）（x ＋2）≤0，解得⎩⎪⎨⎪⎧x >2或x <－1，－2≤x ≤3.借助于数轴，如图所示，原不等式的解集为{x |－2≤x <－1或2<x ≤3}． 答案：[－2，－1)∪(2，3]一元二次不等式恒成立问题(高频考点)一元二次不等式恒成立问题是每年高考的热点，题型多为选择题和填空题，难度为中档题．高考对一元二次不等式恒成立问题的考查有以下三个命题角度：(1)形如f (x )≥0(f (x )≤0)(x ∈R )确定参数的范围； (2)形如f (x )≥0(f (x )≤0)(x ∈[a ，b ])确定参数的范围； (3)形如f (x )≥0(f (x )≤0)(参数m ∈[a ，b ])确定x 的范围．[典例引领]角度一 形如f (x )≥0(f (x )≤0)(x ∈R )确定 参数的范围若不等式(a －2)x 2＋2(a －2)x －4<0对一切x ∈R 恒成立，则实数a 的取值范围是________．【解析】 当a －2＝0，即a ＝2时不等式为－4<0， 对一切x ∈R 恒成立．当a ≠2时，则⎩⎪⎨⎪⎧a －2<0，Δ＝4（a －2）2＋16（a －2）<0，即⎩⎪⎨⎪⎧a <2－2<a <2，解得－2<a <2. 所以实数a 的取值范围是(－2，2]． 【答案】 (－2，2]角度二 形如f (x )≥0(f (x )≤0)(x ∈[a ，b ])确定参数的范围(转化与化归思想)若不等式x 2＋mx －1<0对于任意x ∈[m ，m ＋1]都成立，则实数m 的取值范围是________．【解析】 由题意，得函数f (x )＝x 2＋mx －1在[m ，m ＋1]上的最大值小于0，又抛物线f (x )＝x 2＋mx －1开口向上，所以只需⎩⎪⎨⎪⎧f （m ）＝m 2＋m 2－1<0，f （m ＋1）＝（m ＋1）2＋m （m ＋1）－1<0， 即⎩⎪⎨⎪⎧2m 2－1<0，2m 2＋3m <0， 解得－22<m <0.【答案】⎝⎛⎭⎪⎪⎫－22，0 角度三 形如f (x )≥0(f (x )≤0)(参数m ∈[a ，b ])确定x 的范围求使不等式x 2＋(a －6)x ＋9－3a >0，|a |≤1恒成立的x 的取值范围．【解】 将原不等式整理为形式上是关于a 的不等式(x －3)a ＋x 2－6x ＋9>0.令f (a )＝(x －3)a ＋x 2－6x ＋9，则－1≤a ≤1. 因为f (a )>0在|a |≤1时恒成立，所以(1)若x ＝3，则f (a )＝0，不符合题意，应舍去． (2)若x ≠3，则由一次函数的单调性，可得⎩⎪⎨⎪⎧f （－1）>0，f （1）>0，即⎩⎪⎨⎪⎧x 2－7x ＋12>0，x 2－5x ＋6>0，解得x <2或x >4.则实数x 的取值范围为(－∞，2)∪(4，＋∞)．(1)不等式恒成立问题的求解方法①一元二次不等式在R 上恒成立确定参数的范围时，结合一元二次方程，利用判别式来求解．②一元二次不等式f (x )≥0在x ∈[a ，b ]上恒成立确定参数范围时，要根据函数的单调性，求其最小值，让最小值大于等于0，从而求参数的范围．③一元二次不等式对于参数m ∈[a ，b ]恒成立确定x 的范围，要注意变换主元，一般地，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．(2)求解不等式恒成立问题的数学思想求解此类问题常利用分类讨论思想及转化与化归思想，如例2­2是不等式与函数的转化，例2­3是主元与次元的转化，而例2­1是对二次项系数是否为0进行讨论．[通关练习]1．若函数y ＝mx 2－（1－m ）x ＋m 的定义域为R ，则m 的取值范围是________．解析：要使y ＝mx 2－（1－m ）x ＋m 有意义，即mx 2－(1－m )x ＋m ≥0对∀x ∈R 恒成立，则⎩⎪⎨⎪⎧m >0，（1－m ）2－4m 2≤0，解得m ≥13.答案：m ≥132．若关于x 的不等式4x－2x ＋1－a ≥0在[1，2]上恒成立，则实数a的取值范围为________． 解析：因为不等式4x－2x ＋1－a ≥0在[1，2]上恒成立，所以4x－2x ＋1≥a 在[1，2]上恒成立．令y ＝4x －2x ＋1＝(2x )2－2×2x＋1－1＝(2x－1)2－1.因为1≤x ≤2，所以2≤2x≤4.由二次函数的性质可知：当2x＝2，即x ＝1时，y 取得最小值0， 所以实数a 的取值范围为(－∞，0]． 答案：(－∞，0]解分式不等式的关键是先将给定不等式移项，通分，整理成一边为商式，另一边为0的形式，再通过等价转化化成整式不等式(组)的形式进行求解．对于一元二次不等式恒成立问题，恒大于0就是相应的二次函数的图象在给定的区间上全部在x 轴上方，恒小于0就是相应的二次函数的图象在给定的区间上全部在x 轴下方．另外常转化为求二次函数的最值或用分离参数法求最值． 易错防范(1)对于不等式ax 2＋bx ＋c >0，求解时不要忘记讨论a ＝0时的情形．(2)当Δ<0时，ax 2＋bx ＋c >0(a ≠0)的解集是R 还是∅，要注意区别．(3)不同参数范围的解集切莫取并集，应分类表述． 1．设集合A ＝{x |x 2＋x －6≤0}，集合B 为函数y ＝1x －1的定义域，则A ∩B 等于( ) A ．(1，2) B ．[1，2] C ．[1，2)D ．(1，2]解析：选D.A ＝{x |x 2＋x －6≤0}＝{x |－3≤x ≤2}，由x －1>0得x >1，即B ＝{x |x >1}，所以A ∩B ＝{x |1<x ≤2}．2．若不等式ax 2＋bx ＋2<0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <－12，或x >13，则a －ba 的值为( ) A.56 B.16 C ．－16D ．－56解析：选A.由题意得ax 2＋bx ＋2＝0的两根为－12与13，所以－ba＝－12＋13＝－16，则a －b a ＝1－b a ＝1－16＝56. 3．不等式x －43－2x<0的解集是( )A ．{x |x <4}B ．{x |3<x <4}C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32或x >4 D.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪32<x <4 解析：选C.不等式x －43－2x <0等价于⎝ ⎛⎭⎪⎫x －32(x －4)>0，所以不等式的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32或x >4.4．若不等式x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立，则实数a 的取值范围为( ) A ．[－1，4]B ．(－∞，－2]∪[5，＋∞)C ．(－∞，－1]∪[4，＋∞)D ．[－2，5]解析：选A.x 2－2x ＋5＝(x －1)2＋4的最小值为4，所以x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立， 只需a 2－3a ≤4即可，解得－1≤a ≤4.5．(2018·福建龙岩模拟)已知函数f (x )＝(ax －1)(x ＋b )，若不等式f (x )>0的解集是(－1，3)，则不等式f (－2x )<0的解集是( )A.⎝ ⎛⎭⎪⎫－∞，－32∪⎝ ⎛⎭⎪⎫12，＋∞B.⎝ ⎛⎭⎪⎫－32，12 C.⎝ ⎛⎭⎪⎫－∞，－12∪⎝ ⎛⎭⎪⎫32，＋∞D.⎝ ⎛⎭⎪⎫－12，32 解析：选A.不等式f (x )>0的解集是(－1，3)，故f (x )<0的解集是{x |x <－1或x >3}，故f (－2x )<0的解集为{x |－2x <－1或－2x >3}，即⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <－32或x >12.6．不等式|x (x －2)|>x (x －2)的解集是________．解析：不等式|x (x －2)|>x (x －2)的解集即x (x －2)<0的解集，解得0<x <2.答案：{x |0<x <2}7．函数y ＝lg （1－x ）－2x 2＋12x ＋32的定义域为________． 解析：由题意，得⎩⎪⎨⎪⎧－2x 2＋12x ＋32>0，1－x >0，即⎩⎪⎨⎪⎧x 2－6x －16<0，1－x >0，解得－2<x <1， 即原函数的定义域为{x |－2<x <1}．答案：(－2，1)8．(2018·江西南昌模拟)在R 上定义运算：x *y ＝x (1－y )．若不等式(x －y )*(x ＋y )<1对一切实数x 恒成立，则实数y 的取值范围是________．解析：由题意，知(x －y )*(x ＋y )＝(x －y )·[1－(x ＋y )]<1对一切实数x 恒成立，所以－x 2＋x ＋y 2－y －1<0对于x ∈R 恒成立．故Δ＝12－4×(－1)×(y 2－y －1)<0，所以4y 2－4y －3<0，解得－12<y <32.答案：⎝ ⎛⎭⎪⎫－12，329．若不等式ax 2＋5x －2>0的解集是⎩⎨⎧x ⎪⎪⎪⎭⎬⎫12<x <2.(1)求实数a 的值；(2)求不等式ax 2－5x ＋a 2－1>0的解集．解：(1)由题意知a <0，且方程ax 2＋5x －2＝0的两个根为12，2，代入解得a ＝－2.(2)由(1)知不等式为－2x 2－5x ＋3>0， 即2x 2＋5x －3<0，解得－3<x <12，即不等式ax 2－5x ＋a 2－1>0的解集为⎝⎛⎭⎪⎫－3，12.10．(2018·合肥市第二次教学质量检测)已知函数f (x )＝4－|ax －2|(a ≠0)． (1)求函数f (x )的定义域；(2)若当x ∈[0，1]时，不等式f (x )≥1恒成立，求实数a 的取值范围．解：(1)要使函数有意义，需4－|ax －2|≥0，即|ax －2|≤4，|ax －2|≤4⇔－4≤ax －2≤4⇔－2≤ax ≤6. 当a >0时，函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪－2a≤x ≤6a ；当a <0时，函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪6a≤x ≤－2a .(2)f (x )≥1⇔|ax －2|≤3，记g (x )＝|ax －2|，因为x ∈[0，1]，所以需且只需⎩⎪⎨⎪⎧g （0）≤3g （1）≤3⇔⎩⎪⎨⎪⎧2≤3|a －2|≤3⇔－1≤a ≤5，又a ≠0，所以－1≤a ≤5且a ≠0.1．已知函数f (x )＝－x 2＋ax ＋b 2－b ＋1(a ∈R ，b ∈R )，对任意实数x 都有f (1－x )＝f (1＋x )成立，若当x ∈[－1，1]时，f (x )＞0恒成立，则b 的取值范围是( ) A ．(－1，0) B ．(2，＋∞)C ．(－∞，－1)∪(2，＋∞)D ．不能确定解析：选C.由f (1－x )＝f (1＋x )知f (x )的图象关于直线x ＝1对称，即a2＝1，解得a ＝2.又因为f (x )开口向下，所以当x ∈[－1，1]时，f (x )为增函数，所以f (x )min ＝f (－1)＝－1－2＋b 2－b ＋1＝b 2－b －2，f (x )＞0恒成立，即b 2－b －2＞0恒成立，解得b ＜－1或b ＞2.2．(2018·陕西咸阳模拟)已知a ∈Z ，关于x 的一元二次不等式x2－6x ＋a ≤0的解集中有且仅有3个整数，则所有符合条件的a 的值之和是( ) A ．13 B ．18 C ．21D ．26解析：选C.设f (x )＝x 2－6x ＋a ，其图象为开口向上，对称轴是x ＝3的抛物线，如图所示．若关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数，则⎩⎪⎨⎪⎧f （2）≤0，f （1）>0，即⎩⎪⎨⎪⎧22－6×2＋a ≤0，12－6×1＋a >0，解得5<a ≤8，又a ∈Z ，故a ＝6，7，8.则所有符合条件的a 的值之和是6＋7＋8＝21.3．对于实数x ，当且仅当n ≤x <n ＋1(n ∈N *)时，[x ]＝n ，则关于x 的不等式4[x ]2－36[x ]＋45<0的解集为________．解析：由4[x ]2－36[x ]＋45<0，得32<[x ]<152，又当且仅当n ≤x <n＋1(n ∈N *)时，[x ]＝n ，所以[x ]＝2，3，4，5，6，7，所以所求不等式的解集为[2，8)． 答案：[2，8)4．不等式x 2＋8y 2≥λy (x ＋y )对于任意的x ，y ∈R 恒成立，则实数λ的取值范围为________．解析：因为x 2＋8y 2≥λy (x ＋y )对于任意的x ，y ∈R 恒成立， 所以x 2＋8y 2－λy (x ＋y )≥0对于任意的x ，y ∈R 恒成立，即x 2－λyx ＋(8－λ)y 2≥0恒成立，由二次不等式的性质可得，Δ＝λ2y 2＋4(λ－8)y 2＝y 2(λ2＋4λ－32)≤0，所以(λ＋8)(λ－4)≤0， 解得－8≤λ≤4. 答案：[－8，4]5．某商品每件成本价为80元，售价为100元，每天售出100件．若售价降低x 成(1成＝10%)，售出商品数量就增加85x 成．要求售价不能低于成本价．(1)设该商店一天的营业额为y ，试求y 与x 之间的函数关系式y ＝f (x )，并写出定义域；(2)若要求该商品一天营业额至少为10 260元，求x 的取值范围．解：(1)由题意得y ＝100⎝ ⎛⎭⎪⎫1－x 10·100⎝⎛⎭⎪⎫1＋850x .因为售价不能低于成本价，所以100⎝⎛⎭⎪⎫1－x 10－80≥0，得x ≤2.所以y ＝f (x )＝20(10－x )(50＋8x )，定义域为[0，2]．(2)由题意得20(10－x )(50＋8x )≥10 260，化简得8x 2－30x ＋13≤0.解得12≤x ≤134.所以x 的取值范围是⎣⎢⎡⎦⎥⎤12，2.6．设二次函数f (x )＝ax 2＋bx ＋c ，函数F (x )＝f (x )－x 的两个零点为m ，n (m <n )．(1)若m ＝－1，n ＝2，求不等式F (x )>0的解集； (2)若a >0，且0<x <m <n <1a，比较f (x )与m 的大小．解：(1)由题意知，F (x )＝f (x )－x ＝a (x －m )·(x －n )， 当m ＝－1，n ＝2时，不等式F (x )>0， 即a (x ＋1)(x －2)>0.当a >0时，不等式F (x )>0的解集为{x |x <－1，或x >2}； 当a <0时，不等式F (x )>0的解集为{x |－1<x <2}． (2)f (x )－m ＝a (x －m )(x －n )＋x －m ＝(x －m )(ax －an ＋1)， 因为a >0，且0<x <m <n <1a，所以x －m <0，1－an ＋ax >0. 所以f (x )－m <0，即f (x )<m .。

《第七章从粒子到宇宙》复习教学案【同步知识梳理】1、分子动理论的基本内容：物质是由大量构成的，分子间有；分子处在___________________________________；分子间存在相互作用的___ 力和___ __力。

2、用摩擦的方式使物体带电叫，带电体能够吸引物体，摩擦起电现象证明了电子的普遍存在，从而揭示了。

3、我们把被丝绸摩擦过的玻璃棒所带的电荷称为电荷，把被毛皮摩擦过的橡胶棒所带的电荷称为电荷，同种电荷相互，异种电荷相互。

4、原子核所带的正电荷与电子所带的负电荷在数量上，因此原子呈电中性。

摩擦起电的实质是电子从一个物体到另一个物体，得到电子带电，失去电子带电。

5、原子是由和组成的，原子核是由和组成的，电子带电，质子带电，中子电。

6、散布在宇宙中的星系多达1000亿个，宇宙是个有的天体结构系统。

7、在宇宙尺寸中，米和千米都是非常小的单位，使用米作单位记录和运算都不方便，所以用作为单位比较方便(1 l.y.=9.461×1015m)。

而在很小的原子内部，原子直径为10-10m的数量级，同样也不方便，所以用作为单位较方便。

8、大多数科学家认为宇宙起源于距今约150亿年前的一次。

宇宙大爆炸理论认为，宇宙一开始是一个“原始火球”，原始的火球发生了爆炸，导致宇宙空间处处，温度则（上升/下降/不变）到一定程度时，逐步形成了超星系团，星系团、星系乃至恒星和行星。

___ __ 现象证明了宇宙在膨胀。

【精题精练精讲】例题1：下列例子中，不能说明分子在不停地做无规则运动的是（）A、室内扫地时，在阳光下看见灰尘在空中飞舞B、晒衣服时，水蒸发，衣服变干C、卫生球放在箱里，过几天整个箱子充满了樟脑味D、把一块方糖投入一杯开水中，隔一会整杯水变甜了例题2：有A、B、C三个轻小物体，为判断三个物体带电情况，将三个物体分别互相靠近，发现AB间吸引，BC间排斥，AC间吸引，则下列判断正确的是（）A．A、B带异种电荷 B．B、C带同种电荷C．A、C带异种电荷 D．A、B、C均带电例题3：下列说法正确的是（）A．“破镜难重圆”是因为固体分子间只存在着排斥力B．宇宙大爆炸理论认为宇宙诞生于大爆炸，爆炸引起宇宙膨胀C．在空调房间吸烟时，会看到烟雾在空中弥漫，这是分子的无规则运动D．原子核内质子所带的正电荷数与中子所带的负电荷数相等，所以平常物体不带电例题4：在比较一定量的水和酒精混合前后总体积大小的实验中，在直玻璃管中应先注入_______，为使实验观象更明显，应选用内径较_______的玻璃管（ρ酒精= 0.8×103kg/m3）。

初中物理力学复习教案教学目标：1. 掌握力的概念、作用效果、分类和测量方法。

2. 理解牛顿三定律及其应用。

3. 掌握重力、摩擦力、浮力等常见力的性质和计算方法。

4. 能够运用力学知识解决实际问题。

教学内容：1. 力的概念和作用效果2. 力的分类和测量3. 牛顿三定律4. 重力、摩擦力、浮力5. 力学应用实例教学过程：一、导入（5分钟）1. 复习力的概念：力是物体对物体的作用，是相互的。

2. 复习力的作用效果：改变物体的形状、改变物体的运动状态。

二、力的分类和测量（10分钟）1. 复习力的分类：重力、弹力、摩擦力、浮力等。

2. 复习力的测量：测力计的使用方法。

三、牛顿三定律（15分钟）1. 复习牛顿第一定律：物体静止或匀速直线运动，不受外力或受平衡力。

2. 复习牛顿第二定律：F=ma，力等于质量乘以加速度。

3. 复习牛顿第三定律：作用力和反作用力大小相等、方向相反、作用在同一直线上。

四、常见力（10分钟）1. 复习重力：G=mg，重力与质量成正比。

2. 复习摩擦力：摩擦力与压力、接触面的粗糙程度有关。

3. 复习浮力：F浮=G排，浮力与排开的液体受到的重力相等。

五、力学应用实例（10分钟）1. 分析实际问题，运用力学知识解决问题。

2. 举例说明力学在生活中的应用。

六、总结（5分钟）1. 回顾本节课复习的内容，强调重点知识点。

2. 鼓励学生课后加强练习，巩固力学知识。

教学评价：1. 课后作业：布置有关力学知识的习题，检验学生掌握程度。

2. 课堂表现：观察学生在课堂上的参与程度、提问回答情况。

3. 期中期末考试：检验学生对力学知识的掌握和应用能力。

教学反思：本节课通过复习力的概念、分类、测量、牛顿三定律、常见力和力学应用实例，使学生对力学知识有一个系统的掌握。

在教学过程中，注意引导学生运用力学知识解决实际问题，提高学生的动手能力和解决问题的能力。

在课后，加强对学生的练习指导，提高学生的力学知识水平。

第2节 电场能的性质一、电势能和电势1．电势能 (1)电场力做功的特点：电场力做功与路径无关，只与初、末位置有关。

(2)电势能①定义：电荷在电场中具有的势能，数值上等于将电荷从该点移到零势能位置时电场力所做的功。

②电场力做功与电势能变化的关系：电场力做的功等于电势能的减少量，即W AB ＝E p A －E p B ＝－ΔE p 。

2．电势(1)定义：试探电荷在电场中某点具有的电势能与它的电荷量的比值。

(2)定义式：φ＝E p q 。

(3)矢标性：电势是标量，有正、负之分，其正(负)表示该点电势比零电势高(低)。

(4)相对性：电势具有相对性，同一点的电势因选取零电势点的不同而不同。

3．等势面(1)定义：电场中电势相等的各点组成的面。

(2)四个特点①等势面一定与电场线垂直。

②在同一等势面上移动电荷时电场力不做功。

③电场线方向总是从电势高的等势面指向电势低的等势面。

④等差等势面越密的地方电场强度越大，反之越小。

二、电势差1．定义：电荷在电场中由一点A 移到另一点B 时，电场力做功与移动电荷的电荷量的比值。

2．定义式：U AB ＝W AB q。

3．电势差与电势的关系：U AB ＝φA －φB ，U AB ＝－U BA 。

三、匀强电场中电势差与电场强度的关系1．电势差与电场强度的关系：匀强电场中两点间的电势差等于电场强度与这两点沿电场线方向的距离的乘积。

即U ＝Ed ，也可以写作E ＝U d。

2．公式U ＝Ed 的适用X 围：匀强电场。

1．思考辨析(正确的画“√”，错误的画“×”)(1)电场中电场强度为零的地方电势一定为零。

(×) (2)沿电场线方向电场强度越来越小，电势逐渐降低。

(×)(3)A 、B 两点间的电势差等于将正电荷从A 点移到B 点时静电力所做的功。

(×)(4)A 、B 两点的电势差是恒定的，所以U AB ＝U BA 。

(×)(5)等差等势线越密的地方，电场线越密，电场强度越大。

人教版八年级物理下册第七章力本章复习课教学设计一、教学目标•理解力是使物体发生形变、改变速度或者改变形状的原因；•理解力的大小和方向可以通过力的合成；•掌握解决力的合成问题的方法。

二、教学重点和难点•教学重点：力是使物体发生形变、改变速度或者改变形状的原因。

•教学难点：力的合成问题的解决方法。

三、教学内容和学情分析•教学内容：力的合成问题的解决方法。

•学情分析：学生在上一章节已经学习了力的基本概念和力的作用效果，对于力的合成问题较为陌生，需要引导学生理解力的合成。

四、教学方法和教学过程1.引入新课–引导学生复习上一章节学到的力的概念和作用效果。

–提问：力的合成是什么意思？为什么要进行力的合成？2.示范案例讲解–提供一个力的合成的案例，例如：有一个物体同时受到50N和30N的力，这时物体所受合力是多少？方向是什么？提示：合力的大小可以通过力的矢量合成法解决，合力的方向是力的合成方向。

3.概念解释–解释力矢量的概念：力可以用矢量表示，用力的箭头表示力的大小和方向。

–解释力的合成法：力的合成方法有平行四边形法则和三角形法则。

4.练习与讨论–分组讨论：将学生分成小组，进行力的合成练习。

每个小组根据题目计算合力的大小和方向。

示例题目：1.有一个物体受到30N的力向右和20N的力向上的作用，求合力的大小及方向。

2.有一个物体受到50N的力向左和40N的力向下的作用，求合力的大小及方向。

–每个小组轮流发表答案，并与其他小组的答案进行对比和讨论。

5.概念总结–总结力的合成的概念和解决问题的方法。

6.拓展讨论–引导学生思考：如果有三个力作用于一个物体上，如何计算合力的大小和方向？可以使用什么方法解决？7.巩固练习–让学生独立解决拓展讨论中的问题，并与同学进行讨论和对比答案。

8.作业布置–布置力的合成练习的作业，要求学生独立完成，并要求标明解题过程和答案。

五、教学评价与反思1.教学评价方式：通过观察学生的课堂讨论参与度和解题情况，以及作业的完成情况来评价学生的学习效果。

；。

苏科版物理第七章从粒子到宇宙复习教学案一、走进分子世界1.分子。

物质是由大量组成的。

分子直径以m来度量，数量级是______________。

2.一切物体的分子都在。

①扩散：不同物质在相互接触时，彼此进入对方的现象。

②扩散现象说明：A分子之间有间隙。

B分子在做不停的无规则的运动。

③固体、液体、气体都可扩散固体扩散举例：；液体扩散举例：；气体扩散举例：。

花香扑鼻气体扩散实验一勺盐使整锅汤都有咸味④扩散速度与有关。

温度越，扩散越。

⑤分子运动与物体运动要区分开：扩散、蒸发等是分子运动的结果（微观）飞扬的灰尘，液、气体对流是物体运动的结果（宏观）3.分子间存在和。

①固体和液体很难被压缩说明：；②两滴小水珠靠近结合成一滴大水珠说明：_____________________________，③固体很难被拉断，钢笔写字，胶水粘东西都是因为。

④当分子间距很大时，分子之间作用力十分微弱，可忽略不计。

破镜不能重圆的原因是：。

4.固态、液态、气态的微观模型解释：固体液体气体分子间距离分子间相互作用力分子运动有无固定形状有无固定体积二、探索更小的微粒1.摩擦起电：摩擦过的物体有了的性质，我们就说物体带了电。

（轻小物体指碎纸屑、头发、灰尘、轻质球等。

）2.摩擦起电的实质：。

3.两种电荷：正电荷：规定：实质：物质中的原子电子负电荷：规定：实质：物质中的原子电子4.电荷间的相互作用规律：、。

5.经过100多年众多的科学家的不懈努力，在探索物质组成微粒的进程中取得了了不起的成绩：1897年汤姆逊在真空放电时发现了_______，从而知道原子是由电子和_________组成的；1919年，卢瑟福从氮原子中打出了________，使人们知道原子核是由__________和_________组成的，并提出了_________________模型；1932年，发现了中子；1961年，提出夸克猜想，认为质子和中子由更小的粒子夸克组成。

第7章能量的释放与呼吸一、复习目标1.描述绿色植物的呼吸作用。

2.描述人体呼吸系统的组成。

3.概述发生在肺部和组织细胞处的气体交换过程。

4.说明能量来自细胞中有机物的氧化分解。

二、课时安排1课时三、复习重难点描述绿色植物的呼吸作用。

概述发生在肺部和组织细胞处的气体交换过程。

四、教学过程（一）知识梳理知识点1 呼吸作用1.呼吸作用的概念：在生物体的细胞内，分解有机物生成二氧化碳和水，并且释放能量的过程。

2.绝大部分生物体细胞内，有机物的氧化分解的过程都在有氧条件下进行。

酵母菌在没有氧的条件下进行呼吸，把葡萄糖分解成酒精和二氧化碳，释放少量能量。

通常把酵母菌等微生物在没有氧的环境中进行的呼吸作用叫发酵。

2.生物体呼吸作用产生的能量，一部分以热能的形式释放出来，另一部分以化学能的形式储存在ATP 中。

ATP像一个能量存储库，又像一个能量传递员，直接提供维持生物体各项生命活动的能量。

知识点2 光合作用和呼吸作用区别和联系（一）区别1.部位：光合作用进行的部分必须有叶绿体的细胞，因为叶绿体是进行光合作用的结构基础，形象地比喻为制造有机物的“机器”。

所有的活细胞都要进行呼吸作用，生命活动需要能量支持才能正常完成，而能量是由呼吸作用分解有机物释放得来的，没有呼吸作用，细胞就不能正常生活，就会死亡。

2.条件：光合作需要有光，因为光合作用把光能转变成化学能贮存在有机物中，光能在这里起到了动力作用．呼吸作用与光无关，无论白天黑夜细胞都要进行呼吸作用，提供能量。

3.原料：根据光合作用、呼吸作用的概念可知光合作用原料是二氧化碳和水，呼吸作用的原料是有机物和氧。

4、产物：光合作用的产物是有机物和氧，呼吸作用的产物是二氧化碳和水。

5、能量转变：光合作用是制造有机物，把光能转变成化学能储存起来；呼吸作用是分解有机物，把有机物中的化学能释放出来供生命活动利用，少部分以热的形式散失。

（二）联系光合作用原料的吸收和产物的运输的能量由呼吸作用提供，呼吸作用分解的有机物正是光合作用所制造的。

第2讲化学平衡状态[考纲解读] 1.了解可逆反应的定义。

2.理解化学平衡的定义。

3.理解影响化学平衡的因素。

4.理解化学平衡常数的定义并能进行简单计算。

考点一可逆反应可逆反应的概念：在同一条件下，既能向____反应方向进行，又能向____反应方向进行的化学反应。

1．反应2H2O 电解点燃2H2↑＋O2↑是否为可逆反应？2．向含有2 mol的SO2的容器中通入过量氧气发生2SO2＋O2催化剂加热2SO3，充分反应后生成SO3的物质的量______2 mol(填“<”、“>”或“＝”，下同)，O2的物质的量________0 mol，转化率________100%。

(1)可逆反应的可逆是指同一反应条件下，正、逆反应同时进行，不同条件下的反应不是可逆反应。

(2)可逆反应中任一物质的浓度都不能为零，而是介于完全正向转化与逆向转化之间。

(3)参与反应的物质的转化率不等于100%。

考点二化学平衡状态1．概念一定条件下的可逆反应中，正反应速率与逆反应速率________，反应体系中所有参加反应的物质的____________保持不变的状态。

2．建立过程在一定条件下，将0.3 mol CO和0.2 mol H2O(g)通入2 L密闭容器中，发生反应：CO(g)＋H2O(g) CO2(g)＋H2(g)。

(1)反应刚开始时，________浓度最大，正反应速率最大；______浓度为0，____反应速率为0。

(2)随着反应的进行，反应物浓度逐渐________，正反应速率逐渐________；生成物浓度逐渐________，逆反应速率逐渐________，最终正、逆反应速率________，达到平衡状态，此时反应体系中各物质的浓度均____________。

(3)依据以上叙述画出的反应的v－t图像如下：(4)由v －t 图像可以看出化学平衡是动态平衡，因为______________，即反应仍在进行着。

第五节直线、平面垂直的判定及其性质[考纲传真] 1.以立体几何的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题．1．直线与平面垂直(1)定义：如果直线l与平面α内的任意一条直线都垂直，则直线l与平面α垂直．(2)判定定理：如果一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．(3)推论：如果在两条平行直线中，有一条垂直于一个平面，那么另一条也垂直于这个平面．(4)直线和平面垂直的性质：①垂直于同一个平面的两条直线平行．②直线垂直于平面，则垂直于这个平面内的任一直线．③垂直于同一条直线的两平面平行．2．直线和平面所成的角(1)平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角．(2)当直线与平面垂直和平行(或直线在平面内)时，规定直线和平面所成的角分别为90°和0°.(3)直线和平面所成角的范围是0°≤θ≤90°.3．二面角的有关概念(1)二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．(2)二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角．(3)二面角的范围是0°≤θ≤180°.4．平面与平面垂直(1)定义：如果两个平面所成的二面角是直二面角，就说这两个平面互相垂直．(2)平面与平面垂直的判定定理与性质定理[常用结论]1．若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．2．一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直．3．两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．4．过一点有且只有一条直线与已知平面垂直．5．过一点有且只有一个平面与已知直线垂直．[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)直线l与平面α内的无数条直线都垂直，则l⊥α. ()(2)垂直于同一个平面的两平面平行．()(3)若两条直线与一个平面所成的角相等，则这两条直线平行．()(4)若两个平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面．()[答案](1)×(2)×(3)×(4)×2．“直线a与平面M内的无数条直线都垂直”是“直线a与平面M垂直”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件B[根据直线与平面垂直的定义知“直线a与平面M内的无数条直线都垂直”不能推出“直线a与平面M垂直”，反之可以，所以是必要不充分条件．故选B.]3．(教材改编)设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β.()A．若l⊥β，则α⊥βB．若α⊥β，则l⊥mC．若l∥β，则α∥βD．若α∥β，则l∥mA[∵l⊥β，l⊂α，∴α⊥β(面面垂直的判定定理)，故A正确．]4．如图所示，已知P A⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________．4[∵P A⊥平面ABC，∴P A⊥AB，P A⊥AC，P A⊥BC，则△P AB，△P AC为直角三角形．由BC⊥AC，且AC∩P A＝A，∴BC⊥平面P AC，从而BC⊥PC.因此△ABC，△PBC也是直角三角形．]5．边长为a的正方形ABCD沿对角线BD折成直二面角，则折叠后AC的长为________．a[如图所示，取BD的中点O，连接A′O，CO，则∠A′OC是二面角A′-BD-C的平面角．即∠A ′OC ＝90°，又A ′O ＝CO ＝22a ， ∴A ′C ＝a 22＋a 22＝a ，即折叠后AC 的长(A ′C )为a .]【例1】 (2018·全国卷Ⅱ)如图，在三棱锥P -ABC 中，AB ＝BC ＝22，P A ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且MC ＝2MB ，求点C 到平面POM 的距离． [解] (1)证明：因为AP ＝CP ＝AC ＝4，O 为AC 的中点， 所以OP ⊥AC ，且OP ＝2 3.连接OB .因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2.由OP 2＋OB 2＝PB 2知，OP ⊥OB .由OP ⊥OB ，OP ⊥AC ，OB ⊂平面ABC ，AC ⊂平面ABC ，OB ∩AC ＝O ，知PO ⊥平面ABC .(2)作CH ⊥OM ，垂足为H .又由(1)可得OP ⊥CH ，OP ⊂平面POM ，OM ⊂平面POM ，OP ∩OM ＝O ，所以CH ⊥平面POM .故CH 的长为点C 到平面POM 的距离．由题设可知OC ＝12AC ＝2，CM ＝23BC ＝423，∠ACB ＝45°. 所以OM ＝253，CH ＝OC ·MC ·sin ∠ACB OM ＝455.所以点C 到平面POM 的距离为455. ►考法2 直线与平面垂直的性质【例2】 (2017·江苏高考)如图，在三棱锥A -BCD 中，AB ⊥AD ，BC ⊥BD ，平面ABD ⊥平面BCD ，点E ，F (E 与A ，D 不重合)分别在棱AD ，BD 上，且EF ⊥AD .求证：(1)EF ∥平面ABC ； (2)AD ⊥AC .[证明] (1)在平面ABD 内，因为AB ⊥AD ，EF ⊥AD ， 所以EF ∥AB .又因为EF ⊄平面ABC ，AB ⊂平面ABC ， 所以EF ∥平面ABC .(2)因为平面ABD ⊥平面BCD ， 平面ABD ∩平面BCD ＝BD ， BC ⊂平面BCD ，BC ⊥BD ， 所以BC ⊥平面ABD .因为AD⊂平面ABD，所以BC⊥AD.又AB⊥AD，BC∩AB＝B，AB⊂平面ABC，BC⊂平面ABC，所以AD⊥平面ABC.又因为AC⊂平面ABC，所以AD⊥AC.如图所示，在四棱锥P-ABCD中，P A⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，P A＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.[证明](1)在四棱锥P-ABCD中，∵P A⊥平面ABCD，CD⊂平面ABCD，∴P A⊥CD.又∵AC⊥CD，且P A∩AC＝A，∴CD⊥平面P AC.而AE⊂平面P AC，∴CD⊥AE.(2)由P A＝AB＝BC，∠ABC＝60°，可得AC＝P A.∵E是PC的中点，∴AE⊥PC.由(1)知AE⊥CD，且PC∩CD＝C，∴AE⊥平面PCD.又PD⊂平面PCD，∴AE⊥PD.∵P A⊥底面ABCD，∴P A⊥AB.又∵AB⊥AD，且P A∩AD＝A，∴AB⊥平面P AD，而PD⊂平面P AD，∴AB⊥PD.又AB∩AE＝A，∴PD⊥平面ABE.【例3】(2018·全国卷Ⅰ)如图，在平行四边形ABCM中，AB＝AC＝3，∠ACM＝90°.以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA.(1)证明：平面ACD⊥平面ABC；(2)Q为线段AD上一点，P为线段BC上一点，且BP＝DQ＝23DA，求三棱锥Q-ABP的体积．[解](1)证明：由已知可得，∠BAC＝90°，BA⊥AC.又BA⊥AD，且AC⊂平面ACD，AD⊂平面ACD，AC∩AD＝A，所以AB⊥平面ACD.又AB⊂平面ABC，所以平面ACD⊥平面ABC.(2)由已知可得，DC＝CM＝AB＝3，DA＝3 2.又BP ＝DQ ＝23DA ，所以BP ＝2 2. 作QE ⊥AC ，垂足为E ，则QE 13DC .由已知及(1)可得DC ⊥平面ABC ，所以QE ⊥平面ABC ，QE ＝1.因此，三棱锥Q -ABP 的体积为V Q －ABP ＝13×QE ×S △ABP ＝13×1×12×3×22sin 45°＝1.(2018·江苏高考)在平行六面体ABCD -A 1B 1C 1D 1中，AA 1＝AB ，AB 1⊥B 1C 1. 求证：(1)AB ∥平面A 1B 1C ；(2)平面ABB 1A 1⊥平面A 1BC .[证明] (1)在平行六面体ABCD -A 1B 1C 1D 1中，AB ∥A 1B 1.因为AB ⊄平面A 1B 1C ，A 1B 1⊂平面A 1B 1C ，所以AB ∥平面A 1B 1C .(2)在平行六面体ABCD -A 1B 1C 1D 1中，四边形ABB 1A 1为平行四边形． 又因为AA 1＝AB ，所以四边形ABB 1A 1为菱形，因此AB1⊥A1B.又因为AB1⊥B1C1，BC∥B1C1，所以AB1⊥BC.又因为A1B∩BC＝B，A1B⊂平面A1BC，BC⊂平面A1BC，所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1，所以平面ABB1A1⊥平面A1BC.【例4】AB＝1，AC＝2，∠BAC＝60°.(1)求三棱锥P-ABC的体积；(2)在线段PC上是否存在一点M，使得AC⊥BM，若存在求PMMC的值，并说明理由．[解](1)由题设AB＝1，AC＝2，∠BAC＝60°，可得S△ABC ＝12·AB·AC·sin 60°＝32.由P A⊥平面ABC，可知P A是三棱锥P-ABC的高，又P A＝1，所以三棱锥P-ABC的体积V＝13·S△ABC·P A＝36.(2)在线段PC上存在一点M，使得AC⊥BM，此时PM MC＝13.证明如下：如图，在平面P AC 内，过点M 作MN ∥P A 交AC 于N ，连接BN ，BM .由P A ⊥平面ABC 知P A ⊥AC ， 所以MN ⊥AC .由MN ∥P A 知AN NC ＝PM MC ＝13. 所以AN ＝12，在△ABN 中，BN 2＝AB 2＋AN 2－2AB ·AN cos ∠BAC ＝12＋⎝ ⎛⎭⎪⎫122－2×1×12×12＝34，所以AN 2＋BN 2＝AB 2， 即AC ⊥BN .由于BN ∩MN ＝N ，故AC ⊥平面MBN . 又BM ⊂平面MBN . 所以AC ⊥BM .如图，四边形ABCD 为梯形，AB ∥CD ，PD ⊥平面ABCD ，∠BAD ＝∠ADC ＝90°，DC ＝2AB ＝2，DA ＝ 3.(1)线段BC 上是否存在一点E ，使平面PBC ⊥平面PDE ？若存在，请给出BECE 的值，并进行证明；若不存在，请说明理由．(2)若PD ＝3，线段PC 上有一点F ，且PC ＝3PF ，求三棱锥A -FBD 的体积．[解] (1)存在线段BC 的中点E ，使平面PBC ⊥平面PDE ，即BECE ＝1.证明如下：连接DE ，PE ，∵∠BAD ＝∠ADC ＝90°，AB ＝1，DA ＝3，∴BD ＝DC ＝2， ∵E 为BC 的中点，∴BC ⊥DE ， ∵PD ⊥平面ABCD ，∴BC ⊥PD ， ∵DE ∩PD ＝D ，∴BC ⊥平面PDE ， ∵BC ⊂平面PBC ， ∴平面PBC ⊥平面PDE .(2)∵PD ⊥平面ABCD ，且PC ＝3PF ，∴点F 到平面ABCD 的距离为23PD ＝233，∴三棱锥A -FBD 的体积V A -FBD ＝V F -ABD ＝13×S △ABD ×233＝13×12×1×3×233＝13.【例5】 如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC＝12AD ＝a ，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图2中△A 1BE 的位置，得到四棱锥A 1-BCDE .图1 图2(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1-BCDE 的体积为362，求a 的值．[解] (1)证明：在题图1中，连接EC (图略)， 因为AB ＝BC ＝12AD ＝a ，E 是AD 的中点，∠BAD ＝π2，所以BE ⊥AC . 即在题图2中，BE ⊥A 1O ，BE ⊥OC ， 从而BE ⊥平面A 1OC .又CD ∥BE ，所以CD ⊥平面A 1OC . (2)由已知，平面A 1BE ⊥平面BCDE ， 且平面A 1BE ∩平面BCDE ＝BE ，又由(1)可得A 1O ⊥BE ，所以A 1O ⊥平面BCDE . 即A 1O 是四棱锥A 1-BCDE 的高．由题图1知，A 1O ＝AO ＝22AB ＝22a ，平行四边形BCDE 的面积S ＝BC ·AB ＝a 2，从而四棱锥A 1-BCDE 的体积为V ＝13S ·A 1O ＝13×a 2×22a ＝26a 3.由26a 3＝362，得a ＝6.(2018·鄂州模拟)如图，在Rt △ABC 中，AB ＝BC ＝3，点E ，F分别在线段AB ，AC 上，且EF ∥BC ，将△AEF 沿EF 折起到△PEF 的位置，使得二面角P -EF -B 的大小为60°.(1)求证：EF ⊥PB ；(2)当点E 为线段AB 的靠近B 点的三等分点时，求四棱锥P -EBCF 的侧面积．[解] (1)证明：在Rt △ABC 中，∵AB ＝BC ＝3，∴BC ⊥AB .∵EF ∥BC ，∴EF ⊥AB ，翻折后垂直关系没变，仍有EF ⊥PE ，EF ⊥BE ， ∴EF ⊥平面PBE ，∴EF ⊥PB .(2)∵EF ⊥PE ，EF ⊥BE ，∴∠PEB 是二面角P -EF -B 的平面角， ∴∠PEB ＝60°，又PE ＝2，BE ＝1，由余弦定理得PB ＝3， ∴PB 2＋BE 2＝PE 2，∴PB ⊥BE ，∴PB ，BC ，BE 两两垂直， 又EF ⊥PE ，EF ⊥BE ，∴△PBE ，△PBC ，△PEF 均为直角三角形． 由△AEF ∽△ABC 可得，EF ＝23BC ＝2，S △PBC ＝12BC ·PB ＝332，S △PBE ＝12PB ·BE ＝32，S △PEF ＝12EF ·PE ＝2. 在四边形BCFE 中，过点F 作BC 的垂线，垂足为H (图略)，则FC 2＝FH 2＋HC 2＝BE 2＋(BC －EF )2＝2，∴FC ＝ 2.在△PFC 中，FC ＝2，PC ＝BC 2＋PB 2＝23，PF ＝PE 2＋EF 2＝22， 由余弦定理可得cos ∠PFC ＝PF 2＋FC 2－PC 22PF ·FC ＝－14， 则sin ∠PFC ＝154，S △PFC ＝12PF ·FC sin ∠PFC ＝152.∴四棱锥P -EBCF 的侧面积为S △PBC ＋S △PBE ＋S △PEF ＋S △PFC ＝2＋23＋152.1．(2018·全国卷Ⅲ)如图，矩形ABCD 所在平面与半圆弧︵CD 所在平面垂直，M 是︵CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)在线段AM 上是否存在点P ，使得MC ∥平面PBD ？说明理由． [解] (1)证明：由题设知，平面CMD ⊥平面ABCD ，交线为CD .因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM .因为M 为︵CD 上异于C ，D 的点，且DC 为直径，所以DM ⊥CM . 又BC ∩CM ＝C ，所以DM ⊥平面BMC . 而DM ⊂平面AMD ，故平面AMD ⊥平面BMC . (2)当P 为AM 的中点时，MC ∥平面PBD . 证明如下：如图，连接AC 交BD 于O .因为ABCD 为矩形，所以O 为AC 中点．连接OP ，因为P 为AM 中点，所以MC ∥OP .MC ⊄平面PBD ，OP ⊂平面PBD ，所以MC ∥平面PBD .2．(2017·全国卷Ⅰ)如图，在四棱锥P -ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°。

第二节空间几何体的表面积与体积[考纲传真]了解球、棱柱、棱锥、台的表面积和体积的计算公式．1．多面体的表(侧)面积因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．2．圆柱、圆锥、圆台的侧面展开图及侧面积公式3.1．正四面体的表面积与体积棱长为a的正四面体，其表面积为3a2，体积为2 12a3.2．几个与球有关的切、接常用结论 (1)正方体的棱长为a ，球的半径为R ， ①若球为正方体的外接球，则2R ＝3a ； ②若球为正方体的内切球，则2R ＝a ； ③若球与正方体的各棱相切，则2R ＝2a .(2)若长方体的同一顶点的三条棱长分别为a ，b ，c ，外接球的半径为R ，则2R ＝a 2＋b 2＋c 2.(3)正四面体的外接球与内切球的半径之比为3∶1，棱长为a 的正四面体，其内切球半径R 内＝612a ，外接球半径R 外＝64a .[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)锥体的体积等于底面面积与高之积． ( ) (2)球的体积之比等于半径比的平方． ( ) (3)台体的体积可转化为两个锥体的体积之差． ( )(4)已知球O 的半径为R ，其内接正方体的边长为a ，则R ＝32a . ( )[答案] (1)× (2)× (3)√ (4)√2．(教材改编)已知圆锥的表面积等于12π cm 2，其侧面展开图是一个半圆，则底面圆的半径为( )A ．1 cmB ．2 cmC ．3 cm D.32 cm B [S 表＝πr 2＋πrl ＝πr 2＋πr ·2r ＝3πr 2＝12π，∴r 2＝4， ∴r ＝2(cm)．]3．圆柱的底面直径与高都等于球的直径，则球的体积与圆柱的体积比V 球∶V 柱为( ) A ．1∶2 B ．2∶3C ．3∶4D ．1∶3B [设球的半径为R .则V 球V 柱＝43πR 3πR 2×2R＝23.]4．(教材改编)某几何体的三视图如图所示：则该几何体的体积为( )A ．6B ．3 3C ．2 3D ．3B [由三视图可知，该几何体是一个直三棱柱，其底面为侧视图，该侧视图是底边为2，高为3的三角形，正视图的长为三棱柱的高，故h ＝3，所以几何体的体积V ＝S ·h ＝⎝ ⎛⎭⎪⎫12×2×3×3＝3 3.]5．如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为________．1∶47 [设长方体的相邻三条棱长分别为a ，b ，c ，它截出棱锥的体积为V 1＝13×12×12a ×12b ×12c ＝148abc ，剩下的几何体的体积V 2＝abc －148abc ＝4748abc ，所以V 1∶V 2＝1∶47.]【例1】 (1)若某空间几何体的三视图如图所示，则该几何体的表面积是( )A．48＋πB．48－πC．48＋2π D．48－2π(2)(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为()A．122π B．12πC．82π D．10π(1)A(2)B[(1)该几何体是正四棱柱挖去了一个半球，正四棱柱的底面是正方形(边长为2)，高为5，半球的半径是1，那么该几何体的表面积为S＝2×2×2＋2×4×5－π×12＋2π×12＝48＋π，故选A.(2)因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为22，底面圆的直径为22，所以该圆柱的表面积为2×π×(2)2＋2π×2×22＝12π.](1)一个四面体的三视图如图所示，则该四面体的表面积是()A．1＋ 3 B．1＋2 2C．2＋ 3 D．2 2(2)(2016·全国卷Ⅲ)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为()A．18＋36 5B．54＋18 5C．90D．81(1)C(2)B[(1)由题意知题中的几何图形就是如图所示的四面体，其中AB＝AD＝CB＝CD＝2，BD＝2，且平面ABD⊥平面CBD.所以△ABD与△CBD都是等腰直角三角形，而△ABC与△CAD都是边长是2的等边三角形．所以表面积是12×2×2×2＋34×(2)2×2＝2＋3，故选C.(2)由三视图可知该几何体是底面为正方形的斜四棱柱，其中有两个侧面为矩形，另两个侧面为平行四边形，则表面积为(3×3＋3×6＋3×35)×2＝54＋18 5.故选B.]►考法1 公式法求体积【例2】 (1)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm 3)是( )A.π2＋1 B.π2＋3 C.3π2＋1D.3π2＋3(2)(2018·江苏高考)如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．(1)A (2)43 [(1)由三视图可知该几何体是由底面半径为1，高为3的半个圆锥和三棱锥S-ABC 组成的，如图，三棱锥的高为3，底面△ABC 中，AB ＝2，OC ＝1，AB ⊥OC .故其体积V ＝13×12×π×12×3＋13×12×2×1×3＝π2＋1.故选A.(2)正方体的棱长为2，以其所有面的中心为顶点的多面体是正八面体，其中正八面体的所有棱长都是2，则该正八面体的体积为13×(2)2×1×2＝43.]►考法2 割补法求体积【例3】 (1)(2017·全国卷Ⅱ)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )A ．90πB ．63πC ．42πD ．36π(2)如图所示，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE ，△BCF 均为正三角形，EF ∥AB ，EF ＝2，则该多面体的体积为( )A.23B.33C.43D.32(1)B (2)A [(1)法一：(割补法)如图所示，由几何体的三视图，可知该几何体是一个圆柱被截去上面虚线部分所得．将圆柱补全，并将圆柱体从点A 处水平分成上下两部分．由图可知，该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12，所以该几何体的体积V ＝π×32×4＋π×32×6×12＝63π.故选B.法二：(估值法)由题意，知12V 圆柱＜V 几何体＜V 圆柱．又V 圆柱＝π×32×10＝90π，∴45π＜V几何体＜90π.观察选项可知只有63π符合．故选B.(2)法一：如图所示，分别过A ，B 作EF 的垂线，垂足分别为G ，H ，连接DG ，CH ，则原几何体分割为两个三棱锥和一个直三棱柱，因为三棱锥高为12，直三棱柱高为1，AG ＝12－⎝ ⎛⎭⎪⎫122＝32，取AD 的中点M ，则MG ＝22， 所以S △AGD ＝12×1×22＝24， 所以V ＝24×1＋2×13×24×12＝23.法二：如图所示，取EF 的中点P ，则原几何体分割为两个三棱锥和一个四棱锥，易知三棱锥P -AED 和三棱锥P -BCF 都是棱长为1的正四面体，四棱锥P -ABCD 为棱长为1的正四棱锥．所以V ＝13×12×22＋2×13×34×63＝23.]►考法3 等积法求体积【例4】 如图所示，已知三棱柱ABC -A 1B 1C 1的所有棱长均为1，且AA 1⊥底面ABC ，则三棱锥B 1-ABC 1的体积为( )A.312B.34C.612D.64A [三棱锥B 1-ABC 1的体积等于三棱锥A -B 1BC 1的体积，三棱锥A -B 1BC 1的高为32，底面积为12，故其体积为13×12×32＝312.]A ．2B ．1C.23D.13(2)(2018·天津高考)如图，已知正方体ABCD -A 1B 1C 1D 1的棱长为1，则四棱锥A 1-BB 1D 1D 的体积为________．(1)C (2)13 [(1)几何体如图，由三视图得底面为对角线为2的正方形，高为1，所以体积为13×12×2×1×2×1＝23，故选C.(2)法一：连接A 1C 1交B 1D 1于点E (图略)，则A 1E ⊥B 1D 1，A 1E ⊥BB 1，则A 1E ⊥平面BB 1D 1D ，所以A 1E 为四棱锥A 1-BB 1D 1D 的高，且A 1E ＝22，矩形BB 1D 1D 的长和宽分别为2，1，故VA 1-BB 1D 1D ＝13×1×2×22＝13.法二：连接BD 1(图略)，则四棱锥A 1-BB 1D 1D 分成两个三棱锥B -A 1DD 1与B -A 1B 1D 1，VA 1-BB 1D 1D ＝VB -A 1DD 1＋VB -A 1B 1D 1＝13×12×1×1×1＋13×12×1×1×1＝13.]►考法1 外接球【例5】 (1)(2017·全国卷Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A ．π B.3π4 C.π2 D.π4(2)(2018·全国卷Ⅲ)设A ，B ，C ，D 是同一个半径为4的球的球面上四点，△ABC 为等边三角形且其面积为93，则三棱锥D -ABC 体积的最大值为( )A ．12 3B ．18 3C ．24 3D ．54 3(1)B (2)B [(1)设圆柱的底面半径为r ，球的半径为R ，且R ＝1，由圆柱两个底面的圆周在同一个球的球面上可知，r ，R 及圆柱的高的一半构成直角三角形．∴r ＝1－⎝ ⎛⎭⎪⎫122＝32. ∴圆柱的体积为V ＝πr 2h ＝34π×1＝3π4. 故选B.(2)如图，E 是AC 中点，M 是△ABC 的重心，O 为球心，连接BE ，OM ，OD ，BO .因为S △ABC ＝34AB 2＝93，所以AB ＝6，BM ＝23BE ＝23AB 2－AE 2＝2 3.易知OM ⊥平面ABC ，所以在Rt △OBM 中，OM ＝OB 2－BM 2＝2，所以当D ，O ，M 三点共线且DM ＝OD ＋OM 时，三棱锥D -ABC 的体积取得最大值，且最大值V ma x ＝13S △ABC ×(4＋OM )＝13×93×6＝18 3.故选B.]►考法2 内切球【例6】 (1)(2017·江苏高考)如图，在圆柱O 1O 2内有一个球O ，该球与圆柱的上、下底面及母线均相切，记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是________．(2)已知棱长为a 的正四面体，则此正四面体的表面积S 1与其内切球的表面积S 2的比值为________．(1)32(2)63π [(1)设球O 的半径为R ， ∵球O 与圆柱O 1O 2的上、下底面及母线均相切， ∴圆柱O 1O 2的高为2R ，底面半径为R . ∴V 1V 2＝πR 2·2R 43πR 3＝32.(2)正四面体的表面积为S 1＝4×34×a 2＝3a 2，其内切球半径r 为正四面体高的14，即r＝14×63a ＝612a ，因此内切球表面积为S 2＝4πr 2＝πa 26，则S 1S 2＝3a 2πa 26＝63π.]球，则能得到的最大球的半径等于( )A ．1B ．2C ．3D ．4(2)正四棱锥P -ABCD 的侧棱和底面边长都等于22，则它的外接球的表面积是( ) A ．16π B ．12πC ．8πD ．4π(1)B (2)A [(1)由三视图可知该几何体是一个直三棱柱，底面为直角三角形，高为12，如图所示，其中AC＝6，BC＝8，∠ACB＝90°，则AB＝10.要使该石材加工成的球的半径最大，只需球与直三棱柱的三个侧面都相切，则半径r等于直角三角形ABC的内切圆半径，即r＝6＋8－102＝2，故能得到的最大球的半径为2，故选B.(2)设正四棱锥的外接球半径为R，顶点P在底面上的射影为O(图略)，因为OA＝12AC＝12AB2＋BC2＝12(22)2＋(22)2＝2，所以PO＝P A2－OA2＝(22)2－22＝2.又OA＝OB＝OC＝OD＝2，由此可知R＝2，于是S球＝4πR2＝16π.]1．(2016·全国卷Ⅱ)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为()A．20πB．24πC．28π D．32πC[由三视图可知，该几何体是由一个圆柱和一个圆锥组成的组合体，上面是一个圆锥，圆锥的高是23，底面半径是2，因此其母线长为4，下面圆柱的高是4，底面半径是2，因此该几何体的表面积是S＝π×22＋2π×2×4＋π×2×4＝28π，故选C.]2．(2015·全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有()A．14斛B．22斛C．36斛D．66斛B[设米堆的底面半径为r尺，则π2r＝8，所以r＝16π，所以米堆的体积为V＝14×13π·r2·5＝π12×⎝⎛⎭⎪⎫16π2×5≈3209(立方尺)．故堆放的米约有3209÷1.62≈22(斛)．故选B.]3．(2018·全国卷Ⅰ)在长方体ABCD-A1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为()A．8 B．6 2C．8 2 D．8 3C[连接BC1，AC1，AC.因为AB⊥平面BB1C1C，所以∠AC1B＝30°，AB⊥BC1，所以△ABC1为直角三角形．又AB＝2，所以BC1＝2 3.又B1C1＝2，所以BB1＝(23)2－22＝22，故该长方体的体积V＝2×2×22＝8 2.]4．(2017·全国卷Ⅱ)长方体的长、宽、高分别为3,2,1，其顶点都在球O的球面上，则球O的表面积为________．14π [∵长方体的顶点都在球O 的球面上， ∴长方体的体对角线的长度就是其外接球的直径． 设球的半径为R ， 则2R ＝32＋22＋12＝14.∴球O 的表面积为S ＝4πR 2＝4π×⎝⎛⎭⎪⎫1422＝14π.]。

第3讲化学平衡移动[考纲解读] 1.理解外界条件(浓度、温度、压强、催化剂等)对化学平衡的影响，认识其一般规律。

2.了解化学平衡的调控在生活、生产和科学研究领域中的重要作用。

考点一化学平衡移动1．概念可逆反应达到平衡状态以后，若反应条件(如________、________、________等)发生了变化，平衡混合物中各组分的浓度也会随之________，从而在一段时间后达到________________。

这种由____________向______________的变化过程，叫做化学平衡的移动。

2．过程3．平衡移动方向与反应速率的关系(1)v正____v逆，平衡向正反应方向移动。

(2)v正____v逆，平衡不移动。

(3)v正____v逆，平衡向逆反应方向移动。

1．化学平衡移动的实质是什么？2．某一可逆反应，一定条件下达到了平衡，①若化学反应速率改变，平衡一定发生移动吗？②若平衡发生移动，化学反应速率一定改变吗？考点二影响化学平衡的外界因素1．影响化学平衡的因素条件的改变(其他条件不变) 化学平衡的移动浓度增大反应物浓度或减小生成物浓度向______方向移动减小反应物浓度或增大生成物浓度向______方向移动压强(对有气体存在的反应) 反应前后气体分子数改变增大压强向______________的方向移动反应前后气体分子数不变减小压强向______________的方向移动改变压强温度升高温度向____反应方向移动降低温度向____反应方向移动催化剂使用催化剂2.勒夏特列原理如果改变影响化学平衡的条件之一(如温度、压强，以及参加反应的化学物质的浓度)，平衡将向着能够____________的方向移动。

3．改变条件，平衡向正反应方向移动，原料的转化率一定提高吗？4．升高温度，化学平衡会向着吸热反应的方向移动，此时放热反应方向的反应速率会减小吗？5. 对于达到平衡的可逆反应：X+Y W+Z，增大压强则正、逆反应速率(v)的变化如图所示，分析可知X、Y、Z、W的聚集状态可能是( )A．Z、W为气体，X、Y中之一为气体B．Z、W中之一为气体，X、Y为非气体C．X、Y、Z皆为气体，W为非气体D．X、Y为气体，Z、W中至少有一种为气体6．将NO2装入带活塞的密闭容器中，当反应2NO2(g)N2O4(g)达到平衡后，改变下列一个条件，其中叙述正确的是( )A．升高温度，气体颜色加深，则此反应为吸热反应B．慢慢压缩气体体积，平衡向右移动，混合气体颜色变浅C．慢慢压缩气体体积，若体积减小一半，压强增大，但小于原来的两倍D．恒温恒容时，充入惰性气体，压强增大，平衡向右移动，混合气体的颜色变浅(1)压强的影响实质是浓度的影响，所以只有当这些“改变”造成浓度改变时，平衡才有可能移动。