控制系统超前校正

定常系统的频率法超前校正1问题描述用频率法对系统进行校正，是利用超前校正网络的相位超前特性来增大系统的相位裕量，从而提高系统的稳定性，致使闭环系统的频带扩展，以达到改善系统暂态响应的目的。

但系统频带的加宽也会带来一定的噪声干扰，为了系统具有满意的动态性能，高频段要求幅值迅速衰减，以减少噪声影响。

2设计过程和步骤2.1题目 已知单位反馈控制系统的开环传递函数：设计超前校正装置，使校正后系统满足：2.2计算校正传递函数（1）根据稳态误差的要求，确定系统的开环增益K则解得100k =（2）由于开环增益100k =,在MATLAB 中输入以下命令：z=[ ] ;p=[0,-10,-100];k=100000;[num,den]=zp2tf(z,p,k);[mag,phase,w]=bode(num,den);margin(mag,phase,w);则可得未校正系统的伯德图如图1所示：图1 校正前系统的伯德图由图中可以看出相位裕量角为061.1（3）谐振峰值为%0.161 1.250.4r M σ-=+=， 给定系统的相位裕量值1arcsin()53.1301r M γ==，由于未校正系统的开环对数幅频特性在剪切频率处的斜率为40/db dec -，一般取005~10ε=，在这里取为10,超前校正装置应提供的相位超前量φ，即:5201.611061.11301.531=+-=+-==εγγφφmε是用于补偿因超前装置的引入，使系统的剪切频率增大而增加的相角迟后量。

（4）根据所确定的最大相位超前角m φ，按下式计算相应的α（5）计算校正装置在m w 处的幅值110log α。

由于校正系统的对数幅频特性图，求得其幅值为110log α-处的频率，该频率m φ就是校正后系统的开环剪切频率c w ，即76.80==m c ωω（6）确定校正网络的转折频率和1ω、2ω4946.200644.076.8011=⨯===αωωm T ，（7）画出校正后系统的伯德图，并验算相应的相位裕量是否满足要求？如果不满足，则改变ε值，从步骤（3）开始重新进行计算。

串联超前校正和滞后校正的不同之处在控制系统中，超前校正和滞后校正是两种常见的校正方法。

它们都是为了提高系统的稳定性和性能而采取的措施。

然而，它们的实现方式和效果却有很大的不同。

本文将从理论和实践两个方面，分别探讨串联超前校正和滞后校正的不同之处。

一、理论分析1. 超前校正超前校正是指在控制系统中，通过提前控制信号的相位，使得系统的相位裕度增加，从而提高系统的稳定性和响应速度。

具体来说，超前校正是通过在控制信号中加入一个比例项和一个积分项，来提高系统的相位裕度。

这样，系统就能更快地响应外部干扰和变化，从而提高系统的性能。

2. 滞后校正滞后校正是指在控制系统中，通过延迟控制信号的相位，使得系统的相位裕度减小，从而提高系统的稳定性和抗干扰能力。

具体来说，滞后校正是通过在控制信号中加入一个比例项和一个微分项，来减小系统的相位裕度。

这样，系统就能更好地抵抗外部干扰和变化，从而提高系统的性能。

二、实践应用1. 超前校正超前校正在实践中的应用非常广泛。

例如，在电力系统中，超前校正可以用来提高电力系统的稳定性和响应速度。

在机械控制系统中，超前校正可以用来提高机械系统的精度和响应速度。

在化工生产中，超前校正可以用来提高化工生产的稳定性和生产效率。

2. 滞后校正滞后校正在实践中的应用也非常广泛。

例如，在飞行控制系统中，滞后校正可以用来提高飞行器的稳定性和抗干扰能力。

在汽车控制系统中，滞后校正可以用来提高汽车的稳定性和安全性。

在医疗设备中，滞后校正可以用来提高医疗设备的精度和稳定性。

总之，串联超前校正和滞后校正是两种常见的校正方法，它们都是为了提高系统的稳定性和性能而采取的措施。

然而，它们的实现方式和效果却有很大的不同。

在实践中，我们需要根据具体的应用场景和需求，选择合适的校正方法，以达到最佳的控制效果。

控制系统的超前校正设计1 设计原理本设计使用频域法确定超前校正参数。

首先根据给定的稳态性能指标，确定系统的开环增益K 。

因为超前校正不改变系统的稳态指标，所以，第一步仍然是调整放大器，使系统满足稳态性能指标。

再利用上一步求得的K ，绘制未校正前系统的伯德图。

在伯德图上量取未校正系统的相位裕度和幅值裕度，并计算为使相位裕度达到给定指标所需补偿角的超前相角εγγσϕ+-=0。

其中γ为给定的相位裕度指标；0γ为未校正系统的相位裕度；ε为附加角度。

（加ε的原因：超前校正使系统的截止频率c ω增大，未校正系统的相角一般是较大的负相角，为补偿这里增加的负相角，再加一个正相角ε，即|)()(||)()(|0''0c c c c j H j G j H j G ωωωωε∠-∠≥其中，c 'ω为校正后的截止频率。

当系统剪切率对应的ε取值为：当剪切率为-20dB 时，deg 10~5=ε，剪切率为-40dB 时，deg 15~10=ε，剪切率为-60dB 时，deg 20~15=ε。

）取σϕϕ=m ，并由mma ϕϕsin 1sin 1-+=求出a 。

即所需补偿的相角由超前校正装置来提供。

为使超前校正装置的最大超前相角出现在校正后系统的截止频率c 'ω上，即cm 'ωω=，取未校正系统幅值为)(lg 10dB a -时的频率作为校正后系统的截止频率c 'ω。

由T a m 1=ω计算参数T ，并写出超前校正的传递函数Ts aTs s G c ++=11)(。

校验指标，绘制系统校正后的伯德图，检验是否满足给定的性能指标。

当系统仍不满足要求时，则增大ε值，从ε取值再次调试计算。

2 控制系统的超前校正初始状态的分析由已知条件，首先根据初始条件调整开环增益。

根据：)3.01)(1.01()(s s s Ks G ++=要求系统的静态速度误差系数6≤v K ，K s s KS sG k s v =++==→)3.01)(1.01()(lim 0可得K=6，则待校正的系统开环函数为)3.01)(1.01(6)(s s s s G ++=上式为最小相位系统，其MATLAB 伯德图如图1所示。

串联超前校正的作用1. 引言串联超前校正是一种用于改善系统的控制性能的技术。

在控制系统中，超前校正是指在控制器的输出中引入一个超前补偿器，以提高系统的稳定性和响应速度。

串联超前校正的作用是通过引入一个超前补偿器来改善系统的响应特性，使得系统能够更快地达到稳定状态并具有更好的稳定性。

2. 超前补偿器的原理超前补偿器是一种控制器，它通过引入一个超前传递函数来改变系统的相位特性。

超前传递函数通常具有一个或多个零点，这些零点位于系统的传递函数的左半平面。

通过引入这些零点，超前补偿器可以提前增加系统的相位，从而改善系统的稳定性和响应速度。

超前补偿器的传递函数通常表示为：Gc(s) = Kc * (Ts + 1) / (αTs + 1)其中，Kc是增益，Ts是一个时间常数，α是超前补偿器的增益调节参数。

3. 串联超前校正的作用串联超前校正通过在控制系统中添加超前补偿器来改善系统的性能。

它的作用主要体现在以下几个方面：3.1 提高系统的稳定性超前补偿器通过引入一个或多个零点来改变系统的相位特性。

这些零点位于系统的传递函数的左半平面，可以提前增加系统的相位。

通过增加系统的相位，超前补偿器可以提高系统的稳定性，减小系统的相位裕度，使得系统对参数变化和扰动的抵抗能力更强。

3.2 加快系统的响应速度超前补偿器的引入可以提高系统的相位裕度，从而加快系统的响应速度。

相位裕度是指系统在幅频特性曲线上的相位与-180°的差值。

通过增加系统的相位裕度，超前补偿器可以使系统更快地达到稳定状态，并且减小系统的超调量和响应时间。

3.3 改善系统的跟踪性能超前补偿器可以通过增加系统的相位来改善系统的跟踪性能。

在控制系统中，跟踪性能是指系统对参考输入信号的跟踪能力。

通过引入超前补偿器，系统可以更快地跟踪参考输入信号，并且减小跟踪误差。

3.4 抑制系统的振荡在一些具有较高增益的系统中，可能会出现振荡现象。

超前补偿器可以通过改变系统的相位特性来抑制系统的振荡。

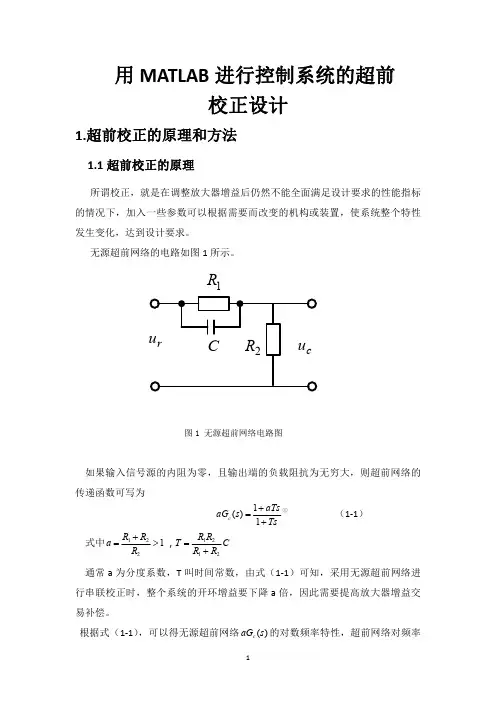
用MATLAB 进行控制系统的超前校正设计1.超前校正的原理和方法1.1超前校正的原理所谓校正，就是在调整放大器增益后仍然不能全面满足设计要求的性能指标的情况下，加入一些参数可以根据需要而改变的机构或装置，使系统整个特性发生变化，达到设计要求。

无源超前网络的电路如图1所示。

图1无源超前网络电路图如果输入信号源的内阻为零，且输出端的负载阻抗为无穷大，则超前网络的传递函数可写为1()1c aTs aG s Ts +=+①（1-1）式中1221R R a R +=>,1212R R T C R R =+通常a 为分度系数，T 叫时间常数，由式（1-1）可知，采用无源超前网络进行串联校正时，整个系统的开环增益要下降a 倍，因此需要提高放大器增益交易补偿。

根据式（1-1），可以得无源超前网络()c aG s 的对数频率特性，超前网络对频率1R在1/aT 至1/T 之间的输入信号有明显的微分作用，在该频率范围内，输出信号相角比输入信号相角超前，超前网络的名称由此而得。

在最大超前角频率m ω处，具有最大超前角m ϕ。

超前网路（1-1）的相角为()c arctgaT arctgT ϕωωω=-（1-2）将上式对ω求导并令其为零，得最大超前角频率（1-3）将上式代入（1-2），得最大超前角频率（1-4）同时还易知''m c ωω=ϕm 仅与衰减因子a 有关。

a 值越大，超前网络的微分效应越强。

但a 的最大值受到超前网络物理结构的制约，通常取为20左右（这就意味着超前网络可以产生的最大相位超前大约为65度）。

利用超前网络行串联校正的基本原理，是利用其相角超前特性。

只要正确地将超前网络的交接频率1/a T 或1/T 选在待校正系统截止频率的两旁，并适当选择参数a 和T ，就可以使已校正系统的截止频率和相角裕度满足性能指标的要求，从而改善系统的动态性能。

②1.2超前校正的应用方法待校正闭环系统的稳态性能要求，可通过选择已校正系统的开环增益来保证。

超前校正的原理超前校正是一种有效的控制系统调节方法，它能够预测系统输出的变化趋势，并在输出达到期望值之前即时采取相应的控制行动，从而减少系统的超调和稳态误差。

超前校正通过提前补偿系统的动态特性，提高系统的响应速度和稳定性，使系统能够更快地达到期望值，并且更好地满足控制要求。

超前校正的原理是基于对系统动态特性的准确建模和对未来输出变化的预测。

首先，需要对系统进行数学建模，将其转化为传递函数的形式，这样可以通过传递函数的特征参数来描述系统的动态响应。

然后，根据已有的系统响应数据，可以通过参数识别方法估计出系统的传递函数。

参数识别方法可以是最小二乘法、极大似然估计法等等。

通过参数估计，可以得到系统的传递函数，从而准确描述系统的动态特性。

一旦得到了系统的传递函数，就可以利用这个函数来进行超前校正。

超前校正的关键是预测系统输出的未来变化趋势。

为了进行预测，可以利用系统的传递函数对输入信号进行处理，得到预测输出信号的响应。

具体的预测方法可以是使用传递函数模型进行数字滤波操作，或者是使用离散化的传递函数进行递推计算等等。

在进行超前校正时，首先需要确定期望输出值和期望时间点。

通过对期望输出值和期望时间点的设置，可以实现对系统输出的精确控制。

当期望输出值和期望时间点确定之后，可以根据系统的传递函数和预测方法进行预测输出信号的计算。

根据预测输出信号和实际输出信号之间的差异，可以计算出校正量。

校正量是控制器输出的补偿值，用来修正系统的动态特性，以便更好地满足期望输出值和期望时间点的要求。

超前校正的关键是如何选择合适的校正量，以实现系统的优化调节。

校正量的选择需要考虑多种因素，包括系统的响应速度、超调量、稳态误差等等。

一般来说，校正量可以是根据经验设置的固定值，也可以是根据系统实时特性进行自适应调节的变量。

通过动态调整校正量，可以使系统的超前校正更加灵活和精确。

总之，超前校正是一种利用数学建模和预测方法进行系统控制的有效技术。

相位超前和滞后在控制系统中的作用如下：
1. 超前校正：目的是改善系统的动态性能，在系统静态性能不受损的前提下，提高系统的动态性能。

通过加入超前校正环节，利用其相位超前特性来增大系统的相位裕度，改变系统的开环频率特性。

一般使校正环节的最大相位超前角出现在系统新的穿越频率点。

2. 滞后校正：通过加入滞后校正环节，使系统的开环增益有较大幅度增加，同时又使校正后的系统动态指标保持原系统的良好状态。

它利用滞后校正环节的低通滤波特性，在不影响校正后系统低频特性的情况下，使校正后系统中高频段增益降低，从而使其穿越频率前移，达到增加系统相位裕度的目的。

3. 滞后-超前校正：是滞后校正与超前校正的组合。

它具有超前校正的提高系统相对稳定性和响应快速性；同时又具有滞后校正的不影响原有动态性能的前提下，提高系统的开环增益，改善系统的稳定性能。

它具有低频端和高频端频率衰减的特性，故又称带通滤波器。

这种校正方式适用于对校正后系统的动态和静态性能有更多更高要求的场合。

用MATLAB进行控制系统的超前校正设计超前校正是一种用于控制系统设计的技术，它通过提前预测系统的动态性质，并校正输出信号，以改善系统的性能和稳定性。

在MATLAB中，我们可以使用控制系统工具箱来进行超前校正的设计。

超前校正的设计步骤如下：1. 确定系统的传递函数模型：首先，我们需要确定待控制系统的数学模型，通常使用传递函数表示。

在MATLAB中，我们可以使用`tf`函数定义传递函数。

例如，如果系统的传递函数为G(s) = (s + 2)/(s^2 + 5s + 6)，可以用以下命令定义该传递函数：```matlabG = tf([1 2], [1 5 6]);```2.确定要求的超前时间常数和相位余量：超前校正的目标是在系统的低频区域增加相位余量，以提高系统的稳定性和性能。

我们需要根据应用需求确定所需的超前时间常数和相位余量。

一般来说，相位余量取值在30到60度之间较为合适。

3.计算所需的超前网络增益：根据所需的超前时间常数和相位余量，可以使用以下公式计算所需的超前网络增益：```matlabKc = 1 / sqrt(phi) * abs(1 / evalfr(G, j * w_c))```其中，phi为所需的相位余量，w_c为所需的截止角频率，evalfr函数用于计算传递函数在复频域上的值。

4. 设计超前校正网络：超前校正网络通常由一个增益项和一个零点组成，用于提高低频响应的相位余量。

使用`leadlag`函数可以方便地设计超前校正网络。

例如，以下命令可以设计一个零点在所需截止频率处的超前校正网络：```matlabw_c=1;%所需的截止角频率phi = 45; % 所需的相位余量Gc = leadlag(w_c, phi);```5. 计算开环传递函数和闭环传递函数：使用`series`函数可以计算超前校正网络和原系统传递函数的乘积，得到开环传递函数。

而使用`feedback`函数可以根据需要计算闭环传递函数。

试验五 系统超前校正（4课时）本试验为设计性试验 一、试验目旳1. 理解和观测校正装置对系统稳定性及动态特性旳影响。

2. 学习校正装置旳设计和实现措施。

二、试验原理工程上常用旳校正措施一般是把一种高阶系统近似地简化成低阶系统, 并从中找出少数经典系统作为工程设计旳基础, 一般选用二阶、三阶经典系统作为预期经典系统。

只要掌握经典系统与性能之间旳关系, 根据设计规定, 就可以设计系统参数, 进而把工程实践确认旳参数推荐为“工程最佳参数”, 对应旳性能确定为经典系统旳性能指标。

根据经典系统选择控制器形式和工程最佳参数, 据此进行系统电路参数计算。

在工程设计中, 常常采用二阶经典系统来替代高阶系统（如采用主导极点、偶极子等概念分析问题）其动态构造图如图7-1所示。

同步还常常采用“最优”旳综合校正措施。

图7-1二阶经典系统动态构造图二阶经典系统旳开环传递函数为)2()1()(2n n s s Ts s Ks G ξωω+=+= 闭环传递函数2222)(nn ns s s ωξωω++=Φ 式中 , 或者 二阶系统旳最优模型 （1）最优模型旳条件根据控制理论, 当 时, 其闭环频带最宽, 动态品质最佳。

把 代入 得到, , 这就是进行校正旳条件。

（2）最优模型旳动态指标为%3.4%100%21/=⨯=--ξξπσe，T t ns 3.43≈=ω三、试验仪器及耗材1．EL —AT3自动控制原理试验箱一台； 2．PC 机一台； 3．数字万用表一块 4．配套试验软件一套。

四、试验内容及规定未校正系统旳方框图如图7-2所示, 图7-3是它旳模拟电路。

图7-2未校正系统旳方框图矫正后未调整电路图图7-3未校正系统旳模拟电路设计串联校正装置使系统满足下述性能指标（1） 超调量%σ≤5% （2） 调整时间t s ≤1秒（3） 静态速度误差系数v K ≥20 1/秒 1. 测量未校正系统旳性能指标 （1）按图7-3接线；（2）加入单位阶跃电压, 观测阶跃响应曲线, 并测出超调量 和调整时间ts 。

第1篇一、实验目的1. 理解超前校正的原理及其在控制系统中的应用。

2. 掌握超前校正装置的设计方法。

3. 通过实验验证超前校正对系统性能的改善效果。

二、实验原理超前校正是一种常用的控制方法，通过在系统的前向通道中引入一个相位超前网络，来改善系统的动态性能。

超前校正能够提高系统的相角裕度和截止频率，从而改善系统的快速性和稳定性。

超前校正装置的传递函数一般形式为：\[ H(s) = \frac{1 + \frac{K}{T_{s}s}}{1 + \frac{T_{s}s}{K}} \]其中，\( K \) 为校正装置的增益，\( T_{s} \) 为校正装置的时间常数。

三、实验设备1. 控制系统实验平台2. 数据采集卡3. 计算机及仿真软件（如MATLAB/Simulink）4. 待校正系统四、实验步骤1. 搭建待校正系统模型：在仿真软件中搭建待校正系统的数学模型，包括系统的传递函数、输入信号等。

2. 分析系统性能：通过仿真软件分析待校正系统的性能，包括稳态误差、超调量、上升时间等。

3. 设计超前校正装置：根据待校正系统的性能要求，设计合适的超前校正装置参数。

4. 仿真验证：将设计好的超前校正装置添加到系统中，进行仿真验证，观察校正后的系统性能。

5. 实验数据分析：对实验数据进行分析，比较校正前后系统的性能差异。

五、实验内容1. 系统模型搭建：搭建一个简单的二阶系统模型，其传递函数为：\[ G(s) = \frac{1}{(s+1)(s+2)} \]2. 系统性能分析：分析该系统的稳态误差、超调量、上升时间等性能指标。

3. 设计超前校正装置：根据系统性能要求，设计一个超前校正装置，其传递函数为：\[ H(s) = \frac{1 + \frac{K}{T_{s}s}}{1 + \frac{T_{s}s}{K}} \]其中，\( K = 2 \)，\( T_{s} = 0.5 \)。

4. 仿真验证：将设计好的超前校正装置添加到系统中，进行仿真验证，观察校正后的系统性能。

超前滞后校正原理你看啊，在控制系统里就像在管理一个小世界一样。

有时候这个系统它表现得不太好，就像一个调皮的小孩，老是达不到我们想要的效果。

这时候呢，超前校正和滞后校正就像是两位神奇的小助手跑出来帮忙啦。

先说说超前校正吧。

超前校正就像是一个充满活力的小机灵鬼。

想象一下，系统就像一辆汽车在行驶，但是它的转向有点慢，不能很快地按照我们想要的方向改变。

超前校正就像是给这辆汽车装了一个超级灵敏的转向助力器。

它的原理呢，就是在系统的某个地方加进去一些东西，让系统能够提前做出反应。

比如说，在信号还没完全变大或者变小之前，就提前调整系统的状态。

这就好比你知道前面的路要拐弯了，你提前就开始转动方向盘，而不是等到到了拐弯的地方才开始转。

超前校正它主要是改变了系统的相角裕度，让系统变得更加稳定而且快速响应。

就像那个提前做好准备的人，不管遇到什么情况都能快速应对，不会手忙脚乱的。

再来说说滞后校正。

滞后校正就像是一个沉稳的老大哥。

它的作用方式有点不一样哦。

如果说超前校正像是快刀斩乱麻，那滞后校正就是慢条斯理地调整。

比如说系统里有些高频的噪声或者干扰，就像一群小苍蝇在捣乱。

滞后校正就像是一个大扇子，慢慢地把这些苍蝇给赶走。

它主要是通过降低系统的高频增益来达到这个目的的。

就像是在一个热闹的派对上，那些吵闹的高音部分被慢慢地降低了音量，让整个系统变得更加平稳。

滞后校正不会像超前校正那样让系统快速反应，但是它能让系统在长期的运行中更加稳定可靠。

它就像是给系统打了一针镇定剂，让那些过度兴奋或者不稳定的因素慢慢平静下来。

这超前校正和滞后校正啊，它们的存在都是为了让系统变得更好。

有时候我们的系统可能既需要快速反应的能力，又需要长期稳定的状态。

这时候呢，我们可能就要把超前校正和滞后校正结合起来用啦。

就像一个超级英雄组合，一个负责冲锋陷阵，快速应对危机，一个负责稳住后方，保证长期的稳定和平静。

你可别小看这两个校正原理哦。

在很多实际的工程应用里，它们可是发挥着巨大的作用呢。