第三章 纤维的力学性质(原文)讲解
- 格式:doc
- 大小:1.50 MB
- 文档页数:193

第三章纤维的力学性质第一节纤维的拉伸与疲劳性能一、拉伸曲线的基本特征表示纤维在拉伸过程中强力和伸长的关系曲线称为拉伸曲线(强力-伸长曲线、应力-应变曲线)。
纤维在拉伸过程中的行为表现和它的结构在拉伸过程中所发生的变化和破坏是有联系的,这样的本构关系可以通过对拉伸曲线的分析加以表述。
拉伸从O′点开始:(1)自O′至O——如果拉伸前纤维未完全伸直,纤维将通过O′O逐渐伸直。
(2)自O至M——曲线基本上是直线段,表示纤维发生的是导致强力与伸长间呈直线相关的虎克变形,纤维中主要是发生了分子内或分子间键角键长的变形。
(3)自M至Q——强力与伸长间关系进入非直线相关阶段,表明纤维中非晶区内大分子链开始发生构象的变化,链与链之间的关系改变。
(4)自Q至S——Q点可称为屈服点,但大多数纤维都没有明晰的屈服点,因为屈服点是结晶物质的特征点,而纤维只有部份结晶态(区)、甚至没有结晶态只有有序区。
自Q点开始,原存在于分子内或分子间的氢键等次价力联系开始破坏,首先是非晶区中大分子的错位滑移,所以,这一阶段,伸长增长快于强力。
(5)自S至A——随拉伸的进行,错位滑移的分子基本伸直平行,并可能在伸直的分子链间创造形成新次价力的机会,同时,纤维的结晶区也开始被破坏。
拉断结晶区与非晶区中分子间联系,需要较大的外力,所以这一阶段强力上升很快,到A点,纤维断裂。
纤维的应力-应变曲线和强力-伸长曲线的特征相似。
表3-1 常见纤维的拉伸性质指标二、表征纤维拉伸断裂特征的指标1.强力强力是指纤维能够承受的最大拉伸力,又名绝对强力、断裂强力。
2.相对强度相对强度是应力指标,简称为强度,用纤维被拉断时单位横截面上承受的拉伸力来表示。
根据采用的表征纤维截面积的指标不同,强度指标有以下几种:(1)断裂应力σ又名强度极限,它是指纤维单位截面积上所能承受的最大拉伸力,单位为N /mm 2(即兆帕)。
(2)比强度tex P指每特纤维所能承受的最大拉伸力,又称断裂强度,单位为N /tex 或cN/dtex 。

2023纤维化学与物理(蔡再生著)课后答案下载2023纤维化学与物理(蔡再生著)课后答案下载第一章高分子化学基础第一节高分子化合物的基本概念第二节高分子化合物的命名和分类第三节高分子化合物的基本合成反应第四节聚合方法概述第五节高分子化合物的分子量及其分布习题与思考题参考文献第二章高分子物理基础第一节高分子化合物的'结构层次第二节高分子链的结构第三节高分子化合物的聚集态结构第四节高分子化合物的力学性能第五节高分子化合物熔体的流变特性第六节高分子深液第七节高分子化合物的结构和性能测定方法概述参考文献第三章纺织纤维的基本理化性能第一节纺织纤维与纺织品第二节纺织纤维的物理结构第三节纺织纤维的吸湿性第四节纺织纤维的力学性质第五节纤维的热学性质第六节纤维的燃烧性第七节纤维的电学性质第八节纤维的光学性质习题与思考题参考文献第四章纤维素纤维第一节纤维素纤维的形态结构第二节纤维素的分子链结构和链间结构第三节纤维素纤维的物理性质第四节纤维素纤维的化学性质第五节再生纤维素纤维参考文献第五章蛋白质纤维第一节蛋白质的基础知识第二节羊毛纤维第三节蚕丝纤维第四节其他动物纤维第五节大豆纤维习题与思考题参考文献第六章合成纤维第一节合成纤维的基础知识第二节聚酯纤维第三节聚酰胺纤维第四节聚丙烯腈纤维第五节聚丙烯纤维第六节聚氨酯弹性纤维第七节聚乙烯醇缩醛化纤维第八节聚氯乙烯纤维第九节其他有机纤维第十节碳纤维习题与思考题参考文献纤维化学与物理(蔡再生著):基本信息点击此处下载纤维化学与物理(蔡再生著)课后答案纤维化学与物理(蔡再生著):目录出版社: 中国纺织出版社; 第1版 (8月1日)丛书名: 纺织高等教育教材平装: 307页语种:简体中文开本: 16ISBN: 7506430029条形码: 9787506430029商品尺寸: 25.6 x 18.2 x 1.6 cm商品重量: 558 g品牌: 中国纺织出版社ASIN: B0011ASQYU用户评分: 平均4.0 星浏览全部评论 (1 条商品评论)亚马逊热销商品排名: 图书商品里排第3,014,655名 (查看图书商品销售排行榜)第1332位 - 图书科技轻工业、手工业纺织工业、染整工业第23005位 - 图书教材教辅与参考书大中专教材教辅本科数理化第30774位 - 图书教材教辅与参考书大中专教材教辅本科工科。






第三章纤维的⼒学性质(原⽂)讲解第三章纤维的⼒学性质第⼀节纤维的拉伸性质纺织纤维在纺织加⼯和纺织品的使⽤过程中,会受到各种外⼒的作⽤,要求纺织纤维具有⼀定的抵抗外⼒作⽤的能⼒。
纤维的强度也是纤维制品其他物理性能得以充分发挥的必要基础,因此,纤维的⼒学性质是最主要的性质,它具有重要的技术意义和实际意义。
纺织纤维的长度⽐直径⼤1000倍以上,这种细长的柔性物体,轴向拉伸是受⼒的主要形式,其中,纤维的强伸性质是衡量其⼒学性能的重要指标。
⼀、拉伸曲线及拉伸性质指标1.纤维的拉伸曲线特征纤维的拉伸曲线由拉伸试验仪得到,图3-1是⼀试样长度为20cm,线密度为0.3 tex,密度为1.5R/cm3的纤维在初始负荷为零开始⼀直拉伸⾄断裂时的⼀根典型的纤维拉伸曲线。
它可以分成3个不同的区域:A为线性区(或近似线性区);B为屈服区,在B区负荷上升缓慢,伸长变形增加较快;C为强化区,伸长变形增加较慢,负荷上升较快,直⾄纤维断裂。
图3-1 纤维的拉伸曲线纤维的拉伸曲线可以是负荷-伸长曲线,也可以将它转换成应⼒-应变曲线,图形完全相同,仅坐标标尺不同⽽已。
纤维拉伸曲线3个不同区域的变形机理是不同的。
当较⼩的外⼒作⽤于纤维时,纤维产⽣的伸长是由于分⼦链本⾝的伸长和⽆定形区中缚结分⼦链伸展时,分⼦链间横向次价键产⽣变形的结果。
所以,A区的变形是由于分⼦链键长(包括横向次价键)和键⾓的改变所致。
变形的⼤⼩正⽐于外⼒的⼤⼩,即应⼒-应变关系是线性的,服从虎克定律。
当外⼒除去,纤维的分⼦链和横向连接键将回复到原来位置,是完全弹性回复。
由于键的变形速度与原⼦热振动速率相近,回复时间的数量级是10-13s,因此,变形的时间依赖性是可以忽略的,即变形是瞬时的。
当施加的外⼒增⼤时,⽆定形区中有些横向连接键因受到较⼤的变形⽽不能承受施加于它们的⼒⽽发⽣键的断裂。
这样,允许卷曲分⼦链伸直,接着分⼦链之间进⾏应⼒再分配,使其他的横向连接键受⼒增加⽽断裂,分⼦链进⼀步伸展。
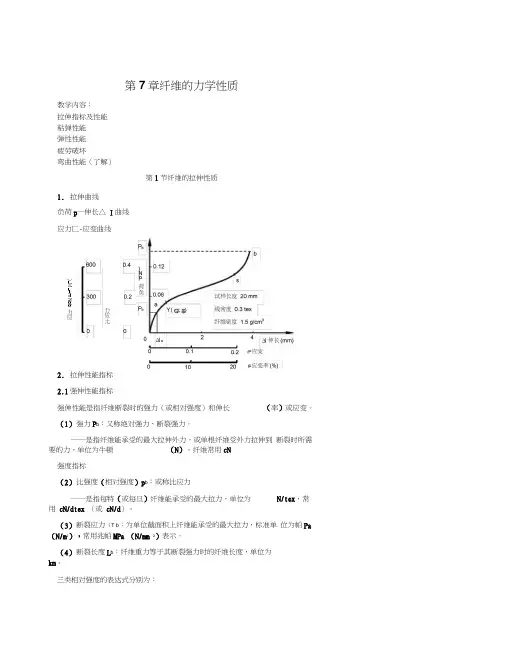
第7章纤维的力学性质教学内容: 拉伸指标及性能 粘弹性能 弹性性能 疲劳破坏 弯曲性能(了解)第1节纤维的拉伸性质1. 拉伸曲线负荷p —伸长△ I 曲线 应力匚-应变曲线2. 拉伸性能指标 2.1强伸性能指标强伸性能是指纤维断裂时的强力(或相对强度)和伸长 (率)或应变。
(1) 强力P b :又称绝对强力、断裂强力。
――是指纤维能承受的最大拉伸外力,或单根纤维受外力拉伸到 断裂时所需要的力,单位为牛顿 (N )。
纤维常用cN 强度指标(2) 比强度(相对强度)p b :或称比应力――是指每特(或每旦)纤维能承受的最大拉力,单位为 N/tex ,常 用 cN/dtex (或 cN/d )。
(3) 断裂应力(T b :为单位截面积上纤维能承受的最大拉力,标准单 位为帕Pa (N/m 2),常用兆帕MPa (N/mm 2)表示。
(4) 断裂长度L b :纤维重力等于其断裂强力时的纤维长度,单位为 km 。
三类相对强度的表达式分别为:)_M_=mNpb力应 力应比R P d =-^ P b 单位为N P t 单位为N/tex N tex N denPb hiL b N mg-b=Pb-b = P 103A(5)断裂伸长率纤维拉伸至断裂时的伸长率(或应变) ,;,100%L0表示纤维断裂时的伸长变形能力的大小2.2 初始模量初始模量是指纤维拉伸曲线的起始部分直线段的应力与应变的比值,即二-;曲线在起始段的斜率。
初始模量的大小表示纤维在小负荷作用下变形的难易程度,即纤维的刚性。
小变形情况下(<1 %),晶区大分子基本不发生形变,只有非晶区分子链发生形变——主要取决于非晶区分子链的取向度。
影响材料的保形、弹性及刚度:大,制品挺括;小,柔软2.3屈服应力与屈服伸长率屈服点:在纤维拉伸曲线上伸长变形随应力增大突然变大时的转折点。
对应屈服点处的应力或伸长率就是屈服应力和屈服伸长率屈服点前后变形情况对比:(1)之前:主要是纤维大分子链本身的键长、键角的伸长和分子链间次价键的剪切一一基本上是可恢复的急弹性变形。
第三章纤维的力学性质1.为何纤维的力学性质较多或近乎全部是讨论拉伸性质(tensile properties)?而对于单纤维的弯曲、压缩、扭转及其对应的高速作用下的讨论很少?2.纤维是微米尺度(micro-scale)的材料,在微尺度下的的弯曲、压缩、扭转甚至拉伸相对宏观尺度有何异同,其测量的主要困难为何?3.试画出常用再生纤维的应力-应变曲线,并讨论其间的不同点,并与对应的结构进行比较。
4.试画出高性能纤维的σ-ε曲线,并比较各自的主特征,并与常规合成纤维进行比较,讨论其间的只要不同点。
5.试就常用合成纤维和天然纤维的比应力-应变曲线进行比较,讨论其间的主要异同性。
如果是要仿生,合成纤维的拉伸纤维应该如何改进?如何进行力学性能配伍的混纺,其拉伸性质又宜作如何变化?6.纤维在拉伸变形中,其截面和伸长在被拉伸段上是否一致或线性变化?这对拉伸行为有何影响?并作图予以讨论。
7.通常的σ-ε曲线是名义应力,即拉伸纤维的截面不变原则。
如果考虑截面随拉伸变化的应力σr(称真应力),其σr-ε曲线与σ-ε曲线有何不同,并作图给出解释。
8.何谓典型拉伸曲线?其如何获得?9.试讨论纤维高聚物的拉伸屈服点与金属材料的屈服点的区别以及产生的基本原理。
10.试表达Peirce“弱环定律”的基本描述,其是否描述了何为“弱环weak-linkage”?11.试述Spencer-Smith的弱环(或弱节)表达,这两位学者是否表述了弱环?12.当ε=kt时,讨论Maxwell模型和Voigt模型的初始模量,以及各自的s=s(*).13.当s=kt时,给出Maxwell模型和Voigt模型的初始模量,以及各自的e=e(t).14.试画出三元件模型的可能组合形式,并分别求其各自的本构方程,并讨论模型间的等效性。
15.试画出下列图的变形曲线。
(1)依据力学模型的本构方程,求E’和E”中主要包含的内容、并讨论与世纪纤维结构的关系。
(2)因为纤维多为原纤结构,而原纤多为结晶或有缺陷的结晶体,因此,作图讨论纤维取向度对交模量E*中的E’和E”的影响。
第三章纤维的力学性质第一节纤维的拉伸性质纺织纤维在纺织加工和纺织品的使用过程中,会受到各种外力的作用,要求纺织纤维具有一定的抵抗外力作用的能力。
纤维的强度也是纤维制品其他物理性能得以充分发挥的必要基础,因此,纤维的力学性质是最主要的性质,它具有重要的技术意义和实际意义。
纺织纤维的长度比直径大1000倍以上,这种细长的柔性物体,轴向拉伸是受力的主要形式,其中,纤维的强伸性质是衡量其力学性能的重要指标。
一、拉伸曲线及拉伸性质指标1.纤维的拉伸曲线特征纤维的拉伸曲线由拉伸试验仪得到,图3-1是一试样长度为20cm,线密度为0.3 tex,密度为1.5R/cm3的纤维在初始负荷为零开始一直拉伸至断裂时的一根典型的纤维拉伸曲线。
它可以分成3个不同的区域:A为线性区(或近似线性区);B为屈服区,在B区负荷上升缓慢,伸长变形增加较快;C为强化区,伸长变形增加较慢,负荷上升较快,直至纤维断裂。
图3-1 纤维的拉伸曲线纤维的拉伸曲线可以是负荷-伸长曲线,也可以将它转换成应力-应变曲线,图形完全相同,仅坐标标尺不同而已。
纤维拉伸曲线3个不同区域的变形机理是不同的。
当较小的外力作用于纤维时,纤维产生的伸长是由于分子链本身的伸长和无定形区中缚结分子链伸展时,分子链间横向次价键产生变形的结果。
所以,A区的变形是由于分子链键长(包括横向次价键)和键角的改变所致。
变形的大小正比于外力的大小,即应力-应变关系是线性的,服从虎克定律。
当外力除去,纤维的分子链和横向连接键将回复到原来位置,是完全弹性回复。
由于键的变形速度与原子热振动速率相近,回复时间的数量级是10-13s,因此,变形的时间依赖性是可以忽略的,即变形是瞬时的。
当施加的外力增大时,无定形区中有些横向连接键因受到较大的变形而不能承受施加于它们的力而发生键的断裂。
这样,允许卷曲分子链伸直,接着分子链之间进行应力再分配,使其他的横向连接键受力增加而断裂,分子链进一步伸展。
在这一阶段,纤维伸长变得较容易,而应力上升很缓慢。
应力-应变曲线具有较小的斜率,这是B区产生的屈服现象。
当外力除去后,变形的回复是不完全的。
因为许多横向连接键已经断裂不能回到原来的位置,或者在新的位置上已经重新形成新的横向次价键变成较稳定的结构状态。
当进一步增加外力时,由于纤维千讦多大分子链经过屈服流动后,分子链因充分伸直,进一步拉伸分子链比较困难。
这时,拉伸曲线斜率增加,如C区,即为强化区,这时增加的变形主要是纤维大分子链键长和键角的改变所引起,最后直至纤维断裂。
不同纺织纤维由于内部结构不同,其拉伸曲线有很大差异,几种常见纺织纤维的应力-应变曲线如图3-2所示。
天然纤维因品种不同,或生长、饲养条件的差异,化学纤维则由于大分子链结构以及纺丝工艺参数的差别,其拉伸性能也会有很大的差别。
常见纺织纤维的有关拉伸性质指标列于表3-1。
图3-2 不同纤维的应力-应变曲线2.拉伸性能指标由纤维拉伸曲线可提取表征纤维拉伸性能的许多重要力学性能指标。
(1)断裂强力和断裂强度纤维断裂强力表示纤维能承受拉伸负荷的最大能力,单位为牛顿(N),或厘牛(cN)。
单根纤维的断裂强力称绝对强力,它与纤维粗细有关,为了相互比较,通常采用断裂强度(或相对强度)来表征。
表示纤维断裂强度常用以下3种指标:①断裂应力:它是单位纤维横截面上纤维所能承受的最大拉力,单位为Pa(N/m2)或 cN/cm2,因Pa的单位很小,常用MPa,且1MPa=106Pa。
②比应力:它是指单位线密度纤维所能承受的最大拉力,单位为N/tex。
③断裂长度:它是指纤维本身重力等于其断裂强力时的纤维长度,单位为千米(km),即(3-1)其中,P为纤维的强力(N);若为重力加速度(9.8m/s2);Nm为纤维的公制支数(m/g)。
纤维相对强度的3个指标间关系为(3-2)(3-3)式中,ζ为纤维断裂应力(N/mm2);p t为纤维的比应力(N/tex);g为重力加速度(9.8m/s2);L 为纤维的断裂长度(km);ν为纤维密度(g/cm3)。
(2)断裂伸长率纤维拉伸断裂时产生的伸长占原来长度的百分率。
它表示纤维承受最大负荷时的伸长变形能力。
(3)初始模量它是纤维应力-应变曲线起始一段直线部分的斜率,其物理含义是表示当试样保持初始斜率不变时,拉伸试样至原来长度的两倍时所需的应力值。
它表征在小变形条件下,纤维承受外力作用时抵抗变形能力的大小,是衡量纤维刚性的指标。
纺织纤维的初始模量与纺织制品的耐磨、耐疲劳、耐冲击、手感、悬垂性和起拱性能等关系密切。
许多纺织品多半是在小变形条件下工作的,因此,初始模量是纤维力学性能中的重要指标。
对于纺织纤维拉伸曲线的起始部分是否存在线性区是有争议的。
前苏联学者库金和索洛维也夫认为,纺织纤维与金属材料不同,拉伸曲线的起始部分是凹向应变轴的,只能近似地接近直线。
澳大利亚学者E.G.Bendit(1978)认为纺织纤维拉伸曲线的起始部分不存在“虎克区”,对粘弹性材料,在理论上其应力-应变曲线是凹向应变轴的。
然而由于纤维截面的转曲和天然卷曲以及试样夹头夹持不当等影响,会使应力-应变曲线的起始部分凹向应力轴,由于这2个相反的弯曲,使应力-应变曲线在外表上似乎有一个不变斜率的“虎克区”。
当有些纤维拉伸曲线起始部分不成直线时,其初始模量常取伸长率为1%(或0.5%)时的应力值,按定义:初始模量=应力/应变计算得到,也称为割线模量。
(4)屈服点纤维拉伸曲线上“虎克区”和屈服区的转变点称为屈服点,所对应的应力和应变分别称为屈服应力和屈服应变。
实验表明:当纤维超过屈服点后,将产生较高比例的塑性变形,纤维的力学性质将起较大的变化,所以在纺织加工和纺织品使用过程中,确定和掌握纤维的屈服点很重要。
有数种确定纤维屈服点的方法可供选择。
①曼列狄斯(Meredith)法如图3-3(a)所示。
连结应力-应变曲线原点O和断裂点A;平行于OA作平行线并与拉伸曲线相切,得切点Y;Y点所对应的应力为屈服应力(ζy),对应的应变为屈服应变(εy)。
图3-3 屈服点的确定方法②考泼伦(Coplan)方法:如图3-3(b),作拉伸曲线在屈服点前后2个区域的近似直线部分的切线,交于K;过K点作平行于应变轴,交拉伸曲线于Y,Y则为屈服点。
③角平分线法:如图3-3(c),作拉伸曲线在屈服点前后2个区域的近似直线部分的切线,交于K;作两切线的夹角平分线,交拉伸曲线于Y,Y即为屈服点。
④三阶导数法:这是1979年阿尔法(E1-Alfy)根据屈服点的定义提出的,应用对拉伸曲线求三阶导数的方法来确定纤维的屈服点,如图3-3(d)所示,三阶导数曲线与伸长轴的交点,即为屈服伸长率。
上述几种方法所决定的屈服点位置略有差异,曼列狄斯法简单,容易求取。
角平分线法较实用,但有时求取屈服点后拉伸曲线部分的切线较困难。
三阶导数法,求取方法麻烦,但有利于计算机自动化。
(5)断裂功、断裂比功和充满系数纤维的负荷-伸长曲线下的面积,表示拉断这根纤维时,外力对它所作的功,表示材料抵抗外力破坏所具有的能量,叫做“断裂功”(W)。
在纤维粗细和试样长度不同时,断裂功不能反映纤维抵抗外力破坏的能力,所以要折算成拉断单位体积或单位纤维重量所需作功的大小,称为“断裂比功”。
在实际应用中,断裂比功采用拉断一单位线密度、1cm长的纤维所需要的功(N·cm)来表示,即断裂比功的单位为N/tex。
断裂比功大的纤维材料能承受冲击破坏的能力强二、纤维代表性拉伸曲线及其绘制纤维性能是结构的反映,天然纤维受到品种、生长条件的影响,化学纤维的拉伸性能与大分子链结构和纺丝工艺的影响很大,使不同纤维在结构上存在着较大的差异,所以力学性能亦在一相当范围内变化。
图3-4为几种主要化学纤维的拉伸曲线。
图中表示出高强低伸型化纤与低强高伸型化纤的拉伸曲线有很大的不同。
图3-4 几种化学纤维的拉伸曲线纺织纤维由于内部结构和外形尺寸的不均匀性,特别是天然纤维,使各根纤维的拉伸曲线存在较大的差异,如何从一批离散性较大的拉伸曲线中,选取一根代表性曲线,以代表这批试样的拉伸性能呢?通常采用下述两种方法。
①单根代表曲线法:根据实测试样所得的断裂强力,断裂伸长和初始模量(或屈服点)的平均值,在n(样本容量)根拉伸曲线中选取其中一根最接近上述指标的平均值的曲线,即为代表性曲线。
这一方法较简单,所得曲线光滑、自然,但在任意拉伸阶段时曲线的平均代表性较差。
②5根曲线平均法:根据上述方法从n根拉伸曲线中选取5根最接近平均断裂强力、断裂伸长率和屈服点(屈服应力和应变)的曲线;将每根曲线等分断裂伸长为若干等分;求出各对应伸长分点的平均强力;以实测的平均断裂伸长为基准,作出各对应伸长分点的平均强力点,然后连接各点所得曲线即为纤维的代表性曲线。
这一方法,绘制较麻烦。
当分点较少时,曲线不光滑。
当取较多分点时,绘制很费时。
但它能较好地代表整个拉伸过程的变形特征,代表性好。
三、纤维结构对力学性能的影响1.相对分子质量(或聚合度)分子链的长短对纤维的力学性能影响很大。
随着相对分子质量的增长,分子链间总的次价键力增大。
分子链间不易滑移,其抗拉强度、断裂伸长、冲击韧性等都随之提高。
当相对分子质量增加到一定程度时,它对力学性能的提高变得不明显,并趋于一极限值,这一临界相对分子质量M c,对于不同纤维聚合物有不同值。
而同一纤维高聚物,对不同的力学性能指标也具有不同的M c值。
2.分子链的刚柔性和极性基团的数量当分子链存在有刚性的基团时如涤纶中的苯环和纤维素纤维中的葡萄糖剩基等,使纤维的模量增加,刚性增大。
分子链上极性基团多时,分子链间次价键力大,同样使纤维具有较高的模量和断裂强度。
3.分子链堆砌的紧密程度、结晶度纤维中大分子链堆砌的紧密程度不同时,对纤维力学性质影响很大。
紧密的堆砌,分子链间作用力大,纤维有较高的强度和屈服应力;反之,疏松的堆砌使纤维有较高的断裂伸长和冲击强度。
一般来说,随着纤维结晶度的增加,其屈服应力、强度、模量和硬度等均会提高,而断裂伸长和冲击韧性则相反。
结晶使纤维高聚物变硬变脆。
聚乙烯高聚物的某些力学性能与结晶度间的关系列于表3-2。
研究表明:结晶的结构常超过结晶度的影响,大的晶粒通常使纤维高聚物的断裂伸长和韧性降低。
小晶粒高聚物的抗张强度、模量、断裂伸长和韧性较大晶粒结构纤维都要高,因为大晶粒内部的空隙和结晶界面的缺陷较多。
4.分子链的取向(取向度)分子链取向使纤维力学性质产生各向异性,使取向方向的强度和模量增加。
其原因主要是分子链取向的结果使化学主价键力和氢键、范德华力的分布不均匀,在纤维轴向以主价键力为主,而在垂直方向上以次价键力为主。
克服次价键力要比克服主价键力容易得多。
其次是,在取向过程中能消除存在于未取向试样中的一些缺陷,或使某些应力集中部分的分子链同时顺力场方向取向。