北京市房山区2016年高三4月一模考试语文试卷

北京市朝阳区高三年级第一次综合练习语文参考答案及评分标准2016．3一、（本大题共8小题，共26分）1．（3分）B（“测量其长度”与原文“拉上来量绳子的长度”不符）2．（4分）指的是考古出土的宋代椗子与《西游记》中对金箍棒的描写极为相像（1分）：大小形制（或“长度、粗细、形状”）一致（1分），都有箍（1分），褐黑色、质地坚密似铁的铁力木与乌铁的颜色质地很相似（1分）。

【评分参考】意思对即可。

3．（3分）D4．（3分）B（A．“全都”有误；C．“有了箍，金箍棒就不结实了”有误；D．“从金箍棒演变而来的”有误）5．（2分）A（B．“丧”读“sànɡ”，意为失去；C．“辟邪”的“辟”读“bì”，意为排除，“辟谣”的“辟”读“pì”，意为驳斥；D．形容做事得心应手，非贬义）6．（2分）C7．（3分）B（A．“武器”有误，应为“金箍棒”；C．“反映了他对自由的矛盾态度”与文意不符；D．“表达了相同的情感”有误）8．（6分）【示例1】赞同“材料一”的观点：金箍棒源于“椗子”。

从外形上看，考古出土的宋代椗子与书中对金箍棒外形的描写极为吻合；从旁证上看，有民间传说将“椗子”与“镇海针”联系起来；从文化内涵上看，金箍棒起源于“椗子”，与大禹治水的传说相关联，体现了人们消灾、安居的愿望，与书中向善的价值取向吻合。

【示例2】赞同“材料二”的观点：金箍棒源于“荆觚棒”。

从读音上看，金箍棒与“荆觚棒”读音相近，很可能是讹传造成的误写；从功能上看，“荆觚棒”是武器，又能辟邪，与孙悟空用金箍棒降妖除怪一致；从文化内涵上看，“荆觚棒”的功能，能够体现金箍棒除暴安良、实现社会公平和谐理想的象征含义。

【评分参考】意思对即可。

如答其他，言之成理可酌情给分。

二、（本大题共6小题，共25分）9．（5分）举三者授之贤者/非为贤赐也/欲其事之成/故当是时/以德就列/以官服事/以劳定赏/量功而分禄/故官无常贵//而民无终贱/人人思贤也【评分参考】答对2处得1分。

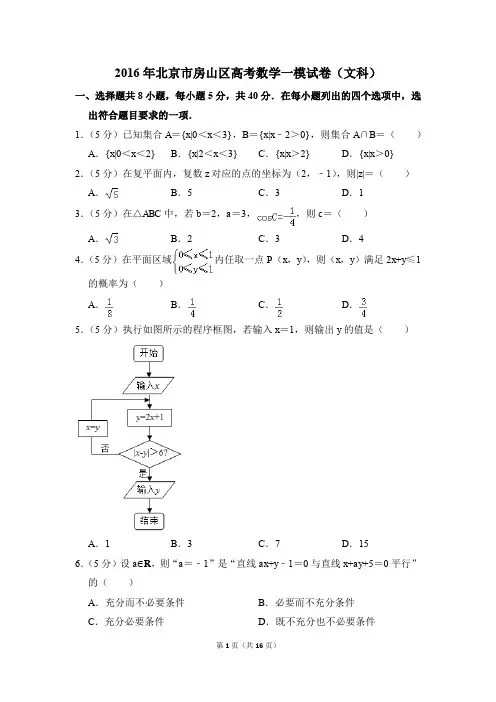
2016年北京市房山区高考数学一模试卷（文科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）已知集合A＝{x|0＜x＜3}，B＝{x|x﹣2＞0}，则集合A∩B＝（）A．{x|0＜x＜2}B．{x|2＜x＜3}C．{x|x＞2}D．{x|x＞0} 2．（5分）在复平面内，复数z对应的点的坐标为（2，﹣1），则|z|＝（）A．B．5C．3D．13．（5分）在△ABC中，若b＝2，a＝3，，则c＝（）A．B．2C．3D．44．（5分）在平面区域内任取一点P（x，y），则（x，y）满足2x+y≤1的概率为（）A．B．C．D．5．（5分）执行如图所示的程序框图，若输入x＝1，则输出y的值是（）A．1B．3C．7D．156．（5分）设a∈R，则“a＝﹣1”是“直线ax+y﹣1＝0与直线x+ay+5＝0平行”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件7．（5分）已知定义在R上的函数f（x）的对称轴为x＝﹣5，且当x≥﹣5时，f （x）＝2x﹣3．若函数f（x）在区间（k，k+1）（k∈Z）上有零点，则k的值为（）A．2或﹣11B．2或﹣12C．1或﹣12D．1或﹣11 8．（5分）某市2015年前n个月空气质量优良的总天数S n与n之间的关系如图所示．若前m月的月平均空气质量优良天数最大，则m值为（）A．7B．9C．10D．12二、填空题共6小题，每小题5分，共30分．9．（5分）双曲线﹣y2＝1的渐近线方程为．10．（5分）圆x2+y2﹣4x+2y+2＝0的圆心坐标为，半径为．11．（5分）若，则＝．12．（5分）已知向量＝（1，1），，若k﹣与垂直，则实数k ＝．13．（5分）某几何体的三视图如图所示，则该几何体的体积等于．14．（5分）数列{a n}满足a1＝3，那么a2016＝，数列{a n}的前n项和S n＝．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）已知函数．（Ⅰ）求f（x）的最小正周期和最大值；（Ⅱ）若，且，求α的值．16．（13分）在等比数列{a n}中，a1＝2，且a2+1是a1，a3的等差中项．（Ⅰ）求{a n}的通项公式及前n项和S n；（Ⅱ）已知{b n}是等差数列，T n为其前n项和，且b2＝a1，b8＝a2+a4，求T n．17．（13分）为了解学生的身体状况，某校随机抽取了一批学生测量体重．经统计，这批学生的体重数据（单位：千克）全部介于45至70之间．将数据分成以下5组：第1组[45，50），第2组[50，55），第3组[55，60），第4组[60，65），第5组[65，70]，得到如图所示的频率分布直方图．现采用分层抽样的方法，从第3，4，5组中随机抽取6名学生做初检．（Ⅰ）求每组抽取的学生人数；（Ⅱ）若从6名学生中再次随机抽取2名学生进行复检，求这2名学生不在同一组的概率．18．（14分）在三棱锥P﹣ABC中，平面P AC⊥平面ABC，P A⊥PC，AC⊥BC，D为AB的中点，M为PD的中点，N在棱BC上．（Ⅰ）当N为BC的中点时，证明：DN∥平面P AC；（Ⅱ）求证：P A⊥平面PBC；（Ⅲ）是否存在点N使得MN∥平面P AC？若存在，求出的值，若不存在，说明理由．19．（13分）已知函数f（x）＝lnx﹣，g（x）＝﹣x．（I）求曲线y＝f（x）在x＝1处的切线方程；（Ⅱ）求f（x）的单调区间；（Ⅲ）设h（x）＝af（x）+（a+1）g（x），其中0＜a≤1，证明：函数h（x）仅有一个零点．20．（14分）已知椭圆C：+＝1（a＞b＞0）的离心率为，右焦点为F（3，0）．N为直线x＝4上任意一点，过点F做直线FN的垂线l，直线l与椭圆C交于A，B两点，M为线段AB的中点，O为坐标原点．（Ⅰ）求椭圆C的标准方程；（Ⅱ）证明：O，M，N三点共线；（Ⅲ）若2|OM|＝|MN|，求l的方程．2016年北京市房山区高考数学一模试卷（文科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）已知集合A＝{x|0＜x＜3}，B＝{x|x﹣2＞0}，则集合A∩B＝（）A．{x|0＜x＜2}B．{x|2＜x＜3}C．{x|x＞2}D．{x|x＞0}【解答】解：由B中不等式解得：x＞2，即B＝{x|x＞2}，∵A＝{x|0＜x＜3}，∴A∩B＝{x|2＜x＜3}，故选：B．2．（5分）在复平面内，复数z对应的点的坐标为（2，﹣1），则|z|＝（）A．B．5C．3D．1【解答】解：由题意可得z＝2﹣i，∴|z|＝＝故选：A．3．（5分）在△ABC中，若b＝2，a＝3，，则c＝（）A．B．2C．3D．4【解答】解：∵b＝2，a＝3，，∴由余弦定理可得：c＝＝＝4．故选：D．4．（5分）在平面区域内任取一点P（x，y），则（x，y）满足2x+y≤1的概率为（）A．B．C．D．【解答】解平面区域为正方形OABC内部（含边界），其面积为1，则满足条件2x+y≤1的点P落在△AOD内部（含边界）．其面积为＝．∴点P满足2x+y≤1的概率为＝．故选：B．5．（5分）执行如图所示的程序框图，若输入x＝1，则输出y的值是（）A．1B．3C．7D．15【解答】解：根据题意，模拟执行程序，可得输入x＝1，第一次循环：y＝2×1+1＝3，x＝3；第二次循环：y＝2×3+1＝7，x＝7；第三次循环：y＝2×7+1＝15，∵|x﹣y|＝8＞6，∴结束循环，输出y＝15．故选：D．6．（5分）设a∈R，则“a＝﹣1”是“直线ax+y﹣1＝0与直线x+ay+5＝0平行”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：当a＝﹣1时，两直线方程分别为﹣x+y﹣1＝0与直x﹣y+5＝0，满足两直线平行．当a＝1时，两直线方程分别为x+y﹣1＝0与直x+y+5＝0满足平行，但a＝﹣1不成立，∴“a＝﹣1”是“直线ax+y﹣1＝0与直线x+ay+5＝0平行”的充分不必要条件．故选：A．7．（5分）已知定义在R上的函数f（x）的对称轴为x＝﹣5，且当x≥﹣5时，f （x）＝2x﹣3．若函数f（x）在区间（k，k+1）（k∈Z）上有零点，则k的值为（）A．2或﹣11B．2或﹣12C．1或﹣12D．1或﹣11【解答】解：当x≥﹣5时，f（x）＝2x﹣3，∵f（1）＝2﹣3＝﹣1＜0，f（2）＝22﹣3＝1＞0，由函数零点存在性定理，可得函数f（x）＝2x﹣3有一个零点在（1，2）内，此时k＝1；又定义在R上的函数f（x）的对称轴为x＝﹣5，由对称性可知，函数f（x）＝2x﹣3有另一个零点在（﹣12，﹣11）内，此时k ＝﹣12．∴k的值为1或﹣12．故选：C．8．（5分）某市2015年前n个月空气质量优良的总天数S n与n之间的关系如图所示．若前m月的月平均空气质量优良天数最大，则m值为（）A．7B．9C．10D．12【解答】解：前n个月的总天数S n与n在图中对应P（n，S n）点则前n个月的月平均值即为直线OP的斜率，由图易得当n＝10时，直线OP的斜率最大，即前10个月的月平均值最高，故m的值为10．故选：C．二、填空题共6小题，每小题5分，共30分．9．（5分）双曲线﹣y2＝1的渐近线方程为±．【解答】解：∵双曲线的a＝2，b＝1，焦点在x轴上而双曲线的渐近线方程为y＝±∴双曲线的渐近线方程为y＝±故答案为：y＝±10．（5分）圆x2+y2﹣4x+2y+2＝0的圆心坐标为（2，﹣1），半径为．【解答】解：将圆方程x2+y2﹣4x+2y+2＝0化为标准方程：（x﹣2）2+（y+1）2＝3，则圆心坐标为（2，﹣1），半径等于，故答案为：（2，﹣1），．11．（5分）若，则＝2．【解答】解：∵，∴＝＝＝2．故答案为：2．12．（5分）已知向量＝（1，1），，若k﹣与垂直，则实数k＝﹣1．【解答】解：∵向量＝（1，1），，∴k﹣＝（k+3，k﹣1），若k﹣与垂直，则（k﹣）•＝（k+3，k﹣1）•（1，1）＝k+3+k﹣1＝2k+2＝0，求得实数k＝﹣1，故答案为：﹣1．13．（5分）某几何体的三视图如图所示，则该几何体的体积等于．【解答】解：根据三视图得：该几何体是放倒的四棱锥，直观图如图所示：E是棱CD的中点，且PE⊥平面ABCD，PE＝2，四棱锥的底面是边长为4、2的矩形，高为PE，所以该几何体的体积V＝＝，故答案为：．14．（5分）数列{a n}满足a1＝3，那么a2016＝2，数列{a n}的前n项和S n＝．【解答】解：依题意，a1＝3，a2＝a1﹣1＝2，a3＝a2﹣1＝1，a4＝2a3＝2，…∴数列{a n}从第二项起，构成以2为周期的周期数列，∵2016＝1+2×1007+1，∴a2016＝a2＝2，}是首项、公差均为3的等差数列，又∵数列{S2n﹣1数列{S2n}是首项为5、公差为3的等差数列，∴当n为奇数时，S n＝3+3（﹣1）＝；当n为偶数时，S n＝5+3（﹣1）＝；∴S n＝，故答案为：2，．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）已知函数．（Ⅰ）求f（x）的最小正周期和最大值；（Ⅱ）若，且，求α的值．【解答】解：（Ⅰ）∵函数＝sin2x+﹣＝sin（2x﹣），∴f（x）的最小正周期为＝π，函数的最大值为．（Ⅱ）若，2α﹣∈（﹣，）；∵＝sin（2α﹣），∴sin（2α﹣）＝1，∴2α﹣＝，∴α＝．16．（13分）在等比数列{a n}中，a1＝2，且a2+1是a1，a3的等差中项．（Ⅰ）求{a n}的通项公式及前n项和S n；（Ⅱ）已知{b n}是等差数列，T n为其前n项和，且b2＝a1，b8＝a2+a4，求T n．【解答】解：（Ⅰ）设等比数列{a n}的公比为q，则a2＝2q，a3＝2q2，∵a2+1是a1，a3的等差中项，∴2（1+2q）＝2+2q2，即q2＝2q，解得：q＝2或q＝0（舍），∴数列{a n}是首项、公比均为2的等比数列，∴a n＝2n，S n＝＝2n+1﹣2；（Ⅱ）由（I）可知b2＝a1＝2，b8＝a2+a4＝4+16＝20，∴等差数列{b n}的公差d＝＝3，b1＝b2﹣d＝1，∴T n＝nb1+d＝n+n（n﹣1）＝．17．（13分）为了解学生的身体状况，某校随机抽取了一批学生测量体重．经统计，这批学生的体重数据（单位：千克）全部介于45至70之间．将数据分成以下5组：第1组[45，50），第2组[50，55），第3组[55，60），第4组[60，65），第5组[65，70]，得到如图所示的频率分布直方图．现采用分层抽样的方法，从第3，4，5组中随机抽取6名学生做初检．（Ⅰ）求每组抽取的学生人数；（Ⅱ）若从6名学生中再次随机抽取2名学生进行复检，求这2名学生不在同一组的概率．【解答】解：（Ⅰ）解：由频率分布直方图知，第3，4，5组的学生人数之比为3：2：1．所以，每组抽取的人数分别为：第3组：×6＝3；第4组：＝2；第5组：＝1．∴从3，4，5组应依次抽取3名学生，2名学生，1名学生．（Ⅱ）记第3组的3位同学为①，②，③；第4组的2位同学为A，B；第5组的1位同学为C．则从6位同学中随机抽取2位同学所有可能的情形为：（①，②），（①，③），（①，A），（①，B），（①，C），（②，③），（②，A），（②，B），（②，C），（③，A），（③，B），（③，C），（A，B），（A，C），（B，C）共15种可能．其中，（①，②），（①，③），（②，③），（A，B）四种为2名学生在同一组，∴有11种可能符合2名学生不在同一组的要求，∴所求概率P＝．18．（14分）在三棱锥P﹣ABC中，平面P AC⊥平面ABC，P A⊥PC，AC⊥BC，D为AB的中点，M为PD的中点，N在棱BC上．（Ⅰ）当N为BC的中点时，证明：DN∥平面P AC；（Ⅱ）求证：P A⊥平面PBC；（Ⅲ）是否存在点N使得MN∥平面P AC？若存在，求出的值，若不存在，说明理由．【解答】证明：（Ⅰ）∵D为AB的中点，N为BC的中点，∴DN∥AC，∵DN⊄平面P AC，AC⊂平面P AC，∴DN∥平面P AC．（Ⅱ）∵平面P AC⊥平面ABC，AC⊥BC，∴BC⊥平面P AC，∵P A⊂平面P AC，∴P A⊥BC，∵P A⊥PC，PC∩BC＝C，∴P A⊥平面PBC．解：（Ⅲ）存在点N，当时，MN∥平面P AC．理由如下：取AD中点E，连结ME、NE，∵M为PD中点，∴ME∥P A，∵D为AB中点，E为AD中点，∴，又∵＝，∴EN∥AC，∵ME∩NE＝E，ME、EN⊂平面MEN，P A、AC⊂平面P AC，∴平面MEN∥平面P AC，∵MN⊂平面MEN，∴MN∥平面P AC．∴存在点N，当时，MN∥平面P AC．19．（13分）已知函数f（x）＝lnx﹣，g（x）＝﹣x．（I）求曲线y＝f（x）在x＝1处的切线方程；（Ⅱ）求f（x）的单调区间；（Ⅲ）设h（x）＝af（x）+（a+1）g（x），其中0＜a≤1，证明：函数h（x）仅有一个零点．【解答】解：（Ⅰ）函数f（x）＝lnx﹣，（x＞0）f′（x）＝﹣x，在x＝1处的切线方程的斜率为k＝f′（1）＝0，∴求曲线y＝f（x）在x＝1处的切线方程y＝，（Ⅱ）f′（x）＝﹣x，令f′（x）＝0，得x＝1，当0＜x＜1时，f′（x）＞0，f（x）单调递增，x＞1时，f′（x）＜0，f（x）单调递减，f（x）的单调递增区间为[1，+∞），f（x）的单调递减区间为（0，1）；（Ⅲ）证明：h（x）＝af（x）+（a+1）g（x）＝+alnx﹣（a+1）x，（x＞0）∴h′（x）＝x﹣（a+1）+≥2﹣（a+1），当且仅当x＝，x＝，设g（x）＝2﹣（a+1）g′（x）＝，0＜a≤1，g′（x）＞0，g（x）单调递增，当a＝1取最大值，最大值为0，∴h′（x）＞0，∴h（x）单调递增，h（a）＝0＜a≤1∴h（a）＜0，当x＞1时，h（x）＞0，利用零点定理，∴函数h（x）仅有一个零点．20．（14分）已知椭圆C：+＝1（a＞b＞0）的离心率为，右焦点为F（3，0）．N为直线x＝4上任意一点，过点F做直线FN的垂线l，直线l与椭圆C交于A，B两点，M为线段AB的中点，O为坐标原点．（Ⅰ）求椭圆C的标准方程；（Ⅱ）证明：O，M，N三点共线；（Ⅲ）若2|OM|＝|MN|，求l的方程．【解答】（I）解：∵椭圆C：+＝1（a＞b＞0）的离心率为，右焦点为F（3，0），∴c＝3，．∴a＝，b＝．∴椭圆C的标准方程为；（Ⅱ）证明：设N（4，m），A（x1，y1），B（x2，y2），AB的中点为M（x0，y0），k NF＝m，由F（3，0），可设直线AB的方程为x＝﹣my+3，代入椭圆方程可得（m2+4）y2﹣6my﹣3＝0，∴y1+y2＝，y1y2＝﹣，于是M（），则直线OM的斜率k OM＝，又k ON＝，∴k OM＝k ON，∴O，N，N三点共线；（Ⅲ）由（Ⅱ）知，M（），N（4，m），且O，M，N三点共线；又2|OM|＝|MN|，则2＝，解得：m＝．∴l的方程为，即．。

2016年北京市房山区高考数学一模试卷（理科）一、选择题共8小题，每小题5分，共40分．在每小题列出得四个选项中，选出符合题目要求得一项．1．在复平面内，复数z对应得点得坐标为（2，﹣1），则|z|=（）A．B．5 C．3 D．12．设不等式组表示得平面区域为D，在区域D内随机取一点M，则点M落在圆（x﹣1）2+y2=1内得概率为（）A．B．C．D．3．执行如图所示得程序框图，若输入x=1，则输出y得值就是（）A．7 B．15 C．23 D．314．在极坐标系中，过点且平行于极轴得直线方程就是（）A．ρ=1 B．ρsinθ=1 C．ρcosθ=1 D．ρ=2sinθ5．函数f（x）得定义域为R，“f（x）就是奇函数”就是“存在x∈R，f（x）+f（﹣x）=0”得（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件6．某几何体得三视图如图所示，则该几何体得体积就是（）A．32 B．16 C．D．7．已知函数若存在实数k使得该函数值域为[0，2]，则实数a得取值范围就是（）A．（﹣∞，﹣2]B．[﹣2，﹣1]C．[﹣2，﹣）D．[﹣2，0]8．在股票买卖过程中，经常用两种曲线来描述价格变化情况：一种就是即时价格曲线y=f （x），另一种就是平均价格曲线y=g（x），如f（3）=4表示开始交易后第3小时得即时价格为4元；g（3）=2表示开始交易后三个小时内所有成交股票得平均价格为2元．下面给出四个图象，实线表示y=f（x），虚线表示y=g（x），其中可能正确得就是（）A．B．C．D．二、填空题共6小题，每小题5分，共30分．9．双曲线得渐近线方程为．10．已知向量=（1，1），，若k﹣与垂直，则实数k=．11．在△ABC中，若a=3，c=4，cosC=﹣，则b=．12．在某校召开得高考总结表彰会上有3位数学老师、2位英语老师与1位语文老师做典型发言．现在安排这6位老师得发言顺序，则3位数学老师互不相邻得排法共有种．（请用数字作答）13．设T n为等比数列{a n}得前n项之积，且a1=﹣6，，则公比q=，当T n最大时，n得值为．14．对于函数f（x）与实数M，若存在m，n∈N+，使f（m）+f（m+1）+f（m+2）+…+f（m+n）=M成立，则称（m，n）为函数f（x）关于M得一个“生长点”．若（1，2）为函数f（x）=cos（x+）关于M得一个“生长点”，则M=；若f（x）=2x+1，M=105，则函数f（x）关于M得“生长点”共有个．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．已知函数．（Ⅰ）求f（x）得最小正周期与最大值；（Ⅱ）若，且，求α得值．16．为降低雾霾等恶劣气候对居民得影响，某公司研发了一种新型防雾霾产品．每一台新产品在进入市场前都必须进行两种不同得检测，只有两种检测都合格才能进行销售，否则不能销售．已知该新型防雾霾产品第一种检测不合格得概率为，第二种检测不合格得概率为，两种检测就是否合格相互独立．（Ⅰ）求每台新型防雾霾产品不能销售得概率；（Ⅱ）如果产品可以销售，则每台产品可获利40元；如果产品不能销售，则每台产品亏损80元（即获利﹣80元）．现有该新型防雾霾产品3台，随机变量X表示这3台产品得获利，求X得分布列及数学期望．17．在三棱锥P﹣ABC中，平面PAC⊥平面ABC，△PAC为等腰直角三角形，PA⊥PC，AC⊥BC，BC=2AC=4，M为AB得中点．（Ⅰ）求证：AC⊥PM；（Ⅱ）求PC与平面PAB所成角得正弦值；（Ⅲ）在线段PB上就是否存在点N使得平面CNM⊥平面PAB？若存在，求出得值，若不存在，说明理由．18．已知函数f（x）=lnx+ax2﹣（2a+1）x，其中．（Ⅰ）当a=﹣2时，求函数f（x）得极大值；（Ⅱ）若f（x）在区间（0，e）上仅有一个零点，求a得取值范围．19．已知椭圆C：=1（a＞b＞0）得离心率就是，且椭圆C上任意一点到两个焦点得距离之与就是4．直线l：y=kx+m与椭圆C相切于点P，且点P在第二象限．（Ⅰ）求椭圆C得标准方程；（Ⅱ）求点P得坐标（用k表示）；（Ⅲ）若过坐标原点O得直线l1与l垂直于点Q，求|PQ|得最大值．20．已知数集M={a1，a2，…，a n}（0≤a1＜a2＜…＜a n，n≥2）具有性质P：对任意得i，j （1≤i≤j≤n），a i+a j与a j﹣a i两数中至少有一个属于M．（Ⅰ）分别判断数集{0，1，3}与{0，2，3，5}就是否具有性质P，并说明理由；（Ⅱ）证明：a1=0，且a n=；（Ⅲ）当n=5时，证明：a1，a2，a3，a4，a5成等差数列．2016年北京市房山区高考数学一模试卷（理科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出得四个选项中，选出符合题目要求得一项．1．在复平面内，复数z对应得点得坐标为（2，﹣1），则|z|=（）A．B．5 C．3 D．1【考点】复数求模．【分析】由复数得几何意义可得z=2﹣i，由复数得模长公式可得．【解答】解：由题意可得z=2﹣i，∴|z|==故选：A2．设不等式组表示得平面区域为D，在区域D内随机取一点M，则点M落在圆（x﹣1）2+y2=1内得概率为（）A．B．C．D．【考点】几何概型．【分析】作出不等式组对应得平面区域，求出对应得面积，结合几何概型得概率公式进行求解即可．【解答】解：作出不等式组对应得平面区域，则平面区域为D得面积S=2×2=4，点M落在圆（x﹣1）2+y2=1内面积S=，则在区域D内随机取一点M，则点M落在圆（x﹣1）2+y2=1内得概率P==，故选：A．3．执行如图所示得程序框图，若输入x=1，则输出y得值就是（）A．7 B．15 C．23 D．31【考点】程序框图．【分析】首先分析程序框图，按照循环结构进行运算，求出满足题意时得y．【解答】解：根据题意，模拟执行程序，可得输入x=1，第一次循环：y=2×1+1=3，不满足条件|x﹣y|＞8，x=3；第二次循环：y=2×3+1=7，不满足条件|x﹣y|＞8，x=7；第三次循环：y=2×7+1=15，不满足条件|x﹣y|＞8，x=15第四次循环：y=2×15+1=31，∵|x﹣y|=16＞8，∴结束循环，输出y=31．故选：D．4．在极坐标系中，过点且平行于极轴得直线方程就是（）A．ρ=1 B．ρsinθ=1 C．ρcosθ=1 D．ρ=2sinθ【考点】简单曲线得极坐标方程．【分析】设P（ρ，θ）为直线上得任意一点，利用直角三角形得边角关系即可得出．【解答】解：设P（ρ，θ）为直线上得任意一点，由题意可得：1=ρcosθ．故选：C．5．函数f（x）得定义域为R，“f（x）就是奇函数”就是“存在x∈R，f（x）+f（﹣x）=0”得（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件得判断．【分析】由“f（x）就是奇函数”⇒“存在x∈R，f（x）+f（﹣x）=0”，反之不成立．即可判断出结论．【解答】解：由“f（x）就是奇函数”⇒“存在x∈R，f（x）+f（﹣x）=0”，反之不成立．∴“f（x）就是奇函数”就是“存在x∈R，f（x）+f（﹣x）=0”得充分不必要条件．故选：A．6．某几何体得三视图如图所示，则该几何体得体积就是（）A．32 B．16 C．D．【考点】由三视图求面积、体积．【分析】根据三视图得该几何体就是放倒得四棱锥，由三视图求出几何元素得长度、判断出线面得位置关系，由锥体得体积公式求出该几何体得体积．【解答】解：根据三视图得：该几何体就是放倒得四棱锥，直观图如图所示：E就是棱CD得中点，且PE⊥平面ABCD，PE=2，四棱锥得底面就是边长为4、2得矩形，高为PE，所以该几何体得体积V==，故选：D．7．已知函数若存在实数k使得该函数值域为[0，2]，则实数a得取值范围就是（）A．（﹣∞，﹣2]B．[﹣2，﹣1]C．[﹣2，﹣）D．[﹣2，0]【考点】分段函数得应用；函数得值域．【分析】分别作出函数y=log2（x+1）+1与y=2（x+1）2得图象，观察函数值在[0，2]内得图象，讨论最小值与最大值得情况，即可得到结论．【解答】解：由分段函数得表达式得﹣1＜k≤1，此时函数f（x）在[k，1]上为增函数，此时f（1）=log22+1=1+1=2，f（k）=log2（k+1）+1，此时log2（k+1）+1≤f（x）≤2，当a≤x＜k时，f（x）=2（x+1）2在[a，k）上不就是增函数，若f（x）=2（x+1）2=2得（x+1）2=1，即x=0或﹣2，若f（x）=2（x+1）2=0得x=﹣1，若log2（x+1）+1=0，则log2（x+1）=﹣1，则x+1=，即x=﹣，若存在实数k使得该函数值域为[0，2]，则﹣≤k≤1，若a＜﹣2，则此时函数f（x）＞2，不满足条件．排除A．当a=﹣2时，f（﹣2）=2，此时当﹣≤k≤1满足条件，当a=0时，f（0）=2，当0≤x＜k时，f（x）≥2，不存在实数k使得该函数值域为[0，2]，排除D．若存在实数k使得该函数值域为[0，2]，则﹣2≤a＜﹣，故选：C．8．在股票买卖过程中，经常用两种曲线来描述价格变化情况：一种就是即时价格曲线y=f （x），另一种就是平均价格曲线y=g（x），如f（3）=4表示开始交易后第3小时得即时价格为4元；g（3）=2表示开始交易后三个小时内所有成交股票得平均价格为2元．下面给出四个图象，实线表示y=f（x），虚线表示y=g（x），其中可能正确得就是（）A．B．C．D．【考点】函数得图象．【分析】根据即时价格与平均价格得价格波动关系进行判断即可．【解答】解：刚开始交易时，即时价格与平均价格应该相等，A，D错误；开始交易后，平均价格应该跟随即时价格变动，即时价格与平均价格同增同减，故A，B，D均错误．故选：C．二、填空题共6小题，每小题5分，共30分．9．双曲线得渐近线方程为y=±x．【考点】双曲线得简单性质．【分析】先确定双曲线得焦点所在坐标轴，再确定双曲线得实轴长与虚轴长，最后确定双曲线得渐近线方程．【解答】解：∵双曲线得a=2，b=1，焦点在x轴上而双曲线得渐近线方程为y=±∴双曲线得渐近线方程为y=±故答案为：y=±10．已知向量=（1，1），，若k﹣与垂直，则实数k=﹣1．【考点】平面向量数量积得运算．【分析】由条件利用两个向量坐标形式得运算法则求得k﹣得坐标，再利用两个向量得数量积公式，两个向量垂直得性质，求得k得值．【解答】解：∵向量=（1，1），，∴k﹣=（k+3，k﹣1），若k﹣与垂直，则（k﹣）•=（k+3，k﹣1）•（1，1）=k+3+k﹣1=2k+2=0，求得实数k=﹣1，故答案为：﹣1．11．在△ABC中，若a=3，c=4，cosC=﹣，则b=．【考点】余弦定理．【分析】利用余弦定理即可得出．【解答】解：由余弦定理可得：c2=a2+b2﹣2abcosC，∴42=32+b2﹣2×3b×，化为：2b2﹣3b﹣14=0，解得b=．故答案为：．12．在某校召开得高考总结表彰会上有3位数学老师、2位英语老师与1位语文老师做典型发言．现在安排这6位老师得发言顺序，则3位数学老师互不相邻得排法共有144种．（请用数字作答）【考点】计数原理得应用．【分析】把3位数学老师插入2位英语老师与1位语文老师全排，形成了4个空中，问题得解决．【解答】解：先把2位英语老师与1位语文老师全排，形成了4个空，再把3位数学老师插入，故有A33A43=144种，故答案为：144．13．设T n为等比数列{a n}得前n项之积，且a1=﹣6，，则公比q=，当T n最大时，n得值为4．【考点】等比数列得通项公式．【分析】a1=﹣6，，可得：=﹣6q3，解得q=．可得a n．于就是T n=（﹣6）n．只考虑n为偶数时，与1比较即可得出．【解答】解：∵a1=﹣6，，∴=﹣6q3，解得q=．∴a n=．∴T n=（﹣6）n×=（﹣6）n．T2n=36n．==36•．n=1时，=＞1；n≥2时，＜1．∴T2＜T4＞T6＞T8＞…．则公比q=，当T n最大时，n得值为4．故答案分别为：；4．14．对于函数f（x）与实数M，若存在m，n∈N+，使f（m）+f（m+1）+f（m+2）+…+f（m+n）=M成立，则称（m，n）为函数f（x）关于M得一个“生长点”．若（1，2）为函数f（x）=cos（x+）关于M得一个“生长点”，则M=﹣；若f（x）=2x+1，M=105，则函数f（x）关于M得“生长点”共有3个．【考点】数列与函数得综合；函数得值．【分析】根据“生长点”得定义建立方程即可求M，结合等差数列得求与公式进行判断即可．【解答】解：若（1，2）为函数f（x）=cos（x+）关于M得一个“生长点”，则M=f（1）+f（2）+f（3）=cos（+）+cos（×2+）+cos（×3+）=﹣sin﹣cos+cos（﹣）=﹣﹣+=﹣，若f（x）=2x+1，M=105，则f（m）就是公差为2得等差数列，则由f（m）+f（m+1）+f（m+2）+…+f（m+n）=105得（n+1）（2m+1）+=105即（n+1）（2m+1）+n（n+1）=105，即（n+1）（2m+n+1）=105，∵105=1×105=3×35=5×21=7×15，∴由得，此时“生长点”为（2，16），由得，此时“生长点”为（4，8），由得，此时“生长点”为（6，4），故函数f（x）关于M得“生长点”共有3个，故答案为：﹣，3三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．已知函数．（Ⅰ）求f（x）得最小正周期与最大值；（Ⅱ）若，且，求α得值．【考点】三角函数得最值；三角函数得周期性及其求法．【分析】（Ⅰ）由条件利用三角恒等变换化简f（x）得解析式，再利用正弦函数得周期性、最值，得出结论．（Ⅱ）由条件求得sin（2α﹣）=1，再根据2α﹣∈（﹣，）；可得2α﹣=，从而求得α得值．【解答】解：（Ⅰ）∵函数=sin2x+﹣=sin （2x﹣），∴f（x）得最小正周期为=π，函数得最大值为．（Ⅱ）若，2α﹣∈（﹣，）；∵=sin（2α﹣），∴sin（2α﹣）=1，∴2α﹣=，∴α=．16．为降低雾霾等恶劣气候对居民得影响，某公司研发了一种新型防雾霾产品．每一台新产品在进入市场前都必须进行两种不同得检测，只有两种检测都合格才能进行销售，否则不能销售．已知该新型防雾霾产品第一种检测不合格得概率为，第二种检测不合格得概率为，两种检测就是否合格相互独立．（Ⅰ）求每台新型防雾霾产品不能销售得概率；（Ⅱ）如果产品可以销售，则每台产品可获利40元；如果产品不能销售，则每台产品亏损80元（即获利﹣80元）．现有该新型防雾霾产品3台，随机变量X表示这3台产品得获利，求X得分布列及数学期望．【考点】离散型随机变量得期望与方差；离散型随机变量及其分布列．【分析】（Ⅰ）（Ⅰ）记“每台新型防雾霾产品不能销售”为事件A，由此利用对立事件概率计算公式能求出每台新型防雾霾产品不能销售得概率．（Ⅱ）由已知，可知X得取值为﹣240，﹣120，0，120．分别求出相应得概率，由此能求出X得分布列及EX．【解答】解：（Ⅰ）（Ⅰ）记“每台新型防雾霾产品不能销售”为事件A，则P（A）=1﹣（1﹣）（1﹣）=．所以，该产品不能销售得概率为．（Ⅱ）由已知，可知X得取值为﹣240，﹣120，0，120．P（X=﹣240）=（）3=，P（X=﹣120）==，P（X=0）==，P（X=120）=（）3=，∴X得分布列为：X ﹣240 ﹣120 0 120PEX=﹣240×﹣120×+0×+120×=30．17．在三棱锥P﹣ABC中，平面PAC⊥平面ABC，△PAC为等腰直角三角形，PA⊥PC，AC⊥BC，BC=2AC=4，M为AB得中点．（Ⅰ）求证：AC⊥PM；（Ⅱ）求PC与平面PAB所成角得正弦值；（Ⅲ）在线段PB上就是否存在点N使得平面CNM⊥平面PAB？若存在，求出得值，若不存在，说明理由．【考点】直线与平面所成得角；空间中直线与直线之间得位置关系．【分析】（I）取AC中点O，连接OP，OM，可证AC⊥平面POM，故而AC⊥PM；（II）以O为原点建立坐标系，求出与平面PAB得法向量得坐标，于就是PC与平面PAB所成角得正弦值为|cos＜＞|；（III）设，用λ表示出得坐标，求出，求出平面CNM得法向量，令=0得出λ．【解答】证明：（I）取AC中点O，连接OP，OM．∵PA=PC，∴PO⊥AC，∵平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，∴PO⊥平面ABC．∵M就是AB得中点，∴OM∥BC，∵BC⊥AC，∴OM⊥AC．又OP∩OM=O，∴AC⊥平面POM，∵PM⊂平面POM，∴AC⊥PM．（II）以O为原点，以OA，OM，OP为坐标轴建立空间直角坐标系，如图所示：则A（1，0，0），C（﹣1，0，0），P（0，0，1），B（﹣1，4，0）．∴=（﹣1，0，﹣1），=（﹣1，0，1），=（﹣2，4，0）．设平面PAB得法向量为=（x，y，z），则，∴，令y=1得=（2，1，2），∴cos＜＞==﹣．∴PC与平面PAB所成角得正弦值为．（III）∵M（0，2，0），∴=（﹣1，4，﹣1），=（1，0，1），=（1，2，0）．设线段PB上存在点N使得平面CNM⊥平面PAB．设=（﹣λ，4λ，﹣λ），（0≤λ≤1）．则==（1﹣λ，4λ，1﹣λ）．设平面CNM得法向量为=（x，y，z），则，∴，设y=1得=（﹣2，1，）．∵平面CNM⊥平面PAB，∴．即﹣4+1+=0，解得．∴线段PB上存在点N使得平面CNM⊥平面PAB，=．18．已知函数f（x）=lnx+ax2﹣（2a+1）x，其中．（Ⅰ）当a=﹣2时，求函数f（x）得极大值；（Ⅱ）若f（x）在区间（0，e）上仅有一个零点，求a得取值范围．【考点】利用导数研究函数得极值；函数零点得判定定理；利用导数研究函数得单调性．【分析】（Ⅰ）当a=﹣2时，求导数，确定函数得单调性，即可求函数f（x）得极大值；（Ⅱ）若f（x）在区间（0，e）上仅有一个零点，分类讨论，即可求a得取值范围．【解答】解：（Ⅰ）当a=﹣2时，f（x）=lnx﹣2x2+3x，∴f′（x）=﹣4x+3=﹣，∴函数在（0，1）上单调递增，在（1，+∞）上单调递减，∴x=1时，函数取得极大值1；（Ⅱ）因为f′（x）=a≤0，函数在（0，1）上单调递减，（1，+∞）上单调递增，∵f（x）在区间（0，e）上仅有一个零点，∴f（e）≤0，∴1+ae2﹣（2a+1）e≤0，∴a≥，∴≤a≤0；a＞0，令f′（x）=0，x1=1，x2=＞1因为f（1）＜0，f（x）在区间（0，e）上仅有一个零点，∴f（e）≥0，∴1+ae2﹣（2a+1）e≥0，∴a≤，不合题意，综上所述，≤a≤0．19．已知椭圆C：=1（a＞b＞0）得离心率就是，且椭圆C上任意一点到两个焦点得距离之与就是4．直线l：y=kx+m与椭圆C相切于点P，且点P在第二象限．（Ⅰ）求椭圆C得标准方程；（Ⅱ）求点P得坐标（用k表示）；（Ⅲ）若过坐标原点O得直线l1与l垂直于点Q，求|PQ|得最大值．【考点】椭圆得简单性质．【分析】（Ⅰ）由椭圆得定义可得a=2，再由离心率公式可得c，由a，b，c得关系可得b，进而得到椭圆方程；（Ⅱ）将直线y=kx+m代入椭圆方程，消去y，可得x得方程，运用判别式为0，解方程可得P得坐标；（Ⅲ）由于l1与l垂直于点Q，则|PQ|即为P到直线l1得距离，设l1：y=﹣x，即x+ky=0，运用点到直线得距离公式，化简整理，再由基本不等式可得最大值．【解答】解：（Ⅰ）由椭圆得定义可得2a=4，即a=2，由e==，可得c=，b==1，即有椭圆C得方程为+y2=1；（Ⅱ）将直线y=kx+m代入椭圆方程x2+4y2=4，可得（1+4k2）x2+8kmx+4m2﹣4=0，由直线与椭圆相切，可得△=64k2m2﹣4（1+4k2）（4m2﹣4）=0，化为m 2=1+4k 2，可得P 得横坐标为﹣=﹣=﹣， 纵坐标为﹣+=，即有P （﹣，）；（Ⅲ）由于l 1与l 垂直于点Q ，则|PQ |即为P 到直线l 1得距离，设l 1：y=﹣x ，即x +ky=0，可得|PQ |= ==≤==1．当且仅当4k 2=，即k=时，|PQ |取得最大值1．20．已知数集M={a 1，a 2，…，a n }（0≤a 1＜a 2＜…＜a n ，n ≥2）具有性质P ：对任意得i ，j （1≤i ≤j ≤n ），a i +a j 与a j ﹣a i 两数中至少有一个属于M ．（Ⅰ）分别判断数集{0，1，3}与{0，2，3，5}就是否具有性质P ，并说明理由； （Ⅱ）证明：a 1=0，且a n =；（Ⅲ）当n=5时，证明：a 1，a 2，a 3，a 4，a 5成等差数列．【考点】集合得表示法．【分析】（Ⅰ）利用新定义，可以判断集合{0，1，3}不具有性质P ，{0，2，3，5}具有性质P ；（Ⅱ）令j=n ，i ＞1，可得a n ﹣a i 属于M ，证明a n =a i +a n+1﹣i ，倒序相加即可得到结论； （Ⅲ）当 n=5时，取j=5，当i ≥2时，a i +a 5＞a 5，由M 具有性质P ，结合等差数列得定义逐步可得．【解答】（Ⅰ）解：由于3﹣1与3+1都不属于集合{0，1，3}，∴该数集不具有性质P ； 由于2+0、3+0、5+0、3+2、5﹣2、5﹣3、0﹣0、2﹣2、3﹣3、5﹣5都属于集合{0，2，3，5}，∴该数集具有性质P ．（Ⅱ）证明：令j=n ，i ＞1，则∵“a i +a j 与a j ﹣a i 两数中至少有一个属于M ”，∴a i +a j 不属于M ，∴a n ﹣a i 属于M ．令i=n ﹣1，那么a n ﹣a n ﹣1就是集合M 中某项，a 1不行，就是0，a 2可以．如果就是a 3或者a 4，那么可知a n ﹣a 3=a n ﹣1，那么a n ﹣a 2＞a n ﹣a 3=a n ﹣1，只能就是等于a n 了，矛盾．∴令i=n ﹣1可以得到a n =a 2+a n ﹣1，同理，令i=n﹣2、n﹣3，…，2，可以得到a n=a i+a n+1，﹣i∴倒序相加即可得到a1+a2+a3+…+a n=a n，即a n=；（Ⅲ）证明：当n=5时，取j=5，当i≥2时，a i+a5＞a5，由M具有性质P，a5﹣a i∈M，又i=1时，a5﹣a1∈M，∴a5﹣a i∈M，i=1，2，3，4，5．∵0=a1＜a2＜a3＜a4＜a5，∴a5﹣a1＞a5﹣a2＞a5﹣a3＞a5﹣a4＞a5﹣a5=0，则a5﹣a1=a5，a5﹣a2=a4，a5﹣a3=a3，从而可得a2+a4=a5，a5=2a3，故a2+a4=2a3，即0＜a4﹣a3=a3﹣a2＜a3，又∵a3+a4＞a2+a4=a5，∴a3+a4∉M，则a4﹣a3∈M，则有a4﹣a3=a2=a2﹣a1．又∵a5﹣a4=a2=a2﹣a1，∴a5﹣a4=a4﹣a3=a3﹣a2=a2﹣a1=a2，即a1，a2，a3，a4，a5就是首项为0，公差为a2得等差数列．2016年8月22日。

北京顺义区2016届高三第一次统练语文试题2016.3一、本大题共8小题，共25分。

阅读下面材料，完成1-8题。

【材料一】在话剧市场一直稳步成长的开心麻花娱乐文化传媒有限公司，手握22部原创话剧IP（知识产权Intellectual Property），凭借《夏洛特烦恼》的成功，其成长空间一下子被打开了。

在国内电影IP热潮下，话剧改编电影前景广阔。

《夏洛特烦恼》的成功源于当下的IP热潮。

在热门小说、热门网络剧、热门电视剧，甚至一首歌都被改编成电影的当下，质量上乘又与电影有着天然联系的话剧有望成为电影改编的下一个洼地，一批话剧正在被改编成电影。

华泰证券．指出，今年国庆档的影片集中体现了娱乐内容产业的几大趋势，其中之一便是IP正成为市场的敲门砖，国庆档排名前三的《夏洛特烦恼》《港囧》《九层妖塔》均带有IP光环。

自9月30日上映以来，《夏洛特烦恼》票房一路飙．升，最后以832万元的优势超越《港囧》，将国庆档票房冠军收入囊中。

这不能不说是一场由IP带来的口碑的胜利，也是中国电影在自媒体时代发展的大趋势。

无论从IP背景、导演与演员阵容以及制作投入上来看，《夏洛特烦恼》都难与《港囧》和《九层妖塔》媲．美，其逆袭靠的是实实在在的口碑，尤其是观众自发的力量，这点与暑期热映的《大圣归来》有一定相似之处。

开心麻花总裁刘洪涛称，“话剧和话剧是不一样的，并不是每一部话剧都适合改编成电影，还要看它是不是大众化的产品。

我们的话剧一开始就是面向大众的，做的是商业话剧。

同时，我们的话剧一演就是几百场甚至上千场，是真正经过市场考验的，有市场的基础在这里，改编成电影的风险是很低的。

”当然，有好的IP，还要把IP用好。

IP具备的粉丝基础，使影片在上映初期可以获得关注，但最终的票房还是取决于对IP的运营能力。

《九层妖塔》就成为了IP运营的一个反面教材，该片只借《鬼吹灯》的噱．头，故事改编薄弱，把盗墓片拍成了怪兽片，使得前期聚拢的人气快速流失，票房表现也不尽如人意。

第一节单项填空（共15小题；每小题1分，共15分）
从每题所给的A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。
例：It’s so nice to hear from her again.________, we last met more than thirty years ago.
— Sorry, I didn’t quite follow him. I________a message to my mum just now.
听第6段材料，回答第6至7题。
6. When was the woman supposed to arrive?
A. 11:30.B. 10:20.C. 12:30.
7. What is the relationship between the two speakers？
A. Strangers.B. Friends.C. Neighbors.
听第8段材料，回答第10至12题。
10. What are the speakers mainly talking about?
A. A hall.B. A palace.C. A garden.
11. What does the man like best?
A. The paintings.B. The decoration.C. The lights.
A. What’s moreB. That’s to say
C. In other wordsD. Believe it or not
答案是D。
21. There is a job available in the small town,________no one wants it.

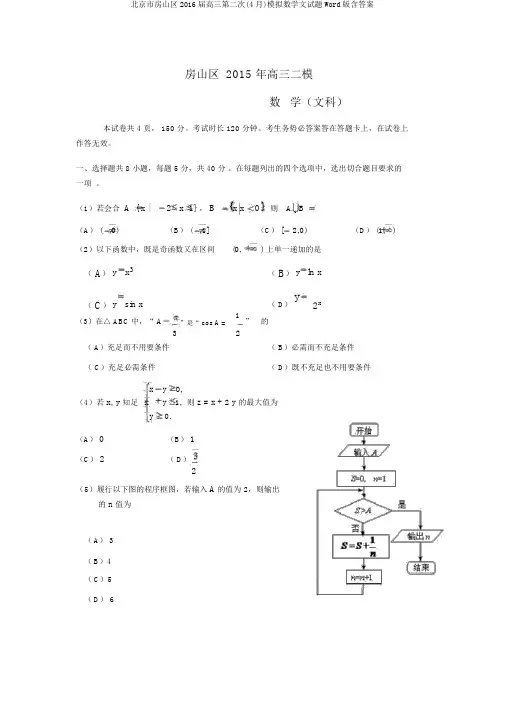
房山区 2015 年高三二模数学（文科）本试卷共 4 页， 150 分。

考试时长 120 分钟。

考生务势必答案答在答题卡上，在试卷上作答无效。

一、选择题共 8 小题，每题 5 分，共 40 分。

在每题列出的四个选项中，选出切合题目要求的一项。

（1）若会合A { x |2x 1} ， B x x0 ，则 A B（A）( ,0)（B）( ,1]（C）[2,0)（D）(1, )（2）以下函数中，既是奇函数又在区间(0,) 上单一递加的是（A） y x3（B） y ln x（C） y sin x（ D）y2x（3）在△ ABC 中，“A＝1” 的”是“ cos A =32（ A）充足而不用要条件（ B）必需而不充足条件（ C）充足必需条件（ D）既不充足也不用要条件x y0,（4）若x, y知足x y1, 则 z = x + 2 y 的最大值为y0.（A）0（B）1（C）2（ D）2（5）履行以下图的程序框图，若输入A的值为2，则输出的 n 值为（A） 3（B）4（C）5（D） 6（6）已知△ ABC 外接圆的圆心为O ，且 AO1(AB AC) ，则 AB 与 AC 的夹角为2（A ）（ B ）（ C ） 3 （ D ）642（7）直线 ykx 3 被圆 ( x 2)2( y 3)2 4截得的弦长为 2 3 ，则 k =（A ） ±3 （ B ）±3 （ C ）3 （D ） 333（ 8）为促使资源节俭型和环境友善型社会建设，指引居民合理用电、节俭用电，北京居民生活用电试行阶梯电价 . 其电价标准以下表：分档电量电价标准用户类型（千瓦时 / 户. 月） （元 / 千瓦时）一档1-240 （含）0.4883试行阶梯电 二档 241-400 （含）0.5383价的用户400 以上三档0.7883北京市某户居民 2016 年 1 月的均匀电费为 0.4983（元 / 千瓦时），则该用户 1 月份的用电量为（A ） 350 千瓦时 （ B ） 300 千瓦时 （ C ） 250 千瓦时（ D ） 200 千瓦时二、填空题共 6 小题，每题 5 分，共 30 分。

绝密★启用前本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本市卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）（1）已知集合{|24},{|3>5}A x x B x x x =<<=<或，则A B =（A ）{|2<<5}x x （B ）{|<45}x x x >或 （C ）{|2<<3}x x （D ）{|<25}x x x >或【答案】C考点： 集合交集 （2）复数12i=2i+- （A ）i （B ）1+i （C ）i - （D ）1i - 【答案】A 【解析】 试题分析：12(12)(2)2422(2)(2)5i i i i i i i i i +++++-===--+，故选A. 考点：复数运算（3）执行如图所示的程序框图，输出的s 值为（A ）8 （B ）9 （C ）27 （D ）36 【答案】B考点： 程序框图（4）下列函数中，在区间(1,1)- 上为减函数的是 （A ）11y x=- （B ）cos y x = （C ）ln(1)y x =+ （D ）2x y -= 【答案】D 【解析】试题分析：由12()2xx y -==在R 上单调递减可知D 符合题意，故选D. 考点：函数单调性（5）圆（x +1）2+y 2=2的圆心到直线y =x +3的距离为（A ）1 （B ）2 （C （D ） 【答案】C 【解析】试题分析：圆心坐标为(1,0)-，由点到直线的距离公式可知d ==，故选C.考点：直线与圆的位置关系（6）从甲、乙等5名学生中随机选出2人，则甲被选中的概率为（A）15（B）25（C）825（D）925【答案】B 【解析】试题分析：所求概率为142525CPC==，故选B.考点：古典概型（7）已知A（2，5），B（4，1）.若点P（x，y）在线段AB上，则2x−y的最大值为（A）−1 （B）3 （C）7 （D）8【答案】C考点：函数最值（8）某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩，其中有三个数据模糊.在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则（A）2号学生进入30秒跳绳决赛（B）5号学生进入30秒跳绳决赛（C）8号学生进入30秒跳绳决赛（D）9号学生进入30秒跳绳决赛【答案】B【解析】试题分析：将确定成绩的30秒跳绳成绩的按从大到小的顺寻排，分别是3，6，7，10，（1，5并列），4，其中，3，6，7号进了立定跳远的决赛，10号没进立定跳远的决赛，故9号需进30秒跳绳比赛的前8名，此时确定的30秒跳绳比赛决赛的名单为3，6，7，10，9，还需3个编号为1-8的同学进决赛，而（1，5）与4的成绩仅相隔1，故只能1，5，4进30秒跳绳的决赛，故选B. 考点：统计第二部分（非选择题共110分）二、填空题（共6小题，每小题5分，共30分）（9）已知向量=a b ，则a 与b 夹角的大小为_________. 【答案】30.考点： 向量数量积与夹角公式,数形结合 （10）函数()(2)1xf x x x =≥-的最大值为_________. 【答案】2 【解析】试题分析：1()11121f x x =+≤+=-，即最大值为2. 考点：函数最值,数形结合（11）某四棱柱的三视图如图所示，则该四棱柱的体积为___________.【答案】3.2【解析】试题分析：四棱柱高为1，底面为等腰梯形，面积为13(12)122⨯+⨯=，因此体积为3.2考点：三视图(12) 已知双曲线22221x y a b-= （a ＞0，b ＞0）的一条渐近线为2x +y =0，一个焦点为,0），则a =_______；b =_____________. 【答案】1,2a b ==考点：双曲线的基本概念 (13)在△ABC 中，23A π∠= ，c ，则bc =_________.【答案】1 【解析】试题分析：由正弦定理知sin sin A aC c==2sin1sin 2C π==，则6C π=，所以2366B ππππ=--=，所以b c =，即1bc =．考点：解三角形(14)某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品有3种，后两天都售出的商品有4种，则该网店①第一天售出但第二天未售出的商品有______种； ②这三天售出的商品最少有_______种. 【答案】①16；②29 【解析】试题分析：①由于前二天都售出的商品有3种，因此第一天售出的有19-3=16种商品第二天未售出；答案为 16．②同①第三售出的商品中有14种第二天未售出，有1种商品第一天未售出，三天总商品种数最少时，是第三天中14种第二天未售出的商品都是第一天售出过的，此时商品总数为29．分别用,,A B C 表示第一、二、三天售出的商品，如图最少时的情形．故答案为29．CBA139142考点： 统计分析三、解答题（共6题，共80分.解答应写出文字说明，演算步骤或证明过程）（15）（本小题13分）已知{a n }是等差数列，{b n }是等差数列，且b 2=3，b 3=9，a 1=b 1，a 14=b 4. （Ⅰ）求{a n }的通项公式；（Ⅱ）设c n = a n + b n ，求数列{c n }的前n 项和.【答案】（Ⅰ）21n a n =-（1n =，2，3，⋅⋅⋅）；（Ⅱ）2312-+n n（II ）由（I ）知，21n a n =-，13n n b -=．因此1213n n n n c a b n -=+=-+．从而数列{}n c 的前n 项和()11321133n n S n -=++⋅⋅⋅+-+++⋅⋅⋅+()12113213nn n +--=+- 2312n n -=+． 考点：等差、等比数列的通项公式和前n 项和公式，考查运算能力. （16）（本小题13分）已知函数f （x ）=2sin ωx cos ωx + cos 2ωx （ω>0）的最小正周期为π. （Ⅰ）求ω的值；（Ⅱ）求f （x ）的单调递增区间. 【答案】（Ⅰ）1ω=（Ⅱ）3,88k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）．函数sin y x =的单调递增区间为2,222k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）．由222242k x k πππππ-≤+≤+，得388k x k ππππ-≤≤+． 所以()f x 的单调递增区间为3,88k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）． 考点：两角和的正弦公式、周期公式、三角函数的单调性. （17）（本小题13分）某市民用水拟实行阶梯水价，每人用水量中不超过w 立方米的部分按4元/立方米收费，超出w 立方米的部分按10元/立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如下频率分布直方图：（I ）如果w 为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w 至少定为多少？（II ）假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费.【答案】（Ⅰ）3；（Ⅱ）10.5元.所以该月用水量不超过3立方米的居民占85%，用水量不超过2立方米的居民占45%．依题意，w 至少定为3．（II ）由用水量的频率分布直方图及题意，得居民该月用水费用的数据分组与频率分布表：根据题意，该市居民该月的人均水费估计为：40.160.1580.2100.25120.15170.05220.05270.05⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯10.5=（元）． 考点：频率分布直方图求频率，频率分布直方图求平均数的估计值. （18）（本小题14分）如图，在四棱锥P-ABCD 中，PC ⊥平面ABCD ，,AB DC DC AC ⊥∥ （I ）求证：DC PAC ⊥平面； （II ）求证：PAB PAC ⊥平面平面；（III ）设点E 为AB 的中点，在棱PB 上是否存在点F ，使得//PA 平面C F E ?说明理由.【答案】（Ⅰ）见解析；（Ⅱ）见解析；（III ）存在.理由见解析. 【解析】试题分析：（Ⅰ）利用线面垂直判定定理证明；（Ⅱ）利用面面垂直判定定理证明；（III ）取PB 中点F ，连结F E ，则F//E PA ，根据线面平行定理则//PA 平面C F E . 试题解析：（I ）因为C P ⊥平面CD AB ， 所以C DC P ⊥． 又因为DC C ⊥A ， 所以DC ⊥平面C PA ．考点：空间垂直判定与性质；空间想象能力，推理论证能力 （19）（本小题14分）已知椭圆C ：22221x y a b+=过点A （2,0），B （0,1）两点.（I ）求椭圆C 的方程及离心率；（Ⅱ）设P 为第三象限内一点且在椭圆C 上，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，求证：四边形ABNM 的面积为定值.【答案】（Ⅰ）2214x y +=；2=e （Ⅱ）见解析.（II ）设()00,x y P （00x <，00y <），则220044x y +=． 又()2,0A ，()0,1B ，所以，直线PA 的方程为()0022y y x x =--． 令0x =，得0022y y x M =--，从而002112y y x M BM =-=+-． 直线PB 的方程为0011y y x x -=+． 令0y =，得001x x y N =--，从而00221x x y N AN =-=+-． 所以四边形ABNM 的面积12S =AN ⋅BM 00002121212x y y x ⎛⎫⎛⎫=++ ⎪⎪--⎝⎭⎝⎭()22000000000044484222x y x y x y x y x y ++--+=--+00000000224422x y x y x y x y --+=--+ 2=．从而四边形ABNM 的面积为定值．考点：椭圆方程，直线和椭圆的关系，运算求解能力.（20）（本小题13分）设函数()32.f x x ax bx c =+++（I ）求曲线().y f x =在点()()0,0f 处的切线方程；（II ）设4a b ==，若函数()f x 有三个不同零点，求c 的取值范围； （III ）求证：230a b -＞是().f x 有三个不同零点的必要而不充分条件. 【答案】（Ⅰ）y bx c =+;（Ⅱ）320,27c ⎛⎫∈ ⎪⎝⎭;（III ）见解析.()f x 与()f x '在区间(),-∞+∞上的情况如下：所以，当0c >且32027c -<时，存在()14,2x ∈--，222,3x ⎛⎫∈-- ⎪⎝⎭， 32,03x ⎛⎫∈- ⎪⎝⎭，使得()()()1230f x f x f x ===． 由()f x 的单调性知，当且仅当320,27c ⎛⎫∈ ⎪⎝⎭时，函数()3244f x x x x c =+++有三个不同零点．考点：利用导数研究曲线的切线；函数的零点。

顺义区2016届九年级第一次统一练习语文试卷一、基础运用（23分）1.阅读下面文字，完成（1）-（4）小题。

（共9分）松树四季常青，姿态挺拔，叶密生而有层云簇拥之势，欹斜层叠。

在万物（iāo shǖ）的隆冬，松树依旧郁郁葱葱，精神抖擞，象征着青春常在和坚强不屈。

正如甲。

竹是高雅、纯洁、虚心、有节的象征，正如乙。

古今庭园几乎无园不竹，居而有竹，则幽簧拂窗，清气满院；竹影婆娑，姿态入画，碧叶经冬不凋，清秀而又潇洒。

古往今，“不可一日无此君”已成了众多文人雅士的偏好。

梅花为中国传统十大名花之一，姿、色、香、韵俱佳。

丙，将梅花的姿容、神韵描绘得淋漓尽致。

漫天飞雪之际，独有梅花笑傲严寒，破蕊怒放，这是何等的可爱、可贵！松竹梅这三种植物被称为“岁寒三友”。

在南宋林景熙《王云梅舍记》记载：“即其居累土为山，种梅百本，与乔松修篁为岁寒友。

”松、竹经冬不凋，梅则迎寒开花，因这三种植物在寒冬时节仍可保持顽强的生命力而得名。

“岁寒三友”还与宋代大文豪苏东坡有一段不解之缘。

北宋神宗元丰二年，苏轼遭权臣迫害，被贬到黄州。

初到此地时，心情很苦闷。

稍后，家眷依，朋友访，苏轼的心绪慢慢好转，为了解决生活上的（拮据），便向黄州府讨了数十亩荒地开垦种植，借以改善生活。

这块地，当地人唤作“东坡”，苏轼便自取别号为“东坡居士”。

苏轼在东坡栽了稻、麦等到农作物，又筑园围墙，造起房屋。

房子取名“雪堂”，并在四壁都画上雪花；园子里，则遍植松、柏、竹、梅等花木。

一年春天，黄州知州徐君猷雪堂看望他，打趣道：“你这房间起居睡卧，环顾侧看处处是雪。

当真天寒飘雪时，人迹难至，不觉得太冷清吗？”苏轼手指院内（yáo yè）花木，爽朗大笑：“风泉两部乐，松竹三益友。

”意思是说，清风吹拂和泉水（淙淙）的声音就是两曲优美的音乐，枝叶常青的松柏、经冬不凋的竹子和傲霜开放的梅花，就是可伴冬寒的三位益友。

徐君猷对苏东坡更加敬仰。

后，松、竹、梅合称“岁寒三友”，一方面取其玉洁冰清、傲立霜雪的高尚品格，一方面也将其视作长青不老、旺盛生命力的象征。

2024北京房山初三一模语 文本试卷共10页，满分100分，考试时长150分钟。

考生务必将答案填涂或书写在答题卡上，在试卷上作答无效。

考试结束后，将试卷和答题卡一并交回。

一、基础·运用（共13分）班级开展了“寻龙之旅”综合实践活动，你所在的小组准备以手抄报的形式汇报活动所得。

下面是手抄报的初稿，请根据要求修改。

1. 请用正楷书写“我的寻龙之旅”六个字作为手抄报的标题。

（一）走进展馆寻“龙”为了弘扬中华优秀传统文化，首都博物馆将馆藏文物中的“龙”元素进行梳理提炼，策画了“遇见铜坐龙”系列活动。

活动的主角铜坐龙为青铜实心铸造，它弓身踞坐，造型别致，吸引了众多观展者的目光。

这尊铜坐龙于1990年在北京金中都正殿大安殿遗址出土。

它有力地证明了金代宫城核心区与当代北京城的关系，是北京城历史的重要见证。

它两肋有飞翼，带有从丝路传来的西亚、中亚地区翼兽的特征，是草原文化与中原文化交融的典型代表。

铜坐龙是民族文化交流融合的象征，也是北京城历史的见证。

2. 小组成员对文段中加点词语的字形作出判断。

下列说法正确的一项是（ ）A. 因为表达的是“光大、发扬”的意思，所以“弘扬”一词中有错字。

B. 因为表达的是“筹谋、设计”的意思，所以“策画”一词中有错字。

C. 因为表达的是“把熔化后的金属倒在模子里制成器物”的意思，所以“铸造”一词中有错字。

D. 因为表达的是“创造出来的物体形象”的意思，所以“造型”一词中有错字。

3. 根据语境，文段中的画线句表达欠妥，请你做出修改。

（二）翻阅书卷觅“龙”我国的文学作品中不乏“龙”的身影。

它显身在神话传说中，如盘古成龙相、伏羲为龙种；它出没在成语故事里，如卧虎藏龙、画龙点睛；它潜藏在古诗文中，如“水不在深，有龙则灵”“雨过不知龙去处，一池草色万蛙鸣”；它奔腾在古典名著里，如《西游记》中一路驮着唐僧前往西天取经的小白龙；它腾飞在近代佳作中，如《少年中国说》中的“潜龙腾渊，鳞爪飞扬”……遍览古今书卷，龙影随处可寻。

顺义区2016届九年级第一次统一练习语文试卷一、基础运用（23分）1.阅读下面文字，完成（1）-（4）小题。

（共9分）松树四季常青，姿态挺拔，叶密生而有层云簇拥之势，欹斜层叠。

在万物（iāo shǖ）的隆冬，松树依旧郁郁葱葱，精神抖擞，象征着青春常在和坚强不屈。

正如甲。

竹是高雅、纯洁、虚心、有节的象征，正如乙。

古今庭园几乎无园不竹，居而有竹，则幽簧拂窗，清气满院；竹影婆娑，姿态入画，碧叶经冬不凋，清秀而又潇洒。

古往今，“不可一日无此君”已成了众多文人雅士的偏好。

梅花为中国传统十大名花之一，姿、色、香、韵俱佳。

丙，将梅花的姿容、神韵描绘得淋漓尽致。

漫天飞雪之际，独有梅花笑傲严寒，破蕊怒放，这是何等的可爱、可贵！松竹梅这三种植物被称为“岁寒三友”。

在南宋林景熙《王云梅舍记》记载：“即其居累土为山，种梅百本，与乔松修篁为岁寒友。

”松、竹经冬不凋，梅则迎寒开花，因这三种植物在寒冬时节仍可保持顽强的生命力而得名。

“岁寒三友”还与宋代大文豪苏东坡有一段不解之缘。

北宋神宗元丰二年，苏轼遭权臣迫害，被贬到黄州。

初到此地时，心情很苦闷。

稍后，家眷依，朋友访，苏轼的心绪慢慢好转，为了解决生活上的（拮据），便向黄州府讨了数十亩荒地开垦种植，借以改善生活。

这块地，当地人唤作“东坡”，苏轼便自取别号为“东坡居士”。

苏轼在东坡栽了稻、麦等到农作物，又筑园围墙，造起房屋。

房子取名“雪堂”，并在四壁都画上雪花；园子里，则遍植松、柏、竹、梅等花木。

一年春天，黄州知州徐君猷雪堂看望他，打趣道：“你这房间起居睡卧，环顾侧看处处是雪。

当真天寒飘雪时，人迹难至，不觉得太冷清吗？”苏轼手指院内（yáo yè）花木，爽朗大笑：“风泉两部乐，松竹三益友。

”意思是说，清风吹拂和泉水（淙淙）的声音就是两曲优美的音乐，枝叶常青的松柏、经冬不凋的竹子和傲霜开放的梅花，就是可伴冬寒的三位益友。

徐君猷对苏东坡更加敬仰。

后，松、竹、梅合称“岁寒三友”，一方面取其玉洁冰清、傲立霜雪的高尚品格，一方面也将其视作长青不老、旺盛生命力的象征。

2015—2016学年北京卷高三年级综合能力测试语文本试卷共8页，共150分。

考试时长150分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、本大题共8小题，共25分。

阅读下面材料，完成1一8题。

材料一①今年3月，由中国南车株洲电力机车有限公司输出技术，在南非当地化生产的第95台20E型电力机车下线，南非总统祖马亲自为机车剪彩时感慨：“中国南车在实现本地化生产和采购，技术转让和本土员工培训等方面功不可没。

”②从卖装备到卖技术，从一锤子买卖到赢得回头客，将高铁打造成国家名片的中国南车，顺着轨道的延伸，向世界展示着“中国制造”的崭新形象。

2004年，中国铁路平均运营时速仍停留在百公里之时，中国南车便引进时速200公里的高速动车组，开始了学徒生涯。

四年后，时速300——350公里CRH2C型高速动车组在南车下线，中国成为继日，法，德之后,世界上第四个能够自主研制时速300公里及以上动车组的国家。

又两年，中国南车研制的具有完全自主知识产权的时速380公里CRH380A 型高速动车组,在京沪高铁创造了486.1公里的世界铁路运营试验最高时速。

③拥有着高铁技术与重载技术的双桂冠，中国南车去年签下37亿美元的海外订单，是历年合同总额的两倍。

今年，中国南车仍将不遗余力地推动中国高铁“走出去”。

目前，泰国铁路项目，新马高铁项目都在积极推进，其中3月14日中泰铁路合作项目正式签署合同。

中国相关机构将对该项目建设进行可行性调研，预计于5月将公布调研结果并对货款等事项进行进一步磋商。

④“中国速度”震惊世界！⑤作为国家领导人每逢出访必定推销的“中国制造”，中国南车的触角正伸向高新技术的前沿阵地。

今年3月，南车四方股份研制出世界首列氢能源有轨电车，填补了氢能源在全球有机电车领域应用的空白，也使我国成为世界上第一个掌握氢能源有轨电车技术的国家。

4月15日，中国南车还将斥资12亿元，收购全球第二大深海机器人供应商——英国SMD公司100%的股权。

房山区2015年高三二模数 学（文科）本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）若集合{|21}A x x =-≤≤，B ={}0x x <，则A B = （A ）(,0)-∞（B ）(,1]-∞（C ）[2,0)-（D ）(1,)+∞（2）下列函数中，既是奇函数又在区间(0,)+∞上单调递增的是（A ）3y x =（B ）ln y x =（C ）sin y x =（D ）2xy =（3）在△ABC 中，“3A π＝”是“1cos 2A =” 的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件（4）若,x y 满足0,1,0.x y x y y -≥⎧⎪+≤⎨⎪≥⎩则2z x y =+的最大值为（A ）0 （B ）1 （C ）2（D ）23 （5）执行如图所示的程序框图，若输入A 的值为2，则输出的n 值为 （A ）3 （B ）4 （C ）5 （D ）6（6）已知△ABC 外接圆的圆心为O ，且1()2AO AB AC =+，则AB 与AC 的夹角为 （A ）6π （B ）4π （C ）3π （D ）2π（7）直线3y kx =+被圆22(2)(3)4x y -+-=截得的弦长为k =（A ）（B（C（D（8）为促进资源节约型和环境友好型社会建设，引导居民合理用电、节约用电，北京居民生活用电试行阶梯电价. 其电价标准如下表：用电量为 （A ）350千瓦时（B ）300千瓦时（C ）250千瓦时（D ）200千瓦时二、填空题共6小题，每小题5分，共30分。

（9）若(2i)i i a b -=-，其中,a b R ∈，i 是虚数单位，则22a b +=___.（10）为了调查野生动物保护区内某种野生动物的数量，调查人员某天捕到这种动物120只，做好标记后放回，经过一星期后，又捕到这种动物错误！未找到引用源。

房山区2016年高三二模数 学（文科）本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）若集合{|21}A x x =-≤≤，B ={}0x x <，则A B = （A ）(,0)-∞（B ）(,1]-∞（C ）[2,0)-（D ）(1,)+∞（2）下列函数中，既是奇函数又在区间(0,)+∞上单调递增的是（A ）3y x =（B ）ln y x =（C ）sin y x =（D ）2xy =（3）在△ABC 中，“3A π＝”是“1cos 2A =” 的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件（4）若,x y 满足0,1,0.x y x y y -≥⎧⎪+≤⎨⎪≥⎩则2z x y =+的最大值为（A ）0 （B ）1 （C ）2（D ）23 （5）执行如图所示的程序框图，若输入A 的值为2，则输出的n 值为 （A ）3 （B ）4 （C ）5 （D ）6（6）已知△ABC 外接圆的圆心为O ，且1()2AO AB AC =+ ，则AB 与AC的夹角为（A ）6π （B ）4π （C ）3π （D ）2π（7）直线3y kx =+被圆22(2)(3)4x y -+-=截得的弦长为k =（A ）（B（C（D（8）为促进资源节约型和环境友好型社会建设，引导居民合理用电、节约用电，北京居民生活用电试行阶梯电价. 其电价标准如下表：用电量为 （A ）350千瓦时（B ）300千瓦时（C ）250千瓦时（D ）200千瓦时二、填空题共6小题，每小题5分，共30分。

（9）若(2i)i i a b -=-，其中,a b R ∈，i 是虚数单位，则22a b +=___.（10）为了调查野生动物保护区内某种野生动物的数量，调查人员某天捕到这种动物120只，做好标记后放回，经过一星期后，又捕到这种动物100只，其中做过标记的有8只，按概率方法估算，该保护区内有___只这种动物.（11）33,0,()1log ,0.x f x x x x ⎧-<⎪=⎨⎪+>⎩ 则 ((1))f f -等于___.（12）某几何体的正（主）视图和俯视图如图所示，则该几何体的体积的最大值为___ .（13）抛物线24x y =的焦点F 的坐标为___，过F 的直线与抛物线交于,A B 两点，若线段AB 的中点M 的纵坐标为4，则线段AB 的长度为___.正（主）视图俯视图（14）观察下面的数表2 4 6 8 10 12 14 16 18 20 2224 26 28 30……该表中第6行最后一个数是___；设2016是该表的m 行第n 个数，则m n +=___.三、解答题共6小题，共80分。