- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
位压强势能)
z p
单位重量流体所具有的总势能 (简称单位总势能)
伯努利积分
p u2
z
2g
Cl
单位重量流体所具有的动能(简称单
u 2 位动能) 2g
****************
p u2 z
2g
单位重量流体所具有的总机 械能(简称单位总机械能)
欧
在理想流体的恒定
拉 流动中,位于同一条
观
流线上任意两个流体
• 迹线是流体质点
运动的轨迹,是与 拉格朗日观点相对 应的概念。
• 拉格朗日法中位移表达式
r r(a,b,c,t)
即为迹线的参数方程。
t 是变数,a,b,c 是参
数。
18
(2)迹线的微分方程
式中,ux,uy,uz 均为时空t,x,y,z的函数, 且t是自变量。 注意:恒定流时流线和迹线重合;
非恒定流时流线和迹线不重合;
四.流量(discharge)
指单位时间内通过河渠、管道等某一过水横断 面的流体数量。
体积流量(m3/s): 质量流量(kg/s):
• 过水断面
Байду номын сангаас
与流动方向正交的流管的横断面
• 过水断面为面积微元的流管
叫元流管,其中的流动称为元
流。
dA1
u1
dA2
u2 • 过水断面为有限面积的流管中的流动叫总流。总流可看作无数
2. 过流断面为渐变流;
3. 均匀不可压缩流体;
4.质量力只有重力
三.能量方程的扩展
分叉恒定流
在有分流汇入及流出的情况下,连续方程只须 作相应变化。质量的总流入 = 质量的总流出。
Qm1 Qm2 Qm3
Qm1
Qm2
Qm3
第七节 能量方程的应用
一.求解问题: 流量流速, 压强, 流量流速和压强 二.能量方程的解题步骤:
H z p u2 总水头
2g
水头线 将各项水头沿程变化的情况几何表示出来。
u2 2g
Hp
z
o
总水头线 测压管水头线
位置水头线
水平基准线 o
理想流体 恒定元流 的总水头 线是水平 的。
假定
1. 理想流体 2.恒定流; 3. 均匀不可压缩流体; 4.质量力只有重力,即X=Y=0,Z=-g; 5. 沿同一条流线
解: uz =0,所以是二维流动,二维流动的流线方程微分为
dx dy
ux uy
将两个分速度代入流线微分方程,得到
dx dy
ky kx
即
xdx+ydy=0
积分上式得到 x2+y2=c
即流线簇是以坐标原点为圆心的同心圆。
2.迹线
(1)迹线的定义 迹线(path line)某一质 点在某一时段内的运动 轨迹线。
举例
已知直角坐标系中的速度场 ux=x+t; uy= -y+t;uz=0,试求t =
0 时过 M(-1,-1) 点的迹线。
解:
由迹线的微分方程:
d x d y d z dt
ux
uy
uz
ux=x+t;uy=-y+t;uz=0
t = 0 时过 M(-1,-1):
C1 = C2 = 0
dx xt dt
1.选择基准面:基准面可任意选定,但应以简化计算为原则。
例如选过水断面形心(z=0),或选自由液面(p=0)
等。 2.选择计算断面:计算断面应选择均匀流断面或渐变流断面,
20 2 1 V22 15 0 V22
16 2g
2g
管中流量
V2
19.6 7 16 12.(1 m/s) 15
qV
4
d 22V2
0.052 12.1 0.02(4 m3/s)
4
4/8/2020
43
第六节 恒定总流能量方程
一、总流能量方程
设单位重量上的某流线的能量为 e z p u 2 2g
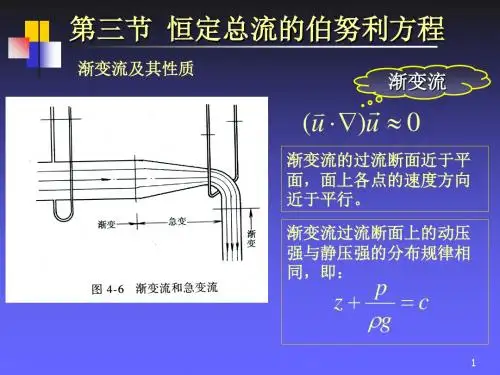
• 渐变流和急变流是工程意义上对流动是否符合均匀流条件的
划分,两者之间没有明显的、确定的界限,需要根据实际情况 来判定
45
渐变流:流线的曲率很小接近平行,过流断面上
的压力基本上是静压分布者为渐变流 (gradually varied flow),否则为急变流。
渐变流——沿程逐渐改变的流动。
对渐变流, p z C
12
(2)流线的性质
a.同一时刻的不同流线, 不能相交。
b.流线不能是折线,而是 一条光滑的曲线。
c.流线簇的疏密反映了速 度的大小
(3)流线的方程
根据流线的定义,可以求得流线的微分方程, 设ds为流线上A处的一微元弧长:
u为流体质点在A点的流速:
因为 所以
——流线方程
【例】
有一流场,其流速分布规律为:ux= -ky, uy = kx, uz=0, 试求其流线方程。
,x方向有:
理想流体的运动微分方程(欧拉运动微分方程)
(3-10)
适用范围:恒定流或非恒定流,可压缩流或不 可压缩流体。
恒定流
恒定流的时变加速度为零,但位变加速度可以不为零。
u 0 t
u u(x, y, z)
对于不可压缩流体的流动,连续方程为
u ux u y uz 0 x y z
dG重量上的能量为 dE e • dG ( z p u 2 )udA
2g
总能量
E
Ae • dG
A (z
p
u 2 )udA
2g
平均单位重量上的能量为:
e
E
Q
1
Q
A (z
p
u 2 )udA
2g
是 否
是 流渐
变
接
近
均
匀 否 流急
流
变
?
流线虽不平行,但夹角较小; 流线虽有弯曲,但曲率较小。
流线间夹角较大; 流线弯曲的曲率较大。
Ⅱ管测压孔
【例】 水流通过所示管路流入大气,已知:U形测压
管中水银柱高差Δh=0.2m,h1=0.72m H2O,管径d1=0.1m ,管嘴出口直径d2=0.05m,不计管中水头损失,试求管 中流量qv。
4/8/2020
41
【解】 首先计算1-1断面管路中心的压强。因为A-B为 等压面,列等压面方程得:
空间坐标
(a,b,c)为t=t0起始时刻质点所在的空间位置坐标,称为拉 格朗日数。所以,任何质点在空的位置(x,y,z)都可看 作是(a,b,c)和时间t的函数.
(1)(a,b,c)=const , t为变数,可以得出某个指 定质点在任意时刻所处的位置。
(2)(a,b,c)为变数,t=const,可以得出某一瞬间 不同质点在空间的分布情况。
各水力运动要素均不随时间而变化。
即:
三者都等于0。
(2)非恒定流
非恒定流(unsteady flow):
又称非定常流, 是指流场中的流体 流动空间点上各水 力运动要素中,只 要有任何一个随时 间的变化而变化的 流动。
• 流动是否恒
定与所选取的 参考坐标系有 关,因此是相对 的概念。
10
二. 流线与迹线
个元流的集合。总流的过水断面一般为曲面。
25
五. 断面平均流速v
总流过水断面上各点 的流速是不相同的,所 以常采用一个平均值来 代替各点的实际流速, 称断面平均流速v。
第三节 连续性方程
根据质量守恒: 因为 当流体不可压缩时,密度为常数 ρ1= ρ1
1
第四节 理想流体运动微分方程
1. Euler方程
由于流体质点的运动轨迹非常复杂,而实用上无
须知道个别质点的运动情况,所以除了少数情况(如 波浪运动)外,在工程流体力学中很少采用。
2.欧拉法
欧拉法(euler method)是以流体质点流 经流场中各空间点的运动即以流场作为描 述对象研究流动的方法。——流场法
它不直接追究质点的运动过程,而是以 充满运动流体质点的空间——流场为对象。 研究各时刻质点在流场中的变化规律。
恒定条件下理想流体运动方程沿流线的积分:
d ux dt
ux
d
t
duy dt
uy
d
t
d uz dt
uz
d
t
X
d
x
Y
d
y
Z
d
z
1
r
p x
d
x
p y
d
y
p z
d
z
上式左边可改写为:
dux dt
ux
dt
duy dt
uy
dt
duz dt
uz
dt
ux
dux
uy
duy
uz
duz
d
u
2 x
2
d
u
2 y
2
d
u
• 元流能量方程的应用举例
毕
托
h
管
测
Ⅰ管
速
pA
A
u
B
uA u uB 0 zA zB
代入 伯努利方程
pA u2 pB 0
2g
假设
Ⅰ、Ⅱ管
的存在不
扰动原流
pB
场。
Ⅱ管
u 2g( pB pA) 2gh
Ⅰ管 —— 测压管,开口方向与流速垂直。 Ⅱ管 —— 总压管,开口方向迎着流速。
从理想流体中任取 一(x,y,z)为中心的微元六 面体为控制体,边长为 dx,dy,dz,中心点压强为 p(x,y,z) ,如图.
受力分析(x方向为例):
1.表面力 因为理想流体,所以t=0 左表面
右表面
2.质量力