第三章 练习题-理论分布与抽样分布

抽样分布习题及答案抽样分布习题及答案抽样分布是统计学中一个重要的概念，它描述了从总体中抽取样本后，样本统计量的分布情况。

在实际应用中，我们经常需要利用抽样分布来进行统计推断，因此对于抽样分布的理解和掌握是十分必要的。

本文将介绍一些常见的抽样分布习题，并提供相应的答案。

1. 问题：某公司有1000名员工，其中400人是女性。

现从中随机抽取100人，求抽取样本中女性人数的抽样分布。

解答：在这个问题中，我们可以将女性的出现看作是一个二项分布的实验，成功的概率为0.4。

因此，抽取样本中女性人数的抽样分布是一个二项分布。

根据二项分布的性质，我们可以计算出不同女性人数的概率。

2. 问题：某电商平台有1000个用户，他们的购买金额服从均值为100元，标准差为20元的正态分布。

现从中随机抽取50个用户，求抽取样本的平均购买金额的抽样分布。

解答：在这个问题中，样本的平均购买金额的抽样分布是一个服从均值为100元，标准差为20/√50元的正态分布。

根据正态分布的性质，我们可以计算出不同平均购买金额的概率。

3. 问题：某城市的居民年收入服从均值为50000元，标准差为10000元的正态分布。

现从中随机抽取200个居民，求抽取样本的平均年收入的抽样分布。

解答：在这个问题中，样本的平均年收入的抽样分布是一个服从均值为50000元，标准差为10000/√200元的正态分布。

根据正态分布的性质，我们可以计算出不同平均年收入的概率。

4. 问题：某医院每天接诊的患者数服从均值为50人，标准差为10人的泊松分布。

现从中随机抽取30天，求抽取样本的平均每天接诊的患者数的抽样分布。

解答：在这个问题中，样本的平均每天接诊的患者数的抽样分布是一个服从均值为50人，标准差为10/√30人的正态分布。

根据正态分布的性质，我们可以计算出不同平均每天接诊的患者数的概率。

通过以上几个习题的解答，我们可以看到不同问题中抽样分布的情况是不同的，需要根据具体的问题来确定抽样分布的类型和参数。

抽样分布习题答案抽样分布习题答案随着统计学的发展，抽样分布成为了统计推断的重要基础。

在统计学中，我们经常需要从总体中抽取一部分样本，然后通过对样本的分析来推断总体的特征。

而抽样分布则是描述样本统计量的分布情况的概率分布。

在这篇文章中，我们将回答一些关于抽样分布的习题，帮助读者更好地理解和应用这一概念。

1. 假设某个总体的均值为μ，标准差为σ，从该总体中抽取样本容量为n的简单随机样本。

则样本均值的抽样分布的均值为多少？标准差为多少？答案：样本均值的抽样分布的均值为总体均值μ，标准差为总体标准差σ除以样本容量n的平方根，即σ/√n。

这意味着随着样本容量的增加，样本均值的抽样分布的标准差将减小，从而更加接近总体均值。

2. 假设某个总体服从正态分布，均值为μ，标准差为σ。

从该总体中抽取样本容量为n的简单随机样本，计算样本均值。

当n足够大时，样本均值的抽样分布将近似服从什么分布？答案：当样本容量n足够大时，样本均值的抽样分布将近似服从正态分布。

这是由于中心极限定理的适用，即当样本容量足够大时，样本均值的抽样分布将趋于正态分布，无论总体的分布形态如何。

3. 假设某个总体服从正态分布，均值为μ，标准差为σ。

从该总体中抽取样本容量为n的简单随机样本，计算样本标准差。

当n足够大时，样本标准差的抽样分布将近似服从什么分布？答案：当样本容量n足够大时，样本标准差的抽样分布将近似服从正态分布。

这是由于当样本容量足够大时，样本标准差的抽样分布可以通过中心极限定理近似为正态分布。

4. 假设某个总体的比例为p，从该总体中抽取样本容量为n的简单随机样本，计算样本比例。

样本比例的抽样分布的均值和标准差分别为多少？答案：样本比例的抽样分布的均值为总体比例p，标准差为√(p(1-p)/n)。

这意味着当样本容量足够大时，样本比例的抽样分布将近似服从正态分布，均值为总体比例p，标准差为√(p(1-p)/n)。

通过以上习题的解答，我们可以看到抽样分布在统计推断中的重要性。

抽样分布与理论分布一、抽样分布总体分布：总体中所有个体关于某个变量的取值所形成的分布。

样本分布：样本中所有个体关于某个变量大的取值所形成的分布。

抽样分布：样品统计量的概率分布，由样本统计量的所有可能取值和相应的概率组成。

即从容量为N 的总体中抽取容量为n 的样本最多可抽取m 个样本，m 个样本统计值形成的频率分布，即为抽样分布。

样本平均数的抽样分布：设变量X 是一个研究总体，具有平均数μ和方差σ2。

那么可以从中抽取样本而得到样本平均数x ，样本平均数是一个随机变量，其概率分布叫做样本平均数的抽样分布。

由样本平均数x 所构成的总体称为样本平均数的抽样总体。

它具有参数μx 和σ2x ，其中μx 为样本平均数抽样总体的平均数，σ2x 为样本平均数抽样总体的方差，σx 为样本平均数的标准差，简称标准误。

统计学上可以证明x 总体的两个参数 μx 和σ2x 与X 总体的两个参数μ和σ2有如下关系：μx = μσ2x = σ2 /n 由中心极限定理可以证明，无论总体是什么分布，如果总体的平均值μ和σ2都存在，当样本足够大时（n>30），样本平均值x 分布总是趋近于N （μ，n2σ)分布。

但在实际工作中，总体标准差σ往往是未知的，此时可用样本标准差S 估计σ。

于是，以nS估计σx ，记为X S ，称为样本标准误或均数标准误。

样本平均数差数的抽样分布：二、正态分布2.1 正态分布的定义：若连续型随机变量X 的概率密度函数是⎪⎭⎫ ⎝⎛--=σμπσx e x f 22121)( （-∞＜x ＜+∞）则称随机变量X 服从平均数为μ、方差为σ2的正态分布，记作X~N （μ，σ2）。

相应的随机变量X 概率分布函数为 F （x ）=⎰∞-x dx x f )(它反映了随机变量X 取值落在区间（-∞，x ）的概率。

2.2 标准正态分布当正态分布的参数μ=0，σ2=1时，称随机变量X 服从标准正态分布，记作X~N （0,1）。

抽样分布习题及答案1. 题目：从一个容器中随机取出30个样本，每个样本的体积服从正态分布，均值为150，标准差为10。

计算样本均值的抽样分布的标准差。

解答：我们知道，样本均值的抽样分布的标准差（也称为标准误差）可以通过总体标准差除以样本容量的平方根来计算。

标准误差 = 总体标准差/ √样本容量在本题中，总体标准差为10，样本容量为30，代入公式可得：标准误差= 10 / √30 ≈ 1.83因此，样本均值的抽样分布的标准差约为1.83。

2. 题目：某电视台进行了一项调查，随机抽取了500名观众，其中有380人表示喜欢该电视节目。

根据该样本数据，计算其样本比例的抽样分布的标准差。

解答：样本比例的抽样分布的标准差可以通过以下公式计算：标准误差= √((样本比例 × (1 - 样本比例)) / 样本容量)在本题中，样本比例为380/500 = 0.76，样本容量为500，代入公式可得：标准误差= √((0.76 × (1 - 0.76)) / 500) ≈ 0.018因此，样本比例的抽样分布的标准差约为0.018。

3. 题目：某商品的包装袋上注明每袋重量服从正态分布，均值为500克，标准差为10克。

为了确定该注明是否准确，随机抽取了100袋该商品，计算抽取样本的平均重量的抽样分布的标准差。

解答：抽取样本的平均重量的抽样分布的标准差可以通过总体标准差除以样本容量的平方根来计算。

标准误差 = 总体标准差/ √样本容量在本题中，总体标准差为10克，样本容量为100，代入公式可得：标准误差= 10 / √100 = 1因此，抽取样本的平均重量的抽样分布的标准差为1克。

4. 题目：某超市进行了一次促销活动，随机抽取了50个顾客进行调查，得知他们购买的平均金额为200元，标准差为50元。

计算该样本的平均金额的抽样分布的标准差。

解答：样本的平均金额的抽样分布的标准差可以通过总体标准差除以样本容量的平方根来计算。

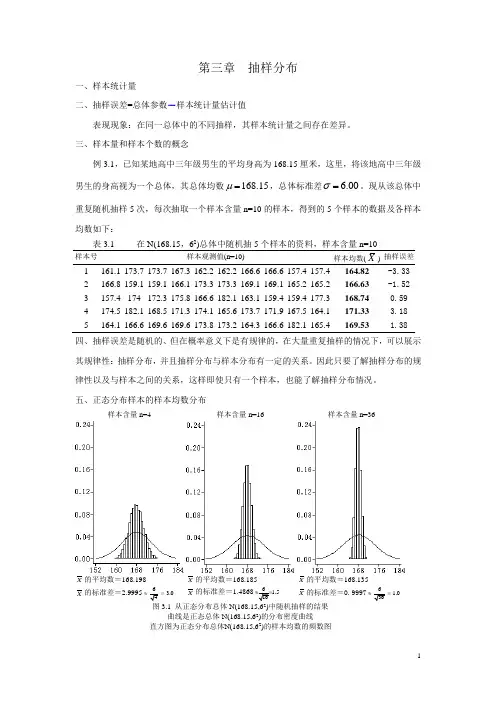
第三章 抽样分布一、样本统计量二、抽样误差=总体参数－样本统计量估计值表现现象：在同一总体中的不同抽样，其样本统计量之间存在差异。

三、样本量和样本个数的概念例3.1，已知某地高中三年级男生的平均身高为168.15厘米，这里，将该地高中三年级男生的身高视为一个总体，其总体均数168.15μ=，总体标准差 6.00σ=。

现从该总体中重复随机抽样5次，每次抽取一个样本含量n=10的样本，得到的5个样本的数据及各样本均数如下：2样本号样本观测值(n=10)X 抽样误差1 161.1 173.7 173.7 167.3 162.2 162.2 166.6 166.6 157.4 157.4 164.82 -3.33 2 166.8 159.1 159.1 166.1 173.3 173.3 169.1 169.1 165.2 165.2 166.63 -1.52 3 157.4 174 172.3 175.8 166.6 182.1 163.1 159.4 159.4 177.3 168.74 0.59 4 174.5 182.1 168.5 171.3 174.1 165.6 173.7 171.9 167.5 164.1 171.33 3.18 5164.1 166.6 169.6 169.6 173.8 173.2 164.3 166.6 182.1 165.4169.531.38四、抽样误差是随机的、但在概率意义下是有规律的，在大量重复抽样的情况下，可以展示其规律性：抽样分布，并且抽样分布与样本分布有一定的关系。

因此只要了解抽样分布的规律性以及与样本之间的关系，这样即使只有一个样本，也能了解抽样分布情况。

五、正态分布样本的样本均数分布样本含量n=4样本含量n=16样本含量n=36X 的平均数＝168.198X的标准差＝2.9995 3.0≈=X 的平均数＝168.185X 的标准差＝1.4868 1.5 X 的平均数＝168.135X 的标准差＝0.9997 1.0≈= 图3.1 从正态分布总体N(168.15,6)中随机抽样的结果曲线是正态总体N(168.15,62)的分布密度曲线直方图为正态分布总体N(168.15,62)的样本均数的频数图表3.2 从正态总体N(168.15，62)随机抽样，样本含量分别为4，16和36●大多数的样本均数相互之间存在差异，绝大多数的样本均数X不等于总体均数，但都离总体均数比较近。

抽样分布练习题
抽样分布是统计学中一个重要的概念，它是指从总体中抽取样
本并计算样本统计量的分布。

通过对抽样分布的理解和应用，我们
可以进行各种统计推断和假设检验。

以下是几个关于抽样分布的练
习题，希望能帮助大家理解和掌握这一概念。

1. 抽样分布的定义是什么？请简要解释。

2. 在一个总体中，平均值为μ，标准差为σ的情况下，从该总体
中随机抽取样本大小为n，计算平均值。

当n趋近于∞时，这个样
本平均值的抽样分布是什么？
3. 如果从一个服从正态分布的总体中抽取样本大小为n，计算
平均值，这个样本平均值的抽样分布是什么？
4. 抽样分布和总体分布之间有什么关系？请解释。

5. 如何通过样本均值的抽样分布来进行统计推断？
6. 抽样方法对于抽样分布的形状和性质有何影响？请举例说明。

7. 在进行假设检验时，抽样分布起到了什么作用？请解释。

8. 为了确定一个样本平均值的抽样分布，我们应该进行几次抽样？为什么？
9. 抽样分布的中心位置和变异性如何影响统计推断的结果？
10. 抽样分布理论适用于哪些统计推断方法？请列举几个例子。

11. 你了解的抽样分布的相关公式有哪些？请简要介绍。

12. 抽样分布在质量控制和市场研究等领域有什么应用？请举例说明。

以上是关于抽样分布的练习题，希望通过这些练习题，大家能够更好地理解和应用抽样分布的概念，并在统计推断和假设检验中能够灵活运用。

抽样分布是统计学中非常重要的一个概念，对于数据分析和研究具有重要的指导意义。

希望大家能够通过不断练习和实践，掌握和运用好抽样分布的知识。

课后练习：一、单项选择：1、抽样误差是指：（）A.抽样推断中各种原因引起的全部误差B.工作性误差C.系统性代表误差D.随机误差 D2、重复抽样的抽样误差（）A.大于不重复抽样的抽样误差B.小于不重复抽样的抽样误差C.等于不重复抽样的抽样误差D.不一定 A3、在简单重复抽样下，若总体标准差不变，要使抽样平均误差变为原来的一半，则样本单位数必须（）A.扩大为原来的2倍B.减少为原来的一半C.扩大为原来的4倍D.减少为原来的四分之一 C4、在抽样之前对每一个单位先进行编号，然后使用随机数字表抽取样本单位，这种方式是（）A.等距抽样B.分层抽样C.简单随机抽样D.整群抽样 C5、一个连续性生产的工厂，为检验产品的质量，在一天中每隔1小时取5分钟的产品做全部检验，这是（）A.等距抽样B.分层抽样C.整群抽样D.简单随机抽样 C6、某工厂连续生产，为检验产品质量，在一天中每隔半小时取一件产品做检验，这是（）A.简单随机抽样B.整群抽样C.机械抽样D.类型抽样 C7、为了了解某工厂职工家庭收支情况，按该厂职工名册依次每50人抽取1人，对其家庭进行调查，这种调查属于（）A.简单随机抽样B.等距抽样C.类型抽样D.整群抽样 B8、抽样平均误差的实质是（）A. 总体标准差B. 抽样总体的标准差C. 抽样误差的标准差D. 抽样平均数的标准差 D9、为调查某消费群体的消费习惯，将消费者按受教育层次分类后，再确定比例抽取样本，此抽样方法属于（）A. 纯随机抽样B. 分层抽样C. 机械抽样D. 整群抽样 B10. 抽样调查必须遵循的基本原则是（）A. 灵活性原则B. 准确性原则C. 随机原则D. 可靠性原则 C11. 抽样误差是（）A. 代表性误差B. 登记性误差C. 系统性误差D. 随机误差 D12. 抽样平均误差和极限误差的关系是（）A. 抽样平均误差小于极限误差B．抽样平均误差大于极限误差C. 抽样平均误差等于极限误差D. 抽样平均误差可能大于、等于或小于极限误差 D13. 在其他条件不变的情况下，如果允许误差缩小为原来的1/2，则样本容量（）A. 扩大为原来的4倍B. 每个大为原来的2倍C. 缩小为原来的1/4倍D. 缩小为原来的1/2倍 A14. 一般来说, 在抽样组织形式中，抽样误差较大的是（）A. 简单抽样B. 分层抽样C. 整群抽样D. 等距抽样 C15. 根据抽样的资料, 一年级优秀生比重为10％, 二年级为20％，在人数相等时，优秀生比重的抽样误差（）A. 一年级较大B. 二年级较大C．相同 D. 无法判断16. 根据重复抽样的资料, 甲单位工人工资方差为25，乙单位为100，乙单位人数比甲单位多3倍, 则抽样误差（）A. 甲单位较大B. 无法判断C．乙单位较大 D. 相同17. 最符合随机原则地抽样组织形式是（ ）A. 整群抽样B. 类型抽样C. 阶段抽样D. 简单随机抽样二、判断题1、 抽样调查必须遵循的原则是灵活性原则。

统计学习题(抽样分布、参数估计)练习题第1章绪论（略）第2章统计数据的描述2.1某家商场为了解前来该商场购物的顾客的学历分布情况，随机抽取了100名顾客。

其学历表示为：1.初中;2.高中/中专;3.大专;4.本科及以上学历。

调查结果如下：4222434414 2244432422 3121441424 2332134344 3312424324 2322212244 2123333334 2343313232 4313434214 2242334121（1）制作一张频数分布表。

（2）绘制一张条形图，反映学历分布。

2.2为了解某电信客户对该电信公司的服务的满意度情况，某调查公司分别对两个地区的电信用户在以下五个方面对受访用户的满意情况进行了问卷调查得到的数据如下（表中数据为平均满意度打分，从1分到10分满意度依次递增）：地区企业形象客户期望质量感知价值感知客户总体满意度A 8.269504 7.51773 9.2624117.9148948.411348B 7.447368 8.3684218.9736848.1052637.394737试用条形图反映将两地区的满意度情况。

2.3下面是一个班50个学生的经济学考试成绩：88569179699088718279 988534744810075956092 83646569996445766369 6874948167818453912484628183698429667594（1）对这50名学生的经济学考试成绩进行分组并将其整理成频数分布表，绘制直方图。

（2）用茎叶图将原始数据表现出来。

2.4如下数据反映的是某大学近视度数的情况，共120名受访同学，男女同学各60名。

男149 161761821310 80 951081414 0 144145151515161681882121 0 21211052121211116817521 0 356462121212121312121 0 2121212121375375383838 8 45566065120 30120 7521女120 3334537437538700 90700 60141516212121211517170 0 0 0 0 0 0 0 5 521 0 1752121214043451217517 8 181818518519195196202021 0 21212121212121333335 0 3636363840474865055（1）按近视度数分别对男女学生进行分组。

抽样分布与中心极限定理例题和知识点总结在统计学中，抽样分布和中心极限定理是非常重要的概念，它们为我们从样本数据推断总体特征提供了坚实的理论基础。

下面，让我们通过一些具体的例题来深入理解这两个重要的知识点。

一、抽样分布抽样分布是指从一个给定的总体中抽取一定容量的样本，由样本统计量所形成的概率分布。

常见的抽样分布有样本均值的抽样分布、样本比例的抽样分布等。

以样本均值的抽样分布为例，如果总体服从正态分布，那么无论样本容量大小，样本均值都服从正态分布。

如果总体不服从正态分布，当样本容量足够大（通常 n ≥ 30）时，根据中心极限定理，样本均值近似服从正态分布。

例题 1假设一个总体的均值为 50，标准差为 10。

从这个总体中抽取样本容量为 25 的简单随机样本，求样本均值的抽样分布的均值和标准差。

解析根据抽样分布的性质，样本均值的抽样分布的均值等于总体均值，即 50。

样本均值的抽样分布的标准差（也称为标准误差）等于总体标准差除以样本容量的平方根，即 10 ／√25 ＝ 2。

二、中心极限定理中心极限定理指出：从均值为μ、方差为σ² 的任意一个总体中抽取样本量为 n 的样本，当 n 充分大时，样本均值的抽样分布近似服从均值为μ、方差为σ² ／ n 的正态分布。

中心极限定理的重要意义在于，即使原始总体不是正态分布，只要样本量足够大，我们就可以利用正态分布的性质来进行统计推断。

例题 2某工厂生产的零件重量服从均值为 10 克、标准差为 2 克的分布。

现随机抽取 49 个零件，求这 49 个零件平均重量的抽样分布。

解析由于样本容量 n ＝ 49 较大，根据中心极限定理，样本均值的抽样分布近似服从正态分布。

均值为总体均值，即 10 克。

方差为总体方差除以样本容量，即 2²／ 49 ＝ 4 ／ 49 ，标准差为√（4 ／ 49) ＝ 2 ／ 7 克。

三、应用举例例题 3一家公司有 1000 名员工，他们的平均工资为 5000 元，标准差为1000 元。

《食品试验优化设计》习题集第一章绪论一、简答题1、什么是试验设计与统计分析？它在食品科学研究中有何作用？2、统计分析的两个特点是什么？3、食品试验设计与统计分析的主要内容、知识框架结构。

第二章统计资料的整理与分析一、名词解释总体个体样本样本容量随机样本参数统计量随机误差系统误差准确性精确性数量性状资料质量性状资料半定量（等级）资料计数资料计量资料全距（极差）组中值次数分布表次数分布图算术平均数无偏估计几何平均数中位数众数调和平均数标准差方差离均差的平方和（平方和）变异系数二、简答题1、如何提高试验的准确性与精确性？2、如何控制、降低随机误差，避免系统误差？3、资料可以分为哪几类？它们有何区别与联系？4、为什么要对资料进行整理？对于计量资料，整理的基本步骤怎样？5、在对计量资料进行整理时，为什么第一组的组中值以接近或等于资料中的最小值为好？6、统计表与统计图有何用途？常用统计图有哪些？常用统计表有哪些？列统计表、绘统计图时，应注意什么？7、统计中常用的平均数有几种？各在什么情况下应用？8、算术平均数有哪些基本性质？9、标准差有哪些特性？10、为什么变异系数要与平均数、标准差配合使用？三、计算对食品科学专业2004级1班10位同学的体重进行测定，测定结果见表1。

试求其平均数、方差、变异系数、标准差、极差、最大值、最小值等。

表1 10位学生的体重测定结果第三章 理论分布与抽样分布一、名词解释必然现象 随机现象 随机试验 随机事件 概率的统计定义 小概率原理 概率分布 随机变量 离散型随机变量 连续型随机变量 概率分布密度函数 正态分布 标准正态分布 标准正态变量（标准正态离差） 双侧概率（两尾概率） 单侧概率（一尾概率） 贝努利试验 二项分布 波松分布 返置抽样 不返置抽样 标准误 样本平均数的抽样总体 中心极限定理 t 分布 二、简答题1、事件的概率具有那些基本性质？2、离散型随机变量概率分布与连续型随机变量概率分布有何区别？3、正态分布的密度曲线有何特点?4、标准误与标准差有何联系与区别?5、样本平均数抽样总体与原始总体的两个参数间有何联系？6、t 分布与标准正态分布有何区别与联系？ 三、计算题1、已知随机变量u 服从N(0，1)，求P(u ＜-1.4)， P(u ≥1.49)， P （｜u ｜≥2.58）， P(-1.21≤u ＜0.45)，并作图示意。