有限元试卷11级 期末考试试卷

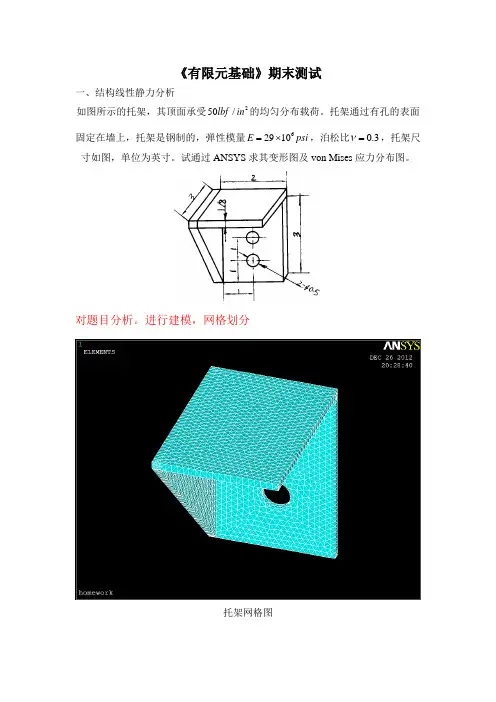
《有限元基础》期末测试一、结构线性静力分析如图所示的托架，其顶面承受2lbf in的均匀分布载荷。

托架通过有孔的表面50/ν=，托架尺固定在墙上，托架是钢制的，弹性模量6=⨯，泊松比0.3E psi2910寸如图，单位为英寸。

试通过ANSYS求其变形图及von Mises应力分布图。

对题目分析。

进行建模，网格划分托架网格图施加约束后，就可以对实体进行加载求解，托架变形图托架变形图输出的是原型托架和施加载荷后托架变形图的对比，虚线部分即为托架的原型，托架变形图可看出，由于载荷的作用，托架上面板明显变形了，变形最严重的就是红色部分，这是因为其离托板就远，没有任何物体与其分担载荷，故其较容易变形甚至折断。

这是我们在应用托架的时候应当注意的。

节点位移图托架von Mises 应力分布图上面两个图为托架的应力分布图，由图可看出主要在两孔处出现应力集中，也就是说这些地方所受的应力的最大的，比较容易出现裂痕。

我们在应用托架的时候，应当注意采取一些设施，以便减缓其应力集中。

特别是在施加载荷时，绝对不能够超过托架所能承受的极限，否则必将导致事故的发生。

二、动力分析如图1有一梁板结构，板的四角由四根梁固定支撑，板质量集中于中央。

梁板材料相关参数为弹性模量112210/E Nm =⨯，泊松比0.3ν=，密度337.810/kg m ρ=⨯。

板的厚度0.02t =，板长2000L mm =，宽1000B mm =，板的质量100M kg =。

梁长1000h mm =，截面面积为42210A m -=⨯，惯性矩为84210J m -=⨯，现在板的表面施加均匀压力载荷如图2。

试研究该梁板结构的瞬态动力响应。

图1图2建立有限元分析模型并附加动力节点146的位移时间历程结果三、非线性屈曲分析如图，一根长200L in =，截面高度0.5h in =，截面面积20.25A in =，惯性矩24/120.0052083J Ah in ==的细长杆受轴向载荷的作用，若沿X 方向取10个主自由度，求其屈曲模态。

有限元考试试题及答案一、简答题（5道，共计25分）。

1.有限单元位移法求解弹性力学问题的基本步骤有哪些？(5分）答：（1）选择适当的单元类型将弹性体离散化；（2）建立单元体的位移插值函数；（3）推导单元刚度矩阵;（4）将单元刚度矩阵组装成整体刚度矩阵；（5）代入边界条件和求解.2. 在划分网格数相同的情况下，为什么八节点四边形等参数单元精度大于四边形矩形单元？（5分）答：在对于曲线边界的边界单元，其边界为曲边,八节点四边形等参数单元边上三个节点所确定的抛物线来代替原来的曲线，显然拟合效果比四边形矩形单元的直边好。

3。

轴对称单元与平面单元有哪些区别？(5分）答：轴对称单元是三角形或四边形截面的空间的环形单元,平面单元是三角形或四边形平面单元;轴对称单元内任意一点有四个应变分量，平面单元内任意一点非零独立应变分量有三个.4。

有限元空间问题有哪些特征？（5分)答:（1）单元为块体形状。

常用单元：四面体单元、长方体单元、直边六面体单元、曲边六面体单元、轴对称单元。

（2）结点位移3个分量。

（3）基本方程比平面问题多。

3个平衡方程，6个几何方程，6个物理方程。

5.简述四节点四边形等参数单元的平面问题分析过程。

（5）分）答：（1）通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元，并选取单元的唯一模式；（2）通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式；（3）将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程，得到平面四节点等参数单元的应力矩阵；(4）用虚功原理求得单元刚度矩阵,最后用高斯积分法计算完成。

二、论述题（3道，共计30分)。

1. 简述四节点四边形等参数单元的平面问题分析过程.（10分)答:(1）通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元，并选取单元的唯一模式；（2）通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式；（3）将四节点四边形等参数单元的位移模式代入平面问题的几何方程，得到单元应变分量的计算式，再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵;(4）用虚功原理求得单元刚度矩阵，最后用高斯积分法计算完成。

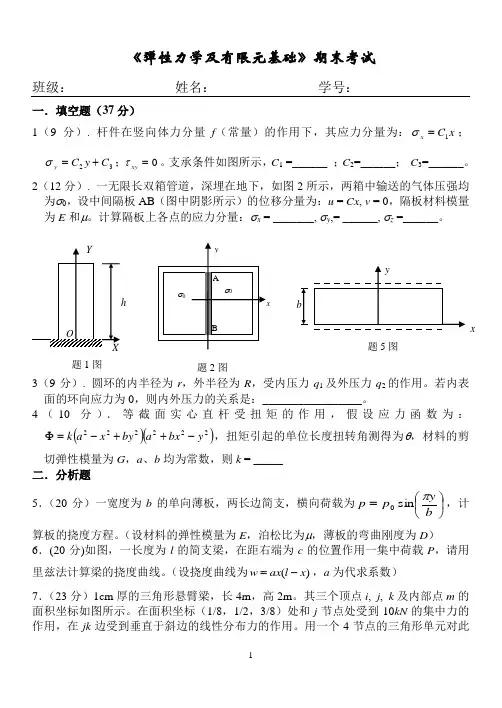
《弹性力学及有限元基础》期末考试班级： 姓名： 学号：一．填空题（37分）1（9分）. 杆件在竖向体力分量f （常量）的作用下，其应力分量为：x C x 1=σ；32C y C y +=σ；0=xy τ。

支承条件如图所示，C 1 =______ ；C 2=______； C 3=______。

2（12分）. 一无限长双箱管道，深埋在地下，如图2所示，两箱中输送的气体压强均为σ0，设中间隔板AB （图中阴影所示）的位移分量为：u = Cx , v = 0，隔板材料模量为E 和μ。

计算隔板上各点的应力分量：σx = _______, σy ,= ______, σz =______。

3（9分）. 圆环的内半径为r ，外半径为R ，受内压力q 1及外压力q 2的作用。

若内表面的环向应力为0，则内外压力的关系是：_________________。

4（10分）．等截面实心直杆受扭矩的作用，假设应力函数为：()()222222y bx a by x a k -++-=Φ，扭矩引起的单位长度扭转角测得为θ，材料的剪切弹性模量为G ，a 、b 均为常数，则k = _____ 二．分析题5．（20分）一宽度为b 的单向薄板，两长边简支，横向荷载为⎪⎭⎫⎝⎛=b y p p πsin 0，计算板的挠度方程。

（设材料的弹性模量为E ，泊松比为μ，薄板的弯曲刚度为D ）6．(20分)如图，一长度为l 的简支梁，在距右端为c 的位置作用一集中荷载P ，请用里兹法计算梁的挠度曲线。

（设挠度曲线为)(x l ax w -=，a 为代求系数）7．（23分）1cm 厚的三角形悬臂梁，长4m ，高2m 。

其三个顶点i , j , k 及内部点m 的面积坐标如图所示。

在面积坐标（1/8，1/2，3/8）处和j 节点处受到10kN 的集中力的作用，在jk 边受到垂直于斜边的线性分布力的作用。

用一个4节点的三角形单元对此题1图 题2图 x 题5图悬臂梁进行有限元分析，域内任一点的位移都表示成⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=+++=m m k k j j i i m m k k j j i i v N v N v N v N v u N u N u N u N u 。

e an dAl l t h i ng si nt he i rb ei n ga re go o2. 如图2所示，有一正方形薄板，沿对角承受压力作用，厚度t=1m ，载荷F=20KN/m ，设泊松比µ=0，材料的弹性模量为E ，试求它的应力分布。

（15分）图23. 图示结点三角形单元的124边作用有均布侧压力q ，单元厚度为t ，求单元的等效结点荷载。

图3图1一、简答题1. 答：1）合理安排单元网格的疏密分布2）为突出重要部位的单元二次划分3）划分单元的个数4）单元形状的合理性5）不同材料界面处及荷载突变点、支承点的单元划分6）曲线边界的处理，应尽可能减小几何误差7）充分利用结构及载荷的对称性，以减少计算量2. 答：形函数应满足的三个条件：a.必须能反映单元的刚体位移，就是位移模式应反映与本单元形变无关的由其它单元形变所引起的位移。

b.能反映单元的常量应变，所谓常量应变，就是与坐标位置无关，单元内所有点都具有相同的应变。

当单元尺寸取小时，则单元中各点的应变趋于相等，也就是单元的形变趋于均匀，因而常量应变就成为应变的主要部分。

c.尽可能反映位移连续性；尽可能反映单元之间位移的连续性，即相邻单元位移协调。

3. 答：含义：所谓的等参数单元，就是在确定单元形状的插值函数和确定单元位移场的插值函数中采用了完全相同的形函数。

意义：构造出一些曲边地高精度单元，以便在给定地精度下，用数目较少地单元，解决工程实际地具体问题。

4. 答：有限单元法是基于变分原理的里兹（Ritz）法的另一种形式，从而使里兹法分析的所有理论基础都适用子有限单元法，确认了有限单元法是处理连续介质问题的一种普遍方法．利用变分原理建立有限元方程和经典里兹法的主要区别是有限单元法假设的近似函数不是在全求解域而是在单元上规定的，面且事先不要求满足任何边界条件，因此它可以用来处理很复杂的连续介质问题。

有nl⎥⎦⎤⎢⎣⎡5.0025.025.011212－－－＝＝E k k ⎥⎦⎤⎢⎣⎡5.0025.0011313－＝＝E k k ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡5.125.025.05.125.0005.05.00025.075.025.025.075.032222212222E E E E k k k k ＋＝＋＋＝⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---5.025.025.0125.025.005.025.0025.05.032312323E E E k k k ＝＋＝⎥⎦⎤⎢⎣⎡---5.0025.025.022424E k k ＝＝⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡025.025.00025.0000025.0032522525E E E k k k ＝＋＝⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡5.125.025.05.15.00025.075.025.025.075.025.0005.043333313333E E E E k k k k ＝＋＋＝⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---125.025.05.05.0025.025.05.025.0025.043533535E E E k k k ＝＋＝⎥⎦⎤⎢⎣⎡0025.0043636E k k ＝＝⎥⎦⎤⎢⎣⎡75.025.025.075.024444E k k ＝＝⎥⎦⎤⎢⎣⎡---25.0025.05.024545E k k ＝＝ ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡5.125.025.05.175.025.025.075.05.00025.025.0005.045535525555E E E E k k k k ＝＋＋＝⎥⎦⎤⎢⎣⎡---25.0025.05.045656E k k ＝＝⎥⎦⎤⎢⎣⎡25.0005.046666E k k ＝＝把上面计算出的，…，对号入座放到总刚矩阵中去，于是得到11k 66k []K的具体表达式。

有限元期末考试题及答案一、选择题1. 有限元方法是一种数值分析方法，主要用于求解什么类型的数学问题？A. 线性代数方程B. 微分方程C. 积分方程D. 代数方程答案：B2. 在有限元分析中，单元的划分是基于什么原则？A. 单元数量B. 单元形状C. 问题域的几何特性D. 计算资源答案：C3. 下列哪项不是有限元分析中常用的单元类型？A. 三角形单元B. 四边形单元C. 六面体单元D. 圆形单元答案：D二、填空题4. 有限元方法中，______是指将连续的物理域离散成有限数量的小区域，这些小区域称为单元。

答案：离散化5. 在进行有限元分析时，通常需要定义材料属性，包括______、密度和弹性模量等。

答案：泊松比三、简答题6. 简述有限元方法的基本步骤。

答案：有限元方法的基本步骤包括：定义问题域、离散化问题域、选择单元类型、定义材料属性、构建全局刚度矩阵、施加边界条件、求解线性代数方程、提取结果。

7. 解释什么是有限元分析中的收敛性，并说明影响收敛性的因素。

答案：收敛性是指随着单元数量的增加，有限元分析结果逐渐接近真实解的性质。

影响收敛性的因素包括单元的类型、形状、大小以及网格的布局等。

四、计算题8. 假设有一个长度为2米的杆，两端固定，中间施加了一个向下的力F=1000N。

如果杆的材料是钢，其弹性模量E=210 GPa，泊松比ν=0.3，请计算杆的弯曲位移。

答案：首先，根据Euler-Bernoulli梁理论，可以写出弯曲位移的方程为：\[ w(x) = \frac{F}{384EI} L^3 \]其中，\( w(x) \) 是位移，\( F \) 是施加的力，\( L \) 是杆的长度，\( E \) 是弹性模量，\( I \) 是截面惯性矩。

对于一个矩形截面，\( I \) 可以表示为：\[ I = \frac{bh^3}{12} \]假设杆的截面宽度为b，高度为h，代入上述公式，可以计算出位移。

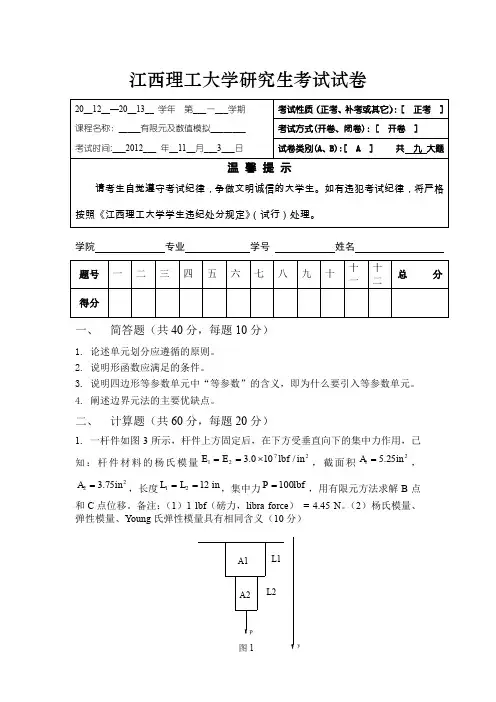
江西理工大学研究生考试试卷一、 简答题（共40分，每题10分）1. 论述单元划分应遵循的原则。

2. 说明形函数应满足的条件。

3. 说明四边形等参数单元中“等参数”的含义，即为什么要引入等参数单元。

4. 阐述边界元法的主要优缺点。

二、 计算题（共60分，每题20分）1. 一杆件如图3所示，杆件上方固定后，在下方受垂直向下的集中力作用，已知：杆件材料的杨氏模量2721/100.3in lbf E E ⨯==，截面积2125.5in A =，2275.3in A =，长度in L L 1221==，集中力lbf P 100=，用有限元方法求解B 点和C 点位移。

备注：（1）1 lbf （磅力，libra force ） = 4.45 N 。

（2）杨氏模量、弹性模量、Young 氏弹性模量具有相同含义（10分）20__12__—20__13__ 学年 第___一___学期 课程名称：_____有限元及数值模拟________ 考试时间:___2012___ 年__11__月___3___日考试性质（正考、补考或其它）：[ 正考 ] 考试方式(开卷、闭卷)：[ 开卷 ] 试卷类别(A 、B):[ A ] 共 九 大题温 馨 提 示请考生自觉遵守考试纪律，争做文明诚信的大学生。

如有违犯考试纪律，将严格按照《江西理工大学学生违纪处分规定》（试行）处理。

学院 专业 学号 姓名 题号 一二三四五六七八九十十一十二总 分得分pyA1A2L1L2图12. 如图2所示，有一正方形薄板，沿对角承受压力作用，厚度t=1m，载荷F=20KN/m，设泊松比µ=0，材料的弹性模量为E，试求它的应力分布。

（15分）图23. 图示结点三角形单元的124边作用有均布侧压力q，单元厚度为t，求单元的等效结点荷载。

图3一、简答题1. 答：1）合理安排单元网格的疏密分布2）为突出重要部位的单元二次划分3）划分单元的个数4）单元形状的合理性5）不同材料界面处及荷载突变点、支承点的单元划分6）曲线边界的处理，应尽可能减小几何误差7）充分利用结构及载荷的对称性，以减少计算量2. 答：形函数应满足的三个条件：a.必须能反映单元的刚体位移，就是位移模式应反映与本单元形变无关的由其它单元形变所引起的位移。

一、填空（共10个空，每空2分，共20分）11、有限元法是近似求解连续场问题的数值方法。

2、有限元法将连续的求解域离散，得到有限个单元，单元和单元之间用节点相连。

3、直梁在外力作用下，横截面上的内力有剪力和弯矩两个。

4、平面刚架结构在外力作用下，横截面上的内力有剪力、弯矩和轴力。

5、进行直梁的有限元分析，梁单元上每个节点的节点位移为挠度和转角。

、平面刚架结构中，已知单元e的坐标变换矩阵[T e]及局部坐标系x´O´y ´下的单元刚度矩阵[K´]e，则单元在整体坐标系xOy下的单元刚度矩阵为 P31 。

7、平面刚架结构中，已知单元e的坐标变换矩阵[T e]及整体坐标系xOy下的单元节点力矩阵{p}e，则单元在局部坐标系x´O´y´下的单元节点力矩阵为 P30 。

8、在弹性范围和小变形的前提下，节点力和节点位移之间是线性系。

9、弹性力学问题的方程个数有 15个，未知量个数有 15 个。

10、弹性力学平面问题的方程个数有个，未知量个数有个。

11、把经过物体内任意一点各个截面的应力状况叫做一点的应力状态。

12、形函数在单元节点上的值，具有本点为 1 、它点为零的性质，并且在三角形单元的任一节点上，三个形函数之和为 1 。

13、形函数是定义于元内部坐标连续函数。

14、在进行节点编号时，要尽量使同一单元的相邻节点的号码差尽可能小，以便最大限度地缩小刚度矩阵带宽，节省存储、提高计算效率。

15、三角形单元的位移模式为。

16、矩形单元的位移模式为。

17、在选择多项式位移模式的阶次时，要求所选的位移模式应该与局部坐标系的方位无关，这一性质称为几何各向同性。

18、单元刚度矩阵描述了节点力和节点位移之间的关系。

19、在选择多项式作为单元的位移模式时，多项式阶次的确定，要考虑解答的收敛性，即要满足单元的完备性和协调性的要求。

20、三节点三角形单元内的应力和应变是常数，四节点矩形单元内的应力和应变是线性变化的。

有限元期末考试试题有限元期末考试试题有限元分析是一种数值计算方法，广泛应用于工程领域中的结构分析、热传导、流体力学等问题。

作为有限元分析的基础，期末考试试题将涵盖有限元的基本原理、方法和应用。

本文将以期末考试试题为主线，深入探讨有限元分析的相关知识。

一、选择题1. 有限元分析的基本思想是什么？A. 将连续体划分为有限个单元B. 将连续体划分为无限个单元C. 将连续体划分为两个单元D. 将连续体划分为三个单元2. 有限元分析中，单元是指什么？A. 物理实体B. 离散区域C. 数学模型D. 计算节点3. 有限元分析的目的是什么？A. 求解连续体的精确解B. 求解连续体的近似解C. 求解连续体的数值解D. 求解连续体的解析解二、填空题1. 有限元分析中，单元的划分应满足什么条件？单元的划分应满足连续性和完整性的条件。

2. 有限元分析中，刚度矩阵的维度是多少？刚度矩阵的维度与单元自由度的个数相关。

三、简答题1. 有限元分析的步骤是什么？有限元分析的步骤包括建立有限元模型、确定边界条件、求解方程、后处理结果。

2. 有限元分析中，如何选择适当的单元类型？选择适当的单元类型需要考虑问题的特点、几何形状和边界条件等因素。

四、计算题1. 对于一个矩形截面的梁，长度为L，宽度为b，高度为h，杨氏模量为E，应力为σ，根据弹性力学理论，梁的弯曲刚度EI与梁的几何尺寸和材料性质有关。

请推导出梁的弯曲刚度的表达式。

解：根据弹性力学理论，梁的弯曲刚度EI与梁的几何尺寸和材料性质有关。

对于矩形截面的梁，弯曲刚度的表达式为：EI = (E * b * h^3) / 12其中，E为杨氏模量，b为梁的宽度，h为梁的高度。

通过以上计算题，我们可以看出有限元分析的应用范围广泛，可以用于解决各种工程问题。

通过对试题的分析和解答，我们对有限元分析的基本原理、方法和应用有了更深入的了解。

总结：本文以有限元期末考试试题为主线，辅以相关知识的解析和讨论，深入探讨了有限元分析的基本原理、方法和应用。

有限元期末考试试题一、选择题（每题2分，共20分）1. 在有限元分析中，单元的刚度矩阵通常通过以下哪种方式计算？A. 直接积分B. 线性插值C. 经验公式D. 试验数据2. 以下哪个选项不是有限元分析中的边界条件？A. 固定边界B. 自由边界C. 周期边界D. 热边界3. 有限元方法中，节点的自由度数量取决于什么？A. 单元类型B. 材料属性C. 几何形状D. 载荷类型4. 在进行热传导问题的有限元分析时，以下哪个方程是正确的？A. 牛顿第二定律B. 热平衡方程C. 动量守恒定律D. 质量守恒定律5. 以下哪个不是有限元分析中常用的单元类型？A. 四节点矩形单元B. 三角形单元C. 六面体单元D. 八节点等参单元二、简答题（每题10分，共30分）1. 简述有限元方法的基本步骤，并举例说明其在工程中的应用。

2. 解释什么是等参单元，并说明它在有限元分析中的重要性。

3. 描述在有限元分析中如何处理非线性问题，并给出一个具体的例子。

三、计算题（每题25分，共50分）1. 给定一个由四个节点构成的二维平面应力问题，节点坐标如下：节点1: (0, 0)节点2: (1, 0)节点3: (1, 1)节点4: (0, 1)已知材料的弹性模量E=210 GPa，泊松比ν=0.3。

若在节点1和节点3上施加单位力（1 N），试求该结构的位移场和应力场。

2. 考虑一个长方体热传导问题，其尺寸为Lx=0.5m，Ly=0.3m，Lz=0.2m。

该长方体的热导率为k=50 W/m·K，初始温度分布为T(x, y, z, 0) = 300 K。

若在x=0和x=Lx的面上施加恒定的边界温度T=400 K，试求经过时间t=10s后长方体内部的温度分布。

四、论述题（共30分）1. 论述有限元分析在结构优化设计中的作用，并讨论其在现代工程设计中的重要性。

有限单元法期末考试试题# 有限单元法期末考试试题## 一、选择题（每题2分，共20分）1. 有限元法中，单元划分的目的是：A. 简化问题B. 增加计算量C. 便于数值计算D. 增加模型复杂度2. 在有限元分析中，以下哪个不是单元的自由度：A. 位移B. 速度C. 转动D. 压力3. 下列哪一项不是有限元法的基本假设：A. 连续性假设B. 线性假设C. 均匀性假设D. 非均匀性假设4. 有限元法中，位移函数的选择应满足：A. 物理意义B. 几何意义C. 边界条件D. 所有上述条件5. 在有限元分析中，以下哪个不是常见的数值积分方法：A. 单点积分B. 高斯积分C. 牛顿-科特斯积分D. 梯形积分## 二、简答题（每题10分，共30分）1. 简述有限元法的基本原理及其在工程中的应用。

2. 解释什么是高斯积分，它在有限元分析中的作用是什么？3. 描述有限元分析中单元刚度矩阵的组装过程。

## 三、计算题（每题25分，共50分）1. 假设有一个二维平面应力问题，其材料的杨氏模量为210 GPa，泊松比为0.3。

给定一个矩形板，尺寸为2m x 1m，四边固定。

在板的中心施加一个向下的集中力P=10 kN。

使用有限元法求解板的中心位移。

(a) 描述问题并建立控制方程。

(b) 选择合适的单元类型并进行网格划分。

(c) 写出单元刚度矩阵的一般形式。

(d) 组装整体刚度矩阵。

(e) 应用边界条件和载荷向量，求解位移。

2. 考虑一个简单的桁架结构，由三个杆件组成，形成一个等腰三角形。

已知杆件的材料属性相同，杨氏模量E=200 GPa，截面积A=0.01 m²。

桁架的底边长度为2m，高为1m。

在顶点施加一个向下的集中力P=10 kN。

使用有限元法计算每个杆件的轴向应力。

(a) 画出桁架结构的示意图。

(b) 确定每个杆件的自由度。

(c) 写出杆件的局部刚度矩阵。

(d) 组装整体刚度矩阵。

(e) 应用载荷向量，求解每个杆件的轴向应力。

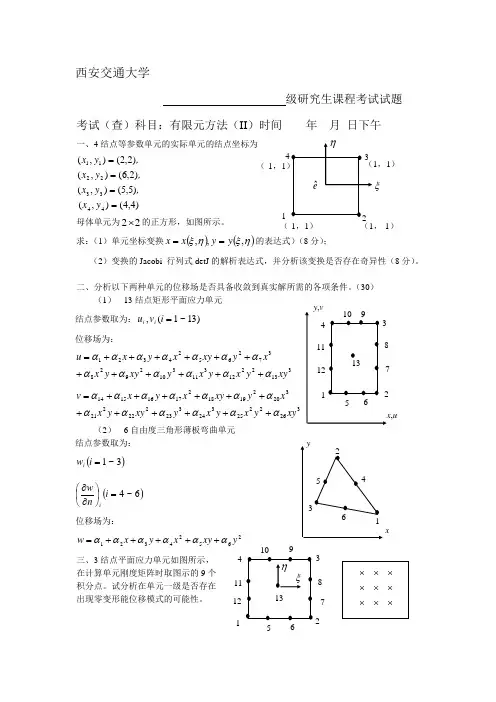
西安交通大学级研究生课程考试试题考试（查）科目：有限元方法（II ）时间 年 月 日下午一、4)4,4(),()5,5(),()2,6(),()2,2(),(44332211====y x ，y x ，y x ，　y x母体单元为22⨯的正方形，如图所示。

求：（1）单元坐标变换()(ξηξ,,,y y x x == （2）变换的Jacobi 行列式detJ 的解析表达式，并分析该变换是否存在奇异性（8分）。

二、分析以下两种单元的位移场是否具备收敛到真实解所需的各项条件。

（30）（1） 13结点矩形平面应力单元结点参数取为：)13~1(,=i v u i i 位移场为：313221231131029283726524321xyy x y x y xy y x x y xy x y x u ααααααααααααα++++++++++++=326222532432322222132021918217161514xyy x y x y xy y x x y xy x y x v ααααααααααααα++++++++++++=（2） 6自由度三角形薄板弯曲单元 结点参数取为：()3~1=i w i()6~4=⎪⎭⎫ ⎝⎛∂∂i n w i位移场为：26524321y xy x y x w αααααα+++++=三、3结点平面应力单元如图所示， 在计算单元刚度矩阵时取图示的9个 积分点。

试分析在单元一级是否存在 出现零变形能位移模式的可能性。

,ux78 10911 12 1234 56四、图示8结点平面应力单元厚度为t ， 沿结点481－－所在边作用图示分布载 荷，最大压强为q 。

求与上述载荷对应的结点8处的等效结点力的大小，并图 示其方向（16分）。

五、图示二维问题，在结点A 、B 与C 、D之间为光滑接触。

试用罚函数法实现对此约束关系的描述，（1）写出对总体坐标系的约束关系式（5分），（2）若该问题的能量泛函为请写出相应的“修正泛函”的表达式（5分）。

有限元考试试题一、选择题（每题5分，共30分）1、在有限元分析中，我们通常使用什么方法来求解偏微分方程？A.积分法B.差分法C.有限差分法D.有限元法2、下列哪个不是有限元法的优点？A.可以处理复杂几何形状B.可以处理非线性问题C.可以处理大规模问题D.可以处理不稳定问题3、在有限元分析中，我们通常将连续的物理场离散化为一系列的什么？A.有限个点B.无限个小段C.有限个小段D.无限个点4、下列哪个不是有限元分析的基本步骤？A.划分网格B.建立模型C.执行计算D.编写代码5、在有限元分析中，我们通常使用什么来描述物理场的性质？A.偏微分方程B.泛函方程C.常微分方程D.边界条件6、下列哪个不是有限元分析的应用领域？A.结构分析B.流体动力学C.电磁学D.社会科学二、填空题（每题10分，共40分）7、______是一种将连续的物理场离散化为一系列有限个点的方法，是有限元分析的基础。

8、在有限元分析中，我们通常使用______来对物理场进行离散化处理。

9、______是一种求解偏微分方程的数值方法，广泛应用于有限元分析。

10、在有限元分析中，我们通常使用______来描述物理场的性质。

三、解答题（每题20分，共60分）11、请简述有限元分析的基本步骤，并解释其在结构分析中的应用。

12、请说明在有限元分析中，如何处理边界条件，并举例说明。

13、请简述有限元分析的优点和局限性。

有限空间培训考试试题及答案一、选择题1、在有限空间内，以下哪个行为是危险的？A.带压操作B.穿著宽松衣服C.使用电动工具D.所有上述答案：D.所有上述。

在有限空间内，带压操作、穿著宽松衣服和使用电动工具都是危险的。

2、当进入有限空间前，应该进行哪项操作？A.排放内部气体B.测试内部气体C.对内部进行冲洗D.所有上述答案：D.所有上述。

在进入有限空间前，应该进行排放内部气体、测试内部气体并对内部进行冲洗。

3、有限空间内的危险因素不包括以下哪个？A.缺氧B.有毒气体C.电击D.所有上述答案：C.电击。

湖南大学研究生课程考试命题专用纸考试科目：有限单元法专业年级：土木工程2011级考试形式：开卷考试A 考试时间：120分钟………………………………………………………………………………………………………………………注：答题（包括填空题）必须答在专用答卷纸上，否则无效。

统一在答卷纸右上角写上学号，姓名。

一、填空题（共30分，每个空2分）4铰接在中柱左侧，结点9受水平链杆约束。

若按图示结点顺序进行自由度编号，每个结点考虑三个位移分量，按水平、竖向、转角位移顺序排列。

用先处理法形成的总刚度矩阵阶数为(1) 阶，若采用等半带储存总刚度矩阵，其半带宽是(2) 。

设所有柱子的高度均为h，所有梁的跨度均为l，梁、柱单元的截面积均为A，弹性模量均为E，抗弯刚度均为EI，拉压刚度均为EA，则按先处理法形成的总刚度矩阵中，其元素K17,17为(3) ，K19,19为(4) ，K17,7为(5) 。

若不考虑梁的轴向变形，用先处理法形成的总刚度矩阵阶数为(6) 阶，若采用等半带储存总刚度矩阵，其半带宽是(7) 阶，总刚中元素K6,6为(8) ，K8,8为(9) ，K14,17为(10) 。

2．三结点三角形单元的形函数在其形心处的值是(11) 。

3．一个有限元解的必要条件是要求该单元的位移函数必须能表示(12) 和常应变状态。

4．平面问题的有限元中，坐标（x, y）表达式的插值函数和位移场（u, v）表达式的插值函数采用同一函数的单元称为(13) 单元。

5．在用有限单元法求解动力问题时，通常把考虑质点惯性力运动的结点位移分量（自由度）称为(14) ，把与运动无关的结点位移分量称为(15) 。

二、采用先处理法，以结点分块的子块形式形成图2所示平面问题的结构总刚度矩阵[K]中的前6行（利用总刚对称性，可以只写出一半），三角形单元的结点编号（1，2，3…）和单元编号（①，②，③……）如图所示，要求在总刚度矩阵元素的右上角标示出单元号，可写成“②① 22K ”的形式。

有限元试题及答案一判断题（20分）（×）1. 节点的位置依赖于形态，而并不依赖于载荷的位置（√）2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元（×）3. 不能把梁单元、壳单元和实体单元混合在一起作成模型（√）4. 四边形的平面单元尽可能作成接近正方形形状的单元（×）5. 平面应变单元也好，平面应力单元也好，如果以单位厚来作模型化处理的话会得到一样的答案（×）6. 用有限元法不可以对运动的物体的结构进行静力分析（√）7. 一般应力变化大的地方单元尺寸要划的小才好（×）8. 所谓全约束只要将位移自由度约束住，而不必约束转动自由度（√）9. 同一载荷作用下的结构，所给材料的弹性模量越大则变形值越小（√）10一维变带宽存储通常比二维等带宽存储更节省存储量。

二、填空（20分）1．平面应力问题与薄板弯曲问题的弹性体几何形状都是薄板，但前者受力特点是：平行于板面且沿厚度均布载荷作用，变形发生在板面内；后者受力特点是：垂直于板面的力的作用，板将变成有弯有扭的曲面。

2．平面应力问题与平面应变问题都具有三个独立的应力分量：σx，σy，τxy ，三个独立的应变分量：εx，εy，γxy，但对应的弹性体几何形状前者为薄板，后者为长柱体。

3．位移模式需反映刚体位移，反映常变形，满足单元边界上位移连续。

4．单元刚度矩阵的特点有：对称性，奇异性，还可按节点分块。

5．轴对称问题单元形状为：三角形或四边形截面的空间环形单元，由于轴对称的特性，任意一点变形只发生在子午面上，因此可以作为二维问题处理。

6．等参数单元指的是：描述位移和描述坐标采用相同的形函数形式。

等参数单元优点是：可以采用高阶次位移模式，能够模拟复杂几何边界，方便单元刚度矩阵和等效节点载荷的积分运算。

7．有限单元法首先求出的解是节点位移，单元应力可由它求得，其计算公式为。

（用符号表示即可）8．一个空间块体单元的节点有 3 个节点位移： u，v，w 9．变形体基本变量有位移应变应力基本方程平衡方程物理方程几何方程 10.实现有限元分析标准化和规范化的载体就是单元三选择题（14分）1 等参变换是指单元坐标变换和函数插值采用__B___的结点和______的插值函数。