流体力学发展简史.

流体力学发展历程流体力学是研究流体的运动和力学性质的学科，其发展历程可以追溯到古代。

本文将从古代到现代，梳理流体力学的发展历程。

古代，人们对水的运动和性质有了初步的认识。

古希腊的亚里士多德提出了流体的连续性原理，他认为流体是连续不断的。

在古代中国，张衡发明了地动仪，通过水的流动来模拟地震，这也是古代流体力学的重要成果之一。

17世纪，随着科学革命的兴起，流体力学开始得到系统的发展。

英国科学家牛顿提出了流体的黏性理论，他认为流体的黏性是导致流体摩擦的原因。

此后，德国数学家伯努利提出了伯努利原理，揭示了流体运动中能量守恒的基本原理。

18世纪，瑞士数学家欧拉为流体力学奠定了坚实的理论基础。

他提出了欧拉方程，描述了理想流体的运动规律。

欧拉方程是流体力学的基本方程之一，对后来的研究具有重要影响。

19世纪，流体力学的研究逐渐扩展到气体和空气动力学领域。

德国物理学家克劳修斯提出了克劳修斯方程，描述了气体的运动规律。

克劳修斯方程是流体力学中重要的方程之一，被广泛应用于航空航天领域。

20世纪初，爱尔兰数学家雷诺为流体力学的发展做出了重要贡献。

他提出了雷诺数，用于描述流体流动的稳定性。

雷诺数在流体力学中具有重要的应用价值，被广泛用于流体力学实验和数值模拟中。

20世纪中叶以后，随着计算机技术和数值模拟方法的发展，流体力学得到了广泛的应用和研究。

计算流体力学（CFD）成为流体力学研究的重要工具之一，可以通过数值方法模拟和预测流体的运动和性质。

近年来，随着科学技术的不断进步，流体力学的研究也在不断深入。

人们开始研究微观尺度下的流体力学问题，如纳米流体力学和微流体力学。

此外，流体力学在生物医学领域的应用也越来越广泛，如血液流动、呼吸系统等。

总结起来，流体力学的发展历程可以追溯到古代，经过了古代的初步认识、17世纪的理论建立、18世纪的基础奠定、19世纪的扩展应用以及20世纪的数值模拟和应用拓展。

随着科学技术的发展，流体力学的研究也在不断深入，为我们认识和应用流体提供了重要的理论和方法。

计算流体力学的发展历程与未来前景计算流体力学（Computational Fluid Dynamics, CFD）是运用数值方法对流体力学问题进行模拟和分析的学科，它结合了流体力学、数值计算和计算机学科的知识。

在过去的几十年中，计算流体力学在科学研究、工程设计和工业应用中起到了重要的作用。

本文将介绍计算流体力学的发展历程，并展望其未来的前景。

计算流体力学的发展历程源远流长。

早在20世纪40年代，人们开始使用数值方法来解决流体力学问题，并发展了有限差分法等基本方法。

然而，当时的计算能力非常有限，只能处理简单的二维问题。

到了20世纪60年代，随着计算机的发展，计算流体力学的发展进入了快速发展期。

有限元法的引入使得计算流体力学能够处理复杂的流动问题，并为工业应用提供了新的解决方案。

此后，随着计算能力的不断提升和计算方法的改进，计算流体力学的应用范围和精度不断提高。

进入21世纪以来，计算流体力学的发展进入了一个全新的阶段。

首先，计算能力的大幅提升使得可以模拟和研究更加复杂的流动问题，如湍流、多相流和自由面问题等。

借助高性能计算技术和并行计算方法，计算流体力学已经成为一种强大的工具，可以模拟包括飞机、汽车、火箭等工程领域中的复杂流动。

其次，计算流体力学与其他学科的交叉应用也日益增多，如结构力学、热传导、化学反应等。

这种多学科的融合为解决复杂多物理场耦合问题提供了新的思路和方法。

未来，计算流体力学有着广阔的发展前景。

随着计算能力的继续提升和计算方法的不断改进，计算流体力学可以更加精确地预测流动的行为，并提供更准确的工程设计依据。

例如，在航空航天领域，计算流体力学可以用于优化飞机的气动外形和减少燃料消耗，提高飞行效率和降低排放。

在能源领域，计算流体力学可以用于优化燃烧过程和提高能源转化效率，减少环境污染。

在环境保护领域，计算流体力学可以用于模拟河流、海洋和大气中的环境问题，帮助解决河流污染、海洋污染和空气污染等问题。

流体力学发展流体力学是物理学中一门重要的分支，它是研究物质运动的一门科学，其研究的内容覆盖水流、气体运动和物质的运动规律性，它可以描述物体在流动状态下的运动强度和变形程度。

流体力学的发展历程可以追溯到古埃及，其伟大的研究成果和发明，为了后来的流体力学技术奠定了基础，为今天的社会乃至世界带来了极大的科学发展。

18世纪以后，由于科学技术的发展，流体力学发展变得越来越快，专业研究者也逐步增多。

1851年，英国数学家贝克发表了他著名的《流体力学定律》，他的定律解释了适用于实际流体的速度场的物理性质，这一定律为流体力学提供了一个强有力的理论和技术支持。

1855年，德国物理学家埃里斯布劳恩定义了液体黏度，提出了经典的压力梯度理论，从而推动了流体力学的发展。

随后，由于科学技术的进步，市场的变革，经济的发展，社会的进化，流体力学的运用也更加广泛。

20世纪50年代中期，美国数学家约翰卢瑟福提出了有关流体力学的电磁学的理论；20世纪60年代，布鲁克曼教授提出了有关流体力学的“分块”理论，解决了瞬态流动情况和复杂流体系统问题；20世纪90年代，瑞士数学家多贝尔曼提出了贝尔曼方法，改善了流体力学计算技术，为大体积流体系统问题提供了一种新的解决方案。

今天，流体力学在社会科学中被广泛应用，它主要应用于航空航天、飞行技术、水力发电、流体机械、生物系统、热力学、农业灌溉，以及石油工程、生态学、环境工程等多个领域。

因此，流体力学发挥着越来越重要的作用，它的运用范围也越来越广泛。

总之，流体力学发展经历了众多伟大的科学家和发明家的不断努力，从古代皇家农场，到18世纪，再到20世纪，流体力学已经走向现代化，并且为各个领域带来了极大的发展和进步。

流体力学发展的过程，也提醒我们要以开放的心态勇敢探索新的技术，努力提升自己的能力。

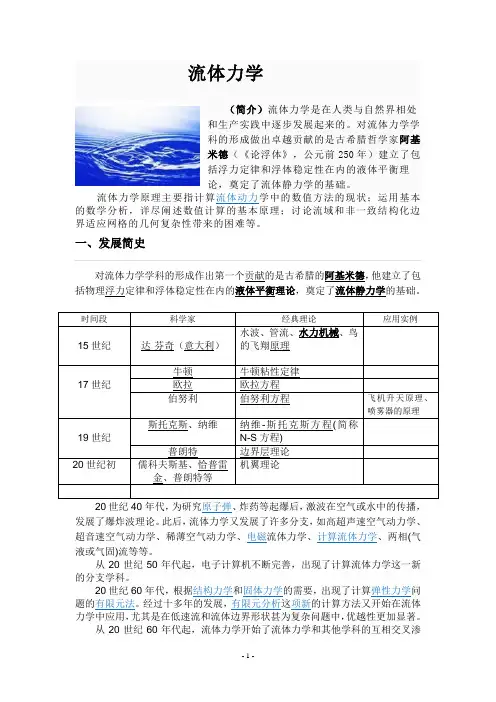
流体力学（简介）流体力学是在人类与自然界相处和生产实践中逐步发展起来的。

对流体力学学科的形成做出卓越贡献的是古希腊哲学家阿基米德（《论浮体》，公元前250年）建立了包括浮力定律和浮体稳定性在内的液体平衡理论，奠定了流体静力学的基础。

流体力学原理主要指计算流体动力学中的数值方法的现状；运用基本的数学分析，详尽阐述数值计算的基本原理；讨论流域和非一致结构化边界适应网格的几何复杂性带来的困难等。

一、发展简史各物理量关系构成牛顿内摩擦定律,τ=μ*du/dy动压和总压。

显然，流动中速度增大，压强就减小；速度减小，压强就增大；速度降为零，压强就达到最大(理论上应等于总压)。

飞机机翼产生举力，就在于下翼面速度低而压强大，上翼面速度高而压强小，因而合力向上。

据此方程，测量流体的总压、静压即可求得速度，成为皮托管测速的原理。

在无旋流动中，也可利用无旋条件积分欧拉方程而得到相同的结果但涵义不同，此时公式中的常量在全流场不变，表示各流线上流体有相同的总能量，方程适用于全流场任意两点之间。

在粘性流动中，粘性摩擦力消耗机械能而产生热，机械能不守恒，推广使用伯努利方程时，应加进机械能损失项[1]。

图为验证伯努利方程的空气动力实验。

补充：p1+1/2ρv1^2+ρgh1=p2+1/2ρv2^2+ρgh2（1）p+ρgh+(1/2)*ρv^2=常量（2）均为伯努利方程其中ρv^2/2项与流速有关，称为动压强，而p和ρgh称为静压强。

伯努利方程揭示流体在重力场中流动时的能量守恒。

由伯努利方程可以看出，流速高处压力低，流速低处压力高。

后人在此基础上又导出适用于可压缩流体的N-S方程。

N-S方程反映了粘性流体（又称真实流体）流动的基本力学规律，在流体力学中有十分重要的意义。

它是一个非线性偏微分方程，求解非常困难和复杂，目前只有在某些十分简单的流动问题上能求得精确解；但在有些情况下，可以简化方程而得到近似解。

例如当雷诺数Re1时，绕流物体边界层外，粘性力远小于惯性力，方程中粘性项可以忽略，N-S方程简化为理想流动中的欧拉方程（=－Ñp+ρF）；而在边界层内，N-S方程又可简化为边界层方程，等等。

流体力学的发展现状流体力学是研究流体运动和力学特性的学科，涵盖了广泛的应用领域，包括工程、地球科学、生物医学和环境科学等。

本文将详细介绍流体力学的发展现状，并探讨其在不同领域的应用。

一、流体力学的概述流体力学是研究流体运动和力学特性的学科，主要研究流体的力学性质、流动规律和流体与固体的相互作用等问题。

它可以分为两个主要分支：流体静力学和流体动力学。

流体静力学研究静止流体的力学性质，而流体动力学研究流体在外力作用下的运动规律。

二、流体力学的发展历程流体力学的发展可以追溯到古代，早在公元前300年，古希腊的亚历山大港就有人开始研究流体力学。

在17世纪，伽利略和牛顿等科学家对流体的运动进行了初步的研究。

到了18世纪，伯努利和欧拉等学者提出了一系列的流体力学理论和方程，为流体力学的发展奠定了基础。

20世纪，随着计算机技术的发展，流体力学得到了极大的推动，数值摹拟和实验研究成为流体力学研究的重要手段。

三、流体力学的应用领域1. 工程领域：流体力学在工程领域的应用非常广泛。

例如，飞机的气动设计、汽车的空气动力学性能、船舶的流体力学特性等都需要流体力学的研究。

此外，流体力学还应用于管道输送、水力发电等工程问题的分析和设计。

2. 地球科学：流体力学在地球科学中的应用主要体现在大气科学和海洋科学领域。

通过对大气和海洋中的流体运动进行研究，可以预测天气、气候变化以及海洋循环等现象，对于环境保护和资源开辟具有重要意义。

3. 生物医学：流体力学在生物医学领域的应用主要涉及血液流动、呼吸系统和心血管系统等方面。

通过研究流体在生物体内的运动规律，可以匡助医生诊断疾病、设计医疗器械以及进行药物输送等。

4. 环境科学：流体力学在环境科学中的应用主要涉及大气污染和水污染等问题。

通过研究流体的运动和传输规律，可以预测和摹拟污染物在大气和水体中的扩散过程，为环境保护提供科学依据。

四、流体力学的研究方法1. 数值摹拟：数值摹拟是流体力学研究中最常用的方法之一。

第一章绪论本章主要阐述了流体力学的概念与发展简史；流体力学的概述与应用；流体力学课程的性质、目的、基本要求；流体力学的研究方法及流体的主要物理性质。

流体的连续介质模型是流体力学的基础，在此假设的基础上引出了理想流体与实际流体、可压缩流体与不可压缩流体、牛顿流体与非牛顿流体概念。

第一节流体力学的概念与发展简史一、流体力学概念流体力学是力学的一个独立分支，是一门研究流体的平衡和流体机械运动规律及其实际应用的技术科学。

流体力学所研究的基本规律，有两大组成部分。

一是关于流体平衡的规律，它研究流体处于静止（或相对平衡）状态时，作用于流体上的各种力之间的关系，这一部分称为流体静力学；二是关于流体运动的规律，它研究流体在运动状态时，作用于流体上的力与运动要素之间的关系，以及流体的运动特征与能量转换等，这一部分称为流体动力学。

流体力学在研究流体平衡和机械运动规律时，要应用物理学及理论力学中有关物理平衡及运动规律的原理，如力系平衡定理、动量定理、动能定理，等等。

因为流体在平衡或运动状态下，也同样遵循这些普遍的原理。

所以物理学和理论力学的知识是学习流体力学课程必要的基础。

目前，根据流体力学在各个工程领域的应用，流体力学可分为以下三类：水利类流体力学：面向水工、水动、海洋等；机械类流体力学：面向机械、冶金、化工、水机等；土木类流体力学：面向市政、工民建、道桥、城市防洪等。

二、流体力学的发展历史流体力学的萌芽，是自距今约2200年以前，西西里岛的希腊学者阿基米德写的“论浮体”一文开始的。

他对静止时的液体力学性质作了第一次科学总结。

流体力学的主要发展是从牛顿时代开始的，1687年牛顿在名著《自然哲学的数学原理》中讨论了流体的阻力、波浪运动，等内容，使流体力学开始成为力学中的一个独立分支。

此后，流体力学的发展主要经历了三个阶段：1.伯努利所提出的液体运动的能量估计及欧拉所提出的液体运动的解析方法，为研究液体运动的规律奠定了理论基础，从而在此基础上形成了一门属于数学的古典“水动力学”（或古典“流体力学”）。