sas统计分析报告
- 格式:doc
- 大小:52.89 KB
- 文档页数:7

手把手教你使用SAS进行数据分析SAS(Statistical Analysis System)是一款强大的数据分析和统计软件,广泛应用于学术研究、商业分析、医学统计等领域。
本篇文章旨在手把手教读者如何使用SAS进行数据分析,并将内容按照类别划分成不同章节,以便提供更具体且丰富的内容。
第一章:SAS基础本章将介绍SAS的安装和基本设置,帮助读者快速上手。
首先,读者需要从SAS官方网站下载并安装SAS软件。
安装完成后,可以根据需要进行个性化设置,例如选择语言和界面风格等。
此外,还将介绍SAS的基本语法和常见命令,让读者了解如何打开、保存和导入数据集。
第二章:数据处理与清洗数据处理是数据分析的首要步骤,本章将详细介绍如何使用SAS进行数据处理和清洗。
首先,会介绍如何检查数据集的完整性,包括数据类型、缺失值和异常值等。
然后,会讲解如何进行数据变换,例如数据排序、合并和拆分等。
最后,会介绍如何处理缺失值,包括插补和删除处理。
第三章:数据探索和可视化数据探索和可视化是数据分析的关键环节,本章将重点介绍如何使用SAS进行数据探索和可视化。
首先,会介绍如何计算和描述性统计量,例如均值、中位数和标准差等。
然后,会讲解如何绘制常见的数据图表,例如直方图、散点图和箱线图等。
此外,还将介绍如何使用SAS进行数据透视和交叉分析,以便更深入地挖掘数据关系。
第四章:统计分析统计分析是数据分析的核心步骤,本章将介绍如何使用SAS进行常见的统计分析。
首先,会介绍基本的假设检验,例如t检验和方差分析等。
然后,会讲解回归分析的基本原理和应用,包括线性回归和逻辑回归等。
此外,还将介绍如何使用SAS进行聚类分析和因子分析等高级统计技术。
第五章:预测建模预测建模是数据分析的高级技术,本章将介绍如何使用SAS进行预测建模。
首先,会讲解时间序列分析的基本原理和应用,包括趋势分析和季节性分析等。
然后,会介绍如何使用SAS进行机器学习建模,例如决策树和随机森林等。

sas数据分析报告摘要:本文介绍了基于SAS软件进行的数据分析报告。
首先,对数据进行了简要的介绍和处理,并对数据进行了可视化处理。
然后我们使用SAS建立了模型,并对模型进行了评估。
最后,我们对结果进行了解释和分析,并提出了相关的建议。
关键词:SAS,数据分析,模型建立,可视化,结果解释1. 简介SAS是一款广泛应用于数据分析领域的统计软件,其丰富的统计函数和数据可视化功能使得它成为了数据分析师不可或缺的工具。
本文使用SAS对某公司的销售数据进行分析,以帮助公司管理者更好地了解企业的经营情况和预测未来的发展趋势。
2. 数据处理与可视化我们先对数据进行了初步的清理和整理,去除了缺失值和异常值,并对数据进行了标准化处理。
然后,我们使用SAS的数据可视化功能对数据进行了可视化处理,包括制作散点图、直方图和箱线图等,以便更好地了解数据的分布情况和相关性。
3. 模型建立与评估我们基于数据建立了模型,并使用SAS对模型进行了评估。
在模型建立过程中,我们采用了多元线性回归模型,考虑了各个变量之间的相互关系和影响。
在模型评估过程中,我们采用了交叉验证和R方值等指标,对模型的预测能力进行了评估。
4. 结果解释与分析根据模型的预测结果,我们对数据进行了解释和分析,并提出了相关的建议。
我们确定了销售额、广告投放、促销活动等因素对销售额的影响,根据模型结果提出了优化销售策略的建议。
同时,我们进一步分析了销售额的趋势,预测了未来的销售情况,为公司的经营决策提供了有力的支持。
结论:本文基于SAS进行了数据分析报告,利用SAS的数据处理、可视化、模型建立和评估等功能,全面分析了某公司的销售数据。
通过对数据的解释和分析,我们提出了相关的建议,为公司的经营决策提供了参考。
这表明SAS在数据分析领域的应用效果显著,对于企业的发展和决策具有重要的意义。

院系:数学与统计学学院专业:__统计学年级:2009 级课程名称:统计分析 ____学号:____________姓名:_________________指导教师:____________2012年4月28日(一)实验名称1. 编程计算样本协方差矩阵和相关系数矩阵;2. 多元方差分析MANOVA。
(二)实验目的1. 学习编制sas程序计算样本协方差矩阵和相关系数矩阵;2. 对数据进行多元方差分析。
(三)实验数据第一题:第二题:(四)实验内容1. 打开SAS软件并导入数据;2. 编制程序计算样本协方差矩阵和相关系数矩阵;3. 编制sas程序对数据进行多元方差分析;4. 根据实验结果解决问题,并撰写实验报告;(五)实验体会(结论、评价与建议等)第一题:程序如下:proc corr data=sasuser.sha n cov;proc corr data=sasuser.sha n no simple cov;with x3 x4;partial x1 x2;run;结果如下:(1)协方差矩阵$AS亲坯曲;15 Friday, Apr: I SB,沙DOCOUR过程x4目由度=30Xi x2x3x4x5X?-10.I9B4944-0.45E2GJ5I.3347097-G.1193E48-£0.e75»GS-ID. 188494669,36&Q3?9-7.22IO&OS1J5692043I5.49ee^91S.Oa97SM-8.45S2645■7,221050829.S78&S46-6.372E47I-15.3084183-21.7352376-11.56747851.3841097 1.G5S2M7t.3726171IJ24«17B 4.e093011 4.4C124732.B747CM-G. I1S3S49 1.GS92043-is.soul aa 4.B09B01I68.7978495劣』S670971S.57ai1B3-IH.05l6l?a15.43S6569-J1.73S2376孔耶124TB27.0387097105.103225&S7.3505S7E:-2D K5752??319-11337204-1L55M7S52r9747?3i19,573118337.3S0&87E33.3SQ6452 (2) 相关系数矩阵Pearson相关系数” N =引当HO: Rho=0 时.Prob > |r|Xi Xixl1.QQ000x2-C.239540.2061x3-0,304590.0957x40.18975Q.3092x5'0.141570.4475x6-0.837870.0630-0.492920.0150x2-0.23354 1.00000-0.162750.143510.022700.181520.24438 x20.20C10.31:1?0.441?0.90350.32640.1761x3-0.30459-0.16275 1.00000-0.06219-0.34641-0.^797-0.23674 x30.095?0.381?<.00010.0563o.oses0 JS97x40.1S8760.14351-0.86219L000000.400540,313650.22610 x40.30920.4412<.0001 D.02EG Q.085S0.2213x5-0J 41570.02270-0.946410.40054 1.000000.317370.26750 x50.4J750.90350.0G68Q.025&0.08130+1620x6-0.33?e?0.1S162-0.397970.813650.31787LOOOOO0.82976 x60.0S300.32840.02660.08580.0813C0001辺-0.432920.24938-0.288740.22810 D.267600.92976 1.00000 x70,01500J7610.19970.22130JG20<.0001第二题:程序如下:proc anova data=sasuser.hua ng;class kind;model x1-x4=k ind;manova h=k ind;run;结果如下:(1)分组水平信息The ANNA ProcedureCla^s Level Informat ionClass Level®Valueskind 3 123Number of observatIons CO(2) x1、x2、x3、x4的方差分析Dependent Variable : xl xlSource DFSum of SquaresMea n Square F Value Pr > F Model 25221.30000 2610.650003.380.0411Error57 44069.55000773.15000Corrected Total 5949290.85000R-Square Coeff Var Rcot MSE xl Mean 0.10592832.3508727.8055785.95000Source DF Anova SS Mean Square F ValuePr > F kind25221.300000 2610.6500003.380.0411The ANOVA ProcsdureDependent Variable : x2 x2S UB ofSource DFSquares Mean Square F ValuePr > F Model 2 518.533333 259.26666?1.620.2078Error57 9148.050000160.492105Corrected Total 599666.583333R-Square Coeff Var Root MSE 0.05364222.9988812.6685555.08333Source DF Anova SS Mean Square F ValuePr > Fkind2518.5333333259.26666671.620.2078The ANOVA Procedure)epende 「t Variable : x:3 x3S UM ofSource DF Squares Mean SquareF Value Pr > FModel2 2480.8333 1240.41670.170.8478Error57 427028.50007491.7281Corrected Total 59429509.3333R-Square Coeff Var Root MSE x3 Mean0.00577621.1798088.55477408.66672480.8333331240.4166670.17 0.8478The ANOVA Procedurex2 Mean SourceAnova SS Mean Square F Value Pr > Fkind(3) 多元方差分析The ProcedureMulti var I ate Ana lysis of Vari sinceCharacteri st ic Roots and Vectors of :: E Inverse 水 H, whereH =舫ow SSCP Matrix for kindE = Error SSCP MatrixChareucteri st icRoot Percent Characteristic Vector V F EV=1x1 x2 x30.33804686 73J7 -0.00045795 -0.00379096 0.00090988 0.00279339 0.12323983 26,C3 0.00424111 0.00236878 0.00D01B42 0.00002832 0.00000000 0.00 0.00121062 -0.00032401 0.00157046 -0.00006539 0.000000000,00-0.003177880.010435260.000070140.00078872MANOVA Test Criteria and F ApproxI nat Ions for the Hypothesis of No Overall kind EffectH 二 Anova SSCP Matr ix for kindE = Error SSCP MatrixS=2M=0*5 N=26 Stat ist icVa 1 ueF Value Num DFDsn DF Pr > F Wilks' Lambda0*660359533.04 8 IDS 0.0040 Pi 1lai f s Trace0.36123585 3,03 e 110 0.0041 Hote11 ing-Law 1ey Trace Q.45927921 3.07 e 74.85G0.0048 Roy s Greatest Root 0.336045804.624550.0027NOTE : F Statistic for Roy's Greatest Root iis an upper boundsNOTE: F Statist ic f or Wilks' Lambdei is exact.根据多元分析结果,p 指小于0.05,表明在0.05的显著水平下,四个变量有 显著差异SourceDF Sum of Squares Mean iSouare F ValuePr > F Model239529,3000 192B4.8E0D 8.010.0009Error57 197115.10002405.5281Corrected Totiii59175644.4000R-SqusreGreff Vir Root M SE x4 Mean0.21936018.96604 49.04610 250.6000SourceDFA JWVI SSMean ^4j&re F V&luePr > F kind2 38529.3000019264.650008.010.0009The ANOVA ProcedureDependent Var iabls : x4 x4。

(一)院系:数学与统计学学院专业:__ _统计学年级: 2009级课程名称:统计分析学号:姓名:指导教师:2012年 4月 28 日(一)实验名称1.编程计算样本协方差矩阵和相关系数矩阵;2.多元方差分析MANOVA。
(二)实验目的1.学习编制sas程序计算样本协方差矩阵和相关系数矩阵;2.对数据进行多元方差分析。
(三)实验数据第一题:第二题:(四)实验内容1.打开SAS软件并导入数据;2.编制程序计算样本协方差矩阵和相关系数矩阵;3.编制sas程序对数据进行多元方差分析;4.根据实验结果解决问题,并撰写实验报告;(五)实验体会(结论、评价与建议等)第一题:程序如下:proc corr data=sasuser.shan cov;proc corr data=sasuser.shan nosimple cov;with x3 x4;partial x1 x2;run;结果如下:(1)协方差矩阵(2)相关系数矩阵第二题:程序如下:proc anova data=sasuser.huang; class kind; model x1-x4=kind; manova h=kind; run;结果如下:(1)分组水平信息(2)x1、x2、x3、x4的方差分析(3)多元方差分析根据多元分析结果,p指小于0.05,表明在0.05的显著水平下,四个变量有显著差异。
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注!)。


多元统计分析实验报告计算协方差矩阵相关矩阵SAS实验目的:通过对多元统计分析中的协方差矩阵和相关矩阵的计算,探究变量之间的相关性,并使用SAS进行实际操作。
实验步骤:1.数据准备:选择一个数据集,例如学生的成绩数据,包括数学成绩、语文成绩和英语成绩。
2.数据整理:将数据转化为矩阵形式,每一行代表一个学生,每一列代表一个变量(即成绩),记为X。
3. 计算协方差矩阵:根据公式计算协方差矩阵C,其中元素Cij表示变量Xi和Xj之间的协方差。
计算公式为Cij = cov(Xi, Xj) = E((Xi - u_i)(Xj - u_j)),其中E为期望值,u_i和u_j分别是变量Xi和Xj的均值。
4. 计算相关矩阵:根据协方差矩阵计算相关矩阵R,其中元素Rij表示变量Xi和Xj之间的相关性。
计算公式为Rij = cov(Xi, Xj) / (sigma_i * sigma_j),其中sigma_i和sigma_j分别是变量Xi和Xj的标准差。
5.使用SAS进行实际操作:使用SAS软件导入数据集,并使用PROCCORR和PROCPRINT命令进行协方差矩阵和相关矩阵的计算和输出。
实验结果:通过计算协方差矩阵和相关矩阵,可以得到变量之间的相关性信息。
协方差矩阵的对角线上的元素表示每个变量的方差,非对角线上的元素表示不同变量之间的协方差。
相关矩阵的对角线上的元素都是1,表示每个变量与自身的相关性为1,非对角线上的元素表示不同变量之间的相关性。
使用SAS进行实际操作后,我们可以得到一个包含协方差矩阵和相关矩阵的输出表格。
该表格可以帮助我们更直观地理解变量之间的相关性情况,从而为后续的统计分析提供参考。
实验总结:通过本次多元统计分析实验,我们了解了协方差矩阵和相关矩阵的计算方法,并使用SAS软件进行实际操作。
这些矩阵可以帮助我们评估变量之间的相关性,为后续的统计分析提供重要的基础信息。
在实际应用中,我们可以根据协方差矩阵和相关矩阵的结果,选择合适的统计方法和模型,并做出恰当的推断和决策。

利用SAS解决两个独立样本的t检验班级:学号:指导教师:姓名:目录1. SAS简介 (2)1.1 SAS的设计思想 (2)1.2 SAS的功能 (2)1.3 SAS的特点 (3)2. 方法及原理——两个独立样本的t检验 (4)2.1假设检验的思想和步骤 (4)2.2 t检验的原理与方法 (4)2.3 检验统计量t的公式 (5)2.4两个独立样本的t检验的步骤 (5)3.SAS常用命令 (6)4.题目与解答 (6)4.1题目 (6)4.2解答与分析 (6)1. SAS简介SAS是美国使用最为广泛的三大著名统计分析软件(SAS,SPSS和SYSTAT)之一,是目前国际上最为流行的一种大型统计分析系统,被誉为统计分析的标准软件。
SAS为“Statistical Analysis System”的缩写,意为统计分析系统。
它于1966年开始研制,1976年由美国SAS软件研究所实现商品化。
1985年推出SAS PC 微机版本,1987年推出DOS下的SAS6.03版,之后又推出6.04版。
以后的版本均可在WINDOWS下运行,目前最高版本为SAS6.12版。
SAS集数据存取,管理,分析和展现于一体,为不同的应用领域提供了卓越的数据处理功能。
它独特的“多硬件厂商结构”(MV A)支持多种硬件平台,在大,中,小与微型计算机和多种操作系统(如UNIX,MVS WINDOWS 和DOS等)下皆可运行。
SAS 采用模块式设计,用户可根据需要选择不同的模块组合。
它适用于具有不同水平于经验的用户,处学者可以较快掌握其基本操作,熟练者可用于完成各种复杂的数据处理。
目前SAS已在全球100多个国家和地区拥有29000多个客户群,直接用户超过300万人。
在我国,国家信息中心,国家统计局,卫生部,中国科学院等都是SAS系统的大用户。
SAS以被广泛应用于政府行政管理,科研,教育,生产和金融等不同领域,并且发挥着愈来愈重要的作用。

SAS数据分析实验报告摘要:本文使用SAS软件对一组数据集进行了分析。
通过数据清洗、数据变换、数据建模和数据评估等步骤,得出了相关的结论。
实验结果表明,使用SAS软件进行数据分析可以有效地处理和分析大型数据集,得出可靠的结论。
1.引言数据分析在各个领域中都扮演着重要的角色,可以帮助人们从大量的数据中提取有用信息。
SAS是一种常用的数据分析软件,被广泛应用于统计分析、商业决策、运营管理等领域。
本实验旨在探究如何使用SAS软件进行数据分析。
2.数据集描述本实验使用了一个包含1000个样本的数据集。
数据集包括了各个样本的性别、年龄、身高、体重等多种变量。
3.数据清洗在进行数据分析之前,首先需要对数据进行清洗。
数据清洗包括缺失值处理、异常值处理和重复值处理等步骤。
通过使用SAS软件中的相应函数和命令,我们对数据集进行了清洗,确保数据的质量和准确性。
4.数据变换在进行数据分析之前,还需要对数据进行变换。
数据变换包括数据标准化、数据离散化和数据归一化等操作。
通过使用SAS软件中的变换函数和操作符,我们对数据集进行了变换,使其符合分析的需要。
5.数据建模数据建模是数据分析的核心过程,包括回归分析、聚类分析和分类分析等。
在本实验中,我们使用SAS软件的回归、聚类和分类函数,对数据集进行了建模分析。
首先,我们进行了回归分析,通过拟合回归模型,找到了自变量对因变量的影响。
通过回归模型,我们可以预测因变量的值,并分析自变量的影响因素。
其次,我们进行了聚类分析,根据样本的特征将其分类到不同的群组中。
通过聚类分析,我们可以发现样本之间的相似性和差异性,从而做出针对性的决策。
最后,我们进行了分类分析,根据样本的特征判断其所属的类别。
通过分类分析,我们可以根据样本的特征预测其所属的类别,并进行相关的决策。
6.数据评估在进行数据分析之后,还需要对结果进行评估。
评估包括模型的拟合程度、变量的显著性和模型的稳定性等。
通过使用SAS软件的评估函数和指标,我们对数据分析的结果进行了评估。

proc compare输出报告ProcCompare是统计软件SAS中一种重要的统计分析工具,它可以比较两个或更多的变量、表或数据集,来评估他们之间的差异。
本文将讨论Proc Compare的输出报告,以及如何使用它。
1. Proc Compare的简介Proc Compare是SAS中一种常用的统计分析工具,它可以用于比较两个或更多的变量、表或数据集之间的差异。
Proc Compare能够识别两个变量、表或数据集之间的重大差异,以及在变量层面上是否存在某种差异。
2. Proc Compare的使用使用Proc Compare首先要确定目标变量或数据集,然后在SAS 语句中指定两个变量或数据集,并指定相应的设置参数。
接下来,执行Proc Compare,它会输出比较结果报告,包括变量的统计信息、差异指标、重大差异检测结果等。
3. Proc Compare的输出报告Proc Compare输出报告主要有三个部分:(1)量比较报告:这部分报告显示了两个变量或数据集之间的比较结果,包括每个变量的统计信息、缺失值比较结果等。
(2)总体差异报告:这部分报告显示了两个变量或数据集整体上的差异情况,包括是否存在重大差异、重大差异的检验结果等。
(3)差异指标:这部分报告显示了两个变量或数据集之间的差异程度,主要有均值差异、比例差异和变异系数差异等。
4.结本文介绍了Proc Compare的使用方法及其输出报告,以及如何使用它。
Proc Compare可以帮助统计分析者快速比较两个或更多变量、表或数据集之间的差异,从而确定其中的重大差异,并识别重大差异的原因。
因此,Proc Compare是研究及项目中非常有用的统计分析工具。
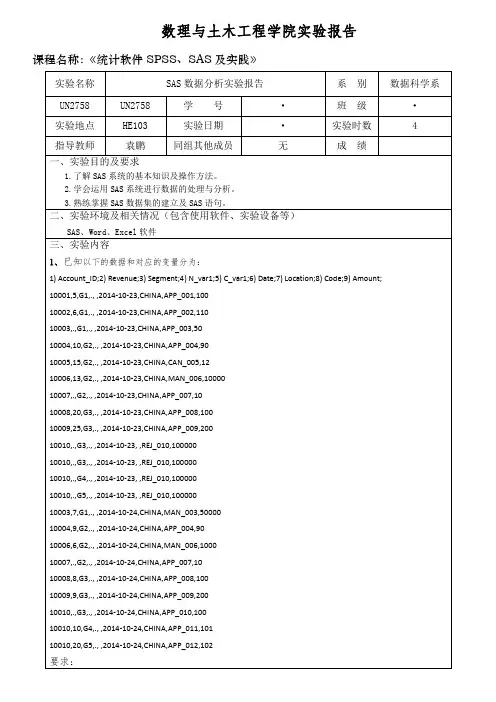
数理与土木工程学院实验报告课程名称:《统计软件SPSS、SAS及实践》实验结果(包括程序代码、程序结果分析)第一题:②基于数据集transaction,将变量“Revenue”中的缺失数据用其均值代替;data a;set a;array s(*) aa1-aa2;n=n(of s(*));mean=mean(of s(*));sum=sum( of s(*));do i=1to dim(s);if s(i)=.then s(i)=mean;end;run;proc print;run;③基于②,将取值全部缺失的变量删除。
data a;set a;array aa aa1-aa2;do over aa;if col=.then delete;end;run;proc transpose data=a out=transaction(drop=_name_);var aa1-aa2;run;proc print;run;第二题:a) 建立一个数据集合读入数据,变量为length,width和 height;data b;input length width height;cards;32 18 1216 15 2448 12 3215 30 4520 30 36;run;proc print data=b;run;b) 使用 set 语句,利用a)的数据集建立一个新数据集,它包括a)的所有数据,并建立三个新变量:每个c) 使用b)建立的数据集建立一个新数据集,只包括其中的volume 和 cost 变量。
data d;set c(keep=volume cost);run;proc print data=d;run;第三题:a)对车的标志(brand)的频数画竖直条形图。
libname mydata 'D:\data';proc print data=edcar;run;data e;set edcar; run;proc gchart;vbar brand;run;b)c)data g;set f;proc means data=g ;run;第四题:试分析:该地区单身人士的收入与住房面积之间是否相关?如果线性相关,确定一元线性回归方程,并做显著性检验。

SAS统计分析介绍SAS(Statistical Analysis System)是一种流行的统计分析软件,被广泛应用于数据分析、数据管理和预测建模等领域。
它提供了一套全面的工具和功能,可以帮助用户有效地收集、分析和解释数据,以支持数据驱动的决策。
SAS具有丰富的功能和应用领域。
首先,它可以用于数据准备和数据管理。
用户可以使用SAS对数据进行清洗、整合、转换和重组,以确保数据的质量和一致性。
此外,SAS还提供了强大的数据查询和处理功能,可以高效地处理大规模和复杂的数据集。
其次,SAS可以用于描述性统计分析。
用户可以使用SAS计算各种统计指标,例如平均值、中位数、标准差、相关系数等,以了解数据的分布和变化。
此外,SAS还支持绘制各种图表和图形,例如直方图、散点图和箱线图,以可视化地展示数据的特征和模式。
SAS还提供了广泛的统计分析功能。
用户可以使用SAS进行假设检验、方差分析、回归分析等常见的统计分析任务。
此外,SAS还支持更高级的统计方法,例如生存分析、因子分析、聚类分析、时间序列分析等。
这些方法可以帮助用户发现数据中的关联和模式,从而支持更深入的数据解释和预测建模。
SAS的预测建模功能也非常强大。
用户可以使用SAS构建各种预测模型,例如线性回归模型、逻辑回归模型、决策树模型、神经网络模型等。
此外,SAS还支持模型评估和模型比较,以帮助用户选择最佳的预测模型。
这些预测模型可以应用于各种领域,例如市场营销、金融风险管理、医疗保健等。
除了数据分析和预测建模,SAS还提供了数据可视化和报告生成的功能。
用户可以使用SAS创建漂亮而有效的报告和图表,以呈现分析结果。
此外,SAS还支持自动化和批处理,可以帮助用户高效地处理和分析大规模的数据集。
总的来说,SAS是一种功能强大的统计分析软件,可以帮助用户从数据中提取有价值的信息和洞察。
它提供了丰富的功能和工具,适用于各种统计分析任务,从简单的数据描述到复杂的预测建模。
如何用SAS进行统计分析SAS(统计分析系统)是一种用于数据分析和统计建模的软件工具。
它提供了一系列功能和程序,用于数据处理、统计分析、预测建模、图形展示和报告生成等。
本文将介绍如何使用SAS进行统计分析,涵盖数据导入、数据清洗、描述性统计分析、假设检验、回归分析和聚类分析等内容。
1. 数据导入和数据清洗在使用SAS进行统计分析之前,你需要将待分析的数据导入到SAS软件中。
SAS支持多种数据格式,包括CSV、Excel、Access等。
你可以使用SAS提供的PROC IMPORT过程将数据导入到SAS的数据集中。
导入数据后,你需要对数据进行清洗。
数据清洗的目的是去除数据中的错误、缺失或异常值,以确保数据的质量。
你可以使用SAS的数据步骤(DATA STEP)来处理数据,例如删除缺失值、填补缺失值、去除异常值等。
2. 描述性统计分析描述性统计分析是对数据进行总结和描述的过程。
它包括计算数据的中心趋势(均值、中位数、众数)、数据的离散程度(标准差、方差、极差)、数据的分布形态(偏度、峰度)等。
在SAS中,你可以使用PROC MEANS过程进行描述性统计分析。
该过程可以计算多个变量的均值、标准差、最小值、最大值、中位数等统计指标。
此外,你还可以使用PROC UNIVARIATE过程计算数据的偏度、峰度等统计值,并绘制直方图和箱线图来展示数据的分布情况。
3. 假设检验假设检验是对样本数据进行推断性统计分析的一种方法。
它用于判断观察到的样本差异是否显著,从而对总体参数进行推断。
在SAS中,你可以使用PROC TTEST过程进行双样本t检验、单样本t检验和相关样本t检验等。
此外,PROC ANOVA过程可以用于方差分析,PROC FREQ过程可以用于卡方检验。
4. 回归分析回归分析是研究因变量与自变量之间关系的一种统计分析方法。
它用于预测和解释因变量的变化,并评估自变量对因变量的影响程度。
在SAS中,你可以使用PROC REG过程进行简单线性回归分析和多元线性回归分析。
sas分析报告:分析报告sas sas结果分析如何用sas显著性分析sas结果读取篇一:sas统计分析报告《统计软件》报告聚类分析和方差分析在统计学成绩分析中的应用班级:精算0801班姓名:张倪学号:2008111500 报告2011年11月指导老师:郝际贵成绩:目录一、背景及数据来源.................................................... 1 二、描述性统计分析.................................................... 2 三、聚类分析................................................................ 4 四、方差分析................................................................ 6 五、结果分析与结论. (8)聚类分析和方差分析在统计学成绩分析中的应用一、背景及数据来源SAS 系统全称为Statistics Analysis System,最早由北卡罗来纳大学的两位生物统计学研究生编制,并于1976年成立了SAS软件研究所,正式推出了SAS软件。
SAS是用于决策支持的大型集成信息系统,但该软件系统最早的功能限于统计分析,至今,统计分析功能也仍是它的重要组成部分和核心功能。
SAS 系统是一个组合软件系统,它由多个功能模块组合而成,其基本部分是BASE SAS模块。
BASE SAS模块是SAS系统的核心,承担着主要的数据管理任务,并管理用户使用环境,进行用户语言的处理,调用其他SAS模块和产品。
也就是说,SAS系统的运行,首先必须启动BASE SAS模块,它除了本身所具有数据管理、程序设计及描述统计计算功能以外,还是SAS系统的中央调度室。
它除可单独存在外,也可与其他产品或模块共同构成一个完整的系统。
实验报告实验项目名称SAS描述统计分析所属课程名称现代统计软件实验类型验证性实验实验日期2014-10-28班级学号姓名成绩实验报告说明1.实验项目名称:要用最简练的语言反映实验的内容。
要求与实验指导书中相一致。
2.实验类型:一般需说明是验证型实验还是设计型实验,是创新型实验还是综合型实验。
3.实验目的与要求:目的要明确,要抓住重点,符合实验指导书中的要求。
4.实验原理:简要说明本实验项目所涉及的理论知识。
5.实验环境:实验用的软硬件环境(配置)。
6.实验方案设计(思路、步骤和方法等):这是实验报告极其重要的内容。
概括整个实验过程。
对于操作型实验,要写明依据何种原理、操作方法进行实验,要写明需要经过哪几个步骤来实现其操作。
对于设计型和综合型实验,在上述内容基础上还应该画出流程图、设计思路和设计方法,再配以相应的文字说明。
对于创新型实验,还应注明其创新点、特色。
7.实验过程(实验中涉及的记录、数据、分析):写明上述实验方案的具体实施,包括实验过程中的记录、数据和相应的分析(原程序、程序运行结果、结果分析解释)。
8.结论(结果):即根据实验过程中所见到的现象和测得的数据,做出结论。
9.小结:对本次实验的心得体会、思考和建议。
10.指导教师评语及成绩:指导教师依据学生的实际报告内容,用简练语言给出本次实验报告的评价和价值。
注意:∙每次实验开始时,交上一次的实验报告。
∙实验报告文档命名规则:“实验序号”+“_”+ “班级”+“_”+“学号”+“姓名”+“_”+ “.doc”例如:管信11班的张军同学学号为:2011312299 本次实验为第2次实验即:实验二、SAS编程基础;则实验报告文件名应为:实验二_管信11 _2011312299_张军.doc 。
sas 中的proc summary的简易用法在SAS(统计分析系统)中,proc summary是一个非常常用的过程,用于对数据进行汇总和统计分析。
它可以帮助用户快速、准确地计算数据的各种统计量,并生成相应的汇总报告。
本文将介绍proc summary的基本用法,包括如何使用它进行简单的数据汇总和统计分析。
一、简介1.1 proc summary概述proc summary是SAS中用于汇总和统计数据的过程。
它可以对数据进行求和、平均值、中位数、标准差等统计计算,还可以生成频数表、交叉表等汇总报告。
通过proc summary,用户可以快速了解数据的整体特征,发现数据的规律和异常值,为后续的分析和建模工作奠定基础。
1.2 proc summary的优势相比于手动编写数据统计分析的代码,proc summary有以下几个显著的优势:- 简洁高效:proc summary只需要一行或几行代码,就可以完成对数据的多种统计计算,极大地提高了统计分析的效率。
- 灵活多样:proc summary支持对多个变量进行统计计算,可以通过选项参数指定不同的统计方法和输出格式,满足用户不同的统计需求。
- 结果可读性好:proc summary生成的汇总报告结构清晰,包含多种统计量和描述性统计信息,便于用户直观地理解和解释数据。
二、基本用法2.1 proc summary语法proc summary的基本语法如下所示:```sasproc summary data=dataset;var variable1 variable2 ...;output out=summary_data mean=mean_value sum=sum_value; run;```其中,data=dataset指定输入的数据集名称;var variable1 variable2 ...指定需要进行统计计算的变量;outputout=summary_data mean=mean_value sum=sum_value指定输出的汇总数据集和需要计算的统计量。
使用SAS进行数据挖掘和统计分析的入门教程一、简介SAS(Statistical Analysis System)是全球最为流行的商业智能和数据分析软件之一。
它提供了一套完整的解决方案,用于数据挖掘、统计分析、预测建模和报告生成等领域。
本教程将带你入门使用SAS进行数据挖掘和统计分析。
二、安装与配置在开始使用SAS之前,首先需要进行安装和配置。
SAS提供了不同版本的软件,可以根据自己的需要选择合适的版本。
安装完成后,还需要进行相应的许可证注册和配置,以确保软件正常运行。
三、数据准备进行数据挖掘和统计分析之前,首先需要准备好相应的数据。
数据可以来自不同的来源,如Excel文件、数据库或者其他外部文件。
在SAS中,可以使用PROC IMPORT命令导入数据,将其转化为SAS数据集的形式。
同时,还需要进行数据清洗和预处理,以确保数据的质量和完整性。
四、数据探索与描述性统计分析在进行数据挖掘和统计分析之前,可以先进行数据的探索和描述性统计分析,以了解数据的基本情况。
SAS提供了多种统计过程和过程步骤,可用于计算变量的均值、标准差、最大值、最小值等统计指标,生成频数表和交叉表等。
利用这些过程,可以对数据的分布情况和变量之间的关系进行初步的了解和分析。
五、建立预测模型数据挖掘的一大应用就是建立预测模型。
在SAS中,可以使用PROC REG或PROC GLM等过程来进行回归分析,通过寻找变量之间的关系,建立线性回归模型。
同时,SAS还提供了其他的预测建模过程,如PROC LOGISTIC用于逻辑回归分析,PROC ARIMA用于时间序列分析等。
通过这些过程,可根据实际需求,选择合适的模型进行建模并进行模型评估。
六、数据挖掘技术应用除了传统的统计分析方法,SAS还提供了多种数据挖掘技术,用于探索隐藏在数据背后的模式和规律。
其中,最为常用的技术包括关联规则挖掘、分类与预测、聚类分析和异常检测等。
通过使用这些技术,可以从数据中发现潜在的价值和信息,为决策提供支持和参考。
使用SAS进行数据分析的步骤第一章:引言数据分析是现代商业和科学领域中不可或缺的一部分。
它可以帮助我们从数据中获取有价值的信息和见解,用以支持决策制定和问题解决。
而SAS(Statistical Analysis System)作为一种流行的数据分析工具,被广泛应用于各个领域。
本文将介绍使用SAS进行数据分析的步骤,并以实例来说明每个步骤的具体操作。
第二章:数据准备一个成功的数据分析过程必须以正确的数据准备开始。
首先,收集所需数据,并确保数据的完整性和准确性。
然后,对数据进行清洗和预处理,包括处理缺失值、异常值和重复值等。
接下来,对数据进行变量选择和变换,以便更好地适应后续的分析需求。
第三章:探索性数据分析在进行正式的统计分析之前,我们需要对数据进行探索性分析,以了解数据的基本特征和潜在关系。
这包括计算和绘制描述性统计指标,如均值、中位数、方差等,以及创建图表和图形,如直方图、散点图、箱线图等。
通过这些分析,我们可以对数据的分布、相关性和异常情况有一个初步的了解。
第四章:假设检验当我们想要通过数据来验证一个假设时,可以使用假设检验进行统计分析。
首先,我们需要明确研究的问题和假设,并选择适当的假设检验方法。
然后,我们将数据导入SAS,并根据所选的假设检验方法进行相应的计算和分析。
最后,根据分析结果来判断是否拒绝或接受原假设。
第五章:建立模型在一些情况下,我们希望通过建立数学模型来解释和预测数据。
在SAS中,我们可以使用线性回归、逻辑回归、时间序列分析等方法来建立模型。
首先,我们需要选择适当的变量和模型类型。
然后,我们可以使用SAS的建模工具来进行变量筛选、模型拟合和验证。
最后,我们可以评估模型拟合的好坏,并通过模型预测来进行决策支持。
第六章:结果解释和报告当我们完成数据分析时,需要将结果进行解释和报告,以便他人理解和使用。
首先,我们需要对分析结果进行解释,包括各个变量的作用和解释、模型的拟合程度、假设检验的结论等。
《统计软件》报告
聚类分析和方差分析
在统计学成绩分析中的应用
班级:精算0801班
姓名:张倪
学号:2008111500
报告时间:2011年11月
指导老师:郝际贵
成绩:
1
目录
一、背景及数据来源 (1)
二、描述性统计分析 (2)
三、聚类分析 (4)
四、方差分析 (6)
五、结果分析与结论 (8)
聚类分析和方差分析在统计学成绩分析中的应用
一、背景及数据来源
SAS 系统全称为Statistics Analysis System,最早由北卡罗来纳大学的两位生物统计学研究生编制,并于1976年成立了SAS软件研究所,正式推出了SAS软件。
SAS是用于决策支持的大型集成信息系统,但该软件系统最早的功能限于统计分析,至今,统计分析功能也仍是它的重要组成部分和核心功能。
SAS 系统是一个组合软件系统,它由多个功能模块组合而成,其基本部分是BASE SAS模块。
BASE SAS模块是SAS系统的核心,承担着主要的数据管理
任务,并管理用户使用环境,进行用户语言的处理,调用其他SAS模块和产品。
也就是说,SAS系统的运行,首先必须启动BASE SAS模块,它除了本身所具有数据管理、程序设计及描述统计计算功能以外,还是SAS系统的中央调度室。
它除可单独存在外,也可与其他产品或模块共同构成一个完整的系统。
各模块的安装及更新都可通过其安装程序非常方便地进行。
本文利用SAS软件进行描述性统计、聚类分析等统计分析方法,将学生按照多指标综合考虑进行聚类。
数据来源:选取2010—2011第一学期统计学选教课成绩单,选取性别系别等变量进行考察。
将中文名称改为英文。
数据类型如下所示:
学号性别班级系部课程名称老师平时成绩期末成绩总评学年
数值型数值型字符型字符型数值型数值型数值型字符型字符型数值型S3
Sn
Sex
class
S1
S2
year
title
teacher
dept
当输入字符型的变量时,需要加上符号$在该变量的后面,用于区分数值型变量,所以用$来作为后缀。
删除缺考错误分数等异常值。
命名为2010stat.xls
1
二、描述性统计分析(一)导入数据stat 首先建立永久磁盘
路径,导入数据集libname path D:\sas\;
;
run(二)描述性统计分析然后进行描述性统计对性别、平时成绩、期末成绩、总评成绩进行计算,代码如下:proc means data=path.stat;
var sex s1 s2 s3;
run;
输出结果如下:
分,总评成绩均分为86.28从结果可以分析出,总体学生平时成绩平均分为分。
77.15 按照系别分类,每个系进行描述性统计,代码如下:means data=path.stat; proc
var sex s1 s2 s3;
class dept;
run;
运行的输出结果如下所示:
2
标准差及最大值从结果可以分析得出,各个系别学生成绩的均值、观测值、和最小值。
其中,会计系、财政系和市场营销系人数众多,除了经济系、市场营分。
销系和留学生以外,各系都有100(三)统计图代码如下绘制频率直方图,
直方图可以良好的反映各系的人数和性别比例。
所示:proc gchart
data=path.stat;
vbar dept/type=sum subgroup=sex;
;
run统计直方图如下所示:3
根据直方直方图的横轴是系别变量,纵轴是人数。
蓝色是男生红色是女生。
分别表示各系别男女生人数分布。
图显示会计系、营销系、财政系三系人数最高。
三、聚类分析输入代码:data=path.stat method=ward outtree=tree standard pseudo ccc; clusterproc
data=tree graphics horizontal; proc tree;
run并且绘制出聚类分析结果的树上述程序说明了使用系统聚类法来进行研究,状图。
22F统计量。
这三个统计量和下面的伪和CCCccc说明需要计算半偏R、R2和伪T统计量主要用于检验聚类的效果。
2统计量说明了本次合并信息的损R 类时,G+1类合并为G半偏当把数据从2统计量大说明信息的损失程度大。
失程度,半偏R22统计量大说明类内离差平方和统计量反映了类内离差平方和的大小,RR 小。
CCC统计量的值大说明聚类的效果好。
2统计量在出现峰值的是F 和伪说明要计算伪PseudoFT统计量一般认为伪4
2T类时,如果伪G+1类合并为G所对应的分类是较佳的分类选择。
当把数据从统计量的值大,说明不应该合并这两类。
后面的tree过程是用来绘制聚类分析结果的树状图。
运行结果如下:
2RSQ统计量、上面的运行结果给出了对样品的聚类过程。
SPRSQ为半偏R22统T为伪统计量、为伪为立方聚类标准、为R统计量、CCC PSFFPST2 计量。
5
223结果分析:从半偏R类合并为统计量的结果可以看出,当样本数据从2统计量的结果可以类时,信息的损失程度较前面的的合并有明显的增加。
从R2统计量较前面的合并显著减小,这看出,当样本数据从3R2类时,类合并为,统计量的结果从Word违背了CCCs的分类原则。
意味着类内离差平方和增加,2统计量
显著类时,伪T53可以看出,最大值对应的类数为类。
从6类合并为2统计量
下降显著。
增加,伪T综合各类统类也是符合图形的。
由聚类分析的分析结果
的树状图可知分为3 计量的结果,学生的统计学成绩分为3类比较合适。
四、方差分析输入代码:glm;proc
sex s3;
class
/ ss1 ss2 ss3 ss4; model s3=sex s3 sex*s1/duncan; means s1run;
输出结果如下所示:6
性别对成绩影响从输出结果可以看出,平时成绩对总评成绩有显著的影响。
中,女生成绩要优于男生,平均分比男生高,方差比男生小。
可见,在平时成绩和性别对学生统计学总评成绩的影响。
7
五、结果分析与结论
本文选取2010—2011年统计学成绩作为样本数据,运用SAS软件先对学生成绩进行描述性统计分析,再选用聚类分析法,最后进行方差分析。
聚类分析(Cluster Analysis)根据样品的统计量将相似程度较大的样品聚合到一个小的分类单位,相似程度较小的聚合到一个大的分类单位,使得同一类中的对象之间的相似性比与其他类的对象的相似性更强,直到把所有的样品都聚合完毕,形成一个由小到大的分类系统,并将整个分类系统画成一张谱系图。
方差分析(Analysis of Variance)由于各种因素的影响,研究所得的数据呈现波动状。
造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
根据描述性统计得到全部学生以及各系别学生的成绩以及性别的描述性统计,聚类分析将学生按照成绩系别等变量分为三大类。
整体分析结果良好的反映学生的学习水平。
结合上文的结论,可以分析出:女生由于出勤高,因而平时成绩优秀,这样期末总评成绩也普遍比男生高。
8。