下载文档原格式
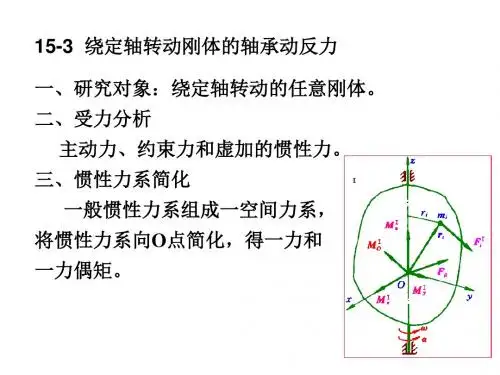
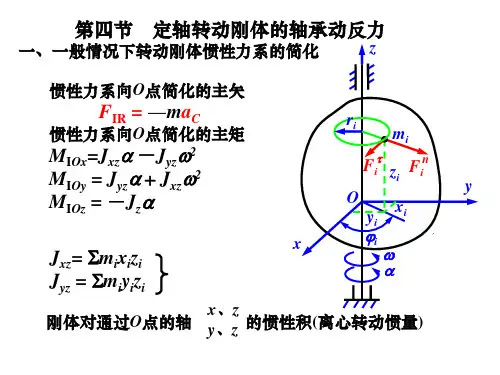
1、轴承约束力、动约束力刚体的角速度w ，角加速度a （逆时针），主动力系向O 点简化: 主矢F R , 主矩M O ，惯性力系向O 点简化: 主矢F IR , 主矩M IO 。
轴承A 处的约束力：F Ax ，F Ay轴承B 处的约束力：F Bx ，F By ，F Bz 根据动静法，列平衡方程:0 0 =+=+++=+++Rz Bz Iy Ry By Ay Ix Rx Bx Ax F F F F F F F F F F 00 =++×-×=++×-×Iy y Bx Ax Ix x Ay By M M OB F OA F M M OA F OB F 000=å=å=åz y x F F F 00=å=åy x M M w aF RMOF IRM IOF AxF Ay F BxF ByF Bz 1、轴承约束力、动约束力全约束力由两部分组成：•一部分由主动力引起的，不能消除，称为静约束力；•另一部分是由于惯性力系引起的，称为动约束力。
后者可以通过调整加以消除。
Rz Bz Iy Ix Ry x By Ix Iy Rx y Bx Iy Ix Ry x Ay Ix Iy Rx y Ax F F OA F M OA F M ABF OA F M OA F M AB F OB F M OB F M AB F OB F M OB F M AB F -=×++×+-=×-+×-=×-+×-=×++×+-=)]()[(1)]()[(1)]()[(1)]()[(1由此求得两轴承的全约束力：1、轴承约束力、动约束力使动约束力为零，须有：静约束力动约束力轴承全约束力==Iy Ix M M 0==Iy Ix F F 当刚体转轴为中心惯性主轴时，轴承的动约束力为零。
五、刚体绕定轴的转动（一）前言前两章质点力学讨论的是物体平动的情况，力学中，在一般情况下，一个物体的运动包含平动、转动、振动等是很复杂的，一物体在平动时，若把物体看成是一刚体（无形变）物体上每一点的运动情况都是一样的，无需考虑物体的形状，大小如何。
故物体可抽象为一质点，其运动情况如前两章质点力学所述。
但在转动中，情况就不一样了。
例如飞轮高速旋转时，其上的各点运动情况各不相同，因而不能简化为质点。
这一章与前两章相比，发生了两点变化：一是主要研究对象变了，由质点变为刚体。
即从物体来说，必须考虑它的形状，大小。
但忽略形变；二是主要研究的问题也变了，由平动变为转动。
即从运动来说突出了转动，暂时忽略振动或其他运动。
若将刚体分成许多细微部分，并把每一细微部分看成一个质点，那么刚体可以看成是有无数质点构成的质点组，这个质点组与平动所讨论的质点组是有区别的，其特征是：构成刚体的任意二质点间的距离，在运动中恒定不变，这种看法使我们有可能在上一章质点动力学的基础上来研究刚体情况。
讲授本章内容时，我们采取类比法，把物体的平动与刚体的定轴转动进行类比，其目的就是使同学们能更好地理解刚体定轴转动中一些物理量的物理含义。
一、刚体绕定轴转动的运动特征：什么是刚体绕定轴的转动呢？刚体中某一直线上的点保持不动（对固定参考系而言），其它各点都以该直线上的相应点为圆心，在垂直于该点的平面内作大小不同的圆周运动。
这种运动称刚体绕定轴的转动。
相对于参照系不动的直线称为转轴，刚体绕定轴的转动有三个特点：(在下面的讨论中要用到这些知识。
)1）刚体上各质点都在各自的平面内作半径不同的圆周运动。
而圆周运动是用角量来描述的，因此，质点运动学中讨论的角位移θ∆，角速度ω，角加速度β等概念都适用刚体定轴转动。
2）各质点作圆周运动的平面垂直于轴线，圆心在轴线上。
3）尽管各质点绕轴运动的线速度不同，但角速度是相同的，这就意味着角速度的时间变化率也是相同的，即各质元的角加速度β相同。
