信息论基础与编码复习2
- 格式:doc
- 大小:260.50 KB
- 文档页数:5


第二章习题解答2-1、试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍? 解:四进制脉冲可以表示4个不同的消息,例如:{0, 1, 2, 3}八进制脉冲可以表示8个不同的消息,例如:{0, 1, 2, 3, 4, 5, 6, 7} 二进制脉冲可以表示2个不同的消息,例如:{0, 1} 假设每个消息的发出都是等概率的,则:四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n X H / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===所以:四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。
2、 设某班学生在一次考试中获优(A )、良(B )、中(C )、及格(D )和不及格(E )的人数相等。
当教师通知某甲:“你没有不及格”,甲获得了多少比特信息?为确定自己的成绩,甲还需要多少信息? 解:根据题意,“没有不及格”或“pass”的概率为54511pass =-=P 因此当教师通知某甲“没有不及格”后,甲获得信息在已知“pass”后,成绩为“优”(A ),“良”(B ),“中”(C )和“及格”(D ) 的概率相同:41score )pass |()pass |()pass |()pass |(=====D P C P B P A P P 为确定自己的成绩,甲还需信息bits 241loglog score score =-=-=P I 3、中国国家标准局所规定的二级汉字共6763个。
设每字使用的频度相等,求一个汉字所含的信息量。
设每个汉字用一个1616⨯的二元点阵显示,试计算显示方阵所能表示的最大信息。
显示方阵的利用率是多少?解:由于每个汉字的使用频度相同,它们有相同的出现概率,即67631=P 因此每个汉字所含的信息量为bits 7.1267631loglog =-=-=P I 字每个显示方阵能显示256161622=⨯种不同的状态,等概分布时信息墒最大,所以一个显示方阵所能显示的最大信息量是bits322.054log log passpass =-=-=P Ibits 25621loglog =-=-=P I 阵显示方阵的利用率或显示效率为0497.02567.12===阵字I I η 4、两个信源1S 和2S 均有两种输出:1 ,0=X 和1 ,0=Y ,概率分别为2/110==X X P P ,4/10=Y P ,4/31=Y P 。


第二章习题解答2-1、试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍? 解:四进制脉冲可以表示4个不同的消息,例如:{0, 1, 2, 3} 八进制脉冲可以表示8个不同的消息,例如:{0, 1, 2, 3, 4, 5, 6, 7} 二进制脉冲可以表示2个不同的消息,例如:{0, 1} 假设每个消息的发出都是等概率的,则:四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n X H / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===所以:四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。
2、 设某班学生在一次考试中获优(A )、良(B )、中(C )、及格(D )和不及格(E )的人数相等。
当教师通知某甲:“你没有不及格”,甲获得了多少比特信息?为确定自己的成绩,甲还需要多少信息? 解:根据题意,“没有不及格”或“pass”的概率为54511pass =-=P 因此当教师通知某甲“没有不及格”后,甲获得信息在已知“pass”后,成绩为“优”(A ),“良”(B ),“中”(C )和“及格”(D ) 的概率相同:41score )pass |()pass |()pass |()pass |(=====D P C P B P A P P 为确定自己的成绩,甲还需信息bits 241loglog score score =-=-=P I 3、中国国家标准局所规定的二级汉字共6763个。
设每字使用的频度相等,求一个汉字所含的信息量。
设每个汉字用一个1616⨯的二元点阵显示,试计算显示方阵所能表示的最大信息。
显示方阵的利用率是多少?解:由于每个汉字的使用频度相同,它们有相同的出现概率,即67631=P 因此每个汉字所含的信息量为bits 7.1267631loglog =-=-=P I 字每个显示方阵能显示256161622=⨯种不同的状态,等概分布时信息墒最大,所以一个显示方阵所能显示的最大信息量是bits 322.054loglog passpass =-=-=P Ibits 25621loglog 256=-=-=P I 阵显示方阵的利用率或显示效率为0497.02567.12===阵字I I η 4、两个信源1S 和2S 均有两种输出:1 ,0=X 和1 ,0=Y ,概率分别为2/110==X X P P ,4/10=Y P ,4/31=Y P 。


《信息论和编码技术》复习提纲复习题《信息论与编码技术》复习提纲复习题纲第0章绪论题纲:I.什么是信息?II.什么是信息论?III.什么是信息的通信模型?IV.什么是信息的测度?V.自信息量的定义、含义、性质需掌握的问题:1.信息的定义是什么?(广义信息、狭义信息——Shannon信息、概率信息)2.Shannon信息论中信息的三要素是什么?3.通信系统模型图是什么?每一部分的作用的是什么?4.什么是信息测度?5.什么是样本空间、概率空间、先验概率、自信息、后验概率、互信息?6.自信息的大小如何计算?单位是什么?含义是什么(是对什么量的度量)?第1章信息论基础㈠《离散信源》题纲:I.信源的定义、分类II.离散信源的数学模型III.熵的定义、含义、性质,联合熵、条件熵IV.离散无记忆信源的特性、熵V.离散有记忆信源的熵、平均符号熵、极限熵VI.马尔科夫信源的定义、状态转移图VII.信源的相对信息率和冗余度需掌握的问题:1.信源的定义、分类是什么?2.离散信源的数学模型是什么?3.信息熵的表达式是什么?信息熵的单位是什么?信息熵的含义是什么?信息熵的性质是什么?4.单符号离散信源最大熵是多少?信源概率如何分布时能达到?5.信源的码率和信息率是什么,如何计算?6.什么是离散无记忆信源?什么是离散有记忆信源?7.离散无记忆信源的数学模型如何描述?信息熵、平均符号熵如何计算?8.离散有记忆多符号离散平稳信源的平均符号熵、极限熵、条件熵(N阶熵)的计算、关系和性质是什么?9.什么是马尔科夫信源?马尔科夫信源的数学模型是什么?马尔科夫信源满足的2个条件是什么?10.马尔科夫信源的状态、状态转移是什么?如何绘制马尔科夫信源状态转移图?11.马尔科夫信源的稳态概率、稳态符号概率、稳态信息熵如何计算?12.信源的相对信息率和冗余度是什么?如何计算?㈡《离散信道》题纲:I.信道的数学模型及分类II.典型离散信道的数学模型III.先验熵和后验熵IV.互信息的定义、性质V.平均互信息的定义、含义、性质、维拉图VI.信道容量的定义VII.特殊离散信道的信道容量需掌握的问题:1.信道的定义是什么?信道如何分类?信道的数学模型是2.二元对称信道和二元删除信道的信道传输概率矩阵是什么?3.对称信道的信道传输概率矩阵有什么特点?4.根据信道的转移特性图,写出信道传输概率矩阵。


信息论与编码复习
去年考点(部分):
简答题:香农第一定理P106、香农第二定理P141
计算题:马尔可夫信源P37、香农编码P110、霍夫曼编码P111、费诺编码P115、平均错误概率P131(例6.3)、例5.10。
重点:
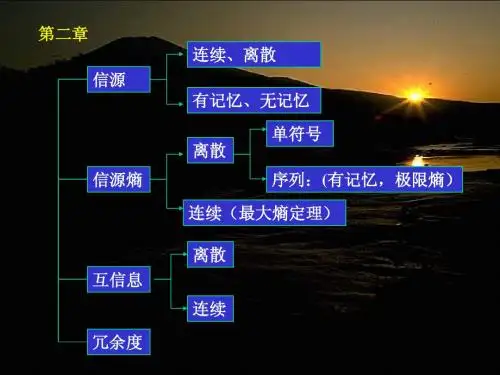
第二章:本章为基础性内容,主要是理解专业词语的含义,记住公式,可参考笔记。
第三章:
重点3.3节,特别是马尔可夫信源P37~P40,会画状态转移图,会求状态转移概率矩阵(例3.5 P38、例3.6 P40)。
第四章:
各种信道容量的计算P58(例4.1、4.2、4.3)、离散对称信道的判别和信道容量计算P61~P64。
第五章:
定长码、码的分类P91、定长码及定长编码定理P94、编码效率P97、Kraft和McMillan不等式、唯一可译码存在条件P100、编码效率及剩余度P108、变长码编码(例 5.5 P108、例5.6 P110、例5.7 P112、例5.8 P115、例5.9 P116)。
第六章:
最大后验概率译码准则、极大似然译码规则P131、平均错误概率P131(例6.3 P131)、编码效率P150、线性分组码P150(例6.6 、6.7、6.8 P154、例5.10 P161)。


《信息论基础》参考答案一、填空题 1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2、信源的剩余度主要来自两个方面,一是信源符号间的相关性,二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0,最大熵为32log bit/符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= H r (S))。
5、当R=C 或(信道剩余度为0)时,信源与信道达到匹配。
6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。
7、根据是否允许失真,信源编码可分为无失真信源编码和限失真信源编码。
8、若连续信源输出信号的平均功率为2σ,则输出信号幅度的概率密度是高斯分布或正态分布或()222x f x σ-=时,信源具有最大熵,其值为值21log 22e πσ。
9、在下面空格中选择填入数学符号“,,,=≥≤〉”或“〈”(1)当X 和Y 相互独立时,H (XY )=H(X)+H(X/Y)=H(Y)+H(X)。
(2)()()1222H X X H X =≥()()12333H X X X H X =(3)假设信道输入用X 表示,信道输出用Y 表示。
在无噪有损信道中,H(X/Y)> 0, H(Y/X)=0,I(X;Y)<H(X)。
二、若连续信源输出的幅度被限定在【2,6】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
()1,2640,x f x ⎧≤≤⎪=⎨⎪⎩其它()()()62log f x f x dx ∴=-⎰相对熵h x=2bit/自由度 该信源的绝对熵为无穷大。
三、已知信源1234560.20.20.20.20.10.1S s s s s s s P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用霍夫曼编码法编成二进制变长码;(6分) (2)计算平均码长L ;(4分) (3)计算编码信息率R ';(2分) (4)计算编码后信息传输率R ;(2分) (5)计算编码效率η。
《信息论与编码技术》复习提纲复习题《信息论与编码技术》复习提纲复习题纲第0章绪论题纲:I.什么是信息?II.什么是信息论?III.什么是信息的通信模型?IV.什么是信息的测度?V.自信息量的定义、含义、性质需掌握的问题:1.信息的定义是什么?(广义信息、狭义信息——Shannon信息、概率信息)2.Shannon信息论中信息的三要素是什么?3.通信系统模型图是什么?每一部分的作用的是什么?4.什么是信息测度?5.什么是样本空间、概率空间、先验概率、自信息、后验概率、互信息?6.自信息的大小如何计算?单位是什么?含义是什么(是对什么量的度量)?第1章信息论基础㈠《离散信源》题纲:I.信源的定义、分类II.离散信源的数学模型III.熵的定义、含义、性质,联合熵、条件熵IV.离散无记忆信源的特性、熵V.离散有记忆信源的熵、平均符号熵、极限熵VI.马尔科夫信源的定义、状态转移图VII.信源的相对信息率和冗余度需掌握的问题:1.信源的定义、分类是什么?2.离散信源的数学模型是什么?3.信息熵的表达式是什么?信息熵的单位是什么?信息熵的含义是什么?信息熵的性质是什么?4.单符号离散信源最大熵是多少?信源概率如何分布时能达到?5.信源的码率和信息率是什么,如何计算?6.什么是离散无记忆信源?什么是离散有记忆信源?7.离散无记忆信源的数学模型如何描述?信息熵、平均符号熵如何计算?8.离散有记忆多符号离散平稳信源的平均符号熵、极限熵、条件熵(N阶熵)的计算、关系和性质是什么?9.什么是马尔科夫信源?马尔科夫信源的数学模型是什么?马尔科夫信源满足的2个条件是什么?10.马尔科夫信源的状态、状态转移是什么?如何绘制马尔科夫信源状态转移图?11.马尔科夫信源的稳态概率、稳态符号概率、稳态信息熵如何计算?12.信源的相对信息率和冗余度是什么?如何计算?㈡《离散信道》题纲:I.信道的数学模型及分类II.典型离散信道的数学模型III.先验熵和后验熵IV.互信息的定义、性质V.平均互信息的定义、含义、性质、维拉图VI.信道容量的定义VII.特殊离散信道的信道容量需掌握的问题:1.信道的定义是什么?信道如何分类?信道的数学模型是2.二元对称信道和二元删除信道的信道传输概率矩阵是什么?3.对称信道的信道传输概率矩阵有什么特点?4.根据信道的转移特性图,写出信道传输概率矩阵。
信息理论与编码基础复习题1.从通信的实质意义来讲,如果信宿收到的消息是已知的,则等于没有收到任何消息。
2.当一个信源中所有的符号消息为等概时,该信源的熵最大。
3.即时码一定是单义可译码。
4.不使用间隔即可区分码字,就必然要求码字具有惟一性。
5.噪声熵为0的信道称为确定信道。
#000000#99CC00#999933#9933336.从通信的实质意义来讲,人们对消息中所包含的未知成分更感兴趣,用概率论的术语来说,就是具有不确定性的成分。
7.当两个集合相互独立时,它们的共熵最大。
8.等长码都是即时码。
9.无记忆离散信源发出的各个消息符号是相互独立的,即信源发出的符号序列中的各个符号之间没有关联性,各个符号的出现概率统计独立。
10.定长非奇异码肯定是惟一可译码。
11.消息中未知的或不确定的成分,通常被称为消息中所包含的信息,而消息的传递需要由信号来载荷。
12.代码组集合中的所有代码组都包含相同个数的码元的编码称为等长码。
13.信源编码器的主要任务是完成输入消息集合与输出代码集合之间的映射。
14.译码时不需要考察后续码元,称之为即时码。
15.在即时码中,任何一个码字都不是其他码字的延长。
16.通信系统的任务是将信源的消息有效可靠地传送到信宿。
17.在通信系统中,人们习惯于将通信分为数字通信和模拟通信,其实质亦是根据信源消息是数字还是模拟来划分的。
18.信源能够用随机过程来建模,从描述信源消息的随机过程的平稳性角度,信源可以分为平稳信源和非平稳信源,也可以按随机过程的类别将其分为高斯信源和马尔可夫信源等。
19.文本信源和语音信源都是针对人类语言、文字、声乐等感知的,又通称为自然语信源。
20.若信源发出的消息是由K个离散符号构成的符号序列,且各个消息相互统计独立,则称这种信源为发出符号序列消息离散无记忆信源。
21.若单符号离散无记忆信源的信源空间为[X∙P],对其进行K重扩展得到符号序列X=X1X2… X k,则称扩展后的信源为离散无记忆信源[X∙P]的K重扩展信源,记为X K。
“信息论与编码”总复习*****************************************************************************简要***************************************************************************** 第二章 信源与信息熵1.每次只发出一个符号代表一个消息的信源叫做发出单个符号的无记忆信源。
2.由一系列符号组成,这种用每次发出1组含2个以上符号序列来代表一个信息的信源叫做发出符号序列的信源。
3.信源发出的序列的统计性质与时间的推移无关,是平稳的随机序列。
4.当信源的记忆长度为m+1时,该时刻发出的符号与前m 个符号有关联性,而与更前面的符号无关,这种有记忆信源叫做m 阶马尔可夫信源。
若上述条件概率与时间起点无关,则信源输出的符号序列可看成齐次马尔可夫链,这样的信源叫做齐次马尔可夫信源。
5.例题:稳态分布概率|稳定后的符号概率分布:符号条件概率矩阵:1/22/33/44/5⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦j i 1/21/3[p(s |s )]=1/41/5状态转移概率矩阵1/20001/32/33/40004/5⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦j i 1/20[p(s |s )]=1/41/50令各稳态分布概率为W1,W2,W3,W4:1131124W W W =+ 2131324W W W =+ 3241135W W W =+ 4242435W W W =+ 12341W W W W +++= 得稳态分布的概率:W1=3/35 W2=6/35 W3=6/35 W4=4/7稳定后的符号概率分布:11131616149()(|)()2353354355735i i i p a p a s p s ==⨯+⨯+⨯+⨯=∑ 221326364426()(|)()2353354355735i i ip a p a s p s ==⨯+⨯+⨯+⨯=∑6.定义具有概率为()i p x 的符号i x 的自信息量为:()log ()i i I x p x =-7.自信息量具有下列特性:(1)()1,()0i i p x I x ==(2)()0,()i i p x I x ==∞(3)非负性(4)单调递减性(5)可加性8.信源熵是在平均意义上来表征信源的总体特征,它是信源X 的 函数,一般写成H (X )。
“信息论与编码”复习1.消息、信号、信息的含义、定义及区别。
信息是指各个事物运动的状态及状态变化的方式。
消息是指包含信息的语言,文字和图像等。
信号是消息的物理体现。
消息是信息的数学载体、信号是信息的物理载体信号:具体的、物理的消息:具体的、非物理的信息:非具体的、非物理的同一信息,可以采用不同形式的物理量来载荷,也可以采用不同的数学描述方式。
同样,同一类型信号或消息也可以代表不同内容的信息2.信息的特征与分类。
1接收者在收到信息之前,对其内容是未知的,所以信息是新知识,新内容;2信息是能使认识主体对某一事物的未知性或不确定性减少的有用知识;3信息可以产生,也可以消失,同时信息可以被携带,被存储及处理;4信息是可以量度的,信息量有多少的差别。
3.狭义信息论、广义信息论、一般信息论研究的领域。
狭义信息论:信息论是在信息可以量度的基础上,对如何有效,可靠地传递信息进行研究的科学。
它涉及信息量度,信息特性,信息传输速率,信道容量,干扰对信息传输的影响等方面的知识。
广义信息论:信息是物质的普遍属性,所谓物质系统的信息是指它所属的物理系统在同一切其他物质系统全面相互作用(或联系)过程中,以质、能和波动的形式所呈现的结构、状态和历史。
包含通信的全部统计问题的研究,除了香农信息论之外,还包括信号设计,噪声理论,信号的检测与估值等。
概率信息:信息表征信源的不定度,但它不等同于不定度,而是为了消除一定的不定度必须获得与此不定度相等的信息量4.信息论的起源、历史与发展。
⏹1924年,Nyquist提出信息传输理论;⏹1928年,Hartly提出信息量关系;⏹1932年,Morse发明电报编码;⏹1946年,柯切尼柯夫提出信号检测理论;⏹1948年,Shannon提出信息论,“通信中的数学理论”—现代信息论的开创性的权威论文,为信息论的创立作出了独特的贡献。
5.通信系统的物理模型(主要框图),各单元(方框)的主要功能及要解决的主要问题。
信息论基础与编码复习一、已知信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡5.05.021x x P X 接到信道⎪⎪⎭⎫⎝⎛=8.02.002.098.0)|(X Y P 上,求在该信道上传输的平均互信息量);(Y X I 、疑义度)|(Y X H ,噪声熵)|(X Y H 和联合熵)(XY H 。
参考答案:不要求计算结果,只要与出公式,每份5分,共20分()()(|)P Y P X P Y X =)|(X Y H =-22211()log (|)i j j i i j p x y p y x ==∑∑)|(Y X H =-22211()log (|)i j i j i j p x y p x y ==∑∑)(XY H =-22211()log ()i j i j i j p x y p x y ==∑∑);(Y X I =()()()H X H Y H XY +-二、一维随机变量X 在区间],[b a 内均匀分布,试求此连续信源的熵)(x H c 。
参考答案:1222()()log ()log ()log ()bc b a aH X p x p x dx b a dx b a +∞--∞=-=-=-⎰⎰(bit ) (10分)三、一维随机变量X 的取值是),(+∞-∞,其概率密度函数为222)(221)(σμπσ--=x ex p (高斯信道),试求此连续信源的熵)(x H c 。
参考答案:()EX xp x dx μ+∞-∞==⎰22()()DX x p x dx μσ+∞-∞=-=⎰ (5分)2122()()log ()log (2)c H X p x p x dx e πσ+∞-∞=-=⎰(bit ) (10分)五、一个三状态马尔可夫信源的转移概率矩阵为⎪⎪⎪⎭⎫ ⎝⎛=4121412121212100P ,请绘制状态转移图,并求该马尔可夫信源的稳态分布。
( 10 分) 参考答案:1、绘制状态转移图 (5分) 2、稳态分布731)(=s P ,722)(=s P ,723)(=s P (5分)六、试求以下列信道矩阵代表的信道容量。
⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100010001001001001][654321321x x x x x x y y y P 参考答案:归并信道,2max(;)max ()log 3()C I X Y H Y p x === /b i t s i g n (10分)七、设一四元对称信源⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡414141413210)(X P X ,接收符号{}3,2,1,0=Y ,其其失真矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0111101111011110D ,试求max D ,min D 及信息率失真函数)(D R 。
(15分) 参考答案:min D =1()min (,)0niijji p x d x y ==∑ (5分)max D =34min j jD = (5分)()ln ln (1)ln(1)DD D D R D n α=++--32ln (1)ln(1)D D D D =++-- (5分) 八、设有一单符号离散信源:1234()0.50.20.20.1X x x x x P X ⎧⎫⎡⎤=⎨⎬⎢⎥⎣⎦⎩⎭,试求其信源熵、二进制哈夫曼编码(最优编码),并计算平均码长。
(15分)参考答案:画出最优二元树 (5分) 编码1234010110111x x x x ⎧⎫⎨⎬⎩⎭ (5分)平均码长:0.5*10.2*20.2*30.1*3 1.8K =+++= (5分)九、设有一单符号离散信源:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X ,试求其信源熵、二进制香农编码,并计算平均码长。
(15分) 参考答案:求信源熵 (5分) 按概率从大到小的排序,计算概率和 编码111111011101011000110010007654321x x x x x x x (5分)平均码长:14.37*01.04*1.03*)15.017.018.019.02.0(=++++++=K (5分)十、设1a ,2a 分别代表某工厂合格品和废品,设该厂产品的合格率)(1a p =99%,废品率)(2a p =1%,若合格品出厂、废品报废,则不会造成损失;若将一个合格品报废,则损失1元;若将一个废品出厂,则损失100元。
现检测系统把合格品误判为废品、废品误判为合格品的概率均为10%,试计算这种检测系统的信息价值率。
(15分) 参考答案: )01.099.0()(21a a X P =,)9.01.01.09.0()|(=X Y P()()(|)i i i i i p x y p x p y x =)010010(=D0min =D21()(,)j i i j i D p x d x y ==∑99.0}99.0,1{min min max ===jj jD D 元, (10分)D =0.199元,∴D D -max =0.791元,(|)()()min(;)j i p y x p D R D I X Y ∈=2222221111(|)(|)(;)()log ()log ()()i j j i i j i j i j i j i i p x y p y x I X Y p x y p x y p x p x =====-=-∑∑∑∑=0.025(sign bit /)所以信息价值率为:max ()D DV R D -==31.6元/比特。
(15分)十一、设某地区的“晴天”概率6/5)(1=a p ,“雨天”概率6/1)(2=a p ,把“晴天”预报为“雨天”、把“雨天”预报为“晴天”造成的损失均为a 元。
又设该预报系统把“晴天”预报为“雨天”、把“雨天”预报为“晴天”的概率均为0.1,把“晴天”预报为“晴天”、把“雨天”预报为“雨天”的概率均为0.9。
试计算这种预报系统的信息价值v (元比特) (15分)参考答案:由题意有:0.90.1(|)0.90.1P Y X ⎛⎫= ⎪⎝⎭12()5166x x P X ⎛⎫ ⎪= ⎪ ⎪⎝⎭()()(|)i i i i i p x y p x p y x =4.50.566()0.90.166P XY ⎛⎫ ⎪=⎪ ⎪ ⎪⎝⎭00a D a ⎛⎫= ⎪⎝⎭0a > (5分)21()(,)j i i j i D p x d x y ==∑1111221()(,)()(,)6a D p x d x y p x d x y =+=21122225()(,)()(,)6aD p x d x y p x d x y =+=max 12min 6j j aD D ≤≤==2211()(|)(,)0.1i j i i j i j D p x p y x d x y a ====∑∑ (10分)∴ max 15aD D -=(|)()()min(;)j i p y x p D R D I X Y ∈=2222221111(|)(|)(;)()log ()log ()()i j j i i j i j i j i j i i p x y p y x I X Y p x y p x y p x p x =====-=-∑∑∑∑所以信息价值率为:max ()D DV R D -=(15分)十二、设有一(7,4)循环码的生成多项式为3()1g x x x =++,试求其生成矩阵和一致校验矩阵,检验接收码字1110011=R 是否有错? (15分) 参考答案:1)(3++=x x x g ,7()(1)/()h x x g x =+=421x x x +++ (5分)按()g x 的升幂()h x 降幂(或者按()g x 的降幂()h x 升幂)生成矩阵11010000110100()00110100001101G =一致校验矩阵1011100(0101110)0010111H = (5分)*T H R =(0,0,1)0T ≠,所以检验出有错误,第七个符号错。
(5分)十三、选择帧长64=N ,对0000000000000000000000000100000000000000000000000000000000000000编冗余位L —D 编码,并译码。
参考答案:264,[log (1)]7N N =+=,用七位编码表示Q (5分)编码:1Q =,126n =,2[log ]6QN c =,11225(11001)Qn T C -===所以,编码为0000001011001 (5分) 译码:前七位表示1Q =,后六位表示25T = 所以126n = (5分)十四、设有一线性分组码的生成多项式为⎪⎪⎪⎭⎫⎝⎛=110100011010101001G ,试求:1、 此分组码??,==k n ,共有多少码字?2、 求此分组码的较验矩阵H ;3、 接收到001001=R 是否有错? (15分)参考答案:1、3,6==k n , 共有823=个码字 (5分)2、较验矩阵⎪⎪⎪⎭⎫⎝⎛=100101010110001011H (5分)*T H R =0)0,1,0(≠T ,所以检验出有错误,第第五个符号错。
(5分)。