2012高考数学 单元检测卷15套8

山东省各地市2012年高考数学（理科）最新试题分类大汇编：第8部分：立体几何（3）一选择题【山东省青州市2012届高三上学期期中理】5．已知α、β是两上不同的平面，m ，n 是两条不同的直线，给出下列命题： ①若,,m m αβαβ⊥⊂⊥则；②若,,//,//m n m n ααββ⊂⊂，则//αβ③如果,,,m n m n αα⊂⊄是异面直线，那么n 与α相交； ④若,//,,,m n m n n αβαβ=⊄⊄且则////n n αβ且。

其中正确的命题是 （ ） A ．①② B ．②③ C ．③④ D ．①④ 【答案】D【山东省日照市2012届高三上学期期末理】（5）下列四个几何体中，各几何体的三视图有且仅有两个视图相同的是（A ）①② （B ）②③ （C ）②④ （D ）①③【答案】C 解析：①的三个视图都相同；②的主视图与左视图相同，与俯视图不同；③的三个视图互不相同；④的主视图与左视图相同，而与俯视图不同。

【山东省日照市2012届高三上学期期末理】（8）已知m ，n 是两条不同直线，βα,是两个不同平面，下列命题中的假命题的是（A ）βαβα//,,则若⊥⊥m m（B ）αα⊥⊥n m n m 则若,,// （C ）n m n m //,,//则若=βαα（D ）βαβα⊥⊂⊥则若,,m m【答案】C 解析：由n m =βαα ,//无法得到m ，n 的确切位置关系。

【山东省青州市2012届高三2月月考理】9. 已知某几何体的三视图如右图所示，其中，正（主）视图，侧（左）视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为12+ B.4136π+16+ D.2132π+ 【答案】C【山东省青岛市2012届高三期末检测 理】5.的尺寸（单位：cm ），可得这个几何体的体积是 Ａ．34000cm 3 Ｂ．38000cm 3Ｃ．3【答案】B【山东省青岛市2012届高三期末检测 理】8.已知a 、b 、c 为三条不重合的直线，下面有三个结论：①若c a b a ⊥⊥,则b ∥c ； ②若c a b a ⊥⊥,则b ⊥c ；③若a ∥,b b ⊥c 则c a ⊥. 其中正确的个数为A ．0个B ．1个C ． 2个D ． 3个【答案】B【山东省实验中学2012届高三第三次诊断理】设有直线m 、n 和平面βα、,下列四个命题中，正确的是（ ）A.若n m n m //,//,//则ααB.若βαββαα//,//,//,,则n m n m ⊂⊂正视图俯视图C.若βαβα⊥⊂⊥m m 则,,D.若ααββα//,,,m m m 则⊄⊥⊥【答案】D【山东省实验中学2012届高三第三次诊断理】在正三棱锥S-ABC 中，M 、N 分别是SC 、BC 的中点，且AM MN ⊥，若侧菱SA=32，则正三棱 S-ABC 外接球的表面积为（ ） A.12π B.32π C.36π D.48π【答案】C【山东省潍坊一中2012届高三阶段测试理】7.设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，给出一列四个命题：①若,α⊥m α//n ，则n m ⊥；②若βα//，γβ//，,α⊥m 则γ⊥m ； ③若,//αm α//n ，则n m //； ④若γα⊥，γβ⊥，则βα//. 其中正确．．命题的序号是 A.①和② B.②和③ C.③和④ D.①和④ 【答案】A【山东省潍坊一中2012届高三阶段测试理】 8.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形，俯 视图是直径为2的圆(如右图），则这个几何体的表面积为A.12+πB.7πC.π8D.π20【答案】C【山东省烟台市2012届高三期末检测理】3.设b ，c 表示两条直线，α，β表示两个平面，则下列命题正确的是A. b c c b //,//,则若αα⊂B. αα//,//,c c b b 则若⊂C. ββαα⊥⊥c c 则若,,//D. βαβα⊥⊥则若,,//c c【答案】D【山东省潍坊市重点中学2012届高三2月月考理】4. 某空间几何体的三视图如图所示，则该几何体的体积是A ．2B ．1C ．32D ．31【答案】B【山东省日照市2012届高三12月月考理】（6象如图所示，为了得到x x g 2sin )(=（A ）向右平移6π个长度单位（B ）向右平移3π个长度单位（C ）向左平移6π个长度单位（D ）向左平移3π个长度单位【答案】A 解析：由图象可知A=1ππ=⇒=T 4，从而22==Tπω，将)1,127(-π代入到)2sin()(ϕ+=x x f 1)-=，根据2πϕ<得到3πϕ=，所以函数)(x f 的解析式为)32sin()(π+=x x f 。

读下面的材料，根据要求作文。

每一个人的心灵深处都希望能得到别人的肯定，而来自他人的一句普普通通的喝彩，也将给我们的生活注入鲜活的美丽，有时甚至会影响一个人的一生。

请以"喝彩"为话题写一篇文章。

【要求】①思想健康，感情真挚，立意自定；②文体不限；③题目自拟；④不少于600字。

【提示】本题属思想感情的限制。

所谓思想健康，具体要做到"三不要"： ①不要选择毫无意义的材料；②不要流露出低沉消极的情绪；③不要表现片面或错误的观点。

所谓感情真挚，要注重"三贵"：①贵亲历；②贵坦诚；③贵自然。

思想感情的限制是考纲的要求，我们写任何文章都必须坚定不移地遵循。

为 自 己 喝 彩 ? 中国古代伟大的思想家老子说：“知人者智，自知者明。

”在古希腊德尔斐阿波罗神庙入口处的一块石头上刻着“认识你自己”这句名言。

这些充满睿智的箴言告诉我们，人的一生，认识自己最重要，也最困难。

“金无足赤，人无完人。

”每个人都像是天空中的一颗星，无论是显赫的，还是普通的，都能找到自己的位置。

只要闪烁着，就有辉煌的机会。

我总认为自己是被上帝忽略的孩子：其貌不扬，大大咧咧，小肚鸡肠，又不聪明，粗心大意……诸多缺点构成了一个极其平凡的我。

我没有女生应有的矜持，却有男生应有的热情；我没有女生的“多愁善感”，却有男孩子的“不拘小节”──明天要考试，晚上还啃着苹果听音乐，白球鞋三天便面目全非，书本乱放，没有规律……我没有女孩子的“温文而雅”，却有男孩子的野，也因为我有男孩子的开朗，所以不会“为赋新词强说愁” …… 执着，是我的另一大闪光点。

“不到长城非好汉”，有时，为了一道题，我与同学喋喋不休，最后灰头灰脑地转过身握着笔在纸上龙飞凤舞地验算。

一次，我买了个改正带，结果还不到一天就被同学给弄坏了，这可把我给气坏了，与他大打出手。

中午回到家，我对着改正带，左思右想地不甘心，决定修好它。

第八章 单元能力测试一、选择题(本大题共12小题，每小题5分，共60分．每小题中只有一项符合题目要求) 1.如右图所示，是一个正方体的表面展开图，A 、B 、C 均为棱的中点，D 是顶点，则在正方体中，异面直线AB 和CD 的夹角的余弦值为( )A.25B.35C.105D.55 答案 C 解析把展开图复原为正方体后示意图如右图所示，∠EGF 为AB 和CD 所成的角，F 为正方体一棱的中点．∴EF ＝GF ＝52，EG ＝ 2.∴cos ∠EGF ＝105.2．用与球心距离为1的平面去截球，所得的截面面积为π，则球的体积为( ) A.8π3 B.82π3 C ．82π D.32π3 答案 B解析 S 圆＝πr 2＝1⇒r ＝1，而截面圆圆心与球心的距离d ＝1，∴球的半径为R ＝r 2＋d 2＝2，∴V ＝43πR 3＝82π3，故选B.3.已知某个几何体的三视图如图所示，根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )A.13cm 3B.23cm 3C.43cm 3D.83cm 3 答案 C解析 由三视图可知该几何体为三棱锥，如图所示，其中AC ＝AD ，平面ACD ⊥平面BCD ，E 为CD 的中点，则AE ⊥平面BCD ，且BE ＝AE ＝2，DC ＝2，∴V ＝13×12×BE ×DC ×AE ＝13×12×2×2×2＝43cm 3，故选C.4．已知m 、n 是两条不同的直线，α、β是两个不同的平面，给出下列命题：①若α⊥β，m ∥α，则m ⊥β；②若m ⊥α，n ⊥β，且m ⊥n ，则α⊥β；③若m ⊥β，m ∥α，则α⊥β；④若m ∥α，n ∥β，且m ∥n ，则α∥β.其中真命题的序号是( )A ．①④B ．②③C ．②④D ．①③ 答案 B解析 若α⊥β，m ∥α，则m 与β可能相交、平行或m 在平面β内，故①错；m ∥α，n ∥β，m ∥n ，则α与β可能平行，可能相交，故④错．故选B.5．(2010·湖北卷)用a ，b ，c 表示三条不同的直线，γ表示平面，给出下列命题： ①若a ∥b ，b ∥c ，则a ∥c ； ②若a ⊥b ，b ⊥c ，则a ⊥c ； ③若a ∥γ，b ∥γ，则a ∥b ； ④若a ⊥γ，b ⊥γ，则a ∥b . 其中真命题的序号是( )A ．①②B ．②③C ．①④D ．③④ 答案 C解析 对于①，由公理“平行于同一直线的两条直线平行”可知，①正确；对于②，如在长方体ABCD －A 1B 1C 1D 1中，AB ⊥AD ，CD ⊥AD ，此时AB 平行于CD ，因此②不正确．对于③，如当平面α∥γ时，平面α内的任意两条直线a ，b 都平行于平面γ，显然此时直线a ，b 可能相交，因此③不正确．对于④，由“垂直于同一平面的两条直线平行”可知其正确性．综上所述，其中真命题的序号是①④，选C.6.如右图所示，正四棱锥P －ABCD 的底面积为3，体积为22，E 为侧棱PC 的中点，则P A 与BE 所成的角为( )A.π6B.π4C.π3D.π2答案 C解析 连结AC 、BD 交于点O ，连结OE ，易得OE ∥P A . ∴所求角为∠BEO .由所给条件易得OB ＝62，OE ＝12P A ＝22，BE ＝2，∴cos ∠OEB ＝12，∴∠OEB ＝60°，选C. 7.如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝BC ＝2，AA 1＝1，则BC 1与平面BB 1D 1D 所成角的正弦值为( )A.63B.255C.155D.105 答案 D解析 连结A 1C 1，交B 1D 1于O ，依题意得，A 1C 1⊥B 1D 1，BB 1⊥A 1C 1，又B 1D 1∩BB 1＝B 1，∴A 1C 1⊥平面BB 1D 1D .连结BO ，则∠C 1BO 为所求角，又OC 1＝2，BC 1＝5，∴sin C 1BO ＝C 1O BC 1＝25＝105，选D.8．圆台上、下底面面积分别是π、4π，侧面积是6π，这个圆台的体积是( ) A.233π B ．23π C.736π D.733π 答案 D解析 上底半径r ＝1，下底半径R ＝2.∵S 侧＝6π，设母线长为l ，则π(1＋2)·l ＝6π，∴l＝2，∴高h ＝l 2－(R －r )2＝3，∴V ＝13π·3(1＋1×2＋2×2)＝733π.故选D.9．如图，四棱锥P －ABCD 的底面为正方形，PD ⊥底面ABCD ，PD ＝AD ＝1，设点C 到平面P AB 的距离为d 1，点B 到平面P AC 的距离为d 2，则有( )A ．1<d 1<d 2B ．d 1<d 2<1C ．d 1<1<d 2D ．d 2<d 1<1 答案 D解析 ∵CD ∥平面P AB .∴C 到平面P AB 的距离等于D 到平面P AB 的距离．过D 作DE ⊥P A ，则DE ⊥平面P AB ，d 1＝DE ＝22. B 与D 到平面P AC 的距离相等．设AC ∩BD ＝O ，则平面PDO ⊥平面P AC ，∴d 2等于D 到PO 的距离，可计算d 2＝33，∴d 2<d 1<1.10．半径为4的球面上有A ，B ，C ，D 四点，且满足AB →·AC →＝0，AD →·AC →＝0，AB →·AD →＝0，则△ABC ，△ACD ，△ADB 面积之和S △ABC ＋S △ACD ＋S △ADB 的最大值为( ) A ．8 B ．16 C ．32 D ．64 答案 C解析 设AB ＝a ，AC ＝b ，AD ＝c ，则S △ABC ＋S △ACD ＋S △ADB ＝12(ab ＋ac ＋bc )≤12(a 2＋b 22＋a 2＋c 22＋b 2＋c 22) ＝12(a 2＋b 2＋c 2) ＝12×4R 2＝12×4×42＝32，当且仅当a ＝b ＝c 时取“＝”．11．二面角的棱上有A 、B 两点，直线AC 、BD 分别在这个二面角的两个半平面内，且都垂直于AB .已知AB ＝4，AC ＝6，BD ＝8，CD ＝217，则该二面角的大小为( )A ．150°B ．45°C ．60°D ．120° 答案 C解析 由条件，知CA →·AB →＝0，AB →·BD →＝0，CD →＝CA →＋AB →＋BD →.∴|CD →|2＝|CA →|2＋|AB →|2＋|BD →|2＋2CA →·AB →＋2AB →·BD →＋2CA →·BD →＝62＋42＋82＋2×6×8cos 〈CA →，BD →〉＝(217)2，∴cos 〈CA →，BD →〉＝－12，〈CA →，BD →〉＝120°，∴二面角的大小为60°，故选C.12．已知正方体ABCD －A 1B 1C 1D 1棱长为1，点P 在线段BD 1上，当∠APC 最大时，三棱锥P －ABC 的体积为( )A.124B.118C.19D.112答案 B解析 以B 为坐标原点，BA 为x 轴，BC 为y 轴，BB 1为z 轴建立空间直角坐标系，设BP→＝λBD 1→，可得P (λ，λ，λ)，再由cos ∠APC ＝AP →·CP →|AP →||CP →|可求得当λ＝13时，∠APC 最大，故V P －ABC ＝13×12×1×1×13＝118.二、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中横线上)13．若一个底面是正三角形的三棱柱的正视图如图所示，则其表面积等于________． 答案 6＋2 3解析 由正视图可知此三棱柱是一个底面边长为2的正三角形、侧棱为1的直三棱柱．则此三棱柱的侧面积为2×1×3＝6，上、下底面面积都为34×22＝3，所以此三棱柱的表面积为6＋2 3.14．如图，在直四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 是菱形，∠BAD ＝60°，AA 1＝AB ＝1，则截面ACC 1A 1的面积为________；异面直线AD 与D 1C 所成角的余弦值为________．答案 3 24解析 截面ACC 1A 1为矩形．AA 1＝1，AC ＝3，其面积S ＝3；BD ＝1，BD 1＝2，在△BCD 1中，BC ＝1，CD 1＝2，cos ∠BCD 1＝24.则异面直线AD 与D 1C 所成角的余弦值为24. 15.如图是一几何体的平面展开图，其中ABCD 为正方形，E 、F 、分别为P A 、PD 的中点，在此几何体中，给出下面四个结论：①直线BE 与直线CF 异面； ②直线BF 与直线AF 异面 ③直线EF ∥平面PBC ； ④平面BCE ⊥平面P AD . 其中正确的有______个． 答案 2解析 将几何体展开拼成几何体(如图)，因为E 、F 分别为P A 、PD 的中点，所以EF ∥AD ∥BC ，即直线BE 与CF 共面，①错；因为B ∉平面P AD ，E ∈平面P AD ，E ∉AF ，所以BE 与AF 是异面直线，②正确；因为EF ∥AD ∥BC ，EF ⊄平面PBC ，BC ⊂平面PBC ，所以EF ∥平面PBC ，③正确；平面P AD 与平面BCE 不一定垂直，④错．16．直三棱柱ABC －A 1B 1C 1的各顶点都在同一球面上．若AB ＝AC ＝AA 1＝2，∠BAC ＝120°，则此球的表面积等于______．答案 20π解析 设球心为O ，球半径为R ，△ABC 的外心是M ，则O 在底面ABC 上的射影是点M ，在△ABC 中，AB ＝AC ＝2，∠BAC ＝120°，∠ABC ＝12(180°－120°)＝30°，AM ＝AC2sin30°＝2.因此，R 2＝22＋(AA 12)2＝5，此球的表面积等于4πR 2＝20π.三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)在下面三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出(单位：cm)．(1)在正视图下面，按照画三视图的要求画出该多面体的俯视图； (2)按照给出的尺寸，求该多面体的体积；(3)在所给直观图中连结BC ′，证明：BC ′∥平面EFG .解析 (1)如图．(2)所求多面体的体积V ＝V 长方体－V 正三棱锥＝4×4×6－13×⎝ ⎛⎭⎪⎫12×2×2×2＝2843(cm 3)．(3)证明：如图，在长方体ABCD －A ′B ′C ′D ′中，连结AD ′，则AD ′∥BC ′. 因为E 、G 分别为AA ′、A ′D ′的中点， 所以AD ′∥EG ，从而EG ∥BC ′.又BC ′⊄平面EFG ，所以BC ′∥平面EFG . 18．(本小题满分12分)(2010·新课标全国，文)如图，已知四棱锥P －ABCD 的底面为等腰梯形，AB ∥CD ，AC ⊥BD ，垂足为H ，PH 是四棱锥的高．(1)证明：平面P AC ⊥平面PBD ； (2)若AB ＝6，∠APB ＝∠ADB ＝60°，求四棱锥P －ABCD 的体积． 解析 (1)因为PH 是四棱锥P －ABCD 的高，所以AC ⊥PH .又AC ⊥BD ，PH ，BD 都在平面PBD 内，且PH ∩BD ＝H ， 所以AC ⊥平面PBD ， 故平面P AC ⊥平面PBD .(2)因为ABCD 为等腰梯形，AB ∥CD ，AC ⊥BD ，AB ＝6， 所以HA ＝HB ＝ 3.因为∠APB ＝∠ADB ＝60°，所以P A ＝PB ＝6，HD ＝HC ＝1. 可得PH ＝3，等腰梯形ABCD 的面积为S ＝12AC ×BD ＝2＋ 3.所以四棱锥的体积为V ＝13×(2＋3)×3＝3＋233.19．(本小题满分12分)在几何体ABCDE 中，∠BAC ＝π2，DC ⊥平面ABC ，EB ⊥平面ABC ，AB ＝AC ＝BE ＝2，CD ＝1.(1)设平面ABE 与平面ACD 的交线为直线l ，求证：l ∥平面BCDE ； (2)设F 是BC 的中点，求证：平面AFD ⊥平面AFE ； (3)求几何体ABCDE 的体积．解析 (1)∵CD ⊥平面ABC ，BE ⊥平面ABC ， ∴CD ∥BE .∵CD ⊄平面ABE ，BE ⊂平面ABE ，∴CD ∥平面ABE . 又l ＝平面ACD ∩平面ABE ，∴CD ∥l . 又l ⊄平面BCDE ，CD ⊂平面BCDE ， ∴l ∥平面BCDE .(2)在△DFE 中，FD ＝3，FE ＝6，DE ＝3. ∴FD ⊥FE .∵CD ⊥平面ABC ，∴CD ⊥AF ，又BC ⊥AF ，CD ∩BC ＝C ，∴AF ⊥平面BCDE ， ∴AF ⊥FD ，∵EF ∩AF ＝F ， ∴FD ⊥平面AFE .又FD ⊂平面AFD ，∴平面AFD ⊥平面AFE .(3)∵DC ⊥平面ABC ，BE ⊥平面ABC ，∴DC ∥BE∵AB ＝AC ＝2，且∠BAC ＝π2 ∴BC ＝2 2∴SBEDC ＝12(DC ＋BE )×BC ＝3 2由(2)知AF ⊥平面BCED∴V E －BCDE ＝13S BEDC ·AF ＝13×32×2＝2. 20．(本小题满分12分)如图，在六面体ABCDEFG 中，平面ABC ∥平面DEFG ，AD ⊥平面DEFG ，ED ⊥DG ，EF ∥DG .且AB ＝AD ＝DE ＝DG ＝2，AC ＝EF ＝1.(1)求证：BF ∥平面ACGD ； (2)求二面角D -CG -F 的余弦值．解析 方法一 (1)设DG 的中点为M ，连接AM ，FM . 则由已知条件易证四边形DEFM 是平行四边形．∴MF ∥DE ，且MF ＝DE .∵平面ABC ∥平面DEFG ，∴AB ∥DE ， ∵AB ＝DE .∴MF ∥AB ，且MF ＝AB ，∴四边形ABFM 是平行四边形， ∴BF ∥AM .又BF ⊄平面ACGD ，AM ⊂平面ACGD ， 故BF ∥平面ACGD .(2)由已知AD ⊥平面DEFG ，∴DE ⊥AD .又DE ⊥DG ，∴DE ⊥平面ADGC .∵MF ∥DE ，∴MF ⊥平面ADGC .在平面ADGC 中，过M 作MN ⊥GC ，垂足为N ，连接NF ，则∠MNF 为所求二面角的平面角．连接CM .∵平面ABC ∥平面DEFG ，∴AC ∥DM ，又AC ＝DM ＝1，所以四边形ACMD 为平行四边形，∴CM ∥AD ，且CM ＝AD ＝2.∵AD ⊥平面DEFG ，∴CM ⊥平面DEFG ，∴CM ⊥DG.在Rt △CMG 中，∵CM ＝2，MG ＝1，∴MN ＝CM ·MG CG ＝25＝255.在Rt △FMN 中，∵MF ＝2，MN ＝255，∴FN ＝4＋45＝2305.∴cos ∠MNF ＝MN FN ＝2552305＝66.∴二面角D -CG -F 的余弦值为66.方法二 由题意可得，AD ，DE ，DG 两两垂直，故可建立如图所示的空间直角坐标系． 则A (0,0,2)，B (2,0,2)，C (0,1,2)，E (2,0,0)，G (0,2,0)，F (2,1,0)． (1)BF→＝(2,1,0)－(2,0,2)＝(0,1，－2)，CG →＝(0,2,0)－(0,1,2)＝(0,1，－2)，∴BF →＝CG →，所以BF ∥CG .又BF ⊄平面ACGD ，故BF ∥平面ACGD . (2)FG→＝(0,2,0)－(2,1,0)＝(－2,1,0)． 设平面BCGF 的法向量为n 1＝(x ，y ，z )，则⎩⎪⎨⎪⎧n 1·CG →＝y －2z ＝0，n 1·FG →＝－2x ＋y ＝0.令y ＝2，则n 1＝(1,2,1)．则平面ADGC 的法向量n 2＝i ＝(1,0,0)．∴cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝1×112＋22＋12×12＋02＋02 ＝66.由于所求的二面角为锐二面角，∴二面角D -CG -F 的余弦值为66.21．(本小题满分12分)(2010·重庆卷，理)如图，四棱锥P －ABCD 中，底面ABCD 为矩形，P A ⊥底面ABCD ，P A ＝AB ＝6，点E 是棱PB 的中点．(1)求直线AD 与平面PBC 的距离；(2)若AD ＝3，求二面角A －EC －D 的平面角的余弦值．解析 解法一：(1)如图，在矩形ABCD 中，AD ∥BC ，从而AD ∥平面PBC ，故直线AD与平面PBC 的距离为点A 到平面PBC 的距离．因P A ⊥底面ABCD ，故P A ⊥AB ，由P A ＝AB 知ΔP AB 为等腰直角三角形，又点E 是棱PB 的中点，故AE ⊥PB .又在矩形ABCD 中，BC ⊥AB ，而AB 是PB 在底面ABCD 内的射影，由三垂线定理得BC ⊥PB ，从而BC ⊥平面P AB ，故BC ⊥AE ，从而AE ⊥平面PBC ，故AE 之长即为直线AD 与平面PBC 的距离．在Rt ΔP AB 中，P A ＝AB ＝6，所以AE ＝12PB ＝12P A 2＋AB 2＝ 3.(2)过点D 作DF ⊥CE ，交CE 于F ，过点F 作FG ⊥CE ，交AC 于G ，则∠DFG 为所求的二面角的平面角．由(1)知BC ⊥平面P AB ，又AD ∥BC ，得AD ⊥平面P AB ，故AD ⊥AE ，从而DE ＝AE 2＋AD 2＝ 6.在Rt ΔCBE 中，CE ＝BE 2＋BC 2＝ 6.由CD ＝6，所以ΔCDE 为等边三角形，故F 点为CE 的中点，且DF ＝CD ·sin π3＝322.因为AE ⊥平面PBC ，故AE ⊥CE ，又FG ⊥CE ，知FG 綊12AE ，从而FG ＝32，且G 点为AC 的中点．连接DG ，则在Rt ΔADC 中，DG ＝12AC ＝12AD 2＋CD 2＝32.所以cos ∠DFG ＝DF 2＋FG 2－DG 22·DF ·FG ＝63.解法二：(1)如图，以A 为坐标原点，射线AB 、AD 、AP 分别为x 轴、y 轴、z 轴正半轴，建立空间直角坐标系A －xyz .设D (0，a,0)则B (6，0,0)，C (6，a,0)，P (0,0，6)，E (62，0，62)．因此AE →＝(62，0，62)，BC →＝(0，a,0)，PC →(6，a ，－6)， 则AE →·BC →＝0，AE →·PC →＝0，所以AE ⊥平面PBC . 又由AD ∥BC 知AD ∥平面PBC ，故直线AD 与平面PBC 的距离为点A 到平面PBC 的距离，即为|AE →|＝ 3.(2)因为|AD →|＝3，则D (0，3，0)，C (6，3，0)．设平面AEC 的法向量n 1＝(x 1，y 1，z 1)，则n 1·AC →＝0，n 1·AE →＝0，又AE →＝(6，3，0)，AE →＝(62，0，62)，故⎩⎨⎧ 6x 1＋3y 1＝0，62x 1＋62z 1＝0，所以y 1＝－2x 1，z 1＝－x 1，可取x 1＝－2，则n 1＝(－2，2，2)． 设平面DEC 的法向量n 2＝(x 2，y 2，z 2)，则n 2·DC →＝0，n 2·DE →＝0.又DC →＝(6，0,0)，DE →＝(62，－3，62)，故⎩⎨⎧ x 2＝0，62x 2－3y 2＋62z 2＝0.所以x 2＝0，z 2＝2y 2.可取y 2＝1，则n 2＝(0,1，2)．故cos 〈n 1·n 2〉＝n 1·n 2|n 1|·|n 2|＝63. 所以二面角A －EC －D 的平面角的余弦值为63.22．(本小题满分12分)如图，在长方体ABCD －A 1B 1C 1D 1中，AD ＝AA 1＝1，AB >1，点E 在棱AB 上移动，小蚂蚁从点A 沿长方体的表面爬到点C 1，所爬的最短路程为2 2.(1)求证：D 1E ⊥A 1D ；(2)求AB 的长度；(3)在线段AB 上是否存在点E ，使得二面角D 1－EC －D 的大小为π4，若存在，确定点E的位置；若不存在，请说明理由．解析 方法一：(1)连结AD 1，由长方体的性质可知：AE ⊥平面AD 1，∴AD 1是ED 1在平面AD 1内的射影．又∵AD ＝AA 1＝1，∴AD 1⊥A 1D ，∴D 1E ⊥A 1D (三垂线定理)．(2)设AB ＝x ，∵四边形ADD 1A 1是正方形，∴小蚂蚁从点A 沿长方体的表面爬到点C 1，可能有四种途径，如图甲、乙的最短路程为|AC 1|＝x 2＋4，如图丙、丁的最短路程为|AC 1|＝(x ＋)2＋1＝x 2＋2x ＋2，∵x >1，∴x 2＋2x ＋2>x 2＋2＋2＝x 2＋4， ∴x 2＋4＝22，∴x ＝2.(3)假设存在，连结DE ，设EB ＝y ，过点D 在平面ABCD 内作DH ⊥EC ，连结D 1H ，则∠D 1HD 为二面角D 1－EC －D 的平面角，∴∠D 1HD ＝π4，∴DH ＝DD 1＝1，在Rt △EBC 内，EC ＝y 2＋1，而EC ·DH ＝DC ·AD ， 即y 2＋1＝2解得y ＝ 3.即存在点E ，且离点B 为3时，二面角D 1－EC －D 的大小为π4.方法二：(1)如图建立空间直角坐标系，设AE ＝a ，则E (1，a,0)，D 1(0,0,1)，A 1(1,0,1)，∴DA 1→＝(1,0,1)，D 1E →＝(1，a ，－1)， ∴DA 1→·D 1E →＝0∴D 1E ⊥A 1D ，(2)同方法一．(3)假设存在，平面DEC 的法向量n 1→＝(0,0,1)，D 1C →＝(0,2，－1)， 设平面D 1EC 的法向量n 2→＝(x ，y ，z )，则⎩⎪⎨⎪⎧D 1C →·n 2→＝0D 1E →·n 2→＝0 即⎩⎨⎧ 0·x ＋2y －z ＝0x ＋ay －z ＝0， 解得⎩⎨⎧ z ＝2y x ＝－ay ，∴n 2→＝(2－a,1,2)， 由题意得cos n 1→，n 2→＝2(2－a)2＋12＋22＝22. 解得a ＝2－3或2＋3(舍去)，即当点E 离B 为3时，π二面角D1－EC－D的大小为4.。

第十章 单元能力测试卷(B 版)一、选择题(本大题共12小题，每小题5分，共60分．)1．如右图所示，是一个正方体的表面展开图，A 、B 、C 均为棱的中点，D 是顶点，则在正方体中，异面直线AB 和CD 的夹角的余弦值为( )A.25B.35 C.105 D.55答案 C解析 把展开图复原为正方体后示意图如右图所示，∠EGF 为AB 和CD 所成的角，F 为正方体一棱的中点．∴EF ＝GF ＝52，EG ＝ 2. ∴cos ∠EGF ＝105. 2．空间四点A 、B 、C 、D 满足|AB →|＝3，|BC →|＝7，|CD →|＝11，|DA →|＝9，则AC →·BD →的取值( )A ．只有一个B ．有两个C ．有四个D ．有无穷多个答案 A解析 注意到32＋112＝72＋92＝130，由于AB →＋BC →＋CD →＋DA →＝0，则|DA →2|＝DA →2＝(AB →＋BC →＋CD →)2＝AB →2＋BC →2＋CD →2＋2(AB →·BC →＋BC →·CD →＋CD →·AB →) ＝AB →2－BC →2＋CD →2＋2(BC →2＋AB →·BC →＋BC →·CD →＋CD →·AB →) ＝AB →2－BC →2＋CD →2＋2(AB →＋BC →)·(BC →＋CD →)．即2AC →·BD →＝AD →2＋BC →2－AB →2－CD →2＝0，所以AC →·BD →只有一个值0，故选A.3．在半径为10 cm 的球面上有A 、B 、C 三点，且AB ＝8 3 cm ，∠ACB ＝60°，则球心O 到平面ABC 的距离为( )A ．2 cmB ．4 cmC ．6 cmD ．8 cm 答案 C解析 设平面ABC 对应的小圆圆心为M ，即三角形ABC 的外接圆的圆心，设小圆的半径为r ，根据正弦定理有2r ＝AB sin ∠ACB ＝83sin60°， ∴r ＝8 cm.根据球体的性质OM ⊥平面ABC ，即球心O 到平面ABC 的距离d ＝OM ，且三角形OCM 为直角三角形，所以d ＝R 2－r 2＝d ＝102－82，∴d ＝6 cm.∴选C.4．已知直线m 、n 、l 和平面α、β、γ，下列条件中，能推出α∥β的是( ) A ．m ⊂α，n ⊂β，m ∥n B ．m ⊥α，m ⊥βC ．m ⊂α，n ⊂α，m ∥β，n ∥βD ．α⊥γ，β⊥γ 答案 B解析 如果两个平面垂直于同一条直线，那么这两个平面平行． 本题也可以通过反例否定错误选项，从而筛选出正确结论． 例如，对于A ，如果α∩β＝l ，m ∥l ，n ∥l ， 那么α与β不平行，对于选项C ，当α与β相交时，存在直线m⊂α、n⊂α，使得m∥β，n∥β，从而可排除C.对于选项D，设α、β为正方体相邻两个侧面，γ为底面，则满足α⊥γ，β⊥γ，但α与β不平行，从而可剔除D.5．如右图所示，正四棱锥P－ABCD的底面积为3，体积为22，E为侧棱PC的中点，则PA与BE所成的角为( )A.π6B.π4C.π3D.π2答案 C解析连结AC、BD交于点O，连结OE，易得OE∥PA.∴所求角为∠BEO.由所给条件易得OB＝62，OE＝12PA＝22，BE＝2，∴cos∠OEB＝12，∴∠OEB＝60°，选C.6．已知平面α⊥平面β，m是α内一条直线，n是β内一条直线，且m⊥n，那么，①m⊥β；②n⊥α；③m⊥β或n⊥α；④m⊥β且n⊥α.这四个结论中，不正确．．．的三个是( ) A．①②③B．①②④C．①③④D．②③④答案 B解析对于结论③，可用反证法证明其正确性．假设m⊥β和n⊥α都不成立，因为m⊥n，根据三垂线定理的逆定理，m垂直于n在α上的射影．由于m和n不可能都与α、β的交线平行，不妨设n与α、β的交线不平行，从而n与它在α上的射影相交，故m⊥β.这与假设矛盾，故m⊥β或n⊥α.7．正三棱锥P－ABC中，M、N是侧棱PB、PC的中点，若截面AMN垂直于侧面PBC，则棱锥的侧面积与底面积的比为( )A ．1∶2B.2∶ 3 C.3∶2 D.6∶1 答案 D解析 如右图所示，∵M 、N 为正三棱锥的侧棱PB 、PC 之中点，∴MN ∥BC ，AM ＝AN . 设MN 的中点为F ，连结AF ，连结PF 并延长交BC 于E ， 连结AE ，则E 为BC 的中点．∵平面AMN ⊥侧面PBC ，而MN ＝平面AMN ∩平面PBC ， ∴AF ⊥PE .又F 为PE 之中点， ∴PA ＝AE .设底面边长为a ，斜高为h ′. 则S 侧＝12×3a ·h ′，S 底＝34a 2.又PB ＝PA ＝AE ＝32a ，BE ＝12a ， ∴h ′＝PE ＝PB 2－BE 2＝22a . ∴S 侧S 底＝12×3a ·h ′34a 2＝12×3a ×22a34a 2＝6∶1. 8．位于北纬x 度的A 、B 两地经度相差90°，且A 、B 两地间的球面距离为π3R (R 为地球半径)，那么x 等于( )A ．30B ．45C ．60D ．75 答案 B解析 记球心为点O ，依题意得∠AOB ＝π3，OA ＝OB ＝R ，因此AB ＝R .又A 、B 两地经度相差90°，因此A 、B 两地所在的纬线圈的半径是22R ，x ＝45，选B. 9．ABCD －A 1B 1C 1D 1为正方体，点P 在线段A 1C 1上运动，异面直线BP 与AD 1所成角为θ，则θ的取值X 围是( )A ．0<θ<π2B ．0<θ≤π2C ．0<θ<π3D ．0<θ≤π3 答案 D解析 因为AD 1∥BC 1，所以BP 与AD 1所成的角θ＝∠C 1BP ，因为P 在A 1C 1上运动，所以0<θ≤π3，故选D. 10．如右图所示的多面体是过正四棱柱的底面正方形ABCD 的点A 作截面AB 1C 1D 1而截得的，且B 1B ＝D 1D .已知截面AB 1C 1D 1与底面ABCD 成30°的二面角，AB ＝1，则这个多面体的体积为( )A.62B.63 C.64D.66答案 D解析 将多面体补形，补成一个高为CC 1 的正四棱柱，则V 棱柱＝2V 多． 又∵截面与底面成30°， ∴∠C 1AC ＝30°.在Rt △ACC 1中，AC ＝2， ∴C 1C ＝2tan30°＝33×2＝63. ∴V 柱＝S ABCD ·CC 1＝63. ∴V 多＝12V 柱＝66.11．半径为4的球面上有A ，B ，C ，D 四点，且满足AB →·AC →＝0，AD →·AC →＝0，AB →·AD →＝0，则△ABC ，△ACD ，△ADB 面积之和S △ABC ＋S △ACD ＋S △ADB 的最大值为( )A ．8B ．16C ．32D ．64 答案 C解析 设AB ＝a ，AC ＝b ，AD ＝c ， 则S △ABC ＋S △ACD ＋S △ADB ＝12(ab ＋ac ＋bc )≤12(a 2＋b 22＋a 2＋c 22＋b 2＋c 22) ＝12(a 2＋b 2＋c 2) ＝12×4R 2＝12×4×42＝32， 当且仅当a ＝b ＝c 时取“＝”．12．二面角的棱上有A 、B 两点，直线AC 、BD 分别在这个二面角的两个半平面内，且都垂直于AB .已知AB ＝4，AC ＝6，BD ＝8，CD ＝217，则该二面角的大小为( )A ．150° B．45° C ．60° D．120° 答案 C解析 由条件，知CA →·AB →＝0，AB →·BD →＝0，CD →＝CA →＋AB →＋BD →.∴|CD →|2＝|CA →|2＋|AB →|2＋|BD →|2＋2CA →·AB →＋2AB →·BD →＋2CA →·BD →＝62＋42＋82＋2×6×8cos 〈CA →，BD →〉＝(217)2，∴cos 〈CA →，BD →〉＝－12，〈CA →，BD →〉＝120°，∴二面角的大小为60°，故选C.二、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中横线上)13．已知△ABC 的顶点坐标为A (1,1,1)、B (2,2,2)、C (3,2,4)，则△ABC 的面积是________． 答案62解析AB →＝(1,1,1)，AC →＝(2,1,3)， cos 〈AB →，AC →〉＝63·14＝427，∴sin A ＝77. 因为S △ABC ＝12|AB →||AC →|sin A ＝123·14·77＝62.14．已知正方体ABCD －A 1B 1C 1D 1棱长为1，点P 在线段BD 1上，当∠APC 最大时，三棱锥P －ABC 的体积为________．答案118解析 以B 为坐标原点，BA 为x 轴，BC 为y 轴，BB 1为z 轴建立空间直角坐标系，设BP →＝λBD 1→，可得P (λ，λ，λ)，再由cos ∠APC ＝AP →·CP→|AP →||CP →|可求得当λ＝13时，∠APC 最大，故V P －ABC ＝13×12×1×1×13＝118.15．已知四边形ABCD 中，AB →＝a －2c ，CD →＝5a ＋6b －8c ，对角线AC ，BD 的中点分别为E ，F 则EF →＝________.答案3a ＋3b －5c解析EF →＝EA →＋AB →＋BF →，又EF →＝EC →＋CD →＋DF →，两式相加，得 2EF →＝(EA →＋EC →)＋AB →＋CD →＋(BF →＋DF →)， 因为E 是AC 中点，故EA →＋EC →＝0， 同理BF →＋DF →＝0，所以2EF →＝AB →＋CD →＝(a －2c )＋(5a ＋6b －8c )＝6a ＋6b －10c ， ∴EF →＝3a ＋3b －5c16．如图是一几何体的平面展开图，其中ABCD 为正方形，E 、F 、分别为PA 、PD 的中点，在此几何体中，给出下面四个结论：①直线BE 与直线CF 异面； ②直线BF 与直线AF 异面 ③直线EF ∥平面PBC ； ④平面BCE ⊥平面PAD . 其中正确的有______个． 答案 2解析 将几何体展开拼成几何体(如图)，因为E 、F 分别为PA 、PD 的中点，所以EF ∥AD ∥BC ，即直线BE 与CF 共面，①错；因为B ∉平面PAD ，E ∈平面PAD ，E ∉AF ，所以BE 与AF 是异面直线，②正确；因为EF ∥AD ∥BC ，EF⊄平面PBC ，BC ⊂平面PBC ，所以EF ∥平面PBC ，③正确；平面PAD 与平面BCE 不一定垂直，④错．三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)如右图所示，在四棱锥P —ABCD 中，PA ⊥底面ABCD ，PB 与底面所成的角是30°，∠BAD ＝90°.AB ∥CD ，AD ＝CD ＝a ，AB ＝2a .(1)若AE ⊥PB 于E ，求证：DE ⊥PB . (2)求异面直线AE 与BC 的夹角的余弦．解析 (1)以A 为原点，AB 、AD 、AP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系． ∵PA ⊥平面ABCD ，∴∠PBA 是PB 与底面ABCD 所成的角． ∵∠PBA ＝30°，∴PA ＝233a .A (0,0,0)，B (2a,0,0)，D (0，a,0)，P (0,0，233a )， AD →＝(0，a,0)，PB →＝(2a,0，－233a )． ∵AD →·PB →＝(0，a,0)·(2a,0，－233a )＝0，∴PB →⊥AD →.又PB →⊥AE →， ∴PB ⊥平面ADE ，∴PB ⊥DE . (2)过E 作EF ⊥AB 于F ，AE ＝a ，EF ＝32a ，AF ＝12a ，E (12a,0，32a )， ∴AE →＝(12a,0，32a )．又C (a ，a,0)，∴BC →＝(－a ，a,0)．设AE →与BC 的夹角是θ，则 cos θ＝AE →·BC →|AE →|·|BC →|＝－24，∴异面直线AE 与BC 的夹角的余弦是24. 18．(本小题满分12分)如右图所示，直三棱柱ABC —A 1B 1C 1，底面△ABC 中，CA ＝CB ＝a ，∠BCA ＝90°，AA 1＝2a ，M 、N 分别是A 1B 1、A 1A 的中点．(1)求BN 的长； (2)求cos 〈BA 1→，CB 1→〉； (3)求证：A 1B ⊥C 1M .解析 以C 为原点建立空间直角坐标系． (1)B (0，a,0)，N (a,0，a )， |BN →|＝a －02＋0－a2＋a －02＝3a .(2)A 1(a,0,2a )，C (0,0,0)，B 1(0，a,2a )，∴BA 1→＝(a ，－a,2a )，CB 1→＝(0，a,2a )，BA 1→·CB 1→＝a ·0＋(－a )·a ＋2a ·2a ＝3a 2， |BA 1→|＝a －02＋0－a2＋2a －02＝6a ， |CB 1→|＝0－02＋a －02＋2a －02＝5a ，∴cos 〈BA 1→，CB 1→〉＝BA 1→·CB 1→|BA 1→||CB 1→|＝36×5＝3010.(3)C 1(0,0,2a )，M (a 2，a 2，2a )，C 1M →＝(a 2，a 2，0)，A 1B →＝(－a ，a ，－2a )，∴A 1B →·C 1M →＝(－a )·a 2＋a ·a 2＋(－2a )·0＝0，∴A 1B →⊥C 1M →，∴A 1B ⊥C 1M .19．(本小题满分12分)已知M 、N 分别是正方体ABCD —A 1B 1C 1D 1的棱B 1C 1和B 1B 的中点．(1)求MN 与A 1C 1所成角的大小； (2)求MN 与平面ACC 1A 1所成角的大小．解析 (1)设正方体的棱长为1，建立直角坐标系D －xyz (如图)．则A 1(1,0,1)，C 1(0,1,1)，M (12，1,1)，N (1,1，12)．∴MN →＝(12，0，－12)，A 1C 1→＝(－1,1,0)．∴cos 〈MN →，A 1C 1→〉＝MN →·A 1C 1→|MN →||A 1C 1→|＝－1222×2＝－12，∴〈MN →，A 1C 1→〉＝120°.而异面直线所成角在(0,90°]内，∴MN 与A 1C 1成60°角．(2)设平面ACC 1A 1的法向量n ＝(1，α，β)，则n ⊥AA 1→，(1，α，β)·(0,0,1)＝0，∴β＝0，又n ⊥AC →.∴(1，α，β)·(－1,1,0)＝0，∴a ＝1， ∴n ＝(1,1,0)，∴cos 〈n ，MN →〉＝n ·MN →|n ||MN →|＝12，∴〈n ，MN →〉＝60°， ∴MN 与面ACC 1A 1成30°角．20．(本小题满分12分)如右图所示，已知四棱锥P —ABCD 的底面是正方形，PA ⊥底面ABCD ，且PA ＝AD ＝2，点M 、N 分别在棱PD 、PC 上，且PN →＝12NC →，PM ＝MD .(1)求证：PC ⊥AM ；(3)求二面角B —AN —M 的大小．解析 (1)证明：因为四棱锥P －ABCD 的底面是正方形，PA ⊥底面ABCD ，故建立如右图所示的空间直角坐标系A —xyz ，又PA ＝AD ＝2，则有P (0,0,2)，D (0,2,0)，∴M (0,1,1)，C (2,2,0)， ∴PC →＝(2,2，－2)，AM →＝(0,1,1)， ∵PC →·AM →＝0＋2－2＝0，∴PC ⊥AM .(2)证明：设N (x ，y ，z )，∵PN →＝12NC →，则有x －0＝12(2－x )，∴x ＝23.同理可得y ＝23，z ＝43.即N (23，23，43)．由PC →·AN →＝43＋43－83＝0，∴PC ⊥AN .又∵PC ⊥AM ，AM ∩AN ＝A ，∴PC ⊥平面AMN .(3)解：连接BN ，设平面BAN 的法向量为n ＝(x ，y ，z )， 由⎩⎨⎧n ·AB→＝2x ＝0，n ·AN →＝23x ＋23y ＋43z ＝0，取n ＝(0，－2,1)．而PC →＝(2,2，－2)为平面AMN 的法向量． ∴cos 〈n ，PC →〉＝n ·PC →|n |·|PC →|＝－4－25·12＝－155.结合图形可知，所求二面角B —AN —M 的大小为π－arccos155. 21．(本小题满分12分)(2010·某某卷，文)如图，四棱锥P －ABCD 中，底面ABCD 为矩形，PA ⊥底面ABCD ，PA ＝AB ＝2，点E 是棱PB 的中点．(2)若AD ＝1，求二面角B －EC －D 的平面角的余弦值．解析 (1)如图，由PA ⊥底面ABCD ，得PA ⊥AB .又PA ＝AB ，故△PAB 为等腰直角三角形，而点E 是棱PB 的中点，所以AE ⊥PB .由题意知BC ⊥AB, 又AB 是PB 在平面ABCD 内的射影，由三垂线定理得BC ⊥PB ，从而BC ⊥平面PAB ，故BC ⊥AE .因为AE ⊥PB ，AE ⊥BC ，所以AE ⊥平面PBC .(2)由(1)知BC ⊥平面PAB ，又AD ∥BC ，得AD ⊥平面PAB ，故AD ⊥AE .在Rt △PAB 中，PA ＝AB ＝2，AE ＝12PB ＝12PA 2＋AB 2＝1.从而在Rt △DAE 中，DE ＝AE 2＋AD 2＝ 2.在Rt △CBE 中，CE ＝BE 2＋BC 2＝ 2.又CD ＝2，所以△CED 为等边三角形．取CE 的中点F ，连接DF ，则DF ⊥CE .因为BE ＝BC ＝1，且BC ⊥BE ，则△EBC 为等腰直角三角形，连接BF ，则BF ⊥CE ，所以∠BFD 为二面角B －EC －D 的平面角．连接BD ，在△BFD 中，DF ＝CD ·sin π3＝62，BF ＝12CE ＝22，BD ＝BC 2＋CD 2＝ 3.所以cos BFD ＝DF 2＋BF 2－BD 22·DF ·BF ＝－33.故二面角B －EC －D 的平面角的余弦值为－33. 22．(本小题满分12分)如图所示，已知直三棱柱ABC —A 1B 1C 1的底面是以∠C 为直角的等腰直角三角形，AC ＝BC ＝CC 1＝2，M ，N 分别在棱CC 1，A 1B 1上，N 是A 1B 1的中点．(1)若M 是CC 1的中点，求异面直线AN 与BM 所成的角；(2)若点C 关于平面ABM 的对称点恰好在平面ABB 1A 1上，试确定M 点在CC 1上的位置． 解析 (1)以CB 、CA 、CC 1所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系．则C (0,0,0)，A (0，－2,0)，B (2,0,0)，C 1(0,0,2)，A 1(0，－2,2)，B 1(2,0,2)，由于N 是A 1B 1的中点，M 是CC 1的中点，所以M (0,0,1)，N (1，－1,2)，于是AN →＝(1,1,2)，BM →＝(－2,0,1)，因此cos 〈AN →，BM →〉＝06×5＝0，所以异面直线AN 与BM 所成的角等于90°.(2)设M (0,0，z )(0<z ≤2)，由于点C 关于平面ABM 的对称点恰好在平面ABB 1A 1上， 取AB 的中点D ，连接CD 、DN 、MD ，易知CD ⊥AB ，ND ⊥AB ，所以AB ⊥平面C 1NDC ，而AB ⊂平面ABM ，所以平面ABM ⊥平面C 1NDC ，又平面ABM ∩平面C 1NDC ＝DM ，过C 作CH ⊥DM ，则CH ⊥平面ABM ，延长CH 至P ，使PH ＝CH ， 则点P 就是点C 关于平面ABM 的对称点，所以P 点在平面C 1NDC 中，又P 点恰好在平面ABB 1A 1上，所以P 点应该在直线ND 上． 由于D (1，－1,0)，所以MD →＝(1，－1，－z )，而点H 在线段MD 上，所以设MH →＝λ·MD →＝(λ，－λ，－λz )，则CH →＝CM →＋MH →＝(λ，－λ，z －λz )，故CP →＝2CH →＝(2λ，－2λ，2z －2λz )，所以P (2λ，－2λ，2z －2λz )， 于是DP →＝(2λ－1，－2λ＋1,2z －2λz )，而DN →＝(0,0,2)，由于P 点应该在直线ND 上，且DC ＝DP ，所以⎩⎨⎧2λ－1＝0，－2λ＋1＝0，|2z －2λz |＝2，得z ＝2，所以当点C 关于平面ABM 的对称点恰好在平面ABB 1A 1上时，CM ＝ 2.。

2012年全国统一高考数学试卷（新课标版）（理科）一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={1，2，3，4，5}，B={（x，y）|x∈A，y∈A，x﹣y∈A}，则B 中所含元素的个数为（）A ．3B．6C．8D．102．（5分）将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（）A ．12种B．10种C．9种D．8种3．（5分）下面是关于复数的四个命题：其中的真命题为（），p1：|z|=2，，p3：z的共轭复数为1+i，p4：z的虚部为﹣1．A ．p2，p3B．p1，p2C．p2，p4D．p3，p44．（5分）设F1、F2是椭圆的左、右焦点，P为直线x=上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为（）A ．B．C．D．5．（5分）已知{a n} 为等比数列，a4+a7=2，a5a6=﹣8，则a1+a10=（）A ．7B．5C．﹣5D．﹣76．（5分）如果执行右边的程序框图，输入正整数N（N≥2）和实数a1，a2，…，a n，输出A，B，则（）A．A+B为a1，a2，…，a n的和B．为a1，a2，…，a n的算术平均数C ．A和B分别是a1，a2，…，a n中最大的数和最小的数D．A和B分别是a1，a2，…，a n中最小的数和最大的数7．（5分）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）A ．6B．9C．12D．188．（5分）等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，，则C的实轴长为（）A ．B．C．4D．89．（5分）（2012•黑龙江）已知ω＞0，函数在上单调递减．则ω的取值范围是（）A ．B．C．D．（0，2]10．（5分）已知函数；则y=f （x ）的图象大致为（ ） A ．B ．C ．D ．11．（5分）已知三棱锥S ﹣ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC=2，则此棱锥的体积为（ ） A ．B ．C ．D ．12．（5分）设点P 在曲线上，点Q 在曲线y=ln （2x ）上，则|PQ|最小值为（ ） A ． 1﹣ln2 B ．C ．1+ln2 D ．二．填空题：本大题共4小题，每小题5分． 13．（5分）（2012•黑龙江）已知向量夹角为45°，且，则= _________ ．14．（5分）设x ，y 满足约束条件：；则z=x ﹣2y 的取值范围为_________ ．15．（5分）某个部件由三个元件按下图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作，设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常相互独立，那么该部件的使用寿命超过1000小时的概率为_________．16．（5分）数列{a n}满足，则{a n}的前60项和为_________．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（12分）已知a，b，c分别为△ABC三个内角A，B，C的对边，（1）求A；（2）若a=2，△ABC的面积为；求b，c．18．（12分）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理．（1）若花店一天购进16枝玫瑰花，求当天的利润y（单位：元）关于当天需求量n （单位：枝，n∈N）的函数解析式．（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：日需求量n14151617181920频数10201616151310以100天记录的各需求量的频率作为各需求量发生的概率．（i）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列，数学期望及方差；（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由．19．（12分）如图，直三棱柱ABC﹣A1B1C1中，，D是棱AA1的中点，DC1△BD（1）证明：DC1△BC（2）求二面角A1﹣BD﹣C1的大小．20．（12分）设抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点；（1）若△BFD=90°，△ABD的面积为；求p的值及圆F的方程；（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值．21．（12分）（2012•黑龙江）已知函数f（x）满足；（1）求f（x）的解析式及单调区间；（2）若，求（a+1）b的最大值．四、请考生在第22，23，24题中任选一题作答，如果多做，则按所做的第一题计分，作答时请写清题号．22．（10分）（2012•黑龙江）选修4﹣1：几何证明选讲如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF△AB，证明：（1）CD=BC；（2）△BCD～△GBD．23．选修4﹣4；坐标系与参数方程已知曲线C1的参数方程是，以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为（1）求点A，B，C，D的直角坐标；（2）设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围．24．选修4﹣5：不等式选讲已知函数f（x）=|x+a|+|x﹣2|（1）当a=﹣3时，求不等式f（x）≥3的解集；（2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．。

吉林省各地市2012年高考数学最新联考试题分类大汇编（8）立体几何 一、选择题： 4. (2012年东北三省四市教研协作体第二次调研测试文科)如图所示是一个几何体的三视图，则该几何体的体积为 A.B. 1 C.D. 4.A　由题意可知，该几何体为一个四棱锥，底面面积为，高为1，体积为.故选A. 8．一个几何体的三视图及尺寸如下图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的表面积是（ ） A． B． C． D． 9．(东北四校2012届高三第一次高考模拟文科)一个几何体的三视图及尺寸如下图所示，其中正视图是直角三角形，侧视图是半圆，则该几何体的表面积是（ C ） A． B． C． D． 5．(吉林省吉林市普通高中2012届高三下学期期中教学质量检测理科)某几何体的三视图如右图所示，则其侧面积为( A ) A． B．C．D．的外接球的球心在上，且平面，,若四面体的体积为，则该球的体积为( D ) A．B．C．D．6．(吉林省吉林市普通高中2012届高三下学期期末教学质量检测文科)已知几何体的三视图如图所示，可得这个几何体的体积是A）4 （B）6 （C）12 （D）18 3．(吉林省延吉市2012年2月高三教学质量检测理科)设 、、是三个互不重合的平面，是两条不重合的直线，则下列命题中正确的是（ ） A． B． C． D． 已知正四棱锥中，，那么当该棱锥的体积最大时，它的高为 A． B．C． D．36.(吉林省实验中学2012届高三第六次模拟理科)一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积是 A． B． C． D．16. (2012年东北三省四市教研协作体第二次调研测试文科)如图所示，正方体的棱长为6，则以正方体的中心为顶点，以平面截正方体外接球所得的圆为底面的圆锥的全面积为__________. 16.为正方体外接球的球心，也是正方体的中心， 到平面的距离是体对角线的，即为， 又球的半径是正方体体对角线长的一半，即为， 由勾股定理可知，截面圆的半径为， 圆锥底面面积为； 圆锥的母线即为球的半径， 圆锥的侧面积为； 因此圆锥的表面积为. 16．，它的外接球的球心为，点是的中点，点是球的球面上任意一点，有以下判断：①该正方体外接球的体积是；②异面直线与所成角为；③长的最大值为；④过点的平面截球的截面面积的最小值为.其中所有正确判断的序号是. ①②③ 三、解答题： 19. (2012年东北三省四市教研协作体第二次调研测试文科)（本小题满分12分） 如图，正方形与直角梯形所在平面互相垂直，，，. ⑴求证：平面； ⑵求点到平面的距离. 19.(本小题满分12分) 【命题意图】本小题主要考查立体几何的相关知识，具体涉及到线面的平行关系、点到平面距离的求法等知识. 【试题解析】解：⑴证明：设，取中点，连结， 则∥且＝. ∵，，∴∥且＝， ∴四边形是平行四边形，∴. ∵平面,平面, ∴平面，即平面.(5分)△中，， 在△中，， 在直角梯形中，， 所以， ， 由于,即， ， 即点到平面的距离为. (12分)19．（本小题满分12分） 已知斜三棱柱ABC—A1B1C1的底面是正三角形，侧面ABB1A1是菱形，且，M是A1B1的中点， （1）求证：平面ABC； （2）求二面角A1—BB1—C的余弦值。

8 立体几何一、选择题：（ 3） ( 北京市东城区 2012 年 1 月高三考试文科） 一个几何体的三视图以下图，则该几何体的体积为（ A ）a 3 （ B ）a 3a26（ C ）a 3（ D ）a 3aa 1218正（主）视图侧（左）视图【答案】 C【分析】该几何体为底面是直角边为a 的等腰直角三角形，3 俯视图高为 a 的直三棱柱，其体积为1a a aa。

2 27．( 北京市西城区 2012 年 1 月高三期末考试理科 ) 某几何体的三视图以下图，该几何体的体积是（）（ A ） 8（ B ） 83（ C ） 4（ D ） 43【答案】 D【分析】将三视图复原直观图，可知是一个底面为正方形（其对角线长为2），高为2 的四棱锥，其体积为V 1S正方形ABCD 2 1 1 2 2 2 4.3 3 2 3B．m , n C．m ,n //A．m //, n //且//，则m // n且，则m // n且，则 m n//D．m // ,n 且，则m // n【答案】 C 体的体积为. 3 23 321 1正视图侧视图2 1俯视图（9） ( 北京市东城区2012 年 4 月高考一模文科) 已知一个四棱锥的三视图以下图，则该四棱锥的体积是.4310. (2012 年 4 月北京市房山区高三一模理科一个几何体的三视图以下图，则这个几何体的体积为.23三、解答题：（17）(北京市东城区2012 年 1 月高三考试文科）（本小题共14 分）如图，在四棱锥P ABCD 中，底面 ABCD 是正方形，PA平面ABCD， E 是PC 中点， F 为线段 AC 上一点.（Ⅰ）求证：BD EF ；P （Ⅱ）试确立点 F 在线段 AC 上的地点，使EF //平面 PBD ，并说明原因.【命题剖析】此题考察线线垂直和线面探究性问题等综合问题。

考察学生的A 空间想象能力。

证明线线垂直的方法：（ 1）异面直线所成的角为直角；（2）线面垂直的性质定理；（ 3）面面垂直的性质定理；（ 4）三垂线定理和逆定理；（5）B勾股定理；（ 6）向量垂直 .要注意线面、面面垂直的性质定理的成立条件.解题过程中要特别领会平行关系性质的传达性，垂直关系的多样性.此题第一问利用方法二进行证明；探究某ED FC证明（Ⅰ）由于因此PA 平面 ABCD ，PA BD ．又四边形 ABCD 是正方形，因此因此因此分AC BD，PA AC A，BD 平面PAC,又EF平面PAC,BD EF.7PBD . ⋯⋯⋯⋯⋯⋯ 14 分(16) （ 2012 年 4 月北京市海淀区高三一模理科）（本小分14 分）在四棱 P - ABCD 中， AB// CD， AB^ AD，AB= 4,AD= 2 2,CD= 2，PA ^ 平面 ABCD ， PA= 4.m ，求： CD //m；P（Ⅰ）平面 PAB 平面 PCD（Ⅱ）求： BD 平面 PAC ；（Ⅲ）点 Q 段 PB 上一点，且直 QC 与平面 PAC 所成角的正弦3，求PQ的．A3 PBDC(16) （本小分14 分） B⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分因此BD ( 4,2 2,0) ， AC (2,2 2,0) ，z AP (0,0,4) ，P因此BDAC (4)2222200 0 ，BDAP(4)0220040.因此BD AC，BD AP. A Dy因AP AC A， AC 平面 PAC ，B CPA 平面 PAC ，x因此BD 平面 PAC .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分由（Ⅱ）知平面PAC 的一个法向量BD ( 4,2 2,0) .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分17. (2012 年 3 月北京市旭日区高三一模文科) （本分13 分）在如所示的几何体中，四形ABCD 平行四形，ABD = 90 ， EB 平面ABCD ， EF//AB ，AB= 2，EF =1，BC= 13，且M是BD F . E的中点（Ⅰ）求：EM // 平面ADF；DCMA B（Ⅱ）在 EB 上能否存在一点 P ，使得CPD 最大？若存在，恳求出 CPD 的正切值；若不存在，请说明原因 .（17）（本小题满分 13 分）（Ⅱ）解：假定在EB 上存在一点 P ，使得CPD 最大 .由于EB平面 ABD ，因此EBCD .又由于CDBD，因此CD平面EBD .8 分在 Rt CPD 中， tan CPD =CD.DP17． ( 北京市西城区 2012 年 4 月高三第一次模拟文) （本小题满分 14 分）如图，矩形 ABCD中，AB 3，BC 4． E ，F分别在线段BC 和 AD上，EF∥AB ，将矩形 ABEF 沿 EF 折起．记折起后的矩形为MNEF，且平面MNEF平面ECDF．（Ⅰ）求 ：NC ∥平面 MFD；（Ⅱ）若EC3 ，求 ：NDFC；（Ⅲ）求四周体NFEC 体 的最大 ．17. （本小 分 14 分）（Ⅰ） 明：因 四 形MNEF ，EFDC 都是矩形，因此 MN∥EF∥CD ，MNEFCD．因此 四 形 MNCD 是平行四 形， ⋯⋯⋯⋯⋯2 分因此 NC ∥MD，⋯⋯⋯⋯⋯⋯ 3 分因NC平面 MFD ，因此 NC ∥平面MFD．⋯⋯⋯⋯⋯⋯ 4 分（Ⅱ） 明： 接ED，ED FCO．因 平面MNEF平面ECDF，且NEEF，因此 NE 平面ECDF，⋯⋯5分因此 FCNE．⋯⋯⋯⋯ 6 分9 分（Ⅲ）解：NE x ， EC 4 x ，此中 0 x 4 ．由（Ⅰ）得NE平面 FEC ，因此四周体 NFEC 的体11V NFECS EFC NEx(4 x)32．⋯⋯⋯ 11 分因此1 [ x (4 x) ]2 ．⋯⋯⋯⋯⋯ 13 分VNFEC22 2当且 当 x 4 x，即x2 ，四周体 NFEC 的体 最大．⋯⋯⋯⋯⋯⋯ 14 分（17） ( 北京市 城区2012 年 4 月高考一模理科 ) （本小 共 13 分）12（17）（共 13 分）（Ⅰ） 明：取BE 中点 D ， DF .因 AECF 1， DE 1，因此 AFAD 2 ，而A 60 ，即△ ADF 是正三角形 .又因 AEED 1, 因此 EF AD .⋯⋯⋯⋯ 2 分因此在图 2 中有 A 1E EF ，BEEF .3分所以A 1 E 为B二面角A 1EF 的B 平面 角.图 1又二面角 A 1 EF B 为直二面角，因此 A 1E BE .5 分又由于 BEEFE ,因此 A 1E ⊥平面 BEF ,即 A 1E ⊥平面 BEP .6 分（Ⅱ）解：由（Ⅰ）可知 A 1E ⊥平面 BEP ， BEEF ，如图，以 E 为原点，成立空间直角坐标系 Exyz ，则 E(0 ,0,0) ， A 1(0,0,1) ， B(2 ,0,0) ，F(0, 3 , 0) .在图１中，连接 DP .由于CFCP 1 ，FAPB 2因此 PF ∥BE ，且 PF1BEDE .2 因此四边形 EFPD 为平行四边形 . 因此EF ∥DP ，且EF DP .故点 P 的坐标为（ ， 3 ， ）图210 .因此 A 1B (2 ,0, 1)， BP ( 1, 3,0) ， EA 1(0,0,1) . 8 分不如设平面 A 1BP 的法向量 nA 1B n0,( x, y, z) ，则0.BP n2 x z 0,3 ，得 n (3,3,6) .10 分即3y令 yx0.因此 cosn, EA 1n EA 163 .12 分1 3| n || EA 1 |4 2故直线 A 1E 与平面 A 1BP 所成角的大小为.13 分3（17） ( 北京市东城区 2012 年 4 月高考一模文科 ) （本小题共 14 分）如图 1，在边长为 3 的正三角形 ABC 中， E ， F ， P 分别为 AB ， AC ， BC 上的点，且知足 AE FC CP 1 .将△ AEF 沿 EF 折起到△A1EF的地点，使平面A1EF 平面 EFB ，连接AB1 ， A1P.（如图2）（Ⅰ）若 Q 为A B中点，求证： PQ ∥平面 A EF；1 1（Ⅱ）求证：A1E EP .图1图2（17）（共 14 分）证明：（Ⅰ）取 A1E 中点M，连接QM , MF．在△ A1BE 中，Q, M分别为 A1B, A1 E 的中点，因此 QM ∥BE，且QM 1BE．由于CFCP 12，FA PB 2因此 PF ∥BE,且PF 1 BE，2因此QM ∥PF ，且QM PF ．因此四边形 PQMF 为平行四边形．因此 PQ∥FM ． 5 分又由于 FM 平面 A1 EF ，且PQ 平面 A1EF ，因此 PQ ∥平面A1EF．7 分（Ⅱ）取BE中点D，连接DF.因AE CF 1，DE 1，因此AF AD 2 ，而 A 60 ，即△ADF 是正三角形.又因 AE ED 1, 因此在 2 中有A1E 因此EFEF.AD .⋯⋯⋯⋯ 9 分因平面A1EF 平面EFB ，平面A1 EF 平面EFB EF ，因此A1E ⊥平面BEF . ⋯⋯⋯⋯ 12 分又 EP平面BEF 因此 A1E⊥EP. ，⋯⋯⋯⋯ 14 分17. (2012年3月北京市丰台区高三一模文科) （本小共14 分）如，四棱P-ABCD中，底面ABCD是菱形， PA=PD，∠ BAD=60o， E 是点 Q 在棱 PC上．（Ⅰ）求：AD⊥平面 PBE；（Ⅱ）若 Q 是 PC的中点，求：PA //平面BDQ；AD 的中点，（Ⅲ）若V P-BCDE=2V Q - ABCD，求CP的．CQ17．明：（Ⅰ）因所PE E 是 AD 的中点，以PA=PD，AD ⊥．⋯⋯⋯⋯⋯⋯⋯⋯ 1 分因底面ABCD是菱形，∠ BAD=60o，因此AB=BD，又因 E 是 AD 的中点，因此AD⊥BE．⋯⋯⋯⋯⋯⋯⋯⋯ 2分因PE∩BE=E，⋯⋯⋯⋯⋯⋯⋯⋯ 3分因此AD⊥平面PBE．⋯⋯⋯⋯⋯⋯⋯⋯ 4分（Ⅱ）接AC 交BD 于点O，OQ．⋯⋯⋯⋯⋯⋯⋯⋯ 5 分因O 是AC中点，Q 是PC的中点，因此OQ △ PAC中位．所以OQ //因h1 CP因此CP 8⋯⋯⋯⋯⋯⋯⋯⋯ 14 分h2，CQ．CQ 317. (2012 年 4 月北京市房山区高三一模理科（本小共14 分）在直三棱柱 ABC ABC中， BC CC AB=2 ,AB BC.点M , N 分是1 1 1 1CC1, B1C 的中点，G是棱AB 上的点.（ I）求：B1C平面BNG；(II)若CG // 平面AB1M，确立G 点的地点，并出明；(III)求二面角M AB1 B 的余弦.17．（本小共14 分）(I) 明：∵在直三棱柱ABC A1B1C1中，BC CC1，点N 是B1C 的中点，∴ BN B1C ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分AB BC , AB BB1, BB1 BC B∴ AB ⊥平面B1 BCC1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分B1 C 平面B1 BCC1∴ B1 C AB ，即 B1 C GB ⋯⋯⋯⋯⋯⋯⋯ 3 分又BN BG B∴ B1C 平面BNG ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分（ II）当G是棱AB的中点，CG // 平面AB1M .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分明以下 :AB1,取 AB1的中点H，接HG , HM ,GC,HG AB1 B 的中位∴ GH ∥BB1， GH 1BB1⋯⋯⋯⋯⋯⋯⋯6分2∵由已知条件， B1 BCC1正方形∴ CC1∥ BB1， CC1 BB1∵ M CC1的中点，(III) ∵直三棱柱ABC A1B1C1且AB BC又平面 B1 AB 的法向量 BC1 (2,0,0) ，1cos BC , n = B1C1 n = 1 ，⋯⋯⋯⋯⋯⋯⋯⋯ 13 分1 1 B1C1 n 3二面角M AB1 B 的平面角，且角cos cos B1C1, n 1．⋯⋯⋯⋯⋯⋯⋯⋯ 14 分3。

2012年高考理科数学试卷及答案全国卷word版2012年高考理科数学试卷及答案全国卷word版第一部分:选择题1. 根据分式的定义，下列分式正确的是（）A. 0/1B. -1/0C. 1/-1D. 0/0答案: A解析: 根据分式的定义，分母不能为0，所以选项B、C均不正确；0/0是不确定的数，所以选项D也不正确。

2. 在(1,2)处的切线方程是（）A. y=x-1B. y=x+1C. y=2x-3D. y=2x-1答案: D解析: 函数y=x^2-1在点(1,0)处的切线斜率为2，因此在(1,2)处的切线斜率也为2，即y=2x+b。

同时，该点在函数图像上，所以代入函数方程可得b=0-1=-1，因此切线方程为y=2x-1。

3. 若x, y>0，且log3x-log3y=log9x-log9y，则x/y等于（）A. 1/3B. 1/9C. 3D. 9答案: B解析: 按照对数的性质，log9x=log3( x^(1/2) )，所以原式可以变形为log3(x/y)=log3( x^(1/2)/y^(1/2) )。

然后两边取3的指数，得到x/y=(x/y)^(1/2)，解得x/y=1/9。

4. 如图，在正方形ABCD中，点P在AC边上，$AP=\frac{1}{3}AC$，点Q在AD边上，$AQ=\frac{1}{4}AD$，则三角形CPQ的面积是正方形ABCD的面积的（）A. 1/12B. 1/16C. 1/24D. 1/36答案: C解析: 因为AP:AC=1:3、AQ:AD=1:4，所以$$\frac{AP}{AC}=\frac{AQ}{AD}=\frac{1}{12}$$因此，三角形APQ与三角形ACD相似。

可以设正方形边长为a，则AC=AD=a√2，AP=1/3×a√2=√2/3a，AQ=1/4×a√2=√2/4a，因此PQ=AP+AQ=7√2/12a，h=AC×PQ/2=49/72a^2，所以三角形CPQ的面积为S=h×PQ/2=7/144a^2，也就是正方形ABCD面积的1/24。

2012年管理类联考综合能力测试数学真题一、问题求解：第1~15小题，每小题3分，共45分。

下列每题给出的,,,,A B C D E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母涂黑。

1、某商品定价200元，受金融危机影响，连续2次降价20%后的售价为（）.114 B.120 C.128 D.144 E.160A2、如图2，三个边长为1的正方形所组成区域（实线区域）的面积（）A. 3B.3C.3D.3E.33、在一次捐赠活动中，某人将捐赠的物品打包成件，其中帐篷和食品共320件，帐篷比食品多80件，则帐篷的件数是（）A.180B.200C.220D.240E.2604、如图2，三角形ABC 是直角三角形，，，为正方形，已知,,a b c 分别是为，，的边长，则：（）--------------------------可以编辑的精品文档，你值得拥有，下载后想怎么改就怎么改---------------------------222222333333 =+=+=+=+=+A a b cB a b cC a b cD a b cE a b c...22.22 Array 5、如图3，一个储物罐的下半部分是底面直径与高均是20m的圆柱体，上半部分（顶部）是半球形的，已知底面与项部的造价是400元/，侧面的造价是300元/，该储物罐的造价是（）万元A.56.52B.62.8C.75.36D.87.92E.100.486、在一次商品促销活动中，主持人出示了一个9位数，让顾客猜测商品的价格，商品的价格是该9位数中从左到右面相邻的3个数字组成的3位数，若主持人出示的是的513535319，则一顾客猜中价格的概率是（）11121.....A B C D E965727、某商店经营15种商品，每次在橱窗内陈列5种，若每两次陈列的商品不完全相同，则最多可陈列（）次A.3000 B.3003 C.4000 D.4003 E.43008、甲、乙、丙三个地区公务员参加一次测评，其人数和如下表：三个地区按平均分从高到低的排列顺序为（）A.乙、丙、甲B. 乙、甲、丙C. 甲、丙、乙D.丙、甲、乙E. 丙、乙、甲--------------------------可以编辑的精品文档，你值得拥有，下载后想怎么改就怎么改-----------------------------------------------------可以编辑的精品文档，你值得拥有，下载后想怎么改就怎么改---------------------------9、经统计，某机构的一个安检口每天中午办理安检手续的乘客人数及对应的概率如下表：.0.2.0.25 .0.4 .0.5E. 0.75A B C D10、某人在保险柜中存放了M 元现金，第一天取出它的，以后每天取出的前一天所取的，共取了7天，保险柜中剩余的现金为（ ）77766222.....[1()]33333MM M M A B C D E M- 11、在直角坐标系中，若平面区域D 中虽有的点的坐标（x,y ）均满足：，，，则面积是（ ）999.(14).9(4).9(3).(2).(1)44444A B C D E πππππ+--++ 12、某单位春季植树100棵，前2天安排乙组植树，其余任务由甲、乙两组共用3天完成，已知甲组每天比乙组多植树4棵，则甲组每天植树（ ）棵A.11B.12C.13D.15E.1713、有两队打羽毛球，每队派出3男2女参加5局单打比赛，第二局和第四局为女生，那么每队派队员出场的方式有几种？（ ）--------------------------可以编辑的精品文档，你值得拥有，下载后想怎么改就怎么改---------------------------A. 12B.10C.8D.6E.414、若能被整除，则（ ）.4,4.4,4.10,8.10,8.2,0A a b B a b C a b D a b E a b ===-=-==-=-==-=15.某公司计划运送180台电视机和110台洗衣机下乡，现有两种货车，甲种货车每辆最多可载40台电视机和10台洗衣机，乙种货车每辆最多可载20台电视机和20台洗衣机，已知甲、乙两种货车的租金分别是每辆400元和360元，则最少的运费是（ ）元A. 2560B.2600C.2640D.2680E.2720二、充分性条件判断：第16～25小题小题，每小题3分，共30分。

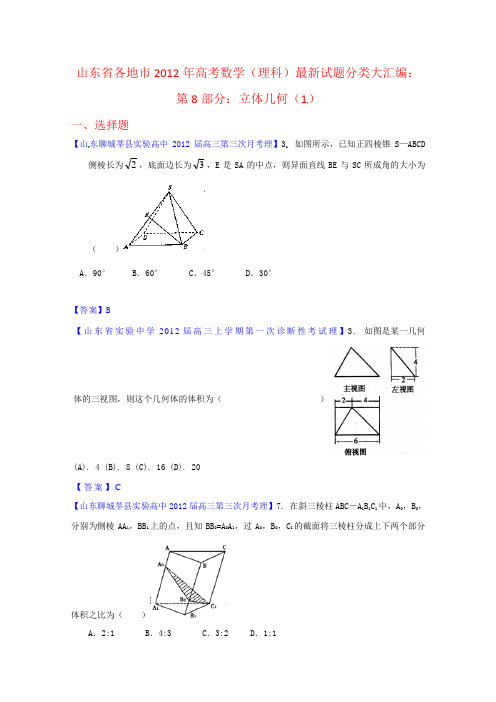
山东省各地市2012年高考数学（理科）最新试题分类大汇编：第8部分：立体几何（1）一、选择题【山东聊城莘县实验高中2012届高三第三次月考理】3. 如图所示，已知正四棱锥S—ABCD 侧棱长为2，底面边长为3，E是SA的中点，则异面直线BE与SC所成角的大小为（）A．90° B．60° C．45°D．30°【答案】B【山东省实验中学2012届高三上学期第一次诊断性考试理】3. 如图是某一几何体的三视图，则这个几何体的体积为（）(A). 4 (B). 8 (C). 16 (D). 20【答案】C【山东聊城莘县实验高中2012届高三第三次月考理】7. 在斜三棱柱ABC－A1B1C1中，A0，B0，分别为侧棱AA1，BB1上的点，且知BB0=A0A1，过A0，B0，C1的截面将三棱柱分成上下两个部分体积之比为（）A．2:1 B．4:3 C．3:2 D．1:1【答案】A【山东聊城莘县实验高中2012届高三第三次月考理】11. m 和n 是分别在两个互相垂直的面α、β内的两条直线，α与β交于l ，m 和n 与l 既不垂直，也不平行，那么m 和n 的位置关系是 （ ）A.可能垂直，但不可能平行B.可能平行，但不可能垂直C.可能垂直，也可能平行D.既不可能垂直，也不可能平行 【答案】D【山东省东营市2012届高三上学期期末（理）】4．某几何体的三视图如图所示，则该几何体的体积为A ．21B ．31C ．41D ．61【答案】A【山东省东营市2012届高三上学期期末（理）】16．设m 、n,是两条不同的直线，βα、是两个不同的平面，给出下列四个命题， ①若m ⊥n ,m ⊥α，α⊄n ，则α//n ；②若βαβαβα⊥⊥⊥=⊥n n m n m 或则,,, ； ③若αβαβ//,,m m 则⊥⊥； ④若βαβα⊥⊥⊥⊥则,,,n m n m .其中正确命题的序号是 (把所有正确命题的序号都写上)． 【答案】①④【山东省滨州市沾化一中2012届高三上学期期末理】7．下列命题中不正确的是（ ）A ．若ααα⊂==⊂⊂lB b l A a l b a 则，,,,B ．若a ∥c ，b ∥c ，则a ∥bC ．若a ⊄α，b ⊂α，a ∥b ，则a ∥αD ．若一直线上有两点在已知平面外，则直线上所有点在平面外 【答案】D【山东省滨州市沾化一中2012届高三上学期期末理】8．如果三棱锥S-ABC 的底面是不等边三角形，侧面与底面所成的二面角都相等，且顶点S 在底面的射影O 在△ABC 内，那么O 是△ABC 的 （ ） A ．垂心 B ．重心 C ．外心 D ．内心 【答案】D【山东省冠县武训高中2012届高三第二次质检理6.某几何体的三视图如图所示，则它的体积是A.283π-B.8-3πC.82π-D.23π 【答案】A【山东省冠县武训高中2012届高三第二次质检理】10.已知a 、b 、l 表示三条不同的直线，αβγ、、表示三个不同的平面，有下列四个命题： ①若,b αβαβγ⋂=⋂=且a //b,则//αγ；②若a 、b 相交，且都在αβ、外，a //,a //,b //,b //αβαβ，则//αβ； ③若αβ⊥，a,b ,a b αββ⋂=⊂⊥，则b α⊥； ④若a ,b ,l a,l b,αα⊂⊂⊥⊥则l α⊥.其中正确的是（ ） A.①② B.②③ C.①④ D.③④ . 【答案】B【山东省冠县武训高中2012届高三第二次质检理3.已知正三棱柱111ABC A B C -的棱长与底面边长相等，则1AB 与侧面11ACC A 所成角的正弦值等于（ ）【答案】B【山东济南市2012界高三下学期二月月考理】如右图，一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形，则其体积是AB.C ．D. 83【答案】C【山东省济宁市2012届高三上学期期末检测理】5.一个几何体的三视图如图所示，则该几何体的表面积为A.22+B.23+C.221+D. 5【答案】A【山东省济南一中2012届高三上学期期末理】9. 已知正三棱锥V ABC -的主视图、俯视图如下图所示，其中VA=4，AC=32,则该三棱锥的左视图的面积；A ．9B ．6C ．33D ．39 【答案】B【山东省济宁市鱼台二中2012届高三11月月考理】1．设 l 、m 、n 为不同的直线，α、β为不同的平面，则正确的命题是( ) A ．若 α⊥β，l ⊥α，则 l ∥β B ．若 α⊥β，l α⊂，则 l ⊥β俯视图第4题C ．若 l ⊥m ，m ⊥n ，则 l ∥nD ．若m ⊥α，n ∥β且α∥β，则 m ⊥n【答案】D【山东省济宁市汶上一中2012届高三11月月考理】9．若一个底面是正三角形的三棱柱的主视图如右图所示，其顶点都在一个球面上，则该球的表面积是（ ）A ．π4B ．1912πC ．193πD ．43π【答案】C【山东省潍坊市2012届高三上学期期末考试理】4．某几何体的三视图如图所示，则该几何体的体积为A ．21 B ．31 C ．41 D ．61 【答案】A【山东省苍山县2012届高三上学期期末检测理】7．已知直线,l m ，平面,αβ，且,l m αβ⊥⊂，给出下列四个命题：①若α//β，则l m ⊥； ②若,//l m αβ⊥则 ③若αβ⊥，则//l m ；④若//,.l m αβ⊥则其中正确命题的个数是 （ ） A ．0 B ．1 C ．2 D ．3 【答案】C【山东省苍山县2012届高三上学期期末检测理】10．如图是一个几何体的三视图，根据图中数据，可得该几 何体的体积是 （ ）A ．3πB ．43πC ．133πD ．683π【答案】C填空题【山东聊城莘县实验高中2012届高三第三次月考理】14.下图是一个物体的三视图，根据图中尺寸（单位：cm ），计算它的体积为 cm 3.【答案】64(4)π+【山东省济南一中2012届高三上学期期末理】16. 关于直线,m n 与平面,αβ，有以下四个命题：① 若//,//m n αβ且//αβ，则//m n ； ② 若,m n αβ⊥⊥且αβ⊥，则m n ⊥； ③ 若,//m n αβ⊥且//αβ，则m n ⊥； ④ 若//,m n αβ⊥且αβ⊥，则//m n ；其中正确命题的序号是 。

单元测试(一)　数与式 (时间：100分钟　满分：150分)题号一二三四五六七八总分合分人复分人得分 一、选择题(本10小题每小题4分满分40分)与－的积是1的是( ) B.C．－－计算(－2)－3的值是( )－1 ．－2－4－5这四个数中最小的是( )－4 ．－5为了加快4网络建设我市电信运营企业将根据各自发展规划今年预计完成4投资7 800万元左右将万元用科学记数法表示为多少元时下列记法正确的是( )C．7.8×107 D．7.8×108 5．使分式－有意义的x的取值范围为( )－2 ．＞－2 ．＜2若x为实数且＋＝0则的值为( )－1 ．－3将多项式x－xy分解因式结果正确的是( )(x2－y) B．(x－y)(x＋y)(x＋y)(x－y)8．(2014·新疆改编)下列运算正确的是( )＋a＝a(3a－b)＝9a－b＝a(a2)3＝a(2014·山东)化简的结果是( )－a－1 ．－a＋1 －ab＋1．－ab＋b甲、乙、丙三家超市为了促销一种定价为m元的商品甲超市先降价20后又降价10；乙超市连续两次降价15；丙超市一次降价30那么顾客购买这种商品更合算的超市是( )甲 ．乙 ．丙 ．一样二、填空题(本大题共4小题每小题5分满分20分)(2015·巴中)分解因式：2a－4a＋2＝________.当x＝时代数式x－3x＋3的值是________．代数式中x的取值范围是________．(2015·淮安)将连续正整数按如下规律排列： 第1列第2列第3列第4列第5列第1行12345第2行8765第3行9101112第4行16151413第5行17181920…若正整数565位于第a行第b列则a＋b＝________.提示：每两行共8个数所以565÷8＝70……5所以前70个8共计140行后面5个数则排第142行第5列所以a＝142＝5所以a＋b＝147.三、(本大题共2小题每小题8分满分16分)计算：－245°＋(2－)0－化简：(x＋2)(x－2)－2(x－5)．四、(本大题共2小题每小题8分满分16分)已知A＝2a－a＋2＝2其中a＞1.求证：A－B＞0.先化简再求值：－，其中a＝－3.五、(本大题共2小题每小题10分满分20分)化简并求值：(m＋n)＋(m＋n)(m－3n)其中m＝＝1.先化简再求值：其中a＝＋1.六、(本题满分12分)(2015·广州)A＝－(1)化简A；(2)当x满足不等式组且x为整数时求A的值．七、(本题满分12分)(2014·黄山模拟)如果一个正整数能表示为两个连续偶数的平方差那么称这个正整数为“神秘数”．如：4＝2－0＝4－2＝6－4因此4都是“神秘数”．(1)36和2 016这两个数是“神秘数”吗？为什么？(2)设两个连续偶数为2k和2k－2(其中k取大于1的整数)由这两个连续偶数构造的神秘数是4的倍数吗？为什么？八、(本题满分14分)观察下列算式：－22＝3－4＝－1－3＝8－9＝－1－4＝15－16＝－1(1)请你按以上规律写出第④个算式；(2)把这个规律用含字母的式子表示出来；你认为(2)中所写出的式子一定成立吗？并说明理由． 2.　3.　4.　5.　6.　7.　8.　9.　10.　11.2(a－1)　12.2　13.x>1　14.147 15.原式＝2－2×＋1－3＝－2. 16.原式＝x－4－2x＋10＝－x＋6. 17.A－B＝(2a－a＋2)－2＝2a－a＝a(2a－1)＞1－1＞0(2a－1)＞0(2a2－a＋2)－2＞0－B＞0. 18.原式＝－ ＝－＝当a＝－3时原式＝＝5. 19.原式＝(m＋2mn＋n)＋(m－3mn＋mn－3n) ＝m＋2mn＋n＋m－3mn＋mn－3n＝2m－2n当m＝＝1时原式＝2×()－2×1＝2×2－21＝2. 20.原式＝＝当a＝＋1时原式＝＝＝ 21.(1)A＝－ ＝－ ＝－＝ ＝(2)不等式组的解集为：1≤x<3. ∵x为整数＝1或2. ∵A＝当x＝2时＝＝＝1. 22.(1)36＝10－8；2 016＝505－50336是“神秘数”不是“神秘数”； (2)(2k)－(2k－2)＝(2k－2k＋2)(2k＋2k－2)＝4(2k－1)由2k和2k－2构造的神秘数是4的倍数． 23.(1)第④个算式为：4×6－5＝24－25＝－1. (2)答案不唯一．如n(n＋2)－(n＋1)＝－1. (3)一定成立． 理由：　n(n＋2)－(n＋1)＝n＋2n－(n＋2n＋1) ＝n＋2n－n－2n－1 ＝－1. 故n(n＋2)－(n＋1)＝－1成立． 初中学习网，资料共分享！我们负责传递知识！。

2012届高考数学第一轮立体几何单元练习题(含答案)高三数学单元练习题：立体几何（Ⅱ）第Ⅰ卷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（本大题共12个小题，每小题5分，共60分）. 1．一条直线与一个平面所成的角等于，另一直线与这个平面所成的角是 . 则这两条直线的位置关系（） A．必定相交 B．平行 C．必定异面 D．不可能平行 2．在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1∶3，则锥体被截面所分成的两部分的体积之比为（） A．1∶ B．1∶9 C．1∶ D．1∶ 3．正方体中，、、分别是、、的中点．那么，正方体的过、、的截面图形是（） A．三角形 B．四边形 C．五边形 D．六边形 4．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（）A．75° B．60° C．45° D．30° 5．对于直线m、n和平面，下面命题中的真命题是（） A．如果、n是异面直线，那么 B．如果、n是异面直线，那么相交 C．如果、n共面，那么 D．如果、n共面，那么 6．已知正方体ABCD－A1B1C1D1的棱长为a，长为定值的线段EF在棱AB上移动（EF<a），若P是A1D1上的定点，Q是C1D1上的动点，则四面体PQEF的体积是（） A．有最小值的一个变量B．有最大值的一个变量 C．没有最值的一个变量 D．是一个常量 7．已知平面所成的二面角为80°，P为、外一定点，过点P的一条直线与、所成的角都是30°，则这样的直线有且仅有（） A．1条B．2条 C．3条 D．4条 8．如图所示，在水平横梁上A、B两点处各挂长为50cm的细线AM、 BN、AB的长度为60cm，在MN处挂长为60cm的木条MN平行于横梁，木条中点为O，若木条绕O的铅垂线旋转60°，则木条比原来升高了（） A．10cm B．5cm C．10 cm D．5 cm 9．如图，棱长为5的正方体无论从哪一个面看，都有两个直通的边长为1的正方形孔，则这个有孔正方体的表面积（含孔内各面）是（） A．258 B．234 C．222 D．210 10．在半径为的球内有一内接正三棱锥，它的底面三个顶点恰好都在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三点后返回，则经过的最短路程是（） A． B． C． D． 11．底面边长为a，高为h的正三棱锥内接一个正四棱柱（此时正四棱柱上底面有两个顶点在同一个侧面内），此棱柱体积的最大值（） A． B． C． D． 12．将半径都为１的４个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为（） A． B．2+ C．4+ D．第Ⅱ卷二、填空题：请把答案填在题中横线上（本大题共4个小题，每小题4分，共16分）. 13．某地球仪上北纬纬线的长度为，该地球仪的半径是__________cm，表面积是______________cm2. 14．如图，矩形ABCD中，DC= ，AD=1，在DC上截取DE=1，将△ADE沿AE翻折到D1点，点D1在平面ABC上的射影落在AC上时，二面角D1¬―AE―B 的平面角的余弦值是 . 15．多面体上位于同一条棱两端的顶点称为相邻的，如图，正方体的一个顶点A在平面内，其余顶点在的同侧，正方体上与顶点A相邻的三个顶点到的距离分别为1，2和4，P是正方体的其余四个顶点中的一个，则P到平面的距离可能是：①3；②4；③5；④6；⑤7 以上结论正确的为______________. （写出所有正确结论的编号） 16．如图，在透明材料制成的长方体容器ABCD―A1B1C1D1内灌注一些水，固定容器底面一边BC于桌面上，再将容器倾斜根据倾斜度的不同，有下列命题：（1）水的部分始终呈棱柱形；（2）水面四边形EFGH的面积不会改变；（3）棱A1D1始终与水面EFGH平行；（4）当容器倾斜如图所示时，BE•BF是定值。

凭祥高中2012届选择题特训专题1姓名 班别 得分一、选择题：本大题共12小题，每小题5分，共60分。

请把答案涂在答题卡指定的位置上。

1．把复数z 的共轭复数记作z ，i 为虚数单位，若1,(1)z z i z =++⋅则=（ ）A ．3i -B ．3i +C ．13i +D ．3 2．函数1ln(1)(1)2x y x +-=>的反函数是（ ） A ．211(0)x y e x -=-> B ．211(0)x y e x -=+>C ．211()x y e x R -=-∈ D ．211()x y e x R -=+∈ 3．“0a >”是“||0a >”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知{}n a 为等差数列，其公差为2-，且7a 是3a 与9a 的等比中项，n S 为{}n a 的前n 项和，则10S 的值为（ ） A ．110- B ．90- C ．90 D ．1105．已知角α的终边过点(8,6sin30)P m --︒，且4cos 5α=-，则m 的值为（ ）A ．12-B ．C ．12D 6．平面α⊥平面β，,A B αβ∈∈，AB 与两平面,αβ所成的角分别为4π和6π，过,A B 分别作两平面交线的垂线，垂足为'',A B ，则'':AB A B ＝（ ） A ． 4:3 B ． 3:2 C ． 2:1 D ． 3:17．某班选派6人参加两项公益活动，每项活动最多安排4人，则不同的安排方法有（ ）A ．50种B ．70种C ．35种D ．55种8．若曲线12y x-=在点12,a a -⎛⎫ ⎪⎝⎭处的切线与两个坐标轴围成的三角形的面积为18，则a =（ ） A ．64 B ．32 C ．16 D ．89 . ()f x R 是上的奇函数，)()2(x f x f -=+，当10≤≤x 时，x x f =)(，则(7.5)f =( )A ．0.5B ．0.5-C ．1.5D ． 1.5-10．椭圆2212516x y +=的左右焦点分别为12,F F ，弦AB 过1F ，若2ABF ∆的内切圆周长为π，,A B 两点的坐标分别为1122(,),(,)x y x y ，则12y y -值为（ ）A ．3 B ．53 C ．103 D ．20311．已知球O 为棱长为1的正方体1111ABCD A B C D -的内切球，则平面1ACD 截球O 的截面面积为（ ）A．6 B．3 C ．6π D ．3π 12．若在直线l 上存在不同的三个点C B A ，，，使得关于实数x 的方程20x OA xOB BC ++= 有解（点O不在l 上），则此方程的解集为（ ） A ．{1}- B ．{0} C．⎪⎪⎩⎭ D ．{}1,0-二、填空题：本大题共4小题，每小题5分，共20分。