2019-2020学年高中数学 2.2.2对数函数(二)教案 新人教必修1.doc

2019-2020年人教版高中数学必修一说课稿：2-2对数函数及其性质一、教材分析本节课选自人教版高一数学（必修一）第二单元2.2.2《对数函数及其性质》第一课时。

对数函数是重要的基本初等函数之一，是指数函数知识的拓展和延伸. 它的教学过程，体现了“数形结合”的思想，同时蕴涵丰富的解题技巧，这对培养学生的观察、分析、概括的能力、发展学生严谨论证的思维能力有重要作用．本节课也为后面进一步探究对数函数的应用及指数函数、对数函数的综合应用起到承上启下的作用。

二、学情分析学生前面已经学习了指数函数，用研究指数函数的方法，进一步研究和学习对数函数的概念、图像和性质以及初步应用，启发引导学生进一步完善初等函数的知识的系统性，加深对函数的思想方法的理解。

教学过程中，发挥大多数学生动手能力较强的特点，让学生自己通过列表、描点、连线画对数函数图像。

这样也利于对对数函数性质的理解。

三、教学目标1.知识目标：让学生掌握对数函数的概念，能正确描绘对数函数的图象，掌握对数函数的性质.2.能力目标：通过对对数函数的学习，培养学生观察，思考，分析，归纳的思维能力.3.情感目标：培养学生勇于探索的精神，让学生主动融入学习．四、教学重点和难点重点：在理解对数函数定义的基础上，掌握对数函数的图象和性质。

难点：对数函数性质的应用。

五、教法与学法说教法教学过程是教师和学生共同参与的过程，启发学生自主性学习,教师主导,学生为主体,根据这样的原则和所要完成的教学目标，我采用如下的教学方法：(1)启发引导学生思考、分析、实验、探索、归纳。

(2)采用“从特殊到一般”、“从具体到抽象”的方法。

(3)体现“对比联系”、“数形结合”及“分类讨论”的思想方法。

(4)多媒体演示法。

说学法教给学生方法比教给学生知识更重要，本节课注重调动学生积极思考、主动探索，尽可能地增加学生参与教学活动的时间和空间，我进行了以下学法指导：(1)对照比较学习法：学习对数函数,处处与指数函数相对照。

高中数学 2.2.2对数函数及其性质（二）教案新人教A版必修1
3.2.2对数函数（二）
教学目标：进一步理解对数函数的定义,掌握对数函数的图象和性质
教学重点：掌握对数函数的图象和性质.
教学过程：
1、 复习对数函数的概念
2、 例子：
（一）求函数的定义域
1． 已知函数)23lg()(2+-=x x x f 的定义域是F,
函数)2lg()1lg()(-+-=x x x g 的定义域是N,
确定集合F 、N 的关系？
2．求下列函数的定义域：
（1）3)1log(1)(-+=x x f （2）2312log )(--=x x x f
（二）求函数的值域
]2,1[log )(2
∈=x x x f 2．]2,1[log
)(∈=x x x f a
3．2log )(22+=x x f 4.求函数（1）)2(log )(2
2+=x
x f （2）21
log )(22+=x x f 的值域
（三）函数图象的应用
x y a log = x y b log = x y c
log =的
课堂练习：略
小结：本节课进一步复习了对数函数的定义、图象和性质
课后作业：略。

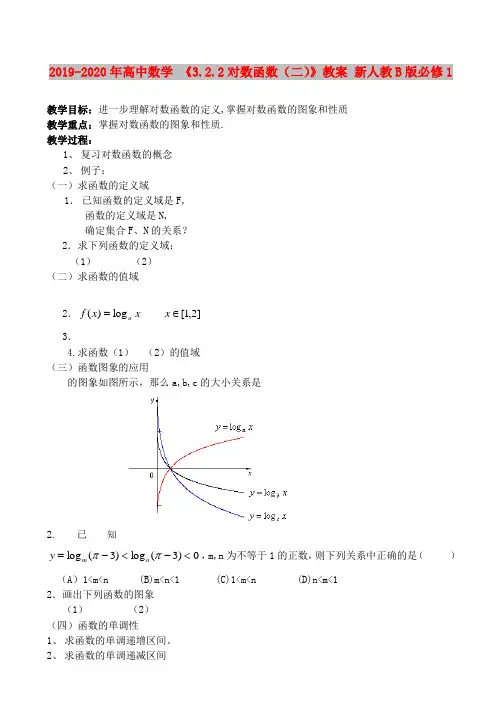
2019-2020年高中数学 《3.2.2对数函数（二）》教案 新人教B 版必修1教学目标：进一步理解对数函数的定义,掌握对数函数的图象和性质教学重点：掌握对数函数的图象和性质.教学过程：1、 复习对数函数的概念2、 例子：（一）求函数的定义域1． 已知函数的定义域是F,函数的定义域是N,确定集合F 、N 的关系？2．求下列函数的定义域：（1） （2）（二）求函数的值域2．]2,1[log )(∈=x x x f a3．4.求函数（1） （2）的值域（三）函数图象的应用的图象如图所示，那么a,b,c 的大小关系是2.已知0)3(l o g )3(l o g <-<-=ππn m y ，m,n 为不等于1的正数，则下列关系中正确的是（） （A ）1<m<n (B)m<n<1 (C)1<m<n (D)n<m<12．画出下列函数的图象（1） （2）（四）函数的单调性1、 求函数的单调递增区间。

2、 求函数的单调递减区间（五）函数的奇偶性1、函数))(1(log22Rxxxy∈++=的奇偶性为[ ]A．奇函数而非偶函数 B．偶函数而非奇函数C．非奇非偶函数 D．既奇且偶函数（五）综合1．若定义在区间（－1，0）内的函数满足，则a的取值范围（）课堂练习：略小结：本节课进一步复习了对数函数的定义、图象和性质课后作业：略2019-2020年高中数学《3.2.3指数函数与对数函数的关系》教案新人教B版必修1教学目标：知道指数函数与对数函数互为反函数教学重点：知道指数函数与对数函数互为反函数教学过程：1、复习指数函数、对数函数的概念2、反函数的概念：一般地，函数中x是自变量，y是x的函数，设它的定义域为A，值域为C，由可得，如果对于y在C中的任何一个值，通过，x在A中都有唯一的值和它对应，那么就表示x是自变量y的函数。

这样的函数叫函数的反函数，记作：。

习惯上，用x表示自变量，y表示函数，因此的反函数通常改写成：注：①明确反函数存在的条件：当一个函数是一一映射时函数有反函数，否则如等均无反函数；②与互为反函数。

2019-2020年高中数学《对数函数》教案12 新人教A版必修1教学目标：知识与技能理解指数函数与对数函数的依赖关系，了解反函数的概念，加深对函数的模型化思想的理解．过程与方法通过作图，体会两种函数的单调性的异同．情感、态度、价值观对体会指数函数与对数函数内在的对称统一．教学重点：重点难两种函数的内在联系，反函数的概念．难点反函数的概念．教学程序与环节设计：由函数的观点分析例题，引出反函数的概念．关联性角度试着给指数函数、对教学过程与操作设计：2019-2020年高中数学《对数函数》教案13 新人教A版必修1教材分析：1、对数函数及其性质为必修内容，而且对数函数及其相关知识历来是高考的重点，既有中档题，又能和其它知识相结合、综合性较强、考查也比较深刻。

2、对数函数是函数中一类重要的基本初等函数，它是在学生已经学过指数函数、对数与对数运算基础上引入的，是对上述知识的应用，也是对函数这一重要数学思想的进一步认识与理解。

3、对数函数是解决有关自然科学领域中实际问题的重要工具，是学生今后学习对数方程，对数不等式的基础。

4、对数函数及其性质的学习使学生的知识体系更加完整、系统，同时又是对数和函数知识的拓展与延伸。

5、本节课内容为反函数知识，应重视数学知识之间的内在联系，突出对数函数是现实世界中的重要数学模型。

教学设计：教学目标：知识与技能理解指数函数与对数函数的依赖关系，了解反函数的概念，加深对函数的模型化思想的理解．过程与方法通过作图，体会两种函数的单调性的异同．情感、态度、价值观对体会指数函数与对数函数内在的对称统一．教学重点：难两种函数的内在联系，反函数的概念．教学难点：反函数的概念．教学程序与环节设计：由函数的观点分析例题，引出反函数的概念．两种函数的内在联系，图象关系．关联性角度试着给指数函数、对教学过程与操作设计：附表1：巩固练习：1.求下列函数的反函数： y =(x ∈R )； y = (a ＞0,a ≠1,x ＞0)2．己知函数的图象过点（1，3）其反函数的图象过（2，0）点，求的表达式. 归纳小结，强化思想：本节课的目的要求是在学习了指数函数与对数函数后，以两个底数相同的指数函数与对数函数介绍反函数的概念，可以初步尝试求一个已知简单函数的反函数，但根据课程标准安排应不作过多强调。

§2.2.2 对数函数及其性质（第一、二课时）一．教学目标1．知识技能①对数函数的概念，熟悉对数函数的图象与性质规律. ②掌握对数函数的性质，能初步运用性质解决问题. 2．过程与方法让学生通过观察对数函数的图象，发现并归纳对数函数的性质. 3．情感、态度与价值观①培养学生数形结合的思想以及分析推理的能力； ②培养学生严谨的科学态度. 二．学法与教学用具1．学法：通过让学生观察、思考、交流、讨论、发现函数的性质； 2．教学手段：多媒体计算机辅助教学． 三．教学重点、难点1、重点：理解对数函数的定义，掌握对数函数的图象和性质.2、难点：底数a 对图象的影响及对数函数性质的作用. 四．教学过程 1．设置情境在2．2．1的例6中，考古学家利用157302logP 估算出土文物或古遗址的年代，对于每一个C 14含量P ，通过关系式，都有唯一确定的年代t 与之对应．同理，对于每一个对数式log xa y =中的x ，任取一个正的实数值，y 均有唯一的值与之对应，所以log x a y x =关于的函数．2．探索新知一般地，我们把函数log a y x =（a ＞0且a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）．提问：（1）．在函数的定义中，为什么要限定a ＞0且a ≠1．（2）．为什么对数函数log a y x =（a ＞0且a ≠1）的定义域是（0，+∞）．组织学生充分讨论、交流，使学生更加理解对数函数的含义，从而加深对对数函数的理解.答：①根据对数与指数式的关系，知log a y x =可化为ya x =，由指数的概念，要使ya x =有意义，必须规定a ＞0且a ≠1．②因为log a y x =可化为y x a =，不管y 取什么值，由指数函数的性质，ya ＞0，所以(0,)x ∈+∞． 例题1：求下列函数的定义域（1）2log a y x = （2）log (4)a y x =- （a ＞0且a ≠1） 分析：由对数函数的定义知：2x ＞0；4x -＞0，解出不等式就可求出定义域． 解：（1）因为2x ＞0，即x ≠0，所以函数2log x a y =的定义域为{}|0x x ≠.（2）因为4x -＞0，即x ＜4，所以函数(4)log x a y -=的定义域为{|x x ＜}4. 下面我们来研究函数的图象，并通过图象来研究函数的性质：先完成P 81表2－3，并根据此表用描点法或用电脑画出函数2log x y =的图象, 再利用电脑软件画出0.5log .x y =的图象x121 2 4 6 8 12 16 y－1122.5833.584y0.5log y x =０ x2log y x =注意到：122log log y x x ==-，若点2(,)log x y y x =在的图象上，则点12(,)log x y y x -=在的图象上. 由于（,x y -）与（,x y -）关于x 轴对称，因此，12log y x =的图象与2log y x =的图象关于x 轴对称 . 所以，由此我们可以画出12log y x =的图象 .先由学生自己画出12log y x =的图象，再由电脑软件画出2log y x =与12log y x =的图象.探究：选取底数(a a ＞0，且a ≠1）的若干不同的值，在同一平面直角坐标系内作出相应的对数函数的图象．观察图象，你能发现它们有哪些特征吗？.作法：用多媒体再画出4log y x =，3log y x =，13log y x =和14log y x =3log y x =42-2-4-55提问：通过函数的图象，你能说出底数与函数图象的关系吗？函数的图象有何特征，性质又如何？先由学生讨论、交流，教师引导总结出函数的性质. (投影)图象的特征函数的性质（1）图象都在y 轴的右边 （1）定义域是（0，+∞） （2）函数图象都经过（1，0）点 （2）1的对数是0（3）从左往右看，当a ＞1时，图象逐渐上升，当0＜a ＜1时，图象逐渐下降 .（3）当a ＞1时，log xa y =是增函数，当0＜a ＜1时，log a y x =是减函数. （4）当a ＞1时，函数图象在（1，0）点右边的纵坐标都大于0，在（1，0）点左边的纵坐标都小于0. 当0＜a ＜1时，图象正好相反，在（1，0）点右边的纵坐标都小于0，在（1，0）点左边的纵坐标都大于0 .（4）当a ＞1时x ＞1，则log a x ＞00＜x ＜1，log a x ＜0 当0＜a ＜1时x ＞1，则log a x ＜00＜x ＜1，log a x ＜0由上述表格可知，对数函数的性质如下（先由学生仿造指数函数性质完成，教师适当启发、引导）：a ＞10＜a ＜1图象性 质（1）定义域（0，+∞）； （2）值域R ； （3）过点（1，0），即当x =1，y =0； （4）在（0，+∞）上是增函数在（0，+∞）是上减函数例题训练：1. 比较下列各组数中的两个值大小（1）22log 3.4,log 8.54log y x =14log y x =13log y x =（2）0.30.3log 1.8,log 2.7（3）log 5.1,log 5.9a a （a ＞0，且a ≠1）分析：由数形结合的方法或利用函数的单调性来完成：（1）解法1：用图形计算器或多媒体画出对数函数2log y x =的图象.在图象上，横坐标为3、4的点在横坐标为8.5的点的下方：所以，22log 3.4log 8.5<解法2：由函数2log y x R =在+上是单调增函数，且3.4＜8.5，所以22log 3.4log 8.5<. 解法3：直接用计算器计算得：2log 3.4 1.8≈，2log 8.5 3.1≈（2）第（2）小题类似（3）注：底数是常数，但要分类讨论a 的范围，再由函数单调性判断大小. 解法1：当a ＞1时，log a y x =在（0，＋∞）上是增函数，且5.1＜5.9. 所以，log 5.1a <log 5.9a当a <1时，log a y x =在（0，＋∞）上是减函数，且5.1＜5.9. 所以，log 5.1a >log 5.9a解法2：转化为指数函数，再由指数函数的单调判断大小不一，令 11log 5.1, 5.1,b a b a ==则 令22log 5.9, 5.9,b a b a ==则 则2 5.9ba =则 当a ＞1时，xy a =在R 上是增函数，且5.1＜5.9 所以，1b ＜2b ，即log 5.1a ＜log 5.9a当0＜a ＜1时，x y a =在R 上是减函数，且5.1＞5.9 所以，1b ＜2b ，即log 5.1a ＞log 5.9a 说明：先画图象，由数形结合方法解答 课堂练习：Ｐ73 练习 第２，３题 补充练习1．已知函数(2)x y f =的定义域为[-1，1]，则函数2(log )y f x =的定义域为 2．求函数22log (1)y x x =+≥的值域.3．已知log 7m ＜log 7n ＜0，按大小顺序排列m, n, 0, 1 4．已知0＜a ＜1, b ＞1, ab ＞1. 比较1log ,log ,log aa b b b 1的大小b归纳小结：②对数函数的概念必要性与重要性;②对数函数的性质，列表展现.。

2019-2020年高中数学 2.2.1对数与对数运算（二）全册精品教案新人教A版必修1（一）教学目标1．知识与技能：理解对数的运算性质．2．过程与方法：通过对数的运算性质的探索及推导过程，培养学生的“合情推理能力”、“等价转化”和“演绎归纳”的数学思想方法，以及创新意识．3．情感、态态与价值观通过“合情推理”、“等价转化”和“演绎归纳”的思想运用，培养学生对立统一、相互联系，相互转化以及“特殊—一般”的辩证唯物主义观点，以及大胆探索，实事求是的科学精神．（二）教学重点、难点1．教学重点：对数运算性质及其推导过程.2．教学难点：对数的运算性质发现过程及其证明.（三）教学方法针对本节课公式多、思维量大的特点，采取实例归纳，诱思探究，引导发现等方法．（四）教学过程备选例题例1 计算下列各式的值：（2）22)2(lg 20lg 5lg 8lg 325lg +⋅++.【解析】（1）方法一：原式=2122325)57lg(2lg 34)7lg 2(lg 21⨯+--=5lg 217lg 2lg 27lg 2lg 25++-- = =.方法二：原式== =.（2）原式=2lg5 + 2lg2 + lg5 (2lg2 + lg5) + (lg2)2 =2lg10 + (lg5 + lg2)2 = 2 + (lg10)2 = 2 + 1 = 3.【小结】易犯lg52 = (lg5)2的错误.这类问题一般有两种处理方法：一种是将式中真数的积、商、方根运用对数的运算法则将它们化为对数的和、差、积、商，然后化简求值；另一种方法是将式中的对数的和、差、积、商运用对数的运算法则将它们化为真数的积、商、幂、方根，然后化简求值. 计算对数的值时常用到lg2 + lg5 = lg10 = 1.例2：（1）已知lg2 = 0.3010，lg3 = 0.4771，求lg ； （2）设log a x = m ，log a y = n ，用m 、n 表示； （3）已知lg x = 2lg a + 3lg b – 5lg c ，求x .【分析】由已知式与未知式底数相同，实现由已知到未知，只须将未知的真数用已知的真数的乘、除、幂表示，借助对数运算法则即可解答.【解析】（1）1190lg 45lg 222==0.4771+0.5 – 0.1505（2）1113412log log log a a a a x y =+-.1213141log 121log 3141m n y x a a -+=-+=（3）由已知得：532532lglg lg lg lg cb ac b a x =-+=，∴.【小结】①比较已知和未知式的真数，并将未知式中的真数用已知式的真数的乘、除、乘方表示是解题的关键，并且应注意对数运算法则也是可逆的；②第（3）小题利用下列结论：同底的对数相等，则真数相等. 即log a N = log a MN = M ..。

（4）由表格中的数据：
碳14的含量P
0.5
0.3
0.1
0.01
0.001
生物死亡年数t
5730
9953
19035
39069
57104
可读出精确年份为39069，当P值为0.001时，t大约为57104年，所以每一个P值都与一个t值相对应，是一一对应关系，所以p与t之间是函数关系。
（5）数学知识不但可以解决猛犸象的封存时间，也可以与其他学科的知识相结合来解决视频中的遗留问题，就是不知道咱们中国的猛犸象克隆问题会由班里的哪位同学解决，我们拭目以待。
课后作业的设计意图：
一、巩固学生本节课所学的知识并落实教学目标；二、让不同基础的学生学到不同的技能，体现因材施教的原则；
三、使同学们体会到科学的探索永无止境，为数学的学习营造一种良好的科学氛围。
对数函数及其性质教学设计
教学过程
设计意图
一、创设情境，导入新课
活动1：（1）同学们有没有看过《冰河世纪》这个电影?先播放视频，引入课题。
（2）考古学家经过长期实践，发现冻土层内某微量元素的含量P与年份t的关系： ，这是一个指数式，由指数与对数的关系，此指数式可改写为对数式 。
（3）考古学家提取了冻土层内微量元素，确定它的残余量约占原始含量的1％，即P=0.01，代入对数式，可知
教学过程中，评价学生的情绪、状态、积极性、自信心、合作交流的意识与独立思考的能力；
在学习互动中，评价学生思维发展的水平；
在解决问题练习和作业中，评价学生基础知识基本技能的掌握.
适时地组织和指导学生归纳知识和技能的一般规律，有助于学生更好地学习、记忆和应用，发挥知识系统的整体优势，并为后续学习打好基础。
解：（1） 函数 的定义域是 。