《平行线的性质定理和判定定理》

A．
平行
B．
垂直
C．
平行或垂直
D．
无法确定
3．若两个角的两边分别平行，且这两个角的差为40°，则这两角的度数分别是（ ）
A．
150°和110°
B．
140°和100°
C．
110°和70°
D．
70°和30°
4．如图所示，AC⊥BC，DE⊥BC，CD⊥AB，∠ACD=40°，则∠BDE等于（ ）
A．
40°
①不相交的两条直线叫做平行线②平面内，过一点有且只有一条直线与已知直线垂直
③平行于同一条直线的两条直线互相平行④在同一平面内，两条直线不是平行就是相交
A．
1个
B．
2个
C．
3个
D．
4个
2．在同一平面内，有8条互不重合的直线，l1，l2，l3…l8，若l1⊥l2，l2∥l3，l3⊥l4，l4∥l5…以此类推，则l1和l8的位置关系是（ ）
A．
50°
B．
130°
C．
100°
D．
50°或130°
2、能力提升问题
11．如图所示，DE∥BC，DC∥FG，则图中相等的同位角共有（ ）
A．
6对
B．
5对
C．
4对
D．
3对
12．如图所示，AD∥EF∥BC，AC平分∠BCD，图中和α相等的角有（ ）
A．
2个
B．
3个
C．
4个
D．
5个
13．如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角是（ ）
2、突破重、难点、，规范过程、梳理方法、总结规律、提升能力的问题或题组
问题二:、证明平行等的角有_________个．

5.4平行线的性质定理和判定定理东平四中备课人：邓海燕学习目标:1.掌握平行线的性质定理和判定定理的证明。

会区分平行线的判定定理及性质定理，体会二者之间的区别与联系；2.了解互逆命题的概念，知道原命题成立，逆命题不一定成立；了解逆定理的概念。

3培养自己的观察、语言表达能力。

重难点: 会写出一个命题的逆命题，会判断定理的逆命题的真假。

教学过程一、知识回顾：命题都有两部分组成：（）和（）。

二、自主学习课本166——168页（约7分钟）三、预习检测：1、在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做（2、“内错角相等，两直线平行”的逆命题是（）。

3、“对顶角相等”的逆命题是（）。

这个逆命题是真命题还是假命题？说明理由。

四、新知探究思考：平行线的判定方法有哪些？平行线有哪些性质？你还记得吗？、同位角相等，两直线平行。

、内错角相等，两直线平行。

3、同旁内角互补，两直线平行。

1、两条平行直线被第三条直线所截，同位角相等。

2、两条平行直线被第三条直线所截，内错角相等。

3、两条平行直线被第三条直线所截，同旁内角互补。

五、典例精析 例1．证明平行线的性质定理2.两条平行线被第三条直线所截，内错角相等。

：已知：求证：证明：思考：你会证明 “平行线的性质定理3：两条平行直线被第三条直线所截，同旁内角互补”吗？试一试。

例2.证明 平行线的判定定理1：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行。

已知：求证：证明：思考：你会证明 “平行线的判定定理2：两条直线被第三条直线所截，如果同旁内角互补，那么两条直线平行。

”吗？与同学交流六、合作探究：例1，例2这两个命题，你能发现它们的条件和结论之间有什么关系？结论;__________________________________________________1、互逆命题：在两个命题中，如果第一个命题的条件是第二个命题的 ，而第一个命题的结论是第二个命题的 ，那么这两个命题互逆命题，如果把 其中一个命题叫做原命题，那么另一个命题叫做它的。

性质定理：1、两直线平行，同位角相等。

2、两直线平行，内错角相等。

3、两直线平行，同旁内角互补。

判定方法：1、同位角相等，两直线平行。

2、内错角相等，两直线平行。

3、同旁内角互补，两直线平行。

两直线平行的判定定理
1、两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行。

（内错角相等，两直线平行）
2、两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行。

（同旁内角互补，两直线平行）
3、两直线都与第三条直线平行，那么这两条直线也互相平行。

（若直线a平行于直线b，直线b平行于直线c，那么直线a也平行于直线c）（等量代换）。

两直线平行的性质定理
1、同一平面内，垂直于同一条直线的两条线段（直线）平行；
2、（同一平面内），平行于同一条直线的两条线段（直线）平行；
3、同一平面内，永不相交的两条直线叫平行线；
4、过直线外一点有且仅有一条直线与已知直线平行。

7.3平行线的判定【知识沙盘】【学习目标】1.会根据基本事实“同位角相等，两直线平行”来规范证明“内错角相等，两直线平行”“同旁内角互补，两直线平行”.2.能用平行线的判定解决一些简单的问题.【重点】1. 能规范证明平行线的判定定理.2.平行线判定定理的简单应用.【难点】用数学语言和符号语言对文字命题的表述.【学情分析】经过前面的学习我们发现，我们得打的任何一个结论都要有依据。

而我们根据这些“依据”推理、证明，从而得到结论的过程叫做证明。

在“同位角相等，两直线平行”的基本事实下，我们将通过演绎推理得到“内错角相等，两直线平行”和“同旁内角互补，两直线平行”，从而得到平行线的判定定理.【教学过程】一、导入你能用折纸的方法折出两条平行线吗？你的依据是什么？通过前面的学习，我们知道了“同位角相等，两直线平行”的基本事实，那我们能利用它证明另外两个判定定理吗？让我们一起来探究吧！二、自主学习阅读并完成学习指导书的知识储备，完成【自主学习】A级和B级.三、交流研讨出示答案，自主订正四、精讲部分（一）不讲内容：①知识储备、归类总结②A级1,2（二）略讲内容：①B级 33.蜂房的顶部由三个全等的四边形围成，每个四边形的形状如图所示，其中o=B70=∠.试确定这个四边形对边的位置关系，并证明你的结论.D∠=CA110=∠∠，o直线平行）　（同旁内角互补，两ＢＤ（等式的性质）Ｂ（已知）Ｂ，直线平行）　（同旁内角互补，两（等式的性质）（已知），理由：ＢＤ解：C A A A DC AB D A D A CA DC AB O O //18070110//18070110////o o o o ∴=∠+∠∴=∠=∠∴=∠+∠∴=∠=∠ （三）精讲内容：① C 级 44.如图，点Ｄ，Ｅ分别在AB 和AC 上，.ABC BE ∠平分 （１）若DEB DBE ∠=∠,求证：BC DE //.（２）若BC DE //，求证：BDE ∆为等腰三角形.（３）在(1)的条件下，若O EBC 25=∠，求BDE ∠的度数．(130180//)(502)(25)(21)(//1)3()DE//BC( )(21)()2()DE//BC()()( )(21)()1(互补两直线平行，同旁内角等式的基本性质已知角平分线的性质已知平分）知由（（等量代换）相等）（两直线平行，内错角已知角平分线的性质已知平分证明：行内错角相等，两直线平等量代换已知角平分线的性质已知平分证明：O O OOABC BDE BCDE EBC ABC EBC ABC EBC DBE ABC BE BCDE EBC DBE DEB EBC ABC EBC DBE ABC BE DEB EBC DEB DBE ABC EBC DBE ABC BE =∠-=∠∴=∠=∠∴=∠∠=∠=∠∴∠∠=∠∴∠=∠∴∠=∠=∠∴∠∴∠=∠∴∠=∠∠=∠=∠∴∠五、【归类总结】1.知识小结：平行线的判定定理；同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行．2.思想方法: 转化的数学思想方法；3.核心素养：几何直观、逻辑推理、数学运算的数学核心素养.六、自我检测七、课堂小结八、布置作业九、教后反思十、预测生成(1）文字命题的已知、画图、求证的转化.(2）运用平行线判定定理解决简单问题时逻辑推理不明确. 十一、板书设计十二、实际生成记录。

自主探究3 1、 例1、例2的两个命题，你发现它们的
条件和结论有什么关系？ 在两个命题中，如果第一个命题的条件 是第二个命题的结论，而第一个命题的 结论是第二个命题的条件，那么这两个 命题叫做互逆命题。 如果把其中一个命题叫做原命题，那么 另一个命题叫做它的逆命题。

自主探究
说出下列命题的逆命题？它们的逆命题是真命题 还是假命题？ （1）两平行直线被第三条直线所截，同旁内角 互补。 （2）对顶角相等。
温馨提示：请 根据上节课所 学习的几何证 明的步骤说说 你的思路.
3
1 2
4
a b
∴∠3=∠2 (两直线平行，同位角相等) ∵ ∠3=∠1 (对顶角相等) ∴∠1=∠2 (等量代换)
自主探究2：
例2：证明平行线的判定 定理1 ：两条直线 被第三条直线所截，如果内错角相等，那 么两直线平行.
已知:如图,∠1和∠2是直线a,b被直线c 截出的内错角,且∠1=∠2. 求证:a∥b. 证明:∵ ∠1=∠2 (已知), ∠2=∠3 (对顶角相等),
3
c
a
2 1
b
∴∠1=∠3(等量代换).
∵ ∠1=∠3 (已证), ∴ a∥b(同位角相等,两直线平行).
已知:如图,∠1和∠2是直 c 线a,b被直线c截出的同旁内 a 1 角,且∠1与∠2互补. 2 求证:a∥b. b 3 证明:∵ ∠1与∠2互补 (已知), ∴∠1+∠2=1800(互补的定义). 平行线的判定定 0 ∴∠1= 180 -∠2(等式的性质). 理2：同旁内角互 又∵∠3+∠2=1800 (平角的定义), 补两直线平行 0 ∴∠3= 180 -∠2(等式的性质). ∴∠1=∠3(等量代换). ∴ a∥b(同位角相等,两直线平行).

简单说成：同旁内角互补，两直线平行. ∵ ∠1+ ∠2=180°， ∴ a∥b.
证明一个命题的一般步骤： (1)弄清题设和结论；
a1 b2
c
(2)根据题意画出相应的图形；
(3)根据题设和结论写出已知,求证；
(4)分析证明思路,写出证明过程.
【议一议】 据说,人类知识的75%是在操作中学到的.
小明用下面的方法作出平行线，你认为他的作法对吗？为 什么？ 通过这个操作活动,得 到了什么结论?
每一个命题都有逆命题，只要将原命题的条件改成 结论，并将结论改成条件，便可得到原命题的逆命题．
但是原命题正确，它的逆命题未必正确．例如真命 题“对顶角相等”的逆命题为“相等的角是对顶角”， 此命题就是假命题．
【跟踪训练】
1.举例说明下列命题的逆命题是假命题. （1）如果一个整数的个位数字是5 ，那么这个整数能被 5整除. 逆命题：如果一个整数能被5整除，那么这个整数的个位 数字是5. 例如，10能被5整除，但它的个位数字是0. （2）如果两个角都是直角，那么这两个角相等. 逆命题：如果两个角相等，那么这两个角是直角. 例如，60°= 60°，但这两个角不是直角.
4.到一个角的两边距离相等的点，在这个角的平分线上.
条件：到一个角的两边距离相等的点. 结论：它在这个角的平分线上. 逆命题：角平分线上的点到角两边的距离相等. 5.线段的垂直平分线上的点到这条线段的两个端点的距离相等. 条件：线段垂直平分线上的点. 结论：它到这条线段的两个端点的距离相等. 逆命题：到一条线段的两个端点的距离相等的点在这条线段 的垂直平分线上.
a
∵∠1+∠2=180°, ∴ a∥b.
b
c
1
2
c

（2）推理的过程要步步有据.
（3）在推理的过程中，已经推出的结论可以作为后面继续推证的依据.
【模拟试题】（答题时间：50分钟）
一.选择题
1.在同一平面内，下列说法：①过两点有且只有一条直线；②两条不同的直线，有且只有一个公共点；③过一点有且只有一条直线与已知直线垂直；④过一点有且只有一条直线与已知直线平行.其中正确的有（）
又∵EF∥AB（已知），
∴∠EFC＝∠B（两直线平行，同位角相等），
∴∠ADE＝∠EFC（等量代换）.
评析：本题关键是利用平行线的性质，来证明角度相等，要注意角的位置.
例4.如图所示，直线MN分别和直线AB、CD、EF相交于G、H、P，∠1＝∠2，∠2＋∠3＝180°，求证：AB∥EF.
分析：要证AB∥EF，可先证AB∥CD和EF∥CD.根据平行于同一条直线的两条直线平行可得AB∥EF.
（1）∵CE∥AB（已知），
∴∠1＝∠B（）
（2）∵CE∥AB（已知），
∴∠2＝∠A（）
（3）∵∠1＝∠B，∠2＝∠A（已证），
∴∠1＋∠2＝∠B＋∠A（）
即∠ACD＝∠B＋∠A（）
（4）∵BCD是一直线（已知），
∴∠1＋∠2＋∠ACB＝180°（），
∴∠A＋∠B＋∠ACB＝180°（）.
*2.如图所示，已知AD⊥BC，EF⊥BC，∠1＝∠2，求证：DG∥BA.
5.提示：因为∠BAC是△ACD的一个外角，所以∠BAC＞∠1.因为∠1＝∠2，所以∠BAC＞∠2.因为∠2是△BCD的一个外角，所以∠2＞∠B.所以∠BAC＞∠B.
3.提示：因为AB∥CD，所以∠EMB＝∠END，即∠1＋∠3＝∠2＋∠4.因为MG∥NH，所以∠3＝∠4.所以∠1＝∠2.
4.提示：过点E作EF∥AB，所以∠B＋∠BEF＝180°，因为AB∥CD，所以EF∥CD（平行于同一条直线的两条直线平行），所以∠D＋∠DEF＝180°，所以∠B＋∠BEF＋∠DEF＋∠D＝360°，即∠B＋∠BED＋∠D＝360°.

平行线的判定方法： （1）两条直线被第三条直线所截，如果同位角相等，那么 两直线平行． （2）两条直线被第三条直线所截，如果内错角相等，那么 两直线平行．
（3）两条直线被第三条直线所截，如果同旁内角互补，那
么两直线平行．
4
探究一：平行线的性质定理 1．平行线的性质定理1：
两条平行直线被第三条直线所截，同位角相等．
14
3．练一练：说出下面命题的逆命题，它的逆命题是真命题
还是假命题？
（1）两条平行直线被第三条直线所截，同旁内角互补；
（2）对顶角相等．
答：（1）逆命题：两条直线被第三条直线所截，如果同旁
内角互补，那么两直线平行．
这是个真命题．
（2）逆命题：如果两个角相等，那么这两个角是对顶角．
这是个假命题．
15
∴∠1＋∠2＝180°（等量代换）．
7
4．归纳：平行线的性质定理．
答：平行线的性质定理 1 ：两条平行直线被第三条直线所
截，同位角相等．
平行线的性质定理 2 ：两条平行直线被第三条直线所截，
内错角相等．
平行线的性质定理 3 ：两条平行直线被第三条直线所截，
同旁内角互补．
8
探究二：平行线的判定定理
相等）．
∵∠AFE＝∠E（已知），
∴∠FAD＝∠DAC（等量代换），
即AD平分∠BAC．
平行线的性质定理 和判定定理
1
c
Hale Waihona Puke 1．如图，已知直线 a，b被直线
1
2 3
a
5
4 6 7
c所截．
b
8
其中对顶角有________________________________________ ∠1和∠3，∠2和∠4，∠5和∠7，∠6和∠8 ； 同位角有___________________________________________ ； ∠1和∠5，∠2和∠6，∠3和∠7，∠4和∠8 内错角有_____________________________ ； ∠4和∠6，∠3和∠5

小学六年级数学重点知识平行线与垂直线的性质及判定方法小学六年级数学重点知识：平行线与垂直线的性质及判定方法在小学六年级的数学学习中，平行线与垂直线是一个重要的知识点。

了解平行线与垂直线的性质及判定方法，对于解决几何问题和数学推理具有重要意义。

本文将介绍平行线与垂直线的性质以及判定方法，并提供相关例题进行说明。

一、平行线的性质平行线是指在同一个平面上，永远不会相交的两条直线。

平行线具有以下性质：1. 直线与平行线的交角关系当一条直线与两条平行线相交时，相交的两个角分别为内角和外角。

性质如下：- 内角：当直线与两条平行线相交时，内角相等。

- 外角：当直线与两条平行线相交时，外角相等且它们之和为180°。

2. 平行线的性质定理平行线具有以下性质定理：- 平行线定理：如果一条直线与另一条直线分别平行，那么这两条直线之间的所有直线都是平行线。

- 平行线的性质：如果一条直线与平行线的其中一线相交，那么它与另一条平行线的关系也是相应的。

比如，如果线l与平行线m相交，并且线l与另一条平行线n的关系为垂直，那么线m与线n也是垂直的。

二、垂直线的性质垂直线是指两条直线之间的夹角为900的直线。

垂直线具有以下性质：1. 垂直线的性质定理垂直线具有以下性质定理：- 垂直线定理：如果两条直线相互垂直，那么它们之间的所有直线也与这两条直线垂直。

- 直线与垂直线的交角关系：当一条直线与两条互相垂直的直线相交时，它与这两条直线的夹角分别为90°。

三、平行线和垂直线的判定方法判定两条直线是否平行或垂直，有以下几种方法：1. 观察法通过观察两条直线的方向、形状和位置来判断其关系。

如果两条直线的方向完全相同或者互为相反方向，则它们平行；如果两条直线交叉形成直角，则它们垂直。

2. 使用角度利用两条直线的交角来判定其关系。

如果两条直线的交角为90°，则它们垂直；如果两条直线的交角为180°，则它们是平行线。

青岛版八年级上册数学说课稿《5-4平行线的性质定理和判定定理》一. 教材分析《5-4平行线的性质定理和判定定理》这一节的内容主要来源于青岛版八年级上册的数学教材。

在这一节中，学生将学习到平行线的性质定理和判定定理。

这些定理是几何学习中的重要基础，对于学生理解和掌握几何学的本质具有重要意义。

教材中首先介绍了平行线的性质定理，包括同位角相等、内错角相等、同旁内角互补等。

这些性质定理可以帮助学生更好地理解和判断平行线之间的关系。

接着，教材又介绍了平行线的判定定理，包括同位角相等、内错角相等、同旁内角互补等。

这些判定定理可以帮助学生快速准确地判断两条直线是否平行。

二. 学情分析在教学《5-4平行线的性质定理和判定定理》这一节之前，学生已经学习了直线、射线、线段等基本概念，并对这些概念有了初步的理解。

同时，学生还学习了角的概念和性质，这为学习平行线的性质定理和判定定理奠定了基础。

然而，由于平行线的性质定理和判定定理较为抽象，学生可能对这些定理的理解和运用存在一定的困难。

因此，在教学过程中，需要注重引导学生通过观察、思考、交流等方式，深入理解平行线的性质定理和判定定理，提高他们的几何思维能力。

三. 说教学目标1.知识与技能目标：使学生理解和掌握平行线的性质定理和判定定理，能够运用这些定理判断两条直线是否平行。

2.过程与方法目标：通过观察、思考、交流等过程，培养学生的几何思维能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养他们勇于探索、积极思考的精神。

四. 说教学重难点1.教学重点：平行线的性质定理和判定定理。

2.教学难点：如何引导学生理解和运用平行线的性质定理和判定定理。

五. 说教学方法与手段1.教学方法：采用问题驱动法、合作学习法、引导发现法等。

2.教学手段：黑板、粉笔、多媒体课件等。

六. 说教学过程1.导入新课：通过复习直线、射线、线段等基本概念，引导学生进入新课。

2.探究平行线的性质定理：让学生观察平行线之间的对应角关系，引导学生发现同位角相等、内错角相等、同旁内角互补等性质定理。

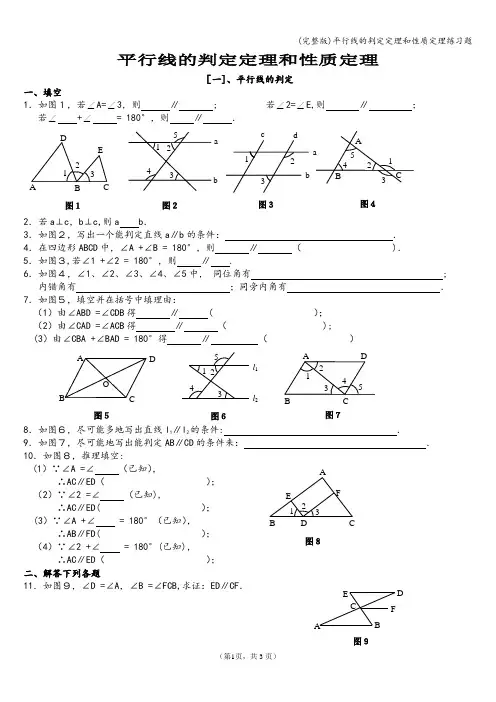
(完整版)平行线的判定定理和性质定理练习题平行线的判定定理和性质定理［一]、平行线的判定一、填空1．如图１，若∠A=∠3，则 ∥ ; 若∠2=∠E,则 ∥ ；若∠ +∠ = 180°，则 ∥ ．2．若a⊥c，b⊥c,则a b ．3．如图２，写出一个能判定直线a ∥b 的条件： ． 4．在四边形ABCD 中，∠A +∠B = 180°，则 ∥ （ )． 5．如图３,若∠1 +∠2 = 180°，则 ∥ .6．如图４，∠1、∠2、∠3、∠4、∠5中， 同位角有 ; 内错角有 ；同旁内角有 ． 7．如图５，填空并在括号中填理由：（1）由∠ABD =∠CDB 得 ∥ ( ）； （2）由∠CAD =∠ACB 得 ∥ （ );(3）由∠CBA +∠BAD = 180°得 ∥ （ ）8．如图６，尽可能多地写出直线l 1∥l 2的条件: ．9．如图７，尽可能地写出能判定AB∥CD 的条件来： ． 10．如图８，推理填空:(1）∵∠A =∠ （已知）， ∴AC∥ED（ ）；（2）∵∠2 =∠ （已知), ∴AC∥ED( ）； (3）∵∠A +∠ = 180°（已知）， ∴AB∥FD( ）；（4）∵∠2 +∠ = 180°(已知)， ∴AC∥ED（ ）； 二、解答下列各题11．如图９，∠D =∠A，∠B =∠FCB,求证：ED∥CF．ACB41 23 5图４ab c d 123 图３A B C ED 1 2 3 图１ 图２43 2 1 5ab1 2 3A F C DB E图８EBAF D C图９ADCBO图５图６5 1 243 l 1 l 2图７54 32 1 A DC B12．如图10，∠1∶∠2∶∠3 = 2∶3∶4， ∠AFE = 60°，∠BDE =120°,写出图中平行的直线,并说明理由．13．如图11，直线AB 、CD 被EF 所截，∠1 =∠2，∠CNF =∠BME。

平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

考点一平行线的判定：1．两直线被第三条直线所截，如果同位角相等，那么这两条直线平行．2．两直线被第三条直线所截，如果内错角相等，那么这两条直线平行．3. 两直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．注意：证明两直线平行，关键是找到与特征结论相关的角.例1．如下图，当∠1=∠3时，直线a、b平行吗？当∠2+∠3=180°时，直线a、b平行吗？为什么？你有几种方法。

例2．请将下面的空补充完整1．如右图，若∠1=∠2，则_______∥_______（）若∠3=∠4，则_________∥_________（）若∠5=∠B，则_________∥_________（）若∠D+∠DAB=180°，则______∥_______（）2．如右图，∠1+∠2=180°（已知）∠3+∠2=180°（）∴∠1=_________∴AB∥CD（）课堂练习：1．如图6－21，已知∠B=142°,∠BFE=38°,∠EFD=40°,∠D=140°,求证：AB∥C D．2．已知，如下图（1），（2），直线AB∥ED．求证：∠ABC+∠CDE=∠BCD．（1） （2） 3．如图，如果AB∥CD，求角α、β、γ与180º之间的关系式．4．如图，已知CD 是∠ACB 的平分线，∠ACB = 500，∠B = 700，DE ∥BC，求：∠EDC 和 ∠BDC 的度数。

达标训练： 一．选择题1．下列命题中，不正确的是( )A ．两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行B ．两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行C ．两条直线被第三条直线所截，那么这两条直线平行D ．如果两条直线都和第三条直线平行，那么这两条直线也互相平行2．如右图，直线a 、b 被直线c 所截，现给出下列四个条件： ( ) (1)∠1=∠2，(2)∠3=∠6，(3)∠4+∠7=180°，(4)∠5+∠8=180°， 其中能判定a ∥b 的条件是( ) A ．(1)(3) B ．(2)(4) C ．(1)(3)(4) D ．(1)(2)(3)(4) 3．如右图，如果∠1=∠2，那么下面结论正确的是( ) A ．AD ∥BC B ．AB ∥CD C ．∠3=∠4 D ．∠A =∠C4．一辆汽车在笔直的公路上行驶，两次拐弯后，行驶的方向与原来 的方向相同，这两次拐弯的角度可能是( ) A ．第一次向右拐40°，第二次向左拐40° B ．第一次向右拐50°，第二次向左拐130° C ．第一次向右拐50°，第二次向右拐130° D ．第一次向左拐50°，第二次向左拐130° 二．填空题αγβED C BAAB D E12FOCABDE5．如右图，∠1=∠2=∠3，则直线l 1、l 2、l 3的关系是________．6．如果两条直线被第三条直线所截，一组同旁内角的度数之比为3∶2，差为36°，那么这两条直线的位置关系是________ ． 7．同垂直于一条直线的两条直线________． 8．根据图形及上下文的含义推理并填空． （1）∵∠A =_______（已知）∴AC ∥ED （ ） （2）∵∠2=_______（已知）∴AC ∥ED （ ） （3）∵∠A +_______=180°（已知） ∴AB ∥FD （ ） 三．解答题9．已知：如图7，∠1=∠2，且BD 平分∠ABC ． 求证．AB ∥CD ．10、.如图，∠A BC =∠BCD, ∠1=∠2,求证：BE ∥CF.11．如图，是大众汽车的标志图案,其中蕴涵着许多几何知识． 根据下面的条件完成证明．已知：如图，BC//AD ，BE//AF ． (1) 求证：B A ∠=∠；(2) 若︒=∠135DOB ，求A ∠的度数．12.已知:如图,∠3与∠1互余,∠3与∠2互余.求证:AB ∥CD.考点二：1．平行线的性质．公理：两直线平行，同位角相等. 定理：两直线平行，内错角相等.CFDEBAOHG321ED C BA定理：两直线平行，同旁内角互补.例1．如图，BE∥DF，∠B =∠D，求证．AD∥BC．课堂作业：1．如上图，AB∥CD，AD∥BC则下列结论成立的是( )A．∠A+∠C=180°B．∠A+∠B=180°C．∠B+∠D=180°D．∠B=∠D2．若两个角的一边在同一条直线上，另一边互相平行，那么这两个角的关系是( )A．相等B．互补C．相等或互补D．相等且互补3．如右图，已知∠1=∠2，∠BAD=57°，则∠B=________．4．已知：如图，AD⊥BC，EF⊥BC，∠4=∠C．求证：∠1=∠2．5．如图所示，已知AB⊥BD于点B，ED⊥BD于点D，且AB=CD，BC=DE，那么AC与CE有什么关系？写你的猜想，并说明理由6、如图所示：已知：AB∥DE。

∴ ∠2=∠3(等量代换).
1 3
2
c
合作交流
两直线平行， 同旁内角互补。
如图,已知a//b,
那么2与4有
什么关系呢？ a
1
为什么?
4
b
2
c
基本事实：同位角相等，两直线平行
例2
如图：已知2=3
a
求证： a//b
b
证明：
∵ ∠2=∠3 (已知)
又∵ ∠1=∠3(对顶角相等)
∴∠1=∠2(等量代换)
基本事实
a
1
平行线的性质1
b
2
两条平行线被第三条直线所截，
同位角相等.
c
简写为：两直线平行，同位角相等.
符号语言: ∵a∥b,
∴∠1=∠2.
例1
两直线平行， 内错角相等。
如图：已知a//b,那么2与3相等吗？ 为什么?
证明∵a∥b(已知),
∴∠1=∠2(两直线平行,
a
同位角相等). b

又∵ ∠1=∠3(对顶角相等),
∴ a∥b(同位角相等，两直线平行).
1 3
2
c
合作交流
同旁内角互补， 两直线平行。
如图,已知
a
2+4=180 那么a//b吗？为什么?
b
1 4 2
c
性质：两直线平行，同位角相等. 判定：同位角相等，两直线平行.
两个命题的条件 和结论正好相反
互逆命题
原命题 逆命题

性质定理一
如果一条直线与平面平行， 那么这条直线与平面内的 任何直线都不相交。
性质定理二
如果两个平面平行，那么 这两个平面内的任何直线 都不相交。
性质定理三
如果两个平面垂直，那么 其中一个平面内的任何直 线都垂直于另一个平面。
平行线和垂直线的综合判定定理和性质定理的应用
应用一
在建筑学中，利用判定定理和性 质定理判断建筑物的稳定性，如 判断墙、柱、梁等是否垂直或平
垂直线的性质定理
垂直线之间的角度都是直角，且垂直线之间的距 离是零。
3
平行四边形的性质定理
平行四边形的对角线互相平分，且对角相等。
空间几何中的其他重要定理的应用
在几何图形中，判定定理和性质定理的应用非常广泛，例如在计算面积、周长、 角度等几何量时，需要使用判定定理和性质定理来证明某些几何关系或求解某些 几何问题。
在机械工程中，垂直线的判定定理和 性质定理被用于确定机械零件的位置 和角度，以确保机械设备的正常运行。
应用二
在建筑学中，垂直线的判定定理和性 质定理被广泛应用于确定建筑物的垂 直度和平行度，以确保建筑物的稳定 性和安全性。
03
平行线和垂直线的综合判定
定理和性质定理
平行线和垂直线的综合判定定理
01
立体几何平行垂直判 定定理和性质定理
• 平行线的判定定理和性质定理 • 垂直线的判定定理和性质定理 • 平行线和垂直线的综合判定定理
和性质定理 • 空间几何中的其他重要定理
目录
01
平行线的判定定理和性质定
理
平行线的判定定理
01
02
03
04
同一平面内，不相交的两条直 线判定为平行线。
平行于同一直线的两条直线互 相平行。

教学课件
数学 八年级上册 青岛版
第5章 几何证明初步
5.4 平行线的性质定理和判定定理
一条公路两次拐弯后，和原来的方向相同，第一次拐的 角∠B是130°，第二次拐的角∠C是多少度？
C
B
议一议
画出直线AB的平行线CD，结合画图过程思考画出的平行线， 已有一对同位角的关系是怎样的？是不是每一对同位角 都具有这样的关系呢？
练一练
1、已知平行线AB、CD被直线AE所截 从∠1＝110°，可以知道 ∠2是多少度，为什么？ A 从∠1=110°，可以知道 ∠3是多少度，为什么？ 从∠1=110°，可以知道 ∠4是多少度，为什么？ B C
1
D
2 4 3
E
练一
练 2、如图是梯形有上底的一部分，量得
∠A=115°，∠D＝100°，梯形另外两 个角各是多少度？
A D
B
C
练一练
3、如图，A、B、C、D在同一直线上，AD∥EF．
∠E=78°时，∠1、∠2各等于多少度？为什么？
∠F=58°时，∠3、∠4各等于多少度？为什么？ A
B
C
D
E
F
平行的的判定与性质： 同位角相等 两定 同旁内角互补
证明的一般步骤
前面我们探索过直线平行的条件．大家来想一想：两条直 线在什么情况下互相平行呢？ ——— 公理
同位角相等，两直线平行
内错角相等，两直线平行 同旁内角互补，两直线平行
两条直线都和第三条直线平行，则这 两条直线互相平行 在同一平面内，不相交的两条直线叫 做平行线．
证明：两条直线被第三条直线所截，如 果同旁内角互补，那么这两条直线平行．
分析：这是一个文字证明题，需要先把命题的文 字语言转化成几何图形和符号语言。

青岛版数学八年级上册5.4《平行线的性质定理和判定定理》教学设计一. 教材分析《平行线的性质定理和判定定理》是青岛版数学八年级上册第五章第四节的内容。

本节内容主要介绍了平行线的性质定理和判定定理，是学生进一步理解几何图形性质、提高解题能力的基础。

教材通过生活中的实例引入平行线的性质定理和判定定理，让学生感受数学与生活的紧密联系，激发学习兴趣。

二. 学情分析八年级的学生已经学习了平面几何的基本概念和性质，对图形的认识有一定的基础。

但是，对于证明过程的严谨性和逻辑性还需加强。

此外，学生的学习兴趣和积极性需要进一步激发，使他们更主动地参与到课堂中来。

三. 教学目标1.理解平行线的性质定理和判定定理，并能运用其解决实际问题。

2.培养学生的逻辑思维能力和证明能力。

3.激发学生对数学学习的兴趣，提高课堂参与度。

四. 教学重难点1.平行线的性质定理和判定定理的理解及运用。

2.证明过程的严谨性和逻辑性的培养。

五. 教学方法1.采用问题驱动的教学方法，引导学生通过观察、思考、探究，发现平行线的性质定理和判定定理。

2.利用多媒体辅助教学，展示实例和图形，增强学生的直观感受。

3.采用小组合作学习，培养学生的团队协作能力和沟通能力。

4.以练习题的形式巩固所学知识，提高学生的应用能力。

六. 教学准备1.多媒体教学设备。

2.教学PPT。

3.练习题及答案。

4.几何画板或黑板。

七. 教学过程1.导入（5分钟）利用生活实例，如道路规划、建筑设计等，引导学生关注平行线的应用，激发学生的学习兴趣。

提出问题：“你知道平行线有哪些性质和判定方法吗？”让学生思考并回答。

2.呈现（10分钟）通过PPT展示平行线的性质定理和判定定理，引导学生观察和理解定理的内容。

同时，给出定理的证明过程，让学生初步感受证明的逻辑性和严谨性。

3.操练（10分钟）让学生利用平行线的性质定理和判定定理，解决一些实际问题。

如给出一些图形，让学生判断其中是否包含平行线，并说明理由。

3
1 2
几何语言 ☞ 平行线的判定定理
判定定理1:
两条直线被第三条直线所截如果内 错角相等,那么两直线平行
a
1
c
∵ ∠1=∠2, ∴ a∥b.
b
2
判定定理2:
c
两条直线被第三条直线所截如果同旁 a
1
内角互补,那么两直线平行.
∵∠1+∠2=1800 , ∴ a∥b.
b
2
这里的结论,以后可以直接运用.
b
2
两条平行直线被第三条
c
直线所截，同旁内角互补。 a
1
∵ a∥b ∴ ∠1+∠2= 180° b
2
活动二：证明平行线的判定定理1和判定定理2
两条直线被第三条直线所截，如果同位角相等，那 么两直线平行.(基本事实) 判定定理1：两条直线被第三条直线所截，如果内 错角相等，那么两直线平行. 判定定理2：两条直线被第三条直线所截，如果同 旁内角互补，那么两直线平行.
3 B
2
求证: ∠1 +∠2=180°
C
1
D
证明： ∵AB∥CD(已知) ∴∠3=∠1（两直线平行，同F 位角相等） ∵∠2+∠3 =180°（平角的定义） ∴∠1+∠2=180°（等量代换）
几何语言 ☞ 平行线的性质定理
两条平行直线被第三条
直线所截，内错角相等. ∵ a∥b. ∴∠1=∠2
c
a1
作业 课本第169页 1.2.3
[课堂小结]
性质
两直线平行，同位角相等
定理 两直线平行，内错角相等
平
两直线平行，同旁内角互补
互逆命题
行
线
同位角相等，两直线平行