1 .4 解直角三角形

解直角三角形的五种常见类型解直角三角形是中考的重要内容之一，直角三角形边、角关系的知识是解直角三角形的基础．解直角三角形时，要注意三角函数的选取，避免计算复杂．在解题中，若求解的边、角不在直角三角形中，应先添加辅助线，构造直角三角形．类型一、已知两直角边解直角三角形【例1】如图，在Rt△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，a＝2，b＝6，解这个直角三角形．类型二、已知一直角边和斜边解直角三角形【例2】如图，∠ACB＝90°，AB＝13，AC＝12，∠BCM＝∠BAC，求sin ∠BAC的值和点B到直线MC的距离．类型三、已知一直角边和一锐角解直角三角形【例3】如图，在△ABC中，∠B＝90°，∠C＝30°， AB＝3.(1)求AC的长；(2)求BC的长类型四、已知斜边和一锐角解直角三角形【例4】如图，在Rt△ABC中，∠C＝90°，∠B＝45°，a，b，c分别为∠A，∠B，∠C的对边，c＝10，解这个直角三角形类型五、已知非直角三角形中的边(或角或三角函数值)解直角三角形题型一：化斜三角形为直角三角形问题(化斜为直法)【例5】如图，在△ABC中，点D是AB的中点，DC⊥AC，1，求∠A的三角函数值．且tan ∠BCD＝3题型2:化解四边形问题为解直角三角形问题【例6】【中考·北京】如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC＝90°，∠CED＝45°，∠DCE＝30°，DE＝2，BE＝22 .求CD的长和四边形ABCD的面积．题型3、化解方程问题为解直角三角形问题【例7】已知a，b，c分别是△ABC中∠A，∠B，∠C的对边，关于x 的一元二次方程a(1－x2)＋2bx＋c(1＋x2)＝0有两个相等的实数根，且3c＝a＋3b.(1)判断△ABC的形状；(2)求sin A＋sin B的值．。

2022-2023学年北师大版九年级数学下册《1.4解直角三角形》同步练习题（附答案）一．选择题1．在Rt△ABC中，∠C＝90°，BC＝2，，则AC的长是（）A．B．3C．D．2．在△ABC中，∠A和∠C都是锐角，且sin A＝，tan C＝，则△ABC是（）A．直角三角形B．钝角三角形C．等边三角形D．不能确定3．在平面直角坐标系xOy中，已知点P（1，3）与原点O的连线与x轴的正半轴的夹角为α（0°＜α＜90°），那么cosα的值是（）A．3B．C．D．4．如图，在Rt△ABC中，∠C＝90°，sin A＝，BC＝，则AC的长为（）A．B．3C．D．25．在Rt△ABC中，∠B＝90°，如果∠A＝α，BC＝a，那么AC的长是（）A．a•tanαB．a•cotαC．D．6．等腰三角形底边与底边上的高的比是2：，则它的顶角为（）A．30°B．45°C．60°D．120°7．阅读理解：为计算tan15°三角函数值，我们可以构建Rt△ACB（如图），使得∠C＝90°，∠ABC＝30°，延长CB使BD＝AB，连接AD，可得到∠D＝15°，所以tan15°＝＝＝＝2﹣．类比这种方法，请你计算tan22.5°的值为（）A．+1B．﹣1C．D．8．如图，在△ABC中，AD⊥BC于点D．若BD＝9，DC＝5，cos B＝，E为边AC的中点，则cos∠ADE的值为（）A．B．C．D．9．如图，在△ABC中，AB＝AC＝10，BC＝12，点D为BC的中点，DE⊥AB于点E，则tan∠BDE的值等于（）A．B．C．D．10．如图，在△ABC中，∠BAC＝120°，AC＝8，AB＝4，则BC的长是（）A．B．C．6D．8二．填空题11．如图，Rt△ABC中，∠C＝90°，点D在AC上，∠DBC＝∠A，若AC＝4，cos A＝，则BD的长度为．12．已知等腰三角形两条边的长分别是4，6，底角为α，则cosα＝．13．如图，在△ABC中，∠ACB＝90°，点D在AB的延长线上，连接CD，若AB＝2BD，tan∠BCD＝，则的值为．14．如图，已知点A（4，3），点B为直线y＝﹣2上的一动点，点C（0，n），﹣2＜n＜3，AC⊥BC于点C，连接AB．若直线AB与x轴正半轴所夹的锐角为α，当n＝2时，则tanα＝；当tanα的值最大时，n的值为．15．如图，在△ABC中，AD⊥BC于D，点E在AC上，∠ABE＝45°，tan∠CBE＝，若AD＝BC，AC＝2，则线段BC的长是．三．解答题16．根据下列条件解直角三角形：（1）在Rt△ABC中，∠C＝90°，c＝8，∠A＝60°；（2）在Rt△ABC中，∠C＝90°，a＝3，b＝9．17．如图，在平面直角坐标系中，OB＝4，sin∠AOB＝，点A的坐标为（，0）．（1）求点B的坐标；（2）求sin∠OAB的值．18．如图，点C在线段AB上，点D，E在直线AB的同侧，∠A＝∠DCE＝∠CBE＝90°，∠ADC＝∠ABD，AC＝3，BC＝，求tan∠CDB的值．19．如图，在Rt△ABC中，∠ACB＝90°，D是边AB的中点，过B作BE⊥CD，交CD的延长线于点E，AC＝30，sin B＝，求：（1）线段CD的长．（2）cos∠BDE的值．20．如图（1），在Rt△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，以下是某同学推理证明的过程：证明：∵sin A＝，sin B＝∴c＝，c＝∴根据你掌握的三角函数知识，请在图（2）中的锐角△ABC中，求证：．参考答案一．选择题1．解：如图，在Rt△ABC中，∠C＝90°，BC＝2，∴sin A＝＝＝，∴AB＝3，∴AC＝＝＝．故选：A．2．解：∵sin A＝，∴∠A＝60°，∵tan C＝，∴∠C＝60°，∴∠B＝180°﹣∠A﹣∠C＝180°﹣60°﹣60°＝60°．∴△ABC是等边三角形．故选：C．3．解：如图，过P点作P A⊥x轴于A，则∠POA＝α，∵点P的坐标为（1，3），∴OA＝1，P A＝3，∴tan∠POA＝＝＝3，即tanα＝3．故选：D．4．解：∵∠C＝90°，sin A＝＝，BC＝，∴AB＝BC＝×＝2，∴AC＝＝＝＝．故选：C．5．解：如图：在Rt△ABC中，AC＝＝．故选：D．6．解：如图，AB＝AC，AD⊥BC，∴BD＝CD，∵BC：AD＝2：，∴tan B＝＝，∴∠B＝60°，∵AB＝AC，∴△ABC是等边三角形，∴∠BAC＝60°，故选：C．7．解：如图：在Rt△ACB中，∠C＝90°，∠ABC＝45°，延长CB使BD＝AB，连接AD，∴∠BAD＝∠D＝22.5°，设AC＝BC＝1，则AB＝BD＝AC＝，∴CD＝BC+BD＝1+，在Rt△ADC中，tan22.5°＝＝＝﹣1，故选：B．8．解：∵AD⊥BC，BD＝9，cos B＝，∴AB＝＝15，AD＝＝12，∵DC＝5，∴AC＝＝13，∵E为边AC的中点，∴ED＝，∴∠EDA＝∠DAE，∴cos∠EDA＝cos∠DAE＝，故选：D．9．解：连接AD，∵△ABC中，AB＝AC＝10，BC＝12，D为BC中点，∴AD⊥BC，BD＝BC＝6，∴AD＝，∴tan∠BAD＝．∵AD⊥BC，DE⊥AB，∴∠BDE+∠ADE＝90°，∠BAD+∠ADE＝90°，∴∠BDE＝∠BAD，∴tan∠BDE＝tan∠BAD＝，故选：C．10．解：如图，过点C作CE⊥BA交BA的延长线于E．∵∠BAC＝120°，∴∠CAE＝180°﹣120°＝60°，∴AE＝AC•cos60°＝4，EC＝AC•sin60°＝4，∵AB＝4，∴BE＝AB+AE＝8，∴BC＝＝＝4，故选：B．二．填空题11．解：∵∠C＝90°，AC＝4，cos A＝，∴AB＝5，∴BC＝＝＝3，∵∠DBC＝∠A．∴cos∠DBC＝cos∠A＝＝，∴BD＝3×＝，故答案为：．12．解：分两种情况：当等腰三角形的腰长为4，底边长为6时，如图：过点A作AD⊥BC，垂足为D，∵AB＝AC＝4，AD⊥BC，∴BD＝DC＝BC＝3，在Rt△ABD中，cos B＝＝，当等腰三角形的腰长为6，底边长为4时，如图：过点A作AD⊥BC，垂足为D，∵AB＝AC＝6，AD⊥BC，∴BD＝DC＝BC＝2，在Rt△ABD中，cos B＝＝＝，综上所述：cosα＝或，故答案为：或．13．解：过点D作DM⊥BC，交CB的延长线于点M，∵∠ACB＝∠DMB＝90°，∠ABC＝∠DBM，∴△ABC∽△DBM，∴＝＝，∵AB＝2BD，∴＝＝＝，在Rt△CDM中，由于tan∠MCD＝＝，设DM＝2k，则CM＝3k，又∵＝＝，∴BC＝2k，AC＝4k，∴＝＝2，故答案为：2．14．解：过点A作AM⊥y轴于点M，作AN⊥BG于点N，如图所示：则∠AMC＝90°，∠ANB＝90°，∵直线y＝﹣2与x轴平行，∴∠ABN＝α，∠CGB＝90°，∵AC⊥BC，∴∠ACB＝90°，∵∠ACM+∠MAC＝90°，∠ACM+∠BCG＝90°，∴∠CAM＝∠BCG，∵∠AMC＝∠CGB＝90°，∴△AMC∽△CGB，∴，设BG＝m，∵点A坐标为（4，3），点C坐标为（0，n），∴AM＝4，GC＝n+2，CM＝3﹣n，∴＝，当n＝2时，可得，解得m＝1，∴GB＝1，BN＝3，∴tanα＝＝；∵tanα＝，当BN最小，即BG最大时，tanα最大，∵＝，∴m＝﹣（n﹣3）（n+2）＝﹣（n﹣）2+，∵﹣＜0，∴当n＝时，m取得最大值，即tanα最大，故答案为：，．15．解：如图，过点A作AF⊥BE于点F，设AD与BF交于点G，∵∠ABE＝45°，∴△ABF是等腰直角三角形，∴AF＝BF，∵∠GDB＝∠AFG＝90°，∠BGD＝∠AGE，∴∠GBD＝∠F AG，∴tan∠GBD＝tan∠F AG，∴＝＝，设DG＝x，则BD＝2x，∴BG＝＝x，设FG＝a，则AF＝2a，∴BF＝AF＝2a，AG＝＝a，∴BG＝BF﹣FG＝a，∴a＝x，∴AD＝AG+DG＝a+x＝6x，∵DC＝BC﹣BD＝AD﹣BD＝a+x﹣2x＝a﹣x＝4x，在Rt△ADC中，根据勾股定理得AD2+DC2＝AC2，∴（6x）2+（4x）2＝（2）2，∴x＝1（负值舍去），∴BC＝AD＝6x＝6．故答案为：6．三．解答题16．解：（1）∵∠C＝90°，∠A＝60°，∴∠B＝90°﹣∠A＝30°，∴b＝c＝4，∴a＝b＝12，∴∠B＝30°，b＝4，a＝12；（2）在Rt△ABC中，∠C＝90°，a＝3，b＝9，∴tan A＝＝＝，∴∠A＝30°，∴∠B＝90°﹣∠A＝60°，c＝2a＝6，∴∠A＝30°，∠B＝60°，c＝6．17．解：（1）过点B作BC⊥OA于点C，在Rt△BOC中，OB＝4，sin∠AOB＝，∴BC＝OB•sin∠AOB＝4×＝3，∴，∴点B的坐标为（，3）；（2）∵点A的坐标为（，0），∴OA＝，∴AC＝OA﹣OC＝＝，∵∠ACB＝90°，∴，∴，∴sin∠OAB的值为．18．解：如图，设CE交BD于G．∵∠A＝∠A＝90°，∠ADC＝∠ABD，∴△ADC∽△ABD，∴，，解得AD＝5，∴DC＝＝，DB＝＝，∵∠A＝∠ECD＝∠CBE＝90°，∴∠ACD+∠ECB＝90°，∠ACD+∠ADC＝90°，∴∠ADC＝∠ECB，设∠DBA＝∠CDA＝α，则∠ECB＝α，∴∠GCB＝∠GBC＝α，∴CG＝GB，设CG＝GB＝x，∴DG＝﹣x，∴（）2+x2＝（﹣x）2，解得x＝，∴tan∠CDB＝＝．19．解：（1）∵∠ACB＝90°，AC＝30，sin B＝＝，∴AB＝50，∵D为直角三角形ABC斜边上的中点，∴CD＝AB＝25；（2）∵AB＝50，D为AB的中点，∴AD＝BD＝25，∵BE⊥CD，∴∠E＝90°，由勾股定理得：BC＝＝＝40，由勾股定理得：BE2＝BD2﹣DE2＝BC2﹣CE2，即252﹣DE2＝402﹣（25+DE）2，解得：DE＝7，∴cos∠BDE＝＝．20．解：过C点作CD⊥AB于D，过B点作BE⊥AC于E，∴sin A＝，sin B＝，∴CD＝b sin∠A＝a sin B，∴，同理，∴．。

《解直角三角形》教学模式介绍：数学的核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析．这些数学学科素养既相对独立，又互相交融，是一个有机的整体．核心素养下的教学设计是利用设计好的核心问题在课堂中培养学生的数学核心素质，重视学生在学习活动中的主体地位，让学生在积极参与学习活动的过程中得到发展．教师创设情境设计问题，或通过富有启发性的讲授，或引导学生独立思考、自主探索、合作交流，组织学生操作实验、观察现象、提出猜想、推理论证等，有效地启发学生思考，使学生成为学习的主体，学会学习．课堂教学中，要注重让学生理解和掌握数学的基础知识和基本技能，让学生感悟数学思想，积累数学活动经验，在学习数学和应用数学的过程中，发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养，让学生能与他人建立良好关系，有效地管理自己的学习、生活，能够发掘自身潜力，战胜学习数学中的困难，让学生能够适应未来社会、进行终身学习，实现全面发展．设计思路说明：1.解直角三角形的关键是找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作辅助线构造直角三角形（作某边上的高是常用的辅助线）；2.一些解直角三角形的问题往往与其他知识联系，所以在复习时要形成知识结构，要把解直角三角形作为一种工具，能在解决各种数学问题时合理运用.教材分析本节主要学习解直角三角形及其在实际问题中的应用。

我们知道，在直角三角形中，勾股定理反映了三边之间的关系，三角形的内角和定理反映了三个角之间的关系，而锐角三角函数反映了边与角之间的关系。

本节利用锐角三角函数，结合勾股定理、三角形内角和定理等知识解直角三角形.通过本节的学习，学生应全面掌握直角三角形中各个元素之间的关系，并能利用这些关系解直角三角形。

教学目标知识与技能：1、使学生理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形．2、通过综合运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形，逐步培养学生分析问题、解决问题的能力．3、渗透数形结合的数学思想，培养学生良好的学习习惯．过程与方法：通过综合运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形，逐步培养学生分析问题、解决问题的能力．情感态度与价值观：渗透数形结合的数学思想，培养学生良好的学习习惯．重点难点1．重点：直角三角形的解法．2．难点：三角函数在解直角三角形中的灵活运用．课前准备:多媒体课件教学过程：一、复习旧知、引入新课【引入】我们一起来解决关于比萨斜塔问题。

湘教版数学九年级上册4.3《解直角三角形》教学设计1一. 教材分析湘教版数学九年级上册4.3《解直角三角形》是本册教材中关于直角三角形知识的重要内容。

通过本节课的学习，学生能了解直角三角形的性质，掌握解直角三角形的方法，并能运用所学知识解决实际问题。

本节课的内容为后续学习勾股定理和三角函数等知识打下基础。

二. 学情分析学生在学习本节课之前，已经掌握了锐角三角形和钝角三角形的性质，了解了三角形的分类。

在此基础上，学生需要进一步掌握直角三角形的性质，并学会解直角三角形。

此外，学生需要具备一定的观察能力、动手操作能力和逻辑思维能力，以便在学习过程中更好地理解和掌握所学知识。

三. 教学目标1.知识与技能目标：学生能掌握直角三角形的性质，了解解直角三角形的方法，并能运用所学知识解决实际问题。

2.过程与方法目标：通过观察、操作、思考、交流等过程，培养学生动手操作能力、观察能力和逻辑思维能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的团队合作精神，使学生感受到数学在生活中的应用。

四. 教学重难点1.教学重点：直角三角形的性质，解直角三角形的方法。

2.教学难点：解直角三角形的灵活运用，解决实际问题。

五. 教学方法1.情境教学法：通过设置情境，引导学生观察、操作、思考，激发学生学习兴趣。

2.合作学习法：学生进行小组讨论、合作探究，培养学生团队合作精神。

3.启发式教学法：教师引导学生发现问题、分析问题、解决问题，培养学生的逻辑思维能力。

4.实践操作法：让学生动手操作，加深对知识的理解和记忆。

六. 教学准备1.教学课件：制作直角三角形的相关课件，包括图片、动画、例题等。

2.教学道具：准备直角三角形模型、三角板等道具，以便进行实物演示。

3.练习题：挑选一些有关直角三角形的练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）利用课件展示一些生活中的直角三角形图片，如教室的黑板、楼梯的扶手等，引导学生关注直角三角形。

解直⾓三⾓形知识点总结 解直⾓三⾓形是中考数学的⼀⼤考点，但相关的知识点其实并不是⼗分的难，下⾯解直⾓三⾓形知识点总结是⼩编为⼤家带来的，希望对⼤家有所帮助。

解直⾓三⾓形知识点总结 【知识梳理】 1.解直⾓三⾓形的依据(1)⾓的关系:两个锐⾓互余;(2)边的关系:勾股定理;(3)边⾓关系:锐⾓三⾓函数 2.解直⾓三⾓形的基本类型及解法：(1)已知斜边和⼀个锐⾓解直⾓三⾓形;(2)已知⼀条直⾓边和⼀个锐⾓解直⾓三⾓形;(3)已知两边解直⾓三⾓形. 3.解直⾓三⾓形的应⽤：关键是把实际问题转化为数学问题来解决 【课前预习】 1、在Rt△ABC中，∠C=90°，根据已知量，填出下列表中的未知量： a b c ∠A ∠B 6 30° 10 45° 2、所⽰，在△ABC中，∠A=30°，，AC= ，则AB= . 变式：若已知AB，如何求AC? 3、在离⼤楼15m的地⾯上看⼤楼顶部仰⾓65°，则⼤楼⾼约 m. (精确到1m， ) 4、铁路路基横断⾯为⼀个等腰梯形，若腰的坡度为1：，顶宽为3⽶，路基⾼为4⽶， 则坡⾓= °，腰AD= ,路基的下底CD= . 5、王英同学从A地沿北偏西60°⽅向⾛100m到B地，再从B地向正南⽅向⾛200m到C地，此时王英同学离A地 m. 【解题指导】 例1 在Rt△ ABC中，∠C=90°，AD=2AC=2BD，且DE⊥AB. (1)求tanB;(2)若DE=1，求CE的长. 例2 34-4所⽰，某居民⼩区有⼀朝向为正南⽅向的居民楼，该居民楼的⼀楼是⾼6m的⼩区超市，超市以上是居民住房，在该楼的前⾯15m处要盖⼀栋⾼20m的新楼.当冬季正午的阳光与⽔平线的夹⾓为32°时. (1)问超市以上的居民住房采光是否有影响，为什么? (2)若新楼的影⼦刚好部落在居民楼上，则两楼应相距多少⽶? (结果保留整数，参考数据： ) 例3某校初三课外活动⼩组，在测量树⾼的⼀次活动中，34-6所⽰，测得树底部中⼼A到斜坡底C的⽔平距离为8.8m.在阳光下某⼀时刻测得1m的标杆影长为0.8m，树影落在斜坡上的部分CD=3.2m.已知斜坡CD的坡⽐，求树⾼AB.(结果保留整数，参考数据 ) 例4 ⼀副直⾓三⾓板放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求CD的长. 【巩固练习】 1、某坡⾯的坡度为1: ，则坡⾓是_______度. 2、已知⼀斜坡的坡度为1:4，⽔平距离为20m，则该斜坡的垂直⾼度为 . 3、河堤的横断⾯1所⽰，堤⾼BC是5m，迎⽔斜坡AB长13m，那么斜坡AB的坡度等于 . 4、菱形在平⾯直⾓坐标系中的位置2所⽰, ,则点的坐标为 . 5、先锋村准备在坡⾓为的⼭坡上栽树，要求相邻两树之间的⽔平距离为5⽶，那么这两树在坡⾯上的距离AB为 . 6、⼀巡逻艇航⾏⾄海⾯处时,得知其正北⽅向上处⼀渔船发⽣故障.已知港⼝处在处的北偏西⽅向上,距处20海⾥; 处在A处的北偏东⽅向上,求之间的距离(结果精确到0.1海⾥) 【课后作业】 ⼀、必做题： 1、4,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为 cm. 2、某⼈沿着有⼀定坡度的坡⾯前进了10⽶,此时他与⽔平地⾯的垂直距离为⽶,则这个坡⾯的坡度为__________. 3、已知5,在△ABC中,∠A=30°,tanB= ,BC= ,则AB的长为__ ___. 4、6,将以A为直⾓顶点的等腰直⾓三⾓形ABC沿直线BC平移得到△，使点与C重合，连结，则的值为 . 5、7所⽰，在⼀次夏令营活动中，⼩亮从位于A点的营地出发，沿北偏东60°⽅向⾛了5km到达B 地，然后再沿北偏西30°⽅向⾛了若⼲千⽶到达C地，测得A地在C地南偏西30°⽅向，则A、C两地的距离为( ) (A) (B) (C) (D) 6、8，⼩明要测量河内岛B到河边公路l的距离，在A测得，在C测得，⽶，则岛B到公路l的距离为( )⽶. (A)25 (B) (C) (D) 7、9所⽰，⼀艘轮船由海平⾯上A地出发向南偏西40°的⽅向⾏驶40海⾥到达B地，再由B地向北偏西10°的⽅向⾏驶40海⾥到达C地，则A、C两地相距( ). (A)30海⾥ (B)40海⾥ (C)50海⾥ (D)60海⾥ 8、是⼀⽔库⼤坝横断⾯的⼀部分，坝⾼h=6m，迎⽔斜坡AB=10m，斜坡的坡⾓为α，则tanα的值为( ) (A) (B) (C) (D) 9、11，A，B是公路l(l为东西⾛向)两旁的两个村庄，A村到公路l的距离AC=1km，B村到公路l的距离BD=2km，B村在A村的南偏东45°⽅向上. (1)求出A，B两村之间的距离; (2)为⽅便村民出⾏，计划在公路边新建⼀个公共汽车站P，要求该站到两村的距离相等，请⽤尺规在图中作出点P的位置(保留清晰的作图痕迹，并简要写明作法). 10、是⼀个半圆形桥洞截⾯⽰意图,圆⼼为O,直径AB是河底线,弦CD是⽔位线,CD∥AB,且CD = 24 m,OE⊥CD于点E.已测得sin∠DOE = .(1)求半径OD;(2)根据需要,⽔⾯要以每⼩时0.5 m的速度下降,则经过多长时间才能将⽔排⼲? 11、所⽰，A、B两城市相距100km. 现计划在这两座城市间修筑⼀条⾼速公路(即线段AB)，经测量，森林保护中⼼P在A城市的北偏东30°和B城市的北偏西45°的⽅向上. 已知森林保护区的范围在以P 点为圆⼼，50km为半径的圆形区域内. 请问：计划修筑的这条⾼速公路会不会穿越保护区?为什么?(参考数据：， ) 12、，斜坡AC的坡度(坡⽐)为1: ，AC=10⽶.坡顶有⼀旗杆BC，旗杆顶端B点与A点有⼀条彩带AB 相连，AB=14⽶.试求旗杆BC的⾼度. ⼆、选做题： 13、,某货船以每⼩时20海⾥的速度将⼀批重要物资由A处运往正西⽅向的B处,经过16⼩时的航⾏到达.此时,接到⽓象部门的通知,⼀台风中⼼正以40海⾥每⼩时的速度由A向北偏西60o⽅向移动,距台风中⼼200海⾥的圆形区域(包括边界)均会受到影响.⑴ B处是否会受到台风的影响?请说明理由.⑵为避免受到台风的影响，该船应在到达后多少⼩时内卸完货物? 14、所⽰，在Rt△ABC中，∠ACB=90°，半径为1的圆A与边AB相交于点D，与边AC相交于点E，连接DE并延长，与线段BC的延长线交于点P. (1)当∠B=30°时，连接AP，若△AEP与△BDP相似，求CE的长; (2)若CE=2，BD=BC，求∠BPD的正切值; (3)若tan∠BPD= ，设CE=x，△ABC的周长为y，求y关于x的函数关系式.。

1.3 解直角三角形(1)一、教学内容解析：本节是在学习锐角三角函数之后，结合已学过的勾股定理和三角形内角和定理，研究解直角三角形的问题.本课内容既能加深对锐角三角函数概念的理解，又为后续解决与其相关的实际问题打下基础，在本章起到承上启下作用.二、教学目标：1、使学生理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形．2、通过综合运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形，逐步培养学生分析问题、解决问题的能力．3、渗透数形结合的数学思想，培养学生良好的学习习惯．三、教学重难点重点：直角三角形的解法.难点：三角函数在解直角三角形中的灵活运用.四、教学手段与教学方法教学手段：多媒体教学.教学方法：启发式教学、小组合作学习.五、教学过程：（一）、设疑，激发兴趣1、组织教学，激情口号：我自信、我出色，我努力、我成功.2、情景导入：同学们，幻灯片上的这幅图片是意大利著名的比萨斜塔，它已经有800多年的历史了，在它落成的时候由于地基等问题就已经发生了倾斜，但是在1972年比萨地区发生地震，造成塔顶中心点偏离垂直中心线达到了5.2米.比萨斜塔的高为54.5米，根据以上信息，我们可以把这道实际问题抽象成什么样的几何图形呢？在这个直角三角形中，AB代表比萨斜塔的高54.5米.BC代表塔顶到垂直中心线的距离5.2米，我们能否根据已知条件求出比萨斜塔的倾斜角∠A，或者∠B以及AB的长呢？你们有多少种求法？这就是本节课我们要学习的内容，解直角三角形.3、板书课题：1.3解直角三角形（1）4、请同学们齐读本节课的学习目标.（二）、活动一：自学初探各组组长检查各小组导学案第二部分主“动”展示完成情况.由各小组举牌主动展示以下三个问题.1、什么叫做解直角三角形？2、在一个直角三角形中，一共有几个元素，这五个元素分别是什么？那这五个元素之间有没有什么关系呢？哪组同学愿意主动展示一下第2道题？(1)三边之间关系：(2)两锐角之间关系：(3)边角之间关系：以上三点就是解直角三角形的依据，我们熟知后就可以拿来运用了.3、在直角三角形中，知道几个已知元素就可以求其余未知元素？（三）、活动二：合作再探现在我们回到比萨斜塔这道题，哪名同学愿意上黑板上写出已知元素和要求的未知元素，把它变成解直角三角形的问题.（教师通过这个过程可以观察到学生是否真的理解了什么叫做解直角三角形。

解直角三角形及其应用—知识讲解【学习目标】1．了解解直角三角形的含义，会综合运用平面几何中有关直角三角形的知识和锐角三角函数的定义解直角三角形；2．会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题．【要点梳理】要点一、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：①三边之间的关系：a2+b2=c2(勾股定理).②锐角之间的关系：∠A+∠B=90°.③边角之间的关系：，，，，，.④，h为斜边上的高.要点诠释：(1)直角三角形中有一个元素为定值(直角为90°)，是已知值.(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解.已知条件解法步骤Rt△ABC两边两直角边(a，b)由求∠A，∠B=90°－∠A，斜边，一直角边(如c，a)由求∠A，∠B=90°－∠A，一边一直角边和一锐角锐角、邻边(如∠A，b)∠B=90°－∠A，一角，锐角、对边(如∠A，a)∠B=90°－∠A，，斜边、锐角(如c，∠A)∠B=90°－∠A，，要点诠释：1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.要点三、解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念：(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.(2)仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.(3)方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(4)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.要点诠释：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解.3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.【典型例题】 类型一、解直角三角形1．在Rt △ABC 中，∠C ＝90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，根据下列条件，解这个直角三角形．(1)∠B=60°，a ＝4； (2)a ＝1，3b =． 【答案与解析】(1)∠A ＝90°－∠B ＝90°－60°＝30°．由tan bB a =知，tan 4tan6043b a B ==⨯=°． 由cos a B c =知，48cos cos 60a c B ===°． (2)由tan 3bB a==得∠B ＝60°，∴ ∠A ＝90°-60°＝30°．∵ 222a b c +=，∴ 2242c a b =+==．【总结升华】解直角三角形的两种类型是：(1)已知两边；(2)已知一锐角和一边．解题关键是正确选择边角关系．常用口诀：有弦(斜边)用弦(正弦、余弦)，无弦(斜边)用切(正切)． (1)首先用两锐角互余求锐角∠A ，再利用∠B 的正切、余弦求b 、c 的值；(2)首先用正切求出∠B 的值，再求∠A 的值，然后由正弦或余弦或勾股定理求c 的值． 举一反三：【高清课程名称：解直角三角形及其应用 高清ID 号：395952 关联的位置名称（播放点名称）：例1（1）-（3）】【变式】（1）已知∠C=90°，a=23，b=2 ，求∠A 、∠B 和c ；（2）已知sinA=23, c=6 ，求a 和b ； 【答案】（1）c=4；∠A=60°、∠B=30°； （2）a=4；b=252．（2015•湖北）如图，AD 是△ABC 的中线，tanB=，cosC=，AC=．求：（1）BC 的长；（2）sin ∠ADC 的值．【答案与解析】解：过点A 作AE ⊥BC 于点E ， ∵cosC=，∴∠C=45°，在Rt△ACE中，CE=AC•cosC=1，∴AE=CE=1，在Rt△ABE中，tanB=，即=，∴BE=3AE=3，∴BC=BE+CE=4；（2）∵AD是△ABC的中线，∴CD=BC=2，∴DE=CD﹣CE=1，∵AE⊥BC，DE=AE，∴∠ADC=45°，∴sin∠ADC=．【总结升华】正确作出辅助线构造直角三角形是解题的关键，注意锐角三角函数的概念的正确应用．类型二、解直角三角形在解决几何图形计算问题中的应用3．如图所示，BC是半圆⊙O的直径，D是AC的中点，四边形ABCD的对角线AC、BD交于点E，(1)求证：△ABE∽△DBC；(2)已知BC＝52，CD＝52sin∠AEB的值；(3)在(2)的条件下，求弦AB的长．【答案与解析】(1)∵AD CD，∴∠1＝∠2，又BC是⊙O的直径，∴∠BAC＝∠BDC＝90°．∴△ABE∽△DBC．(2)由△ABE∽△DBC，∴∠AEB＝∠DCB．在Rt△BDC中，BC＝52，CD＝5∴ BD ＝225BC CD -=， ∴ sin ∠AEB ＝sin ∠DCB＝52552BD BC ==． (3)在Rt △BDC 中，BD ＝5，又∠1＝∠2＝∠3，∠ADE ＝∠BDA ，∴ △AED ∽△BAD ． ∴AD DEDB AD=，∴ 2AD DE DB =． 又∵ 5CD AD ==，∴ CD 2＝(BD －BE)·BD ， 即25(5)5BE ⎛⎫=- ⎪ ⎪⎝⎭，∴ 35BE =． 在Rt △ABE 中，AB ＝BEsin ∠AEB ＝32355452⨯=． 【总结升华】本题综合了三角函数、相似三角形、勾股定理、圆等方面知识，尤其涉及三角函数问题，都是通过找出或构造直角三角形来解决问题． (1)根据圆周角定理易证△ABE ∽△DBC ．(2)利用(1)的结论，将∠AEB 转化为Rt △BCD 中的DCB ∠．(3)在Rt △ABE 中求AB ．举一反三：【高清课程名称：解直角三角形及其应用 高清ID 号：395952 关联的位置名称（播放点名称）：例2】【变式】 （2015•河南模拟）如图，在等腰Rt △ABC 中，∠C=90°，AC=6，D 是AC 上一点，若tan ∠DBA=，则AD 的长为多少?【答案与解析】解：作DE ⊥AB 于E ，如图， ∵∠C=90°，AC=BC=6，∴△ACB 为等腰直角三角形，AB=AC=6， ∴∠A=45°，在Rt △ADE 中，设AE=x ，则DE=x ，AD=x ， 在Rt △BED 中，tan ∠DBE==，∴BE=5x ，∴x+5x=6，解得x=，∴AD=×=2．类型三、解直角三角形在解决实际生活、生产问题中的应用4．某过街天桥的截面图为梯形，如图所示，其中天桥斜面CD 的坡度为1:3i =（i ＝1:3是指铅直高度DE 与水平宽度CE 的比)，CD 的长为10 m ，天桥另一斜面AB 的坡角∠ABC ＝45°．(1)写出过街天桥斜面AB 的坡度； (2)求DE 的长；(3)若决定对该过街天桥进行改建，使AB 斜面的坡度变缓，将其45°坡角改为30°，方便过路群众，改建后斜面为AF ，试计算此改建需占路面的宽度FB 的长(结果精确到.0.01 m)． 【答案与解析】(1)作AG ⊥BC 于G ，DE ⊥BC 于E ，在Rt △AGB 中，∠ABG ＝45°，AG ＝BG ． ∴ AB 的坡度1AGi BG'==． (2)在Rt △DEC 中，∵ 3tan DE C EC ∠==，∴ ∠C ＝30°． 又∵ CD ＝10 m ．∴ 15m 2DE CD ==． (3)由(1)知AG ＝BG ＝5 m ，在Rt △AFG 中，∠AFG ＝30°，tan AG AFG FG ∠=，即355FB =+，解得535 3.66(m)FB =-=． 答：改建后需占路面的宽度FB 的长约为3.66 m ．【总结升华】（1）解梯形问题常作出它的两条高，构造直角三角形求解．（2）坡度是坡面的铅直高度与水平宽度的比，它等于坡角的正切值．5．腾飞中学在教学楼前新建了一座“腾飞”雕塑．为了测量雕塑的高度，小明在二楼找到一点C ，利用三角板测得雕塑顶端A 点的仰角为30°，底部B 点的俯角为45°，小华在五楼找到一点D ，利用三角板测得A 点的俯角为60°(如图所示)．若已知CD 为10米，请求出雕塑AB 的高度．(结果精确到0.1米，参考数据3＝1.73)．【答案与解析】过点C作CE⊥AB于E．∵∠D＝90°－60°＝30°，∠ACD＝90°－30°＝60°，∴∠CAD＝180°－30°－60°＝90°．∵ CD＝10，∴ AC＝12CD＝5．在Rt△ACE中，AE＝AC·sin∠ACE＝5×sin 30°＝52，CE＝AC·cos ∠ACE＝5×cos 30°＝53 2，在Rt△BCE中，∵∠BCE＝45°，∴5553(31)222AB AE BE=+=+=+≈6.8(米)．∴雕塑AB的高度约为6.8米．【总结升华】此题将实际问题抽象成数学问题是解题关键，从实际操作（用三角形板测得仰角、俯角）过程中，提供作辅助线的方法，同时对仰角、俯角等概念不能模糊．。

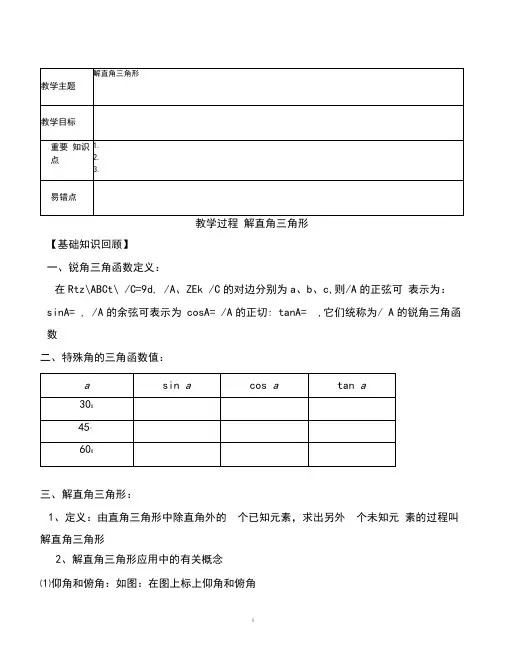
教学过程解直角三角形【基础知识回顾】一、锐角三角函数定义：在Rtz\ABCt\ /C=9d, /A、ZEk /C的对边分别为a、b、c,则/A的正弦可表示为：sinA= , /A的余弦可表示为cosA= /A的正切: tanA= ,它们统称为/ A的锐角三角函数二、特殊角的三角函数值：三、解直角三角形：1、定义：由直角三角形中除直角外的个已知元素，求出另外个未知元素的过程叫解直角三角形2、解直角三角形应用中的有关概念⑴仰角和俯角：如图：在图上标上仰角和俯角i视线水平线⑵坡度坡角：如图：斜坡AB的垂直度h和水平宽度l的比叫做坡度，用i表示, 即1= 坡面与水平面得夹角为用字母％表示，则i=tan %=上。

11 T⑶方位角：是指南北方向线与目标方向所成的小于900的水平角如图：OA^Z K OB 表木OC 表木O味示（也可称东南方向）北_ A南例2 在Rtz\ABOt\ /C=90° , AB=2BC现给出下歹U结论：①sinA= § ;②cosB=■1 ;③tanA=殍；④tanB=#,其中正确的结论是（只需填上正确结论的序号）解：如图所示：故答案为：②③④.对应训练2.计算6tan45 -2cos60 °的结果是（）A. 4 3B. 4C. 5 3D. 52. D考点三：化斜三角形为直角三角形例3 在△ABC^, AB=AC=5 sin /ABC=0.8,贝U BC=故答案为：6.对应训练3.如图，四边形ABCD勺对角线AG BD相交于点Q且B阡分AC若BD=8 AC=6/BOC=120,则四边形ABCD勺面积为 .（结果保留根号）3.12 .3考点四：解直角三角形的应用4.如图，益阳市梓山湖中有一孤立小岛，湖边有一条笔直的观光小道AR现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据：AB=80.0米,/PAB=38.5 , / PBA=26.5.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.（以A, B为参照点，结果精确到0.1米）（参考数据:sin38.5 =0.62 , cos38.5 =0.78 , tan38.5 =0.80 , sin26.5 =0.45, cos26.5 =0.89 , tan26.5 =0.50）4.解：设PD=x^,・.PDL AB,・•・/ADPN BDP=90 ,在Rt^PAD中，tan / PAD=^ ,AD・•・ AD=-—= 5x, tan38.5o0.8 4在RtWBD中，tan/PBD-DB又.78=80.0 米,55x+2x=80.0 ,4解得：x=24.6,即P[> 24.6 米,・•. DB=2x=492答：小桥PD的长度约为24.6米，位于AB之间距B点约49.2米.【聚焦中考】1.6cos30 °的值是1,但22.河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1:收，则AB的长为( )A.12B.4石米C. 5痣米D. 673米B2. A3.一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处处，望见渔船D在南偏东60方向，若海监船的速度为50海里/小时，则A, B之间的距离为（取4=1.7,结果精确到0.1海里）.5. 67.56.如图，有一艘渔船在捕鱼作业时出现故障，急需抢修，调度中心通知附近两个小岛A、B上的观测点进行观测，从A岛测得渔船在南偏东37方向C处，B岛在南偏东66°方向，从B岛测得渔船在正西方向，已知两个小岛间的距离是72海里, A岛上维修船的速度为每小时20海里，B岛上维修船的速度为每小时28.8海里，为及时赶到维修，问调度中心应该派遣哪个岛上的维修船？(参考数据：cos37 =0.8, sin37 =0.6, sin66 =0.9, cos66 =0.4)6.解：如图，作ADLBC的延长线于点D.北D C B在Rt^ADB中，AD=ABcos/BAD=72< cos66 =72X 0.4=28.8 （海里），BD=ABsin / BAD=72 sin66 =72X 0.9=64.8 （海里）.在Rt/XADC^, AC=—AD— ^88- 空=36（海里），cos DAC cos37o0.8CD=ACsin / CAD=36 sin37 =36X 0.6=21.6 （海里）.BC=BD-CD=64.8-21.6=43.2 （海里）.A岛上维修船需要时间t A=^ ^=1.8 （小时）.20 20B岛上维修船需要时间t B=坨432=1.5 （小时）.28.8 28.8- t A> t B,.•・调度中心应该派遣B岛上的维修船.10.校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CDW l垂直，测得CD的长等于21米，在l上点D的同侧取点A B,使/ CAD=30 , / CBD=60 .（1）求AB的长（精确到0.1米，参考数据：石=1.73, 72=1.41 ）;（2）已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒, 这辆校车是否超速？说明理由.S DC10.解：（1）由题意得，在Rtz\ADC^, AD= CD”马=21 阴=36.33 （米），tan30o .33在Rt^BDC^ , BD=_CD V=Z1 =75/3 = 12.11 （米），tan60 3贝U AB=AD-BD=36.33-12.11=24.22= 24.2 （米）。

1.3解直角三角形第1课时解直角三角形【基础练习】知识点已知一边一角或两边解直角三角形,BC=6,则AB的长为()1.在Rt△ABC中,△C=90°,sin A=35A.4B.6C.8D.102.如图1,在Rt△ABC中,△C=90°,△B=30°,AB=8,则BC的长为()图1A.4√3B.4C.8√3D.4√333.在Rt△ABC中,已知△C=90°,△A=40°,BC=3,则AC等于()A.3sin40°B.3sin50°C.3tan40°D.3tan50°4.在Rt△ABC中,△C=90°,a,b,c分别为△A,△B,△C的对边,c=10,△A=45°,则a=,b=,△B=°.5.在Rt△ABC中,△C=90°,a,b,c分别为△A,△B,△C的对边,a=6,b=2√3,则△B的度数为.6.如图2,在Rt△ABC中,△C=90°,△B=37°,BC=32,则AC的长约为.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)图27.如图3所示,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是米(假设夏至的正午时刻阳光与地平面的夹角为60°).图38.如图4,在Rt△ABC 中,△C=90°,a ,b ,c 分别为△A ,△B ,△C 的对边,由下列条件解直角三角形. (1)△A=60°,b=4; (2)a=13,c=√23;(3)c=2√2,△B=30°;(4)a=8,sin B=√22.图49.如图5,在△ABC 中,△ABC=90°,△A=30°,D 是边AB 上一点,△BDC=45°,AD=4,求BC 的长.(结果保留根号)图5【能力提升】10.某简易房的示意图如图6所示,它是一个轴对称图形,则AC的长为()图6A.511sinα米B.511cosα米C.115sinα米D.115cosα米11.等腰三角形的腰长为2√3,底边长为6,则底角等于()A.30°B.45°C.60°D.120°12.[2019·杭州]如图7,一块矩形木板ABCD斜靠在墙边(OC△OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,△BCO=x,则点A到OC的距离等于()图7A.a sin x+b sin xB.a cos x+b cos xC.a sin x+b cos xD.a cos x+b sin x13.如图8,已知在Rt△ABC中,△ABC=90°,点D沿BC边从点B向点C运动(点D与点B,C不重合),作BE△AD于点E,CF△AD,交AD的延长线于点F,则在点D运动的过程中,BE+CF的值()图8A.不变B.逐渐增大C.逐渐减小D.先增大后减小14.如图9,小明将一张矩形纸片ABCD沿CE折叠,点B恰好落在AD边上,设此点为F.若AB∶BC=4∶5,则tan△ECB的值为.图915.在学习《解直角三角形》一章时,小明同学对一个角的倍角的三角函数值是否具有关系产生了浓厚的兴趣,进行了一些研究.(1)初步尝试:我们知道:tan60°=,tan30°=,发现结论:tan A2tan A2(填“=”或“≠”).(2)实践探究:如图10△,在Rt△ABC中,△C=90°,AC=2,BC=1,求tan A2的值.小明想构造包含12△A的直角三角形:延长CA至点D,使得DA=AB,连结BD,可得到△D=12△BAC,即转化为求△D的正切值.请按小明的思路进行余下的求解.(3)拓展延伸:如图△,在Rt△ABC中,△C=90°,AC=3,tan A=13.△tan2A=;△求tan3A的值.图10答案1.D2.D3.D4.5√2 5√2 455.30° [解析] ∵tan B=ba ,b=2√3,a=6, ∴tan B=2√36=√33,∴∠B=30°. 6.24 [解析] 因为在Rt △ABC 中,∠C=90°, 所以tan B=ACBC ,即tan37°=AC32, 所以AC=32·tan37°≈32×0.75=24. 7.√38.解:(1)∵∠A=60°,∠C=90°,∴∠B=30°. ∵b=4,cos A=bc,∴4c=12,解得c=8,∴a=√82-42=4√3.(2)∵a=13,c=√23,∴b=√c 2-a 2=13. ∵sin A=a c =13÷√23=√22, ∴∠A=45°,∴∠B=45°. (3)∵∠B=30°,c=2√2,sin B=bc , ∴12=2√2,∠A=60°,∴b=√2,∴a=√c 2-b 2=√(2√2)2-(√2)2=√6. (4)∵sin B=√22,∴∠B=45°, ∴∠A=45°,∴b=a=8, ∴c=√a 2+b 2=8√2.9.解:∵∠ABC=90°,∠BDC=45°, ∴BD=BC.∵∠ABC=90°,∠A=30°, ∴AB=√3BC ,∴AD+BD=√3BC ,即AD+BC=√3BC. 又∵AD=4,∴4+BC=√3BC , 解得BC=2√3+2.10.D [解析] 如图,过点A 作AH ⊥BC 于点H.由题意,得AB=AC ,BC=4+0.2+0.2=4.4(米). ∵AH ⊥BC , ∴BH=CH=2.2米. 在Rt △ABH 中,cos α=BH AB,∴AB=BHcosα=2.2cosα=115cosα(米),即AC=115cosα米. 故选D . 11.A [解析] 如图所示,在△ABC 中,AB=AC=2√3,BC=6,过点A 作AD ⊥BC 于点D , 则BD=12BC=12×6=3.在Rt △ABD 中,cos B=BDAB =2√3=√32,∴∠B=30°.故选A .12.D [解析] 如图,过点A 分别作AE ⊥OC 于点E ,AF ⊥OB 于点F .∵四边形ABCD 是矩形, ∴∠ABC=90°.∵∠ABC=∠AEC ,∠BCO=x ,∴∠EAB=x,∴∠FBA=x.∵AB=a,AD=b,∴AE=FO=FB+BO=a cos x+b sin x.故选D.13.C[解析] ∵BE⊥AD,CF⊥AD,∴CF∥BE,∴∠DCF=∠DBE.设∠DCF=∠DBE=α,则CF=CD·cosα,BE=DB·cosα,∴BE+CF=(DB+CD)cosα=BC·cosα.∵∠ABC=90°,∴0°<α<90°,当点D从点B向点C运动时,α是逐渐增大的,∴cosα的值是逐渐减小的,∴BE+CF=BC·cosα的值是逐渐减小的.故选C.14.12[解析] 设AB=4k,则BC=5k.在△DFC中,FC=BC=5k,CD=AB=4k,∴DF=3k,∴AF=2k.由折叠的性质可知∠CFE=∠B=90°,∴∠CFD+∠AFE=90°.又∵∠CFD+∠DCF=90°,∴∠AFE=∠DCF.又∵∠D=∠A=90°,∴△DFC∽△AEF,∴DFAE =FCEF,即3kAE=5k4k-AE,解得AE=1.5k,∴BE=2.5k,∴tan∠ECB=2.5k5k =1 2 .15.解:(1)√3√33≠(2)在Rt△ABC中,∵∠C=90°,AC=2,BC=1,∴AB=√AC 2+BC 2=√5. ∵DA=AB ,∴∠D=∠ABD ,CD=DA+AC=√5+2, ∴∠BAC=2∠D , ∴tan A2=tan D=BCCD =√5+2=√5-2.(3)①34 [解析] 如图ⓐ,作AB 的垂直平分线交AC 于点E ,连结BE ,则AE=BE ,∠A=∠ABE ,∴∠BEC=2∠A. ∵在Rt △ABC 中,∠C=90°,AC=3,tan A=13, ∴BC=1,则AB=√AC 2+BC 2=√10. 设AE=x ,则BE=x ,EC=3-x.在Rt △EBC 中,由勾股定理,得BE 2=EC 2+BC 2,即x 2=(3-x )2+1, 解得x=53,即AE=BE=53,∴EC=43,∴tan2A=tan ∠BEC=BC EC=34.故答案为34.②如图ⓑ,作AB 的垂直平分线交AC 于点E ,连结CE ,作BM 交AC 于点M , 使∠MBE=∠ABE ,则∠BMC=∠A+∠MBA=3∠A. 设EM=y ,则CM=EC -EM=43-y. ∵∠MBE=∠ABE ,∠A=∠ABE ,∴∠A=∠MBE ,∠ABM=2∠A=∠BEC , ∴△ABM ∽△BEM , ∴AB BE =BM EM,即√1053=BM y,∴BM=3√105y. 在Rt △MBC 中,BM 2=CM 2+BC 2, 即3√105y 2=43-y 2+1,整理得117y 2+120y -125=0, 解得y 1=2539,y 2=-53(不合题意,舍去), 即EM=2539,则CM=43-2539=913,∴tan3A=tan ∠BMC=BCCM=1913=139.。