高一年级寒假培优数学教材

第1讲集合理清双基1、集合的有关概念（1）、集合的含义与表示：研究对象的全体称为集合。

对象为集合的元素。

通常用大写字母A 、B 、C 、D 表示。

元素与集合的关系∈与∉（2）、集合元素的特征（三要素）：①确定性：②互异性：③无序性：【例】1.设R b a ∈,，集合},,0{},,1{b aba b a =+，则=-a b ________.（3）、集合的分类：①有限集②无限集③空集：∅（4）、集合的表示方法:①自然语言②列举法③描述法④venne 法【例】2.分析下列集合间的关系}1{2+==x y y A }1{2+==x y x B }1),{(2+==x y y x C }1{2+==x t t D 3.集合}{抛物线=A }{直线=B ，则B A 的元素个数下列说法正确的是（）一个（B ）二个（C ）一个、二个或没有（D ）以上都不正确变式：集合})0(),{(2≠++==a c bx ax y y x A })0(|),{(≠+==k b kx y y x B ，则B A 的元素个数为（）说明：列举法与描述法各有优点，应该根据具体问题确定采用哪种表示法，要注意，一般集合中元素较多或有无限个元素时，不宜采用列举法。

2.集合间的关系（1）子集：（2）相等关系：（3）真子集：说明：任何一个集合是它本身的子集空集是任何集合的子集，是任何非空集合的真子集。

【例】4.设⎭⎬⎫⎩⎨⎧∈+==Z k k x x M ,412,⎭⎬⎫⎩⎨⎧∈+==Z k k x x N ,214，则M 与N 的关系正确的是（）A.NM = B.NM ≠⊂ C.NM ≠⊃ D.以上都不对5.已知集合}.121|{},72|{-<<+=≤≤-=m x m x B x x A 。

若A B ⊆，则实数m 的取值范围是()A ．43≤≤-m B ．43<<-m C ．42≤<m D ．4≤m 3.集合的基本运算（1）交集（2）并集（3）补集全集【例】6.已知集合}1{2+==x y y M ，}9{2x y x N -==，则=N M ________4、集合运算中常用结论（1）等价关系B A A B A ⊆⇔= AB A B A ⊆⇔=【例】7.已知集合}{},1{a x x B x x A ≥=≤=，且R B A = ，则实数a 的取值范围为____（2）反演律（德摩根定律）)()()(B C A C B A C U U U =)()()(B C A C B A C U U U =【例】8.设全集}5,4,3,2,1{=U ，集合S 与T 都是U 的子集，满足}2{=T S ，}4{)(=T S C U ，}5,1{)()(=T C S C U U 则有()A ．TS ∈∈3,3B ．TC S U ∈∈3,3C ．TS C U ∈∈3,3D ．TC S C U U ∈∈3,39.由)(+∈N n n 个元素组成的集合A 的子集个数：A 的子集有n2个，非空子集有)12(-n 个，真子集有)12(-n 个，非空真子集有)22(-n 个【考点分析】考点一集合的基本概念【例1】1.已知集合},,|),{(},5,4,3,2,1{A y x A y A x y x B A ∈+∈∈==则B 中所含元素的个数为()A ．3B ．6C ．8D ．102.集合A 是由形如()Z n Z m n m ∈∈+,3的数构成的，判断321-是不是集合A 中的元素.3.数集A 满足条件：若A a ∈，则)1(11≠∈-+a A a a ．若A ∈31，求集合中的其他元素.4.已知},,2|{R k N x k x x P ∈∈<<=，若集合P 中恰有3个元素，则实数k 的取值范围是________.5.已知集合}023|{2=+-=x ax x A .（1）若A 是单元素集合，求集合A ；（2）若A 中至少有一个元素，求a 的取值范围．►归纳提升解答集合的概念问题应关注两点(1)研究集合问题，一定要抓住元素，看元素应满足的属性，对于含有字母的集合，在求出字母的值后，要注意检验集合的元素是否满足互异性。

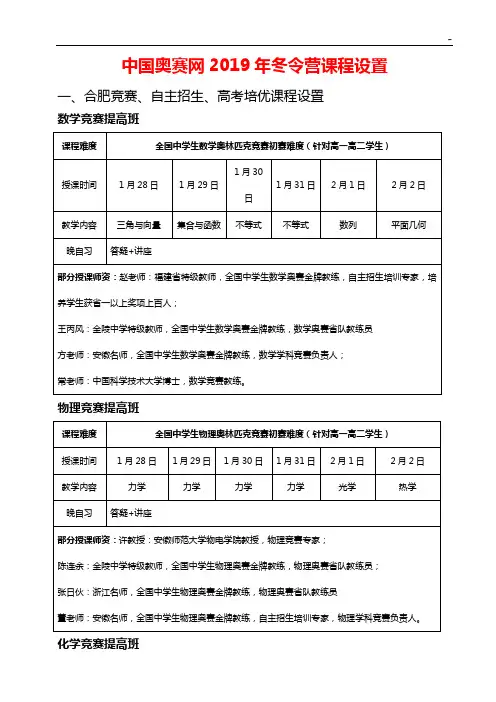
中国奥赛网2019年冬令营课程设置一、合肥竞赛、自主招生、高考培优课程设置
数学竞赛提高班
物理竞赛提高班
化学竞赛提高班
生物竞赛提高班
自主招生班
高考培优理科提高班
高考培优理科冲刺班
高考培优文科冲刺班
电脑制作活动冲刺班
二、南京冬令营竞赛专题精讲+刷题班课程设置数学
物理
化学
三、上课时间、地点
（一）时间：元月27号报到，28日上课，2月2日结束；电脑营1号结束。

（二）地点：培优营：安徽大学老校区（黄山路校区）；竞赛冲刺营：南京。

四、费用标准
（一）学科竞赛营、高考培优营学费1980元/每生；
（二）电脑制作营学费3980元/每生；
（三）南京竞赛冲刺营：2380元/每生；
（四）食宿费用：合肥：80元/每生每天（伙食、住宿各40元）；南京：160元/天（住宿酒店100元，伙食60元）。

（五）食宿标准：住宿校内招待所、留学生公寓，每间4人；学生食堂统一用餐。

南京酒店上课，住宿标间，酒店桌餐。

【新教材】2019统编人教版高中数学A版必修第二册教学计划高一下学期数学教师教育教学工作计划（含教学进度表培优补差等）XX高级中学高一数学组XXX2019统编人教版高中数学A版必修第二册教学计划高一数学是高中数学的重要组成部分，通过本学期的教学，要使学生学会适应日常生活，参加生产和进一步学习所必须的基础知识与基本技能，进一步培养运算能力、思维能力和空间观念：能够运用所学的知识解决简单的实际问题，培养学生的数学创新意识、良好个性品质及初步的辩证唯物主义的观点。

一、学情分析：根据分班考试的情况来分析学生的数学成绩并不理想，总体的水平一般，尖子生少、低分的学生较多，而且学习欠缺勤奋，学习的自觉性不高。

高一年级学生往往沿用初中的学习方法，死记硬背，这样既没读懂弄透，又使其自学能力和实际应用能力得不到很好的训练，要重视对学生的读法指导。

高一年级学生往往对课程增多、课堂学习容量加大不适应，顾此失彼，精力分散，使听课效率下降，要重视听法的指导。

学习离不开思维，善思则学得活，效率高，不善思则学得死，效果差。

高一年级学生常常固守小学算术中的思维定势，思路狭窄、呆滞，不利于后继学习，要重视对学生进行思法指导。

学生在解题时，在书写上往往存在着条理不清、逻辑混乱的问题，要重视对学生进行写法指导。

学生是否掌握良好的记忆方法与其学业成绩的好坏相关，高一学生由于正处在初级的逻辑思维阶段，识记知识时机械记忆的成份较多，理解记忆的成份较少，这就不能适应高一教学的新要求，要重视对学生进行记法指导。

学生大多存在学习粗心,作业马虎,对数学学习缺乏兴趣和信心的整体弱点，学习习惯差。

在知识结构上：学生在小学已学过的概率的运算，相应的较为简单的应用题，对图形、图形的面积、体积，数据的收集与整理上有了初步的认识，无论是代数的知识，图形的知识都有待于进一步系统化、理论化，这就是高中的内容，本学期将要学习有关统计与概率的认识，对图形的进一步认识；在数学的思维上：学生正处于形象思维向逻辑抽象思维的转变期，这期间，结合教学，让学生适当思考部分有利于思维的题目，无疑是对学生终身有用的；另一方面关注一题多解，多题一解，从不同的角度看问题，培养学生数学思维的活跃性和敏感性。

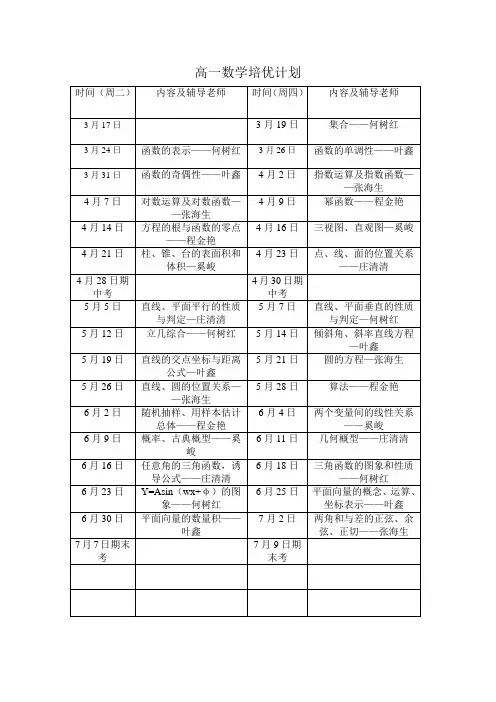
高一年段数学培优教材第二讲 二次函数一、 基础知识： 1． 二次函数的解析式（1）一般式：2()(0)f x ax bx c a =++≠（2）顶点式：2()()f x a x h k =-+，顶点为(,)h k （3）两根式：12()()()f x a x x x x =-- （4）三点式：132312321313221231213()()()()()()()()()()()()()()()()x x x x x x x x x x x x f x f x f x f x x x x x x x x x x x x x ------=++------2．二次函数的图像和性质（1）2()(0)f x ax bx c a =++≠的图像是一条抛物线，顶点坐标是24(,)24b ac b a a--，对称轴方程为2bx a=-，开口与a 有关。

（2）单调性：当0a >时，()f x 在(,]2b a -∞-上为减函数，在[,)2ba-+∞上为增函数；0a <时相反。

（3）奇偶性：当0b =时，()f x 为偶函数；若()()f a x f a x +=-对x R ∈恒成立，则x a =为()f x 的对称轴。

（4）最值：当x R ∈时，()f x 的最值为244ac b a -，当[,],[,]2b x m n m n a ∈-∈时，()f x 的最值可从(),(),()2b f m f n f a -中选取；当[,],[,]2bx m n m n a∈-∉时，()f x 的最值可从(),()f m f n 中选取。

常依轴与区间[,]m n 的位置分类讨论。

3．三个二次之间的关联及根的分布理论：二次方程2()0(0)f x ax bx c a =++=≠的区间根问题，一般情况需要从三个方面考虑：判别式、区间端点函数值的符号；对称轴与区间端点的关系。

二、 综合应用：例1：已知二次函数()f x 的图像经过三点(1,6),(1,0),(2.5,0)A B C --，求()f x 的解析式。

安徽省示范高中培优联盟2023年冬季联赛（高一）数学（答案在最后）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1至第3页，第Ⅱ卷第4至第6页.全卷满分150分，考试时间120分钟.考生注意事项：1.答题前，务必在试题卷、答题卡规定的地方填写自己的姓名、座位号，并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。

2.答第Ⅰ卷时，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.3.答第Ⅱ卷时，必须使用0.5毫米的黑色墨水签字笔在答题卡上书写，要求字体工整、笔迹清晰.作图题可先用铅笔在答题卡规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效.4.考试结束，务必将试题卷和答题卡一并上交.第Ⅰ卷（选择题共60分）一、选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知集合()(){}23270xA x x =--=∣，{}0ln 1B x x =∈Z∣ ，则A B = （）A.{}2B.{}3 C.{}2,3 D.{}1,2,32.若命题：0x ∃>，2210x mx -+ 是真命题，则实数m 的取值范围是（）A.[)1,+∞B.[)2,+∞C.)⎡+∞⎣D.[)3,+∞3.已知函数()2y f x =的定义域为3,22⎡⎤-⎢⎥⎣⎦，则函数()()1ln 2f x y x -=+的定义域为（）A.70,4⎡⎤⎢⎥⎣⎦B.[)(]3,11,4---C.(]2,4- D.()(]2,11,4--- 4.若:3p a >，q ：关于x 的方程210x ax ++=有两个不相等的实数根，则p 是q 成立的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知定义域为R 的函数()f x 和()g x ，函数()f x 图象关于原点对称，函数()g x 满足()()0g x g x --=，若()()321xf xg x x +=+-，则()1f 与()2g -的大小关系为（）A.()()12f g >-B.()()12f g <-C.()()12f g =- D.不确定6.已知1a >，1b >，log 10lg a b =，lg lg 2a b + ，则a b +=（）A.2B.5C.10D.207.已知函数()f x 定义域为D ，若对于12,x x D ∀∈，当12x x ≠时，都有()()()()22121221120x x f x f x x f x x f x ⎡⎤+--<⎣⎦成立，则称函数()f x 是“共建”函数，则下列四个函数中是“共建”函数的是（）A.()()42x xf x x =+ B.()()12log 21f x x x =-C.()2f x x x =+，()0,x ∈+∞ D.()2f x x =，()0,x ∈+∞8.函数()8149431923x x x x xf x --+⋅+⋅+=+⋅的最小值是（）A. B.3C.83 D.103二、选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.）9.若实数x ，y 满足12x y -<<<，则下列说法中正确的是（）A.11x<- B.24x y -<+<C.10x y -<-< D.30x y -<-<10.若点(),8a 在幂函数()()1bf x a x =-的图象上，则以下关于函数()g x =是（）A.()g x 的定义域是[]1,2B.()g x 的值域是[]1,1-C.()g x 是增函数D.()()50g x g x -+=11.若函数()f x 的零点与()4ln 2xg x x =+-的零点之差的绝对值不超过12，则()f x 可以是（）A.()41f x x =- B.()32f x x x =+-C.()33xxf x -=- D.()()2log 32f x x =-12.定义在R 上的函数()f x ，当0x >时，()22f x x =-，当0x 时，()12x f x +=，若关于x 函数()()21y f x mf x =++在定义域内有四个零点，则实数m 的取值可以是（）A.265-B.5- C.103-D.52-第Ⅱ卷（非选择题共90分）考生注意事项：请用0.5毫米黑色墨水签字笔在答题卡上作答，在试题卷上答题无效.三、填空题（本题共4小题，每小题5分，共20分.）13.已知函数()2f x x =()f x 的值域为________.14.已知函数()()log a f x x b =+的图象不经过第二、四象限，请写出满足条件的一组(),a b 的值________.15.设点()1,0A ，()0,1B ，点C 是函数1112y x x x ⎛⎫=+⎪⎝⎭图象上一点，则ABC △面积的最小值为________.16.若函数()()()232f x x x mx n =+++对于x ∀∈R 都有()()20f x f x -+=，则2m n +=________.四、解答题（本题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.）17.（10分）某品牌汽车制造厂引进了一条小型家用汽车装配流水线，本年度第一季度统计数据如下表月份1月2月3月小型汽车数量x （辆）306080创造的收益y （元）480060004800（1）根据上表数据，从下列三个函数模型中：①y ax b =+，②2y ax bx c =++，③xy a b =+选取一个恰当的函数模型描述这条流水线生产的小型汽车数量x （辆）与创造的收益y （元）之间的关系，并写出这个函数关系式；（2）利用上述你选取的函数关系式计算，若这家工厂希望在一周内利用这条流水线创收6020元以上，那么它在一周内大约应生产多少辆小型汽车？18.（12分）（1）已知0b a >>，求证11a ab b+>+；（2）利用（1111111112462n ⎛⎫⎛⎫⎛⎫⎛⎫<---⨯⨯-< ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ （*n ∈N 且2n ）.19.（12分）我们知道存储温度x （单位：℃）会影响着鲜牛奶的保鲜时间T （单位：h ），温度越高，保鲜时间越短.已知x 与T 之间的函数关系式为()e mx n T x +=（e 为自然对数的底数），某款鲜牛奶在5℃的保鲜时间为180h ，在25℃的保鲜时间为45h .（参考数据：2 1.41≈）（1）求此款鲜牛奶在0℃的保鲜时间约为几小时（结果保留到整数）；（2）若想要保证此款鲜牛奶的保鲜时间不少于90h ，那么对存储温度有怎样的要求？20.（12分）定义在R 上的函数()f x ，满足()0f x >，对于任意的,x y ∈R 都有()()ln ln f xy y f x =成立，并且0m ∃>，使得()12f m =.（1）判断函数()f x 的单调性，并证明；（2）若[]2,1x ∀∈--，不等式()212x f a f x ⎛⎫+- ⎪⎝⎭恒成立，求实数a 的取值范围.21.（12分）已知函数()223,0;2ln ,0.x x x f x x x ⎧+-=⎨-+>⎩ （1）请在网格纸中画出()f x 的简图，并写出函数的单调区间（无需证明）；（2）定义函数()()2241,20;12,0 2.2f x x x xg x x x ⎧--+-⎪=⎨-<⎪⎩ 在定义域内的0x ，若满足()00g x x =，则称0x 为函数()g x 的一阶不动点，简称不动点；若满足()()00g g x x =，则称0x 为函数()g x 的二阶不动点，简称稳定点.①求函数()g x 的不动点；②求函数()g x 的稳定点.22.（12分）已知函数()log a f x x =，其中1a >.（1）若存在12x x <，使得()()12f x f x =，求122x x +的最小值；（2）令()()x g x f x f a ⎛⎫= ⎪⎝⎭，若关于x 的方程()g x m =有两个根1x 和2x ，求当221x a x >时，实数m 的取值范围.2023冬季联赛高一数学参考答案123456789101112ACDAADBDBDBCDABDAB一、选择题（本大题共8个题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.【答案】A{}2,3A =，{}1e B x Z x =∈≤≤∣，所以{}2A B = ，故选A.2.【答案】C2Δ8004m m ⎧=-≥⎪⎨>⎪⎩，即)m ⎡∈+∞⎣，故选C.3.【答案】D ∵3,22x ⎡⎤∈-⎢⎥⎣⎦，∴[]23,4x ∈-，∴3142021x x x -≤-≤⎧⎨+>+≠⎩且，即3421x x x -≤≤⎧⎨>-≠-⎩且，故选D.4.【答案】A 由2Δ40a =->解得2a >或2a <-，故p 是q 成立的充分不必要条件，选A.5.【答案】A因为()()0f x f x +-=，()()0g x g x --=，()()321xf xg x x +=+-，故()()321xf xg x x --+-=--，即()()321xf xg x x --+=--，所以()32222x x x f x --+=，()2222x x g x -+-=，计算可得()714f =，()928g -=，故选A.6.【答案】D∵log 10lg a b =，∴lg10lg lg b a=，即lg lg 1a b ⋅=，由基本不等式可知lg lg 2a b +≥=，又因为lg lg 2a b +≤，所以lg lg 2a b +=，即满足基本不等式取等条件lg lg 1a b ==，即10a b ==，故选D.7.【答案】B根据题意，()()()1221120x x x f x x f x ⎡⎤--<⎣⎦，即()()()121212120f x f x x x x x x x ⎡⎤--<⎢⎥⎣⎦，设()()f x g x x=，即()()()1212120x x x x g x g x ⎡⎤--<⎣⎦，选项B 中，()()12log 21g x x =-在定义域上是单调递减函数，满足“共建”函数的定义，故选B.8.【答案】D设3x t =，则()224222222414121222t t t t t f t t t t t t t t t⎛⎫+++++ ⎪⎝⎭===+++++，因为2221133t t t t t +=++≥，所以()110333f t ≥+=，选D.二、选择题：本大题共4个题，每小题5分，共20分.每小题有多项符合题目要求，全部选对得5分，部分选对得2分，有选错得0分.9.【答案】BD 当1x =时，111x=>-，故A 错误；因为12x y -<<<，根据同向可加性易知24x y -<+<，故B 正确；因为12x y -<<<，所以12x -<<，21y -<-<，则30x y -<-<，故C 错误，D 正确，故选BD.10.【答案】BCD因为()()1bf x a x =-为幂函数，所以11a -=，则2a =，由点()2,8在()bf x x =的图象上得3b =，故()g x =.由3020x x -≥⎧⎨-≥⎩解得23x ≤≤，故A 错误；易知函数()g x =单调递增，故C 正确；当23x ≤≤时，求得值域为[]1,1-，故B 正确；由()g x =()5g x -=()()50g x g x -+=，故选BCD11.【答案】ABD计算可得A ，B ，C ，D 选项中的零点分别为14，1，0，1，根据二分法以及零点存在性定理可求出()14220g =-=>，1112ln 2ln 0222g ⎛⎫=+-=< ⎪⎝⎭，)333ln 221ln0444g ⎛⎫=-=+> ⎪⎝⎭所以()g x 的零点所在区间为13,24⎛⎫⎪⎝⎭，故选ABD.12.【答案】AB 令()t f x =，则21y t mt =++，由题意原函数有4个零点，结合函数()t f x =图象可知函数21y t mt =++有两个不同零点1t 和2t ，不妨设12t t <，且12t t m +=-，121t t =，分析函数()t f x =的图象可知，24t ≥，则12221174m t t t t -=+=+≥，解得174m ≤-，故选AB.三、填空题：本题共4小题，每小题5分，共20分13.15,8⎡⎫+∞⎪⎢⎣⎭14.()2,112-16.14-13.【答案】15,8⎡⎫+∞⎪⎢⎣⎭令t =，则0t ≥，21x t =+，()()2211521248y f x t t t ⎛⎫==+-=-+ ⎪⎝⎭，易得值域为15,8⎡⎫+∞⎪⎢⎣⎭.14.【答案】()2,1只要满足1a >，1b =即可15.12-，如图所示，1111111222222ABC ACO BCO ABO S S S S x x x x x ⎛⎫⎛⎫=+-=++-=+- ⎪ ⎪⎝⎭⎝⎭△△△△，因为112x ≤≤，所以12xx +≥=，当且仅当2x =时取等号，此时ABC △12.（另解：利用点到直线距离公式亦可解决）16.【答案】14-，因为对于R x ∀∈都有()()20f x f x -+=，所以函数()f x 的对称中心为()1,0，又因为()30f -=，所以()50f =，故()()()()()()22315321210f x x x x x x x =+--=+-+，即2241014m n +=-+=-.四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤17.（10分）【答案】（1）选取②2y ax bx c =++，由题表可知，随着x 的增大，y 的值先增大后减小，而函数y ax b =+及x y a b =+均为单调函数，故不符合题意，所以选取②2y ax bx c=++2分将()30,4800，()60,6000，()80,4800三点分别代入函数解析式2y ax bx c =++，可得二次函数对称轴为3080552x +==，故可将函数解析式设为2(55)y a x h =-+，即得到2256000254800a h a h ⎧+=⎨+=⎩，解出26050a h =-⎧⎨=⎩，∴2222(55)60502220y x x x ax bx c =--+=-+=++，∴2a =-，220b =，0c =；5分（2）设在一周内大约应生产x 辆小型汽车，根据题意，可得222206020x x -+>，即2222060200x x -+->，即211030100x x -+<，6分因为2Δ11043010600=-⨯=>，所以方程211028000x x -+=有两个实数根155x =，255x =，由二次函数21103010y x x =-+的图象可知不等式的解为5555x <<+.8分因为x 只能取整数值，所以当这条流水线在一周内生产的小型汽车数量5358x ≤≤之间时，这家工厂能够获得6020元以上的收益.10分18.（12分）【答案】（1）证明：因为0b a >>，所以()1011a a b a b b b b +--=>++，于是11a ab b+>+.4分（2135212462n n -<⨯⨯⨯<（*n N ∈且2n ≥）由（1）式可知，2221221221n n nn n n --<<-+，故21352113521124221112462246223521224n n n n n n n n ---⎛⎫⎛⎫⎛⎫⨯⨯⨯>⨯⨯⨯⨯⨯⨯=⨯= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭ （*n N ∈且2n ≥）2135211352124621246224623572121n n n n n n n --⎛⎫⎛⎫⎛⎫⨯⨯⨯<⨯⨯⨯⨯⨯⨯= ⎪ ⎪⎪++⎝⎭⎝⎭⎝⎭ （*n N ∈且2n ≥）135212462n n -<⨯⨯⨯<（*n N ∈且2n ≥），原式得证.12分19.（12分）【答案】（1）根据题意，将()5,180，()25,45分别代入()emx nT x +=得525e 180e45m n m n ++⎧=⎨=⎩，2分所以20451e1804m==，所以5e 2m =，0m <，当0x =时，()5180e 180 1.41253.8e 2n m T x ====≈⨯=，此款鲜牛奶在0℃的保鲜时间为254小时.6分（2）根据题意，即要求()e 90mx nT x +=≥，由（1）可知101e 2m =，所以101551e e e 180902m m n m n ++⋅=⋅=，故15ee mx nm n ++≥，即15e e mx m ≥，即15mx m ≥，因为0m <，所以15x ≤，所以想要保证此款鲜牛奶的保鲜时间不少于90h ，存储温度要低于15℃12分20.（12分）【答案】（1）函数()f x 单调递减.，证明如下：由()()ln ln f xy y f x =得，()()[]yf xy f x =，则12,R x x ∀∈，当12x x <时()()()()()()121122a babf x f x f ma f mb f m f m ⎛⎫⎛⎫⎡⎤⎡⎤-=-==- ⎪ ⎪⎣⎦⎣⎦⎝⎭⎝⎭-4分因为12x x <，所以ma mb <，则a b <，故()()1211022a bf x f x ⎛⎫⎛⎫-=-> ⎪ ⎪⎝⎭⎝⎭所以函数()f x 单调递减.6分（2）不等式()212x f a f x ⎛⎫+-≥ ⎪⎝⎭可等价变形为()212x f a f x⎛⎫+≥ ⎪-⎝⎭，因为()()[]yf xy f x =，所以()()()12221f x f x f x -⎡⎤=-=⎣⎦-，则不等式可变为()22x f a f x ⎛⎫+≥ ⎪⎝⎭8分由（1）知，函数()f x 在定义域内单调递减，故22xa x +≤，[]2,1x ∈--恒成立，则2min2x a x ⎛⎫≤-⎪⎝⎭，解得32a ≤11分因此实数a 的取值范围是3,2⎛⎤-∞ ⎥⎝⎦.12分21.（12分）【答案】（1）()f x 的单增区间为[]1,0-，()0,+∞，()f x 的单减区间为(],1-∞-5分（2）易知()222,2012,022x x g x x x ---≤≤⎧⎪=⎨-<≤⎪⎩①当020x -≤≤时，()0022g x x =--，令()00g x x =得0022x x --=，解得023x =-；当002x <≤时，()200122g x x =-，令()00g x x =得200122x x -=，解得01x =综上所述：函数()g x 的不动点为23-.8分②当021x -≤<-时，()0022g x x =--，且()002g x <≤，则()()()()2200000122222242g g x g x x x x =--=---=+令()()00g g x x =得，200024x x x +=，解得032x =-或00x =（舍）当010x -≤≤时，()0022g x x =--，且()020g x -≤≤，则()()()()000022222242g g x g x x x =--=----=+令()()00g g x x =得0042x x +=，解得023x =-10分当002x <≤时，()200122g x x =-，且()020g x -≤<，则()()2220000112222222g g x g x x x ⎛⎫⎛⎫=-=---=-+ ⎪ ⎪⎝⎭⎝⎭令()()00g g x x =得2002x x -+=，解得01x =或02x =-（舍）综上所述：函数()g x 的稳定点有3个，分别是32-，23-和1.12分22.（12分）【答案】（1）因为()log a f x x =为单调函数，所以当12x x <时，()()12f x f x ≠，则当()()12f x f x =时，有()()12f x f x =-，即12log log 0a a x x +=，解得121x x =，则2分1211122x x x x +=+≥当且仅当12x =时，取等号，故122x x +的最小值为.5分（2）由题意，()()()log log log log 1a a a a x x g x f x f x x x a a ⎛⎫==⋅=- ⎪⎝⎭令log a t x =，则R t ∈，11log a t x =，22log a t x =，若221x a x >，则221log log a a x a x >，即21log log 2a a x x ->，即212t t ->7分由1t 和2t 为方程()1t t m -=，即方程20t t m --=的两根得Δ140m =+>，解得14m >-，且121t t +=，12t t m =-9分因为212t t ->，所以()1112t t -->，解得112t <-，所以()22121111111124m t t t t t t t ⎛⎫=-=--=-=-- ⎪⎝⎭，。

高一年段数学培优教材第四讲 三角函数知识要点:一、角的概念与推广：任意角的概念；角限角、终边相同的角； 二、弧度制：把长度等于半径的弧所对的圆心角叫做1弧度；弧长公式：r l α=扇形面积：S=α22121r r l =⋅三角函数线：如右图，有向线段AT 与MP OM 分别叫做的的正切线、正弦线、余弦线。

三、同角三角函数关系：即：平方关系、商数关系。

四、诱导公式：()ααπg nf ±=⎪⎭⎫⎝⎛±2 记忆：奇变偶不变，符号看象限。

奇双：即看πn 中的n 是2π的奇数倍还是偶数倍，奇数倍后面三角函数名变，偶数不变则三角函数名不变；符号看象限：即把α看成锐角，加上2πn 终边落在第几象限则是第几象限角的符号。

五、有关三角函数单调区间的确定、最小正周期、奇偶性、对称性以及比较三角函数值的大小问题。

六、函数图像的变换。

典型例题：一: 同角三角函数关系,诱导公式的应用。

例1（北京理1）已知0tan cos <θθ，那么角θ是（ ） Ａ．第一或第二象限角 Ｂ．第二或第三象限角 Ｃ．第三或第四象限角Ｄ．第一或第四象限角例2（浙江理科8）若cos 2sin αα+=tan α=（ ） A ．12B ．2C ．12-D ．2-二: 求三角函数的定义域、值域和最值、三角函数的性质（包括奇偶性、单调性、周期性、对称性）例3（广东文9）已知简谐运动ππ()2sin 32f x x ϕϕ⎛⎫⎛⎫=+<⎪⎪⎝⎭⎝⎭的图象经过点(01)，，则该简谐运动的最小正周期T 和初相ϕ分别为（ ）Ａ．6T =，π6ϕ=Ｂ．6T =，π3ϕ=Ｃ．6πT =，π6ϕ=Ｄ．6πT =，π3ϕ=例4（福建理5）已知函数()sin (0)f x x ωωπ⎛⎫=+> ⎪3⎝⎭的最小正周期为π，则该函数的图象（ ）A ．关于点0π⎛⎫ ⎪3⎝⎭，对称B ．关于直线x π=4对称 C ．关于点0π⎛⎫ ⎪4⎝⎭，对称D ．关于直线x π=3对称 例5（江苏5）函数)3sin(2)(π-=x x f ，[]0,π-∈x 的单调递增区间是（ ）Ａ．5ππ6⎡⎤--⎢⎥⎣⎦， Ｂ．5ππ66⎡⎤--⎢⎥⎣⎦， Ｃ．π03⎡⎤-⎢⎥⎣⎦，Ｄ．π06⎡⎤-⎢⎥⎣⎦，例6（辽宁理科16）已知()sin (0)363f x x f f ωωπππ⎛⎫⎛⎫⎛⎫=+>= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，且()f x 在区间63ππ⎛⎫⎪⎝⎭，有最小值，无最大值，则ω＝__________．例7（安徽卷）设0a >，对于函数()sin (0)sin x af x x xπ+=<<，下列结论正确的是（ ）A ．有最大值而无最小值B ．有最小值而无最大值C ．有最大值且有最小值D ．既无最大值又无最小值三: 关于三角函数的图象, 立足于正弦余弦的图象，重点是函数 的图象与y=sinx 的图象关系。

新教材】2019统编版高中数学A版必修第二册教学计划含教学进度表培优补差等(高一下学期数学教学计划)教学计划：高一下学期数学教学工作计划XX高级中学数学组2019统编人教版高中数学A版必修第二册是高中数学的重要组成部分。

通过本学期的教学，学生将学会适应日常生活、参加生产和进一步研究所必须的基础知识与基本技能，进一步培养运算能力、思维能力和空间观念。

学生将能够运用所学的知识解决简单的实际问题，培养数学创新意识、良好个性品质及初步的辩证唯物主义的观点。

一、学情分析：学生的数学成绩并不理想，总体水平一般，尖子生少、低分的学生较多，而且研究欠缺勤奋，研究的自觉性不高。

高一年级学生往往沿用初中的研究方法，死记硬背，这样既没读懂弄透，又使其自学能力和实际应用能力得不到很好的训练。

因此，要重视对学生的读法指导。

高一年级学生往往对课程增多、课堂研究容量加大不适应，顾此失彼，精力分散，使听课效率下降，要重视听法的指导。

研究离不开思维，善思则学得活，效率高，不善思则学得死，效果差。

高一年级学生常常固守小学算术中的思维定势，思路狭窄、呆滞，不利于后继研究，要重视对学生进行思法指导。

学生在解题时，在书写上往往存在着条理不清、逻辑混乱的问题，要重视对学生进行写法指导。

学生是否掌握良好的记忆方法与其学业成绩的好坏相关，高一学生由于正处在初级的逻辑思维阶段，识记知识时机械记忆的成份较多，理解记忆的成份较少，这就不能适应高一教学的新要求，要重视对学生进行记法指导。

学生大多存在研究粗心、作业马虎、对数学研究缺乏兴趣和信心的整体弱点，研究惯差。

在知识结构上：学生在小学已学过的概率的运算、相应的较为简单的应用题，对图形、图形的面积、体积，数据的收集与整理上有了初步的认识。

无论是代数的知识，还是图形的知识，都有待于进一步系统化、理论化。

本学期将要研究有关统计与概率的认识，对图形的进一步认识。

在数学的思维上：学生正处于形象思维向逻辑抽象思维的转变期。

高一培优补差教学计划数学培优补差工作计划范文(精选四篇)培优补差顾名思义，培优就是要在日常教学工作中对成果较好、有较大进步空间的同学重点培育，使他们的成果再上一个新台阶。

以下是为大家整理的高一培优补差教学方案数学培优补差工作方案范文(精选四篇),欢迎品鉴!高一培优补差教学方案数学培优补差工作方案依据学校方案要求，努力做好前20℅与后20℅的辅导工作。

依据对优生增加养分，对差生高看一眼，厚爱三分，以最大限度的急躁和恒心补出成效。

二.差缘由分析查找根源，发觉造成学习困难的缘由：1、同学流淌性强，每个学期十几个进，十几个出，转出的是优生，转进的是差生，由于本班同学来自祖国的十几个省，地域文化与教材的差异，并且这些同学大部分在家是留守儿童或这在老家无人管理成果差劲，家长才把他带到自己身边。

2、不良的学习习惯：学习困难同学通常没有良好的学习习惯，对学习缺乏爱好，把学习当作完成父母老师交给的差事,由于同学基本是外来务工子女，家长忙于工作，疏于管理。

再加上他们一般贪玩，上课留意力不集中，自控力量差，较任凭，上课不听讲，练习不完成，课前不预习，课后不复习，作业不能独立完成,甚至抄袭作业，拖拉作业常有发生，即使有不懂的问题也很少请教他人。

3.家庭因素。

由于同学基本是外来务工子女，父母的文化程度较低，期望水平低，他们大多缺乏辅导力量。

有的家长对子女的教育方式简洁粗暴，缺乏急躁(如佘旺同学，他学习邋遢，作业完成不准时，家长最好的方法是粗暴的打;有的缺乏教育，缺少关怀，放纵孩子，甚至认为读书无所谓，有的说：“我不识字不也过得非常好。

”这大大挫伤了孩子的上进心。

有的家长长年在外打工，孩子在家无人管束……总之，家庭的文化氛围差，使同学的学习受到了干扰，造成了学习上的困难。

三.有效培优补潜措施。

1.课上潜能生板演，中等生订正，优等生解决难题。

2.支配座位时坚持“好潜同桌”结为学习对子。

即“兵教兵”。

高一培优补差教学方案数学培优补差工作方案一班级数学下学期培优补差工作方案勐罕镇曼搭完小董学聪要提高教学质量，还要做好课后辅导工作，一班级的同学爱动、好玩，缺乏自控力量，针对各种问题，我在课后为不同层次的同学进行相应的辅导，以满意不同层次的同学的需求，避开了一刀切的弊端，同时加大了后进生的辅导力度，一班级数学下学期培优补差工作方案。

高一年段数学培优教材第七讲 数列通项公式数列是高考中的重点内容之一，每年的高考题都会考察到，小题一般较易，大题一般较难。

而作为给出数列的一种形式——通项公式，在求数列问题中尤其重要。

本文给出了求数列通项公式的常用方法。

一、 观察法例1：根据数列的前4项，写出它的一个通项公式：（1）9，99，999，9999，…（2） ,17164,1093,542,211 （3） ,52,21,32,1 （4） ,54,43,32,21--二、定义法例2： 已知数列{a n }是公差为d 的等差数列，数列{b n }是公比为q 的(q ∈R 且q ≠1)的等比数列，若函数f (x ) = (x －1)2，且a 1 = f (d －1)，a 3 = f (d +1)，b 1 = f (q +1)，b 3 = f (q －1)，(1)求数列{ a n }和{ b n }的通项公式；三、 叠加法例3：已知数列6，9，14，21，30，…求此数列的一个通项。

四、叠乘法例4：在数列｛n a ｝中，1a =1, (n+1)·1+n a =n ·n a ，求n a 的表达式。

五、公式法若已知数列的前n 项和n S 与n a 的关系，求数列{}n a 的通项n a 可用公式⎩⎨⎧≥-==-211n S S n S a n n n n 求解。

例5：已知下列两数列}{n a 的前n 项和s n 的公式，求}{n a 的通项公式。

（1）13-+=n n S n 。

（2）12-=n s n例6. 设数列{}n a 的首项为a 1=1，前n 项和S n 满足关系),4,3,2,0(3)32(31 =>=+--n t t S t tS n n求证：数列{}n a 是等比数列。

六、待定系数法例7：设数列}{n c 的各项是一个等差数列与一个等比数列对应项的和，若c 1=2，c 2=4，c 3=7，c 4=12，求通项公式c n七、 辅助数列法有些数列本身并不是等差或等比数列，但可以经过适当的变形，构造出一个新的数列为等差或等比数列，从而利用这个数列求其通项公式。

福鼎一中高一年段数学培优教材第五讲 平面向量（1）一、基础知识：1．向量的运算：加法：;AB BC AC +=设1122(,),(,)a x y b x y ==则1212(,)a b x x y y +=++减法：;AB AC CB -=设1122(,),(,)a x y b x y == 则1212(,)a b x x y y -=--实数与向量的积： 向量a λ与a 的关系； 设(,),a x y = 则(,)()a x y R λλλλ=∈||||||||a a a λλ==⋅ 22||a a a a =⋅= 向量的数量积： ||||cos (a b a b θθ⋅=⋅⋅ 是a 与b 的夹角）； 设1122(,),(,)a x yb x y ==则1212a b x x y y ⋅=+2．向量的关系： ①不等关系： ||||||||||||a b a b a b -≤±≤+ ||||||a b a b ⋅≤⋅（注意等号的条件）②设1122(,),(,),0a x y b x y b ==≠ 则a b ⇔,a b λ= 12210a b x y x y ⇔-=12120;0a b a b a b x x y y ⊥⇔⋅=⊥⇔+=3．平面向量的基本定理：如果12,e e 是同一平面内的不共线向量，那么对于这个平面内的任一向量a，有且只有一对实数,λμ，使12a e e λμ=+。

相关结论：如果12,e e 是同一平面内的不共线向量，且120e e λμ+=，则0λμ== 点O 、A 、B 、C 在同一平面内，A 、B 、C 共线的充要条件是：(1)OA xOB yOC x y =++=4．常用公式： 22222()2()()a b a a b ba b a b a b ±=±⋅++⋅-=-ABC ∆中，M 为BC 边的中点，G 为重心， 则10;();02AB BC CA AM AB AC GA GB GC ++==+++=二、综合应用：例1：求证：三角形的三条中线交于一点。

福建省福鼎一中高一年段数学培优教材（第三讲）三角恒等变换高一数学备课组一、 基础知识： 1． 三角的恒等变化：要注意公式间的内在联系和特点，审题时要善于观察差异，寻找联系，实现转化；要熟悉公式的正用和、逆用和变形应用。

化简三角函数式可以采用“切化弦”来减少函数种类，采用“配方法”和“降次公式”来逐步降低各项次数，并设法去分母、去根号、利用特殊值来向目标靠拢。

2． 常见的变形公式：1sin cos sin 22ααα= 221cos 2cos 1cos 2sin 22αααα+=-=22221sin (sincos )2sin ()1sin (sincos )2sin ()22242224αααπαααπαα+=+=+-=-=- tan tan tan()[1tan tan ]αβαβαβ±=±sin cos )a x b x x ωωωϕ+=+3． 通过对角的变换推出万能公式和半角公式以及和差与积的互化公式。

如常见的角的拆并有 2()(),(),,(),)2266424αβαβπππππααβαβααββααααα+-=++-=+-=+=+--=-+（等二、 综合应用：例1：已知角α的终边上一点(2sin3,2cos3)P -，则α的弧度数为_____________已知32,cot 2παπα<<=3cot cot 22αα-=_________________函数2sin cos ()y x x x x R =∈的最大值是____________________ 化简42212cos 2cos 22tan()sin ()44x x x x ππ-+=-+____________________________ 例2：已知1sin cos 4αβ=，求cos sin αβ的取值范围。

例3：求22sin 20cos 50sin 20cos50++的值。

例4：已知222()sin sin ()sin (),f θθθαθβ=++++其中,αβ是适合0αβπ≤<≤的常数，试问,αβ取何值时，()f θ的值恒为定值？例5：求值：cot15cot 25cot 35cot85例6：已知,(0,),sin csc cos()2παββααβ∈⋅=+；（1）求证：2sin cos tan 1sin ααβα=+； （2）求tan β的最大值，并求当tan β取得最大值时tan()αβ+的值。

福鼎一中高一年段数学培优教材高一数学备课组第一讲 函数的性质一、 基本性质： 1. 函数图像的对称性（1） 奇函数与偶函数：奇函数图像关于坐标原点对称，对于任意x D ∈，都有()()f x f x -=-成立；偶函数的图像关于y 轴对称，对于任意x D ∈，都有()()f x f x -=成立。

（2） 原函数与其反函数：原函数与其反函数的图像关于直线y x =对称。

若某一函数与其反函数表示同一函数时，那么此函数的图像就关于直线y x =对称。

（3） 若函数满足()(2)f x f a x =-，则()f x 的图像就关于直线x a =对称；若函数满足()(2)f x f a x =--，则()f x 的图像就关于点(,0)a 对称。

（4） 互对称知识：函数()()y f x a y f a x =-=-与的图像关于直线x a =对称。

2．函数的单调性函数的单调性是针对其定义域的某个子区间而言的。

判断一个函数的单调性一般采用定义法、导数法或借助其他函数结合单调性的性质（如复合函数的单调性）特别提示：函数(0)ay x a x=+>的图像和单调区间。

3．函数的周期性对于函数()y f x =，若存在一个非零常数T ，使得当x 为定义域中的每一个值时，都有()()f x T f x +=成立，则称()y f x =是周期函数，T 称为该函数的一个周期。

若在所有的周期中存在一个最小的正数，就称其为最小正周期。

（1） 若T 是()y f x =的周期，那么()nT n Z ∈也是它的周期。

（2） 若()y f x =是周期为T 的函数，则()(0)y f ax b a =+≠是周期为Ta的周期函数。

（3） 若函数()y f x =的图像关于直线x a x b ==和对称，则()y f x =是周期为2()a b -的函数。

（4） 若函数()y f x =满足()()(0)f x a f x a +=-≠，则()y f x =是周期为2a 的函数。

高一年段数学培优教材(5)宁化一中高一年段数学培优教材高一数学备课小组第五讲平面向量（1）一、基本知识：1．向量的运算：加法：ab?bc?ac;设a?(x1,y1),b?(x2,y2)则a?b?(x1?x2,y1?y2)减法：ab？交流电？cb；设定一个目标？（x1，y1），b？（X2，Y2）然后a？B（x1？x2，y1？y2）实数与向量的乘积：向量？a和a之间的关系；设定一个目标？（x，y），那么？A.（？x，？y）（？r）2???222|a|?x?y,|?a|?|?|?|a|a?a?a?|a|向量的量积：a？b？|a |？|b |？余弦？（？是a和b之间的角度）；设定一个目标？（x1，y1），b？（x2，y2）则a?b?x1x2?y1y22.向量关系：① 不平等关系A.b |？|a |？|b | | a？b |？|a |？|B |（注意等号的条件）② 设定一个目标？（x1，y1），b？（x2，y2），b？0然后是a？BA.BA.Bx1y2？x2y1？0a?b?a?b?0;???a?b?01x2x?1y2y??3．平面向量的基本定理：如果e1,e2是同一平面内的不共线向量，那么对于这个平面内的任一向量a，有且只有一对实数?,?，使a??e1??e2。

相关结论：如果E1和E2是同一平面上的非共线向量，以及？e1？？e2？0，那么0点o、a、b、c在同一平面内，a、b、c共线的充要条件是：oa?xob?yoc(x?y?1)2.2.24.常用公式：（a？B）？A.2a？BBG是重心，那么AB呢？卑诗省？ca？0.2、综合应用：例1：求证：三角形的三条中线交于一点。

2.2（a？b）？（a？b）？A.B在ABC中，M是BC边的中点，1???am?(ab?ac);ga?gb?gc?02.oa？产科医生？oc？Om示例2：设置？ABC的外中心是O，取点m，制造并验证m是？ABC的垂直中心和这个三角形的外中心垂心、重心在一条直线上。