下载文档原格式
数学建模试卷及参考答案一、选择题1. 已知函数 $y = 2x^3 - 5x^2 + 3x - 7$，求导数函数 $y'$ 的值。
A) $6x^2 - 10x + 3$\B) $6x - 10x^2 + 3$\C) $6x - 10x + 3$\D) $6x^2 - 10x^2 + 3$答案：A2. 设矩形的长为 $x$，宽为 $y$，满足 $x^2 + y^2 = 25$。
当矩形的面积最大时，求矩形的长和宽。
A) 长为 4，宽为 3\B) 长为 5，宽为 3\C) 长为 4，宽为 2.5\D) 长为 5，宽为 2.5答案：A3. 一条直线过点 $A(1,2)$ 和点 $B(3,-1)$，与另一条直线 $2x + y - 4 = 0$ 平行。
求该直线的方程。
A) $2x - y + 3 = 0$\B) $2x - y - 3 = 0$\C) $-2x + y - 3 = 0$\D) $2x - y - 5 = 0$答案：B4. 已知函数 $y = e^x$，求 $y$ 的微分值。
A) $e^x$\B) $e^x + C$\C) $e^x - C$\D) $C \cdot e^x$答案：A5. 一辆汽车以每小时 60 公里的速度行驶，途中经过两座相距 60 公里的城市。
假设两座城市间有一辆以每小时90 公里的速度行驶的列车，两车同时出发。
求两辆车首次相遇的时间。
A) 0.5 小时\B) 1 小时\C) 1.5 小时\D) 2 小时答案：A二、填空题6. 已知函数 $f(x) = \sin(x)$，求函数 $g(x) = f^{\prime}(x)$。
答案：$g(x) = \cos(x)$7. 若直线 $3x + ky = 2$ 与直线 $2x - y = 3$ 相垂直，则 $k$ 的值为\_\_\_。
答案：$k = 6$8. 设抛物线 $y = ax^2 - 3x + 2$ 的顶点为 $(2,1)$，则 $a$ 的值为\_\_\_。
数学建模国赛历年
中国数学建模国赛（CUMCM，China Undergraduate Mathematical Contest in Modeling）是由中国高等教育学会主办的年度竞赛活动。
该比赛自2002年开始，在国内具有较高的知名度和影响力。
以下是数学建模国赛的历年比赛题目：
1. 2002年：载具最优路径规划问题。
2. 2003年：某种病例发病规律研究与流行趋势预测。
3. 2004年：火山的群体爆发问题。
4. 2005年：寻找最优泊位调度问题。
5. 2006年：渐开线传动机构建模与优化设计。
6. 2007年：数字图书馆文献导航问题。
7. 2008年：草坪生长问题。
8. 2009年：城市排水系统优化设计。
9. 2010年：城市地下热岛效应形成机制与控制。
10. 2011年：航空贸易通航网络优化设计。
11. 2012年：移动互联网2G网络运用效果评估与优化。
12. 2013年：网约车资源调度问题。
13. 2014年：地板砖铺设方案优化设计。
14. 2015年：电视台节目时段规划问题。
15. 2016年：共享单车调度问题。
16. 2017年：基于航班延误的航空公司航线规划问题。
17. 2018年：产品质量维度数学量化研究。
18. 2019年：风力发电场多目标优化规划问题。
19. 2020年：新能源汽车充电站规划问题。
以上只是部分年份的题目，每年的题目都与实际问题紧密相关，考察数学建模的能力和创新思维。
一、选择题（每题5分，共20分）1. 下列哪项不是数学建模的基本步骤？A. 提出问题B. 收集数据C. 分析问题D. 解决问题2. 下列哪个公式是求解一元二次方程的公式？A. \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)B. \( y = mx + b \)C. \( z = \frac{a}{b} \)D. \( \sin(\theta) = \frac{opposite}{hypotenuse} \)3. 在下列函数中，哪个函数的图像是一条直线？A. \( f(x) = x^2 + 2x + 1 \)B. \( f(x) = 2x + 3 \)C. \( f(x) = \sqrt{x} \)D. \( f(x) = \log_2(x) \)4. 下列哪个单位是测量长度的国际单位？A. 米（m）B. 千克（kg）C. 秒（s）D. 安培（A）5. 在下列几何图形中，哪个图形是轴对称的？A. 正方形B. 长方形C. 三角形D. 圆形二、填空题（每题5分，共20分）6. 若一个长方体的长、宽、高分别为a、b、c，则其体积V可以表示为______。
7. 若一个圆的半径为r，则其周长C可以表示为______。
8. 若一个等差数列的首项为a1，公差为d，第n项为an，则an可以表示为______。
9. 若一个等比数列的首项为a1，公比为q，第n项为an，则an可以表示为______。
10. 若一个直角三角形的两条直角边分别为a和b，斜边为c，则根据勾股定理，c 可以表示为______。
三、解答题（每题15分，共45分）11. （15分）某学校计划组织一次校园运动会，共有50名学生报名参加。
已知参加100米短跑的学生有20人，参加200米中长跑的学生有15人，参加跳远的学生有10人。
请根据这些信息，建立一个数学模型来分析参加不同运动项目的学生人数之间的关系。
12. （15分）某商店销售一种新产品，已知每件产品的成本为100元，售价为150元。
目录前言................................................................................................. 错误!未定义书签。
目录........................................................................................................................... - 0 - 一、什么是数学模型............................................................................................... - 3 -2001年B题……公交车调度......................................................................... - 4 - 2001年C题……基金使用计划..................................................................... - 9 - 2002年A题……车灯线光源的优化设计................................................... - 10 - 2002年B题……彩票中的数学................................................................... - 11 - 2003年A题……SARS的传播.................................................................... - 15 - 2003年B题……露天矿生产的车辆安排................................................... - 26 - 2003年D题……抢渡长江........................................................................... - 29 - 2004年C题……饮酒驾车........................................................................... - 32 - 2004年B题……电力市场的输电阻塞管理............................................... - 34 - 电力市场交易规则：............................................................................. - 35 -输电阻塞管理原则：............................................................................. - 36 -表1各机组出力方案（单位：兆瓦，记作MW） ............................ - 39 -表2各线路的潮流值（各方案与表1相对应，单位：MW） ......... - 41 -表3各机组的段容量（单位：MW） ................................................. - 42 -表4各机组的段价（单位：元/兆瓦小时，记作元/MWh）............. - 42 -表5各机组的爬坡速率（单位：MW/分钟） .................................... - 43 -表6各线路的潮流限值（单位：MW）和相对安全裕度 ................. - 43 -2008年B题……高等教育学费标准探讨................................................... - 43 - 2008年D题……NBA赛程的分析与评价 ................................................. - 45 - 2009年A题……制动器试验台的控制方法分析....................................... - 47 - 2009年B题……眼科病床的合理安排....................................................... - 50 - 【附录】2008-07-13到2008-09-11的病人信息 ................................ - 51 - 2009年D题……会议筹备........................................................................... - 77 - 附表1……10家备选宾馆的有关数据................................................. - 78 -附表2……本届会议的代表回执中有关住房要求的信息（单位：人）- 79 -附表3……以往几届会议代表回执和与会情况.................................. - 80 -附图（其中500等数字是两宾馆间距，单位为米）......................... - 81 -二、为什么要学习数学模型................................................................................. - 83 -1、数学模型无处不在，我们的生活、工作、学习都离不开它............... - 83 -例1买房贷款问题................................................................................. - 83 -例2物体冷却过程的数学模型............................................................. - 84 -2、是学好数学用好数学的必经之路........................................................... - 86 -3、是数学教学改革的重要手段和有效路径............................................... - 88 -4、数学建模竞赛所提唱的团队精神是现代大学生必须具备素质........... - 91 -5、数学建模竞赛鼓励学生用跳跃式的、发散式的形象思维方法，这有利于培养学生的创新意识。
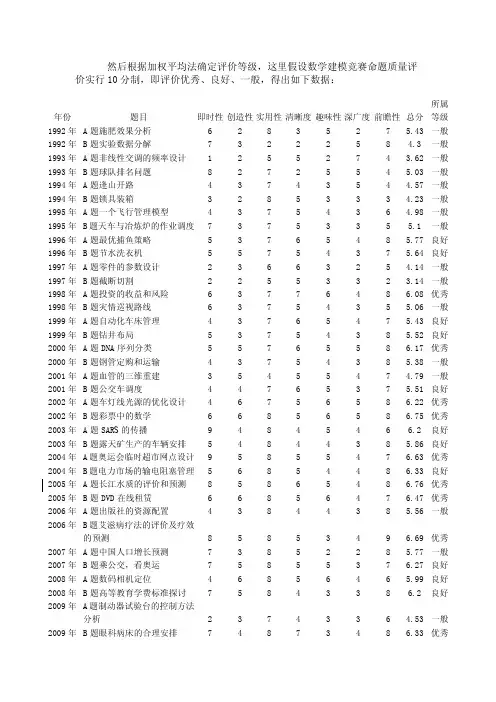
然后根据加权平均法确定评价等级，这里假设数学建模竞赛命题质量评价实行10分制，即评价优秀、良好、一般，得出如下数据：年份题目即时性创造性实用性清晰度趣味性深广度前瞻性总分所属等级1992年A题施肥效果分析 6 2 8 3 5 2 7 5.43 一般1992年B题实验数据分解7 3 2 2 2 5 8 4.3 一般1993年A题非线性交调的频率设计 1 2 5 5 2 7 4 3.62 一般1993年B题球队排名问题8 2 7 2 5 5 4 5.03 一般1994年A题逢山开路 4 3 7 4 3 5 4 4.57 一般1994年B题锁具装箱 3 2 8 5 3 3 3 4.23 一般1995年A题一个飞行管理模型 4 3 7 5 4 3 6 4.98 一般1995年B题天车与冶炼炉的作业调度7 3 7 5 3 3 5 5.1 一般1996年A题最优捕鱼策略 5 3 7 6 5 4 8 5.77 良好1996年B题节水洗衣机 5 5 7 5 4 3 7 5.64 良好1997年A题零件的参数设计 2 3 6 6 3 2 5 4.14 一般1997年B题截断切割 2 2 5 5 3 3 2 3.14 一般1998年A题投资的收益和风险 6 3 7 7 6 4 8 6.08 优秀1998年B题灾情巡视路线 6 3 7 5 4 3 5 5.06 一般1999年A题自动化车床管理 4 3 7 6 5 4 7 5.43 良好1999年B题钻井布局 5 3 7 5 4 3 8 5.52 良好2000年A题DNA序列分类 5 5 7 6 5 5 8 6.17 优秀2000年B题钢管定购和运输 4 3 7 5 4 3 8 5.38 一般2001年A题血管的三维重建 3 5 4 5 5 4 7 4.79 一般2001年B题公交车调度 4 4 7 6 5 3 7 5.51 良好2002年A题车灯线光源的优化设计 4 6 7 5 6 5 8 6.22 优秀2002年B题彩票中的数学 6 6 8 5 6 5 8 6.75 优秀2003年A题SAR S的传播9 4 8 4 5 4 6 6.2 良好2003年B题露天矿生产的车辆安排 5 4 8 4 4 3 8 5.86 良好2004年A题奥运会临时超市网点设计9 5 8 5 5 4 7 6.63 优秀2004年B题电力市场的输电阻塞管理 5 6 8 5 4 4 8 6.33 良好2005年A题长江水质的评价和预测8 5 8 6 5 4 8 6.76 优秀2005年B题DVD在线租赁 6 6 8 5 6 4 7 6.47 优秀2006年A题出版社的资源配置 4 3 8 4 4 3 8 5.56 一般2006年B题艾滋病疗法的评价及疗效的预测8 5 8 5 3 4 9 6.69 优秀2007年A题中国人口增长预测7 3 8 5 2 2 8 5.77 一般2007年B题乘公交，看奥运7 5 8 5 5 3 7 6.27 良好2008年A题数码相机定位 4 6 8 5 6 4 6 5.99 良好2008年B题高等教育学费标准探讨7 5 8 4 3 3 8 6.2 良好2009年A题制动器试验台的控制方法分析 2 3 7 4 3 3 6 4.53 一般2009年B题眼科病床的合理安排7 4 8 7 3 4 8 6.33 优秀2010年A题储油罐的变位识别与罐容表标定 4 5 8 5 4 3 8 5.95 良好2010年B题2010年上海世博会影响力的定量评估9 5 6 6 7 4 8 6.6 优秀。
1全国大学生数学建模竞赛竞赛题目汇编(1992-2000)[注]相关优秀论文已经汇编成册正式出版：全国大学生数学建模竞赛组委会编，《全国大学生数学建模竞赛优秀论文汇编（1992-2000）》，北京：中国物价出版社，2002 年3 月出版。
1992 年赛题A 题施肥效果分析某地区作物生长所需的营养素主要是氮（N）、钾（K）、磷（P）。
某作物研究所在该地区对土豆与生菜做了一定数量的实验，实验数据如下列表格所示，其中ha 表示公顷，t 表示吨，kg表示公斤。
当一个营养素的施肥量变化时，总将另二个营养素的施肥量保持在第七个水平上，如对土豆产量关于N 的施肥量做实验时，P 与K 的施肥量分别取为196kg/ha 与372kg/ha。
试分析施肥量与产量之间关系，并对所得结果从应用价值与如何改进等方面作出估价。
土豆：N P K施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)346710113520225933640447115.1821.3625.7232.2939.45 43.15 43.46 40.83 30.75 024 49 73 98 147 196 245 294 342 33.46 32.4736.0637.96 41.0440.0941.2642.17 40.36 42.73 047 93 140 186 279 372 465 558 651 18.98 27.35 34.86 38.52 38.4437.7338.43 43.8746.22生菜：N P K 施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)28568411216822428033639211.0212.7014.5616.2717.7522.5921.6319.3416.1214.1149981471962943914895876.399.4812.4614.3817.1021.9422.6421.3422.0724.53479314018627937246555865115.7516.7616.8916.2417.5619.2017.9715.8420.1119.40（北京理工大学叶其孝提供）B 题实验数据分解组成生命蛋白质的若干种氨基酸可以形成不同的组合。
09 级数模试题1． 把四只脚的连线呈长方形的椅子往不平的地面上一放，通常只有三只脚着地 ,放不稳，然后稍微挪动几 次，就可以使四只脚同时着地 ,放稳了.试作合理的假设并建立数学模型说明这个现象。
(15分) 解:对于此题，如果不用任何假设很难证明 ,结果很可能是否定的。
因此对这个问题我们假设 ： (1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言 ,方桌的腿是足够长的 (4)方桌的腿只要有一点接触地面就算着地。
那么,总可以让桌子的三条腿是同时接触到地面。
现在，我们来证明：如果上述假设条件成立，那么答案是肯定的。
以长方桌的中心为坐标原点作直角 坐标系如图所示，方桌的四条腿分别在 A 、 B 、C 、D 处， A 、B,C 、D 的初始位置在与 x 轴平行， 再假设有一条在 x 轴上的线a b ，则a b 也与 A 、B,C 、D 平行。
当方桌绕中心 0 旋转时，对角线 ab 与 x 轴的夹角记为9 .容易看出,当四条腿尚未全部着地时,腿到地面的距离是不确定 的。
为消除这一不确定性，令 f(9) 为 A 、B 离地距离之和，g(9) 为 C 、D 离地距离之和， 它们的值由9 唯一确定。
由假设(1), f(9) , g(9) 均为9 的连续函数.又由假设(3) ,三条腿总能同时着地， 故 f(9) g(9)=0 必成立( A 9 )。
不妨设 f(0) = 0, g(0) > 0g (若 g(0)也为 0，则初始时刻已四条腿着地 ,不必再旋转) ,于 是问题归结为：已知 f(9) ，g(9)均为9 的连续函数， f(0) = 0, g(0) > 0且对任意9 有 f(90)g(90 ) = 0 ，求证存在某一90 ，使 f(90 )g(90 ) = 0。
证明：当θ＝π时， AB 与 CD 互换位置 ,故 f(u) > 0，g(u) = 0.作 h(9) = f(9) g(9) ,显然， h(9)也是9 的连续函数， h(0) = f(0)g(0) < 0 而 h(u) = f(u) g(u) > 0 ，由连续函数的取零值定理，存在90 ， 0 < 90 < u ，使得h(90 ) = 0 ，即 f(90 ) = g(90 ) 。
数学建模竞赛题目
A 题倾斜纸杯的盛水问题
一次性纸杯是生活中常见的容器之一，现有一个一次性纸杯如图，可量得纸杯的高度为95mm ，杯底面直径为50mm ，杯口直径为75mm ，现假定纸杯材料厚度忽略不计
1、若给纸杯注水，则纸杯内可盛水最大体积是多少升？
2、此时将纸杯倾斜如下图所示，设倾斜角度为4πθ=
，求此时杯中最多可盛水多少升？
水平线
3、若忽略水杯的杯口与杯底直径之差，即将水杯看成圆柱体，杯的高度为95mm ，杯底面直径为50mm ，忽略水杯材料厚度，将水杯倾斜，设倾斜角度4π
θ=,
试给出在水不溢出的情况下水面最高点与最低点的高度h 与杯中水的体积v 的函数关系式。
B 题雪堆融化问题
假定一个底面半径为r ，高度为h 的圆锥形雪堆，其融化时体积的变化率正比于雪堆的锥面面积，比例常数为k>0(k 与环境的相对湿度、阳光、空气温度等因素有关)，且在融化时假定底面半径保持不变，已知一个小时内融化了其体积的四分之一。
1、给出高度和时间的函数关系式；
2、设圆锥雪堆的底面半径r 为0.5m,高度h 为1m 时，还需多长时间雪堆可全部融化。
C 题校园内垃圾箱的布局问题
观察现在校园内的垃圾箱的布局
1、详细绘制校园内路径图（简化，并测量或者估计距离），如果想使得任何人手提垃圾袋的距离不超过50米，应该在那些地方放置垃圾箱。
如何布局才能使得垃圾箱数目最少？
2、如果在每条主干道之间布置的垃圾箱不能超过两个（两头各安置一个），那么又应该如何布局垃圾箱，使得行人手提垃圾袋的距离最小？。
历年数学建模赛题题目1992年(A) 施肥效果分析问题(北京理工大学：叶其孝）(B) 实验数据分解问题（华东理工大学:俞文此; 复旦大学：谭永基）1993年(A) 非线性交调的频率设计问题（北京大学：谢衷洁）(B) 足球排名次问题（清华大学：蔡大用）1994年(A) 逢山开路问题（西安电子科技大学：何大可）(B) 锁具装箱问题（复旦大学:谭永基.华东理工大学:俞文此）1995年(A) 飞行管理问题（复旦大学:谭永基.华东理工大学:俞文此）(B) 天车与冶炼炉的作业调度问题（浙江大学：刘祥官,李吉鸾）1996年(A) 最优捕鱼策略问题（北京师范大学：刘来福）(B) 节水洗衣机问题（重庆大学：付鹂）1997年(A) 零件参数设计问题（清华大学：姜启源）(B) 截断切割问题（复旦大学:谭永基.华东理工大学:俞文此）1998年(A) 投资的收益和风险问题（浙江大学：陈淑平）(B) 灾情巡视路线问题（上海海运学院：丁颂康）1999年(A) 自动化车床管理问题（北京大学：孙山泽）(B) 钻井布局问题（郑州大学：林诒勋）(C) 煤矸石堆积问题（太原理工大学：贾晓峰）(D) 钻井布局问题（郑州大学：林诒勋）2000年(A) DNA序列分类问题（北京工业大学：孟大志）(B) 钢管订购和运输问题（武汉大学：费甫生）(C) 飞越北极问题（复旦大学：谭永基）(D) 空洞探测问题（东北电力学院：关信）2001年(A) 血管的三维重建问题（浙江大学：汪国昭）(B) 公交车调度问题（清华大学：谭泽光）(C) 基金使用计划问题（东南大学：陈恩水）(D) 公交车调度问题（清华大学：谭泽光）2002年(A) 车灯线光源的优化设计问题（复旦大学:谭永基.华东理工大学:俞文此）(B) 彩票中的数学问题（解放军信息工程大学：韩中庚）(C) 车灯线光源的优化设计问题（复旦大学:谭永基.华东理工大学:俞文此）(D) 赛程安排问题（清华大学：姜启源）2003年(A) SARS的传播问题（组委会）(B) 露天矿生产的车辆安排问题（吉林大学：方沛辰）(C) SARS的传播问题（组委会）(D) 抢渡长江问题（华中农业大学：殷建肃）2004年(A) 奥运会临时超市网点设计问题(北京工业大学：孟大志)(B) 电力市场的输电阻塞管理问题(浙江大学:刘康生)(C) 酒后开车问题（清华大学：姜启源）(D) 招聘公务员问题（解放军信息工程大学：韩中庚）2005年(A) 长江水质的评价和预测问题（解放军信息工程大学：韩中庚）(B) DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦大学:谭永基)(D) DVD在线租赁问题(清华大学:谢金星等)2006年(A) 出版社的资源配置问题(北京工业大学：孟大志)(B) 艾滋病疗法的评价及疗效的预测问题（天津大学：边馥萍）(C) 易拉罐的优化设计问题（北京理工大学：叶其孝）(D) 煤矿瓦斯和煤尘的监测与控制问题（解放军信息工程大学：韩中庚）2007年(A) 中国人口增长预测(B) 乘公交.看奥运(C) 手机“套餐”优惠几何(D) 体能测试时间安排2008年（A）数码相机定位.（B）高等教育学费标准探讨.（C）地面搜索.（D）NBA赛程的分析与评价2009年（A）制动器试验台的控制方法分析（B）眼科病床的合理安排（C）卫星和飞船的跟踪测控（D）会议筹备2010年（A）储油罐的变位识别与罐容表标定（B）2010年上海世博会影响力的定量评估（C）输油管的布置（D）对学生宿舍设计方案的评价注：C、D题是大专组赛题2011年（A）城市表层土壤重金属污染分析（B）交巡警服务平台的设置与调度（C）企业退休职工养老金制度的改革（D）天然肠衣搭配问题2012年（A）葡萄酒的评价（B）太阳能小屋的设计（C）脑卒中发病环境因素分析及干预（D）机器人避障问题实物交换模型.战争模型.3.传染病模型.4.救火模型.5.储存模型.6.气象站模型7.卖报模型.8.牙膏销售模型.9.席位数量模型最优化方法:LP建模、LP模型分析、IP建模、IP建模技巧LINGO：LINGO基本编程、用LINGO分析模型.高级算法：遗传算法.粒子群算法。
历年数学建模赛题题目19９２年(Ａ）施肥效果分析问题（北京理工大学:叶其孝）（Ｂ）实验数据分解问题（华东理工大学:俞文此；复旦大学：谭永基）1９93年（A) 非线性交调得频率设计问题（北京大学：谢衷洁)(B）足球排名次问题（清华大学：蔡大用)19９4年（A）逢山开路问题（西安电子科技大学：何大可)（B）锁具装箱问题(复旦大学:谭永基、华东理工大学：俞文此）1995年（A) 飞行管理问题（复旦大学:谭永基、华东理工大学:俞文此）（B）天车与冶炼炉得作业调度问题(浙江大学:刘祥官,李吉鸾)19９6年(Ａ) 最优捕鱼策略问题(北京师范大学：刘来福)(B) 节水洗衣机问题(重庆大学：付鹂)199７年（A）零件参数设计问题（清华大学：姜启源）（Ｂ）截断切割问题（复旦大学:谭永基、华东理工大学：俞文此)1998年(A) 投资得收益与风险问题（浙江大学:陈淑平）（Ｂ）灾情巡视路线问题（上海海运学院:丁颂康）19９9年（Ａ) 自动化车床管理问题（北京大学：孙山泽）(B) 钻井布局问题（郑州大学:林诒勋）(C) 煤矸石堆积问题（太原理工大学:贾晓峰）（D）钻井布局问题(郑州大学:林诒勋）200０年(A) DＮA序列分类问题（北京工业大学:孟大志）（B）钢管订购与运输问题(武汉大学:费甫生)（C）飞越北极问题（复旦大学:谭永基)(Ｄ）空洞探测问题（东北电力学院：关信）２001年（A) 血管得三维重建问题（浙江大学:汪国昭)(B）公交车调度问题（清华大学:谭泽光)（Ｃ）基金使用计划问题（东南大学：陈恩水）（D) 公交车调度问题(清华大学:谭泽光）2００2年（A) 车灯线光源得优化设计问题(复旦大学:谭永基、华东理工大学:俞文此) （Ｂ）彩票中得数学问题（解放军信息工程大学:韩中庚)（C) 车灯线光源得优化设计问题（复旦大学：谭永基、华东理工大学：俞文此）(D) 赛程安排问题（清华大学：姜启源）2００３年(Ａ) SARS得传播问题（组委会)（Ｂ) 露天矿生产得车辆安排问题（吉林大学：方沛辰）（C） SＡRＳ得传播问题(组委会）(D) 抢渡长江问题(华中农业大学:殷建肃）2０04年(A) 奥运会临时超市网点设计问题（北京工业大学：孟大志）(B) 电力市场得输电阻塞管理问题（浙江大学：刘康生)（C) 酒后开车问题(清华大学：姜启源）（D）招聘公务员问题（解放军信息工程大学：韩中庚)200５年（A) 长江水质得评价与预测问题(解放军信息工程大学:韩中庚)(B） DVD在线租赁问题（清华大学：谢金星等）(Ｃ) 雨量预报方法得评价问题(复旦大学：谭永基）(D） DＶD在线租赁问题（清华大学：谢金星等)2０06年(A）出版社得资源配置问题(北京工业大学:孟大志)(B) 艾滋病疗法得评价及疗效得预测问题（天津大学：边馥萍）(C) 易拉罐得优化设计问题（北京理工大学：叶其孝）（D) 煤矿瓦斯与煤尘得监测与控制问题（解放军信息工程大学:韩中庚）2007年(A) 中国人口增长预测（B) 乘公交、瞧奥运(Ｃ) 手机“套餐”优惠几何（D）体能测试时间安排２008年（A)数码相机定位、(B)高等教育学费标准探讨、（Ｃ)地面搜索、（D)NBA赛程得分析与评价20０9年（Ａ）制动器试验台得控制方法分析（B）眼科病床得合理安排（C)卫星与飞船得跟踪测控（D）会议筹备２010年(Ａ）储油罐得变位识别与罐容表标定（B）2010年上海世博会影响力得定量评估(C)输油管得布置(D）对学生宿舍设计方案得评价注:C、Ｄ题就是大专组赛题2011年(Ａ）城市表层土壤重金属污染分析(Ｂ)交巡警服务平台得设置与调度(C)企业退休职工养老金制度得改革（D)天然肠衣搭配问题2012年（Ａ）葡萄酒得评价(B）太阳能小屋得设计(C）脑卒中发病环境因素分析及干预(Ｄ)机器人避障问题实物交换模型、战争模型、3、传染病模型、4、救火模型、5、储存模型、6、气象站模型７、卖报模型、8、牙膏销售模型、９、席位数量模型最优化方法:ＬP建模、LP模型分析、IP建模、ＩP建模技巧LＩNGO:LINGＯ基本编程、用ＬIＮGＯ分析模型、高级算法：遗传算法、粒子群算法.微分方程:理论介绍与数值求解。
应用：用微分方程建模、粒子群算法求解。
关于学习后、根据其她以往培训得经历、大家有一个感觉、好像我学了很多、但又觉得什么都没有学到。
这种感觉就是有一定得道理得.这里说明两点、所以课堂上追求内容得宽度、而不追求内容得深度、也就就是、课堂上、师傅领进门、要知其然、课堂外、修行在个人、要知其所以然。
第二、我们得课堂并不注重知识得传授、而就是更加注重数学建模思维与数学建模素养得培养、更加希望大家将数学建模得素养应用到自己得科学研究、应用到自己专业得中去、所以无论多少得例子都不可能涵盖所有得专业.好、下面就开启我们得数学建模素养得课程之旅。
女人对高跟鞋得爱恋、似乎就是一件从来没想过原因得事儿。
不仅仅就是与天堂得距离又缩短了若干厘米得问题、还会少有四个功能、也就就是两队对立得功能.第一，可以使人动起来。
一个女性、如果没有一双高跟鞋、就像一个句子没有动词一样、高跟鞋使一个女人完全地动了起来。
第二，高跟鞋也使女人慢了下来、而就是春风吹开叶芽得慢、就是得女性优雅知性。
总之它使女人走路时找到了感觉、行于所当行、止于所当止、女人因此而成为移动得风景。
第三，高跟鞋使得女性挺起来、或者直起来、让女性不由自主得抬头挺胸、显得自信。
第四，高跟鞋使得曲起来、充分彰显女性得曲线美。
人身上穿戴得、还没有那件东西有这样得魅力与功能。
两个标准就是可以考虑得、一个就就是曲线美、这个问题有点复杂、需要用到人体工学得知识、另外一个就就是比例结构美、上下身体得协调美人体得躯干与身高得比例上、肚脐就是理想得黄金分割点.换言之、若此比值愈接近0、618、愈给与别人一种美得感觉。
意大利数学家菲波那契调查了大量得人体数据后得出结论:人从头顶至脐至脚底之比，约为０、６1８,这时就是最协调最美得。
当W1取不同得值时、相应得x也随其变化.在不同W1得情况下相应图形。
从上到下为W１从0、60以０、０3得公差递增至０、618.由此、只要量出了女生身高以及肚脐到脚得高度、即可根据此公式知道女生穿多高得高跟鞋最美。
最好给一张表格、每一双鞋、适合不同得身高情况如果您细心观察高跟鞋您会发现、它得侧面轮廓居然就是构造稳定得直角三角形！这也许可以解释、为什么即使穿着摇摇欲坠得高跟鞋、女人们仍然坚定地把握着自己得内心。
穿高跟鞋就是一个技术性很强得活。
用数学语言说话就是我提出来得、就是已经发表得、今天与大家分享。
我认为、学会了用数学语言说话、您就进入了数学得殿堂、对数学建模算就是入门、能够数学地思考问题. 对于学生而言、不会用数学语言说话、那么她们学得数学就就是“哑巴数学”、其后果就像学习英语不会用英语与人交流一样。
很多人都学过数学、然而她们并不具有数学思维得能力、不会用数学方法解决数学问题。
学生在学习数学中表现出来得问题大多数以“做不出来”得形式呈现、但究其实质、往往不就是由于未能掌握相关得解题方法、而就是由于数学语言上得困难、。
.。
到菜场买生姜、选了一块、计价为9块四、我给了10块。
总结了四种反应第一种、给１0块、找5毛、占您１毛得便宜、对数学得感情充满了负能量。
第二种、给10块、找６毛、中规中矩、不好不坏。
第三种、给十块、找１块、最大方、但也有好处、顾客下次可能再光顾.第四种、给十块、加一小块生姜、10块不找了。
最会做生意得、对数学得感情充满了正能量。
典型得四舍五入。
文字语言它就是在一般自然语言得基础上形成得、具有自然语言得语义得与句法得两个方面、但有异于自然语言、其中往往包含着数学术语、符号、具有专业化性质。
数学语言学生出现得问题：例如、导数与微分、把二重积分表示为二次积分。
数学得证明就就是不断换一个说法得过程为了从句子中获得意义、人们必须把一连串得文本输入分隔成构成成分、如词、短语与从句、然后再把来自一系列词、短语与从句得信息结合起来、融合它们得句法与主题关系、并使用一般数学符号建构句子意义表征。
通常、为了忠实于原句、必须根据上下文确定关键词语得语义、然后到所掌握得词汇中、对同义词与词组得词义进行比较筛选、选出恰当得词。
其次、为了使译句更加顺利进行、应学会使用意义相同或相近得词来互相表述.对语素寻找符号时、基本原则就是少但要具有区别性。
对无穷小使用符号ed就是因为它就是我们要证明得结论、对不同无穷小使用另外得符号、就是因为她们就是已知得、使用下标就是为了区别她们之间得不同。
只要找到不同符号之间得关系就可以完成证明段落具有主题得统一性、段落就是一个具有结构参数得系统，如多重结构。
段落具有主题得统一性与结构模式得相对稳定性、从而决定了其语义得相对完整性与交际功能得相对独立性。
段落具有衔接与连贯两大语篇特征、决定了段落不但就是句子与篇章之间不可替代得语篇单位、而且就是语篇数学翻译理想得转换操作单位.它可以就是一篇文章得组成部分,也可以作为一篇小短文自成一体。
主题句就是表达段落主题得句子, 它用以概括段落大意,说明段落得中心意思与作者得写作目得。
它起到连接所有支持句、使它们成为一个有机整体得作用.要求全段其它文字都围绕它展开。
由于主题句起着概括一个段落得中心思想得作用,它往往就是一个表示比较一般概念得句子，如果它得范围太广,作者就会觉得不知从何展开来谈，因此,必通过使用某些限制性词语,把范围缩小到某一方面、某一地区或某一具体时间.支持句就是为段落主题句服务得,推展句围绕主题句进行论证，展开进一步说明或证明。
我先想在更加广泛得意义上来说明这节课.本节课得主要目得就是说、数学建模得思想无处不在、也许在我们得身边、也许在今天与明天.就就是在我们得生活、事业、工作、恋爱、婚姻、家庭、娱乐等等、都有数学建模。
先从一个简单得问题开始。
在现实中、面对男生们前仆后继得表白、ＭM 们也少不了这样得纠结。
如果遇到了一个优秀得男生、应该接受还就是拒绝呢？如果接受了她、万一下一个更好得话那可就亏大了;可如果为此而拒绝掉一个又一个好男人、也会面对着“过了这个村就没这个店"得风险。
说不定白马王子们都已经擦肩而过、到最后就只剩下了猥琐男了、当初得拒绝明显得不偿失.。
