分离变量法的解题步骤总结

导数分离变量法知识点一、知识概述“导数分离变量法知识点”①基本定义：导数分离变量法就是在解决含有导数的方程或不等式时，把含有变量的式子放在等号或不等号的一边，把不含变量的式子放在另一边，这样可以方便我们进一步分析和求解。

就像是把一群羊和一群牛分开，好分别照顾它们一样。

②重要程度：在数学学科里，尤其是涉及导数的问题中，它是一种非常有用的方法。

很多看似复杂的导数等式或不等式，一用这个方法就条理清晰了，是解决很多导数相关问题的一把“钥匙”。

③前置知识：得先掌握导数的基本概念和求导公式，像幂函数的求导公式(x^n)' = nx^(n - 1)等。

还得了解一些基本的等式和不等式运算规则，不然即便分离了变量，后面也做不了。

④应用价值：在研究函数的单调性、极值、最值等方面有着广泛的应用。

比如在物理学里研究速度随时间的变化规律时可能就会用到，或者经济学里分析成本随产量的变化时也可能涉及。

二、知识体系①知识图谱：在导数这一块知识中，它是属于利用导数解决问题的一个很重要的方法，就像大树上的一个重要树枝。

②关联知识：和求导公式、函数的单调性、函数的极值等知识都有联系。

如果求不出函数的导数，就没办法有效使用分离变量法；而求出的导数也是为了进一步了解函数特性，和函数单调性、极值等相关。

③重难点分析：掌握难度不算特别大，关键是要能准确地把变量分离出来，有时候那些式子看起来乱糟糟的就很棘手。

重难点主要就在准确识别哪些部分是含有变量可以分到一边的，哪些是常数能分到另一边的。

④考点分析：在考试里是比较常考的内容。

可能会单独出一道用分离变量法解导数方程或者不等式的题目，也可能在综合题里涉及。

考查方式就是让你求解变量的取值范围、证明某个不等式什么的。

三、详细讲解【方法技能类】①基本步骤：先把含有导数的等式或者不等式列出来，比如f'(x)+g(x)h(x)=k(x)这种式子（这只是个例子啊）。

然后把含有x这个变量的式子尽可能全地放到一边，假设就是含g(x)h(x)这部分的放到一边，另一边就是k(x)- f'(x)。

分离变量法是求解数学物理方程中的一种常见方法。

它的基本思想是将解函数表示为多个变量的乘积形式，然后将原方程中的偏导数用每个变量的偏导数表示，再将所得的各个方程分别解出。

具体来说，假设有一个二元偏微分方程
其中k 是一个常数。

这样我们将原方程分离成两个单变量的方程，每个方程只含有一个变量和其对应的导数，可以分别解出。

然后将得到的两个解函数相乘，就可以得到原方程的通解。

需要注意的是，分离变量法并不是适用于所有数学物理方程的通用解法，但它在许多情况下是非常有用的。

一阶线性微分方程的解法和分离变量法微积分作为高等数学中的一门重要学科，其涵盖的内容极其广泛，其中线性微分方程是其应用广泛的一部分。

在实际应用中，很多问题可以转化为一阶线性微分方程的形式，这使得解决这些问题变得更加容易和可行。

而分离变量法是解决这类微分方程的一种有效的方法，本文将详细介绍一阶线性微分方程及其解法，重点介绍分离变量法的基本思想和具体步骤。

一. 一阶线性微分方程1. 定义一阶线性微分方程是指形如y' + p(x)y = q(x)的微分方程，其中y是未知函数，p(x)和q(x)是已知函数，y'是对y关于x求导得到的导数。

其中，p(x)和q(x)是一阶齐次线性微分方程的系数函数，即p(x)y=0的一阶微分方程，而加上非齐次项q(x)后就成为了一般的一阶非齐次线性微分方程。

2. 特征一阶线性微分方程有一些特征：（1）是关于未知函数y及其导数y'的方程；（2）系数p(x)和q(x)是已知函数不含y及其导数；（3）在一定范围内有确定的解出现。

这种类型的微分方程的解法非常重要，因为它们出现在数学、工程和科学中的各个领域中。

二. 分离变量法分离变量法是一种非常有效的解决一阶线性微分方程的方法。

其基本思想是将一阶微分方程中的未知函数y及其导数y'分别归成一个变量组的函数，然后将它们分离到方程两边，从而得到一个与求解x有关的对两个纯变量的积分方程。

因为变量已经分离，因此它们可以分别积分，最后便可求得原方程的通解。

下面我们将从分离变量法的基本思想、步骤以及解题策略几个方面详细介绍这种解法的具体方法。

1、基本思想我们现在来考虑一阶线性微分方程y' + p(x)y = q(x)，其中p(x)和q(x)都是已知函数。

我们将y'移向等式左边，将p(x)y和q(x)合并到等式右边，于是有：y' = q(x) - p(x)y现在，我们将y'和y分别看作一个单独的变量，我们有：dy/dx = f(x, y)其中，f(x, y) = q(x) - p(x)y。

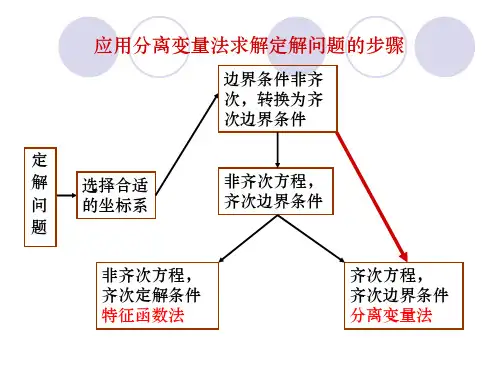
分离变量法的步骤
嘿，咱今儿个就来说说这分离变量法的步骤哈！这分离变量法啊，
就像是解开一道复杂谜题的钥匙呢！
首先呢，咱得把那个复杂的方程给定住咯，就像抓住一只调皮的小
猴子，别让它乱跑。

然后呢，咱试着把能分离开的变量给它分离开来，这就好比把一堆混杂在一起的糖果给分拣出来一样。

比如说有个方程，一边是关于 x 的式子，另一边是关于 y 的式子，
咱就得想法子让它们各在各的一边呆着，井水不犯河水。

这可不是件
容易事儿啊，得有点耐心，有点技巧。

接下来，就该对分离开的两边分别进行处理啦！该积分的积分，该
化简的化简。

这就好像给分开的糖果们穿上漂亮的包装纸一样。

等把两边都处理得差不多了，嘿，神奇的事情可能就发生了，答案
说不定就呼之欲出啦！这感觉，就像是在黑暗中突然找到了那盏明灯
一样，让人兴奋不已呀！
咱再想想，这不就跟咱生活中很多事情一样嘛！有时候遇到个麻烦
事儿，咱也得把它给拆解开来，一步一步地去解决。

不能一股脑儿地
瞎干，得有方法，有策略。

分离变量法不就是教我们怎么有条理地去解决问题嘛！你看，数学
里的这些方法啊，其实都是有大智慧在里面的呢。

咱要是能把这分离变量法掌握得透透的，那以后再遇到类似的问题，还怕啥呀！就像咱有了一把万能钥匙，啥锁都能给它打开咯！
所以啊，大家可别小瞧了这分离变量法的步骤，一步一步走稳了，
才能在数学的道路上越走越远，越走越顺溜呀！这可是咱探索数学奥
秘的重要法宝呢！大家可得好好琢磨琢磨，多练练手，把它变成自己
的拿手好戏！加油吧！。

变量分离法的具体实现过程变量分离法是一种常用的数学方法，用于解决复杂的微积分方程。

它通过对方程中的变量进行适当的分离，简化方程的求解过程，并使得问题更加容易处理。

本文将从实际角度出发，结合一些具体的例子，介绍变量分离法的具体实现过程，希望能够为读者提供一些帮助。

一、什么是变量分离法变量分离法，顾名思义，就是将微积分方程中的变量分离出来，通过对变量的处理，得到简化后的方程，进而求解原始问题的方法。

具体来说，对于形如f(x,y)=0的微积分方程，我们将其视为两个函数之间的关系f(x,y)=g(x)h(y)，然后对该式进行求导，得到g'(x)h(y)+g(x)h'(y)=0。

这里的关键就是要将原方程以一定的形式进行重写，使得它能够被方便地分离成两个独立的变量。

二、需要注意的问题在进行变量分离法的求解过程中，需要注意以下几个问题：1. 变量分离法的适用范围变量分离法只适用于某些特定类型的微积分方程，比如可以被写成g(x)h(y)=0形式的方程。

如果方程无法重写为这种形式，那么这种方法就不适用了。

2. 整合式的处理在对方程求解时，如果出现了整合式的形式，我们往往需要进行一些特殊处理。

一种常见的方法是先将整合式求解出来，然后代入原方程中，得到更加简化后的形式。

3. 分离后的变量的处理在对变量进行分离后，我们往往需要对两个变量分别进行处理。

一种比较常见的方法是将其中一个变量看作常数，只针对另一个变量进行求解。

三、变量分离法的具体实现下面我们将通过两个具体的例子，介绍变量分离法的具体实现过程。

例1：解决二元函数的微分方程假设有一个二元函数f(x,y)，并且它满足以下的微分方程：(1+y^2)f’(x,y)=y(1+f(x,y)^2)我们来看如何使用变量分离法来对该方程进行求解。

首先将方程变形为以下形式：yf(x,y)^2-f’(x,y)y+1=0这时我们发现方程可以被写成yf(x,y)^2=g(x)-1的形式，接着对方程进行求导，得到：2yf(x,y)f’(x,y)-f’’(x,y)y=0将g(x)-1视为常数，只对f(x,y)进行处理，得到：f’’(x,y)/f’(x,y)-2y/f(x,y)=0将其化简，得到：ln|f(x,y)|-y^2=C1x+C2这里C1、C2为常数，通过指定不同的初值，可以求出方程的具体解。

一次微分方程的通解的方法一次微分方程是指一个包含未知函数及其导数的方程。

一次微分方程是一个一元微分方程，其中最高次导数的幂为1、一次微分方程的通解是指能够满足该微分方程的所有解。

在解一次微分方程时，一般使用分离变量、变量代换、常数变易等方法。

下面我将详细介绍这些方法。

1.分离变量法：分离变量法是求解一次微分方程的一种常见方法。

其基本思想是将微分方程中包含未知函数及其导数的项分离到等号两边，并对两边进行积分。

具体步骤如下：(1)将方程中包含未知函数及其导数的项分离到等号两边；(2)对等号两边进行积分；(3)解出未知函数。

例如，考虑一次微分方程dy/dx = f(x)g(y)，其中f(x)和g(y)是已知函数。

可以将dy/dx分离到等号两边得到dy/g(y) = f(x)dx，然后对等号两边进行积分，最后解出y的表达式。

2.变量代换法：变量代换法是求解一次微分方程的另一种常见方法。

其基本思想是通过引入一个新的变量替换原有的变量，从而将一次微分方程转化为另一种形式。

具体步骤如下：(1)选择一个适当的变量代换，将原方程转化为一个新的方程；(2)解出新的方程；(3)将新的方程中的解代回原方程，得到原方程的解。

例如，考虑一次微分方程dy/dx = f(x)，可以通过变量代换y = v(x)将方程转化为dv/dx = f(x)，然后对新方程进行解析，最后将解代回原方程得到y的表达式。

3.常数变易法：常数变易法是求解一次齐次微分方程的一种常见方法。

齐次微分方程是指其非齐次项为零的微分方程。

常数变易法的基本思想是假设未知函数的解具有特定的形式，然后通过适当选择常数的值，使得原方程成立。

具体步骤如下：(1)假设一次微分方程的通解具有特定的形式，并将其代入原方程；(2)解出未知函数的表达式，并将其代回原方程校验；(3)求得未知函数的特解，然后将通解和特解相加得到原方程的通解。

例如，考虑一次齐次微分方程dy/dx + p(x)y = 0，其中p(x)是已知函数。

分离变量求积分分离变量求积分是微积分中的一个重要方法之一，也是计算微积分题目中经常要用到的方法。

它的核心思想是将一个以两个变量为自变量的函数分解成两个只有一个变量的函数的乘积形式，然后分别对这两个只含有一个变量的函数进行积分，并最后将结果相乘得到原始的函数的积分结果。

分离变量求积分可以应用于很多领域，比如物理学、生物学、化学等等。

在这些领域中，我们通常需要对两个或更多变量的函数进行积分计算，这时候就可以采用分离变量的方法来解决问题。

下面我们将对分离变量求积分的方法以及应用进行详细介绍。

一、分离变量的方法假设我们有一个以两个变量x和y为自变量的函数f(x,y)，我们需要对它进行积分计算。

我们可以采用分离变量的方法，将f(x,y)表示为两个只含有一个变量的函数的乘积形式，如下所示：f(x,y) = g(x)h(y)这里g(x)和h(y)都是只含有一个变量的函数。

这个式子的意义在于，我们将x和y分别表示为g(x)和h(y)的函数，然后将它们乘在一起得到原始函数f(x,y)。

在这个式子中，我们需要先选取一个变量（比如说x），然后将其看成是一个参数，代入f(x,y)中，变成如下形式：f(x,y) = g(x)h(y) = G(x)H(y)这里，G(x)和H(y)分别表示g(x)和h(y)的积分函数，它们可以通过积分计算得出。

对于这两个函数，我们可以分别对它们进行积分，得到如下结果：G(x) = ∫g(x)dx H(y) = ∫h(y)dy最后我们将G(x)和H(y)相乘再加上常数项C，即可得到函数f(x,y)的积分结果：∫f(x,y)dx = G(x)H(y) + C这就是分离变量求积分的基本方法。

通过这个方法，我们可以将一个以两个变量为自变量的函数分解成两个只含有一个变量的函数的积分形式，然后分别对这两个函数进行积分，最后将结果相乘得到原始函数的积分结果。

二、分离变量的应用分离变量求积分可以应用于很多领域，比如物理学、生物学、化学等等。

球坐标系中的分离变量法步骤1. 引言球坐标系是一种常用的三维坐标系，它描述了三维空间中的点的位置。

在物理学、数学和工程学等领域中，球坐标系经常用于描述球对称问题的解决方案。

而球坐标系中的分离变量法是一种重要的数学工具，用于解析球坐标系中的微分方程。

本文将介绍球坐标系的基本概念，并详细探讨球坐标系中的分离变量法的步骤和应用。

2. 球坐标系的基本概念球坐标系由径向距离（r），极角（θ）和方位角（φ）三个参数组成。

其中，径向距离表示点到原点的距离，极角表示与正半轴（通常为x轴）之间的夹角，而方位角表示与x轴之间的夹角。

在球坐标系中，点的位置可以通过如下公式表示：x = r * sinθ * cosφy = r * sinθ * sinφz = r * cosθ其中，x、y、z分别代表点在直角坐标系中的坐标。

3. 球坐标系中的分离变量法步骤球坐标系中的分离变量法用于解析球坐标系中的微分方程。

其主要步骤如下：3.1. 确定问题的边界条件首先，需要确定问题的边界条件。

边界条件指定了问题的边界上点的特定值或导数值，这些条件是微分方程求解的一部分。

3.2. 将微分方程转化为球坐标系的形式将要求解的微分方程转化为球坐标系中的形式。

这通常需要将直角坐标系中的微分算子通过适当的变换转换为球坐标系中的形式。

3.3. 假设分离变量的形式假设球坐标系的解可以表示为一系列的分离变量的乘积形式。

这意味着解可以写成：u(r, θ, φ) = R(r) * Θ(θ) * Φ(φ)其中R(r)、Θ(θ)和Φ(φ)分别是关于r、θ和φ的函数。

3.4. 将分离变量代入微分方程将分离变量代入微分方程，并将公式中的对各个变量的偏导数分离开。

这将导致形如下式的一组常微分方程：1/R * (d/dr (r^2 * dR/dr)) + 1/Θ * (1/sinθ * d/dθ (sinθ * dΘ/dθ)) + 1/Φ* d^2Φ/dφ^2 + k^2 * RΘΦ = 0其中k是一个常数。

变量分离方程变量分离方程是解决一元微分方程的常用方法之一。

所谓一元微分方程，是指涉及到一个未知函数及其导数的方程。

变量分离方程的目标是将方程中的已知量和未知量分离在等式的两边，然后分别积分求解，最终得到未知函数的解析表达式。

一般来说，变量分离方程可以写成以下形式：dy/dx = f(x)g(y)，其中f(x)和g(y)是关于x和y的已知函数，dy/dx表示y对x的导数。

我们的目标是将x和y分离到等式的两边。

首先，我们将方程两边关于x积分，得到∫1/g(y)dy = ∫f(x)dx。

左边的积分结果是y的函数，右边的积分结果是x的函数，因此我们将方程变为∫1/g(y)dy = F(x) + C，其中C是积分常数。

然后，我们需要对∫1/g(y)dy进行求解。

这一步可能需要一些数学技巧，例如分部积分、换元法等。

求解后得到∫1/g(y)dy = H(y) = F(x) + C。

最后，我们将解y(x) = H^-1(F(x) + C)，即y是H^-1(F(x) + C)的逆函数。

接下来，我们将通过一个实际的例子来演示变量分离方程的求解过程。

假设我们有一个一元微分方程dy/dx = x/y^2。

我们可以将该方程分解为以下形式：y^2dy = xdx。

然后，我们将方程两边进行积分。

对左边进行积分得到∫y^2dy，对右边进行积分得到∫xdx。

∫y^2dy的积分结果是y^3/3，∫xdx的积分结果是x^2/2。

因此，我们得到y^3/3 = x^2/2 + C，其中C是积分常数。

接着，我们将解y(x) = (3(x^2/2 + C))^(1/3)。

这是方程dy/dx = x/y^2的解析解。

变量分离方程是一种简单而有效的解微分方程的方法。

通过将方程分解以及对两边进行积分，我们可以将已知量和未知量分离，并最终得到未知函数的解析解。

然而，对于一些复杂的微分方程，变量分离可能并不容易实现，此时我们需要借助其他方法，如常数变易法、齐次法等。

微分方程分离变量法微分方程是数学中的重要概念，它描述了自然界中许多现象的变化规律。

在微分方程的求解方法中，分离变量法是一种常用且有效的方法。

本文将以分离变量法为主题，介绍微分方程的基本概念和分离变量法的应用。

一、微分方程的基本概念微分方程是描述函数与其导数之间关系的方程。

它包含了未知函数及其导数的表达式。

常见的微分方程类型有常微分方程和偏微分方程两类。

常微分方程只包含一个自变量，而偏微分方程包含多个自变量。

二、分离变量法的基本思想分离变量法是求解微分方程的一种基本方法。

其基本思想是将微分方程中的未知函数和导数分开，使得方程两边可以分别只含有自变量和未知函数。

具体步骤如下：1. 将微分方程中的未知函数和导数分开，形成两边的因子乘积；2. 对两边的因子进行分离，即将含有自变量的因子移到方程的一边，将含有未知函数的因子移到方程的另一边；3. 对两边的因子进行积分，得到两边的积分结果；4. 将积分结果合并并加上常数项，得到最终的解析解。

三、分离变量法的应用举例下面通过一个具体的例子来说明分离变量法的应用。

例：求解微分方程dy/dx = 2x。

解：根据分离变量法，将方程分离为dy = 2xdx。

对方程两边进行积分，得到∫dy = ∫2xdx。

即y = x^2 + C，其中C为常数。

因此，原微分方程的解为y = x^2 + C。

四、分离变量法的优缺点分离变量法作为求解微分方程的常用方法，具有以下优点：1. 方法简单易懂，容易掌握和应用；2. 适用范围广，可以解决许多常见的微分方程问题。

然而，分离变量法也存在一些局限性：1. 不是所有微分方程都可以使用分离变量法求解，只适用于部分形式的微分方程；2. 在进行变量分离时，可能会出现分母为零的情况，导致无法继续进行求解。

五、总结微分方程的分离变量法是一种常用且有效的求解方法。

它通过将微分方程中的未知函数和导数分开，使得方程能够被分离为两个只含有自变量和未知函数的因子。