4北邮MATLAB实验报告

信号与系统MATLAB第一次实验报告一、实验目的1.熟悉MATLAB软件并会简单的使用运算和简单二维图的绘制。

2.学会运用MATLAB表示常用连续时间信号的方法3.观察并熟悉一些信号的波形和特性。

4.学会运用MATLAB进行连续信号时移、反折和尺度变换。

5.学会运用MATLAB进行连续时间微分、积分运算。

6.学会运用MATLAB进行连续信号相加、相乘运算。

7.学会运用MATLAB进行连续信号的奇偶分解。

二、实验任务将实验书中的例题和解析看懂，并在MATLAB软件中练习例题，最终将作业完成。

三、实验内容1.MATLAB软件基本运算入门。

1). MATLAB软件的数值计算：算数运算向量运算：1.向量元素要用”[ ]”括起来，元素之间可用空格、逗号分隔生成行向量，用分号分隔生成列向量。

2.x=x0:step:xn.其中x0位初始值，step表示步长或者增量，xn为结束值。

矩阵运算：1.矩阵”[ ]”括起来；矩阵每一行的各个元素必须用”,”或者空格分开；矩阵的不同行之间必须用分号”;”或者ENTER分开。

2.矩阵的加法或者减法运算是将矩阵的对应元素分别进行加法或者减法的运算。

3.常用的点运算包括”.*”、”./”、”.\”、”.^”等等。

举例：计算一个函数并绘制出在对应区间上对应的值。

2).MATLAB软件的符号运算：定义符号变量的语句格式为”syms 变量名”2.MATLAB软件简单二维图形绘制1).函数y=f(x)关于变量x的曲线绘制用语：>>plot(x,y)2).输出多个图像表顺序：例如m和n表示在一个窗口中显示m行n列个图像，p表示第p个区域，表达为subplot(mnp)或者subplot(m,n,p)3).表示输出表格横轴纵轴表达范围：axis([xmax,xmin,ymax,ymin])4).标上横轴纵轴的字母：xlabel(‘x’),ylabel(‘y’)5).命名图像就在subplot写在同一行或者在下一个subplot前：title(‘……’)6).输出：grid on举例1：举例2：3.matlab程序流程控制1).for循环：for循环变量=初值:增量:终值循环体End2).while循环结构：while 逻辑表达式循环体End3).If分支：(单分支表达式)if 逻辑表达式程序模块End(多分支结构的语法格式)if 逻辑表达式1程序模块1Else if 逻辑表达式2程序模块2…else 程序模块nEnd4).switch分支结构Switch 表达式Case 常量1程序模块1Case 常量2程序模块2……Otherwise 程序模块nEnd4.典型信号的MATLAB表示1).实指数信号：y=k*exp(a*t)举例：2).正弦信号：y=k*sin(w*t+phi)3).复指数信号：举例：4).抽样信号5).矩形脉冲信号:y=square(t,DUTY) (width默认为1)6).三角波脉冲信号：y=tripuls(t,width,skew)(skew的取值在-1~+1之间，若skew取值为0则对称)周期三角波信号或锯齿波:Y=sawtooth(t,width)5.单位阶跃信号的MATLAB表示6.信号的时移、反折和尺度变换:Xl=fliplr(x)实现信号的反折7.连续时间信号的微分和积分运算1).连续时间信号的微分运算：语句格式：d iff(function,’variable’,n)Function:需要进行求导运算的函数，variable:求导运算的独立变量，n：求导阶数2).连续时间信号的积分运算：语句格式：int(function,’variable’,a,b)Function:被积函数variable:积分变量a:积分下限b:积分上限(a&b默认是不定积分)8.信号的相加与相乘运算9.信号的奇偶分解四、小结这一次实验让我能够教熟悉的使用这个软件，并且能够输入简单的语句并输出相应的结果和波形图，也在一定程度上巩固了c语言的一些语法。

matlab实验报告总结电气工程学院自动化102班 2012年12月21日实验一 MATLAB环境的熟悉与基本运算一、实验目的1．熟悉MATLAB开发环境2．掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。

2.掌握MATLAB常用命令变量与运算符变量命名规则如下：变量名可以由英语字母、数字和下划线组成变量名应以英文字母开头长度不大于31个区分大小写MATLAB中设置了一些特殊的变量与常量，列于下表。

MATLAB运算符，通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式的基本运算表7 两种运算指令形式和实质内涵的异同表的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、新建一个文件夹2、启动，将该文件夹添加到MATLAB路径管理器中。

3、保存，关闭对话框4、学习使用help命令，例如在命令窗口输入help eye，然后根据帮助说明，学习使用指令eye5、学习使用clc、clear，观察command window、command history和workspace等窗口的变化结果。

6、初步程序的编写练习，新建M-file，保存，学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。

注意：每一次M-file的修改后，都要存盘。

练习A：help rand，然后随机生成一个2×6的数组，观察command window、command history和workspace等窗口的变化结果。

学习使用clc、clear，了解其功能和作用。

答：clc是清除命令窗体内容 clear是清除工作区间输入C=1:2:20，则C表示什么？其中i=1,2,3,?,10。

1. 利用符号极限判定函数的连续性。

微积分是数学分析中的一个重要内容，是高等数学建立的基础和整个微分方程体系的基础内容。

Matlab 能够通过符号函数的计算实现微积分运算，如极限、微分、积分、级数等。

极限是当变量无限接近特定值时函数的值，例如，一元函数f(x)的导数f ’(x)的定义为下面的极限：f ’(x)=hx f h x f h )()(0lim -+→ Matlab 符号工具箱利用函数limit 计算符号的极限，其调用格式如下： ● l imit(expr, x , a):求x 趋近于a 的极限，但是当左、右极限不想同时，极限不存在。

● l imit(expr , a): 用 findsym(expr)作为独立变量。

● l imit(expr): 对x 求右趋于a=0的极限。

● l imit(expr, x , a , ‘left ’): 对x 求左趋于a 的极限。

● l imit(expr, x , a , ‘right ’): 对x 求左趋于a 的极限。

函数limit 要求第一个输入变量为符号函数，limit 不支持符号函数的句柄，但是对符号函数句柄f ， 可以将f(x)作为输入变量。

例如：讨论函数f(x)= ｛0x x,0x ,2x 1)(cosx =≠= 的连续性。

求解过程：当x<0, x>0时，f(x)为初等函数，其连续性是显然的，只要考虑在x=0处的连续性。

根据需要，首先创建符号函数的M 文件，其源代码为：保存M 文件，名为ex0.m 。

调用limit 函数判定函数的连续性，代码为由结果可以看出，0lim →x f(x)=+→0lim x f(x)=-→0lim x f(x)=- 1/2 =0=f(0), 所以，在x=0时函数是不连续的。

2.在实际应用中，常常提出这样一种需求：把同一自变量的两个不用量纲、不同数量级的函数量的变化绘制在同一张图上。

例如希望在同一张图上表现出温度、湿度随时间的变化；人口数量、GDP 的变化曲线等。

学生实验报告一、实验目的 熟悉MATLAB 软件的用户环境；了解MATLAB 软件的一般命令；掌握MATLAB 向量、数组、矩阵操作与运算函数；掌握MATLAB 软件的基本绘图命令；掌握MATLAB 语言的几种循环、条件和开关选择结构，及其编程规范。

通过该实验的学习，使学生能灵活应用MATLAB 软件解决一些简单问题，能借助MATLAB 软件的绘图功能，对函数的特性进行探讨，广泛联想，大胆猜想，发现进而证实其中的规律。

二、实验仪器、设备或软件： 电脑,MATLAB 软件三、实验内容 1．MATLAB 软件的数组操作及运算练习；2．直接使用MATLAB 软件进行作图练习；3．用MATLAB 语言编写命令M 文件和函数M 文件。

四、实验步骤1．在D 盘建立一个自己的文件夹；2．开启软件平台——MATLAB ，将你建立的文件夹加入到MATLAB 的搜索路径中；3．利用帮助了解函数max, min, sum, mean, sort, length ，rand, size 和diag 的功能和用法；4．开启MATLAB 编辑窗口，键入你编写的M 文件（命令文件或函数文件）；5．保存文件（注意将文件存入你自己的文件夹）并运行；6．若出现错误，修改、运行直到输出正确结果；7．写出实验报告，并浅谈学习心得体会。

五、实验要求与任务根据实验内容和步骤，完成以下具体实验，要求写出实验报告（实验目的→问题→算法与编程→计算结果或图形→心得体会）1. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321212113A ， ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=101012111B 要求：（1）屏幕输出A 与B ；（2）A 的转置A′；（3）求A+B 的值；（4）求A-B 的值；（5）求4A ；（6）求A×B ；（7）求A -1．2. 有一函数f (x ,y )=x 2+sin xy +2y ，写一程序，输入自变量的值，输出函数值。

3. 用plot ，fplot 分别绘制函数y =cos(tan(πx ))图形。

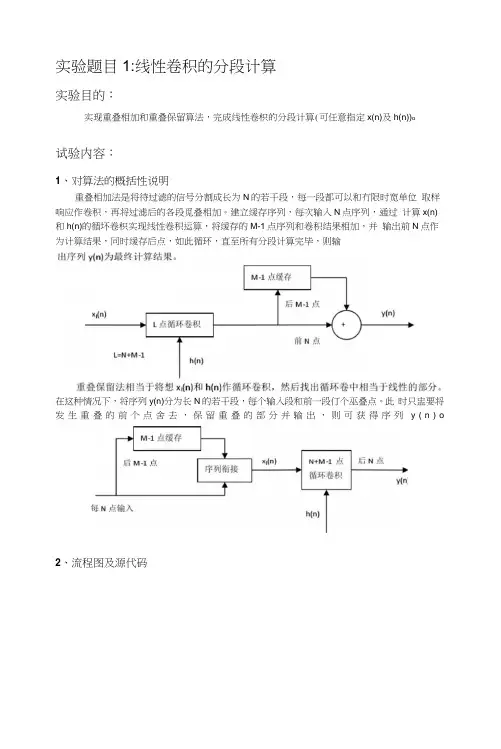
实验题目1:线性卷积的分段计算实验目的：实现重叠相加和重叠保留算法，完成线性卷枳的分段计算(可任意指定x(n)及h(n))o试验内容：1、对算法的概括性说明重叠相加法是将待过滤的信号分割成长为N的若干段，每一段都可以和冇限时宽单位取样响应作卷积，再将过滤后的各段觅叠相加。

建立缓存序列，每次输入N点序列，通过计算x(n)和h(n)的循坏卷枳实现线性卷积运算，将缓存的M-1点序列和卷积结果相加，并输出前N点作为计算结果，同时缓存后点，如此循环，直至所有分段计算完毕，则输在这种情况下，将序列y(n)分为长N的若干段，每个输入段和前一段仃个巫叠点。

此时只盅要将发生重叠的前个点舍去，保留重叠的部分并输出，则可获得序列y(n)o2、流程图及源代码function [ y ] = circular_conv( xl f x2# L )%利用循环卷积计算线性卷积%循环卷积采用频域计算方法，已FFT代薛DFT,降低运篦戢Xlk = fft(xl#L);龟xl 做L点FFTX2k = fft(x2/L);电xl 做L点FFTYk ■ Xlk.*X2k; *频域相乘y = ifft(Yk); %FFT反变换得循环卷积结果endfunction [ y ] = overlap_add( x, h f N )令堪叠相加法实现咎核心为将高点数DFT转化为低点数DFT. R用循环卷积计算线性卷积M = length(h); *获得人5)的长度if N < M &为N选择介适的值保证运算正确N = M+1;endL = M+N-1;电循环卷枳与线性卷枳结果相同时需耍进行运算的赠少点数Lx = length(x);乌获得x(n)的长度T = ceil(Lx/N);乌确定分段数Tt ■ zerosd/M-l);靱初始化序列t(n)x = [x.zerosd, (T+1)*N-Lx) ]; %不足的分段补零y = zerosd, (T+1)*N); $生成输出序列y(n),长度足勢长for i = 0:1:Txi = i*N+l;x_seg = x(xi:xi+N-l);卡选择低点数计算时的分段x(n)y_seg = circular_conv(x_seg, h, L);乌调用循环卷积计算线性卷积y_seg(l:M-l) = y_seg(1:M-l) +t (1:M-l);%完成重叠相加■ y_seg(N+l:L); *重新对t(n)赋ff[为保留的后点y(xi :xi+N-l) = y_seg( 1 :N);为II接输出前N 个点endy=y(l:Lx+M-l); *収岀協终的输出序列endfunction [ y ] = overlap_save( x, h# N )%重叠保留法实现駢亥心为将高点数DFT转化为低点数DFT. II用循环卷积计算线性卷枳Lx = length(x);労获得x(n)的长度M = length(h); *获得h(n)的长度if N < M先为N选择合适的值保证运算正确N - M+1；endL = N+M-1; *为降低点数，取M+N-1点循环卷积即可t = zerosfl/M-l); *初始化序列t(n)T - ceil(Lx/N);乌确定分段数x = [x r zeros(l f (T+1)*N-Lx)];电为不足的分段补牢y = zerosfl, (T+l)*N);for i = 0:1:Txi = i*N4-l;X_seg = (t r x(xi:xi+N-l)];舎确定每个低点数卷积的分段x(n)t = x_seg(N+l:N+M-l);勒为t(n)重新赋值为后M-l个点的值y_seg = circular_conv(x_seg,h,L); *循环卷积计算线性卷积y(xi:xi+N-l) ■ y_seg(M:N+M-l) ;%^[接取出后N个点作为一次计算的输出endy=y(l:Lx+M-l); *収出实际的输出序end3、实验结果输入(参考教材例3.4、3.5)：n - 0:9;xn = n+1;hn = d,0,-l];N = 6;yl = convfhn/ xn)y2 = overlap_add(xn, hn, N)y3 = overlap_save(xn r hn r N)输出: yi ■y2 =2.0000 2.0000 Columns 11 through 12-9.0000 -10.00002.0000 2.0000Columns 11 through 12-9.0000 -10.0000 町见，用重叠相加法和重叠保留发分别计算的卷枳结果与直接利用线性卷枳计算的结果 一致。

实验名称MATLAB编程实验目的和要求：1、熟悉MATLAB的编程。

2、掌握定义和调用MA TLAB函数的方法。

3、掌握利用if语句、switch语句实现选择结构的方法。

4、掌握for语句、while语句实现循环结构的方法。

实验内容和步骤:1、输入一个字符，若为大写字母，则输出其后继字符，若为小写字母，则输出其前导字符，若为数字字符则输出其对应的数值，若为其他字符则原样输出。

c=input('请输入一个字符','s');if c>='A'&c<='Z'disp(setstr(abs(c)+1));else if c>='a'&c<='z'disp(setstr(abs(c)-1));else if c>='0'&c<='9'disp(abs(c)-abs('0'));elsedisp(c);endendend运行结果：请输入一个字符aeyhjgfhgdfgsdfgdxgifegfcefrcef请输入一个字符WEWERETRYTRUYTXFXFSFUSZUSVZU请输入一个字符45445454794 5 4 4 5 4 5 4 7 92、已知5个学生4门功课的成绩，求每名学生的总成绩。

s=0;a=[65,76,56,78;98,83,74,85;76,67,78,79;98,58,42,73;67,89,76,87]for k=as=s+k;enddisp(s);运行结果：a =65 76 56 7898 83 74 8576 67 78 7998 58 42 7367 89 76 872753403002713193、已知多项式h=x^6-10x^5+31x^4-10x^3-116x^2+200x-96,求其根程序：h=roots([1 -10 31 -10 -116 200 -96])运行结果：h =-2.00004.00003.00002.00002.00001.00004、从键盘输入一个三位整数，将它反向输出。

北邮通信原理软件实验报告以下是为大家整理的北邮通信原理软件实验报告的相关范文，本文关键词为北邮,通信,原理,软件,实验,报告,，您可以从右上方搜索框检索更多相关文章，如果您觉得有用，请继续关注我们并推荐给您的好友，您可以在综合文库中查看更多范文。

通信原理软件实验报告学院：信息与通信工程学院班级：学号：班内序号：姓名：1/63一、通信原理matlab仿真实验实验八一、实验内容假设基带信号为m(t)=sin(2000*pi*t)+2cos(1000*pi*t),载波频率为20khz，请仿真出Am、Dsb-sc、ssb信号，观察已调信号的波形和频谱。

二、实验原理1、具有离散大载波的双边带幅度调制信号Am该幅度调制是由Dsb-scAm信号加上离散的大载波分量得到，其表达式及时间波形图为：应当注意的是，m(t)的绝对值必须小于等于1，否则会出现下图的过调制：Am信号的频谱特性如下图所示：由图可以发现，Am信号的频谱是双边带抑制载波调幅信号的频谱加上离散的大载波分量。

2/632、双边带抑制载波调幅（Dsb—scAm）信号的产生双边带抑制载波调幅信号s(t)是利用均值为0的模拟基带信号m(t)和正弦载波c(t)相乘得到，如图所示：m(t)和正弦载波s(t)的信号波形如图所示：若调制信号m(t)是确定的，其相应的傅立叶频谱为m(f)，载波信号c(t)的傅立叶频谱是c(f),调制信号s(t)的傅立叶频谱s(f)由m(f)和c(f)相卷积得到，因此经过调制之后，基带信号的频谱被搬移到了载频fc 处，若模拟基带信号带宽为w，则调制信号带宽为2w，并且频谱中不含有离散的载频分量，只是由于模拟基带信号的频谱成分中不含离散的直流分量。

3、单边带条幅ssb信号双边带抑制载波调幅信号要求信道带宽b=2w,其中w是模拟基带信号带宽。

从信息论关点开看，此双边带是有剩余度的，因而只要利用双边带中的任一边带来传输，仍能在接收机解调出原基带信号，这样可减少传送已调信号的信道带宽。

实验一 matlab 基本操作一、 实验目的熟悉matlab 的安装与启动；熟悉matlab 用户界面；熟悉matlab 功能、建模元素；熟悉matlab 优化建模过程。

二、 实验设备与仪器1.微机2.matlab 仿真软件三、 实验步骤1. 了解matlab 的硬件和软件必备环境；2. 启动matlab ；3. 熟悉标题栏，菜单栏，工具栏，元素选择窗口，状态栏，控制栏以及系统布局区；4. 学习优化建模过程。

四、 实验报告要求1. 写出matlab 系统界面的各个构成；以及系统布局区的组成；以及每一部分的功能；2. 优化建模过程应用举例五、实验内容（一）、Matlab 操作界面1. 命令窗口（command window ）2. 命令历史窗口（command history ）3. 工作空间管理窗口（workspace ）4. 当前路径窗口（current directory ）（二）、优化建模过程应用举例1、简单矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321A 的输入步骤。

（1）在键盘上输入下列内容A = [1,2,3; 4,5,6; 7,8,9]（2）按【Enter 】键，指令被执行。

（3）在指令执行后，MATLAB 指令窗中将显示以下结果：A = 1 2 34 5 67 8 92、矩阵的分行输入。

A=[1,2,34,5,67,8,9]A =1 2 34 5 67 8 93、指令的续行输入S=1-1/2+1/3-1/4+ ...1/5-1/6+1/7-1/8S =0.63454、画出衰减振荡曲线t ey t 3sin 3-=及其它的包络线30t e y -=。

t 的取值范围是]4,0[π。

t=0:pi/50:4*pi;y0=exp(-t/3);y=exp(-t/3).*sin(3*t);plot(t,y,'-r',t,y0,':b',t,-y0,':b')grid5、画出2222)sin(y x y x z ++=所表示的三维曲面。

数学试验报告 一、实验问题： 有一形状较为复杂，但表面很光滑的曲面工件.通过科学手段，将其放置于某一空间坐标系下，测得曲面上若干个点的坐标如下： Y x -5 -4 -3 -2 -1 0 1 2 3 4 5

-5 0 0 -4 0 0 -3 0 0 -2 3 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 2 0 0 3 0 0 4 0 0 5 0 0 要求： （1）、画出该曲面工件的图形. （2）、在已知相邻的横、纵坐标之间插入三个分点，用interp2命令计算出所有点处的竖坐标，画出相应的插值曲面. （3）、分别用不同的方法求出该曲面工件表面积的近似值.

二、问题分析： （1）、由x=-5:1:5;y=-5:1:5产生“格点”矩阵，再用已知的各“格点”的纵坐标z，用surf（x,y,z）命令即可画出未进行插值的工件表面图形。 （2）、要在已知相邻的横、纵坐标之间插入三个分点，则要用xc=-5::5;yc=-5::5产生另一个“格点”矩阵，然后使用interp2命令计算所有“格点”处的纵坐标z，然后再用surf（x,y,z）命令即可画出该插值曲面。 （3）、该工件是一个曲面，要求其表面积的近似值，可以想到的用“分”，“匀”，“和”，“精”的思想，将工件曲面分成n个在xoy平面上的投影是边长为d的矩形的曲面四边形（从第（2）题画出的曲面可以一目了然的看出），分别求出各个曲面四边形的面积再求和，n取的越大，d越小，越接近准确值。 对于如何求每一个曲面四边形的面积: 方法1：如图所示，曲面面积微元S近似等于以OP1和OP2为邻边的平行四边形的面积S=∥𝐎𝐏𝟏×𝐎𝐏𝟐∥，只要n取的值较大，d足够小，误差会较小。 曲面微元： 方法2：由第一型面积分公式：S=∬√1+Fx2+Fy

2

（σ）dxdy ，曲面面积微元

S等于√1+Fx2+Fy2dxdy. 由上述分割工件曲面的思想，dxdy即等于d2. 问题是如何求得曲面方程的对x、y的偏导数通过查找资料，发现Matlab软件中有求梯度的命令gradient，因此，曲面的面积微元S可以求得，而且与方法一类似，当d取足够小时，误差可以忽略不计。

实验题目3：梳状滤波器的应用实验目的：录制一段自己的话音，时间长度及取样频率自定；对该段声音加入一次反射、三次反射和无穷多次反射。

试验内容：1、对试验原理的说明回声可以认为是由原始声音衰减后的多个延迟叠加组成的，因此回声可以用延迟单元来生成。

x(n)表示原始声音信号，a为衰减系数，T为延迟周期，回声信号Y(n)=X(n)+a*x(n‐T）+a^2*x(n‐2T)+……+a^k*x(n‐kT)。

Z变换后的系统函数H(z)可由梳状滤波器实现。

本实验用MATLAB中的filter(b,a,x)函数可用来仿真差分方程a(1)*y(n)=b(1)*x(n)+b(2)*x(n‐1)+...+b(nb+1)*x(n‐nb)‐a(2)*y(n‐1)‐...‐a(na+1)*y(n‐na)。

2、在同一张图上，绘制原声音序列x(n)、加入一次反射后的声音序列x1(n)、加入三次反射后的声音序列x3(n)和加入无穷多次反射后的声音序列x I(n)。

[x, fs] = wavread('a.wav');% sound(x, fs);a = 0.6; T = 0.2;y1 = filter([1, zeros(1,T*fs-1), a], 1, x);% sound(y1, fs); wavwrite(y1, fs, 'echo1.wav');y2 = filter([1, zeros(1,T*fs-1), a, zeros(1,T*fs-1), a^2, zeros(1,T*fs-1), a^3], 1, x);% sound(y2, fs); wavwrite(y2, fs, 'echo2.wav');y3 = filter(1, [1, zeros(1,T*fs-1), a], x);% sound(y3, fs); wavwrite(y3, fs, 'echo3.wav');plot(y3, 'm');hold on; plot(y2, 'r');hold on; plot(y1, 'g');hold on; plot(x, 'b');其中蓝色为原声音序列x(n)，粉红色为加入一次反射后的声音序列x1(n)，绿色为加入三次反射后的声音序列x3(n)，红色为加入无穷多次反射后的声音序列x I(n)。

实验一：MATLAB语言平台与SIMULINK工具箱一、实验目的：1．学习了解MATLAB语言环境；2．练习MATLAB命令；4．掌握SIMULINK工具箱的应用。

二、实验要求：1．实验内容（1）学习了解MATLAB语言环境；（2）练习MATLAB命令的基本操作；（3）掌握SIMULINK仿真环境的使用方法;(4) 掌握线性系统仿真常用基本模块的用法2．要求按照实验文档的要求与步骤完成实验，撰写实验报告。

三、实验基本知识：1.熟悉MATLAB环境：MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。

2.掌握MATLAB常用命令3.了解SIMULINK模块库中各子模块基本功能四、实验内容：1.学习使用help命令，例如在命令窗口输入help eye，然后根据帮助说明，学习使用指令eye（其它不会用的指令，依照此方法类推）help eyeEYE Identity matrix.EYE(N) is the N-by-N identity matrix.EYE(M,N) or EYE([M,N]) is an M-by-N matrix with 1's onthe diagonal and zeros elsewhere.EYE(SIZE(A)) is the same size as A.EYE with no arguments is the scalar 1.EYE(M,N,CLASSNAME) or EYE([M,N],CLASSNAME) is an M-by-N matrix with 1'sof class CLASSNAME on the diagonal and zeros elsewhere.Example:x = eye(2,3,'int8');See also speye, ones, zeros, rand, randn.Reference page in Help browserdoc eyeA=eye(3)A=1 0 00 1 00 0 12．任意创建3个变量，分别为数值、矩阵、字符串,保存到mydat.mat文件，再把my_data.mat文件中的变量读取到MatLab工作空间内；查找已创建变量的信息，删除变量；学习使用clc、clear，观察command window、command history和workspace等窗口的变化结果。

MATLAB实训报告M AT L A B语⾔编程实训报告题⽬MATLAB在信号与系统中的应⽤年级2008 专业电⼦信息⼯程⽬录第⼀章绪论 (2)1.1 本设计课题⽬的及意义，重点解决的问题 (2)1.1.1 MATLAB在信号与系统中应⽤的⽬的及意义 (2)1.1.2 重点解决的问题 (2)1.2 课题的社会和技术背景 (2)1.3 实现的具体功能 (3)第⼆章课题的基本概念和原理 (4)2.1 MATLAB的概念 (4)2.2 信号与系统的概念 (4)2.3 信号与系统分析的基本内容与⽅法 (5)2.4 离散系统的基本概念 (6)2.5连续系统模型及表⽰ (6)第三章系统设计和实现 (7)3.1采⽤的软件及开发平台 (7)3.1.1系统设计软件 (7)3.1.2开发平台和编程环境 (7)3.2系统的详细设计 (8)3.2.1建模 (8)3.2.2解决⽅法 (9)3.3系统设计的亮点 (9)第四章结束语 (10)参考⽂献 (11)第⼀章绪论1.1 本设计课题⽬的及意义，重点解决的问题1.1.1 MATLAB在信号与系统中应⽤的⽬的及意义MATLAB在信号与系统中应⽤能够让学⽣熟悉MATLAB软件平台、⼯具箱、⾼效的数值计算及符号计算功能。

熟悉MATLAB 软件的信号处理编程⽅法和结果的可视化。

了解数字信号处理的计算机仿真⽅法。

进⼀步加深对信号与系统的基本原理、⽅法及应⽤的理解。

MATLAB软件具有强⼤的数值分析和计算结果可视化的功能.运⽤MATLAB软件,通过⼀个应⽤实例,将信号与系统课程的理论与实践教学有机地结合,有效地解决了教学中的难点问题,说明了MATLAB软件在信号与系统课程的实践教学中具有重要的实际意义1.1.2 重点解决的问题matlab的基本使⽤⽅法，matlab的预定义函数，如何⽤matlab绘图，如何在matlab中编程，基于matlab的矩阵运算、符号运算、数值分析等。

1.2 课题的社会和技术背景长期以来，“信号与系统”课程⼀直采⽤⿊板式的单⼀的教学⽅式，学⽣仅依靠做习题来巩固和理解教学内容，对课程中⼤量的应⽤性较强的内容不能实际动⼿设计、调试、分析，严重影响和制约了教学效果。

MATLAB实践报告2016/2017学年第一学期专业：电气工程及其自动化班级：学号：姓名：2017年 2 月目录第1章绪论 (1)1.1 Matlab简介 (1)1.2 Matlab语言特点及优势 (1)1.2.1 语言特点 (1)1.2.2 优势 (2)1.3 Matlab的功能 (5)第2章Matlab实践任务 (6)2.1实验一Matlab环境语法、基本运算及绘图 (6)2.1.1实验目的 (6)2.1.2实验原理 (6)2.1.3实验内容 (6)2.2实验二Matlab数值运算 (10)2.2.1实验目的 (10)2.2.2实验原理 (10)2.2.3实验内容 (10)2.3实验三Matlab的符号计算 (19)2.3.1实验目的 (19)2.3.2实验内容 (19)2.4实验四Matlab基本编程方法 (23)2.4.1实验目的 (23)2.4.2实验内容 (23)第3章小结 (27)参考文献 (28)第1章绪论1.1 Matlab简介Matlab是“Matrix Laboratory”的缩写，意为“矩阵实验室”，是当今美国很流行的科学计算软件．信息技术、计算机技术发展到今天，科学计算在各个领域得到了广泛的应用．在许多诸如控制论、时间序列分析、系统仿真、图像信号处理等方面产生了大量的矩阵及其相应的计算问题．自己去编写大量的繁复的计算程序，不仅会消耗大量的时间和精力，减缓工作进程，而且往往质量不高．美国Mathwork软件公司推出的Matlab软件就是为了给人们提供一个方便的数值计算平台而设计的．Matlab是一个交互式的系统，它的基本运算单元是不需指定维数的矩阵，按照IEEE的数值计算标准（能正确处理无穷数Inf(Infinity)、无定义数NaN(not-a-number)及其运算）进行计算。

系统提供了大量的矩阵及其它运算函数，可以方便地进行一些很复杂的计算，而且运算效率极高。

Matlab命令和数学中的符号、公式非常接近，可读性强，容易掌握，还可利用它所提供的编程语言进行编程完成特定的工作。

计算机与信息工程学院综合性实验报告一、实验目的二、本实验通过MATLAB语言编写程序来实现, 主要培养学生综合运用所学知识和实验方法、实验技能, 提高分析、解决实际问题的能力。

三、实验仪器或设备装MATLAB软件的计算机一台。

四、总体设计（设计原理、设计方案及流程等）1.用if语句实现以下计算, a,b,c,x 的值从键盘输入:五、输入20个数, 求其中最大数和最小数, 要求用while循环结构和MATLAB的max和min 函数来实现。

六、设计一段程序, 用for循环求1+2+3+…+100的和。

七、实验步骤（包括主要步骤、代码分析等）1.求函数(if循环语句)x=input('please input x= ');a=input('please input a= ');b=input('please input b= ');c=input('please input c= ');if(x>=0.5)&&(x<1.5);y=a*x^2+b*x+c;elseif(x>=1.5)&&(x<3.5);y=a*sin(x)+b+c;elseif(x>=3.5)&&(x<5.5);y=log(abs(b+c/x));elsey=0;enddisp('The answer of y= ')disp(y)2.求最大值、最小值i=1;j=1;n=0;m=0;x=0;y=0;while(i<=10)&&(j<=10)a(i)=input('Enter the number of a: ');b(j)=input('Enter the number of b: ');n=max(a,b);m=min(a,b);i=i+1;'i';j=j+1;'j';endx=max(n);y=min(m);disp('The max number is ')disp(x)disp('The min number is ')disp(y)3.求和function [ S ] = Sum( ~ )S=0;for n= 1:1:100if(n<=100)S=S+n;n=n+1;endendend八、结果分析与总结1.刚开始做实验的时候, 由于理论知识基础学不好, 在实验过程遇到了许多的难题, 使我意识到理论知识的重要性；2.在实验过程自己遇到问题, 通过看书、查资料、思考交流, 最终解决问题也使我感到有成就感。