材料的热膨胀

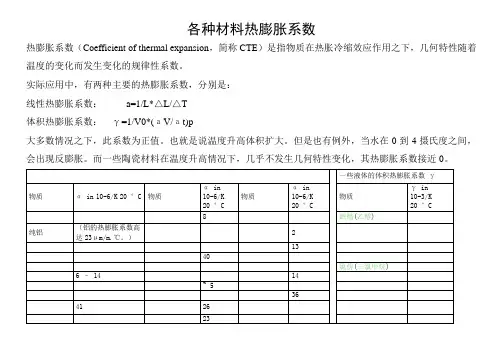
热的膨胀和膨胀系数的计算材料的热膨胀是指由于温度的升高，材料的长度、面积或体积增加的现象。

膨胀系数是一个材料的性质，用来描述其对温度变化的敏感度。

本文将介绍热膨胀的基本原理以及如何计算膨胀系数。

一、热膨胀的原理根据热力学原理，物质的温度升高会导致分子的热运动增强，分子之间的相互作用力减弱，使材料的体积、长度或面积增大。

不同材料的热膨胀性能可能有所不同，这取决于其结构、成分和弹性模量等因素。

热膨胀是一种普遍存在于物质中的现象，对于工程设计和材料选择具有重要意义。

二、线膨胀系数的计算线膨胀系数（α）是描述材料在一定温度下单位长度的膨胀量。

通常用公式表示为：ΔL = αL₀ΔT其中，ΔL是材料长度的变化量，L₀是初始长度，ΔT是温度的变化量。

根据单位换算，线膨胀系数的单位通常是1/℃或者K⁻¹。

线膨胀系数可以通过实验测量或者查阅资料获得，常见材料的线膨胀系数如下：- 钢：11x10⁻⁶ /℃- 铝：23x10⁻⁶ /℃- 铜：16x10⁻⁶ /℃- 玻璃：8x10⁻⁶ /℃三、体膨胀系数的计算体膨胀系数（β）用于描述材料在一定温度下单位体积的膨胀量。

通常用公式表示为：ΔV = βV₀ΔT其中，ΔV是材料体积的变化量，V₀是初始体积，ΔT是温度的变化量。

与线膨胀系数类似，体膨胀系数的单位也是1/℃或者K⁻¹。

体膨胀系数可以通过实验测量或者查阅资料获得，常见材料的体膨胀系数如下：- 钢：3x10⁻⁵ /℃- 铝：7x10⁻⁵ /℃- 铜：5x10⁻⁵ /℃- 玻璃：9x10⁻⁶ /℃四、应用实例假设我们有一根长度为1m的铁管，将其加热到100℃，我们可以根据铁的线膨胀系数计算出其长度的变化量：ΔL = αL₀ΔT= 11x10⁻⁶ /℃ x 1m x 100℃= 0.011m因此，铁管的长度将增加0.011m。

同样地，我们也可以计算铁管的体积变化量：ΔV = βV₀ΔT= 3x10⁻⁵ /℃ x (1m)³ x 100℃= 0.03m³铁管的体积将增加0.03m³。

各种材料热膨胀系数材料的热膨胀系数可以定义为单位温度变化时材料长度、体积或面积的变化量与初始尺寸的比值。

不同材料的热膨胀系数差异很大，以下是一些常见材料的热膨胀系数。

1.金属：铝：铝的线膨胀系数为24×10^-6/℃。

因此，当铝材料从摄氏0度升到100度时，材料长度将增加约0.24%。

铁：铁的线膨胀系数为11.7×10^-6/℃。

在相同条件下，铁材料的长度增加约0.117%。

铜：铜的线膨胀系数为16.6×10^-6/℃。

在相同条件下，铜材料的长度增加约0.166%。

2.塑料：聚乙烯：聚乙烯的线膨胀系数为105×10^-6/℃。

因此，当聚乙烯材料从摄氏0度升至100度时，材料长度将增加约1.05%。

聚丙烯：聚丙烯的线膨胀系数为125×10^-6/℃。

在相同条件下，聚丙烯材料的长度增加约1.25%。

聚四氟乙烯：聚四氟乙烯的线膨胀系数为12×10^-6/℃。

在相同条件下，聚四氟乙烯材料的长度增加约0.12%。

3.陶瓷：石英：石英的膨胀系数为0.5×10^-6/℃。

因此，当石英材料从摄氏0度升至100度时，材料长度将增加约0.005%。

氧化铝：氧化铝的线膨胀系数约为7.4×10^-6/℃。

在相同条件下，氧化铝材料的长度增加约0.074%。

4.玻璃：硼硅酸玻璃：硼硅酸玻璃的线膨胀系数约为3.3×10^-6/℃。

因此，当硼硅酸玻璃材料从摄氏0度升至100度时，材料长度将增加约0.033%。

钠钙玻璃：钠钙玻璃的线膨胀系数约为9×10^-6/℃。

在相同条件下，钠钙玻璃材料的长度增加约0.09%。

总结：不同材料的热膨胀系数可以很大程度上影响材料的热胀冷缩性能。

了解材料的热膨胀系数可以帮助工程师设计和预测材料在不同温度下的性能和变形情况。

常见材料热膨胀系数解析常见材料热膨胀系数解析引言：热膨胀是物体在温度变化时展现出的一种性质，也是工程设计和材料选择中不可忽视的因素。

随着温度的升高，物体的尺寸会发生改变，这可能会对工程结构的稳定性和性能产生重要影响。

理解和掌握常见材料的热膨胀系数是非常重要的。

一、热膨胀系数的概念和定义热膨胀系数是一个描述物体在温度变化时膨胀程度的物理量，通常用符号α表示。

它定义为单位温度变化下单位长度的线膨胀或体膨胀量。

常见的热膨胀系数单位是°C⁻¹。

二、常见材料的热膨胀系数1. 金属材料：金属是一类导热性能较好的材料，它的热膨胀系数一般比较大。

铝的热膨胀系数为22.2×10⁻⁶ °C⁻¹，而钢的热膨胀系数在10×10⁻⁶ - 13×10⁻⁶ °C⁻¹之间。

在工程设计中使用金属材料时，需要考虑温度变化对构件的影响。

2. 石材和混凝土：石材和混凝土是建筑工程中常用的材料，它们的热膨胀系数比金属要小。

石材的热膨胀系数在5×10⁻⁶ - 11×10⁻⁶ °C⁻¹之间，混凝土的热膨胀系数约为10×10⁻⁶ °C⁻¹。

这种相对较小的热膨胀系数使得石材和混凝土在温度变化下变形较小，更适用于建筑结构的使用。

3. 塑料和橡胶：塑料和橡胶是热膨胀系数较大的材料。

由于它们的热膨胀系数较高，温度变化会导致较大的变形。

在使用塑料和橡胶制品的工程中，需要考虑温度变化对构件的影响，特别是在高温环境下。

4. 玻璃：玻璃的热膨胀系数比较小，一般在8×10⁻⁶ - 10×10⁻⁶ °C⁻¹之间。

这使得玻璃在温度变化下变形较小，适用于长时间稳定性要求较高的工程结构和仪器设备。

三、热膨胀系数的影响和应用1. 工程设计中的考虑：在工程设计中，材料的热膨胀系数需要考虑作为一个重要的参数。

常见材料热膨胀系数
【实用版】
目录
1.热膨胀系数的定义和意义
2.常见材料的热膨胀系数
3.热膨胀系数在实际应用中的重要性
4.结论
正文
热膨胀系数是一个重要的物理量，它表征了物体在受热时，其长度、面积或体积变化的程度。

热膨胀系数包括线膨胀系数、面膨胀系数和体膨胀系数，这些系数可以用来描述物质在不同温度下的膨胀情况。

在日常生活中，我们常常会接触到各种材料，如金属、陶瓷、塑料等。

这些材料的热膨胀系数是不同的，因此，在实际应用中，我们需要根据材料的热膨胀系数来设计产品，以确保产品的稳定性和安全性。

例如，在制造金属器件时，我们需要选择具有相近热膨胀系数的金属材料，以避免因温度变化引起的器件变形或破裂。

同样，在焊接或熔接不同材料时，我们也需要选择具有相近热膨胀系数的材料，以确保焊接或熔接处的稳定性。

热膨胀系数在实际应用中的重要性不言而喻。

在工程设计、材料科学、物理学等领域，热膨胀系数都是一个重要的研究课题。

通过研究材料的热膨胀系数，我们可以更好地了解材料的性质和特点，从而更好地利用这些材料来满足我们的需求。

总的来说，热膨胀系数是一个重要的物理量，它对于我们了解和利用材料具有重要的意义。

在实际应用中，我们需要根据材料的热膨胀系数来设计产品，以确保产品的稳定性和安全性。

材料的热膨胀行为及其在工程中的应用材料的热膨胀行为是指当材料受热时，其体积、长度和面积会发生改变的现象。

热膨胀行为是由于物质内部原子的热运动引起的，随着温度的升高，原子的热振动增强，从而使材料的尺寸发生变化。

热膨胀在工程中有着广泛的应用，下面将从材料选择、结构设计和工程实践等方面进行论述。

1. 材料选择在工程设计中，我们需要考虑材料的热膨胀系数。

热膨胀系数是描述材料热膨胀行为的物理量，它表示在单位温度变化下，材料单位长度的形变量。

不同材料的热膨胀系数存在差异，因此在选材时需要根据具体的工程要求和环境条件来选择合适的材料。

例如，在建筑领域中，由于环境温度的变化以及建筑材料的特性差异，我们需要选择具有相似热膨胀系数的材料来减小热膨胀对结构的影响。

另外，在航空航天、核工程等领域，材料的低热膨胀系数是一个重要的考虑因素，以确保材料在极端温度环境下的稳定性与可靠性。

2. 结构设计在工程结构设计中，必须合理考虑材料的热膨胀行为，以避免由于热膨胀引起的变形、开裂等问题。

一种常见的应用是利用热膨胀行为来设计伸缩缝和隔热层。

伸缩缝可以有效地补偿材料由于温度变化而引起的体积变化，防止产生过大的应力，从而减小结构的变形和破坏风险。

在建筑物、桥梁、管道等工程中广泛采用伸缩缝的设计，以确保结构的稳定性与耐久性。

隔热层的设计也是基于材料的热膨胀行为。

在高温环境下，结构材料容易受到热膨胀的影响，从而导致材料性能的下降和破坏。

通过在结构表面覆盖一层隔热材料，可以减少热膨胀对结构的直接作用，提高结构的稳定性和耐用性。

3. 工程实践热膨胀行为在工程实践中的应用包括管道的伸缩补偿、高温设备的设计等。

管道的伸缩补偿是为了解决由于温度变化引起的管道变形和应力增大问题。

通过在管道中安装伸缩补偿器，可以有效地补偿热膨胀引起的管道变形，保证管道的正常运行。

在高温设备的设计中，必须考虑材料的热膨胀特性。

例如，在炉膛的设计中，需合理预留热膨胀空间，以避免设备由于热膨胀而产生应力集中和变形等问题。

第三节材料热膨胀一、固体热膨胀机理线膨胀系数αl ：体膨胀系数αV ：对于各向同性材料，有：00()f f l l l T T l α−−=0l l l TαΔ=Δ（l 0、l f 0V V V TαΔ=Δ（V 0、ΔV 分别是初始体积和体积变化量）3V lαα≅热膨胀本质：从原子的观点看，热膨胀是点阵结构中的质点间平均距离随温度升高而增大现象的宏观反映质点的振动可分为简谐振动和非简谐振动材料热膨胀的物理本质是质点振动的非简谐效应简谐效应：质点围绕其平衡位置作简谐振动，质点之间相互作用势能对平衡位置是对称的，温度升高只能增大振幅，并不改变平衡位置。

质点间平均距离不会因温度升高而改变，即不改变晶体的大小和形状，晶体受热不膨胀非简谐效应：原子之间斥力项（玻恩斥力B/r n，n和原子的电子层有关，电子层越多，n越大，nHe =5，nNe=7，nAr=9）随原子间距的变化比引力项（库仑力A/r2）的变化更快。

热振动不是左右对称的线性振动，而是非线性振动23在质点平衡位置r 0的两侧，合力曲线的斜率是不相等的。

当r <r 0时，曲线的斜率较大；r >r 0时，斜率较小。

r <r 0时斥力随位移变化很快；r >r 0时引力随位移的变化要慢一些在这样的受力情况下，质点振动时的平均位置就不在r 0处，而要向右移。

因此相邻质点间平均距离增加温度越高，振幅越大，质点在r 0两侧受力不对称情况越显著，平衡位置向右移动越多，相邻质点间平均距离就增加得越多，以致晶胞参数增大，晶体膨胀从点阵能曲线的非对称性同样可以得到具体解释非对称势能曲线对称势能曲线T 1T 2T 3T 4T 5对于给定的点阵能曲线，r，β，β’均为常数，似乎α也为常数。

但如再考虑δ4，δ5，…时，则可得α随温度而变化的规律除了质点的非对称振动外，作为次要因素，晶体中的各种热缺陷的形成也将造成局部点阵的畸变和膨胀且随着温度升高，缺陷浓度按指数关系增加。