自动控制原理仿真

一、实验目的1. 熟悉MATLAB/Simulink仿真软件的基本操作。

2. 学习控制系统模型的建立与仿真方法。

3. 通过仿真分析，验证理论知识，加深对自动控制原理的理解。

4. 掌握控制系统性能指标的计算方法。

二、实验内容本次实验主要分为两个部分：线性连续控制系统仿真和非线性环节控制系统仿真。

1. 线性连续控制系统仿真（1）系统模型建立根据题目要求，我们建立了两个线性连续控制系统的模型。

第一个系统为典型的二阶系统，其开环传递函数为：\[ G(s) = \frac{1}{(s+1)(s+2)} \]第二个系统为具有迟滞环节的系统，其开环传递函数为：\[ G(s) = \frac{1}{(s+1)(s+2)(s+3)} \]（2）仿真与分析（a）阶跃响应仿真我们对两个系统分别进行了阶跃响应仿真，并记录了仿真结果。

（b）频率响应仿真我们对两个系统分别进行了频率响应仿真，并记录了仿真结果。

（3）性能指标计算根据仿真结果，我们计算了两个系统的性能指标，包括上升时间、超调量、调节时间等。

2. 非线性环节控制系统仿真（1）系统模型建立根据题目要求，我们建立了一个具有饱和死区特性的非线性环节控制系统模型。

其传递函数为：\[ W_k(s) = \begin{cases}1 & |s| < 1 \\0 & |s| \geq 1\end{cases} \]（2）仿真与分析（a）阶跃响应仿真我们对非线性环节控制系统进行了阶跃响应仿真，并记录了仿真结果。

（b）相轨迹曲线绘制根据仿真结果，我们绘制了四条相轨迹曲线，以分析非线性环节对系统性能的影响。

三、实验结果与分析1. 线性连续控制系统仿真（a）阶跃响应仿真结果表明，两个系统的性能指标均满足设计要求。

（b）频率响应仿真结果表明，两个系统的幅频特性和相频特性均符合预期。

2. 非线性环节控制系统仿真（a）阶跃响应仿真结果表明，非线性环节对系统的性能产生了一定的影响，导致系统响应时间延长。

实验一 MATLAB及仿真实验（控制系统的时域分析）一、实验目的学习利用MATLAB进行控制系统时域分析，包括典型响应、判断系统稳定性和分析系统的动态特性；二、预习要点1、系统的典型响应有哪些？2、如何判断系统稳定性？3、系统的动态性能指标有哪些？三、实验方法（一）四种典型响应1、阶跃响应：阶跃响应常用格式：1、；其中可以为连续系统，也可为离散系统。

2、；表示时间范围0---Tn。

3、；表示时间范围向量T指定。

4、；可详细了解某段时间的输入、输出情况。

2、脉冲响应：脉冲函数在数学上的精确定义：其拉氏变换为：所以脉冲响应即为传函的反拉氏变换。

脉冲响应函数常用格式：①；②③（二）分析系统稳定性有以下三种方法：1、利用pzmap绘制连续系统的零极点图；2、 利用tf2zp 求出系统零极点；3、 利用roots 求分母多项式的根来确定系统的极点 （三） 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1． 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ，试判断其稳定性2． 用Matlab 求出的极点。

%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den) 运行结果： p =-1.7680 + 1.2673i -1.7680 - 1.2673i 0.4176 + 1.1130i 0.4176 - 1.1130i -0.2991P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知，该系统的2个极点具有正实部，故系统不稳定。

实验一 MATLAB 及仿真实验（控制系统的时域分析）一、实验目的学习利用MATLAB 进行控制系统时域分析，包括典型响应、判断系统稳定性和分析系统的动态特性； 二、预习要点1、 系统的典型响应有哪些2、 如何判断系统稳定性3、 系统的动态性能指标有哪些 三、实验方法（一） 四种典型响应1、 阶跃响应：阶跃响应常用格式：1、)(sys step ；其中sys 可以为连续系统，也可为离散系统。

2、),(Tn sys step ；表示时间范围0---Tn 。

3、),(T sys step ；表示时间范围向量T 指定。

4、),(T sys step Y =；可详细了解某段时间的输入、输出情况。

2、 脉冲响应：脉冲函数在数学上的精确定义：0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为：)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。

脉冲响应函数常用格式： ① )(sys impulse ； ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y =（二） 分析系统稳定性 有以下三种方法：1、 利用pzmap 绘制连续系统的零极点图；2、 利用tf2zp 求出系统零极点；3、 利用roots 求分母多项式的根来确定系统的极点 （三） 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1． 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ，试判断其稳定性2． 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。

%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果： p =+ - + -P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知，该系统的2个极点具有正实部，故系统不稳定。

兰州理工大学《自动控制原理》MATLAB分析与设计仿真实验报告院系：电气工程与信息工程学院班级：电气工程及其自动化四班姓名：学号：时间：年月日电气工程与信息工程学院《自动控制原理》MATLAB 分析与设计仿真实验任务书（2014） 一、仿真实验内容及要求 1．MATLAB 软件要求学生通过课余时间自学掌握MATLAB 软件的基本数值运算、基本符号运算、基本程序设计方法及常用的图形命令操作；熟悉MATLAB 仿真集成环境Simulink 的使用。

2．各章节实验内容及要求1）第三章 线性系统的时域分析法∙ 对教材第三章习题3-5系统进行动态性能仿真，并与忽略闭环零点的系统动态性能进行比较，分析仿真结果；∙ 对教材第三章习题3-9系统的动态性能及稳态性能通过仿真进行分析，说明不同控制器的作用；∙ 在MATLAB 环境下选择完成教材第三章习题3-30，并对结果进行分析； ∙ 在MATLAB 环境下完成英文讲义P153.E3.3；∙ 对英文讲义中的循序渐进实例“Disk Drive Read System”，在100=a K 时，试采用微分反馈控制方法，并通过控制器参数的优化，使系统性能满足%5%,σ<3250,510s ss t ms d -≤<⨯等指标。

2）第四章 线性系统的根轨迹法∙ 在MATLAB 环境下完成英文讲义P157.E4.5； ∙ 利用MATLAB 绘制教材第四章习题4-5；∙ 在MATLAB 环境下选择完成教材第四章习题4-10及4-17，并对结果进行分析；∙ 在MATLAB 环境下选择完成教材第四章习题4-23，并对结果进行分析。

3）第五章 线性系统的频域分析法∙ 利用MATLAB 绘制本章作业中任意2个习题的频域特性曲线；4）第六章 线性系统的校正∙ 利用MATLAB 选择设计本章作业中至少2个习题的控制器，并利用系统的单位阶跃响应说明所设计控制器的功能；∙ 利用MATLAB 完成教材第六章习题6-22控制器的设计及验证；∙ 对英文讲义中的循序渐进实例“Disk Drive Read System”，试采用PD控制并优化控制器参数，使系统性能满足给定的设计指标ms t s 150%,5%<<σ。

实验一 典型环节的MATLAB 仿真 一、实验目的1．熟悉MATLAB 桌面和命令窗口，初步了解SIMULINK 功能模块的使用方法。

2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。

3．定性了解各参数变化对典型环节动态特性的影响。

二、实验内容① 比例环节1)(1=s G 和2)(1=s G ；Simulink 图形实现：示波器显示结果：② 惯性环节11)(1+=s s G 和15.01)(2+=s s GSimulink 图形实现：示波器显示结果：③ 积分环节s s G 1)(1Simulink 图形实现：示波器显示结果：④ 微分环节s s G )(1Simulink 图形实现：波器显示结果：⑤ 比例+微分环节（PD ）2)(1+=s s G 和1)(2+=s s G1）、G1（s ）=s+2Simulink 图形实现：示波器显示结果：2）、G2（s）=s+1 Simulink图形实现：示波器显示结果：⑥ 比例+积分环节（PI ）s s G 11)(1+=和s s G 211)(2+=1）、G1（1）=1+1/sSimulink 图形实现：示波器显示结果：2）G2（s）=1+1/2s Simulink图形实现：示波器显示结果：三、心得体会通过这次实验我学到了很多，对课本内容加深了理解，熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法，加深对各典型环节响应曲线的理解，这为对课程的学习打下了一定基础。

实验二线性系统时域响应分析一、实验目的1．熟练掌握step( )函数和impulse( )函数的使用方法，研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。

2．通过响应曲线观测特征参量ζ和nω对二阶系统性能的影响。

3．熟练掌握系统的稳定性的判断方法。

二、实验内容1．观察函数step( )的调用格式，假设系统的传递函数模型为243237()4641s s G s s s s s ++=++++绘制出系统的阶跃响应曲线？2．对典型二阶系统222()2n n n G s s s ωζωω=++1）分别绘出2(/)n rad s ω=，ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线，分析参数ζ对系统的影响，并计算ζ=0.25时的时域性能指标,,,,p r p s ss t t t e σ。

自动控制原理实验报告学 院 电子信息与电气工程学院实验一 MATLAB 及仿真实验（控制系统的时域分析）一、实验目的学习利用MATLAB 进行控制系统时域分析，包括典型响应、判断系统稳定性和分析系统的动态特性； 二、预习要点 1、 系统的典型响应有哪些？ 2、 如何判断系统稳定性？ 3、系统的动态性能指标有哪些？三、实验方法 （一） 四种典型响应 1、阶跃响应： 阶跃响应常用格式：1、)(sys step ；其中sys 可以为连续系统，也可为离散系统。

2、),(Tn sys step ；表示时间范围0---Tn 。

3、),(T sys step ；表示时间范围向量T 指定。

4、),(T sys step Y =；可详细了解某段时间的输入、输出情况。

2、脉冲响应：脉冲函数在数学上的精确定义：0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为：)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。

脉冲响应函数常用格式： ① )(sys impulse ； ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y = （二） 分析系统稳定性 有以下三种方法： 1、 利用pzmap 绘制连续系统的零极点图； 2、 利用tf2zp 求出系统零极点；3、利用roots 求分母多项式的根来确定系统的极点（三） 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1． 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ，试判断其稳定性2．用Matlab求出253722)(2342++++++=s s s s s s s G 的极点。

控制系统的模拟试验和MATLAB 仿真1 MATLAB 简介MATLAB 是Mathworks 公司开发的一种集数值计算、符号计算和图形可视化三大基本功能于一体的功能强大、操作简单的优秀工程计算使用软件。

MATLAB 不仅可以处理代数问题和数值分析问题，而且还具有强大的图形处理及仿真模拟等功能。

从而能够很好的帮助工程师及科学家解决实际的技术问题。

MATLAB 的含义是矩阵实验室（Matrix Laboratory ），最初主要用于方便矩阵的存取，其基本元素是无需定义维数的矩阵。

经过十几年的扩充和完善，现已发展成为包含大量实用工具箱（Toolbox ）的综合使用软件，不仅成为线性代数课程的标准工具，而且适合具有不同专业研究方向及工程使用需求的用户使用。

MATLAB 最重要的特点是易于扩展。

它允许用户自行建立完成指定功能的扩展MATLAB 函数（称为M 文件），从而构成适合于其它领域的工具箱，大大扩展了MATLAB 的使用范围。

目前，MATLAB 已成为国际控制界最流行的软件，控制界很多学者将自己擅长的CAD 方法用MATLAB 加以实现，出现了大量的MATLAB 配套工具箱，如控制系统工具箱（control systems toolbox ），系统识别工具箱（system identification toolbox ），鲁棒控制工具箱（robust control toolbox ），信号处理工具箱（signal processing toolbox ）以及仿真环境SIMULINK 等。

（1） MATLAB 的安装本节将讨论操作系统为Microsoft Windows 环境下安装MATLAB7的过程。

将MATLAB7的安装盘放入光驱，系统将自动运行auto-run.bat 文件，进行安装；也可以执行安装盘内的setup.exe 文件启动MATLAB 的安装程序。

启动安装程序后，屏幕将显示安装MATLAB 的初始界面，根据Windows 安装程序的常识，不断单击[Next],输入正确的安装信息，具体操作过程如下：输入正确的用户注册信息码；选择接收软件公司的协议；输入用户名和公司名；选择MATLAB 组件（Toolbox ）；选择软件安装路径和目录；单击[Next]按钮进入正式的安装界面。

自动控制系统的建模与仿真自动控制系统的建模和仿真是实现控制系统设计、分析、调试和优化的一种重要方法。

本文将从控制系统建模的概念入手，介绍控制系统建模的基本方法，并通过实例介绍控制系统的仿真过程。

一、控制系统建模的基本概念1. 控制系统建模的概念控制系统建模是指将控制系统抽象为数学模型的过程，其目的是方便对控制系统进行设计、分析和优化。

2. 控制系统的分类根据输入输出信号的性质，控制系统可分为模拟控制系统和数字控制系统。

模拟控制系统是指输入输出信号为模拟信号的控制系统，数字控制系统是指输入输出信号为数字信号的控制系统。

3. 控制系统的基本结构控制系统由控制器、执行器和被控对象三部分组成。

控制器负责对被控对象进行信号处理和决策，输出控制信号；执行器接收控制信号，通过转换为相应的动力或能量信号控制被控对象的运动；被控对象是控制系统的实际操作对象，其状态受执行器控制信号影响而改变。

4. 控制系统的数学模型控制系统的数学模型是描述其输入输出关系的数学方程或模型，可将其简化为传递函数的形式。

控制系统的数学模型有两种主要表达方式，一种是状态空间表达式，一种是等效传递函数式。

二、控制系统建模的基本方法1. 确定控制系统类型和目标在建模之前，需要对控制系统的类型和目标进行确定，包括控制系统的输入和输出信号的特征、被控对象的特性等。

2. 建立被控对象的数学模型被控对象的数学模型包括其动态特性和静态特性。

动态特性即描述被控对象内部变化规律的数学模型，静态特性即描述被控对象输入输出关系的数学模型。

3. 建立控制器的数学模型控制器的数学模型要根据被控对象的数学模型和控制系统的控制目标进行设计。

4. 建立控制系统的数学模型将被控对象的数学模型和控制器的数学模型相结合，得到控制系统的数学模型，可推导得到控制系统的传递函数。

5. 对控制系统进行仿真通过仿真软件对控制系统进行仿真，可以实现在不同工作条件下模拟出控制系统的工作状态和性能，以验证控制系统的可行性。

《自动控制原理》的虚拟仿真在课堂教学中的应用【摘要】本文主要探讨了《自动控制原理》课堂教学中虚拟仿真技术的应用。

首先介绍了背景和研究意义，指出虚拟仿真技术在教学中的重要性。

随后分析了自动控制原理课堂教学的特点，探讨了虚拟仿真在课堂教学中的作用。

重点探讨了虚拟仿真在实验和理论教学中的应用，提出了这种技术的推动作用和未来发展方向。

通过本文的研究，可以发现虚拟仿真技术对提高自动控制原理课堂教学效果具有积极作用，为未来教学提供了新的可能性和方向。

【关键词】自动控制原理、虚拟仿真技术、教学应用、课堂教学、实验教学、理论教学、推动作用、未来发展方向1. 引言1.1 背景介绍在自动控制原理课程中，学生需要理解和掌握各种控制系统的原理、结构、性能和设计方法，这对于他们的职业发展至关重要。

传统的理论课堂教学往往无法满足学生的需求，因为很多抽象概念和理论难点需要通过实验操作进行直观展示才能更好地理解。

虚拟仿真技术的应用可以有效地弥补这一不足，提供一个更加生动和直观的学习环境，使学生能够更深入地理解自动控制原理的知识，提高他们的学习效果和技能水平。

1.2 研究意义虚拟仿真技术可以帮助学生更直观地理解自动控制原理中的抽象概念。

通过虚拟仿真，学生可以看到实际系统的运行情况，可以进行仿真实验并观察实验结果，从而更加深入地理解课程内容。

这有助于提高学生的学习兴趣和学习效果。

虚拟仿真技术还可以提高自动控制原理课程的实践性和互动性。

学生可以通过虚拟仿真软件进行实际操作，调整参数，观察系统变化，从而加深对自动控制原理的理解。

学生之间还可以通过虚拟仿真软件进行交流和合作，促进学生之间的互动和合作。

引入虚拟仿真技术到自动控制原理课堂教学中，不仅可以提高教学效果，增强学生的学习兴趣，还可以提高学生的实践能力和创新能力，为学生的职业发展奠定更加坚实的基础。

研究虚拟仿真技术在自动控制原理课堂教学中的应用具有重要的意义。

1.3 研究目的研究目的是探讨虚拟仿真技术在自动控制原理课堂教学中的应用效果，以期为提高教学质量和学生学习效果提供有效的方法和技术支持。

matlab仿真自动控制原理
MATLAB仿真自动控制原理
自动控制原理是研究自动调节系统的基本理论和方法，MATLAB作为一款强大的数学仿真软件，为自动控制原理的研究提供了良好的平台。

MATLAB在自动控制原理的研究中，主要包括以下内容：
1. 系统动态模型的建立：根据自动调节系统的特性及其输入输出关系，建立数学模型，并进行仿真。

2. 系统稳态性能分析：计算系统的稳态误差和静态增益等指标，确定系统的增益校正和调节参数。

3. 系统动态性能分析：分析系统的过渡过程、阻尼比和动态特性，确定系统的控制参数。

4. 设计控制器：根据系统模型和目标性能要求，设计合适的控制器，如比例积分控制器、比例积分微分控制器等。

5. 仿真验证：通过MATLAB仿真，验证控制器的性能和控制效果。

通过MATLAB仿真自动控制原理，不仅可以方便地进行各种控制系统的设计与分析，同时也可以通过仿真验证的方法，快速评估和分析不同控制策略的优劣，提高控制系统的稳定性和性能。

《自动控制原理》控制系统的simulink仿真实验一、实验目的(1)初步了解Matlab中Simulink的使用方法，熟悉simulink模块的操作和信号线的连接(2)通过观察典型环节在单位阶跃信号作用下的动态特性，熟悉各种典型环节的响应曲线。

(3)定性了解各参数变化对典型环节动态特性的影响。

二、实验仪器装配Matlab7.0的计算机三、实验原理Simulink是MATLAB中的一种可视化仿真工具。

Simulink是一个模块图环境，用于多域仿真以及基于模型的设计。

它支持系统设计、仿真、自动代码生成以及嵌入式系统的连续测试和验证。

四、实验内容及步骤1.1 运行Matlab，在命令窗口“Command Window”下键入“Simulink”后回车，则打开相应的系统模型库；或者点击工具栏上的“Simulink”图标，进入系统仿真模型库，然后点击左上角“新文件”图标，打开模型编辑窗口。

1.2 调出模块在系统仿真模型库中，把要求的模块都放置在模型编辑窗口里面。

从信号源模块包(Sources)中拖出1个阶跃信号(step)和1个白噪声信号发生器(band-limited white noise) ；从数学运算模块包(Math Operations)中拖出1个比例环节(gain)和1个加法器(sum) ；从连续系统典型环节模块包(Continuous) 中拖出1个微分环节(Derivative)和3个传函环节(transfer Fcn)；从信号与系统模块包(Signals Routing) 拖出1个汇流排(mux)；从输出模块包(Sinks)中拖出1个示波器(scope)；所有模块都放置在模型编辑窗口里面。

1.3 模块参数设置（鼠标左键双击各典型环节，则可进行参数设置）双击打开白噪声信号发生器，设定功率(Noise power)为0.0001，采样时间(Sample time)为0.05。

打开比例环节，设定比例增益为2；打开3个传函环节(transfer Fcn)，通过参数设定，分别构成积分、惯性和二阶环节；1.4 模块连接五、实验原始数据记录与数据处理（22.1 双击Scope打开示波器，点击按钮“ ”启动仿真，画出输入信号波形图。

实验名称：自动控制系统的MATLAB仿真分析一、实验目的1.熟悉MATLAB在自动控制系统仿真中的应用；2.对自动控制系统进行仿真研究；3.掌握用MATLAB绘制自动控制系统根轨迹及对数频率特性的方法，掌握根据系统根轨迹及对数频率特性分析自动控制系统性能的方法。

二、实验设备1.计算机2.MATLAB软件三、实验内容1.用MATLAB提供的Simulink仿真软件工具对实验一中的各个典型环节及二阶系统进行阶跃响应仿真研究，将仿真获得的阶跃响应结果与模拟电路获得的阶跃响应结果进行比较。

（1）比例环节传递函数为200 ()51 G s=建立仿真模型，得到的输出结果如图所示：（2）积分环节传递函数为9.8 ()G ss=建立仿真模型，得到的输出结果如图所示：（3）一阶惯性环节传递函数为3.9 ()0.21G ss=+建立仿真模型，得到的输出结果如图所示：（4）比例积分环节传递函数为0.39781 ()0.102sG ss+=建立仿真模型，得到的输出结果如图所示：（5）比例微分环节传递函数为10 ()220s G ss=++建立仿真模型，得到的输出结果如图所示：（6）比例微分积分环节传递函数为51050 ()220sG ss s+=+++建立仿真模型，得到的输出结果如图所示：（7） 二阶系统的阶跃响应 ①0.325K ξ==传递函数为2()250()10250C s R s s s =++ 建立的仿真模型与阶跃响应仿真波形如下图所示：②0.510K ξ==传递函数为2()100()10100C s R s s s =++ 建立的仿真模型与阶跃响应仿真波形如下图所示：③0.75K ξ==传递函数为2()50()1050C s R s s s =++ 建立的仿真模型与阶跃响应仿真波形如下图所示：2. 单位负反馈系统的开环传递函数为：(1)()()(21)k s G s H s s s +=+仿真绘制K 从0~∞变化时的根轨迹，分析系统的稳定性。

自动控制原理MATLAB仿真实验实验指导书电子信息工程教研室实验一典型环节的MA TLAB仿真一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。

2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。

3．定性了解各参数变化对典型环节动态特性的影响。

二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。

利用SIMULINK功能模块可以快速的建立控制系统的模型，进行仿真和调试。

1．运行MA TLAB软件，在命令窗口栏“>>”提示符下键入simulink命令，按Enter键或在工具栏单击按钮，即可进入如图1-1所示的SIMULINK仿真环境下。

2．选择File菜单下New下的Model命令，新建一个simulink仿真环境常规模板。

图1-1 SIMULINK仿真界面图1-2 系统方框图3．在simulink仿真环境下，创建所需要的系统。

以图1-2所示的系统为例，说明基本设计步骤如下：1）进入线性系统模块库，构建传递函数。

点击simulink下的“Continuous”，再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。

2）改变模块参数。

在simulink仿真环境“untitled”窗口中双击该图标，即可改变传递函数。

其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数，数字之间用空格隔开；设置完成后，选择OK，即完成该模块的设置。

3）建立其它传递函数模块。

按照上述方法，在不同的simulink的模块库中，建立系统所需的传递函数模块。

例：比例环节用“Math”右边窗口“Gain”的图标。

4）选取阶跃信号输入函数。

用鼠标点击simulink下的“Source”，将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口，形成一个阶跃函数输入模块。

自动控制原理的仿真实验教学设计自动控制原理是现代工程技术领域中的重要基础学科，它涉及到许多方面，如控制系统的设计、分析和优化等。

而仿真实验则是自动控制原理教学中不可或缺的一部分，它可以帮助学生更好地理解和掌握自动控制原理的基本概念和方法。

本文将着重探讨自动控制原理仿真实验教学设计的相关问题。

一、自动控制原理的基本概念和方法自动控制原理是指利用自动化技术和控制理论对各种系统进行控制的方法和技术。

在自动控制原理中，控制系统是一个重要的概念，它是由一组相互作用的元件和设备组成的系统，用于控制某个物理量或变量。

控制系统的设计和分析需要掌握一些基本概念和方法，如反馈控制、开环控制、传递函数、根轨迹等。

这些概念和方法是自动控制原理的基础，也是学生在进行仿真实验时需要掌握的知识点。

二、自动控制原理仿真实验的意义自动控制原理仿真实验是一种重要的教学方法，它可以帮助学生更好地理解和掌握自动控制原理的基本概念和方法。

与传统的实验教学相比，仿真实验具有以下优点：1. 安全性高：传统的实验教学需要使用实际设备和仪器，存在一定的危险性。

而仿真实验则是通过计算机软件进行模拟，不会对学生的安全造成任何威胁。

2. 灵活性强：传统的实验教学需要预定时间和地点，而仿真实验可以随时随地进行，不受时间和地点的限制。

3. 成本低廉：传统的实验教学需要购买实验设备和仪器，费用较高。

而仿真实验只需要购买相应的计算机软件，费用较低。

4. 实验结果可重复性好：传统的实验教学容易受到环境和条件的影响，实验结果不易重复。

而仿真实验则可以通过更改参数和条件进行多次实验，实验结果更易重复。

三、自动控制原理仿真实验教学设计1. 实验内容的选择自动控制原理的仿真实验可以涉及到许多方面，如反馈控制、开环控制、PID控制、根轨迹分析等。

在选择实验内容时，应根据学生的实际情况和教学要求进行选择，尽可能涵盖自动控制原理的基本概念和方法。

2. 实验软件的选择自动控制原理的仿真实验需要使用相应的计算机软件进行模拟。

自动控制原理的仿真实验教学设计自动控制原理是现代工程技术中的重要学科之一，其应用广泛，涉及到许多领域，如工业控制、机械控制、电力系统控制等。

为了使学生更好地掌握自动控制原理，教学应该注重实践和应用，而仿真实验是一种非常有效的教学手段。

本文将介绍一种基于仿真实验的自动控制原理教学设计。

一、教学目标本教学设计的目标是让学生掌握以下内容：1.自动控制原理的基本概念和理论知识。

2.使用Simulink进行仿真实验，掌握仿真实验的基本操作和方法。

3.设计和实现常见控制系统的仿真实验，如比例控制、积分控制、微分控制等。

4.理解控制系统的动态特性，如稳态误差、超调量、调节时间等。

二、教学内容1.自动控制原理的基本概念和理论知识自动控制原理是研究自动控制系统的基本原理和方法的学科。

它主要研究控制系统的结构、动态特性和控制方法等方面的问题。

自动控制系统是由传感器、执行器、控制器和处理器等组成的，它可以自动地调节系统的输出，使其达到预定的目标。

2.使用Simulink进行仿真实验Simulink是MATLAB的一个工具箱，它可以用来建立和仿真动态系统。

在本教学设计中，我们将使用Simulink进行仿真实验。

学生需要掌握Simulink的基本操作和方法，包括建立模型、设置参数、运行仿真等。

3.设计和实现常见控制系统的仿真实验在本教学设计中，我们将设计和实现常见的控制系统仿真实验，如比例控制、积分控制、微分控制等。

学生需要了解这些控制方法的基本原理和实现方法，以及它们对控制系统的影响。

4.理解控制系统的动态特性控制系统的动态特性是指控制系统在响应外部信号时的特性。

它包括稳态误差、超调量、调节时间等。

学生需要理解这些动态特性的概念和意义，以及如何通过调整控制器的参数来改善控制系统的动态特性。

三、教学方法本教学设计采用“理论教学+仿真实验”的教学方法。

在理论教学中，教师将介绍自动控制原理的基本概念和理论知识，以及控制系统的动态特性。

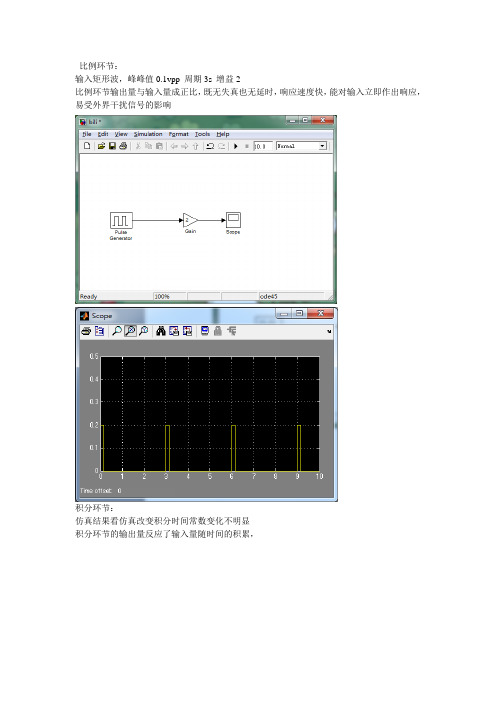
比例环节：
输入矩形波，峰峰值0.1vpp 周期3s 增益2
比例环节输出量与输入量成正比，既无失真也无延时，响应速度快，能对输入立即作出响应，易受外界干扰信号的影响
积分环节：
仿真结果看仿真改变积分时间常数变化不明显
积分环节的输出量反应了输入量随时间的积累，
\微分环节：
峰峰值1vpp 周期10秒.微分环节的输出反应了输入信号的变化速度，微分环节能预示输入信号的变化趋势。

若输入为定值，输出为常数
比例微分环节：
输入信号单位阶跃信号。

比例微分环节使得系统较单独的比例环节稳定
输入常值的时候也有输出。

避免了单独微分环节的零输出。

比例积分环节：。

中国地质大学江城学院《自动控制原理》仿真实验报告姓名吴丽芳班级数控（2）班学号2520110228指导教师祁锋2013年12月9 日目录实验一 MATLAB软件的安装与认知实验二使用软件进行数值运算和绘图实验三采用SIMULINK仿真模块进行系统性能分析实验一 MATLAB软件的认识一、实验目的MATLAB软件是具有数值分析、矩阵运算、复杂的信息处理和完美的图形显示等多种功能的软件包，它具有许多专门用途的工具箱，进一步扩展了MATLAB 的应用领域，使其在自动控制系统的分析和设计方面获得广泛的应用。

1、熟悉启动和退出MATLAB软件的方法；2、熟悉MATLAB软件的运行环境；3、熟悉MATLAB软件的基本操作；4、掌握建立矩阵的方法；5、掌握熟悉MATLAB软件各种表达式的书写规则以及常用函数的使用；6、能够进行基本的数组、矩阵运算。

二、实验内容熟悉MATLAB软件的各个工具箱、指令及常用工具，掌握数值的表示方法、运算符的使用规则及运算表达式的写法。

三、分析讨论题1、MATLAB软件有哪些常用指令？有哪些专用工具箱？help elfun %列出所有基本函数。

lookfor image 查找有关图像的函数和命令。

几个常用的通用命令。

quit 关闭MATLABexit 关闭MATLABclc 清除MATLAB命令窗口中的所有显示内容clear 清除工作空间中保存的所有变量Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱2、用举例的方法说明数值的表示方法是怎样的？MATLAB的数值采用十进制，可以带小数点或负号。