(二)化学因素朗伯—比尔定律的假定

比色分析的基本原理(朗伯-比尔定律,吸光度,消光度,吸光系数)( 关键词：比色分析,吸光光度法,光电比色法,分光光度法,朗伯-比尔定律,吸光度,消光度,吸光系数)比色分析是基于溶液对光的选择性吸收而建立起来的一种分析方法，又称吸光光度法。

有色物质溶液的颜色与其浓度有关。

溶液的浓度越大，颜色越深。

利用光学比较溶液颜色的深度，可以测定溶液的浓度。

根据吸收光的波长范围不同以及所使用的仪器精密程度，可分为光电比色法和分光光度法等。

比色分析具有简单、快速、灵敏度高等特点，广泛应用于微量组分的测定。

通常中测定含量在10-1～1 0-4mg·L-1的痕量组分。

比色分析如同其他仪器分析一样，也具有相对误差较大（一般为1%～5%）的缺点。

但对于微量组分测定来说，由于绝对误差很小，测定结果也是令人满意的。

在现代仪器分析中，有60%左右采用或部分采用了这种分析方法。

在医学学科中，比色分析也被广泛应用于药物分析、卫生分析、生化分析等方面。

一、物质的颜色和光的关系光是一种电磁波。

自然是由不同波长（400～700nm）的电磁波按一定比例组成的混合光，通过棱镜可分解成红、橙、黄、绿、青、蓝、紫等各种颜色相连续的可见光谱。

如把两种光以适当比例混合而产生白光感觉时，则这两种光的颜色互为补色。

图8-1中处于同一直线关系的两种色光（如绿与紫、黄与蓝）互为补色。

当白光通过溶液时，如果溶液对各种波长的光都不吸收，溶液就没有颜色。

如果溶液吸收了其中一部分波长的光，则溶液就蜈现透过溶液后剩余部分光的颜色。

例如，我们看到KMnO4溶液在白光下呈紫红色，就是因为白光透过溶液时，绿色光大部分被吸收，而其他各色都能透过。

在透过的光中除紫红色外都能两两互补成白色，所以KMnO4溶液呈现紫红色。

同理，CuSO4溶液能吸收黄色光，所以溶液呈蓝色。

由此可见，有色溶液的颜色是被吸收光颜色的补色。

吸收越多，则补色的颜色越深。

比较溶液颜色的深度，实质上就是比较溶液对它所吸收光的吸收程度。

比尔-朗伯定律比尔-朗伯定律，通常被称为比尔定律，是指在透明溶剂中发色团的吸光度随着样品池光程以及发色团浓度的变化而呈线性变化。

比尔定律是对描述光与物质的相互关系的麦克斯韦远场方程的简化描述。

事实上，比尔定律对一系列发色团、溶剂和浓缩物品而言都是非常精确的定律，在定量光谱学中被广泛运用。

吸光度通过分光光度计度量，这需要通过一束波长是λ的平行光束，光束要穿过一个类似平面的厚平板，该材料与光束垂直。

对液体而言，样品保存在一个叫做样品池的光学平面透明的容器里。

吸光度(Aλ)的计算是入射光穿过样品(I)的光能与入射在样品(I)表面的光能的比率。

Aλ= -log (I/I0)比尔定律遵从：A λ= ελbcc =波长λ的发色团的分子吸收率或消光系数（1M溶液的1cm厚样品的光密度），ελ 是溶液和材料的特性。

b = 样品路径（厘米）c =样品中化合物浓度，摩尔浓度 (mol L-1)在吸收度实验中，光束不仅通过发色团衰减，也通过从空气和样品之间的界面反射、样品和小型管之间的界面反射、以及溶液的吸收而衰减。

各因素可以分别量化，但常常当光束通过样品“空白”或“基准”或参考样品时，这些因素被通过定义I0的方式被去除了。

（例如，充满溶液但发色团浓度为0的小型管被用做”空白”。

）许多因素可以影响比尔定律的有效性。

它通常通过测量一系列标准的吸光度的方式用来检测发色团比尔定律的线性。

这种校准也可以去除实验、设备以及一批试剂中的误差。

（比如光程未知的样品池）。

紫外可见分光光度法——光的吸收定律一. Lambert-Beer 定律——光吸收基本定律“ Lambert-Beer 定律” 是说明物质对单色光吸收的强弱与吸光物质的浓度（c）和液层厚度（b）间的关系的定律，是光吸收的基本定律，是紫外-可见光度法定量的基础。

Lambert定律——吸收与液层厚度（b）间的关系Beer 定律——吸收与物质的浓度（c）间的关系“ Lambert-Beer 定律”可简述如下：当一束平行的单色光通过含有均匀的吸光物质的吸收池（或气体、固体）时，光的一部分被溶液吸收，一部分透过溶液，一部分被吸收池表面反射；设：入射光强度为 Io，吸收光强度为Ia，透过光强度为It，反射光强度为Ir，则它们之间的关系应为：Io = Ia + It + Ir (4)若吸收池的质量和厚度都相同，则 Ir 基本不变，在具体测定操作时 Ir 的影响可互相抵消（与吸光物质的 c及 b 无关）上式可简化为： Io= Ia +It (5)实验证明：当一束强度为 I0 的单色光通过浓度为 c、液层厚度为 b 的溶液时，一部分光被溶液中的吸光物质吸收后透过光的强度为 It ，则它们之间的关系为：称为透光率，用 T % 表示。

朗伯比尔定律解释1：伯(Lambert)定律阐述为：光被透明介质吸收的比例与入射光的强度无关；在光程上每等厚层介质吸收相同比例值的光。

比尔(Beer)定律阐述为：光被吸收的量正比于光程中产生光吸收的分子数目。

log( Io/I)= εCl (1—4)公式中 Io和I分别为入射光及通过样品后的透射光强度；log（Io/I）称为吸光度(ab—sorbance)旧称光密度(optical density)；C为样品浓度；l为光程；ε为光被吸收的比例系数。

当浓度采用摩尔浓度时，ε为摩尔吸收系数。

它与吸收物质的性质及入射光的波长λ有关。

当产生紫外吸收的物质为未知物时，其吸收强度可用表示：(1—5)公式中 C为lOOml溶液中溶质的克数；b为光程，以厘米为单位；A为该溶液产生的紫外吸收；表示lcm光程且该物质浓度为lg/lOOmL时产生的吸收。

朗伯—比尔定律数学表达式 A=lg(1/T)=Kbc A为吸光度,T为透射比,是透射光强度比上入射光强度 c为吸光物质的浓度 b为吸收层厚度物理意义是当一束平行单色光垂直通过某一均匀非散射的吸光物质时,与其吸光度A与吸光物质的浓度c及吸收层厚度b成正比.朗伯-比耳定律成立的前提 (1) 入射光为平行单色光且垂直照射. (2) 吸光物质为均匀非散射体系. (3) 吸光质点之间无相互作用. (4) 辐射与物质之间的作用仅限于光吸收,无荧光和光化学现象发生.解释2：Lambert-Beer定律是吸收光度法的基本定律，表示物质对某一单色光吸收的强弱与吸光物质浓度和厚度间的关系。

1．Lambert-Beer定律的推导⑴Lambert-Beer定律的数学表达式I0：入射光强（平行单色光）；I：透射光强S：吸光物质截面积；l：吸光物质厚度n：吸光质点（原子、离子或分子）数dS = kdndS/S =（kdn）/S（负号表示光强因被吸收而减弱）∵ S = V（体积）/ l（厚度），n = V·C（浓度）∴n / S = l·CLambert-Beer定律的数学表达式：-lg(I/I0)= ECl[概念]透光率(transmitance，T)：T = I/I0吸光度(absorbance，A)：A = -lg T =-lg(I/I0)= ECl （A与C成正比关系）T = 10-A = 10-ElC（T与C成指数函数关系）⑵Lambert-Beer定律的物理意义及成立条件Lambert-Beer定律：当一束平行单色光通过均匀的非散射样品时，样品对光的吸光度与样品的浓度及厚度成正比，A = ECl。

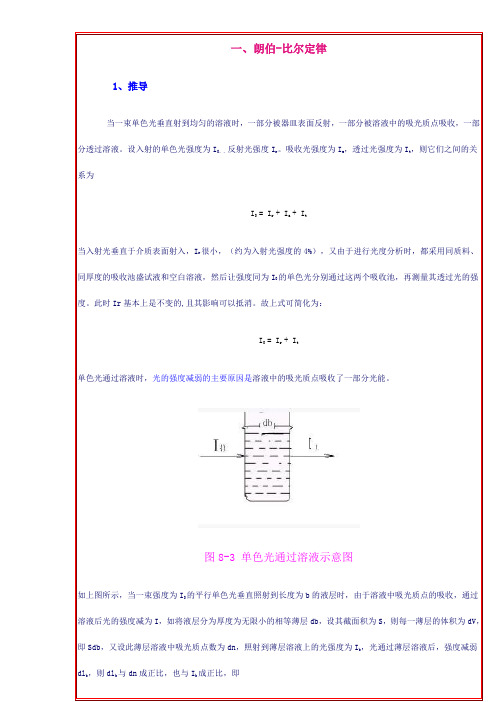
一、朗伯-比尔定律1、推导当一束单色光垂直射到均匀的溶液时，一部分被器皿表面反射，一部分被溶液中的吸光质点吸收，一部分透过溶液。

设入射的单色光强度为I0。

，反射光强度I r。

吸收光强度为I a，透过光强度为I t，则它们之间的关系为I0 = I r + I a + I t当入射光垂直于介质表面射入，I r很小，（约为入射光强度的4%），又由于进行光度分析时，都采用同质料、同厚度的吸收池盛试液和空白溶液，然后让强度同为I0的单色光分别通过这两个吸收池，再测量其透过光的强度。

此时Ir基本上是不变的,且其影响可以抵消。

故上式可简化为：I0 = I r + I t单色光通过溶液时，光的强度减弱的主要原因是溶液中的吸光质点吸收了一部分光能。

图8-3 单色光通过溶液示意图如上图所示，当一束强度为I0的平行单色光垂直照射到长度为b的液层时，由于溶液中吸光质点的吸收，通过溶液后光的强度减为I，如将液层分为厚度为无限小的相等薄层db，设其截面积为S，则每一薄层的体积为dV，即Sdb，又设此薄层溶液中吸光质点数为dn，照射到薄层溶液上的光强度为I b，光通过薄层溶液后，强度减弱dl b，则dl b与dn成正比，也与I b成正比，即-dl b = K · l b · dn (1)负是表示光温度减弱，K 为比例常数。

设吸光物质浓度为C，则上述薄层溶液中的吸光质点数dn为：dn = K2 . C .dV = K2 . C . S . db (2)K2与所取浓度、面积及长度的单位有关，式中S为光束截面积，对一定仪器为定值。

将式（2）带入式（1）中，合并常数项，得到-dI b = K1 . I b. K2 . C . S . db-dI b = K3 . I b . C . dbK3 = K1 . K2 . S这个关系式称为光吸收定律或比耳定律的数学表达式。

lgI0/I称为吸光度，用符号A表示，其物理意义表示有色溶液吸收单色入射光的程度。

朗伯 -比尔定律朗伯-比尔定律（Lambert's cosine law）是光学中一个重要的定律，描述了光线在介质中的传播规律。

该定律表明，光线在通过介质时，其能量随着入射角的变化而发生改变。

下面将详细介绍朗伯-比尔定律及其应用。

朗伯-比尔定律最早由德国数学家约翰·海因里希·朗伯于1760年提出，后来由英国科学家约翰·亨利·比尔在19世纪初进行了推广和证明。

根据朗伯-比尔定律，光线在通过透明介质时，其能量与光线入射角的余弦值成正比。

换句话说，当光线垂直入射时，其能量最大，而当光线与法线成最大入射角时，其能量几乎为零。

朗伯-比尔定律的数学表达式为I = I₀cosθ，其中I表示光线经过介质后的能量，I₀表示光线入射介质前的能量，θ表示光线与法线的夹角。

根据该定律，我们可以推导出一系列与光学相关的现象和规律。

根据朗伯-比尔定律，我们可以解释为什么天空是蓝色的。

当太阳光射向地球大气层时，由于大气层中的分子会散射光线，而蓝色光的波长较短，散射程度较大，因此我们看到的天空是蓝色的。

朗伯-比尔定律还可以解释为什么太阳光在日落时呈现出橙红色。

当太阳处于地平线上方时，太阳光经过较长的传播距离，光线中的蓝色部分被大气层中的颗粒物散射，而红色部分的波长较长，能更好地穿透大气层，因此我们看到的太阳呈现出橙红色。

朗伯-比尔定律还在光学反射和折射中有着重要的应用。

根据该定律，我们可以解释为什么光线从一个介质射向另一个介质时会发生折射现象。

折射是由于入射光线在介质界面上发生了方向变化，根据朗伯-比尔定律，入射角和折射角之间满足一个固定的关系，即入射角的余弦值与折射角的余弦值之比等于两个介质的折射率之比。

朗伯-比尔定律也可以应用于光学测量中。

例如，我们可以利用该定律来测量反射面的光学特性。

通过测量入射光线和反射光线的能量，可以计算出反射率和反射面的光学效率。

这在材料科学研究和光学器件制造中具有重要意义。

伯(Lambert)定律阐述为：光被透明介质吸收的比例与入射光的强度无关；在光程上每等厚层介质吸收相同比例值的光。

目录编辑本段定义朗伯比尔定律又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律（Bouguer–Lambert–Beer law），是光吸收的基本定律，适用于所有的电磁辐射和所有的吸光物质，包括气体、固体、液体、分子、原子和离子。

比尔-朗伯定律是吸光光度法、比色分析法和光电比色法的定量基础。

光被吸收的量正比于光程中产生光吸收的分子数目。

公式及参数意义log( Io/I)= εCl (1—4)公式中 Io和I分别为入射光及通过样品后的透射光强度；log（Io/I）称为吸光度(ab—sorbance)旧称光密度(optical density)；C为样品浓度；l为光程；ε为光被吸收的比例系数。

当浓度采用摩尔浓度时，ε为摩尔吸收系数。

它与吸收物质的性质及入射光的波长λ有关。

当产生紫外吸收的物质为未知物时，其吸收强度可用表示：(1—5)公式中 C为lOOml溶液中溶质的克数；b为光程，以厘米为单位；A为该溶液产生的紫外吸收；表示lcm光程且该物质浓度为lg/lOOmL时产生的吸收。

朗伯—比尔定律数学表达式A=lg(1/T)=Kbc（A为吸光度,T为透射比,是透射光强度比上入射光强度 c为吸光物质的浓度 b 为吸收层厚度）物理意义当一束平行单色光垂直通过某一均匀非散射的吸光物质时,与其吸光度A与吸光物质的浓度c及吸收层厚度b成正比.朗伯-比耳定律成立的前提(1) 入射光为平行单色光且垂直照射.(2) 吸光物质为均匀非散射体系.(3) 吸光质点之间无相互作用.(4) 辐射与物质之间的作用仅限于光吸收,无荧光和光化学现象发生.比尔－朗伯定律维基百科，自由的百科全书（重定向自比尔-朗伯定律）比尔-朗伯定律（Beer–Lambert law），又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律（Bouguer–Lambert–Beer law），是光吸收的基本定律，适用于所有的电磁辐射和所有的吸光物质，包括气体、固体、液体、分子、原子和离子。

试简述偏离朗伯—比尔定律的化学因素
朗伯-比尔定律是描述气体溶解度与其分压之间关系的经验定律。

根据朗伯-比尔定律，溶解度与气体分压成正比，即溶解
度随气体分压的增加而增加。

然而，在某些情况下，化学因素可能会导致气体溶解度偏离朗伯-比尔定律。

以下是一些常见的化学因素：
1. 气体反应：当溶解气体与溶剂之间发生化学反应时，朗伯-
比尔定律不再适用。

例如，二氧化碳与水反应生成碳酸酸性溶液，溶解度随着反应的进行而发生变化。

2. 离子间作用：某些气体在溶解时会产生离子，这些离子可能会发生电荷间的相互作用，从而对溶解度产生影响。

例如，一些气体在水中溶解后会形成酸碱溶液，其中离子间的相互作用对溶解度有影响。

3. 温度变化：溶解度通常随着温度的升高而增加，但在某些情况下可能出现偏离。

例如，某些气体的溶解度在特定温度范围内达到最大值，然后随温度继续升高而降低。

4. 溶剂特性：不同的溶剂对气体的溶解度有不同的影响。

例如，极性溶剂通常会增加气体的溶解度，而非极性溶剂则相对较低。

综上所述，化学因素如气体反应、离子间作用、温度变化和溶剂特性等可能导致气体溶解度偏离朗伯-比尔定律。

这些因素
需要在实际情况中进行考虑和分析。

朗伯- 比尔定律摘要：一、朗伯-比尔定律的概念及意义二、朗伯-比尔定律的数学表达式三、朗伯-比尔定律的应用领域四、影响朗伯-比尔定律的因素五、朗伯-比尔定律在实际生活中的应用案例正文：朗伯-比尔定律（Lambert-Beer law）是一种描述物质在溶液中吸光度与浓度、厚度以及溶液对该光线的吸收波长之间关系的定律。

该定律在光学、环境科学、化学、生物学等领域具有广泛的应用。

一、朗伯-比尔定律的概念及意义朗伯-比尔定律是由约翰·亨利·朗伯（John Herschel）在1852年提出的。

它指出，在一定条件下，物质对某一波长光的吸收程度与该物质的浓度成正比，与溶液的厚度成反比。

这意味着，通过测量物质溶液在特定波长下的吸光度，我们可以推断出溶液中物质的浓度。

二、朗伯-比尔定律的数学表达式朗伯-比尔定律的数学表达式为：A = eb*l*C其中，A 表示吸光度，eb 表示摩尔吸光系数（单位：L/mol·cm），l 表示溶液厚度（单位：cm），C 表示溶液浓度（单位：mol/L）。

三、朗伯-比尔定律的应用领域朗伯-比尔定律在许多领域都有广泛的应用，如化学分析、环境监测、生物医学检测等。

通过测量物质溶液在特定波长下的吸光度，可以快速、准确地测定物质的浓度，从而为各种研究和实际应用提供数据支持。

四、影响朗伯-比尔定律的因素虽然朗伯-比尔定律提供了一种简单、快捷的测量方法，但在实际应用中，一些因素可能会影响到测量结果。

这些因素包括：溶液的温度、溶液的酸碱性、溶剂的种类、测量仪器的精度等。

因此，在应用朗伯-比尔定律进行测量时，需要注意这些因素的影响，并进行相应的校正。

五、朗伯-比尔定律在实际生活中的应用案例在日常生活中，朗伯-比尔定律也有很多实际应用。

例如，在酒类生产中，通过测量酒液对特定波长光的吸光度，可以了解酒中的糖分含量；在医学检测中，通过测量血液或尿液对特定波长光的吸光度，可以快速检测出患者是否患有某些疾病。