弹簧设计计算

弹簧设计的计算公式
常见的弹簧设计绝大部分是压缩螺旋弹簧或拉伸螺旋弹簧。

这两种弹簧设计，涉及下面的项目。

在这里将关于a），b），c）进行解说。

a）在使用范围内，弹簧负载和形变量：弹簧常数
b）安装弹簧的空间：长度x外形
c）弹簧的固定方法：弹簧的两端形状和固定方法
d）其他：弹簧刚度（永久变形），疲劳度
（1）弹簧常数和弹簧形状尺寸的关系式
弹簧的形变量和负载（力）的关系。

P ＝k x δ
P：弹簧负载
k：弹簧常数
δ：弹簧挠度（形变量）
（k：弹簧常数）用弹簧材料特性和弹簧形状可以用下述公式表达。

这个公式压缩螺旋弹簧和拉伸螺旋弹簧都适用。

k ＝P/δ＝G x d4／8 x n x D3 ・・・（A）
G：横向弹性系数（杨氏模量）
d：线径
n：有效匝数
D：平均线圈直径
通过使公式（A）变形，暂时设定D（平均线圈直径），d（线径），
k（弹簧常数）来计算有效匝数：n，或者根据已知的P，D，d，n ，来计算形变量：δ。

（2）弹簧的长度、外形的设计
弹簧长度是根据(允许形变量)与弹簧载荷之间的关系来选择和设计的。

(允许形变量)是会使弹簧变形或损坏的最大变形量（参考图1）。

圆柱螺旋压缩（拉伸）弹簧的设计计算
一、圆柱螺旋压缩（拉伸）弹簧的设计原理
1、圆柱螺旋压缩（拉伸）弹簧原理
圆柱螺旋压缩（拉伸）弹簧是一种特殊的弹簧，其结构设计使用了螺
旋结构，螺旋结构的形状是一个圆柱形的圆柱螺纹。

圆柱螺旋压缩（拉伸）弹簧的压缩（拉伸）受力分布差异，当进行压缩（拉伸）力作用时，弹簧
的整个螺旋节在不同的力矩作用下会产生相应的弹性变形，从而使得弹簧
的中心轴变长，以缩短弹簧的长度。

2、圆柱螺旋压缩（拉伸）弹簧特性
圆柱螺旋压缩（拉伸）弹簧具有对同直径和外径的小变化具有很强的
适应性的特性，同时，压缩（拉伸）力也有必要时可以根据弹性变形率来
改变。

圆柱螺旋压缩（拉伸）弹簧的压缩（拉伸）受力分布差异，当进行
压缩（拉伸）力作用时，弹簧的整个螺旋节在不同的力矩作用下会产生相
应的弹性变形，从而使得弹簧的中心轴变长，从而缩短弹簧的长度。

此外，这种弹簧具有紧凑结构，能够有效地减少设备装置内的多余空间，重量轻，由于采用细小的钢、不锈钢、铜或其它有良好装配性的金属等材料，具有
良好的耐磨性、耐腐蚀性和耐臭氧性等性能。

弹簧参数尺寸及计算公式弹簧是一种用来储存和释放机械能的装置，应用广泛于机械、汽车、电器等领域。

弹簧的参数、尺寸以及计算公式对于设计和选择弹簧十分重要。

1.弹簧的参数：- 预压力（Preload）：弹簧在未加载之前的初始压力。

- 弹性系数（Spring Constant）：弹簧在单位变形下的恢复力。

- 卸载长度（Unloaded Length）：未加载时的弹簧长度。

- 动载荷（Dynamic Load）：弹簧所承受的变动力。

- 疲劳寿命（Fatigue Life）：弹簧能够承受的循环加载次数。

2.弹簧的尺寸：- 线径（Wire Diameter）：弹簧材料的直径，决定着弹簧的承载能力。

- 外径（Outer Diameter）：弹簧的最大直径。

- 内径（Inner Diameter）：弹簧的最小直径。

- 组件高度（Solid Height）：弹簧在最大压缩状态下的高度。

- 活动齿数（Active Coils）：弹簧上具有弹性的齿数。

- 紧齿数（Total Coils）：弹簧上总共的齿数。

3.弹簧的计算公式：-弹性系数（K）的计算公式：K=Gd^4/(8Na^3)其中，G为剪切模量，d为线径，N为齿数，a为活动齿数。

-预压力（P）的计算公式：P=K*δ其中，δ为弹簧的压缩/拉伸变形量。

-力（F）的计算公式：F=K*δ弹簧所受的力正比于弹性系数与变形量之积。

-弹簧的伸长（δ）计算公式：δ=(F*L)/(K*Gd^4)其中，L为弹簧的长度。

-弹簧的疲劳寿命（Nf）计算公式：Nf=(C*S^b)/(F^b)其中，C为常数，S为应力幅值（一般为弹簧的最大变形量）。

以上公式仅为常见的弹簧计算公式，实际应用中可能还需要考虑更多的因素，如安全系数、材料的疲劳强度等。

总结起来，弹簧的参数、尺寸和计算公式对于弹簧的设计和选择至关重要。

具体的参数和尺寸根据实际应用需求和弹簧类型来确定，而计算公式则是根据力学原理和材料特性推导得出的。

弹簧设计基本公式
（1）强度计算公式
式中，K 为曲度系数，；
F 为载荷；
C 为弹簧指数（亦称旋绕比），C = D2/d；
[τ] 为弹簧材料的许用扭转应力。

由此可计算弹簧丝直径d。

（2）刚度计算公式
式中，n 为弹簧的有效圈数；
G 为弹簧的切变模量；
λ为弹簧变形量；
D2 为弹簧圈中径；
其它符号意义同前。

（3）稳定性计算公式
为了限制弹簧载荷F小于失稳时的临界载荷Fcr。

一般取F = Fcr/(2～2.5)，其中临界载荷可按下式计算
Fcr = CBkH0
式中，CB 为不稳定系数
注：1---两端固定；2---一端固定；3---两端自由转动
以上信息由东莞市玖胜五金弹簧有限公司整理发布，不排除有错误可能，请谨慎下载！谢谢。

圆柱弹簧的设计计算圆柱弹簧是一种常见的弹性元件，通常用于机械装置和工具中。

它的设计计算是根据弹簧的工作负载和材料特性来进行的。

本文将详细介绍圆柱弹簧的设计计算过程及注意事项。

首先，设计计算的第一步是确定弹簧的工作负载。

弹簧的工作负载是指它所要承受的力或变形。

根据工程需求，我们需要确定弹簧承受的最大力和变形程度。

最大力通常是指弹簧所承受的静载或动载，而变形程度则是指弹簧的线材变形量。

这两个参数将成为后续计算的基础。

接下来，我们需要选择适当的弹簧材料。

弹簧材料应具备较高的弹性模量和耐久性，以确保弹簧在工作条件下不会发生塑性变形或断裂。

常用的弹簧材料有钢、不锈钢和合金钢等。

根据应用需求和弹簧所承受的最大力，我们可以选择适当的弹簧材料。

在选择弹簧材料后，我们需要计算弹簧的弹性常数。

弹性常数是指单位长度的弹簧线材在单位力下的变形量。

弹性常数可以根据弹簧线材的杨氏模量和截面形状来计算。

对于圆柱弹簧来说，弹性常数可以用以下公式进行计算：k=(G*d^4)/(8*D^3*n)其中，k是弹簧的弹性常数，G是弹簧线材的剪切模量，d是弹簧线材的直径，D是弹簧线材的直径和弹簧的外径之和，n是弹簧的圈数。

接下来，我们需要计算弹簧的刚度。

弹簧的刚度是指单位力下弹簧的变形量。

根据钩-氏定律，弹簧的刚度可以用以下公式计算：F=k*x其中，F是施加在弹簧上的力，k是弹簧的弹性常数，x是弹簧的变形量。

设计计算的最后一步是根据弹簧的刚度和工作负载来确定弹簧的尺寸。

根据弹簧的工作负载，我们可以确定所需的弹簧刚度。

然后，通过选择合适的材料和截面形状，我们可以计算出弹簧线材的直径和弹簧的外径。

此外，还需要考虑弹簧的几何形状和细节设计。

在设计过程中，还应注意以下几点：1.弹簧的刚度应能满足所需的负载要求，并在给定范围内调整。

2.弹簧的线材应具备足够的强度，以防断裂或塑性变形。

3.弹簧的圈数应满足实际应用需求，以确保弹簧在工作过程中具有足够的变形量。

1.1单个钢板弹簧的载荷已知汽车满载静止时汽车前轴荷G1=3000kg，非簧载质量Gu1=285kg，则据此可计算出单个钢板弹簧的载荷:Fw1=（G1－Gu1）／２＝1357.5 kg （１）进而得到：Pw1=Fw1×9.8=13303.5 N （２）1.2钢板弹簧的静挠度钢板弹簧的静挠度即静载荷下钢板弹簧的变形。

前后弹簧的静挠度都直接影响到汽车的行驶性能[1]。

为了防止汽车在行驶过程中产生剧烈的颠簸（纵向角振动），应力求使前后弹簧的静挠度比值接近于1。

此外，适当地增大静挠度也可减低汽车的振动频率，以提高汽车的舒适性。

但静挠度不能无限地增加（一般不超过240 ｍｍ），因为挠度过大，即频率过低，也同样会使人感到不舒适，产生晕车的感觉。

此外，在前轮为非独立悬挂的情况下，挠度过大还会使汽车的操纵性变坏。

一般汽车弹簧的静挠度值通常如表1[2]所列范围内。

本方案中选取fc1=80 ｍｍ。

1.3钢板弹簧的满载弧高满载弧高指钢板弹簧装到车轴上，汽车满载时钢板弹簧主片上表面与两端（不包括卷耳孔半径）连线间的最大高度差[3]。

当H0=0时，钢板弹簧在对称位置上工作。

考虑到使用期间钢板弹簧塑性变形的影响和为了在车架高度已限定时能得到足够的动挠度值，常取H0∈10－20ｍｍ。

本方案中H01初步定为１8ｍｍ。

1.4钢板弹簧的断面形状板弹簧断面通常采用矩形断面，宜于加工，成本低。

但矩形断面也存在一些不足。

矩形断面钢板弹簧的中性轴，在钢板断面的对称位置上。

工作时，一面受拉应力，一面受压应力作用，而且上、下表面的名义拉应力和压应力的绝对值相等。

因材料的抗拉性能低于抗压性能，所以在受拉应力作用的一面首先产生疲劳断裂。

除矩形断面以外的其它断面形状的叶片，其中性轴均上移，使受拉应力的一面的拉应力绝对值减小，而受压应力作用的一面的压应力绝对值增大，从而改善了应力在断面上的分布情况，提高了钢板弹簧的疲劳强度并节约了近10%的材料。

波形弹簧计算公式波形弹簧是一种弹性元件，常用于工程和机械装置中，用于储存和释放能量。

它的形状类似于波浪状，能够承受较大的压力和拉力，同时具有较好的抗变形能力。

波形弹簧的计算公式主要涉及以下几个方面：载荷、变形、刚度和应力等。

一、载荷相关的计算公式：1.弹簧力F=k*x其中，F为弹簧所受的力，k为弹簧的刚度，x为弹簧的变形量。

2.由载荷计算弹簧的刚度：k=F/x其中，F为弹簧所受的力，x为弹簧的变形量，k为弹簧的刚度。

3.计算变形量：x=F/k其中，F为弹簧所受的力，k为弹簧的刚度，x为弹簧的变形量。

二、刚度相关的计算公式：1.刚度系数k：k=G*(D⁴-d⁴)/(8*D³*d)其中，G为弹簧材料的剪切模量，D为弹簧的外直径，d为弹簧的内直径。

2.计算刚度弹性模量E：E=k/(d/2)其中，k为弹簧的刚度，d为弹簧的线径。

三、应力相关的计算公式：1.弹簧的螺旋线应力σ：σ=M*R/W其中，M为弹簧的弯矩，R为弹簧的曲率半径，W为弹簧的截面模量。

2.计算弯矩M：M=F*L其中，F为弹簧所受的力，L为弹簧的力臂长度。

3.计算曲率半径R：R=D²/(8*r)其中，D为弹簧的螺距，r为弹簧的半径。

4.计算截面模量W：W=π*(D⁴-d⁴)/(32*D)其中，D为弹簧的外直径，d为弹簧的内直径。

以上就是波形弹簧计算中常用的几个公式。

需要注意的是，实际计算弹簧时需要考虑更多因素，比如弹簧材料的应力应变关系、疲劳寿命等。

因此，在实际应用中，建议使用专业软件进行详细计算和设计。

弹簧计算公式弹簧计算公式是用来计算弹簧的弹力的数学公式。

弹簧是一种用来存储和释放能量的弹性元件，广泛应用于各种机械装置和工具中。

根据弹簧的形状和用途，可以分为压簧、拉簧和扭簧。

下面将分别介绍这三种弹簧的弹力计算公式。

1.压簧弹力计算公式压簧是一种用于承受压缩力的弹簧，通常由钢丝绕成螺旋形。

压簧的弹力与其形状、材料的物理性质以及受到的压缩力有关。

压簧的弹力计算公式如下：F=k*x其中，F表示弹簧的弹力，k是一个常数，称为簧系数，x是压簧的变形量。

压簧的弹力与其变形量呈线性关系，即弹簧的弹力与其压缩或拉伸的距离成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

2.拉簧弹力计算公式拉簧是一种用于承受拉力的弹簧，通常由钢丝绕成螺旋形。

拉簧的弹力与其形状、材料的物理性质以及受到的拉力有关。

拉簧的弹力计算公式如下：F=k*x其中，F表示弹簧的弹力，k是一个常数，称为拉簧的刚度系数或簧系数，x是拉簧的变形量。

拉簧的弹力与其变形量呈线性关系，即弹簧的弹力与其拉伸或压缩的长度成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

3.扭簧弹力计算公式扭簧是一种用于承受扭转力的弹簧，通常由钢丝绕成螺旋形。

扭簧的弹力与其形状、材料的物理性质以及受到的扭转力矩有关。

扭簧的弹力计算公式如下：T=k*φ其中，T表示弹簧的扭力，k是弹簧的刚度系数或簧系数，φ是弹簧的扭转角度。

扭簧的弹力与其扭转角度成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

需要注意的是，以上的公式都是基于线性弹性假设的情况下推导出来的。

实际上，弹簧的变形行为通常是非线性的，因此在计算弹力时需要考虑非线性效应，例如在变形量较大或载荷较高的情况下。

除了弹力的计算公式，还可以根据实际需要计算弹簧的弹性系数、刚度系数、临界长度等参数。

这些参数对于设计和选择弹簧具有重要意义，可以保证弹簧在工作过程中具有足够的弹性和耐力。

弹簧压力拉力计算弹簧是一种用于储存和释放机械能的弹性元件，广泛应用于机械和工程领域。

在设计和使用弹簧时，计算其压力和拉力是非常重要的。

本文将介绍弹簧压力和拉力的计算方法。

1.弹簧压力的计算方法：弹簧压力是指弹簧在压缩或压摊状态下所受的力。

弹簧的压力可以用胡克定律来计算，胡克定律表示弹簧的变形与所受的力成正比。

1.1一般情况下，弹簧压力的计算公式为：F=k*x其中，F为弹簧受力（压力），k为弹簧的弹性系数，x为弹簧的变形量。

1.2弹簧压力的单位：弹簧的压力一般用牛顿（N）来表示。

1.3弹性系数的计算方法：弹簧的弹性系数可以通过实验或计算得出。

在实验中，可以测量弹簧所受的外力和相应的变形量，然后根据胡克定律计算弹性系数。

在计算中，弹性系数可以通过材料力学性质和弹簧几何参数来确定。

2.弹簧拉力的计算方法：弹簧拉力是指弹簧在拉伸状态下所受的力。

弹簧的拉力可以通过下面的计算方法得出。

2.1一般情况下，弹簧拉力的计算公式为：F=k*x其中，F为弹簧受力（拉力），k为弹簧的弹性系数，x为弹簧的变形量。

2.2弹簧拉力的单位：弹簧的拉力也一般用牛顿（N）来表示。

3.弹簧压力、拉力计算的实例：假设一个弹簧的弹性系数为100N/m，变形量为0.02m，求弹簧的压力和拉力。

根据公式F=k*x，可以计算出弹簧的压力和拉力：压力：F=100N/m*0.02m=2N拉力：F=100N/m*0.02m=2N所以，该弹簧在压缩或拉伸状态下的压力和拉力都为2N。

4.弹簧压力、拉力计算注意事项：4.1在计算弹簧压力和拉力时，需要准确测量弹簧的变形量，以获取正确的结果。

4.2弹簧的弹性系数是一个重要参数，需要根据实际情况选择合适的值。

4.3弹簧的压力和拉力计算仅适用于弹簧的线性变形范围，如果超过线性范围，计算的结果将不准确。

4.4在实际应用中，还需要考虑弹簧的材料性质、弯曲和扭转等因素的影响，以获得更准确的结果。

总结：本文介绍了弹簧压力和拉力的计算方法。

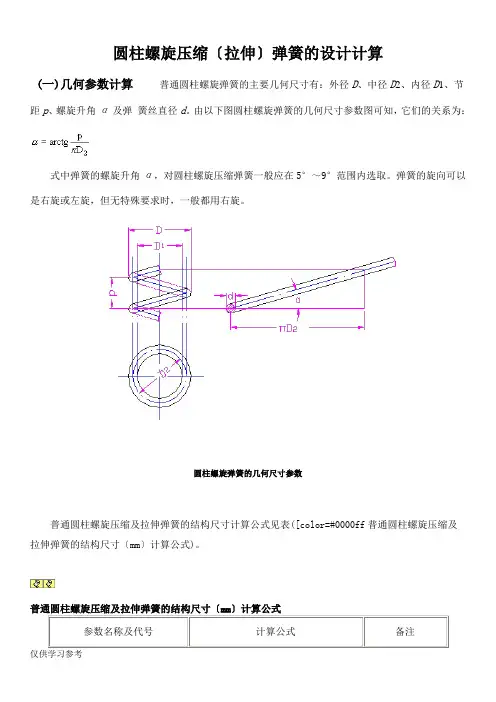
圆柱螺旋压缩〔拉伸〕弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。

由以下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。

弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。

圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff普通圆柱螺旋压缩及拉伸弹簧的结构尺寸〔mm〕计算公式)。

参数名称及代号计算公式备注工作高度或长度H1,H2,…,H nH n=H0-λn H n=H0+λnλn--工作变形量有效圈数n根据要求变形量按式〔16-11〕计算n≥2总圈数n1n1=n+(2～2.5)〔冷卷〕n1=n+(1.5～2)〔YII型热卷〕n1=n拉伸弹簧n1尾数为1/4,1/2,3/4整圈。

推荐用1/2圈节距p p=(0.28～0.5)D2p=d轴向间距δδ=p-d展开长度L L=πD2n1/cosαL≈πD2n+钩环展开长度螺旋角αα=arct g(p/πD2) 对压缩螺旋弹簧，推荐α=5°～9°质量m sm s=γ为材料的密度，对各种钢，γ=7700kg/；对铍青•(二)特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。

因此在设计弹簧时，务必使其工作应力在弹性极限范围内。

在这个范围内工作的压缩弹簧，当承受轴向载荷P时，弹簧将产生相应的弹性变形，如右图a所示。

为了表示弹簧的载荷与变形的关系，取纵坐标表示弹簧承受的载荷，横坐标表示弹簧的变形，通常载荷和变形成直线关系(右图b)。

这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。

对拉伸弹簧，如图<圆柱螺旋拉伸弹簧的特性曲线>所示，图b为无预应力的拉伸弹簧的特性曲线；图c为有预应力的拉伸弹簧的特性曲线。

弹簧压力计算弹簧参数计算弹簧压力计算是机械设计中的重要计算，用于确定弹簧在压缩时的弹性变形及其所产生的压力。

弹簧参数的计算则包括对弹簧的基本结构、工作环境及所需要的压力范围进行分析，以确定适合弹簧的材料、尺寸、线径等。

下面将介绍弹簧压力计算的几个基本要素。

首先要确定弹簧的初始长度，也称为无荷长度。

这个长度通常是指在弹簧无负载时的长度，一般用公称长度来表示。

公称长度是根据标准规定的，是弹簧长度的理论值。

计算压缩弹簧所需要的基本参数时，必须准确地知道公称长度。

其次要确定弹簧的线径。

线径是指弹簧线圈截面上的直径，也称为丝径。

线径的大小直接影响到弹簧的硬度和承载能力。

线径太小会导致弹簧容易变形或损坏，线径太大则会使弹簧过于刚硬，不易变形，不能发挥其弹性作用。

接下来要确定的是弹簧的管径。

管径是指弹簧线圈的外径。

通常管径是由线径和线圈圈数所决定的。

在一定的线径和线圈数量下，管径越大，弹簧的承载能力也越大。

最后要确定的是弹簧的材料。

弹簧材料的选择要考虑弹簧的工作环境及所需的压力范围。

常用的弹簧材料包括高碳钢、合金钢、不锈钢等。

不同材料的弹簧所承载的压力范围不同，选择时要做出合理的判断。

综上所述，弹簧压力计算和弹簧参数计算是机械设计中非常重要的一部分。

只有根据具体的工作环境和所需承载的压力范围来选择合适的材料、尺寸和线径等参数，才能保证弹簧的正常工作和长时间的使用寿命。

在进行设计时，需要根据实际情况综合考虑各参数之间的相互作用，做出准确的计算及合理的设计。

弹簧设计计算步骤
线径d=φ0.45内径Di=4
有效卷数Na=8.5总卷数Nt=10.5
左 座卷数Nzl=1左座研削补正系数Gnl=0（有研削=-0.75右 座卷数Nzr=1右座研削补正系数Gnr=0（有研削=-0.75横弹性系数G=68500（SW-C、SWP-A、SWP-B =78500N/mm2
SUS304-WPB =68500N/mm2
SUS631J1-WPC =73500N/mm2 )
弹性系数k=0.46876k＝G*d4/（8*Na*（Di+d）3）
提供的力N=2发生形变的长度L= 4.27
形变时长度L1=9自由时的长度L0=13.3
密着高度Hs= 4.725
密着时荷重Ps= 4.00395
弹簧系数C=9.88889C=(Di+d)/d
注：弹簧系数C数值，必须符合下面要求。

压力修正系数k= 1.14657k=（4C-1)/(4C-4)+0.615/C
压缩容许压力∫emax=850注：∫emax具体数值，根据材料，从下面表格读取。

最大允许荷重Pmax= 5.96135Pmax=∫emax*∏*d 3/(8*(Di+d)*k)
荷重比
Rp=
33.55%
注：Rp的数值必须在20%-80%之间，才能说明弹簧设
（有研削=-0.75、无研削=0）
（有研削=-0.75、无研削=0）材料，从下面表格读取。

才能说明弹簧设计合理。

弹簧线长度计算公式一、弹簧线长度计算的基本原理。

1. 螺旋弹簧。

- 对于圆柱螺旋弹簧，其线长度（展开长度）计算基于螺旋线的几何形状。

- 假设圆柱螺旋弹簧的中径为D（弹簧外径减去钢丝直径），节距为t，有效圈数为n。

- 弹簧一圈的展开长度可以根据圆周长公式l = π D（这里D为弹簧中径）。

- 那么弹簧的总长度L=π Dn+钩部展开长度（如果有钩部的话）。

- 如果考虑两端并紧磨平，一般并紧圈数为n_1（通常取n_1 = 1.5 - 2.5圈），此时弹簧总长度L=π D(n + n_1)+钩部展开长度。

- 对于节距t，在计算总长度时，如果没有特殊说明，当考虑弹簧的压缩或拉伸行程时，在有效圈数n的范围内，总长度还可以表示为L=(n - 1)t+2d+钩部展开长度（d为弹簧丝直径）。

2. 圆锥螺旋弹簧。

- 圆锥螺旋弹簧的中径是变化的。

设圆锥弹簧的大端中径为D_1，小端中径为D_2，节距为t，有效圈数为n。

- 其一圈的平均展开长度l=π(D_1 + D_2)/(2)。

- 则弹簧的总长度L=π(D_1 + D_2)/(2)n+钩部展开长度（如果有钩部）。

二、实际应用中的注意事项。

1. 材料特性影响。

- 在计算弹簧线长度时，有时需要考虑材料的弹性变形等因素。

例如，当弹簧受到较大的拉力或压力时，其实际长度会发生变化，在精确计算时需要根据材料的弹性模量等参数进行修正。

2. 制造工艺的影响。

- 实际制造过程中，弹簧的绕制工艺可能会导致一定的误差。

如在绕制过程中钢丝的拉伸、弯曲半径的微小变化等，这些因素在高精度要求的弹簧线长度计算中需要考虑。

在设计时，可以根据制造工艺的精度等级，预留一定的长度余量。

聚氨酯弹簧 设计计算
聚氨酯弹簧是一种新型的弹簧材料，常用于汽车悬挂系统、工业机械和航空航天
等领域。

设计计算聚氨酯弹簧需要考虑以下几个因素：
1. 负载：弹簧所承受的最大负载是需要考虑的一个因素，这可以通过伯努利原
理进行计算。聚氨酯弹簧的负载能力与其直径、材料和长度等参数有关。

2. 材料：聚氨酯弹簧的材料特性需要考虑，包括弹性模量、泊松比、密度和热
膨胀系数等。这些参数可以通过实验和材料手册获得。

3. 直径：聚氨酯弹簧的直径对其负载能力有直接影响，因此需要根据负载要求
和材料特性来选择合适的直径。

4. 长度：聚氨酯弹簧的长度也会影响其负载能力，因此需要根据负载要求和材
料特性来选择合适的长度。

5. 预压力：聚氨酯弹簧在设计时需要考虑预压力，即在不承受负载时的初始压
力。预压力通常是根据负载要求来确定的。
综上所述，设计计算聚氨酯弹簧需要综合考虑负载、材料、直径、长度和预压力
等因素，并进行合理的计算和选择。

弹簧设计计算软件弹簧设计计算软件是指一种专门用于计算弹簧设计参数的软件工具。

弹簧作为机械零件的一种，广泛应用于各种机械设备中，如汽车、电器、仪器仪表等，其设计参数直接影响着弹簧的性能和使用寿命。

传统的弹簧设计方法通常需要手工计算，不仅费时费力，而且容易出错。

而弹簧设计计算软件的出现，大大简化了设计过程，提高了计算准确性和设计效率。

1.材料数据库：软件内置了各种弹簧材料的物性参数，用户可以从数据库中选择合适的材料，无需手动输入。

2.弹簧类型选择：根据使用要求，用户可以选择不同类型的弹簧，如压缩弹簧、拉伸弹簧、扭转弹簧等。

3.输入设计参数：用户需要输入一些基本的设计参数，如载荷、变形量、工作环境等。

根据这些参数，软件可以自动计算出最佳的弹簧尺寸和工作特性。

4.强度计算：对于给定的材料和设计参数，软件能够计算出弹簧的最大载荷和最大变形量，以及弹簧的疲劳寿命。

5.迭代优化：在弹簧设计过程中，用户可以根据计算结果进行迭代优化。

软件可以根据用户的修改，自动重新计算设计参数，以达到设计要求。

6.规范标准：软件内置了国内外的弹簧设计规范标准，用户可以选择适合自己需求的规范进行设计。

7.结果输出：软件可以生成弹簧设计计算报告，包括弹簧尺寸、材料和设计参数等详细信息。

用户可以打印或导出报告，方便交流和备案。

1.准确性：软件利用现代计算方法和模型，能够更准确地计算出弹簧的设计参数和工作特性，避免了手工计算中可能出现的错误。

2.高效性：软件自动化的计算过程大大提高了计算效率，节省了设计人员的时间和精力。

3.灵活性：用户可以根据实际需求选择不同的材料、弹簧类型和规范标准，有助于满足不同设计要求。

4.可迭代性：软件支持迭代优化，用户可以根据计算结果进行反复修改和优化，直到达到设计要求。

5.规范性：软件内置了规范标准，能够保证设计结果符合相关的弹簧设计规范和要求。

总之，弹簧设计计算软件是现代机械设计的一种重要工具，其准确性、高效性和灵活性，使得弹簧设计变得更加简单、快捷和可靠。