位移和时间关系

时间位移公式
位移时间公式是x=V0t+1/2at²、x=(V0+Vt)×t、x=v²/2a。

位移（displacement）用位移表示物体(质点)的位置变化。

定义为：由初位置到末位置的有向线段。

其大小与路径无关，方向由起点指向终点。

它是一个有大小和方向的物理量，即矢量。

在瞬时t质点位于Q点，瞬时t+△t位于Q′点，则矢量表示质点从t时刻开始在△t时间间隔内的位移。

它等于Q′点的矢径与Q点的矢径之差，即△r=r（t+△t）－r（t）。

相关信息：
物体在某一段时间内，如果由初位置移到末位置，则由初位置到末位置的有向线段叫做位移。

它的大小是运动物体初位置到末位置的直线距离；方向是从初位置指向末位置。

位移只与物体运动的始末位置有关，而与运动的轨迹无关。

如果质点在运动过程中经过一段时间后回到原处，那么，路程不为零而位移则为零。

匀变速直线运动的位移与时间的关系匀变速直线运动是一种物体在直线上以恒定加速度进行运动的情况。

在这种情况下，位移与时间的关系可以通过所给定的初速度、加速度和时间来计算。

首先，我们要明确一些基本概念。

位移是物体从一个位置到另一个位置的距离，通常表示为Δx。

时间是运动持续的时间长度，通常表示为t。

加速度是速度变化的率，通常表示为a。

初速度是运动开始时的速度，通常表示为v0。

根据匀变速直线运动的原理，我们可以得到物体在某一时刻的速度公式为v = a * t + v0。

这个公式表示了速度随时间变化的关系。

而位移与时间的关系则可以通过速度与时间的积分得到。

积分的过程可以视为速度与时间关系图像下的面积计算。

当物体处于加速度为a的匀变速直线运动时，位移与时间的关系可以分为两个阶段。

1. 初速度阶段（0 ≤ t ≤ T）：在这个阶段，物体的初速度为v0，根据速度公式，可以得到物体的速度为v = a * t + v0。

通过位移的计算，可以得到位移与时间的关系为：Δx = ∫(a * t + v0) dt，即Δx = 1/2 * a * t^2 + v0 * t2. 加速度阶段（T ≤ t）：在这个阶段，物体的速度已经达到了一个恒定的值，由于加速度为恒定值a，所以位移与时间的关系可以表示为：Δx = ∫(a * t) dt，即Δx = 1/2 * a * t^2综上所述，匀变速直线运动的位移与时间的关系可以通过上述公式计算得出。

根据初速度、加速度和时间的不同取值，我们可以根据公式获取物体的位移数据。

这种关系可以帮助我们更好地理解物体在运动过程中的位置变化情况。

匀变速直线运动是物理学中常见的一种运动方式，其有着广泛的应用。

在这样的运动中，物体的速度会随着时间的变化而变化，从而导致物体的位置发生改变。

位移与时间的关系是描述这种运动的重要数学表达式之一。

对于匀变速直线运动，可以通过给定的初速度、加速度和时间来求解位移与时间的关系。

位移和时间的关系以及速度和时间的关系公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]位移和时间的关系以及速度和时间的关系一、匀速直线运动1、定义：在任意相等的时间内位移均相等的直线运动。

2、运动规律：3、特点：二、位移——时间图象（s－t图象或简称位移图象）1、横轴表示时间（t/s），纵轴表示位移（x/m），坐标原点表示位移起点。

2、x－t图象物理意义：反映物体运动位移随时间的变化关系。

3、x－t图象一经确定，在物体实际运动空间中正方向就确定，则x－t图象只能反映直线运动。

4、匀速直线运动：x－t图象是一条倾斜直线5、图1物理含义：(1)从距离规定的位移参考点相距x0的地方开始沿正方向作匀速直线运动。

θ1＞θ2，与水平方向倾角越大，物体运动得越快，速度越大。

(2)x—t图像的交点表示相遇?（3）x－t图象并不表示物体运动（4）x—t图像是曲线时，某一点的切线的斜率表示该点的速度.三、速度和时间的关系：（v-t图像或速度图像）1、纵轴v(m/s) 横轴t(s) 坐标原点速度为零2、匀速直线运动v－t图象。

①匀速直线运动的v－t图象是一条平行于t轴的直线。

②v的正负表示运动的方向③v－t图象与t轴所围面积表示位移的大小。

④v－t图象在坐标系中一经建立，正方向在实际运动空间中就确定，v－t图象只能反映物体速度沿正方向或负方向作直线运动，对于曲线运动的物体只能用速率时间图像反应.?3、4、匀变速直线运动：在变速直线运动中，如果在任意相等的时间内速度的改变均相等，这种运动叫匀变速直线运动。

特点：例：一辆玩具电动车，起动时和刹车时均做匀变速直线运动。

起动时：刹车时：刚好相反。

?启动作匀加速直线运动刹车时作匀减速运动5、匀变速直线运动的v－t图象是一条倾斜直线。

?可以把图象分割成无限的等时间间隔的梯形，这样无限分割下去，每一个小的时间间隔内物体可看作匀速直线运动，则每一个小的时间间隔内的位移可以看成是与t 轴所围成的面积，这样整个0～t0过程物体作匀变速直线运动位移就等于与t轴所围图形的面积。

第六讲位移与时间的关系知识点一、位移时间公式[提出问题]1.在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，如果把每一小段△t内的运动看做匀速运动，则矩形面积之和等于各段匀速直线运动的位移。

如果把整个运动过程划分得非常非常细，当△t→0时，各矩形面积之和趋近于v-t图线下面的面积，如图所示。

设初速度为v0，加速度为a，试通过V-t图像推导其位移公式。

[要点提炼]at21.匀变速直线运动的位移与时间的关系：x＝v0t＋12at2(由静止开始的匀加速直线运动)2.当v0＝0时，x＝123.当a＝0时，x＝(匀速直线运动)4.公式中x、v0、a都是矢量，应用时必须选取的正方向．若选v0方向为正方向，则：物体加速，a取值；物体减速，a取值．若位移为正值，位移的方向与正方向；若位移为负值，位移的方向与正方向at2只适用于5.公式x＝v0t＋12[经典例题]1.做匀加速直线运动的物体初速度是0.50m/s，加速度是20.10m/s，那么第4s末的瞬时速度4v=____，头4秒内的平均速度4v=____，4秒内通过的位移4s=___，第4秒内通过的位移IVs=____。

2.一物体做初速度为零的匀加速直线运动，加速度为a＝2m/s2，求：(1)第5s末物体的速度多大？(2)前4s的位移多大？(3)第4s内的位移多大？3.做匀变速直线运动的物体，在一段时间t内的平均速度等于这段时间内_____的瞬时速度，还等于这段时间初、末速度矢量和的一半。

即022tt v vxv vt +===[变式训练]1.（2020·大石桥市）一列火车以2m/s的初速度，0.5m/s2的加速度做匀加速直线运动，求：(1)火车在第3s末的速度是多少？(2)火车在前4s内的位移是多少？(3)火车在第5s内的位移是多少？2.汽车在高速公路上行驶，起初以54km/h的速度前进10s，接着以20.6m/s的加速度匀加速前进15s。

第3节 匀变速直线运动的位移与时间的关系学习目标核心提炼1.知道匀速直线运动的位移与v －t 图象中矩形面积的对应关系。

1种方法——极限思想解决问题的方法 1个公式——位移与时间关系式x ＝v 0t ＋12at 22种图象——x －t 和v －t 图线的特点及应用 2个重要推论——⎩⎨⎧v ＝v t 2＝v 0＋v 2Δx ＝aT 22.了解位移公式的推导方法，感受利用极限思想解决物理问题的科学思维方法。

3.理解匀变速直线运动的位移与时间的关系式。

会应用此关系式对匀变速直线运动问题进行分析和计算。

4.知道什么是x －t 图象，能应用x －t 图象分析物体的运动。

一、匀速直线运动的位移阅读教材第37～38页“匀速直线运动的位移”部分，知道匀速直线运动的位移x 与v －t 图象中矩形面积的对应关系。

1．位移公式：x ＝v t 。

2．在v －t 图象中的表示位移：对于匀速直线运动，物体的位移在数值上等于v －t 图线与对应的时间轴所包围的矩形的面积。

如图所示阴影图形面积就等于物体t 1时间内的位移。

思维拓展如图1所示，质点在5 s 内的位移是多大？图1★答案★ 0～3 s 位移x 1＝v 1t 1＝9 m 3～5 s 位移x 2＝－v 2t 2＝－4 m 故0～5 s x ＝x 1＋x 1＝5 m 。

二、匀变速直线运动的位移分析教材第38～40页图2.3－2的甲、乙、丙、丁的图解过程，了解位移公式的推导方法，从中感受极限思维方法的应用。

1．在v －t 图象中的表示位移： (1)微元法推导①把物体的运动分成几个小段，如图2甲，每段位移≈每段起始时刻速度×每段的时间＝对应矩形面积。

所以，整个过程的位移≈各个小矩形面积之和。

②把运动过程分为更多的小段，如图乙，各小矩形的面积之和可以更精确地表示物体在整个过程的位移。

图2③把整个过程分得非常非常细，如图丙，小矩形合在一起成了一个梯形，梯形的面积就代表物体在相应时间间隔内的位移。

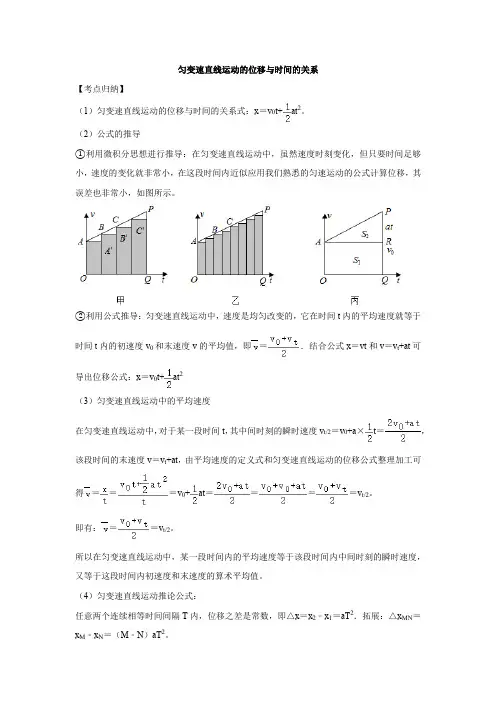
匀变速直线运动的位移与时间的关系【考点归纳】（1）匀变速直线运动的位移与时间的关系式：x＝v0t+at2。

（2）公式的推导①利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示。

②利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值，即＝．结合公式x＝vt和v＝v t+at可导出位移公式：x＝v0t+at2（3）匀变速直线运动中的平均速度在匀变速直线运动中，对于某一段时间t，其中间时刻的瞬时速度v t/2＝v0+a×t＝，该段时间的末速度v＝v t+at，由平均速度的定义式和匀变速直线运动的位移公式整理加工可得＝＝＝v0+at＝＝＝＝v t/2。

即有：＝＝v t/2。

所以在匀变速直线运动中，某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度，又等于这段时间内初速度和末速度的算术平均值。

（4）匀变速直线运动推论公式：任意两个连续相等时间间隔T内，位移之差是常数，即△x＝x2﹣x1＝aT2．拓展：△x MN＝x M﹣x N＝（M﹣N）aT2。

推导：如图所示，x1、x2为连续相等的时间T内的位移，加速度为a。

【命题方向】例1：对基本公式的理解汽车在平直的公路上以30m/s的速度行驶，当汽车遇到交通事故时就以7.5m/s2的加速度刹车，刹车2s内和6s内的位移之比（）A.1：1B.5：9C.5：8D.3：4分析：求出汽车刹车到停止所需的时间，汽车刹车停止后不再运动，然后根据位移时间公式求出2s内和6s内的位移。

解：汽车刹车到停止所需的时间＞2s所以刹车2s内的位移＝45m。

t0＜6s，所以刹车在6s内的位移等于在4s内的位移。

＝60m。

所以刹车2s内和6s内的位移之比为3：4．故D正确，A、B、C错误。

位移与时间的关系位移与时间的关系是物理学中一个重要的概念，在描述物体运动时起着关键作用。

位移是指物体从一个位置到另一个位置的变化，而时间是指这个变化所经历的时长。

研究位移与时间的关系可以帮助我们更好地理解和描述物体的运动规律。

本文将详细探讨位移与时间的关系，并且探讨在不同情况下这种关系的特点和规律。

一、匀速直线运动情况下的位移与时间关系在匀速直线运动中，物体的速度保持恒定，因此它的位移与时间的关系是线性的。

根据物体的匀速直线运动的定义，位移与时间的比值等于物体的速度。

例如，如果一个物体以每秒10米的速度匀速向前运动，那么它在1秒钟内的位移将为10米，在2秒钟内的位移为20米。

可以看出，位移与时间成正比，位移和时间的比例关系由速度来决定。

二、加速度运动情况下的位移与时间关系在加速度运动中，物体的速度在单位时间内发生变化，因此它的位移与时间的关系不再是线性的。

根据牛顿第二定律，物体的加速度等于力对物体施加的作用力。

在这种情况下，位移和时间之间的关系由物体的加速度来决定。

在匀加速直线运动中，物体的速度随时间线性变化，位移与时间的关系呈现二次函数的形式。

具体而言，位移与时间的关系可以用以下公式表示：s = ut + (1/2)at^2其中s表示位移，u表示初始速度，t表示时间，a表示加速度。

这个公式表明，在匀加速直线运动中，位移与时间的平方成正比，与时间一次方成正比，与初始速度无关。

三、自由落体情况下的位移与时间关系自由落体是指物体在无空气阻力作用下由高处自由下落的运动。

在自由落体中，物体的加速度近似为地球上的重力加速度。

根据这个特点，位移与时间的关系可以用以下公式表示：s = (1/2)gt^2其中s表示位移，g表示重力加速度，t表示时间。

这个公式表明，在自由落体运动中，位移与时间的平方成正比。

四、周期性运动情况下的位移与时间关系在周期性运动中，物体经过一段时间后按照相同的模式重复运动。

这种情况下，位移与时间的关系呈现周期性变化的特点。

匀变速直线运动的位移与时间关系一、匀变速直线运动的概念匀变速直线运动是指物体在直线上做运动时，其速度随时间的变化规律不同，即速度并非恒定，而是随着时间的推移而发生变化。

二、匀变速直线运动的位移公式在匀变速直线运动中，物体在某一时刻的位移与它在该时刻前所经过的路程有关。

因此可以通过路程和速度来求得物体在任意时刻的位移。

设物体在t1时刻的位置为S1，在t2时刻的位置为S2，则该物体在时间Δt内所经过的路程为：ΔS = S2 - S1根据定义可知，平均速度Vavg等于位移ΔS与时间Δt之比：Vavg = ΔS/Δt根据匀变速直线运动中平均速度与瞬时速度相等这一性质，可以得到物体在t1时刻瞬时速度v1和在t2时刻瞬时速度v2之间的关系：vavg = (v1 + v2)/2将上式代入平均速度公式中可得：ΔS = (v1 + v2)/2 × Δt进一步化简可得到匀变速直线运动中的位移公式：S2 - S1 = (v1 + v2)/2 × Δt三、匀变速直线运动中的时间与位移关系根据上述位移公式，可以得到匀变速直线运动中时间与位移之间的关系。

当物体在t1时刻的位置为S1，在t2时刻的位置为S2时，它在这段时间内所经过的路程ΔS等于它在这段时间内的平均速度乘以这段时间，即：ΔS = Vavg × Δt将平均速度公式代入上式中可得：ΔS = (v1 + v2)/2 × Δt因此，匀变速直线运动中物体在任意时刻的位移与它在该时刻前所经过的路程有关，而路程又与物体在该段时间内所处的平均速度和时间有关。

因此，在已知物体在某一时刻的瞬时速度和该段时间内加速度不变情况下，可以通过上述位移公式来计算物体在任意时刻的位移。

四、匀变速直线运动中瞬时速度与加速度之间的关系根据牛顿第二定律F=ma和力学基本公式v = at + v0（其中v0为初速度），可以得到匀变速直线运动中瞬时速度与加速度之间的关系。

加速度位移时间的关系
加速度是速度随时间改变的量度，位移是物体位置随时间改变的量度。

加速度、位移和时间之间的关系可以通过运动学方程来描述。

在一维运动中，假设物体的初始位置为x0，初始速度为v0，加速度为a，时间为t。

根据运动学方程，物体在时间t内的位移可以用如下公式表示：
x = x0 + v0t + 0.5at^2
这个公式描述了加速度、位移和时间之间的关系。

根据这个公式，当加速度为常数时，位移随时间的平方关系增加。

在匀加速直线运动中，位移与时间的关系是二次函数关系。

当加速度为正数时，表示物体在正向方向上加速移动；当加速度为负数时，表示物体在负向方向上加速移动或者在正向方向上减速移动。

根据加速度的正负不同，位移与时间的关系也会有所不同。

在其他情况下，也可以根据具体的运动条件，使用其他的运动学方程来描述加速度、位移和时间之间的关系。

学业分层测评(八)(建议用时：45分钟)[学业达标]1．关于匀变速直线运动，下列说法正确的是( )A ．位移与时间的平方成正比B ．位移总是随着时间的增加而增加C ．加速度、速度、位移三者方向一致D ．加速度、速度、位移的方向并不一定都相同【解析】 根据x ＝v 0t ＋12at 2，位移与时间的平方不是正比关系，A 错误；位移可能随时间的增加而增加，也可能随时间的增加而减小，如先减速后反向加速的匀变速直线运动，位移先增加后减小，B 错误；加速度、速度、位移的方向可能相同，也可能不同，C 错误，D 正确．【答案】 D2．在交警处理某次交通事故时，通过监控仪器扫描，输入计算机后得到汽车在水平路面上刹车过程中的位移随时间变化的规律为：x ＝30t －3t 2(x 的单位是m ，t 的单位是s)．则该汽车在路面上留下的刹车痕迹长度为( )A ．25 mB ．50 mC ．75 mD ．150 m【解析】 由x ＝v 0t ＋12at 2得v 0＝30 m/s ，12a ＝－3 m/s 2，即a ＝－6 m/s 2.汽车由v 0刹车到静止，由v ＝v 0＋at 得t ＝v －v 0a ＝5 s ，汽车在路面上留下的刹车痕迹长度，由x ＝v 0t ＋12at 2得x ＝30 m/s ×5 s ＋12×(－6 m/s 2)×(5 s)2＝75 m ，故选项C 正确．【答案】 C3．一质点沿一条直线运动的位移—时间图象如图2-3-6所示，则( )【导学号：57632120】图2-3-6A．t＝0时刻，质点在坐标原点B．从t＝0时刻到t1时刻，质点位移是x0C．从t1时刻到t2时刻，质点位移大小等于路程D．质点在t1时刻的速度比t2时刻的速度大【解析】t＝0时刻，质点在x0处，选项A错误；从t＝0时刻到t1时刻，质点位移大于x0，选项B错误；从t1时刻到t2时刻，质点做单方向匀速直线运动，位移大小等于路程，选项C正确，选项D错误．【答案】 C4．(多选)a、b、c三个质点在一条直线上运动，它们的位移—时间图象如图2-3-7所示，下列说法正确的是()【导学号：57632121】图2-3-7A．在0～t3时间内，三个质点位移相同B．在0～t3时间内，质点c的路程比质点b的路程大C．质点a在t2时刻改变运动方向，质点c在t1时刻改变运动方向D．在t2～t3这段时间内，三个质点运动方向相同【解析】从x-t图象可知，0～t3时间内，三个质点位移大小与方向均相同，选项A正确；0～t3时间内，质点c的路程比质点b的路程大，选项B正确；质点a在t2时刻向负方向运动，质点c在t1时刻向正方向运动，选项C正确；在t2～t3时间内，质点b、c运动方向相同向正方向运动，质点a向负方向运动，故选项D错误．【答案】ABC5．一物体做匀加速直线运动，在第1个t s 内位移为x 1，第2个t s 内位移为x 2，则物体在第1个t s 末的速度是( )【导学号：57632122】A.x 1－x 2tB.x 2＋x 1tC.x 2－x 12t D ．x 2＋x 12t【解析】 v ＝v t 2，所以第1个t s 末的速度v 1＝x 1＋x 22t ，D 正确．【答案】 D6．一辆公共汽车进站后开始刹车，做匀减速直线运动．开始刹车后的第1 s 内和第2 s 内位移大小依次为9 m 和7 m ．则刹车后6 s 内的位移是( )A ．20 mB ．24 mC ．25 mD ．75 m【解析】 由Δx ＝aT 2得：9 m －7 m ＝a ·12s 2，a ＝2 m/s 2，由v 0t 1－12at 21＝x 1得：v 0×1 s －12×2 m/s 2×12s 2＝9 m ，v 0＝10 m/s ，汽车刹车时间t ＝v 0a ＝5 s<6 s ，故刹车后6 s 内的位移为x ＝12at 2＝12×2×52 m ＝25 m ，故选C.【答案】 C7．一质点的x -t 图象如图2-3-8所示，那么此质点的v -t 图象可能是下图中的( )【导学号：57632123】图2-3-8【解析】 x -t 图象的切线斜率表示速度，由图象可知：0～t 12时间内图象的斜率为正且越来越小，在t 12时刻图象斜率为0，即物体正向速度越来越小，t 12时刻减为零；从t 12～t 1时间内，斜率为负值，数值越来越大，即速度反向增大，故选项A 正确．【答案】 A8．一滑块自静止开始，从斜面顶端匀加速下滑(斜面足够长)，第5 s 末的速度是6 m/s ，试求：(1)第4 s 末的速度大小；(2)运动后7 s 内的位移大小；(3)第3 s 内的位移大小．【解析】 (1)滑块做匀加速运动，由v ＝v 0＋at 得v 5＝at 5＝5a ＝6 m/s ，a ＝1.2 m/s 2v 4＝at 4＝1.2×4 m/s ＝4.8 m/s.(2)x 7＝v 0t 7＋12at 27＝0＋12×1.2×72 m ＝29.4 m.(3)第3 s 内的位移等于前3 s 内的位移减去前2 s 内的位移x ′3＝12at 23－12at 22＝3 m.【答案】 (1)4.8 m/s (2)29.4 m (3)3 m[能力提升]9．A 、B 两质点从同一地点运动的x -t 图象如图2-3-9所示，下列说法正确的是( )【导学号：57632124】图2-3-9A ．A 、B 两质点在4 s 末速度相等B ．前4 s 内A 、B 之间距离先增大后减小，4 s 末两质点相遇C ．前4 s 内A 质点的位移小于B 质点的位移，后4 s 内A 质点的位移大于B 质点的位移D ．A 质点一直做匀速运动，B 质点先加速后减速，8 s 末回到出发点【解析】 x -t 图象中，图线的斜率表示速度，4 s 末二者的斜率不同，所以速度不同，故A 错误；前4 s 内A 、B 之间距离先增大后减小，4 s 末两质点位置坐标相同，表示相遇，故B 正确；前4 s 内A 质点的位移等于B 质点的位移，后4 s 内A 质点的位移与B 质点的位移大小相等，方向相反，故C 错误；由图象斜率可知，A 质点一直做匀速运动，B 质点先减速后加速，8 s 末回到出发点，故D 错误．【答案】 B10．一滑块以某一速度从斜面底端滑到顶端时，其速度恰好减为零．已知运动中滑块加速度恒定．若设斜面全长为L ，滑块通过最初12L 所需的时间为t ，则滑块从斜面底端滑到顶端所用时间为( ) A.2tB ．(2＋2)tC ．3tD ．2t【解析】 利用“逆向思维法”把滑块的运动看成逆向的初速度为0的匀加速直线运动．设后L 2所需时间为t ′，则L 2＝12at ′2，全过程L ＝12a (t ＋t ′)2解得t ′＝(2＋1)t所以t 总＝t ′＋t ＝(2＋2)t ，故B 正确．【答案】 B11．(多选)物体做匀变速直线运动，某时刻速度的大小为4 m/s,2 s 后速度的大小变为10 m/s ，在这2 s 内该物体的( )【导学号：57632125】A ．位移的大小一定是14 mB ．位移的大小可能是6 mC．加速度的大小可能是3 m/s2D．加速度的大小可能大于7 m/s2【解析】(1)取初速度方向为正方向，如果末速度与初速度同向，则加速度：a＝v－v0t＝10－42m/s2＝3 m/s2位移：x＝v0＋v2t＝4＋102×2 m＝14 m.(2)取初速度方向为正方向，如果末速度与初速度反向，则加速度：a＝v－v0t＝－10－42m/s2＝－7 m/s2位移：x＝v0＋v2t＝4＋(－10)2×2 m＝－6 m故位移大小为14 m或6 m，加速度大小为3 m/s2或7 m/s2；故A、D错误，B、C正确．【答案】BC12．甲、乙两辆汽车在一条平直公路上沿直线同向行驶，某一时刻甲、乙两车相遇，从该时刻开始计时，甲车的位移随时间变化的关系式为x＝2t2＋2t，乙车的速度随时间变化的关系式为v＝2t＋10，(表达式中各物理量均采用国际单位)试求：(1)两车速度大小相等的时刻；(2)两车速度大小相等的时刻两车相距的距离．【导学号：57632126】【解析】(1)对甲车，根据x＝v0t＋12at2＝2t2＋2t得，甲车的初速度v01＝2m/s，加速度a1＝4 m/s2；对乙车，根据v＝v0＋at＝2t＋10得，乙车的初速度v02＝10 m/s，加速度a2＝2 m/s2；根据速度时间公式得，v01＋a1t＝v02＋a2t解得t＝v02－v01a1－a2＝10－24－2s＝4 s.(2)两车速度相等时，甲车的位移：x1＝(2×42＋2×4) m＝40 m乙车的位移：x2＝10×4＋12×2×42 m＝56 m两车间距：Δx＝x2－x1＝16 m. 【答案】(1)4 s(2)16 m。